NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State

NCERT Solutions Class 12 Chemistry Chapter 1 contains the solved questions and answers provided in the textbook. The answers are provided by subject experts and hence the students can refer to these solutions for better preparations. The explanations are provided in an easy language which the students find easy to understand. The diagrammatic representations make the explanations even clearer.

The NCERT Solutions for Class 12 Chemistry Chapter 1 not only helps the students prepare for their board exams, but also prepares them for competitive exams. The solutions strengthen the conceptual knowledge of the students that clarifies even the minute doubts.

Board	CBSE
Textbook	NCERT
Class	Class 12
Subject	Chemistry
Chapter	Chapter 1
Chapter Name	The Solid State
Number of Questions Solved	50
Category	NCERT Solutions

NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State

“The Solid State” is an important chapter in Chemistry from the examination perspective. We are surrounded by different states of matter. Most of the matter around us is in solid state. The NCERT Solutions for Class 12 Chemistry Chapter 1 explain the structure, classification and properties of solids. The explanation of the structure of solids states the correlation between the structure and properties of solids.

NCERT IN-TEXT QUESTIONS

Question 1.
Why are solids rigid?
Answer:
Solids are rigid because the constituent particles are very closely packed. They don’t have any translatory movement
and can only oscillate about their mean positions.

Question 2.
Why do solids have a definite volume?
Answer:
The constituent particles of a solid have fixed positions and are not free to move about, i.e., they possess rigidity. That is why they have definite volume.

Question 3.
Classify the following as amorphous and crystalline solids; polyurethane, naphthalene, benzoic acid, Teflon,
potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper.
Answer:
Amorphous solids: Polyurethane, naphthalene, Teflon, cellophane, polyvinyl chloride, fiberglass. Crystalline solids: Benzoic acid, potassium nitrate, copper.

Question 4.
Why is glass considered a supercooled liquid?
Answer:
Glass is an amorphous solid. Like liquids, it has a tendency to flow, though very slowly. This can be seen from the glass panes of windows or doors of very old buildings which are thicker at the bottom than at the top. Therefore, glass is considered as a supercooled liquid.

Question 5.
The Refractive index of a solid is observed to have the same value along with all the directions. Comment on the nature of the solid. Would it show cleavage property?
Answer:
As the solid has the same refractive index along with all the directions, it is isotropic in nature and is, therefore, an amorphous solid. It is not expected to show a clean cleavage when cut with a special type of knife. It will break into pieces with irregular surfaces.

Question 6.
Classify .the following solids in different categories based on the nature of intermolecular forces operating in them: Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide
Answer:
Potassium sulphate = Ionic Tin=Metallic.
Benzene = Molecular (non-polar)
Urea=Molecular (polar).
Ammonia=Molecular (H-bonded)
Water = Molecular (H-bonded)
Zinc sulphide = Ionic Graphite=Covalent Rubidipm Metallic Argon = Molecular (non-polar)
Silicon Carbide=Covalent

Question 7.
A solid substance ‘A’ is a very hard and electrical insulator both in the solid-state as well as in the molten state. It has also the very high melting point. Is the solid metal like silver or network solid like silicon carbide (SiC)?
Answer:
Since the solid behaves as an insulator even in the molten state, it cannot be metal like silver. Therefore, it is a covalent or network solid like SiC.

Question 8.
Ionic solids conduct electricity in molten state but not in solid state. Explain
Answer:
In a solid-state, the ions cannot move, they are held by strong electrostatic forces of attraction. So, ionic solids do not conduct electricity in the solid state. However, in the molten state, they dissociate to give tree ions and hence conduct electricity.

Question 9.
What types of solids are electrical conductors, malleable and ductile? (C.B.S.E. Outside Delhi 2013)
Answer:
Metallic solids exhibit these characteristics. Their atoms are linked to one another by metallic bonds.

Question 10.
Give the significance of a ‘lattice point’.
Answer:
Each lattice point represents one constituent particle of the solid. This constituent particle may be an atom, a molecule or an ion.

Question 11.
Name the parameters which characterize a unit cell.
Answer:
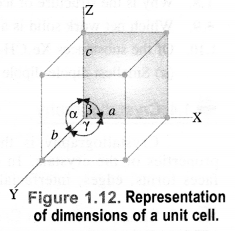
A unit cell is characterized by two types of parameters. These are edges (a, b, c) which may or may not be mutually perpendicular, and angles between the edges (α, β, and γ).
(i) Edges or edge lengths. The edges a, b and c represent the dimensions of the unit cell in space along the three axes. The edges may or may not be mutually perpendicular.
(ii) Angles between the edges. There are three angles between the edges. These are denoted as α (between b and c), β (between a and c), and γ (between a and b). Thus, a unit cell may be characterized by six parameters as shown in Fig. 1.12. The various types of crystal systems differ with respect to edge lengths as well as angles between the edges.

Question 12.
Distinguish between
(i) Hexagonal and monoclinic unit cells
(ii) Face-centred and end-centered unit cells.

Answer:
(i)

Hexagonal unit cell	Monoclinic unit cell
a=b≠c	a≠b≠c
α = β = 90°	α = γ = 90°
γ = 120°	β ≠ 90°

(ii)

Face-centred unit cell	End-centred unit cell
A Face-centred unit cell the constituent particles are present at the corners and one at the centre of each face.	An End-centred unit cell contains particles at the corners and one at the centre of any two opposite faces.
Total no of particles in a face centered unit cell= 4	Total no. of particles in an end centered unit cell = 2

Question 13.
Explain how many portions of an atom located at the
(i) corner and
(ii) body centre of a cubic unit cell is a part of the neighbouring unit cell.
Answer:
(i) An atom located at the corner is shared by eight unit cells. Therefore, its contribution to a particular unit cell is 1/8.
(ii) An atom located at the body of the unit cell is not shared by any unit cell. It belongs to one particular unit cell only.

Question 14.
What is the two-dimensional coordination number of a molecule in a square close-packed layer?
Answer:
In 2D, square close-packed layer, an atom touches 4 nearest neighbouring atoms. Hence, its CN=4

Question 15.
A compound forms a hexagonal close-packed structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?
Answer:
No. of atoms in 0.5 mole of the compound = 0.5 x N₀ = 0.5 x 6.022 x 10²³ = 3.011 x 10²³
No. of octahedral voids = No. of atoms = 3.011 x 10²³
No. of tetrahedral voids = 2 x 3.011 x 10²³ = 6.022 x 10²³
Total no. of voids = (3.011 + 6.022) x 102²³ = 9.033 x 10²³

Question 16.
A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy l/3rd of tetrahedral voids. What is the formula of the compound?
Answer:
Atoms of N from ccp, therefore, if the lattice points are n, then
No.of atoms of N = n
No. of oct voids = n
No. of td voids = 2n= 2 x 1n/3 = 2n/3
∴ Formula of the compound is: M : N
2/3 n : n
2n: 3n
2: 3
i.e., M₂N₃

Question 17.
Which of the following lattices has the highest packing efficiency :
(i) simple cubic
(ii) body-centered cubic and
(iii) hexagonal close-packed lattice?
Answer:
The packing efficiency of the different types of arrangement is :
(i) Simple cubic = 52.4%
(ii) Body-centred cubic = 68%
(iii) Hexagonal close-packed = 74%
his means that hexagonal close-packed arrangement has the maximum packing efficiency (74%).

Question 18.
An element with a molar mass 2.7 x 10^-2 kg  mol^-1 forms a cubic unit cell with an edge length of 405 pm. If its density is 2.7 x 10³ kg m^-3, what is the nature of the cubic unit cell?
Answer:

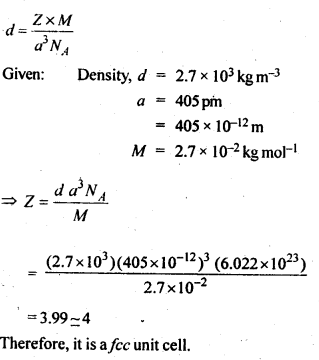
Question 19.
What type of defect can arise when a solid is heated? Which physical property is affected by it and in what
way?
Answer:
When a solid is heated, some atoms or ions may leave the crystal lattice. As a result, vacancies are created and this leads to vacancy defects in the crystalline solid. Since the number of atoms/ions per unit volume decreases, the vacancy defects lead to a decrease in the density.

Question 20.
What type of stoichiometric defect is shown by:
(i) ZnS
(ii) AgBr
Answer:
(i) ZnS shows Frenkel defect
(ii) AgBr shows Frenkel as well as Schottky defect.

Question 21.
Explain how vacancies are introduced in the ionic solid when a cation of higher valence is added as an impurity to it.
Answer:
Let us consider an ionic solid sodium chloride (Na⁺Cl^–) to which a small amount of strontium chloride (SrCl₂) has been added to act as an impurity. Since the crystal as a whole is to remain electrically neutral, two Na+ ions have to leave their sites to create two vacancies. Out of these, one will be occupied by Sr²⁺ ion while the other will be vacant. Thus, vacancies will be created in the ionic solid. When a cation of higher valency is added as an impurity in the ionic solid, some of the sites of the original cations are occupied by the cations of higher valency. Each cation of higher valency replaces two or more original cations and occupies the site of one original cation and the other site(s) remains vacant.

Question 22.
Ionic solids which have anionic vacancies due to metal excess defect, develop colour. Explain with the help of a suitable example.
Answer:
Let us illustrate by sodium chloride (Na⁺Cl^–) crystals. Upon heating in the atmosphere of sodium (Na) vapours, sodium atoms get deposited on the surface of the crystals. The Cl^– ions from the crystal lattice leave their sites and diffuse into the surface. They tend to combine with sodium atoms present in the vapours which in turn get ionised to form Na⁺ ions by releasing electrons. The latter is trapped by the anionic vacancies created by Cl^–ions in order to maintain the crystals electrically neutral. Now, the electrons absorb radiations corresponding to a certain colour from white light and start vibrating. They emit radiations corresponding to yellow colour. That is how the crystals of sodium chloride develop yellow colour. These electrons are called F-centres because these are responsible for colours (In German, F = Farbe meaning colour).

Question 23.
A group 14 element is to be converted into an n-type semiconductor by doping it with a suitable impurity. To which group should the impurity element belong?
Answer:
n-type semiconductors are conducting due to the presence of excess negatively charged electrons. In order to convert group 14 elements (e.g. Si, Ge) into n-type semi-conductors, doping is done with some elements of group 15 (e.g. P, As)

Question 24.
What type of substances would make better permanent magnets; ferromagnetic or ferrimagnetic? Justify your answer. (C.B.S.E. Outside Delhi 2013)
Answer:
Ferromagnetic substances make better permanent magnets than ferrimagnetic substances. The metal ions of a ferromagnetic substance are grouped into small regions known as domains and these are randomly oriented. Under the influence of the applied magnetic field, all domains are oriented in the direction of the magnetic field and as a result, a strong magnetic field is produced. The ferromagnetic substance behaves as a magnet. This characteristic of the domains persists even when the external magnetic field is removed. This imparts permanent magnetic character to these substances. However, this property is lacking in ferrimagnetic substances. Therefore ferromagnetic substances are better magnets.

NCERT EXERCISE

Question 1.
Define the term ‘amorphous’. Give a few examples of amorphous solids.
Answer:
Amorphous solids are those solids in which the constituent particles may have short-range order but do not have a long-range order. They have irregular shapes and are isotropic in nature. They do not undergo a clean cleavage. They do not have sharp melting points or definite heat of fusion. E.g.: Glass, rubber, and plastics.

Question 2.
What makes a glass different from a solid such as quartz? Under what conditions could quartz be converted into glass?
Answer:
Glass is made up of Si04 tetrahedral units. These constituent particles have short-range order only. Quartz is also made up of Si04 tetrahedral units. On heating it softens and melts over a wide range of temperature. It is a crystalline solid having long-range ordered structure. It has a sharp melting point. Quartz can be converted into glass by first melting and then rapidly cooling it.

Question 3.
Classify each of the following solids as ionic, metallic, molecular, network (covalent), or amorphous:
(a) Tetra phosphorus decoxide (P₄O₁₀)
(b) Graphite
(c) Brass
(d) Ammonium phosphate (NH₄)₃PO₄
(e) SiC
(f) Rb
(g)l₂
(h) LiBr
(i) P₄
(j) Si
(k) Plastic.
Answer:
(a) Molecular solid
(b) Covalent (Net-work) solid
(c) Metallic solid
(d) Ionic solid
(e) Covalent solid (Network)
(f) Metallic solid
(g) Molecular solid
(h) lonic solid
(i) Molecular solid
(j) Covalent solid
(k) Amorphous solid.

Question 4.
(a) What is meant by the term coordination number?
(b) What is the coordination number of atoms
(i) in a cubic close-packed structure
(ii) in a body-centered cubic structure?
Answer:
(i) The number of nearest neighbours of a particle in its close packing is called its coordination number.
(ii) (a) 12, (b) 8.

Question 5.
How can you determine the atomic mass of an unknown metal if you know its density and the dimensions of its unit cell? Explain.
Answer:
Let the edge length of a unit cell = a
Density = d
Molar mass = M
The volume of the unit cell = a3
Mass of the unit cell = No. of atoms in unit cell x Mass of each atom = Z × m

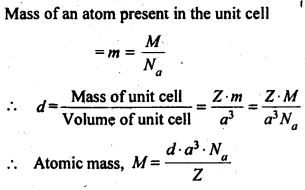
Question 6.
(a) Stability of a crystal is reflected in the magnitude of the melting point. Comment.
(b) Collect the melting point of

• Ice
• ethyl alcohol
• diethyl ether
• methane from a data book. What can you say about intermolecular forces between the molecules?

Answer:
(a) Higher the melting point, greater are tire “forces holding the constituent particles together and hence greater is the stability.

(b) The intermolecular forces in water and ethyl alcohol are mainly hydrogen bonding. The higher melting point of water than alcohol shows that hydrogen bonding in ethyl alcohol molecules is not as strong as in water molecules. Diethyl ether is a polar molecule. The intermolecular forces present in them are the dipole-dipole attraction. Methane is a non-polar molecule. The only forces present in them are the weak Vander Waal’s forces (London / dispersion forces).

Question 7.
How will you distinguish between the following pairs of terms:
(i) Cubic close packing and hexagonal close packing?
(ii) Crystal lattice and unit cell?
(iii) Tetrahedral void and octahedral void?
Answer:
(i) Cubic close packing: When the third layer is placed over the second layer in such a way that the spheres cover the octahedral voids, a layer different from first (A) and second (B) is produced. If we continue packing in this manner, then packing is obtained where the spheres in every fourth layer will vertically aligned. This pattern of packing spheres is called the ABCABC pattern or cubic close packing.

Hexagonal close-packing: When a third layer is placed over the second layer in such a manner that the spheres cover the tetrahedral void, a three-dimensional close packing is obtained where the spheres in every third or alternate layer are vertically aligned. If we continue packing in this manner, then the packing obtained would be called ABAB pattern or hexagonal close packing.

(ii) Crystal lattice: It is a regular arrangement of the constituent particles (i?.e., ions, atoms or molecules) of a crystal in three-dimensional space.
Unit cell: The smallest three-dimensional portion of a complete space lattice which when repeated over and over again in different directions produces the complete crystal lattice is called the unit cell.

(iii) Tetrahedral void: A simple) the triangular void is a crystal is surrounded by four spheres and is called a tetrahedral void.
Octahedral void: A double triangular void is surrounded by six spheres and is called an octahedral void.

Question 8.
How many lattice points are there in one unit cell of each of the following lattices
(a) face-centered-cubic
(b) face centred tetragonal
(c) body-centered cubic?
Answer:
(i) In the face-centered cubic arrangement, a number of lattice points are = 8 (at comers) + 6 (at face centres)
Lattice points per unit cell = 8 × \(\frac { 1 }{ 8 } \) + 6 × \(\frac { 1 }{ 2 } \) = 4.

(ii) In face centred tetragonal, number of lattice points are = 8 (at comers) + 6 (at face centres)
Lattice points per unit cell = 8 × \(\frac { 1 }{ 8 } \) + 6 × \(\frac { 1 }{ 2 } \) = 4

(iii) In body centred cubic arrangement, number of lattice points are = 8 (at comers) + 1 (at body centres)
Lattice points per unit cell = 8 × \(\frac { 1 }{ 8 } \) + 1 = 2

Question 9.
Explain:
(i) The basis of similarities and differences between metallic and ionic crystals.
(ii) Ionic solids are hard and brittle.
Answer:
(i) Basis of similarities. The basis of similarities between the metallic and ionic crystals are the presence of strong electrostatic forces of attraction. These are present among the ions in the ionic crystals and among the kernels and
valence electrons in the metallic crystals. That is why both metals and ionic compounds are good conductors of electricity and have high melting points.
Basis of differences. The basis of differences in the absence of mobility of ions in the ionic crystals while the same is present in the valence electrons and kernels in the case of metallic crystals. As a consequence, the ionic compounds conduct electricity only in the molten state while the metals can do so even in the solid-state.
(ii) The ionic solids are hard and brittle because of strong electrostatic forces of attraction which are present in the oppositely charged ions.
The ionic solids are hard because of the presence of strong inter-ionic forces of attraction in the oppositely charged ions. These ions are arranged in three-dimensional space. The ionic solids are brittle because the ionic bond
is non-directional.

Question 10.
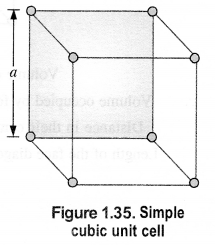
Calculate the efficiency of packing in the case of metal crystal for:
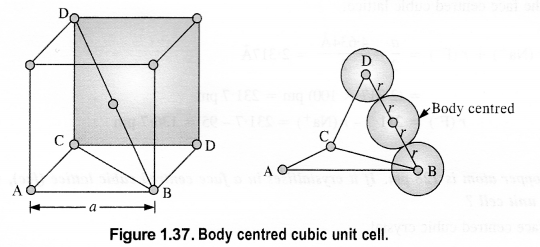
(i) Simple cubic
(ii) Body centered cubic
(iii) Face centered cubic (with the assumption that the atoms are touching each other). (C.B.S.E. Outside Delhi 2011) Answer:
(i) Simple cubic: We know that in a simple cubic unit cell, there is one atom (or one sphere) per unit cell. If r is the radius of the sphere, the volume occupied by one sphere present in the unit cell = 4/3πr³.


(ii) Body-centred cubic: We know that a body-centered cubic unit cell has 2 spheres (atoms) per unit cell. If r is the radius of the sphere Volume of one sphere = 4/3πrsup>3


(iii) Face centred cubic: We know that a face centered cubic unit cell (fcc) contains four spheres (or atoms) per unit cell.

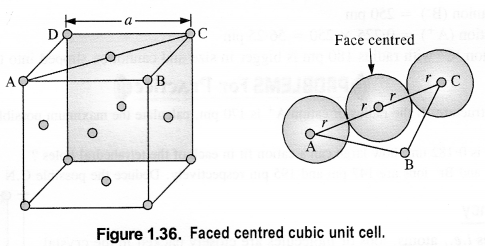
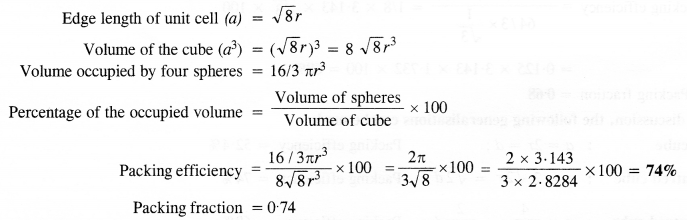
Question 11.
Silver crystallizes in a face centered cubic lattice with all the atoms at the lattice points. The length of the edge of
the unit cell as determined by X-ray diffraction studies is found to be 4.077 x 10^-8 cm. The density of silver is 10.5 g cm^-3. Calculate the atomic mass of silver. (C.B.S.E. Sample Paper 2012)(Uttarakhand Board 2015)
Answer:

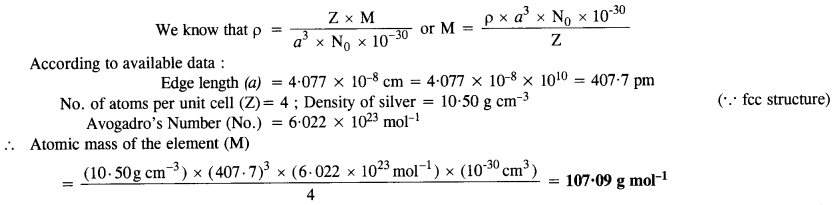
Question 12.
A cubic solid is made up of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body centre. What is the formula of the compound? What are the coordination numbers of P and Q?
Answer:
As atom Q are present at the 8 comers of the cube, therefore, number of atoms of Q in the unit cell = 8 × \(\frac { 1 }{ 8 } \) = 1.
As atoms P are present at the body centre, therefore a number of atoms P in the unit cell = 1.
∴ The formula of the compound = PQ
Co-ordination number of each P and Q = 8.

Question 13.
Niobium crystallizes in a body-centered cubic structure. If the density is 8.55 g cm-1, calculate the atomic radius of niobium given that the atomic mass of niobium is 93 g mol^-1. (C.B.S.E. Delhi 2008)
Answer:
Step I. Calculation of edge length of unit cell.
No. of particles in b.c.c. type unit cell (Z) = 2
Atomic mass of the element (M) = 93 g mol^-1

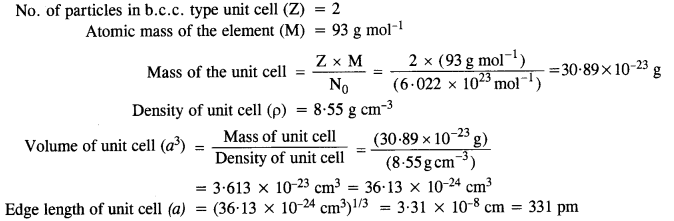
Step II. Calculation of radius of unit cell

Question 14.
If the radius of octahedral void is r and the radius of the atom in close packing is R, derive the relation between r and R. (C.B.S.E. Sample Paper 2017)
Answer:
Let length of each side of the square is a and the radii of the void and the sphere are r and R respectively. Consider the right angled triangle ABC.


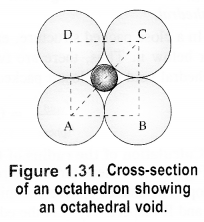
∴ Radius of octahedral void is 0.414R(or 41.4% as compared to that of the sphere).

Question 15.
Copper crystallises into a foc lattice with edge length 3•61 x 10-8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm. (C.B.S.E. Delhi 2009 Comptt.)
Answer:

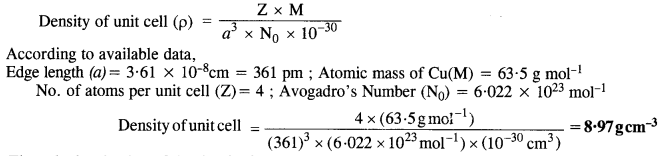
The calculated value of the density is nearly the same as the measured value.

Question 16.
Analysis shows that nickel oxide has formula Nin.os 01.00. What fraction of nickel exists as Ni²⁺ and as Ni³⁺ ions ?
Answer:
The ratio of Ni and O atoms in pure nickel oxide (NiO) = 1:1
Let x be the no. of Ni (II) atoms replaced by Ni (III) atoms in the oxide.
∴ No. of Ni (II) atoms present = (0.98 – x)
Since the oxide is neutral in nature,
Charge on Ni atoms = Charge on oxygen atoms
2(0.98 – x) + 3x = 2
1.96 – 2x + 3x = 2
x = 2 – 1.96 = 0.04

% of Ni (II) atoms in nickel oxide = 100 – 4:01 = 95.99%

Question 17.
What is a semiconductor? Describe the two main types of semiconductors and contrast their conduction mechanism.
Answer:
Those solids which have intermediate conductivities ranging from 10^-6 to 10⁴ ohm^-1 m^-1 are classified as semiconductors. As the temperature rises, there is a rise in conductivity value because electrons from the valence band jump to the conduction band.

(i) n-type semiconductor: When a silicon or germanium crystal is doped with group 15 elements like P or As, the dopant atom forms four covalent bonds like Si or Ge atom but the fifth electron, not used in bonding, becomes delocalized and continues its share towards electrical conduction. Thus silicon or germanium doped with P or As is called an H-type semiconductor, a-indicative of negative since it is the electron that conducts electricity.

(ii) p-type semiconductor: When silicon or germanium is doped with group 13 elements like B or Al, the dopant is present only with three valence electrons. An electron vacancy or a hole is created at the place of the missing fourth electron. Here, this hole moves throughout the crystal-like a positive charge giving rise to electrical conductivity. Thus Si or Ge doped with B or Al is called p-tvpe semiconductor, p stands for the positive hole since it is the positive hole that is responsible for conduction.

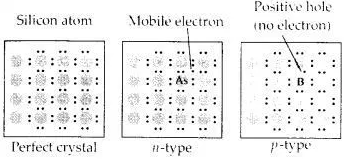
Question 18.
Non-stoichiometric cuprous oxide (Cu₂O) can be prepared in the laboratory. In this oxide, the copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p-type semiconductor?
Answer:
The ratio less than 2: 1 in Cu₂O shows that some cuprous (Cu⁺) ions have been replaced by cupric (Cu²⁺) ions. To maintain electrical neutrality, every two Cu⁺ ions will be replaced by one Cu²⁺ ion thereby creating a hole. As conduction will be due to the presence of this positive hole, hence it is a p-type semiconductor.

Question 19.
Ferric oxide crystallizes in a hexagonal close-packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of ferric oxide.
Answer:
There is one octahedral hole for each atom in the hexagonal close-packed arrangement.
If the number of oxide ions (O^2-) per unit cell is 1, then the number of Fe³⁺ ions = 2/3 x octahedral holes = 2/3 x 1 = 2/3.
Thus, the formula of the compound = Fe^2/3O¹, or Fe²O³.

Question 20.
Classify each of the following as being either a p-type or an n-type semiconductor.
(i) Ge doped with In
(ii) B doped with Si.
Answer:
(i) Ge belongs to group 14 and In belongs to group 13, therefore an electron-deficient hole is created and hence it is an n-type semiconductor.
(ii) B belongs to group 13 and Si belongs to group 14, therefore there will be a free electron and hence it is an n-type semiconductor.

Question 21.
Gold (atomic radius = 0.144 nm) crystallizes in a face-centered unit cell. What is the length of a side of the cell?
Answer:
For fee lattice, edge length,
a = 2 √2 x 0.144 nm = 0.407 nm

Question 22.
In terms of Band Theory, what is the difference
(i) between a conductor and an insulator
(ii) between a conductor and semi-conductor?
Answer:
The variation in the electrical conductivity of the solids can be explained with the help of the band theory.

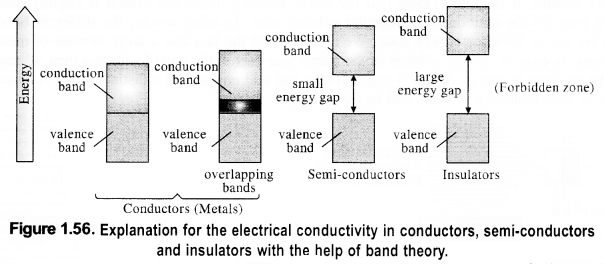
(i) In insulators, the energy gaps are very large and the no electron jump is feasible from the valence band to the conduction band. The energy gaps also called forbidden zones. The insulators, therefore, do not conduct electricity.
(ii) In semi-conductors, there is a small energy gap between the valence band and conduction band. However, some electrons may jump to the conduction band and these semiconductors can exhibit a little electrical conductivity.

Question 23.
Explain the following terms with suitable examples.
(i) Schottky defect,
(ii) Frenkel defect,
(iii) Interstitials,
(iv) F-centres.
Answer:
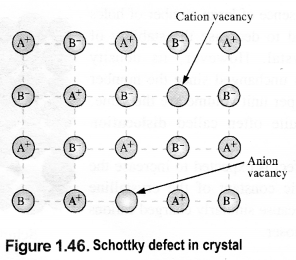
(i) Schottky defect: This rises because certain ions are missing from the crystal lattice and vacancies or holes are created at their respective positions. Since a crystal is electrically neutral, the number of such missing cations (A⁺) and anions (B^–) must be the same. e.g., KCl, NaCl, KBr, etc.

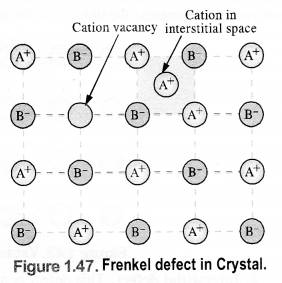
(ii) Frenkel defect: It results when certain ions leave their normal sites and occupy positions elsewhere in the crystal lattice. Holes are created at their respective positions. Since cations are smaller in size as compared to anions normally these are involved in Frenkel defect. e.g., AgBr, ZnS, etc.

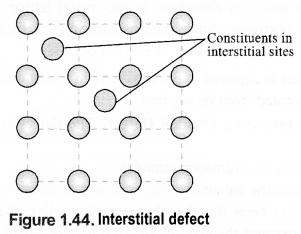
(iii) Interstitials: This defect is noticed when constituent particles (atoms or molecules) occupy the interstitial sites in the crystal lattice. As a result, the number of particles per unit volume increases and so the density of the solid.

(iv) F-centres: These are the anionic sites occupied by unpaired electrons. F-centres impart colour to crystals. The colour results by the excitation of electrons when they absorb energy from the visible light falling on the crystal.

Question 24.
Aluminium crystallises in a cubic close-packed structure. Its metallic radius is 125 pm.
(a) What is the length of the side of the unit cell?
(b) How many unit cells are there in 1.00 cm? of aluminum? (C.B.S.E. Outside Delhi 2013)
Answer:
Step I. Calculation of length of side of the unit cell
For f.c.c. unit cell, a = \(2\sqrt { 2 } r\) = \(2\sqrt { 2 } \) (125pm) = 2 x 1.4142 x (125 pm) = 354 pm.
Step II. Calculation of no. of unit cells in 1:00 cm³ of aluminium.
Volume of one unit cell = (354 pm)3 = (354 x 10^-10 cm)³ = 44174155 x 10^-30 cc.

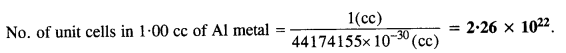
Question 25.
If NaCl is doped with 10^-3 mol % of SrCl₂, what is the concentration of cation vacancies?
Answer:

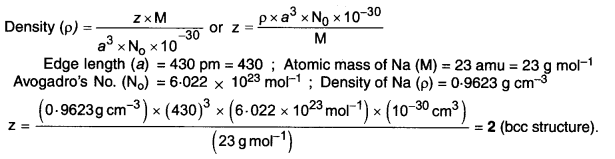
Question 26.
Explain the following with suitable examples.
(a) Ferromagnetism
(b) Piezoelectric effect
(c) Paramagnetism
(d) Ferrimagnetism
(e) Antifluoride structure
(f) 12 – 16 and 13 – 15 compounds.
Answer:
(a) Ferromagnetism: A few solids like iron. cobalt, nickel, gadolinium and CeO₂ are attracted very strongly by magnetic fields. These are known as ferromagnetic solids. Apart from that, they can be even permanently magnetised or become permanent magnet. e.g., Fe, Ni, Co and CrO₂

(b) Piezoelectric effect: A dielectric crystal which has a resultant dipole moment can produce electricity or show the electrical property when external pressure is applied. Such a crystal is known as piezoelectric crystal and this property is called piezoelectricity or pressure electricity. e.g., PbZrO₂, Nh₄H₂PO₄ etc.

(c) Paramagnetism: These are the solids attracted by a magnet. Actually, the atoms of the elements present have certain unpaired electrons. Their spins or magnetic moments may lead to magnetic characters. Many transition metals such as Co, Ni, Fe, Cu, etc. and their ions are paramagnetic. e.g., O₂, Cu²⁺, Fe³⁺, etc

(d) Ferrimagnetism: They have certain resultant magnetic moment or magnetic character which is of permanent nature. However, ferrimanetic solids are less magnetic than ferromagnetic solids. For example, magnetic oxide of iron (Fe₃O₄) and ferrites with general formula MFe₂O₄. e.g., Fe₃O₄

(e) Antifluoride structure: In this structure, the positions of the cations and anions as compared to fluorite structure get reversed i.e. the smaller cations occupy the position of fluoride ions while the anions with bigger size occupy the positions of calcium ions. e.g., Li₂O, K₂O, Rb₂O and Rb₂S.

(f) 12 – 16 and 13 – 15 compounds: A large variety of solid-state materials have been prepared by the combination of elements belonging to groups 13 and 15 or group 12 and 16. A few examples of compounds 13-15 combinations are InSb, Alp and GaAs. Similarly, compounds resulting from 12 – 16 combinations are AdS, CdSe, HgTe.

We hope the NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State help you. If you have any query regarding NCERT Solutions for Class 12 Chemistry Chapter 1 The Solid State, drop a comment below and we will get back to you at the earliest.