Inverse Trigonometric Functions Class 12 Important Extra Questions Maths Chapter 2

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 2 Inverse Trigonometric Functions. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 2 Important Extra Questions Inverse Trigonometric Functions

Inverse Trigonometric Functions Important Extra Questions Very Short Answer Type

Question 1.
Find the principal value of sin^-1 ( \(\frac { 1 }{ 2 }\) )
Solution:
\(\sin ^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{6} \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
Hence, the principal value of sin^-1 ( \(\frac { 1 }{ 2 }\) ) is \(\frac{\pi}{6}\)

Question 2.
What is the principal value of:
cos^-1 (cos \(\frac{2 \pi}{3}\) + sin^-1 (sin \(\frac{2 \pi}{3}\) ) ?
Solution:

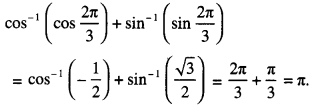
Question 3.
Find the principal value of:
tan^-1 (√3)- sec^-1 (-2). (A.I.C.B.S.E. 2012)
Solution:

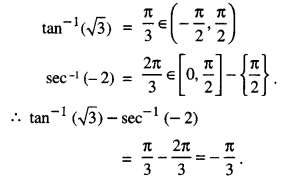
Question 4.
Evaluate : tan ^-1 ( 2 cos (2 sin^-1 ( \(\frac{1}{2}\) )))
Solution:

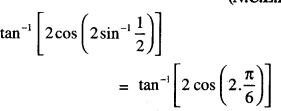
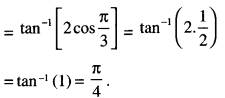
Question 5.
Find the value of tan^-1(√3) – cot^-1(-√3). (C.B.S.E. 2018)
Solution:
tan^-1(√3) – cot^-1(—√3)
\(=\frac{\pi}{3}-\left(\pi-\frac{\pi}{6}\right)=-\frac{\pi}{2}\)

Question 6.
If sin^-1 ( \(\frac { 1 }{ 3 }\) ) + cos^-1 x = \(\frac{\pi}{2}\), then find x.(C.B.S.E. 2010C)
Solution:
sin^-1 ( \(\frac { 1 }{ 3 }\) ) + cos^-1 x = \(\frac{\pi}{2}\)
⇒ x = 1/3
[sin^-1 x + cos^-1 x = \(\frac{\pi}{2}\)

Question 7.
If sec^-1 (2) + cosec^-1 (y) = \(\frac{\pi}{2}\) , then find y.
Solution:
sec^-1 (2) + cosec^-1 (y) = \(\frac{\pi}{2}\)
⇒ y = 2 [∵ sec^-1 x + cosec^-1 x= \(\frac{\pi}{2}\) ]

Question 8.
Write the value of sin [ \(\frac{\pi}{3}\) – sin ^-1 ( \(\frac { -1 }{ 2 }\) ) ]
Solution:
sin [ \(\frac{\pi}{3}\) – sin^-1 ( \(\frac { -1 }{ 2 }\) ) ]
= sin [ \(\frac{\pi}{3}\) + sin^-1 ( \(\frac { 1 }{ 2 }\) ) ]
[∵ sin^-1 (-x) = -sin^-1x]
= sin ( \(\frac{\pi}{3}+\frac{\pi}{6}\) ) = sin \(\frac{\pi}{2}\) = 1

Question 9.
Prove the following:

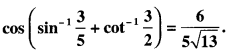
Solution:

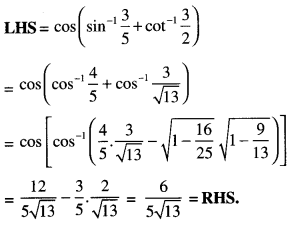
Question 10.
If tan^-1 x + tan^-1y = \(\frac{\pi}{4}\) , xy < 1, then write the value of the x + y + xy (A.I.C.B.S.E. 2014)
Solution:
We have tan^-1 x + tan^-1y = \(\frac{\pi}{4}\)

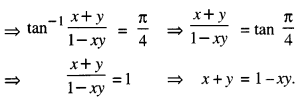
Hence x + y + xy = 1.

Question 11.
Prove that: 3 sin^-1 x = sin^-1(3x – 4x²);
x ∈ [\(\frac { -1 }{ 2 }\) , \(\frac { 1 }{ 2 }\)] (C.B.S.E 2018)
Solution:
To prove: 3 sin^-1 x = sin^-1(3x – 4x²)
Put sin^-1 x = θ
so that x = sin θ.
RHS = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3θ) = 3θ = 3 sin^-1x = LHS.

Inverse Trigonometric Functions Important Extra Questions Short Answer Type

Question 1.
Express sin^-1 ( \(\frac{\sin x+\cos x}{\sqrt{2}}\) )
Where \(-\frac{\pi}{4}\) < x < \(\frac{\pi}{4}\), in the simples form.
Solution:

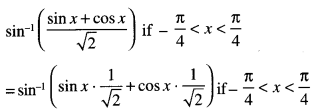
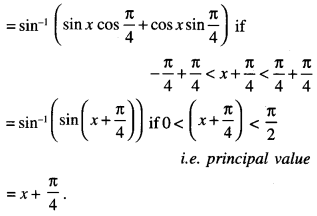
Question 2.
Prove that :
\(\cos ^{-1} \frac{12}{13}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{56}{65}\)   (A.I.C.B.S.E. 2019; C.B.S.E. 2010)
Solution:

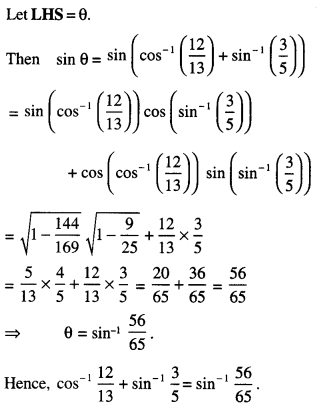
Question 3.
Prove that :
sin ^-1 \(\frac{8}{17}\) + cos ^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{36}{77}\) (A.I.C.B.S.E. 2019)
Solution:
L.H.S = sin^-1 \(\frac{8}{17}\) + cos^-1 \(\frac{4}{5}\)
= tan^-1 \(\frac{8}{15}\) + tan^-1\(\frac{3}{4}\)

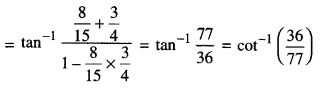
= R.H.S

Question 4.
Solve the following equation:
\(\tan ^{-1}\left(\frac{x+1}{x-1}\right)+\tan ^{-1}\left(\frac{x-1}{x}\right)=\tan ^{-1}(-7)\) (A.I.C.B.S.E. 2019; C)
Solution:

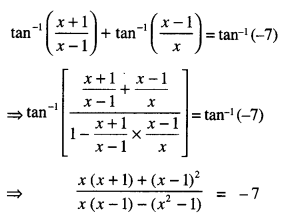
⇒ 2x² – 8x + 8 = 0
⇒ x² – 4x + 4 = 0
⇒ (x – 2)² = 0.
Hence, x = 2.

Question 5.
Solve the following equation:
2 tan^-1(sin x) = tan^-1 (2 sec x), x ≠ \(\frac{\pi}{2}\)   (C.B.S.E. (F) 2012)
Solution:
2 tan^-1(sinx) = tan^-1 (2 secx)

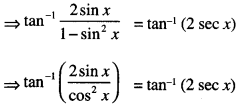
⇒ tan ^-1 (2sec x tan x) = tan^-1 (2sec x)
⇒ 2 sec x tan x = 2 sec x
tan x = 1 [∵ sec x ≠ 0 ]
Hence, x= \(\frac{\pi}{2}\)

Question 6.
Solve the following equation
cos (tan^-1 x) = sin ( cot ^-1\(\frac { 3 }{ 4 }\) )
(A.I.C.B.S.E. 2013)
Solution:
We have:
cos (tan^-1 x) = sin ( cot ^-1\(\frac { 3 }{ 4 }\) )
cos (tan^-1 x) = sin ( sin ^-1\(\frac { 4 }{ 5 }\) )
cos (tan^-1 x) = \(\frac { 4 }{ 5 }\)
tan^-1 x = cos^-1\(\frac { 4 }{ 5 }\)
⇒ tan^-1 x = tan ^-1\(\frac { 3 }{ 4 }\)
Hence x = \(\frac { 3 }{ 4 }\)

Question 7.
Prove that
3cos^-1 x = cos^-1 (4x³ – 3x), x ∈ [ \(\frac { 1 }{ 2 }\) , 1 ]
Solution:
Put x = cos θ in RHS
As 1/2 ≤ x ≤ 1
RHS = cos^-1 (4cos³ θ – 3cos θ),
= cos^-1 (cos 3θ) = 3θ = 3cos^-1 x = L.H.S

Inverse Trigonometric Functions Important Extra Questions Long Answer Type 1

Question 1.
prove that \(\frac { 1 }{ 2 }\) ≤ x ≤ 1, then
\(\cos ^{-1} x+\cos ^{-1}\left[\frac{x}{2}+\frac{\sqrt{3}-3 x^{2}}{2}\right]=\frac{\pi}{3}\) (CBSE. Sample paper 2017 – 18)
Solution:

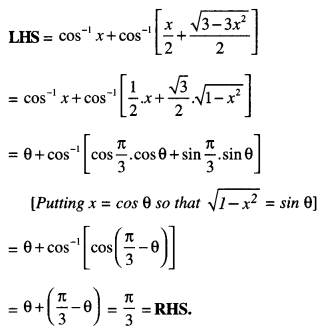
Question 2.
Find the value of :
\(\tan ^{-1}\left(\frac{x}{y}\right)-\tan ^{-1}\left(\frac{x-y}{x+y}\right)\)
Solution:

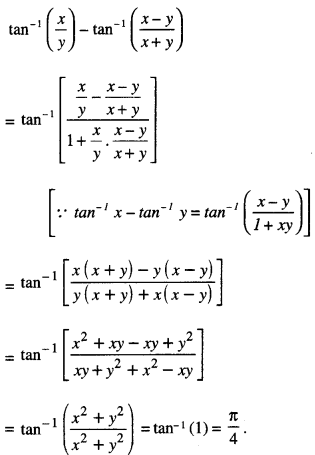
Question 3.
Prove that :
tan ^-1( \(\frac{1}{2}\) ) + tan ^-1 ( \(\frac{1}{5}\) ) + tan ^-1( \(\frac{1}{8}\) ) = \(\frac{\pi}{4}\) (C.B.S.E. 2013: A.I.C.B.S.E. 2011)
Solution:

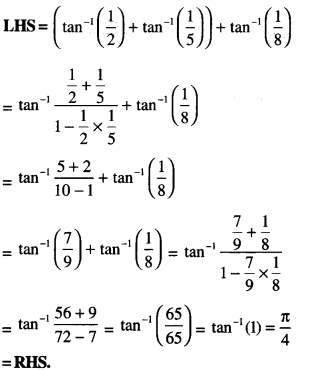
Question 4.

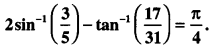
Solution:

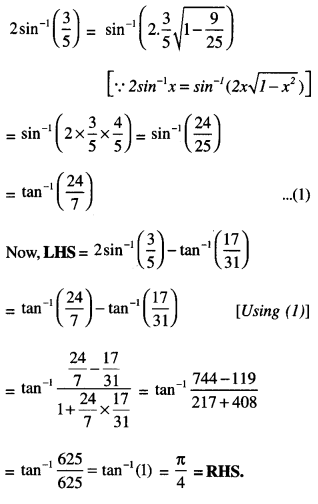
Question 5.

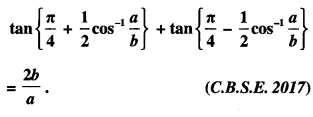
Solution:
Put cos ^-1 (a/b) = θ so that cos θ = a/b.

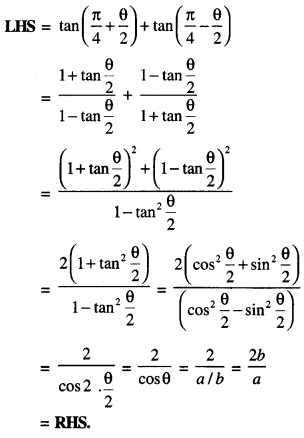
Question 6.

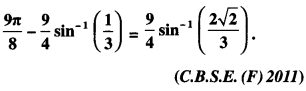
Solution:

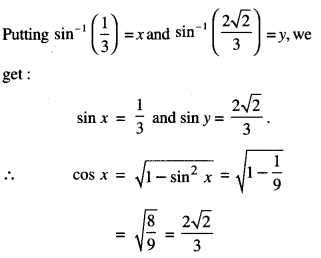
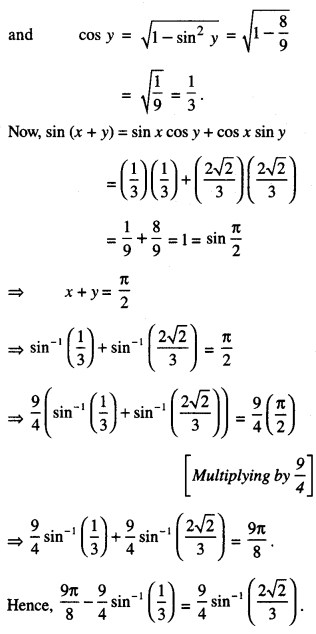
Question 7.

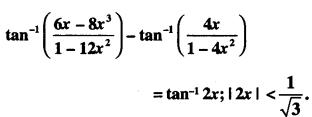
( A.I.C.B.S.E. 2016)
Solution:

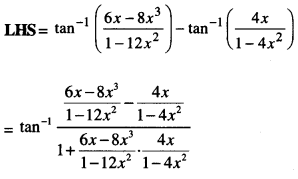
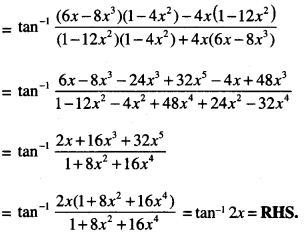
Question 8.
\(\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\) (C.B.S.E. 2016)
Solution:

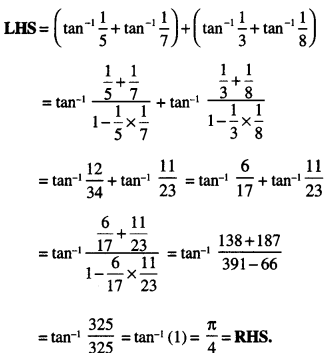
Question 9.
Solve for x : 2 tan^-1 (cos x ) = tan^-1(2 cosec x). (C.B.S.E. 2016)
Solution:
2 tan^-1 (cos x ) = tan^-1 (cos x) + tan^-1 (cos x)


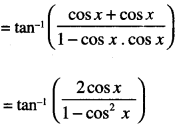
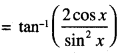
= tan^-1 (2cot x cosec x) …(1)
Now 2 tan^-1(cos x) = tan^-1(2 cosec x)
⇒ tan^-1(2 cot x cosec x) = tan^-1 (2cosec x)
[Using (1)]
⇒ 2 cot x cosec x = 2 cosec x
⇒ cotx cosecx = cosec x
⇒  sin x = tan x sin x
⇒either sin x = 0 or tan x = 1.
Hence, x = nπ ∀ n ∈ Z or x
= πm + \(\frac{\pi}{4}\) ∀ m ∈ Z

Question 10.
If tan^-1 \(\left(\frac{x-2}{x-4}\right)\) + tan^-1 \(\left(\frac{x+2}{x+4}\right)\) = \(\frac{\pi}{4}\) find the value of ‘x’   (A.I.C.B.S.E. 2014)
Solution:
We have

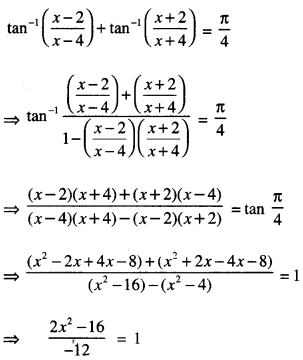
⇒ 2x² – 16 = -12
⇒ 2x² = 16 – 12
⇒ 2x² = 4
⇒ x² = 2
Hence x = ±√2

Question 11.
If tan^-1 \(\left(\frac{x-3}{x-4}\right)\) + tan^-1 \(\left(\frac{x+3}{x+4}\right)\) = \(\frac{\pi}{4}\) find the value of ‘x’ (A.I.C.B.S.E. 2017)
Solution:

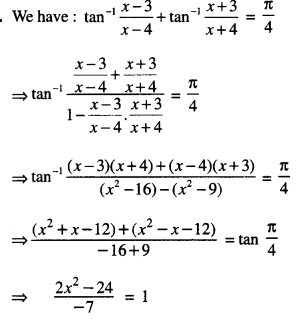
⇒ 2x² – 24 = -7
⇒ 2x² = 17
⇒ 2x² = 4
⇒ x² = 17/2
Hence x = \(\pm \sqrt{\frac{17}{2}}\)

Question 12.
Prove that : \(\tan ^{-1} \sqrt{x}=\frac{1}{2} \cos ^{-1}\left(\frac{1-x}{1+x}\right)\)
x∈ [0,1] (C.B.S.E. 2019C)
Solution:
Let tan ^-1 √x = θ
So that √x = tan θ i.e. x = tan²θ

Question 13.
Solve for x : tan ^-1 (2x) + tan ^-1 (3x) = \(\frac{\pi}{4}\) (C.B.S.E. 2019)
Solution:
The given equation is
tan ^-1 (2x) + tan ^-1 (3x) = \(\frac{\pi}{4}\) …. (1)

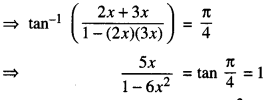
⇒ 5x = 1 – 6x²
⇒ 6x² + 5x – 1 = 0
⇒ x = -1 or x = \(\frac{1}{6}\)
Hence, x = \(\frac{1}{6}\)
[∵ x = -1 does not satisfy (1)]

Question 14.
Solve : tan^-1 4x + tan^-1 6x = \(\frac{\pi}{4}\) (C.B.S.E. 2019)
Solution:
We have tan^-1 4x + tan^-1 6x = \(\frac{\pi}{4}\)

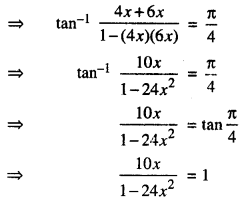
⇒ 10x = 1 – 24x²
⇒ 24x² + 10x – 1 = 0
⇒ 24x²+ 12x – 2x – 1 = 0
⇒ 12x(2x + 1) – 1 (2x + 1) = 0
⇒ (2x+1)(12x – 1) = 0
⇒ 2x + 1 = 0 or 12x – 1 = 0
x = \(-\frac{1}{2}\) or x = \(\frac{1}{2}\).
Hence, x = \(-\frac{1}{2}\) or \(\frac{1}{12}\)
As x = \(-\frac{1}{2}\) does not satisfy the given equation.
Hence x = \(-\frac{1}{12}\)

Question 15.
If (tan^-1 x )² + (cot^-1 x )² = \(\frac{5 \pi^{2}}{8}\) , then find ‘x’ (C.B.S.E. 2015)
Solution:
We have
(tan^-1 x )² + (cot^-1 x )² = \(\frac{5 \pi^{2}}{8}\)
Put tan^-1 x = t so that cot^-1x = \(\frac{\pi}{2}\) – t
∴ (1) become : t² + (\(\frac{\pi}{2}\) – t)² = \(\frac{5 \pi^{2}}{8}\)

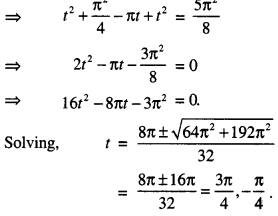
When tan^-1x = \(\frac{3 \pi}{4}\)
then x = tan \(\frac{3 \pi}{4}\) = -1.
When tan^-1 x = \(-\frac{\pi}{4}\),
then x = tan(\(-\frac{\pi}{4}\)) = -1.
Hence, x = -1.

Question 16.
Write : tan ^-1\(\frac{1}{\sqrt{x^{2}-1}}\) , |x| > 1 in the simplest form.
Solution:
Put x = sec θ

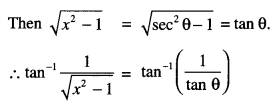
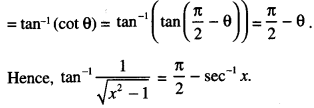
Question 17.
Prove that

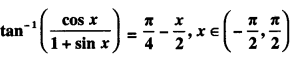
(C.B.S.E. 2012)
Solution:

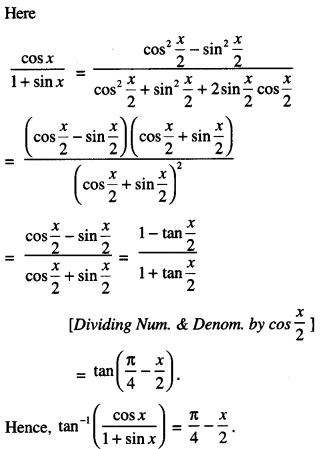
Question 18.
Prove that :
tan^-1x + tan^-1 \(\frac{2 x}{1-x^{2}}\) = tan ^-1\(\frac{3 x-x^{3}}{1-3 x^{2}}\) (N.C.E.R.T
Solution:
Put x = tan θ so that θ = tan ^-1 x

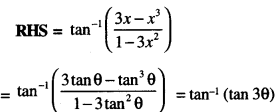
= 3θ = 3 tan^-1x = tan^-1x + 2tan^-1x
= tan^-1x + tan^-1\(\frac{2 x}{1-x^{2}}\)
= L.H.S.

Question 19.
Simplify : tan^-1 [ \(\left[\frac{a \cos x-b \sin x}{b \cos x+a \sin x}\right]\)]
If \(\frac{a}{b}\) tan x > -1    (N.C.E.R.T)
Solution:

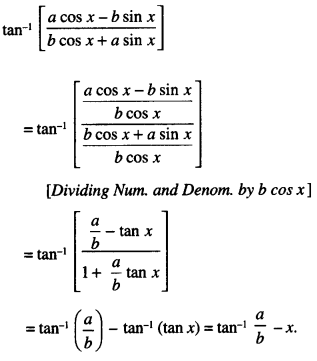
Question 20.
Prove that tan ^-1 [ \(\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}\) ]
= \(\frac{\pi}{4}+\frac{1}{2}\) cos^-1 x ; \(-\frac{1}{\sqrt{2}}\) ≤ x ≤ 1. (C.B.S.E. 2019C)
Solution:

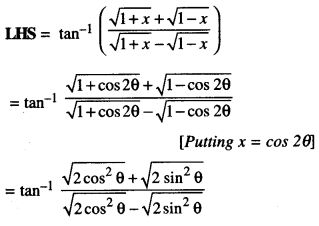
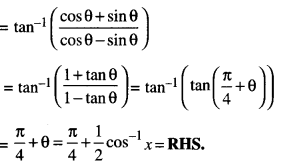
Question 21.
Show that

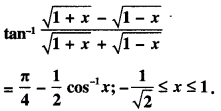
(N.C.E.R.T.A.I. CBSE 2014)
Solution:

Question 22.
cos[tan^-1{sin (cot^-1x)}] = \(\sqrt{\frac{1+x^{2}}{2+x^{2}}}\)
(A.I. C.B.S.E. 2010)
Solution:
Put cot^-1 = θ so that x = cot θ
∴ sin θ = \(\frac{1}{\sqrt{1+x^{2}}}\)

Question 23.
Find the value of sin (2 tan^-1 1/4) + cos (tan^-1 2√2)   (C.B.S.E. Sample Paper 2018 – 2019)
Solution:
Put tan^-1 1/4 = θ so that θ = 1/4
Now, sin 2θ = \(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\)

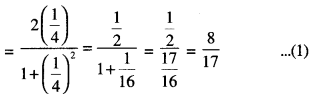
To evaluate cos(tan^-1 2√2) :
Put tan^-12√2 = Φ
So that tan Φ = 2√2
cos Φ = 1/3
Hence, sin (2tan^-1(1/4)) + cos (tan^-12√2)
= sin 2θ + cos Φ = \(\frac{8}{17}+\frac{1}{3}=\frac{41}{51}\)
[Using (1) and (2)]

Question 24.
Solve for x:
tan^-1(x – 1) + tan^-1x + tan^-1(x + 1) = tan^-1(3x).    (A.I.C.B.S.E. 2016)
The given equation is:
tan^-1(x —1) + tan^-1(x) + tan^-1(x + 1) = tan^-13x
tan^-1(x— 1)+tan^-1(x+ 1) = tan^-13x – tan^-1


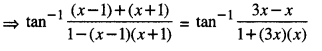
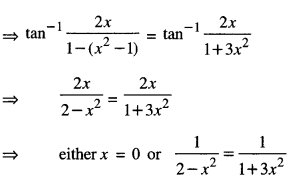
⇒ 1 + 3x² = 2 – x²
⇒ 4x² = 1
⇒ x² = 1/4
⇒ x = \(\pm \frac{1}{2}\)
Hence, x = 0, \(\pm \frac{1}{2}\)