Category: CBSE Class 12

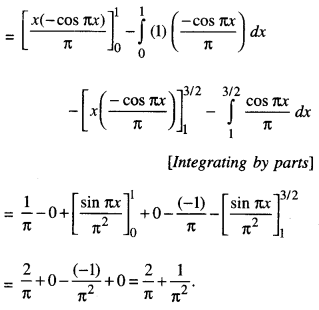
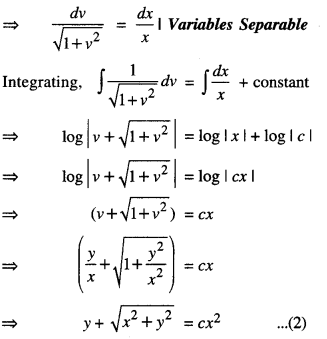
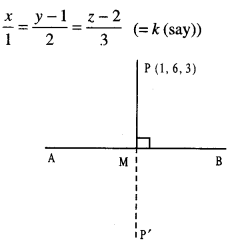
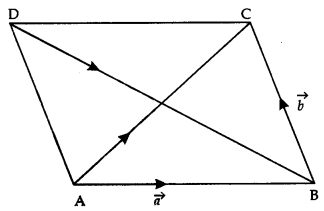
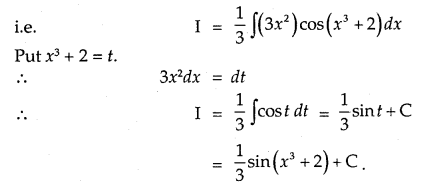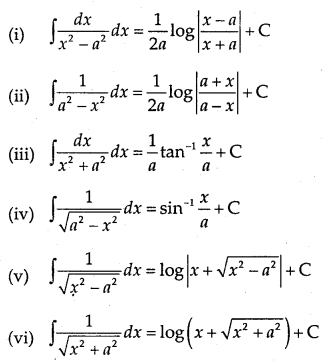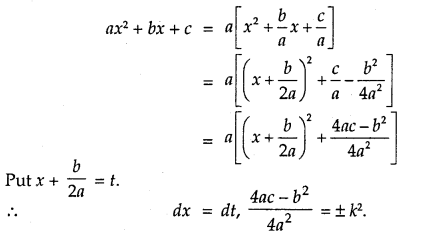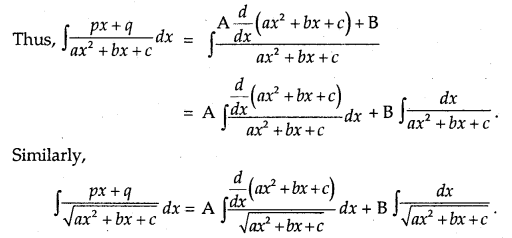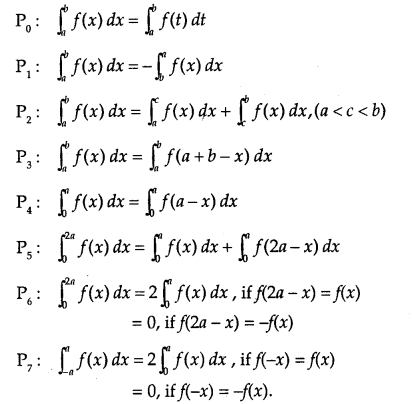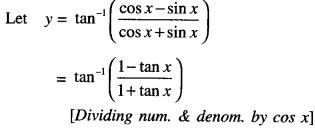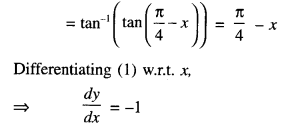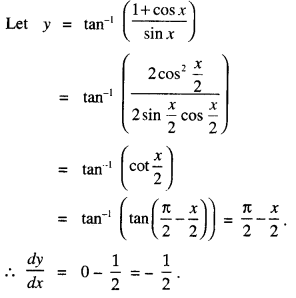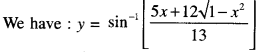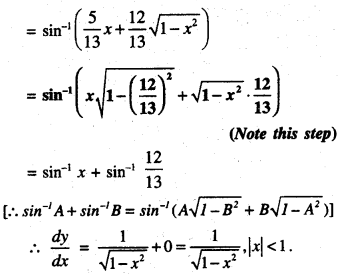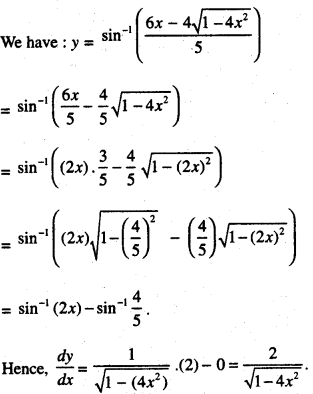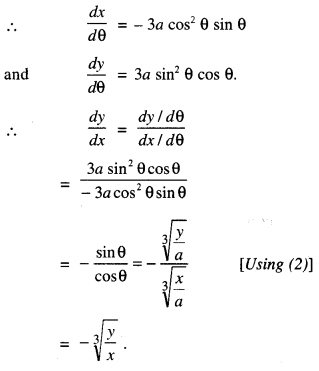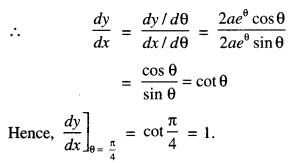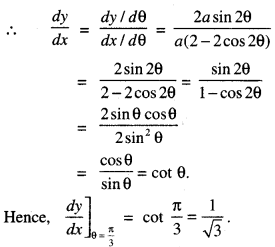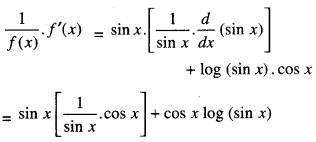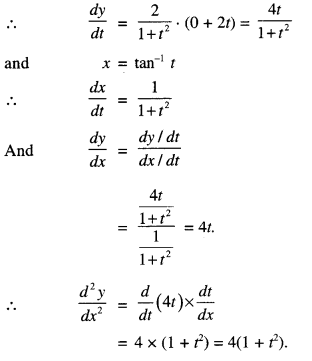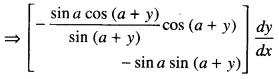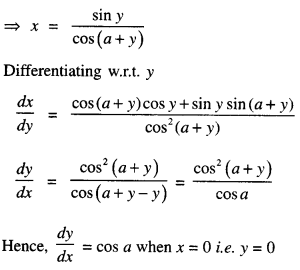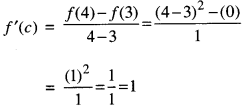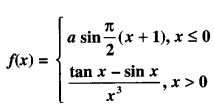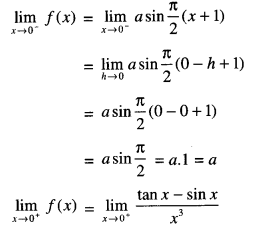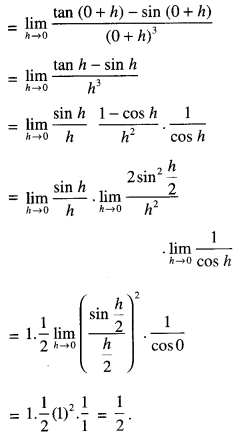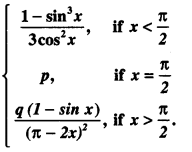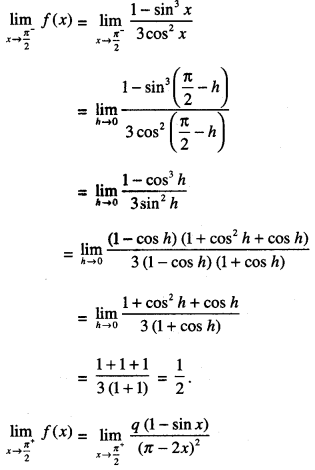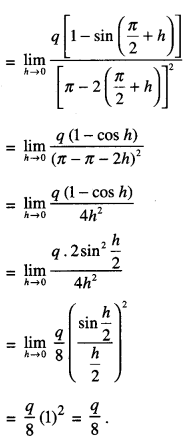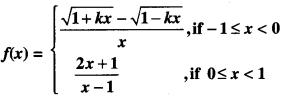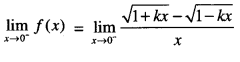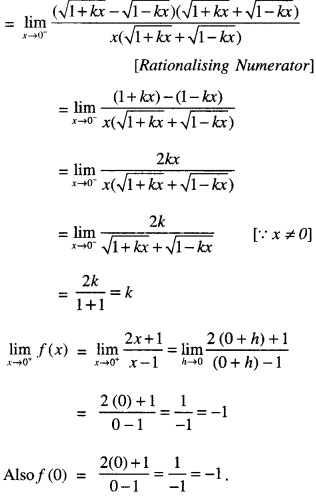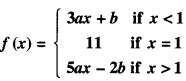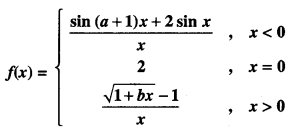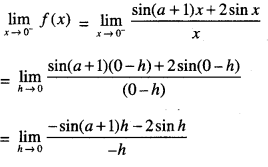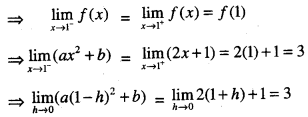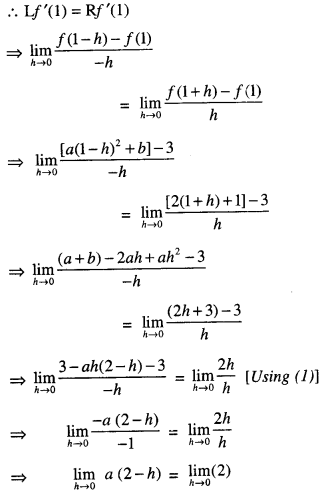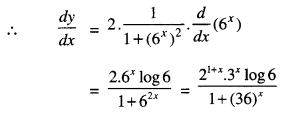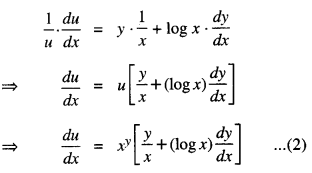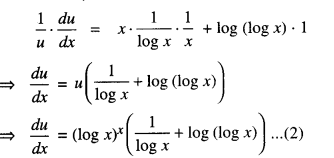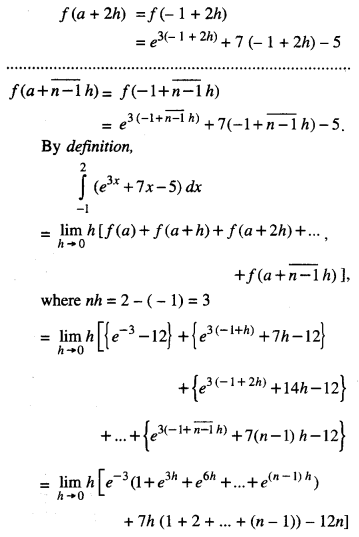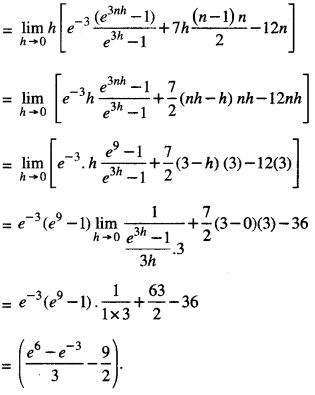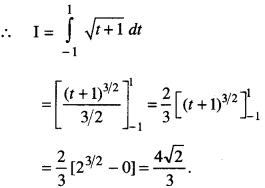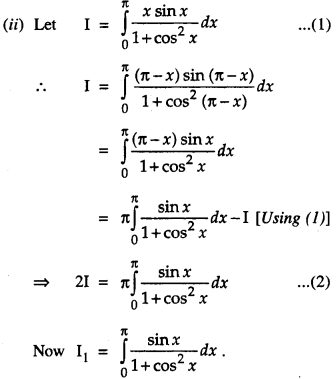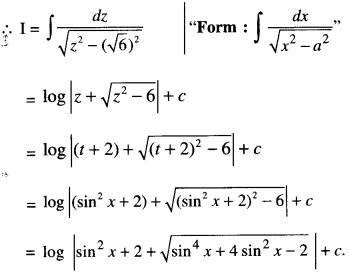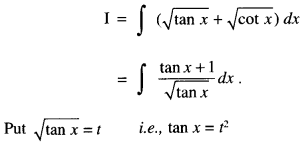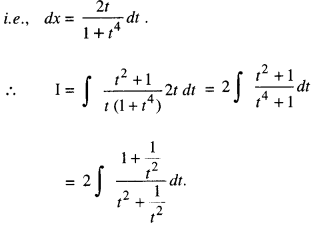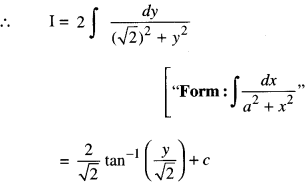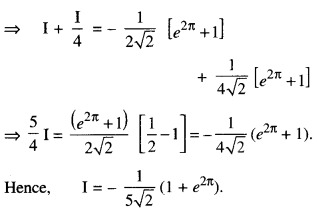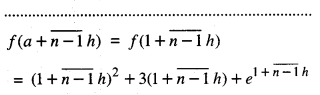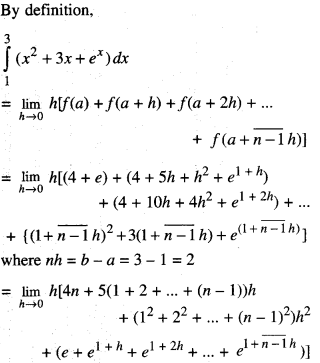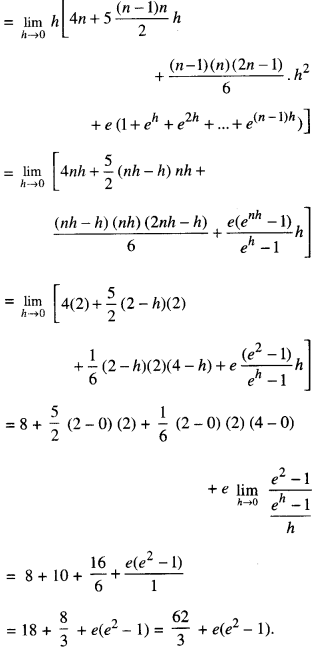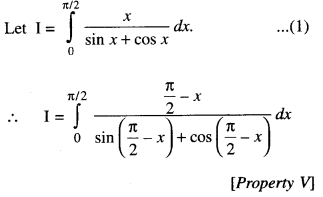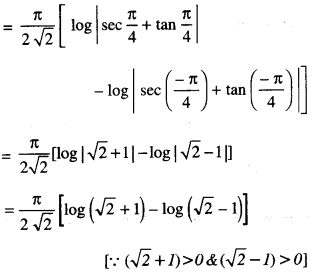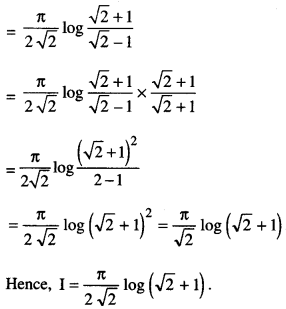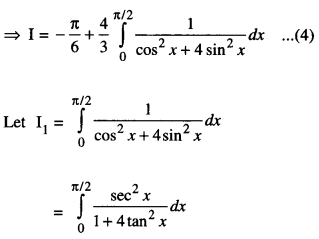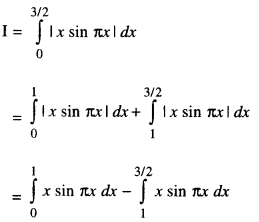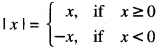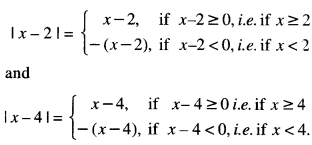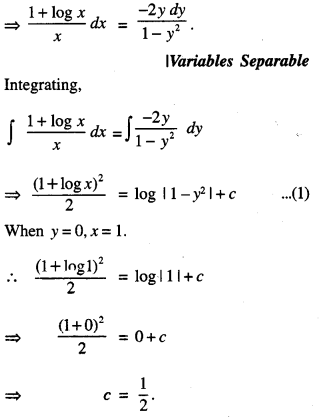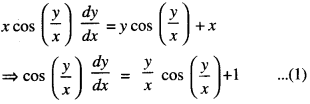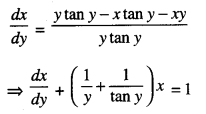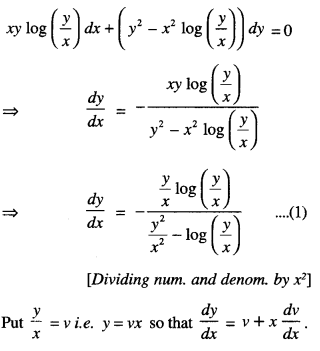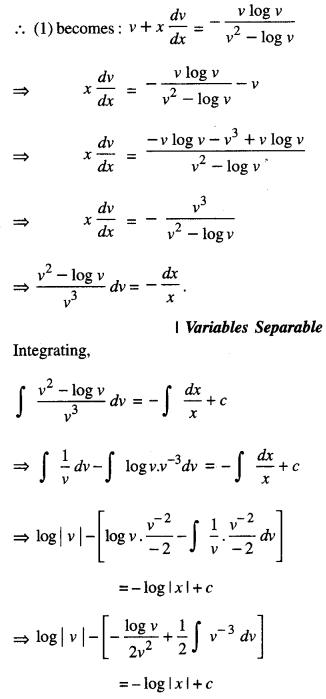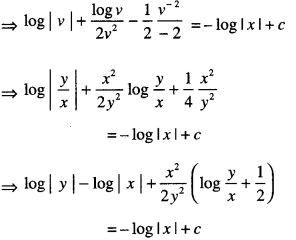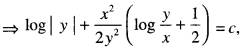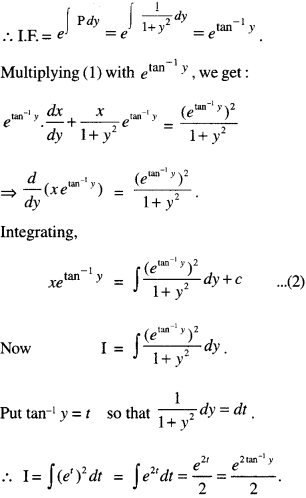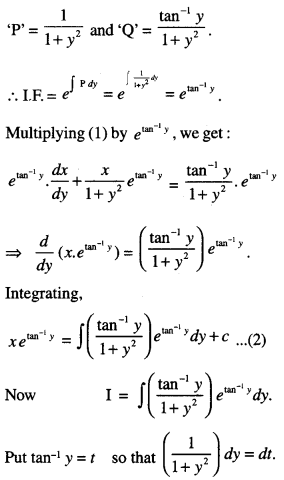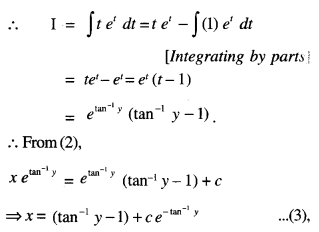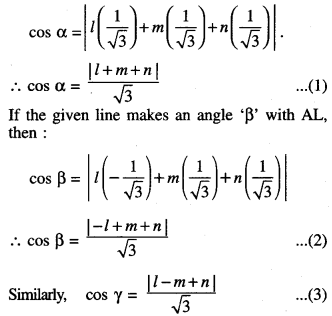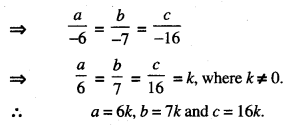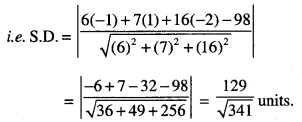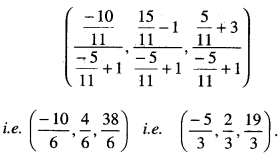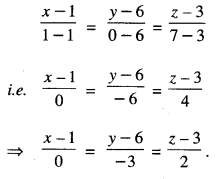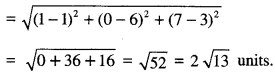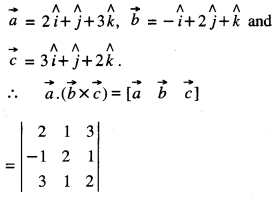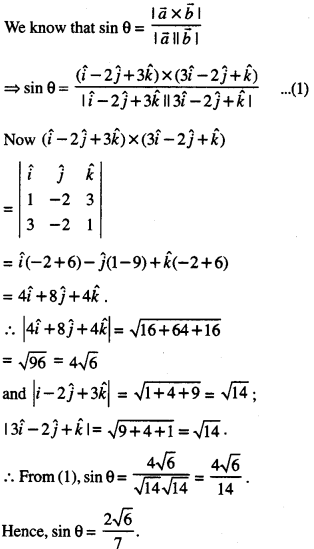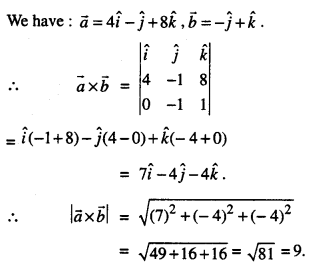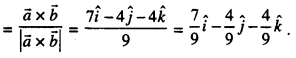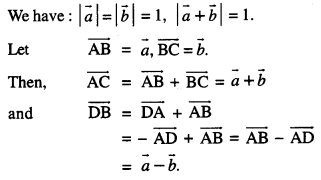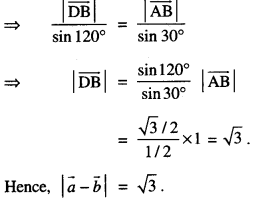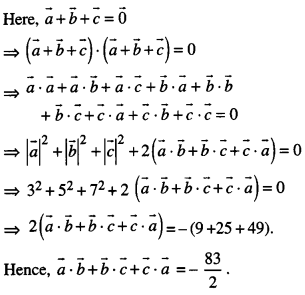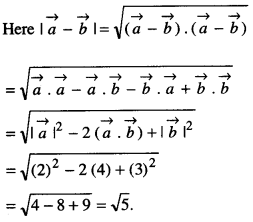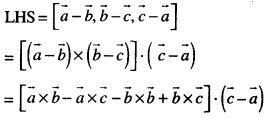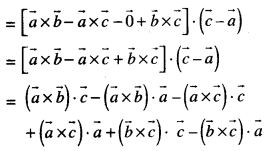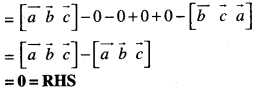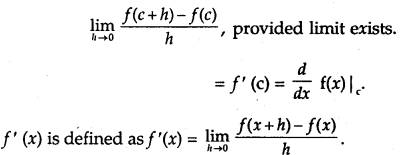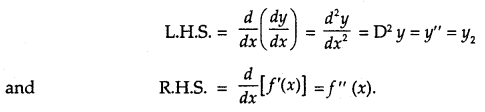By going through these CBSE Class 12 Maths Notes Chapter 6 Application of Derivatives, students can recall all the concepts quickly.

Application of Derivatives Notes Class 12 Maths Chapter 6

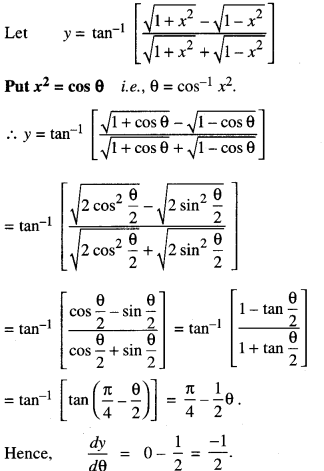
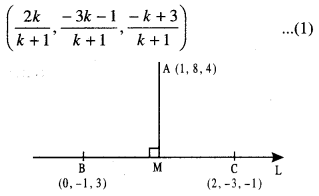
Rate of change of Quantities: Let y =f(x) be a function. If the change in one quantity y varies with another quantity x, then \(\frac{d y}{d x}\) = f ‘ (x) denotes the rate of change of y with respect to x. At x = x₀\(\left.\frac{d y}{d x}\right]_{x=x_{0}}\), or f'(x) represents the rate of change of y w.r.t. x at x = x₀.

Let I will be the open interval contained in the domain of real-valued function f.

Increasing Function: f is said to be increasing function on I, if x₁ < x₂ on I, then f(x₁) ≤ f(x₂) for all x₁, x₂ ∈ I.

Strictly Increasing Function: f is said to be strictly increasing on I if x₁ < x₂ in I ⇒ f(x1) < f(x₂) for all x₁, x₂ ∈ I.

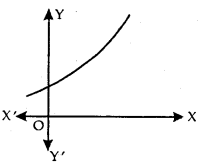
Decreasing Function: f is said to be decreasing function on I, if x₁ < x₂ in I, then f(x₁) ≥ f(x₂) for all x₁, x₂ ∈ I.

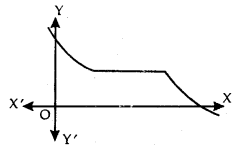
Strictly Decreasing Function: f is said to be strictly decreasing function on I, if x₁ < x₂ in I ⇒ f(x₁) > f(x₂) for all x₁, x₂ ∈ I.

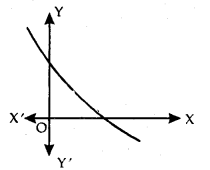
Increasing and Decreasing Functions at x₀:
Let x₀ be a point in the domain of definition of a real valued function f and there exists an open interval I = (x₀ – h, x₀ + h) containing x0 such that

1. f is increasing at x₀, if x₁ < x₂ in I ⇒ f(x₁) ≤ f(x₂).
2. f is strictly increasing at x₀, if x₁ < x₂ in I ⇒ f(x₁) < f(x₂).
3. f is decreasing at x₀, if x₁ < x₂ in I ⇒ f(x₁) ≥ f(x₂).
4. f is strictly decreasing at x₀, if x₁ < x₂ ⇒ f(x₁) >f(x₂).

Test: Increasing/decreasing/constant Functions:
Let f be continuous on [a, b] and differentiable in an open interval (a, b), then

1. f is increasing on [a, b], if f ‘(x) > 0 for each x ∈ (a, b).
2. f is decreasing on [a, b], if f ‘(x) < 0 for each x ∈ (a, b).
3. f is constant on [a, b], if f ‘(x) = 0 for each x ∈ (a, b).

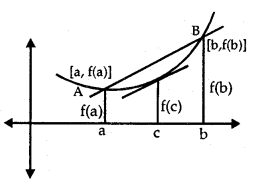
→ Tangent to a curve: Let y = f(x) be the equation of a curve. The equation of the tangent at (x₀, y₀) is y – y₀ = m(x – x₀),
where m = slope of the tangent
= \(\left.\frac{d y}{d x}\right]_{\left(x_{0}, y_{0}\right)}\) = f ‘(x₀).

→ Normal to the curve: Let y = f(x) be the equation of a curve.
Equation of the normal is
y – y₀ = – \(\frac{1}{m}\)(x – x₀)
or
x – x₀ + m(y – y₀) = 0,
where m = slope of the tangent
= \(\left.\frac{d y}{d x}\right]_{\left(x_{0}, y_{0}\right)}\) = f ‘(x₀)

It may be noted that, slope of normal
= – \(\frac{1}{m}=\frac{-1}{f^{\prime}\left(x_{0}\right)}\).

→ Particular case of tangent: Let m = tan θ. If θ = 0, then m = 0.
Equation of tangent is y – y₀ = 0, i.e., y = y₀.
If θ = \(\frac{π}{2}\), m is not defined.
∴ (x – x₀) = \(\frac{1}{m}\) (y – y₀).
when θ = \(\frac{π}{2}\), then cot \(\frac{π}{2}\) = 0.

∴ Equation of tangent is x – x₀ = 0 or x = x₀.

→ Approximation: Let f: D → R, D⊂R such that y = f(x) and Δy is the increment in y corresponding to increment Δx in x, where Δy = f(x + Δx) – f(x).
Now,

1. the differential of x denoted by dx is defined by dx = Δx
2. The differential of y, denoted by dy, is defined by
   dy = f ‘(x)dx
   or
   dy = (\(\frac{dy}{dx}\))Δx

Maximum value, Minimum Value, Extreme Value:
Let f be a function defined in the interval I. Then,
1. Maximum Value:
If there exists a point x = c in I such that f(c) > f(x), for all x ∈ I, then/is maximum in I. Point c is known as a point of the maximum value in I.

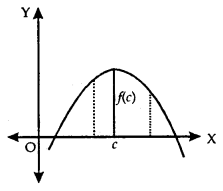
2. Minimum Value:
If there exists a point x = c in I such that f(c) ≤ f(x), for all x ∈ I, then/is minimum in I. Point c is called as a point of the minimum value in I.

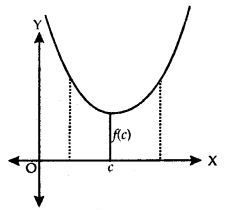
3. Extreme Value:
If there exists a point x = c in I such that f(c) is either a maximum value or a minimum value in I, then f is having an extreme value in I. Point c is said to be an extreme point.

Local Maxima and Minima:
Let f be a real-valued function and x = c be an interior point in the domain of f, then
(a) Local Maxima: c is a point of local maxima, if there is an h > 0, such that f(c) ≥ f(x) for all x ∈ (c – h, c + h).
The value f(c) is called the local maximum value of f.

(b) Local Minimum: c is a point of local minimum, if there is an h > 0, such that f(c) ≤ f(x) for all x ∈ (c – h, c + h).
The value of f(c) is known as the local minimum value of f.

Geometrically if x = c is a point of local maxima of f, then f is increasing (f ‘(x) > 0) in the interval (c – h, c) and decreasing (f ‘(x) < 0) in the interval (c, c + h)

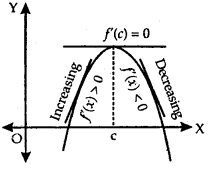
This implies f ‘(c) = 0.

Test of Maxima and Minima:
1. Let f be a function on an open interval I and c ∈ I will be any point. If f has local maxima or local minima at x = c, then either f ‘(c) = 0 or f is not differentiable at c.

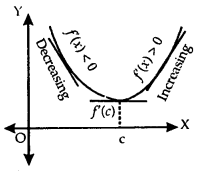
Let f be continuous at a critical point c in it.

2. If f ‘(x) changes sign from positive to negative as x increases through c, i.e.,

1. (i) f ‘(x) > 0 at every point in (c – h, c) and
2. (ii) f ‘(x) < 0 at every point in (c, c + h), where h is sufficiently small, then there is a point of local maxima.

3. If f ‘(x) changes sign from negative to positive as x increases through c, i.e.,

1. f(x) < 0 at every point in (c – h, c) and
2. f ‘(x) > 0 at every point in (c, c + h), where It is sufficiently small, then c is a point of local minima.

4. If f ‘(x) does not change significantly as x increase through c, then c is neither a point of local maxima nor a point of local minima. Such a point is called point of inflection.

Second Derivative Test of Maxima and Minima:
Let f be a function defined on an interval I and c ∈ I and f be differentiable at c. Then,

1. Maxima: x = c is a local maxima, if f'(c) = 0 and f “(c) < 0.
2. Minima: x = c is a local minima, iff'(c) = 0 and f “(c) > 0. Here, f(c) is the local minimum value off.
3. Point of Inflection: If f ‘(c) = 0 and f “(c) = 0, then test fails. Then, we apply the first derivative test as x increases through c.

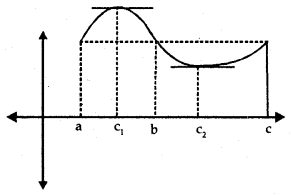
Maximum and Minimum Values in a Closed Interval:
Consider the function f(x) = x+ 3, x ∈ [0,1]. Here f ‘(c) ≠ 0. It has neither maxima nor minima. But f(0) = 3. This is the absolute minimum or global minimum or least value.

Further, f(1) = 4. This is the absolute maximum or global maximum or greatest value.
Further, consider f be any other continuous function having local maxima and minima.

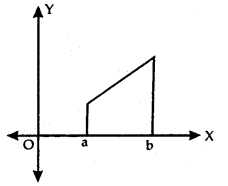
Absolute Maxima and Minima:
Let f be a continuous YA function on an interval I = [a, b].
Then, f has the absolute maximum value and/attains it at least once in I. Similarly,f has the absolute minimum value and attains at least once in I.

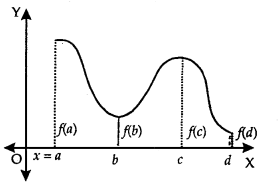
At x = b, there is a minimum.
At x = c, there is a maxima.
At x = a, f(a) is the greatest value or absolute maximum value.
– At x = d,f(d) is the least value or absolute minimum value.

To find absolute maximum value or absolute minimum value:

1. Find all the critical points viz. where f ‘ (x) = 0 or f is not differentiable.
2. Consider the endpoints also.
3. Calculate the values of the function at all the points found in steps (1) and (2).
4. Identify the maximum and minimum values out of the values calculated in step 3. These are absolute maximum and absolute minimum values.

1. DERIVATIVEASARATEMEASURE
f'(x) is the rate measure of fix) w.r.t. x.

2. INCREASING AND DECREASING FUNCTIONS

(i) A function f(x) is said to be increasing function of x
if x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂)
or x₁ ≥ x₂ ⇒ f(x₁) ≥ f(x₂)

(ii) A function f(x) is said to be a strictly increasing function of x
if x₁ < x₂ ⇒ f(x₁) < f(x₂)
or x₁ > x₂ ⇒ f(x₁) > f(x₂)

(iii) A function f(x) is said to be a decreasing function of x,
if x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂)
or x₁ ≥ x₂ ⇒ f(x₁) ≤ f(x₂)

(iv) A function f(x) is said to be a strictly decreasing function of x,
if x₁ < x₂ ⇒ f(x₁) > f(x₂)
or x₁ > x₂ ⇒ f(x₁) < f(x₂)

(v) Monotone Function. A function is said to be monotone if it is either increasing or decreasing.

3. TANGENTSANDNORMALS

(i) lf y = f(x), then the slope of the tangent at P (x = c) is \(\left.\frac{d y}{d x}\right]_{x=c}\)

(ii) Equation of the normal at P(x’, y’) to the curve y = f(x) is y – y’ =\(\left(\frac{d y}{d x}\right)_{\mathrm{P}}\) (x – x’)

(iii) Equation of the normal at P(x’, y’) to the curve y = f(x) is y – y’= \(-\frac{1}{\left(\frac{d y}{d x}\right)_{\mathrm{P}}}\) (x – x’)

4. MAXIMA AND MINIMA

(i) Method to find absolute max. and min., values in a given interval.
(a) Find all points when \(\frac{d y}{d x}\) =0.
(b) Take end points of the interval.
(c) At all these points, calculate values of y.
(d) Take the maximum and minimum values out of these values.

(ii) If f(a) is an extreme value of f(x), then f'(a) = 0.

(iii) Local Maximum and Minimum values.
(a) First Derivative Test GUIDE-LINES:
Let y=f(x).
Step (i) Put \(\frac{d y}{d x}\) = 0. Solve it for getting x = a, b, c,… dx

Step (ii) Select x = a.
Study the sign of \(\frac{d y}{d x}\) when (I) x < a slightly dx (II) x > a slightly.
(a) If the former is + ve and latter is -ve, then f(x) is max. at x = a.
(b) If the former is – ve and latter is +ve, then f(x) is min. at x = a.

Step (iii) Putting those values of x for which f(x) is max. or min. and get the corresponding max. or min. values of f(x).

(b) Second Derivative Test GUIDE-LINES:
Step (i) Put y = f(x) and find \(\frac{d y}{d x}\) i.e., f(x).

Step (ii) Put \(\frac{d y}{d x}\) = 0 i.e. f'(x) = 0 and solve it for x giving 😡 = a, b, c,…

Step (iii) Select x = a. Find \(\frac{d^{2} y}{d x^{2}}\) i.e. f”(x) at x = a.

(I) If \(\left.\frac{d^{2} y}{d x^{2}}\right]_{x=a}\) i. e. f”(a) is -ve, then x = a gives the max. value.
(II) If \(\left.\frac{d^{2} y}{d x^{2}}\right]_{x=a}\)i.e. f”(a) is +ve, then x = a gives the min. value.
Similarly for x = b, c,…

Also Read:

Finnifty 21450

By going through these CBSE Class 12 Maths Notes Chapter 7 Integrals, students can recall all the concepts quickly.

Integrals Notes Class 12 Maths Chapter 7

→ Integration is the inverse process of differentiation. If we are given the derivative of a function and we have to find the function whose derivative is given, the process of finding the primitive or the original function is called the integration or anti-differentation.

Let \(\frac{d}{d x}\)[F(x) + c] = F ‘(x) = f(x)
⇒ F(x) + c is the antiderivative or integal of f(x). This may be written as ∫f(x)dx = F(x) + c,
where c is an arbitrary constant called constant of integration.
∫f(x) dx is called indefinite integral.

Properties of Indefinite Integral.

1. The processes of differentiation and integration are inverse processes of each other, i.e.,
   \(\frac{d}{d x}\)∫f(x) dx = f(x).
2. Indefinite integrals with the same derivatives belong to the same family of curves and so they are equivalent, i.e.,
   in ∫f(x) dx = F(x) + c, [F(x) + c] denotes the same family of indefinite integrals of f(x).
3. ∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx.
4. ∫k f(x) dx = k ∫f(x) dx, where k is real number.
5. If k₁, k₂,………… k_n are the real numbers, then ∫[k₁ f₁(x)+ k₂ f₂(x) +………..+ k_nf_n(x)] dx = k₁∫f₁(x)dx +k₂ ∫f₂(x) dx + +k_n∫f_n(x)dx.

→ We know the formulae for the derivatives of many functions. Corresponding integrals are given below:

Derivatives	Integrals
1. \( \frac{d}{d x}\left(\frac{x^{n+1}}{n+1}\right) \) Where n = 0, \(\frac{d}{d x} \)(x) = 1	1. ∫xn dx = \( \frac{x^{n+1}}{n+1}\) + C ∫dx = x + C
Trigonometric Functions 2. \(\frac{d}{d x} \)(sin x) = cos x	2. ∫cos x dx = sin x + C
3. \(\frac{d}{d x} \)(tan x ) = sin x	3. ∫sin x dx = – cos x + C
4. \(\frac{d}{d x} \)(- cosec x) = cosec x cot x	4. ∫sec2 x dx = tan x + C
5. \(\frac{d}{d x} \)(- cosec x) = cosec x cot x	5. ∫cosec x cot x dx = – cosec x + C
6. \(\frac{d}{d x} \)(sec x) = sec x tan x	6. ∫sec x tan x dx = sec x + C
7. \(\frac{d}{d x} \)(- cot x) = cosec2 x	7. ∫cosec2 x dx = – cot x + C
Inverse Trigonometric Functions 8. \(\frac{d}{d x} \)(sin-1 x) = \( \frac{1}{\sqrt{1-x^{2}}} \)	8. ∫\( \frac{1}{\sqrt{1-x^{2}}} \) dx = sin-1  x + C
9. \(\frac{d}{d x} \)(- cos-1 x) = + \( \frac{1}{\sqrt{1-x^{2}}} \)	9. ∫\( \frac{1}{\sqrt{1-x^{2}}} \) dx = – cos-1 x + C
10. \(\frac{d}{d x} \)(tan-1 x) = \( \frac{1}{1+x^{2}}\)	10. ∫\( \frac{1}{1+x^{2}}\) dx = tan-1 x + C
11. \(\frac{d}{d x} \)(- cot-1 x) = \( \frac{1}{1+x^{2}}\)	11. ∫\( \frac{1}{1+x^{2}}\) dx = – cot-1 x + C
12. \(\frac{d}{d x} \)(sec-1 x) = \( \frac{1}{x \sqrt{x^{2}-1}}\)	12. ∫\( \frac{1}{x \sqrt{x^{2}-1}}\) dx = sec-1 x + C
13. \(\frac{d}{d x} \)(- cosec-1  x) = \( \frac{1}{x \sqrt{x^{2}-1}}\)	13. ∫\( \frac{1}{x \sqrt{x^{2}-1}}\) dx = – cosec-1 x + C
Exponential Functions 14. \(\frac{d}{d x} \)ex = ex	14. ∫ex dx = ex + C
15. \( \frac{d}{d x}\left(\frac{a^{x}}{\log a}\right)\)  =ax	15. ∫ax dx = \( \frac{a^{x}}{\log a}\) + C
Logarithmic Functions 16. \(\frac{d}{d x} \)(loge x) = \(\frac{1}{x}\)	16. ∫\(\frac{1}{x}\) dx = loge x + C
17. \(\frac{1}{2}\)(loga x) = \(\frac{1}{x}\)loga e	17. ∫\(\frac{1}{x}\)loga e dx = loga x + C

Geometrical Interpretation of Indefinite Integral:
∫f(x) dx = F(x) + C = y (say).
y = F(x) + C represents a family of curves. By giving different values to C, we get different members of family. These members can be obtained by shifting any of the curves parallel to itself.

Comparison between Differentiation and Integration:

Differentiation	Integration
1. It is an operation on function.	1. It is an operation on function.
2. \( \begin{aligned}\frac{d}{d x}\left[k_{1} f_{1}(x)+k_{2} f_{2}(x)+\ldots\right.\\\left.+k_{n} f_{n}(x)\right]\end{aligned}\) = k1 \(\frac{d}{d x} \)f1 (x) + k2 \(\frac{d}{d x} \)f2(x) + ……….+ kn \(\frac{d}{d x} \)fn (x)	2. ∫ k1 \(\frac{d}{d x} \)f1 (x) + k2 \(\frac{d}{d x} \)f2 (x) + ……….+ kn \(\frac{d}{d x} \)fn (x) = k1∫f21(x) dx + k2∫f2 (x) dx + ……… + kn∫fn (x) dx
3. Some functions are not differentiable.	3. All functions are not integrable.
4. The derivative of a function, if it exists, is unique.	4. The integral of a function is not unique.
5. ¡f a polynomial function of a degree n is differentiated, we obtain a polynomial of degree n – 1.	5. If a polynomial function of a degree n is integrated, we get a polynomial of degree n + 1.
6. We can obtain a derivative at a point.	6. Integral of a function may be obtained over an interval in which f is defined.
7. Slope of tangent at a point x = x1 is f ‘(x1).	7. Integral of a function represents a family of curves.
8. If the distance traversed at any time f is known, we can find velocity and acceleration.	8. When the velocity or acceleration at any time t is known, we can find the distance traversed in time t,
9. Differentiation is a process involving limits.	9. Integration too involves limits.

Integration by Substitution:
Let I = ∫f(x) dx. This integral can be transformed into another form by changing the independent variable x to t by putting x=g(t).
∴ \(\frac{dx}{dt} \) = g'(t) or dx = g'(t) dt
∴ I = ∫f[g(t)]g'(t) dt

Note: While making a substitution, it should be kept in mind that the f[g(t)] is in the form of some standard formula, whereas g'(t) is a factor, along with f[g(t)] e.g.
Consider the integral I = ∫x² cos(x³ + 2)dx
If we put x³ + 2 = t, its derivative 3x² is a factor and cos t can easily be integrated.

Some Results:

1. ∫tan x = log|sec x| + C
2. ∫cot x = log|sin x| + C
3. ∫sec x = log|sec x + tan x| + C
4. ∫cosec x dx = log|cosec x – cot x| + C

→ Use of Trigonometric Identities:
Use following trigonometric identities for integrating the functions such as sin2x.cos2x, sin3x, cos3x, sin x cos x, etc.

1. sin² x = \(\frac{1-\cos 2 x}{2}\), cos2 x = \(\frac{1+\cos 2 x}{2}\)
2. sin³ x = \(\frac{3 \sin x-\sin 3 x}{4}\), cos2 x = \(\frac{3 \cos x+\cos 3 x}{4}\)
3. 2sinA cosB = sin(A + B) + sin(A – B)
   2cosA sinB = sin(A + B) – sin(A – B)
   2cosA cosB = cos(A + B) + cos(A – B)
   2sinA sinB = cos(A – B) – cos(A + B)

Some more Integrals:

→ How to integrate when the integral has ax² + bx + c or \(\sqrt{a x^{2}+b x+c}\) in the denominator?

So, ax² + bx + c changes to t² ± k².
Thus, \(\frac{1}{a x^{2}+b x+c}\) converts into the form \(\frac{1}{t^{2} \pm k^{2}}\) and
\(\frac{1}{\sqrt{a x^{2}+b x+c}}\) converts into the form \(\frac{1}{\sqrt{t^{2} \pm \dot{k}^{2}}}\).

→ To find the integration of type ∫\(\frac{p x+q}{a x^{2}+b x+c}\) dx or ∫\(\frac{p x+q}{\sqrt{a x^{2}+b x+c}}\) dx:
Put px + q = A\(\frac{d}{d x} \)(ax² + bx + c) + B

Compare the two sides and find the value of A and B.

Partial Fractions of Rational Functions.
(a) Let \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) be a rational function, where P(x) and Q(x) are
polynomials, where Q(x) ≠ 0.

1. If degree of P(x) is less than degree of Q(x), then \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) called a proper rational function.
2. If degree of P(x) is greater than the degree of Q(x), then \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) is known as an improper rational function.

This can be expressed in the form f(x) + \(\frac{\mathrm{P}_{1}(x)}{\mathrm{Q}(x)}\) by dividing P(x) by Q(x), so that degree of P1(x) is less than the degree of Q(x).

(b) 1. Let \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) be a proper rational function. Find the factors of Q(x). Let these factors be linear.
P(x)
Suppose Q(x) = (x + a)(x + b)(x + c), Then, \(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}\) is written as
\(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}=\frac{\mathrm{A}}{x+a}+\frac{\mathrm{B}}{x+b}+\frac{\mathrm{C}}{x+c}\)
or
P(x) = A(x + b)(x + c) + B(x + a)(x + e) + C(x+a)(x+ b)

It is an identity which is true for all values of x ∈ R.
To find A,put x =-a.
To find B, put x = – b.
To find C, put x = – c.
Thus, the fractions so obtained on the R.H.S. are the partial fractions. e.g.
Let us find the partial fraction of \(\frac{1}{(x-1)(x-2)}\)

∴ \(\frac{1}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\)
1 = A(x – 2) + B(x – 1)
Put x = 1, 1 = A(1 – 2) = – A
∴ A = -1

Put x = 2, 1 = B(2 – 1) = B
∴ B = 1

\(\frac{1}{(x-1)(x-2)}=\frac{-1}{x-1}+\frac{1}{x-2}\)

2. Let the linear factor(s) be repeated. Q(x) = (x + a)(x + b)2.
Then,
\(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}=\frac{\mathrm{A}}{x+a}+\frac{\mathrm{B}}{x+b}+\frac{\mathrm{C}}{(x+b)^{2}}\)
Also, P(x) = A(x + b)2 + B(x + n)(x + b) + C(x + a)

3. Suppose one of the factors of Q(x) be quadratic.
Let Q(x) = (x + a)(x² + bx + c). Then,
\(\frac{\mathrm{P}(x)}{\mathrm{Q}(x)}=\frac{\mathrm{A}}{x+a}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+b x+c}\)
Also, P(x) A(x² + b + c) ÷ (x + a)(Bx + c)
Put x = – a, value of A is obtained.
Put x =0, 1, -1, etc., and obtain equations involving A, B, C.

Substitute the value of A in these equations. Then, solve them to find the values of B and C.
OR
Compare the co-efficients of x², x and constant. Solve the equations so obtained e.g.: Let us find the partial fractions of
\(\frac{1}{(x-1)\left(x^{2}+1\right)}\)
\(\frac{1}{(x-1)\left(x^{2}+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^{2}+1}\)
∴ 1 = A(x² + 1) + (x – 1)(Bx + C)
1 = A(x² + 1) + B(x² – x) + C(x – 1)
Put x=1, I =A(1 + 1) = 2A
∴ A = \(\frac{1}{2}\).

Comparing the coefficients of x², we get
O = A + B
∴ B = -A = – \(\frac{1}{2}\)

Comparing the coefficients of x, we get
O = -B + C
∴ C = B = –\(\frac{1}{2}\).
∴ \(\frac{1}{(x-1)\left(x^{2}+1\right)}=\frac{1}{2(x-1)}-\frac{x+1}{2\left(x^{2}+1\right)}\).

Note: It is obvious that by converting the rational function into partial fractions, we can easily integrate the given rational function.

Integration by Parts
Let u and v be the functions of x, then
∫uv dx = u∫v dx – ∫u'[∫vdx]dx
= u × Integral of v – Integral of (derivative of u × Integral of v]

Note: Out of two functions, which function is to be considered as first. Usually, we proceed as follows:
∫xⁿ f(x) dx xⁿ = u is First function.
∫(Inverse trig, function) × f(x) dx

Inverse trig. function = u is First function.
∫(log x)f(x) dx, Take log x = u as first function.

Some Integrals:

Definite Integral as the Limit of Sum
Definite integral as a limit of a sum is defined as

where h = \(\frac{b-a}{n}\). As h → 0, n → ∞.

Note: Some useful series to find the definite integral as the limit of the sum.


Area Function:
∫_a^bf(x) dx is defined as the area of the region bounded by the curve y = f(x), a ≤ x ≤ b,the x-axis and the ordinates x = a and x = b. Let x be a given point in [a, b]. Then,

∫_a^b f(x) dx represents the area of the shaded region. It is as shmmed that f(x) > 0 for x ∈ [a, b].
This function is denoted by A(x) which is known as area function. i.e.,
A(x) = ∫_a^x f(x) dx.

→ First Fundamental Theorem of Integral Calculus
Let f be a continuous function on the closed interval [a, b] and let A(x) be the area function. Then, A'(x) =f(x) for all x E [a, b].

→ Second Fundamental Theorem of Integral Calculus
Let f be a continuous function defined on closed interval [a, b] and F be antiderivative of f Then,
∫a b f(x) = [F(x)]ba = F(b) — F(a).

→ Evaluation of Definite Integral by Substitution

1. To evaluate ∫a b f(x) dx, let the substitution be x = g(t) such that dx = g'(t) dt.
2. Let t = t₁ at x = a, t = t₂ at x = b.

The new limits are t1 to t.
∴ ∫ab f(x) dx = ∫_t1 ^t₂ f[g(t)g'(t) dt
= F(t₂) – F(t₁), where
∫f[g(t)]g'(t) dt = F(t).

Properties of Definite Integrals:

1. DEFINITION
If \(\frac{d}{d x}\) f(x) = F(x), then ∫F(x) dx = f(x) + c, where ‘c’ is a constant of integration.

2. STANDARD RESULTS

(i). Power Rule. ∫ xⁿ dx = \(\frac{x^{n+1}}{n+1}\) + c, provided n ≠ – 1
(ii) ∫ \(\frac{1}{x}\) dx = log |x| + c, x ≠ 0
(iii) ∫a^xdx = \(\frac{a^{x}}{\log a}\) + c, a > 0, a ≠ 1 for all x ∈ R
(iv) ∫ e^x dx = e^x + c ∀ x ∈ R
(v) ∫ sin x dx= -cosx+c ∀ x ∈ R
(vi) ∫ cos x dx = sin x + c ∀ x ∈ R
(vii) ∫ sec² xdx = tan x + c, x ≠ an odd multiple of \(\frac{\pi}{2}\)
(viii) ∫ cosec² x = – cot x + c, x ≠ an even multiple of \(\frac{\pi}{2}\)
(ix) ∫ sec x tan x dx = sec x + c, x ≠ an odd multiple of \(\frac{\pi}{2}\)
(x) ∫ cosec x cot x dx = – cosec x + c,x ≠ an even multiple of \(\frac{\pi}{2}\)
(xi) ∫ tan x dx – – log | cos x | + c = log |sec x| + c, x ≠ x an odd multiple of \(\frac{\pi}{2}\)
(xii) ∫ cot x dx = log |sin x| + c, x ≠ an even multiple of \(\frac{\pi}{2}\)
(xiii) ∫ sec x dx = log |sec x + tan x| + c, x ≠ an odd multiple of \(\frac{\pi}{2}\)
(xiv) ∫ cosec x dx =  log |cosec x – cot x| + c, x ≠ an even multiple of \(\frac{\pi}{2}\).

3. FUNDAMENTAL THEOREMS

(i) ∫ a f(x) dx = a ∫ f(x)dx, where ‘a ’ is any real constant
(ii) ∫ [f₁(x) ± f₂(x)]dx = ∫ f₁(x)dx ± ∫ f₂(x)dx
(iii) \(\frac{d}{d x}\)[∫f(x)dx] = f(x)
(iv) ∫\(\frac{f^{\prime}(x)}{f(x)}\)dx = log |f(x)| + c
(v) ∫ f(x))ⁿ f'(x)dx = (\(\frac{(f(x))^{n+1}}{n+1}\) + c, n ≠ -1
(vi) ∫ \(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = sin^-1\(\frac{x}{a}\) + c
(vii) ∫ \(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = \(\frac{1}{a} \tan ^{-1} \frac{x}{a}\) + c
(viii) ∫ \(\frac{1}{\sqrt{a^{2}+x^{2}}}\)dx = log|x + \(\sqrt{a^{2}+x^{2}}\)|+ c
(ix) ∫ \(\frac{d x}{\sqrt{x^{2}-a^{2}}}\) = log|x + \(\sqrt{x^{2}-a^{2}}\) |+ c
(x) ∫ \(\sqrt{a^{2}-x^{2}} d x=\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}+c\)
(xi) ∫ \(\sqrt{a^{2}+x^{2}} d x=\frac{x}{2} \sqrt{a^{2}+x^{2}}+\frac{a^{2}}{2} \log \left|x+\sqrt{a^{2}+x^{2}}\right|+c\)
(xii) ∫ \(\sqrt{x^{2}-a^{2}} d x=\frac{x}{2} \sqrt{x^{2}-a^{2}}-\frac{a^{2}}{2} \log \left|x+\sqrt{x^{2}-a^{2}}\right|+c\)
(xiii) ∫ \(\frac{1}{a^{2}-x^{2}}\)dx = \(\frac{1}{2 a} \log \left|\frac{a+x}{a-x}\right|\)+ c
(xiv) ∫ \(\frac{1}{x^{2}-a^{2}}\)dx = \(\frac{1}{2 a} \log \left|\frac{x-a}{x+a}\right|\)+ c

4. IMPORTANT RULES

(i) Rule to integrate ∫ sin^m x cosⁿ x dx.
(a) If the index of sin x is a positive odd integer, put cos x = t.
(b) If the index of cos x is a positive odd integer, put sin x = t.

(ii) Rule to integrate : \(\int \frac{1}{a \sin ^{2} x+b \cos ^{2} x} d x, \int \frac{1}{a+b \cos ^{2} x} d x\) ; etc.
a sin x + b cos x J a + b cos x
(a) Divide the numerator and denominator by cos²x
(b) Replace sec²x, if any, in the denominator by 1 + tan²x
(c) Put tan x = t so that sec²x dx = dt.

(iii) Integration of Parts.
Integral of the product of two functions = First function x Integral of second – Integral [(diff. coeff. of first) x (integral of second)].

(iv) Rule to integrate \(\int \frac{1}{\text { linear } \sqrt{\text { linear }}} d x\) or \(\int \frac{1}{\text { quadratic } \sqrt{\text { linear }}} d x\) Put \(\sqrt{\text { linear }}=t\)

(v) Rule of integrate \(\int \frac{1}{\text { linear } \sqrt{\text { quadratic }}} d x\) Put linear = \(\frac { 1 }{ t }\)

(vi) Rule to integrate \(\int \frac{x d x}{\text { (Pure Quad.) } \sqrt{\text { Pure Quad }}}\). Put \(\sqrt{\text { Pure Quad }}\) = t

(vii) Rule to integrate \(\int \frac{d x}{\text { (Pure Quad.) } \sqrt{\text { Pure Quad }}}\) Put x = \(\frac{1}{t}\) and \(\sqrt{\text { Pure Quad }}\) = u.

5. Integral As The Limit of a sum

\(\int_{a}^{b}\) f(x)dx = \(\lim _{h \rightarrow 0}\) h[f(a)+f(a + h)+f(a + 2h)+… + f(a + \(\overline{n-1}\)h)], where h = \(\frac{b-a}{n}\).

6. FUNDAMENTAL THEOREM OF INTEGRAL CALCULUS

\(\int_{a}^{b}\)f(x) dx = F(b) – F(a), where ∫ f(x) dx = F(x).

7. PROPERTIES OF DEFINITE INTEGRALS

I. \(\int_{a}^{b}\) f(x)dx = \(\int_{a}^{b}\) f(t) dt

II. \(\int_{a}^{b}\) f(x)dx = –\(\int_{a}^{a}\)f(x)dx. Particular case: \(\int_{a}^{a}\)f(x)dx = 0

III. \(\int_{a}^{b}\) f(x)dx = \(\int_{a}^{b}\) f(a + b – x)dx.

IV. \(\int_{a}^{b}\) f(x)dx = \(\int_{a}^{c}\)f(x)dx + f(x)dx = \(\int_{c}^{b}\) f(x)dx, where a < b < c

V. \(\int_{0}^{a}\) f(x)dx = \(\int_{a}^{b}\) f(a – x)dx

VI. \(\int_{-a}^{a}\) f(x)dx = 0 if f(-x) = -f(x)
= 2\(\int_{0}^{a}\) f(x)dx if f(-x) = f(x)

VII. \(\int_{0}^{2a}\) f(x)dx = \(\int_{0}^{a}\) f(x)dx =\(\int_{0}^{a}\) f(2a – x)dx

VIII. \(\int_{0}^{2a}\) f(x)dx = 2\(\int_{0}^{a}\) f(x) dx
= 0

f(2a-x)dx = f(x)
if (2a – x) = f(x)

Read More:

Nseix Gift Nifty

1 Mark Questions for Political Science Class 12 Pdf: Here we are providing CBSE 1 Mark Questions for Political Science Class 12 in Hindi and English Chapter Wise Pdf. Students can get Class 12 Political Science Important Questions, Political Science Class 12 One Mark Questions and Answers designed by subject expert teachers.

One Mark Questions for Class 12 Political Science Chapter Wise Pdf

Class 12 Political Science 1 Mark Questions Part A Contemporary World Politics

1. The Cold War Era 1 Mark Questions
2. The End of Bipolarity 1 Mark Questions
3. US Hegemony in World Politics 1 Mark Questions
4. Alternative Centres of Power 1 Mark Questions
5. Contemporary South Asia 1 Mark Questions
6. International Organisations 1 Mark Questions
7. Security in the Contemporary World 1 Mark Questions
8. Environment and Natural Resources 1 Mark Questions
9. Globalisation Important Questions 1 Mark Questions

One Mark Questions for Class 12 Political Science Part B Politics in India Since Independence

1. Challenges of Nation Building 1 Mark Questions
2. Era of One Party Dominance 1 Mark Questions
3. Politics of Planned Development 1 Mark Questions
4. India’s External Relations 1 Mark Questions
5. Challenges to and Restoration of Congress System 1 Mark Questions
6. The Crisis of Democratic Order 1 Mark Questions
7. Rise of Popular Movements 1 Mark Questions
8. Regional Aspirations 1 Mark Questions
9. Recent Developments in Indian Politics 1 Mark Questions

We hope the given NCERT Political Science Class 12 One Mark Questions in Hindi and English Chapter Wise Pdf will help you. If you have any queries regarding Class 12 Political Science 1 Mark Questions and Answers, drop a comment below and we will get back to you at the earliest.

FAQ’s on 1 Mark Questions for Political Science Class 12

Question 1.
Is it possible to score better grades by preparing the 1 Mark Questions for Political Science Class 12?

Answer:
Yes, it is possible to score better grades by preparing the 1 Mark Questions for Political Science Class 12 as they are quite scoring.

Question 2.
Does CBSE repeat the Class 12 Political Science 1 Mark Questions in Board Exams?

Answer:
Yes, CBSE repeats the 12th Class 1 Mark Political Science Questions in board exams. So, try reading the important questions regularly and score better grades in board exams.

Question 3.
Is there any source that provides the 12th Standard Political Science 1 Mark Questions List for free?

Answer:
Yes, Learninsta.com is a reliable online portal where you can get 1 Mark Political Science Questions List for free of cost and make your preparation effective.

Question 4.
How can I get full marks in Class 12 Political Science Board Exams?

Answer:
Understand your syllabus thoroughly and know exactly what to study. Along with studying from Textbooks do prepare notes and highlight the important points. At first, understand the information and read subsequently to remember the information.

Read More:

HS3252 – Professional English II Syllabus

Here we are providing Class 12 Business Studies Important Extra Questions and Answers Chapter 11 Marketing. Business Studies Class 12 Important Questions are the best resource for students which helps in class 12 board exams.

Class 12 Business Studies Chapter 11 Important Extra Questions Marketing

Marketing Important Extra Questions Short Answer Type

Question 1.
What are Marketing and selling? Also, differentiate between the two.
Answer:
Many people confuse ‘Selling’ for marketing They consider these two terms as one and same. Marketing refers to a large set of activities of which selling is just one part. For example, a marketer of television, before marketing the sale does a lot of other activities such as planning the types and model of television to be produced, the price at which it would be sold, and selecting the distribution outlets at which the same would be available, etc. In short, marketing involves a whole range of activities relating to planning, pricing promotion, and distribution of the products that satisfy customers’ needs.

The function of selling, on the other hand, is restricted to the promotion of goods and services through salesmanship, advertising, publicity, and short-term incentives so that title of the product is transferred from seller to buyer or in other word product is converted into cash.

The Major differences between Selling and Marketing are listed below
1. Part of the Process Vs Wider term: Selling is only a part of the process of Marketing and is concerned with promotion and transferring possession and ownership of goods from the seller to the buyer Marketing is a much wider term consisting of a number ofactiviti.es such as identification of the customer. Need, developing the products to satisfy these needs fixing prices, and persuading the potential buyers to buy the same thus selling is merely a part of marketing.

2. Transfer of title Vs Satisfying Customer Need: The main focus of selling is on affecting the transfer of title and possession of goods from sellers to consumers or achieving maximum satisfaction of the customer’s needs and wants.

3. Profit, Through Maximising Sales Vs Customer Satisfaction: All selling activities are directed as Maximising sales and thereby the profit of the firm. In another word, the emphasis is on profit maximization through the maximization of sales. Marketing on the other hand is concerned with customer satisfaction and thereby increasing profit in the long run. Marketing organization thus attaches the highest importance to customer satisfaction as a route to profit maximization.

4. Start and End of the Activities Selling activities start after the product has been developed while marketing activities start much before the product is produced and continue even after the product has been sold.

5. Difference in the Emphasis: In selling the emphasis is on bending the customer according to the product while in marketing the attempt is to develop the product and other strategies as per customer needs.

6. Difference in the Strategies: Selling involves efforts like promotion and persuasion while marketing uses integrated marketing efforts involving strategies in respect of product promotion, pricing, and physical distribution.

Question 2.
Mention in brief the role of Marketing in the Context of the Indian economy?
Answer:
AM profit or pursue some improvement of quality of life or promotion of cause say UNICEF working for the Welfare of children or Help age working for the cause of senior citizens whether it is a profit organization or non-profit organization Marketing plays an important role in achieving its objectives. Marketing plays an important role from its help the individual consumers in raising their standard of living by making available the product and services that satisfy their need and want.lt also plays a significant role in the economic development of a nation. The role of marketing in different situations may be described in brief as follows.

The modern concept of marketing plays a significant role in achieving the objectives of a firm, ft emphasizes that customer satisfaction is the key to the survival and growth of an organization in the contemporary competitive marketing environment. By adopting a marketing organization, an organization-whether profit-making or non-profit making can achieve its goals in the most effective manner, it helps in focusing the activities of an organization or the need and wants of the customers. For example, what products or services will be marketed by a firm will depend upon what do its customers need. Thus an analysis of the need of the customers shall be undertaken in order to decide what to produce and sell.

The product will then be designed according to the need of the potential buyers and be made available through the outlets are convenient to customers and are priced at a level which the target customers can afford. In other words marketing as a business philosophy help in serving the customers by satisfying their needs. It is a well-known fact that a satisfied customer is the most valuable asset of a firm. Thus marketing plays a crucial role in the survival and growth of a firm.

O Role in Economy: Marketing plays a significant role in the development of an economy, it acts as a catalyst in the economic development of a country, and helps in raising the standards of living of people.

The development of a nation can be judged by the level of standard of living of its people. Another important criterion, which is related to the first one is the per capita income of an average citizen of a country. On this basis, an underdeveloped country may be stated to be which is characterized by factors like poverty, Scarcity of goods and services predominance of agriculture, etc.

Marketing can play a significant role in the economic development of a nation. It can inspire people to undertake new activities and to set up enterprises for producing goods that are needed by customers. Marketing can help in overcoming obstacles posed by high prices due to imbalances in the level of production and consumption It can also ensure smooth flow of goods through efficient physical distribution arrangements.

In other words, marketing can help in finding out the right type of products and services that a firm should manufacture the places where it should make such products available for sale. The price at which the product should be sold and the channels that should be used for moving the products to the ultimate place of consumption or use. This linkage between the business and consumption centers accelerates the economic activity leading to higher incomes more consumption and increased saving and investment.

Question 3.
Explain the important characteristics of a good brand name?
Answer:
Characteristics of Good Brand Name: Choosing the right brand name is not an easy decision what makes this decision important is the fact that once a brand name is chosen and the product is launched in the market. Changing the brand name is very difficult. So getting it right the first time is very essential following are some of the considerations which should be kept in mind while choosing a brand name.

1. The brand name should be short easy to Pronounce, spell, recognized, and remember e.g. ponds, VIP, Rin, Vim Etc.
2. A brand should suggest the product’s benefits and qualities. It should be appropriate to the product’s functions, e.g. Rasika, Genteel, Promise, My fair Lady, and Boost.
3. A brand name should be distinctive e.g. Liril, sprit, Safari, Zodiac;
4. The brand name should be adaptable to packaging or Labelling requirements to different advertising media and to different languages.
5. The brand name should be sufficiently versatile to accommodate new products, which are added to the product line e.g. Maggie, Colgate;
6. It should be capable of being registered and protected legally; and
7. The chosen name should have to stay power ie; it should not get out of data.

Question 4.
Explain the term sales promotion and mention, in brief, the merits and limitations of sales promotion.
Answer:
Sales Promotion refers to short-term incentives which are designed to encourage the buyers to make immediate purchase of a product or service these include all promotion effort other than advertising, personal selling, and publicity, used by a company to boost its sale sales promotion activities include offering a cash discount, sales contests, tress gift offers and free sample distribution, sales promotion include only those activities that are u$ed to provide short term. incentives to boost the sales of a firm.

Merits of Sales promotion:

1. Attention ValueSales promotion activities attract the attention of the people because of the use of incentives.
2. Useful in New Product Launch Sales Promotion tools can be very effective at the time of introduction of a new product in the market. It includes people to break away from their regular buying behavior and try the new product.
3. Synergy in total promotional efforts Sales Promotion activities is designed to Supplement the personal selling and advertising efforts used by a firm and add to the overall effectiveness of the promotion efforts of a firm.

Limitation of Sales promotion:

1. Reflects CrisisIt a firm frequently rely on Sales promotion, it may give the impression that it is unable to manage its sales or that there are no takers of its product.
2. Spills Product Image Use of Promotion tools may affect the image of a product. The buyers may start feeling that the product is not of good quality or is not appropriately priced.

Question 5.
Differentiate between the old and new concept of Marketing?
Answer:
The difference between the new and old Marketing. The concept may be made clear as to under
1. Orientation: – The old concept is production-oriented because it emphasizes production on the other hand new concept insists on the consumer’s need for satisfaction and therefore it is consumer-oriented.

2. Scope of Marketing Production and sales were the main
activities included scope. The scope of Marketing under the new concept has been widened to include the pre-production and after-sales problems.

3. Targets: In the old Marketing concept the main target of the firm was to earn profit through more and more production and higher sales volume whereas in the modern concept of Marketing the target of the firm is to earn more profit through customer satisfaction.

4. Market Research: There is no scope of Market research in the old concept of the market whereas, in a new concept of Marketing, market research is a must to know the needs, wants and behavior of the consumers so as to produce goods and services accordingly.

5. Inter-departmental Integration: Under the old concept of Marketing different departments of the firm independent and has no Integration with the Marketing department. They were mainly concerned with the production and not with the sales. A new concept of Marketing has now changed the view. Now activities of each department are directed by the Marketing department and the various department are better integrated with the Marketing department.

6. Consumer Welfare The new concept is fully dedicated to consumer welfare. The main responsibility of Marketing is to raise the standard of living of the society through consumer welfare and consumer satisfaction. There was no place for consumer welfare under the old concept of Marketing.

From the above-mentioned point, it is clear that: The old concept of Marketing is referred to as a system where more and more emphasis was laid on the production of commodities. It was based on the idea that consumers would buy what the seller produces. The modern concept on the other hand concentrates on the satisfaction of the need of customers and the need there. The seller produces what the buyer need and thus new concept emphasizes customers and their need satisfaction. The main point of difference between these two concepts has been explained in the following lines.

Old Concept of Marketing:

New Concept of Marketing:

Before embarking on the production work, the new concept of Marketing starts by finding out the requirement of customers. The businessman has to earn profit by selling and satisfying the customer with the product’s quality.

The Modern Concept of Marketing In India: On the question of the application of the Modem concept of Marketing in India, various scholars are of the view that it does not apply to India. They put forward undermentioned logics in support of their answer

1. Production if India is not according to the taste and needs of the consumers.
2. The marketing program does not include after-sales service.
3. The Concept that “We must have profit irrespective of the fact that consumer feels satisfied or not is adopted in India.

However, consumers are of the opinion that the modem concept of Marketing applies in India due to the following reasons:

1. Many producers produce products after identifying the need of consumers.
2. After-sale services are provided such as a guarantee on products.
3. There are many manufacturers who are not solely concerned with a profit motive.
4. Advertisement and other sales-promotion activities are undertaken by producers, so as to enhance the standard of living of consumers.

Judging and Comparing the two thoughts on Marketing in India, it can be deduced that Modern Marketing Concept applies in India in a partial way. Modern Marketing concepts will play a crucial role in India with the expansion of education, urbanization of the population, increase in per-capital income, and improvement of the standard of living.

Question 6.
Explain in brief the objectives and importance of Physical Distribution Management?
Answer:
The Scope elf Physical Distribution System and its Components

The Marketing process is not complete simply by creating a super product and by creating a customer at the right time and place is an equally important function in Marketing. In the process of Marketing, this vital function is called Physical distribution. Physical distribution means the process of delivering the product to the user or Consumer Promptly safety and its time.

The following are the components of the Physical distribution system:

1. Distribution Planning and accounting
2. Inbound Transport
3. Receiving
4. Inventory Management
5. In-plant Warehousing
6. Order processing
7. Packaging/repackaging where applicable
8. Dispatch of goods
9. Outbound transport
10. Field warehousing
11. Customer service
12. Communication.

Physical distribution components or activities can be used as elements of Marketing strategy. Recognization of Physical distribution service can bring about better customer service. Increase in sales cost reduction and higher profit Margin.

In this full scope for a manufacturer, Physical distribution would involve not only the movement of finished goods from the end of the production line to the final customer but also the flow of raw materials from the supplier to the factory. Similarly, dealers and traders will manage the flow of goods into their shelves as well as from their shelves to the customer’s home or stores.

Importance of Physical Distribution Management – It is a physical distribution that provides place-utility and time-utility to products. In other words, it is the physical distribution that makes the product available at the right place and at the right time thereby Maximising the company’s chance to sell the product and strengthen its competitive position. If any product mode in any place could be consumed in its entirety at the very place of production and at the very time of production, there would no need for Physical distribution for that product.

But such products are very rare. In practice, almost every product gets consumed at places and times that, are different from those of their manufacture. They have to be carried t to places of consumption, they have to be stored and they have to be distributed.

The activity of Physical distribution is necessary for modern Marketing due to the following reasons
1. Control on Distribution CostUnder an efficient system of Physical distribution, a detailed analysis of transportation and storage cost is made in view of controlling or minimizing the distribution cost. It aims at reducing the sale price to the consumer for this purpose stress is laid on improvement in packaging control over channels of distribution simplification of the distribution system and technical improvement:

2. Increase in Sales Volume Marketing Management has realized that there is a definite connection between merchandising programs and physical distribution services (Particularly delivery service and order processing service). Customer often gives more importance to physical distribution than to price and promotion service. Physical distribution is considered by customers second in importance 1 to produce quality a reason for purchasing from a certain firm. Better J Physical distribution service gives higher overall customer satisfaction.

In other words, customers’ buying behavior hinges on the offer of adequate Physical distribution service.

3. Coordination of Demand and SupplyPhysical distribution facilitates the coordination between management got the benefits of a lower and higher level of customer service and thereby could reduce their operating expenses by 10 to 15 percent Many other competing firms were also compelled to adopt Scientific Management of physical distribution service. Thus many companies have now started giving more attention to the management of physical distribution operations in an integrated manner.

4. Product PlanningIncreasing competition in Marketing has necessitated the proper attention to be paid on product planning, production advertisement, and sales promotion, etc. but only this is not enough for an enterprise to get success in its marketing efforts. It also becomes necessary that the goods and services produced by the enterprise must be made available to the consumers at the right time and right place for this reason. Marketing executives of today have come to realize the importance of physical distribution.

5. Important in Marketing Physical distribution system is now recognized as an integral part of Marketing. Hence the marketing concept must apply to the management of physical distribution revolving around customer need can add the utility or want-satisfying power, viz, the availability of product at the right place and time, and at the lowest possible cost.

6. Need for customer satisfaction Physical distribution is not only a cost, it should be regarded as one of the tools in competitive Marketing. A Marketer can attract additional customers and maintain existing customers by offering better and dependable service or lower prices with fair service through improvement in the physical distribution package. The marketer has to evolve an appropriate physical distribution process that will fulfill the objective of adequate customer satisfaction.

7. Stabilisation of Prices The Marketing function of warehousing inventory, control, transport, protective packaging physical handling order processing, etc. is now managed as an integrated whole. An effective physical distribution package gives the customers the service they expect and at the same time, it assures profitable sales. Control oversupply position may help to stabilize the prices in the market. It at any time demand exceeds the supply available in the Market additional supplies can be released from the warehouses on the contrary if the supply position improves the production may be kept in storage in order to arrest the fall in prices.

8. Management Science The development of Management science or operations research has made possible the integration of Physical distribution functions. Physical distribution problems have a large number of variables that are readily measurable. Operations research techniques can be easily applied to secure the solution to the physical distribution problem.

Question 7.
What is market segmentation?. Mention in brief the criteria for market segmentation.
Answer:
Definitions of Market Segmentation:

Following are the definitions of market segmentation:
1. According to, Philip Kotler “Market segmentation is the subdividing of a market into homogeneous subsets of customers, where any subset may be a distinct marketing mix.”

2. According to William J. Stanton “Marketing segmentation consists of taking the total heterogeneous market for a product and dividing it into several sub-markets or segments, each of which tends to be homogeneous in all significant aspects.”

3. According to Rustan S. Davar” Market may be classified in several ways depending on the customer characteristics. Customers may be grouped on the basis of how they use a product or service. This grouping of customers can also be broken up in terms of age, sex, income level, education, or geographical in terms of sales territories. This grouping of buyers or segmenting the market is described as Market segmentation.”

4. According to Cundiff and Still: “Market segments are a grouping of consumers according to such characteristics as income, age, degree of urbanization, race or ethnic classification, geographic location or education.

5. According to Alan A. Robert”Market segmentation is the strategy of dividing markets in order to conquer them.”

6. According to Amerian Marketing Association “Market segmentation refers to dividing the heterogeneous markets into smaller customer divisions having certain homogeneous characteristics that can be satisfied by the firm.”

Basis or Criteria For Market Segmentation: Market segmentation being the key input in a firm’s marketing planning process the important issue is how to identify these market segments. Unfortunately, there is no one best way of segmenting the markets. That is why marketing managers are expected to examine a variety of segmentation criteria so as to identify those that will be most effective in defining their markets. The most prevalent basis for segmentation of the market in several countries broadly industrialized, have the prime objective of buying the product/item.

On the basis of this objective, the product market can be divided into two segments. These are

1. Ultimate Consumer
2. Industrial Consumer

The reason behind the division of the product market lies in the differentiation of consumers’ nature quantum of purchase, the factors influencing purchase, and the marketing efforts made by the seller.

The above division of market segmentation is used by Cundiff and Still. They have mentioned the following criteria for market segmentation:

Bases for Consumer Product	Bases for Industrial Product
1. Income of the Consumer.	1. Kinds business
2. Age of the Consumer	2. Usual purchasing procedure
3. Sex of the Consumer	3. Size of user
4. Degree of urbanization of the consumer	4. Geographical market segmentation.
5. Geographical market segmentation
6. Education attainment of the consumer
7. Religion of the consumer.

Philip Kotter h1s mentioned the following criteria for market segmentation:

1. Geographic Segment
2. Demographic Segment
3. Psychographic Segment
4. Benefit Segment
5. Marketing Segment
6. On the basis of Volume
7. Basis of Brand Loyalty

1. Geographic Segment: The first most popular criterion for segmenting the market may be the geographical segmentation of the whole operational area. The markets are divided on the basis of geographical factors such as area, climate, and the density of population. According to area states may be taken the basis for segmentation. Each state may be recognized as a separate market. The area may further be segmented in rural, town, and urban areas or where the market is international, the division may be a national or international market.

On the basis of climate, markets may be on hill and plain areas. For example, the North-Western cities of India may be important market segments for a manufacturer of woolen textile. Such type of segmentation is best where the customers are stretched over a vast area and the production is done on large scale. the producer may design his marketing strategies taking the characteristics of the individual markets into consideration.

2. Demographic Segment: On this basis, a seller does the segmentation by taking into consideration the age, income, sex, occupation, education, religion, size of family, nationality and the social class, etc, and thus, makes the separate groups. Demographic variables have been popularly made the basis for market segmentation for a long. It is, therefore, necessary to give them a wide description as under

1. Income: Income is a very important factor affecting the nature, attitudes, preferences, and behavior of consumers. Therefore, a market can be segmented on the basis of the income of consumers. Consumers can be divided into three parts on the basis of income

1. High-income group,
2. Middle-income group;
3. Low-income group.

The consumers of the high-income group stress the design, fashion, quality, and the feeling of social prestige. The consumers of the middle-income group stress the durability and utility of products, while the consumers of the low-income group stress the price and quality. Different models of television sets are examples of this type of segmentation.

2. AgeAge is one of the most important factors for segmenting the market. The producer should know for what age group his product would be most suited so that he can plan his pricing polity, advertisement policy, marketing policy, and strategy accordingly. For example, some breakfast products are aimed to suit the tastes of children while others are attractive to consumers within a broader range of ages. Similarly, the cloth market or garment market may be segmented on the basis of age as children, young, adults, and old.

3. Sex Markets may also be divided on the basis of sex, i.e., ladies and gents. Some products are exclusively produced for women while others are for men. For example, lipstick is meant for women and on the other hand, shaving cream is only for men. Because the attitudes, needs, mental and physical attributes, and motivational factors are different in men and women, advertisement strategy may differ for both types of products.

Personality, sense of family security, and social prestige are some of the factors which are given top priority in an advertisement for a product meant exclusively for men. On the other hand, beauty and purchasing ability are some factors for advertising a product meant for women.

4. Educational level The consumers can be divided on the basis of educational levels such as educated, semi-educated, and uneducated, and the marketing activities and strategies are worked out accordingly. For example, a book market may be segmented on the basis of primary, high school, degree, and professional course books.

5. Business or profession It is also an important factor on which market of a product can be divided. Businessmen, employed persons, and professionals are examples of such classification. Employed persons may further be sub-grouped as clerks, officers, teachers, and executives. Similarly, professionals may be sub-grouped as doctors, advocates, chartered accountants, etc.

6. Caste or religion India is a country having a number of varieties of communication, castes, sub-castes, and religions. The feelings, attitudes, and lifestyles of the consumers of different castes and religions are different. Therefore, a market can be segmented on the basis of caste or religion.

3. Psychographic Segment: The characteristics of psychographic buyers are also the basis for market segmentation. These characteristics are added to the personality of the buyers. Customers’ behavior regarding several products is found to be different. The reason for this difference is related to the customer’s personality. For example, some buyer wants to buy new products while some among them prefer second hand or cheap products. The lifestyle of people too influences the buying trends.

4. Benefit Segment: When consumers buy a particular product they have their expectations. Such expectations differ from product to product and from consumer to consumer. These benefits can be durability, economy, efficiency, prestige, etc. For example, a shampoo market may have 4 benefits-cleanliness, economy, protection (protein, enriched, and anti-dandruff), and cosmetic (long silky hair) benefits.

Each segment favors a certain brand. The company can study these features and decide to which segment they want to comply with and should know the characteristics of that segment and the major existing competitive brands. The company can also search for new benefits and launch a brand that delivers them. Benefits segmentation usually implies that a company should focus on satisfying one benefit group.

5. Marketing Segment: Elements of marketing can also be made a basis for market segmentation. They are of different kinds for example,

• buyers with price consciousness,
• buyers influenced by the quality and variety of the product.

A seller will have made different efforts of marketing for each type of market segment.

6. Volume: Market segmentation can be made on the basis of the quantum of the product proposed for buying, for example, customers buying bulk quantity, medium quantity, and Lesser quantity. Flour purchased by a customer for domestic needs and for hotel use may be from different segments.

7. Brand Loyalty can also be made a basis for the market segmentation. The sellers first try to introduce the characteristics of loyal buyers and then endeavor to make them the buyer. However, segmentation of the market is not always possible on the basis of mere brand loyalty.

Question 8.
Explain the various objectives of packaging?
Answer:
Objectives of Packaging:
1. Attraction: As far as possible, the package must possess attraction value, as attraction is the main objective of packaging, so that it may attract customers towards the products concerned.

2. Protection: The second objective of packaging is to provide safety to the product. In other words, the package must protect the contents of the product until it is consumed. The package keeps the product fresh and clean. It protects from adverse effects of weather, temperature, dampness, insects, contamination, breakage, evaporation, leakage, etc. It preserves the flavor and color of the product. It also prevents theft and pilferage.

3. Convenience: The consumers, as well as the middlemen, want packages that are easy to carry, use and dispose of. A good package facilitates easy transportation; storage, display, and usage. Pouch packing is very popular nowadays due to convenience.

4. Economy The next important objective of packaging is economy. Here economy means economic use of the product. The consumer can take out the only quantity to be used at a time and thus, wastage can be avoided.

5. Sales Promotion The objective of packaging is to promote the sale of the product. Whatever is written on the packing acts as an advertisement and sales promotion.

6. Other objectives of packaging are as under,

1. It improves the image of the product and thus increases the profit.
2. It maintains the utility of the package even after the product packed is consumed.
3. Owing to data of manufacturing and the expiry printed on the packing, the freshness or expiry of products can be identified.

Question 9.
Differentiate between Branding and Trade Marks.
Answer:
Difference between Brand and Trade Mark: Difference between brand and trademark can be made on the basis of the following points
1. Registration: Registration of a brand is not essential while registration for a trademark is essential. A brand is called a trademark only when it is registered.

2. Scope: The scope of a brand is limited while the scope of a trademark is very wide. Any business firm can use different brands for its different products while it uses only one trademark for all of them.

3. Legal protection: Brand can be copied by other competing concerns. No legal actions can be taken against them but if trademark denotes the manufacturer who got it registered. So trademark can be used with every brand. ‘

4. Nature: All brands are not trading marks but all trademarks are the brands. Thus, the word brand is more comprehensive than the trademark.

5. Use: Brand can be used by all that but the trademark can be used by the business firm that got it registered in the name of the firm.

In simple words, the main difference between brand and trademark is that brand is not registered, whereas trademark is always registered under Trade and Merchandise Mark Act, 1958.

Question 10.
Explain the term skimming the cream pricing strategy and low penetration pricing strategy and the reasons for adopting the two?
Answer:
Skimming the cream Pricing Strategy: It is also known as the “High Initial Price Strategy”. Under this strategy, the price of a new product is determined very high. Such prices continue to be high till the competitors begin to enter the market. As soon as competitors enter the market, the pioneer producer reduces the price of his product. This strategy is based on a plea that substantial expenses are incurred on research, advertising, and sales promotion activities and the competitors are also absent in the initial price is determined for a product.

By this strategy, the investment made for the development of the product may be quickly realized. The pricing strategy is useful in the case of innovating and specialty products. The manufacturers of computers, mobile phones, calculators, electronic watches, and electronic appliances used this strategy very successfully for pricing their products.

The main reasons for adopting the Skimming the cream strategy are as follows:

1. To recover the heavy amount of expenditure incurred by the firm on the research, development production, advertising, and sales promotion of the new product.
2. To get the highest possible return on capital invested till the competitors enter the market.
3. To get the advantage of a monopoly situation in the market.
4. To attract the consumers of the high-income group.
5. To try the market for the product at a high rate, because it is easy to reduce it than to raise it.
6. When the initial cost of production is very high.
7. Suitable for pricing luxury products, because it creates social status.
8. A high introductory price will produce greater rupee sales and profits than a low introductory price.

Low Penetration Pricing Strategy: Under this strategy, the price of a new product is determined low to speed up its sales and therefore widening the market base. Low price is used as a major tool for rapid penetration into the market to hold a position. This pricing strategy is adopted where there seem to be no distinctive classes of customers with different price, elasticity, and when advantages of mass production drastically reduce the costs, and when the product is not an innovative product but a simple product.

This strategy aims at capturing the market at the very outset. And if there is already a competing product, it aims at capturing the major share of the market. The best example ever seen of this strategy is the pricing of NIRMA washing powder. This strategy also discourages competitors from entering the market. Another feature of this strategy is that when the new product gains popularity or when its market is expanded, the price of the product is increased.

The main reasons for adopting a low penetration strategy are as follows

1. Less cost of research, development, and production.
2. To avoid the competition or to face the competition successfully.
3. To avoid government interference
4. To get the economics of large scale production by increasing the sales.
5. To attract the customers of low-income groups, which are large in number.
6. The demand for new products is highly elastic even in the introductory stage.
7. To expand the market.
8. To obtain large profit.

Comparison of Skimming the cream and low penetration Pricing strategies: Skimming the cream means high initial price and low penetration means low initial price. Now the question arises, which of the two strategies should be followed for price determination of a new product. To compare the two strategies or to answer this question we should consider a number of things.

For example, if excess expenses are made on new product development, advertising, and sales promotion, and there are no prospects for competition in near future, demand for the product is less elastic and the product is related to the consumer of the high-income group, then the marketer should follow, high initial price strategy. Contrary to it, if no many expenses are incurred on new product development, advertising, and sales promotion and there are high prospects for competition in near future, demand for a product is more elastic and the product is related to the consumers of the low-income group than the marketer should follow low initial price strategy.

For revolutionary new products that have large potential markets, penetration pricing is usually the most appropriate strategy. This is because the existence of a large potential market is almost certain to attract many larger competitors soon after the introduction of a new product. Penetration pricing helps to discourage prospective competitors contrary to it, if marketer expects that competitors will need considerable time and will meet great difficulties in coming up with their own version of the product, then, of course, price skimming is an appropriate strategy. Hence, the selection of the strategy depends upon the needs of the circumstances.

Question 11.
Give the objectives of Physical Distribution of consumers and Industrial Products?
Answer:
Objectives of Physical Distribution: Like any other marketing mix component, physical distribution has two broad objectives to attain.

1. Maximization of customer satisfaction
2. Minimization of costs

Physical distribution is concerned with getting the right product to the right place, at right time at the lowest cost. In other words, efficiency and satisfactory services are key goals of physical distribution. The Physical distribution function has the following objectives.
1. To provide better customer services: Customer services are the services provided to the consumers from the time of order placed by them till the products are delivered to them, it also includes after-sale services. In physical distribution customer service consists of providing the right product at the right time and at the right place. However, a high level of customer satisfaction can be attained through a distribution system.

2. To reduce cost: Cost reduction is an important objective of physical distribution. By intelligently managing the physical distribution system and determining the optimum number and locations of warehouses, transportation schedules and modes, material handling, increasing stock turnover, correcting inefficient procedures in order processing and moving offices, plants, retail outlets to low-cost locations, economics can be brought in various costs. By reducing the cost, the profit margin can be improved. This advantage can be shifted to the consumer by lowering the prices.

3. To increase sales: Another objective of physical distribution is to make available the products which have regular demand and also have contingency plans for quick order processing of items so that the product is not out of supply even in the stock or offseason. Moreover, firms can attract additional customers by offering better service or by charging lower prices, this will increase the sales volume of the firm.

4. To create utilities: The physical distribution function by warehousing and transportation creates time and place utility. Warehousing system is known for creating time utility by holding the products from the time of their production till their consumption. Whereas, transportation creates place utility making products more useful by bringing them to the places where they are needed. The main objective is the maximization of customer satisfaction and profits to the firm.

5. To establish a differential advantage over rivals: A firm can establish an advantage over its rivals by performing customer services more effectively, such as arranging rapid and reliable delivery, avoiding errors in order processing, and delivering undamaged products and satisfactory services.

6. To develop a communication system: To develop a communication system which permits the traveling salesmen to transmit orders on a regular basis, so that customer’s inquiries on the order status can be responded to within the shortest possible time and order may also be executed within time.

7. To attain price stability: By physical distribution, the objective of price stabilization can be achieved. With the help of transport and warehousing facilities, an adjustment can be made between the demand and supply of products, and thus, the price fluctuations can be prevented.

8. To increase reputation: With the help of efficient physical distribution management, a firm is able to increase its reputation among buyers and competitors. Buyers like those firms who are able to fulfill their orders as per specification and within the time limit with the help of physical distribution ‘no stock’ situation can be avoided and quality of goods produced can be improved. Better services are always welcomed by the customers.

Question 12.
Explain in brief the importance of promotion mix in marketing?
Answer:
Importance of Promotion in Marketing: Promotion plays an important role in stimulating demand and sales of the product. Its importance may be gathered from the following facts
1. In depression, the importance of promotional activities is greater because, at such a time, the main problem is that of sales of goods and services.

2. The activity of promotion has become important because of the widening of the market. With the physical distance between producers and consumers and also the increase in the number of prospective buyers, the promotion has gained importance. The producer is now to inform all prospective consumers to capture a major share of the market.

3. There are a number of channels of distribution. The producer should not only inform the consumers but he should also inform about the product to the middlemen because they have to present the goods to the middlemen next in the hierarchy and to the consumers. The middlemen should be well versed in the characteristics of the goods.

4. In modern times, there is cut-throat competition in every field. New and new products and producers are entering the market and every producer wants to sell his products first. In order to meet the competition, the producer is to make the customers/prospective customers of his products and their outstanding features along with a comparative view of the competitor’s products. This helps the consumers to select the right type of product.

5. Promotion expenses are the highest of all the marketing expenses. They should be properly and strictly controlled and should be paid due attention.

Question 13.
Explain the term personal selling and its important functions?
Answer:

1. “Personal selling consists of contacting prospective buyer of the product personally.” – Richard Buskirk
2. “Personal selling is an oral presentation in conversation with one or more prospective purchases for the purpose of making sales.” – American Marketing Association
3. “Personal selling consists of individual, personal communication, in contrast to mass relatively impersonal communication of advertising, sales promotion and other promotional tools.” – William J. Stanton
4. “Personal selling is basically a method of communication. It involves not only individual but social behavior each of the person, also in face contrast-salesman and prospect influences the other.” -Cundiff and Still

From the above definitions, we can conclude that personal selling is the art of convincing prospects to buy the given product and services. It is the ability to handle the people to demand the product. It is the science and art of understanding human desires and pointing the ways to their fulfillment. It is the ability to convert human needs into wants. The purpose of personal selling is not to ensure the present sales alone, but to win a regular customer.

Functions of Personal selling is an oral presentation in a face to face conversation with one or more prospective customers for the purpose of making sales. The main functions of personal selling are as follows: ‘
1. Making Sales The first and the foremost function of personal selling is to make sales both to old and new customers.

2. Keep Sales records Another important function of personal selling is to keep the complete record of the sale. This record is sent to the manufacturer.

3. Achieving Sales targets Another function of personal selling is to achieve the Sales targets by increasing the Sales Volumes.

4. Collection of Statistics The Salesman collects the data pertaining to the product, from the market on regular basis and sends it to the manufacturer.

5. Advertising new product The salesman sells in the market, the new products with his skills and expertise and create demand for the new product.

6. Demonstration of products Under personal selling the seller physically demonstrates the product, explains its working and features to the customer, and tries to persuade him to buy the product. The customer buys the product after being satisfied with the demonstration.

7. Increase in goodwill The Salesman provides several services apart from selling under personal selling. These services increase the popularity of the company and the Salesman both.

8. Executive function The experienced Salesman provides training to the new Salesman and assist the management in selling the problems relating to marketing.

9. Customer services The functions of personal selling also include, rendering customer services, such as: to introduce the products, explain the right use of the product, convince the customers about the quality of the product, remove doubts of the customers, etc.

10. Other services Under personal selling the Salesman not only perform the selling activities but other services like market research, complaints redressal, repairs, etc. are also performed by the Salesman.

11. Winning customer’s confidence Modem personal selling aims at educating the customer and providing a solution to his problems. The salesman also provides after-sale services. This helps in winning the confidence of the customers.

12. Persuasion of customers The customer is not to be pressurized but influenced favorably by the Salesman. A Salesman must have the ability to .convince the people to buy the product.

Question 14.
Give the importance of Sales promotion as a tool of enhancement in Sales?
Answer:
Importance of Sales Promotion: In recent years, the importance of Sales promotion has increased to a greater extent. The amount spent on Sales promotion now equals the amount spent on advertising. The Sales promotion increase is due to the changes in the marketing environment. The importance of sales promotion increase is due to the thinking of new ideas for creating a favorable condition of selling promoting sales and future expansion of sales. It is a part of marketing strategy. It is essential for the survival of a manufacturer.

More and more promotional activities are required to induce the consumers to purchase more and more products and thus they produce the demand.

In today’s competitive world, promotional activities play an important role which can be judged from the following facts:
1. Effective Sales support: Basically sales promotion policies supplement the. efforts of personal and impersonal sales-manship (advertising). It is found that good sales promotion materials make the salesman’s effort more productive. Activities reduce his time spent in prospecting and reduce the turndowns.

2. Faster product acceptance: Most of the sales promotion devices (such as contests, premium coupons, etc.) can be used faster than the other promotion methods such as advertisement.

3. Distance between producers and consumers: Due to prevalent market conditions mass selling is quite impossible without promotional activities. The distance between producers and consumers has so widened in present days that to get them acquainted with the product, promotional activities are necessary.

4. Selling in imperfect markets: Every market is an imperfect market. In imperfect market conditions, the product cannot be sold easily only on the basis of price differentiation. It is a promotional activity that provides information about the differences, characteristics, and multitudes of the products of various competitors in the market. The customer is attracted to purchase the goods on the basis of such information. Thus, promotional activities are necessary for selling products successfully.

5. Intense competition: The intense competition has necessitated the sales promotional activities. When one manufacturer increases its promotion spending and adopts an aggressive strategy in creating a brand image, others are also forced to follow the suit. This leads virtually to a ‘promotion-war’. It actually leads to a price reduction of standard goods.

6. Increased trade pressures: The growth of large-scale retailers such as supermarkets, chain stores, etc. have brought greater pressure on manufacturers for support and allowance. So, in order to aid the retailer and also to ensure their share of shelf space, many manufacturers have taken to sales promotion activities.

7. Increased standard of living and employment opportunities large scale production is the theme of the day. Sales promotion is always the result of large scale production. But this could be achieved only with appropriate methods of large scale selling. Large scale selling is possible only with the help of promotional activities.

In this way, promotional activities increase the standard of living by providing better goods at a lower rate (due to large scale production and selling). As the promotional activities cannot be performed without the help of an effective sales force and specialists in the field, employment opportunities are open for a large number of people.

8. Traffic-building: Traffic-building implies encouraging more inflows of new buyers and repurchasers. Traffic-building objective is attained by offering incentives to the buyers like special sales, retailer coupons, and premiums, weekly special, etc.

Marketing Important Extra Questions Long Answer Type

Question 1.
What is Packaging? Explain the importance and functions of packaging?
Answer:
Packaging: One of the most important developments affecting the business world in recent years has been in the area of packaging. Many products, which we thought could never lend themselves to packing because of their nature, have been successfully packed e.g. pulses, ghee, milk, salt, cold drinks, etc. Packaging refers to the act of designing and producing the container or wrapper of a product, packaging plays a very important role in the marketing success or failure of many products, particularly the consumer non-durable products.

In fact, if one makes an analysis of the reasons for the success of some of the successful products in the recent past, it can be noted the packaging has played its due role. For example, it was one of the important factors is the success of products like Maggie Noodles, Uncle Chips, or Crax Wafers.

Importance of Packaging: Packaging has acquired great significance in the marketing of goods and services, because for the following reasons
1. Rising standards of Health and Sanitation: Because of the increasing standards of living in the country, more and more people have started purchasing packed goods as the chances of adulteration as such goods are minimized.

2. Self-Service Outlets: The self-service retail outlets are becoming very popular, particularly in major cities and towns. Because of this, some of the traditional roles assigned to personal selling in respect be promotion have gone to packaging.

3. Innovational Opportunity: Some of the recent development in the area of packaging have completely changed the marketing scene in the country. For example, milk can now be stored for 4-5 days without refrigeration in the recently developed packing materials. Similarly, in the area of pharmaceuticals, soft drinks, etc, lots of new innovations have come in respect of packaging. As a result, the scope for the marketing of such products has increased.

4. Product Differentiation: Packaging is one of the very important means of creating product differentiation. The color, size, materials, etc. of the package makes a real difference in the perception of customers about the quality of the product. For example, by looking at the package of a product say paint or hair oil one can make some guess about the quality of the product contained in it.

Functions of Packaging:
As stated above, packaging performs a no. of functions in the marketing of goods. Some of the important functions are as follows
1. Product Identification: Packaging greatly helps in the identification of the products. For example, Colgate in red color, or Ponds Cream jar can be easily identified by its package.

2. Product Protection: Packaging protects the contents of a product from spoilage, breakage, leakage, pilferage, damage, climatic effect, etc. This kind of protection is required during storing, distribution, and transportation of the product.

3. Facilitating the use of the Product: The size and shape of the package should be such that it should be convenient to open, handle and use for the consumers. Cosmetics, medicines, and tubes of toothpaste are good examples of this.

4. Product Promotion: Packaging is also used for promotion purposes. A startling color scheme, photograph, or typeface may be used to attract the attention of the people at the point of purchase. Sometimes it may work even better than advertising. In self-service stores, this role of packaging becomes all the more important.

Question 2.
What is the pricing of a product? Explain the important factors affecting the pricing of a product?
Answer:
Pricing: When a product is bought, some money is paid for it. This money represents the sum of values that consumers exchange for the benefit of having or using the product and is referred to as the price of the product. Similarly, money paid for the services such as fare for the transport service, premium for an insurance policy, and fee to a doctor for his medical advice represent the price of these services. Price may therefore be defined as the amount of money paid by a buyer (or received by a seller) in consideration of the purchase of a product or a service.

Factors affecting Price Determination: There is a number of factors that affect the fixation of the price of a product. Some of the important factors in this regard are discussed below:
1. Product Cost: One of the most important factors affecting the price of a product or service is cost. This includes the cost of producing, distributing, and selling the product. The cost sets the minimum level or the floor price at which the product may be sold. Generally, all marketing firms strive to cover all their costs, at least in the long run. In addition, they aim at earning a margin of profit over and above the costs.

In certain, circumstances, for example, at the time of introducing a new product or while, entering a new market, the product may be sold at a price, which does not cover all the costs. But in the long run, a firm cannot survive unless at least all its costs are covered.

There, are broadly three types of costs: viz fixed costs, variable costs, and semi-variable costs. Fixed costs are those costs, which do not vary with the level of activity of a firm says the volume of production. or sale. For example, the rent of a building or the salary of a sales manager remains the same whether 1000 units or 10 units are produced in a week.

Those costs which vary in direct proportion with the level of activity are called variable costs, for example, the cost of raw materials, labor, and power is directly related to the quantity of I goods produced. Let us say if the cost of wood for manufacturing one chair comes to Rs. 100/- the cost of wood, for 10 chairs would be Rs 1000/- obviously, there will be no cost of wood if no chair is produced.

Semi variable costs are those costs that vary with the level of activity but not in direct proportion with it change in the volume of sale.

Total costs are the sum total of the fixed variable and semi-variable costs for the specific level of activity say the volume of sales or quantity produced.

2. The Utility and Demand: While the product costs set the lower limits of the price, the utility provided by the product and the intensity of demand of the buyers sets the upper limit of price, which a buyer would be prepared to pay. In fact, the price must reflect the interest of both the parties to the transaction the buyers and the seller. The buyers may be ready to pay up to the point where the utility from the product is at least equal to the sacrifice made in terms of the price paid. The seller would, however, try to at least cover the costs. According to the law of demand, consumers usually purchase more units at a low price than at a high price.

The price of a product is affected by the elasticity of demand of the product. The demand is said to be elastic if a relatively small change in price results in large changes in the quantity demanded. Here numerically the price elasticity is greater than one. In the case of inelastic demand, the total revenue increases when the price is increased and goes down when the price is reduced. If the demand for a product is inelastic, the firm is in a better position to-fix higher prices.

3. Extend of Competition in the market: Between the lower limit and the upper limit where would the price settle down. This is affected by nature and the degree of competition. The price will tend to reach the upper limit in case there is a lesser degree of competition while under conditions of free competitors the price will tend to be set at the lowest level.

Competitor’s prices and their anticipated reactions must be considered before fixing the price of a product. Not only the price but the quality and the features of the competitive products must be examined carefully, before fixing the price.

4. Government and Legal Regulations: In order to protect the interest of the public against unfair practices in the field of price-fixing, the government can intervene and regulate the price of commodities. The government can declare a product as an essential product and regulate its prices. For example, the cost of a drug manufactured by a company having a monopoly in the production of the same was Rs. 20/- per strip of ten and the buyer is prepared to pay any amount for it say Rs. 200/-.

In the absence of any competitor, the seller may be tempted to export the maximum amt. of Rs. 200/- for the drug and intervene to regulate the price. Usually, in such a case, the govt does not allow the first to charge such a high price and intervene to regulate the price of the drug. This can be done by the govt, by declaring the drug as an essential commodity and regulating its prices.

5. Pricing objectives: Pricing objectives are another imp. factor affecting the fixation of the price of a product or a service. Generally, the objective is stated to be to maximize the profits. But there is a difference in maximizing profits in the short run and in the long run. If the firm decides to maximize profits in the short run, it would tend to charge maximum price and its products. But if it is to maximize its total profit in the long run, it would opt for a lower per-unit price so that it can capture a larger share of the market and earn greater profits through increased sales.

Apart from profit maximization, the pricing objectives of a firm may include:
(a) Obtaining market share leadership: If a firm objective is to obtain a larger share of the market, it will keep the price of its products at lower levels so that a greater no. of people are attracted to purchase the products.

(b) Surviving in a competitive market: If a firm is facing difficulties in surviving in the market? because of intense competition or the introduction of a more efficient substitute by a competitor, it may resort to discounting its products or running a promotion campaign to liquidate its shock, and

(c) Attaining product quantity leadership: In this case, normally higher prices are charged to cover high quality and high cost of Research and Development.

Thus, the price of firm products and services is affected by the pricing objective of the firm.

6. Marketing Method Used: The price fixation process is also affected by other elements of marketing such as distribution system quality of salesman employed, quality and amount of advertising, sales promotion efforts the type of packaging product differentiation, credit facility, and customer service provided. For example, if a company provides free home delivery, it has some flexibility in fixing prices. Similarly, the uniqueness of any of the elements mentioned above gives the company competitive freedom in fixing the prices of its products.

Question 3.
Mention the important features or characteristics of personal selling?
Answer:
Characteristics of Personal selling: Following are some imp. characteristics of personal selling

1. Personal selling is a method of sales communication.
2. Personal selling includes commercial and social behavior.
3. Personal selling includes both selling functions and non-selling functions.
4. It involves the persuasion of customers.
5. It involves winning buyers’ confidence.
6. It aims at providing information and services to buyers.
7. It is a two-way process and benefits both buyers and sellers.
8. It helps in solving the problems of the buyers and satisfying their needs.
9. Personal selling is an educative process. It tells consumers the way in which they can satisfy their needs.
10. Personal selling is more flexible and adaptable. Because of face communication, the salesman adjusts himself and his sales talks according to the need, desires, and behavior of the consumers.

Role of Personal Selling: Personal selling plays a very important role in the marketing of goods and services. The importance of personal selling to businessman, customers, and society may be described as below:

Importance to Businessmen: Personal selling is a powerful tool for creating demand for a firm’s products and increasing their sales. The importance of personal selling to a business organization may be described as follows
1. Effective Promotional tool: Personal selling is a very effective promotional tool that helps in influencing the prospects about the merits of a product and thereby increasing its sales.

2. Flexible tool: Personal selling is more flexible than other tools of promotion such as advertising and sales promotion. It helps business persons in adopting their offer in varying purchase situations.

3. Minimise wastage of efforts: Compared with other tools of promotion, the possibility of wastage. of efforts in personal, selling is minimum. This helps the business, persons in bringing economy in their efforts.

4. Consumer attention: There is an opportunity to detect the loss of consumer attention and interest in a personal selling situation. This helps a business person, in successfully completing the? sale.

5. Lasting relationship: Personal selling helps to develop a lasting relationship between the salespersons it the customers, which is very important for achieving the objectives of a business.

6. Personal rapport: The development of personal rapport with customers increases the ‘ competitive strength of a business organization.

7. Role in the introduction stage: Personal selling plays a very important role in the introduction stage ( of a new product as it helps in persuading customers about the merits of the product.

8. Link with customers: Salespeople play their different roles, namely persuasive role, service role, and informative role, and thereby link a business firm to its customer’s importance to Customers

This role of personal selling becomes more imp. for the illiterates and rural customers who do not have many other means of getting product information.

The customers are benefited from personal selling in the following ways

1. Help in identifying needs: Personal selling helps the customers in identifying their needs and wants and in knowing how these can best be satisfied.
2. Latest market information: Customers get the latest market information regarding price changes product availability and shortage and new product introduction which helps them in taking the purchase decisions in a better way.
3. Expert advice: Customers get expert advice and guidance in purchasing various goods and services which help them in making a better purchase.
4. induces Customers: Personal selling induces customers to purchase new products that satisfy their needs in a better way and thereby helps to improve their standards of living.

Importance of society: Personal selling plays a very productive role in the economic progress of a society. The more specific benefits of personal selling to society are as follows
1. Converts latent demand: Personal selling converts latent demand into effective demand. It is through this cycle that the economic activity in the society is fostered, leading to more jobs, more incomes, and more products and services. That is how economic growth is influenced by personal selling.

2. Employment opportunities: Personal selling offers greater income and employment opportunities to unemployed youth.

3. Career opportunities: Personal selling provides an attractive career with greater opportunities for advancement and job satisfaction as well as security, respect, variety, interest, and independence to young men and women.

4. Mobility of Salespeople: There is a greater degree of mobility in salespeople, which promote travels and tourism in the country.

5. Product standardization: Personal selling increases product standardization and uniformity in consumption patterns in a diverse society.

Question 4.
“Money spent on advertising is an investment not waste.” Explain the statement by giving the merits/advantages of advertising?
Answer:
Money spent on advertising is an investment
or
Imp. and Advantages of Advertising

It is an era of advertising. No business or industrial enterprise can survive without advertising in the modern business world, because in every business and industrial activity there is cut-throat competition.

To face and win this competition successfully, it becomes imperative for every enterprise that it advertises what it has and what it wants to sell to the consumers. Advertising is useful not only for the business and industrial enterprise but for the whole community as a whole.

Advertising broader the knowledge of the consumers. With the aid of advertising, consumers find and buy necessary products without much waste of time. This speeds up the sales of commodities, increases the efficiency of labor in distribution, and diminishes the cost of selling. It is an accepted fact that without the market stimulus of heavy advertising, consumers might have waited another sixty years for the product evaluation that took place in less than ten years-it took after all over sixty years from the Invention of the Safety razors before the first acceptable stainless steel blades appeared in the market. These words are more than enough to justify the potentialities of advertising in’ the field of the modem marketing system.

Importance and Advantages of Advertisement:

Advantages        to Producers	Advantages to Middleman	Advantages to Consumers	Advantages to Society
1. Increase in Sale	1. Helpful in Selling	1. Increase Knowledge	1. Rapid economic development
2. Lower Costs	2. Helpful in searching middleman	2. Easy purchase	2. Increase in standard-of-living.
3. Reduction in production selling expenses	3. Helpful in                facing                competition	3. Information regarding avail of goals.	3.Increase in employment
4. Reduced distribution expenses	4. Earning sources	4. Cheap quality goods	4. Increase in knowledge
5. Increase in demand	5. Increase in goodwill	5. Increase in standard of living	5. Quality product
6. Creation of goodwill			6. Development of civilization
7. Steady demand			7. Helpful in foreign trade
8. Prepare the ground for the new product			8. Helpful in the development of the newspaper
9. To receive efficient workers			9. Reduction in costs
10. To increase profit			10. Others

Advantages to Producers:
1. Increase in Sales: By creating the demand for new products, increasing the demand
for existing products, and maintaining the demand for products in all seasons and at all times, advertising helps in increasing the sales of an enterprise.

2. Lower cost: Production cost and marketing cost both can be reduced by manufacturing the product on large scale .because the demand rises through advertising and supply can only be given by manufacturing them on a large scale.

3. Reduction in Production and selling expenses: Selling cost per unit is reduced due to increased sale volume, consequently production cost and overheads are also reduced due to mass production and sale.

4. Reduction in Distribution expenses: Due to large scale selling distribution cost is also reduced.

5. Increase in Demand: Advertising helps in increasing the demand for existing products because it reminds the consumers of a product again and again.

6. Creation of Goodwill: Advertising helps in the creation of goodwill. It increases the sales and increases in sales mean the increase in no. of customers which is apparently the result of the increase in goodwill of the concern.

7. Steady Demand: Advertising helps in stabilizing the demand for a product in all the seasons and all the time. It is only because of advertising that people like to consume eggs, tea, coffee, etc in summer also.

8. Preparation of the ground for New Products: Whenever a producer produces, a new product advertising helps him in creating demand for his product because it is the advertising through which a producer explains the merits of his products to the consumers. It is also the advertisement through which a producer proves the superiority of his products in comparison to the similar products of competitors.

9. To employ efficient workers: As the demand for products is increased through advertising, the employer working with the firm is motivated. This helps in the recruitments of efficient workers.

10. Increase in Profits: Increase in sales results in increased profits also, and thus the enterprise achieves the object of maximizing profits.

Advantages to Middleman:

1. Helpful in selling: Easy sale of the products is possible since consumers are aware of the product and its quality through advertisements.
2. Helpful in searching middleman: Able middleman can be appointed through the advertisements.
3. Helpful in facing competition: Advertising helps the middleman in facing competition successfully. It introduces the products into the market and creates the demand for the products.
4. Earning sources: Advertising stabilizes demand. Customers are thereby available throughout the year which ensures permanent income to the middleman.
5. Increase in goodwill: The reputation created is shared by middlemen also because they need not spend anything on the advertising of already a well-advertised product.

The advantage to consumers:

1. Increase in knowledges: Advertising helps the customers to know about the existence of various products and their prices. They can choose from the various brands to satisfy their wants. Thus, they cannot be exploited by the sellers. Advertising educates people about new products and diverse – uses.
2. Easy purchase: Advertising makes it very convenient for the consumers to make their purchases because they take the decision well in advance about the commodity to purchase.
3. Cheap and quality goods: The goods advertised are cheap and of standard quality. Advertising induces the manufacture to improves quality because otherwise, the customers will switch to competitor’s products.
4. Increase in standard of living: Advertising stimulates the consumption of varied and new products. More the consumption more will be the standard of living of the consumers. Advertising induces the manufactures he improves the quality of their products through research and development. This ensures a supply of products of better quality to the consumers.

Advantages to Society and Nation:
1. Rapid Economic development: Due to advertising sales of products increase in the market, it helps in increasing the scale of production. Large scale production brings industrial progress and prosperity. Advertising also encourages art and design in the country. Due to advertising employment opportunities, research and development also help in the rapid economic development of a country.

2. Increase in standard of living: Advertising promotes the standard of living of the people by increasing the variety and quality in consumption as a result of sustained research and development activities by the manufactures.

3. Increase in employment opportunities: Advertising provides employment to persons engaged in writing, designing, and issuing advertisements. Increased employment brings additional income to the people, which stimulates more demand. Employment is further generated to meet the increased demand.

4. Increase in knowledge: Advertising is very educative. It provides complete information about, the products of their uses to the society. In the words of the late President Roosevelt of the U.S.A. “Advertising brings to the greatest no. of people-actual knowledge consuming useful things.” It is essentially a form of education and the progress of civilization depends on education.

5. Good quality products: Confidence of the public towards the product gets stability through advertisement. This is the reason, the manufacturer is not inclined to end such confidence of the public and enters only goods quality of products or the market. It increases productivity.

6. Development of Civilisation: In the Age of globalization advertising plays a vital role in foreign trade. Exports and imports are possible only due to advertising.

7. Helpful in the development of newspaper: Advertising provides an imp. source of revenue to the publishers of newspapers and magazines. It enables them to increase the circulation of their publication by selling them at lower rates. People are also benefitted because they get publications at cheaper rates.

8. Reduced cost: As already stated cost of production is reduced due to large-scale production. Society also benefits from sour rates of products.

From the above discussion, it is clear that there are a number of advantages of advertising. It is beneficial to all the concerned – Producers, middlemen, customers, and consumers. In this time of throat competition, it is not enough to produce quality products at low costs, it is also necessary that it should be made known to the customer for whose it is produced.

Question 5.
Explain in detail the various pricing policies of a product?
Answer:
Pricing Policies Policies are guidelines for achieving the objectives. Therefore, different policies are framed and adopted for achieving the different objectives. Thus price policy is framed and adopted ‘policies provide the framework and consistency needed by the company to make reasonable, practicable, and effective pricing decisions. It helps the company to attain its pricing objectives.

Any good pricing policy must be aimed at offering a reasonable price to the consumer, ensuring a fair return on investment, and provide, price stability. While adopting the price policy trade traditions, customer preferences, their buying motives, purchase frequency, level of competition, nature of the product, amount of discount and allowances to be given, etc. must be considered.-There are a number of pricing Policies, a brief explanation of them is as follows:

A. On the basis of Cost and Demand. There are two price policies

1. Cost-oriented pricing policy: This policy assures that no product is sold at a loss since the I price covers the full, coat incurred. Pricing under this policy is based on simple arithmetic i.e.; adding a fixed percentage to the Unit Cost.
2. Demand-oriented pricing policy: Under the policy of a product is based upon its demand in the market. For instance, a high price is charged when and where the demand is high and a low price is charged when and where the demand is low. This policy is more suited to small business units and mostly in the case of non-standardized products.

B. On the basis of Price-Level.There are three price policies:
Meeting Competition Policy: If the price is the main basis of competition, then companies adopt this policy and adjust their prices 1 according to that of competitions. If the competitors change their price, the company will do the same. Such a policy is adopted in the case of highly competitive goods. One important feature of the policy is that it may not have any relationship to its cost and demand of the

Under the Market policy: It is a policy in which a company keeps its prices less than those prevailing in the market. Under the market, the policy is adopted when a company wants to enter the market on wants to expand it. Sometimes, a company has low costs because TtSsProducts is of lower quality and therefore, the price of products is usually kept low than those of competitors. At other times, lower prices may be substituted for promotional efforts used by its competitors.

Above the Market policy: Under this policy, the company ‘ eeps? its prices more than those prevailing in the market. This policy is adopted by companies who either enjoy a good reputation in the market or offer a unique product.
The customers get attracted to the company because of its high prestige. Such a company spends highly on advertising. Sometimes, manufacturers keep more than above price to give some more margin to profit to a middleman in return for their aggressive marketing efforts.

C. On the basis of Flexibility.
There are two pricing policies
1. One price Policy: Under this policy, one price is charged from all types of customers irrespective of volume or conditions of purchase. Price is fixed in this policy. It is a fair trade practice. Such a policy helps in clearly estimating the sales and profits. This policy helps in bargaining as such saves time and selling expenses. These companies, who follow this policy lays emphasis on the product’s quality and customs service.

2. Flexible pricing policy: Under this policy, different buyers are charged different prices for the same product. The difference in price depends upon the bargaining power of buyer and seller, place on delivery market conditions, and many other such factors. It is generally adopted in the case of sub-standard products. This policy makes the seller free to adjust the price according to the prevailing market circumstances. In certain cases, the product may be prepared on the basis of specification or design given by the buyer. In such a case, the price has to be negotiated and then fixed.

D. On the basis of Geographical Conditions.
There are six pricing policies
1. Uniform delivery pricing policy is also known as’F.O.R.’ (Free on the rail) or ‘Destination price’ or ‘Postage stamp’ pricing policy. Under this same price is charged from all the buyers irrespective of their location. In other words, the buyers do not bear directly the freight and other charges because the price includes such charges. They actually add in full or average of total freight charges for all the nation to the price quoted. Such a pricing system is used where transport costs are a major change on the seller’s total cost structure as a case of medicines.

2. Production point pricing policy It is that type of pricing policy in which the firm quotes ‘Ex-factory’ or Free on rail’ price. It does not bear the transportation cost, in the case of ex-factory price, the buyer bears all the transportation costs both freight and cartage from the factory point, whereas in the case of F.O.R. price, the firm bears the freight charges up to the railway station as the transport agency.

After that, the buyer has to meet, freight and cartage. It is also called as ‘Free on, Board’ (F.O.B) pricing policy. In simple words, under this policy, the price of the product includes only the price of the product. All the expenses of transportation from the price of the product. All the expenses of transportation from the place of the seller to the place of buyers are paid by the buyer himself.

3. Zonal delivery pricing policy Under this policy, the company divides the country into different zones and quotes uniform prices for each zone. The prices are uniform within a zone. But these prices differ from zone to zone, because of differences in transportation costs, local taxes, etc. The company adds average transportation cost to the basic price to arrive at the zonal price. Such a price benefits the buyer living at a distant place within a zone.

4. Basepoint pricing policy: It implies partial absorption of the transport cost by the company. One or more geographical locations are selected as base points from which the transport costs are, calculated. The buyers pay the er-factory price plus freight calculated from. the nearest base point. This price policy is normally the collective decision of all the firms.

5. Freight absorption pricing policy: To penetrate distant marked a seller may be willing to absorb part of the freight cost. Thus, under the freight absorption policy, the price of a product includes its actual price and a part of transportation cost. Therefore, the total expenses to be incurred on transportation of goods are divided into \ two parts – a part of these expenses is paid by the seller and the remaining part is paid by the buyer. A freight absorption strategy is adopted to offset the competitive disadvantages of F.O.B. or er-factory pricing.

6. Home delivery pricing policy This policy is gaining popularity in cities. Under this policy, dealers quote the price of a product and delivered the goods at the door-step of the customer. Dealers of television, fridge, air-condition, washing machines, steel furniture, and Haryana merchants usually adopt a home delivery pricing policy.

E. On the basis of Speciality:
On the basis of the specialty of the product, market conditions, trade -conditions, different sellers use the following pricing policies:
1. Skimming pricing policy: It involves setting a very high, price for a new product initially and to reduced the price gradually as competitors enter the market. The initial high price serves to skim the cream of the market. This is a policy of recovering the product^ generally adopted in the case of an innovative product.

2. Penetration pricing policy: This policy aims at capturing the market as soon as possible, therefore, the prices are kept at a low level. It helps in the initial stage or till the product is accepted by the majority of the population.

3. Price lining policy: Under this policy, various products are v priced according to their quality standards. The products may be classified as good, better and best – Different prices are charged for different qualities. The price lining has attraction both for the consumers and the retailers. The consumer’s buying decisions are simplified since the no. of prices from which he must make a selection is limited. The retailers also find this policy attractive because it helps them to plan their buying decisions.

4. Full-line pricing policy: When a manufacturer produces a product in different sizes or models and is unable to calculate the fixed expenses incurred on each type of product separately, he priced his product according to sizes or their demand.

5. Unit pricing policy: Under this policy price of the package and price per unit are mentioned on the package. For example, a toothpaste of 100 grams bears the price of a 100 grams package and also the price of 1 gm. This policy facilitates the consumers to make their buying decision and there is no scope of any bargaining.

6. Bait pricing policy to kinds of products are manufactured under this policy i.e. low price products. The marketer attracts the consumer by showing low price products. Thus, low prices act as bait for attracting customers.

7. Psychological Pricing policy: Under this policy prices are forced in such a manner that they have some psychological effect on buyers. Certain consumers have a feeling that high period products are indicated of high quality. As such, they demand high priced products. For example, diamonds, electronic products, cosmetics, etc. The pricing of products according to their quality standards as superior, fine, or economical also puts psychological pressure on consumers.

8. Old Pricing policy: It is another form of psychological pricing policy. Under this policy price is ending in an odd no. or a price just under a round number i.e. setting the price at an off amount such as Rs. 199.95 instead of Rs. 200 or Rs.5.990 instead of 6,000. The rationale for this policy is that consumers perceive off prices as a better buy. Even extensive products appear less expensive when the period in this way. This policy gives the feeling that the company is true to the last paisa, and results in an increase in sales.

9. Customary pricing: The policy is one that is based on the customs prevailing in the market. The prices are fixed to suit local conditions. Such products are typically standard ones. The price of sweets, soft drinks, bread, and other eatables are based on customary pricing policy.

10. Prestige pricing policy: Generally, the prestige pricing policy is adopted in the case of luxury products where the salesman is successful in creating a prestige of his product in the consumer’s mind. In this case, prices so fixed are generally higher than the prevailing market price. Sometimes, to show that our product is a quality product, market fix higher price for his product in comparison to competitors. Because customers judge the quality of a product by its price. If the price is high, they assume that quality is good. This policy is only useful when actually the quality of the product is genuine and high.

11. Captive pricing policy: In a captive pricing policy, the basic product is priced low, often below cost, but the high markup on supplies required to operate the basic product compensates for that low price. The loss on the basic product is recovered in profits from the sale of the required supplies. This policy is adopted by the newspaper. A newspaper costs, more to produce and distribute than the price charged from the subscribers, but increased circulation encouraged by the low price leads to more advertising revenue and greater overall profit.

12. Loss leader pricing policy Under this policy, few popular products are temporarily offered at low prices with a
view to attracting customers. Such products are termed as loss leaders.

13. Leader pricing policy The business firm who wants to present itself pioneer in the industry take the initiative in fixing the price and other firms follow it. This is generally adopted in oligopolistic market conditions where there are few sellers and these products are identical.

14. Monopoly pricing policy: Monopoly pricing policy is adopted when one company has single-handed control over the entire supply, there are a large number of buyers blit only one seller. The product is unique with no close substitutes. The competition is totally is absent and the seller has a free hand in fixing the price. Monopoly prices are generally considered as high prices.

15. Discriminating pricing policy: Under this policy, the marketer sells the same product at different prices to different buyers. This discrimination may be on basis of the use of product type of customer, the difference in a geographical area, etc.

16. Dual pricing policy Under dual pricing policy, a producer is required to sell a part of his production, under compulsion, to the govt, or its authorized agency at a substantially low price.

17. Administrated pricing policy Prices fixed by the govt, of goods sold through fair price shops are administered prices. This policy favors the welfare of low-income group people.

18. Sealed bid pricing policy Big firms or the govt, calls for competitive bids when they want to purchase certain products or specialized terms. The lowest bidder gets the work.

19. Break-even pricing policy The level of output of which the total revenue will be equal to the total cost is known as the break-even point. Sales over this point will yield profit. The sale must be above the break-even point quantity.

20. Promotion pricing policy This policy is based on its sales promotion method. For instance, take the case of ‘Grand Reduction Sale’ which is intended to revive the memory of the customs who might have stopped buying the products they used to buy in past. In this case, the seller tries to get rid of old and outdated stock.

Question 6.
Explain the various methods of determining the price of a product?
Answer:
Methods of Determining Prices There are many methods for the determination of the price of products. For the convenience of study, these methods can be divided into two parts:

1. Methods of determining the price on the basis of cost.
2. Methods of determining the price on the basis of market conditions.

1. Methods of determining the price on the basis of cost: The cost of production of a product is the most important variable and most, an important determinant of its price. There may be many types of costs such as Fixed cost, the variable cost, total cost, avg. cost, and marginal cost, etc.

An analytical study of these costs must be made for t determining the price of a product. Methods of determining the price on the basis of cost are as under
1. Cost-plus pricing method This is the simplest and easiest method of price determination. Under this system of pricing the average, I total cost of each unit of production is calculated, and to it is added the desired margin of profit, and selling is done at this ultimate price.

Cost-plus, pricing involves making a cost estimate and adding a margin to cover making expenses and profit. For example, a manufacturer may set the price for a new product by estimating the producer’s per unit total costs and then adding a certain percentage to provide a gross margin (i.e. expenses of net profit).,

Thus, under this method, the price per unit of product is calculated by adding desired profit to the total cost per unit. Under this policy, the price per unit can be calculated as under:

The amount of desired profit varies from enterprise to enterprise, product to product, and time to time. Some business enterprises determine a certain percentage of profit and calculate the price per unit of their product by adding this much percentage of profit to the cost of production, such as

Price per unit = Total Cost + 10% Profit.

This method assumes that no product is sold at a loss. This method is used when there is no competition in the market or when the cost of production of a product of all the manufacturers is almost equal. This method is used by retail traders also. This method of pricing is based on simple arithmetic of adding a fixed percentage of profit to the unit cost. Thus, the retail price of a product can be the cost of the manufacturer plus the margin of profit of the wholesaler plus s the margin of profit to the retailer. Therefore, this method is also known as “The sum of margin method”.

2. Marginal or Incremental Cost pricing Method Linder this method, price is so set that it covers only the marginal costs and not the total costs. When a new product is introduced, such a method is usually adopted. By this method, labor may be kept employed even during slack seasons. However, this method cannot be followed for long as the fixed cost has also to be taken into consideration. If certain products are period on this basis and others on a cost-plus basis, then some customers would be required to pay higher, prices while others would get the product at the cost of the last unit.

3. Break-Even Analysis: Break-even points is the volume of sales at which the total sales revenue of the product is equal to its total cost. In other words, it can also be said that the break-even point is the volume of sales at which there is no profit and no loss. Therefore, this method is also known as the’ profit No loss Pricing Method’.
Under this method, break-even price (B.E.P.) can be calculated as under

4. Rate of Return of Target pricing method: Under this method, first of all, an arbitrary desired rate of profit on the capital employed/invested is determined by the enterprise. The total desired profit is then calculated on the basis of this rate of return. The total desired profit is then added to the total cost of production and thus, the price per unit of the product is determined. In short, this method is good only when there is no competition in the market. The rate of investment is decided arbitrarily.

2. Methods of determining the price on the basis of market conditions: The price of a product must be determined keeping in view the conditions prevailing in the market. If market conditions are not duly considered before determining the price of products, the marketing objectives of the enterprise can’t be achieved.

Following are the methods of price determination based on market conditions:
1. Pricing to meet Competitions: Under this method, the price of a product is determined on the basis of the price of a competitor’s products. This method is used when the firm is new in the market. ; This method is used when there is tough competition in the market.

The method is based on assumption that a new product will create: demand only when its price is competitive. In such a case, the film follows the market trader.

2. Price below Competitive level: Under this method, the pricing firm determines the price of its. products below the competitive level i.e. below the price of the same products of the competitors. This policy pays where customers are price conscious and the method is used by new firms entering the market.

3. Pricing above Competitive level: Under his policy, the seller may set higher than avg. prices for his product to convey an impression that his products are above avg. equality. The buyer may pay this price in the belief that it is of higher quality.

Manufacturers sometimes keep more than average price to give some margin of profit to a middleman in return for the latter’s aggressive sales promotion. For a consumer product to compete successfully at a price above the market, it must either be so strongly differentiated that consumers believe it is superior to a competitive brand, or middleman must enthusiastically and heavily promote.

4. Purchasing power pricing method: Some commercial undertakings determine the product price by keeping in mind the purchasing power of their consumers. This method is generally used for the determination of the price for fashionable products.

Question 7.
Explain the various methods/Tools of Sales Promotion?
Answer:
Types, Methods/Tools of Sales Promotion: For a marketer resorting to sales promotion, a variety of tools and techniques are available. Sales promotion letters, catalogs, point of purchase displays, customer service programs, demonstrations, free samples discounts, contests, sweepstakes, premiums, and coupons are the Commonly employed methods of sales promotion.

Sales promotion can be divided into the following kinds:

1. Consumer/Customer Promotion Methods.
2. Dealer Sales Promotion
3. SalesForce.

1. Consumer/Customer Promotion Methods: Consumer promotion methods of sales promotion are the methods that directly encourage consumers to buy the product in more and more quantity. These methods may be as follows

1. Distribution of free samples: Under this method, the producer distributes free samples of the product to the consumer. They are also given to introduce a new product and expand the market. It increases the sales volume when the product is a new one to the customers. It is an effective device in which the product is purchased often, i.e. soaps, detergents, tea or coffee, etc. It is a method of demand creation, sampling gives a chance to the consumers to compare the products with other substitutes. Samples are given to doctors by medical representatives.

The samples may be delivered door to door, sent by mail, picked up in a store, attached to another product, etc. It is the most effective way to introduce a new product.

However, sampling is not always a good marketing strategy. It is not justified in the case of
(a) Well established product.
(b) a product that is not the superior in-store way to competing products or whose points of superiority would not easily be recognized by the consumers.
(c) a product with a slow turnover.
(d) a product with a narrow margin of profit.
(e) a highly fragile, perishable, or bulky product.

2. Coupons: A coupon certificate that reduces the price. When a buyer gives a coupon to the dealer, he gets the products at a lower price. Coupons are accepted as cash by retailers coupons normally perform two specific functions for the manufacturer. Firstly, they enthuse the consumers to exploit the bargain. Secondly, they serve as an inducement to the channel for stocking the items. The manufacturer thus succeeds in attracting consumers as well as in promoting the channel to stock the merchandise by introducing coupons. They are useful for introducing a new product as well as for strengthening the sale of an existing product.

According to John F. Luick and Zieglar, “A coupon is a certificate that when presented for redemption at a retail store, entitles the bearer to a stated saving in the purchase of a specific product.”

3. Price Reduction or price off promotion: It stimulates sales during a slump season. It gives a temporary, discount to the consumers, i.e. goods are offered at a rate less than the labeled rate. Fans are sold at a reduced rate in the rainy season.

For example, Hawkins pressure cookers have come up with several sales promotion schemes during the last few years. In one of these schemes, Hawkins announced.

Upto Rs. 150/- off on a new Hawkins in exchange for any old pressure cooker.

4. Contests: These may be conducted to attract new customers or to introduce a new product by asking the prospects to state in a few words why they prefer a particular product. For entering into the contest, the prospect is first required to purchase a product and submit the evidence (e.g. a label or package or card wanted to the product) with an entry form for a contest. Through such contests, even the persons who are not inclined to purchase otherwise, also get interested in using the product.

According to John. F. Lick and W.L. Zieglar, “A contest is sales promotion device in which the participants compete for a prize or prizes on the basis of their skill in fulfilling a certain requirement, usually analytical or creative.”

Sponsor companies on the T.V. are adopting the quiz and contest route as a profitable means of establishing brand equality over a period of time. lit programs like Philips Top ten, four with, Close-up brand equity has been used as a format. These programs have gained considerable popularity and they will be remembered for along time. T.V. has gained a substantial audience in India.

5. Demonstration: It is the introduction to educate the consumers in the manner of using the product. It is a promotional tool that attracts the attention of consumers. When products are complex and of a technical nature, the demonstration is necessary, e.g. computers field machinery, electrical pumping set, etc. The demonstration is done in front of consumers for mixy, wet grinder in retail shops, etc.

6. Premium It is a temporary price reduction wealth increases the instinct of the buyers. Products are offered free or at a reduced cost as an inducement for purchasing. It is offered to consumers for consumer goods like soap, brush, paste, washing powder, glucose, etc. For instance, when the customer buys two soaps, a soapbox is given free along with the soaps. The soapbox is a premium, It certain cases, the price is reduced. The reduced amount is a premium.

According to George Wuistopto is “A Premium is an item of Merchandise that is offered at cost or at relatively low cost as a bonus to purchases of a particular product.”

According to Alfred Gross, “A premium is an article of merchandise or another thing of value offered as an inducement to purchase a product or service.”

7. Money Refund Offers: If the purchaser is not satisfied with the product, a part or all of the purchaser’s money will be refunded. It is stated on the package. It will create new users and will strengthen brand loyalty. Some times, the money will be refunded, if 10 top covers or 10 empty bottles or 10 packages are sent a book to the manufacturers.

8. Trade fairs and Exhibitions: India is a country in which various fairs and exhibitions are organized at different levels in different parts. Some producers take part in these fairs and exhibitions and display their products.

9. Special Prizes: Under this method, every purchase of the product is given a prize coupon during a certain period. All the coupons distributed during this period are put into a box and a lottery is drawn therefrom. The winners are given some attractive prizes. There, this scheme also compels the consumers to purchase and use the product.

10. Bonus Stamps: Such bonus stamps are issued to the consumers by the retailers or manufacturer in proportion to their purchases. The consumer goes on collecting stamps until he has sufficient quantity to obtain the desired merchandise in exchange for the stamps.

11. Buy-Back Allowance: Allowance is given following a previous trade deal. That is, a trader deal offers a certain amount of money for a new purchase based on the purchased quantity. It prevents a decline in the post-trade deal. Buyer’s Motivation is increased because of their co-operation on the first trade deal, for example when Cinthol and Mav soaps are purchased, the salesman gives one mug and two coupons free.

12. After-Sale Service Under this method, the producer gives a guarantee to the consumers to maintain the product for a certain specified period.

2. Dealer Sales Promotion: Dealer promotion methods include all the methods which are adopted with a view to encouraging the dealers and distributors to purchase and resell the product in more and more quantity. Dealer promotion methods include the following methods

1. ContestThis is an indirect way of hosting the sales. This is in the form of the window display, store display, etc. The prize is awarded for outstanding achievements.

2. Buying Allowance Discount The buying allowance or discount is offered to the dealer to induce him to buy the manufacturer’s product.

3. Premium Premium is a product usually offered free at less than its price to encourage consumers to buy other products.

4. Incentive By using this method, producers announce some incentives to their salesman so that they may take maximum interest in the sale of the product.

5. Loan Facility The producer allows credit to their dealers, based on the quantity purchased by them. This enables them to purchase bulk quantities.

6. Advertising Allowance The allowance is offered to the dealer to display the manufacturer’s product.

7. GiftRalli Fan Co. arranges for a free holiday.

8. Point of purchase The point of purchase display is the silent salesman that calls the attention to the product in the hope of buying action.

9. Dealers listed promotion This method induces dealers to stock the products and consumers are encouraged to buy the products from the listed dealers.

10. Training Through this method, producers train their selling force.

Try Once:

BRITANNIA Pivot Calculator

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 5 Continuity and Differentiability. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 5 Important Extra Questions Continuity and Differentiability

Continuity and Differentiability Important Extra Questions Very Short Answer Type

Question 1.
If y = log (cos e^x), then find \(\frac{d y}{d x}\) (Delhi 2019)
Solution:
We have :y = log (cos e^x)
∴ \(\frac{d y}{d x}=\frac{1}{\cos e^{x}}\left(-\sin e^{x}\right) \cdot e^{x}\)
= – e^x tan e^x

Question 2.
Differentiate cos {sin (x)²} w.r.t. x. (Outside Delhi 2019)
Solution:
Let y = cos {sin (x)²}.
∴ \(\frac{d y}{d x}\)= – sin {sin (x)²}. \(\frac{d y}{d x}\){sin (x)²}
= – sin {sin (x)²}. cos(x)² \(\frac{d y}{d x}\) (x²)
= – sin {sin (x)²}. cos(x)²2x
= -2x cos(x)² sin {sin(x)²}.

Question 3.
Differentiate sin²(x²) w.r.t. x².   (C.B.S.E. Sample Paper 2018-19)
Solution:
Let y = sin²(x²).
∴ \(\frac{d y}{d x}\) = 2 sin (x²) cos (x²) = sin (2x²).

Question 4.
Find \(\frac{d y}{d x}\), if y + siny = cos or.
Solution:
We have: y + sin y = cos x.
Differentiating w.r,t. x, we get:
\(\frac{d y}{d x}\) + cos y. \(\frac{d y}{d x}\) = – sin x
(1 + cos y)\(\frac{d y}{d x}\) = -sin x
Hence, \(\frac{d y}{d x}\) = \(-\frac{\sin x}{1+\cos y}\)
where y ≠ (2n + 1)π, n ∈ Z.

Question 5.
If y = \(\sin ^{-1}\left(6 x \sqrt{1-9 x^{2}}\right),-\frac{1}{3 \sqrt{2}}<x<\frac{1}{3 \sqrt{2}}\) then find \(\frac{d y}{d x}\). (C.B.S.E. 2017)
Solution:
Here y = sin^-1\(\left(6 x \sqrt{1-9 x^{2}}\right)\)
Put 3x = sin θ.
y = sin^-1 (2 sin θ cos θ)
= sin^-1 (sin 2θ) = 2θ
= 2 sin^-1 3x
\(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)

Question 6.
Is it true that x = e^logx for all real x? (N.C.E.R.T.)
Solution:
The given equation is x = e^logx
This is not true for non-positive real numbers.
[ ∵ Domain of log function is R+]
Now, let y = e^logx
If y > 0, taking logs.,
log y = log (e^logx) = log x.log e
= log x . 1 = log x
⇒ y = x.
Hence, x = e^logx is true only for positive values of x.

Question 7.
Differentiate the following w.r.t. x : 3^{x + 2}. (N.C.E.R.T.)
Solution:
Let y = 3^{x + 2}.
\(\frac{d y}{d x}\) = 3^{x + 2}.log3. \(\frac{d}{d x}\)(x + 2)
= 3^{x + 2} .log3.(1 + 0)
= 3^{x + 2}. log 3 = log 3 (3^{x + 2}).

Question 8.
Differentiate log (1 + θ) w.r.t. sin^-1θ.
Solution:
Let y = log (1 + θ) and u = sin^-1θ.

Question 9.
If y = x^x , find \(\frac{d y}{d x}\).
Solution:
Here y = x^x …(1)
Taking logs., log y = log x^x
⇒ log y = x log x.
Differentiating w.r.t. x, we get:
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x \(\frac{1}{x}\) + logx.(1)
= 1 + log x.
Hence, \(\frac{d y}{d x}\) = y (1 + log x) dx
= x^x (1 + log x). [Using (1)]

Question 10.
If y = \(\sqrt{2^{x}+\sqrt{2^{x}+\sqrt{2^{x}+\ldots \ldots+0 \infty}}}\) then prove that: (2y – 1)\(\frac{d y}{d x}\) = 2^x log 2.
Solution:
The given series can be written as :
y = \(\sqrt{2^{x}+y}\)
Squaring, y² = 2^x + y
⇒ y² – y = 2^x.
Diff. w.r.t. x, (2y -1)\(\frac{d y}{d x}\) = 2^x log 2.

Question 11.
Discuss the applicability of Rolle’s Theorem for the function f(x) = (x- 1)^2/5 in the interval [0, 3].
Solution:
Since f(x) is a polynomial in x,
∴ it is continuous in [0, 3].
And f'(x) = \(\frac { 2 }{ 5 }\)(x-1) ^-3/5 = \(\frac{2}{5} \cdot \frac{1}{(x-1)^{3 / 5}}\)
which does not exist at x = 1
⇒ f(x) is not derivable in (0, 3).
Hence, Rolle’s theorem is not applicable.

Continuity and Differentiability Important Extra Questions Short Answer Type

Question 1.
Discuss the continuity of the function : f(x) = |x| at x = 0. (N.C.E.R.T.)
Solution:

Hence ‘f’ is continuous at x = 0.

Question 2.
If f(x) = x + 1, find \(\frac{d}{d x}\)(fof)(x). (C.B.S.E. 2019)
Solution:
We have : f(x) = x + 1 …(1)
∴ fof(x) = f (f(x)) =f(x)+ 1
= (x + 1) + 1 = x + 2.
∴ \(\frac{d}{d x}\)(fof)(x).) = \(\frac{d}{d x}\)(x + 2) = 1 + 0 = 1.

Question 3.
Differentiate \(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\) with respect to x. (C.B.S.E. 2018 C)
Solution:

Question 4.
Differentiate: tan^-1 \(\left(\frac{1+\cos x}{\sin x}\right)\) with respect to x. (C.B.S.E. 2018)
Solution:

Question 5.
Write the integrating factor of the differential equation :
(tan^-1 y – x) dy = (1 + y²) dx. (C.B.S.E. 2019 (Outside Delhi))
Solution:
The given differential equation is :
(tan^-1 y – x) dy = (1 + y²) dx
⇒ \(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) Linear Equation
∴ I.F = \(e^{\int \frac{1}{1+y^{2}} d x}=e^{\tan ^{-1} y}\)

Question 6.
Find \(\frac{d y}{d x}\) if y = sin^-1\(\left[\frac{5 x+12 \sqrt{1-x^{2}}}{13}\right]\) (A.I.C.B.S.E. 2016)
Solution:

Question 7.
Find \(\frac{d y}{d x}\) if y = \(\sin ^{-1}\left[\frac{6 x-4 \sqrt{1-4 x^{2}}}{5}\right]\) (A.I.C.B.S.E. 2016)
Solution:

Question 8.
If y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ , prove that \(\frac{d y}{d x}=\frac{n y}{\sqrt{x^{2}+a^{2}}}\)
Solution:
y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ ……… (1)

Question 9.
The total cost C(x) associated with the production of ‘x’ units of an item is given by C(x) = 0.005x³ – 0.02x² + 30x + 5000.
Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of the total cost at any level of output. (C.B.S.E. 2018)
Solution:
We have: 0.005x³ – 0.02x² + 30x + 5000
∴ Marginal cost,
C'(x) = (0.005)(3x²) – 0.02(2x) + 30.
Hence,C'(3) = (0.005) (3×9)- (0.02) (6) + 30
= 0.135-0.12 + 30
= 30.135 – 0.12
= 30.02 units nearly

Question 10.
If (x² + y²)² = xy, find \(\frac{d y}{d x}\). (C.B.S.E. 2018)
Solution:
We have : (x² + y²)² = xy
Diff. w.r.t. x,
2(x² + y²)\(\frac{d}{d x}\)(x²+ y²) = x\(\frac{d y}{d x}\) + y(1)
2(x² + y²) [2x +2y\(\frac{d y}{d x}\) ] = x\(\frac{d y}{d x}\) + y
4x(x² + y²) – y = \(\frac{d y}{d x}\) [x – 4y(x² + y²)]
Hence \(\frac{d y}{d x}=\frac{4 x^{3}+4 x y^{2}-y}{x-4 y x^{2}-4 y^{3}}\)

Question 11.
Fing \(\frac{d y}{d x}\) if x^2/3 + y^2/3 = a^2/3 (N.C.E.R.T)
Solution:
The given equation is
if x^2/3 + y^2/3 = a^2/3
Its parametric equations are :
x = a cos³ θ,
y = a sin³ θ
[x^2/3 + y^2/3 = a^2/3 (cos²θ + sin²θ) = a^2/3(I) = a^2/3]

Question 12.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\), if:
x = ae^θ (sin θ – cos θ)
and y = ae^θ (sin θ + cos θ). (A.I.C.B.S.E. 2014)
Solution:
We have : x= ae^θ (sin θ – cos θ)
and y= ae^θ(sin θ + cos θ).
\(\frac{d x}{d \theta}\) = ae^θ (cos θ + sin θ) + ae^θ(sin θ – cos θ)
= 2ae^θsin θ
and \(\frac{d y}{d \theta}\) = ae^θ (cos θ – sin θ) + ae^θ(sinθ + cosθ)
= 2ae^θ cos θ

Question 13.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ), find \(\frac{d y}{d x}\) where θ = \(\frac{\pi}{3}\) (C.B.S.E 2018)
Solution:
We have :
x = a(2θ – sin 2θ)
and y = a(1 – cos 2θ).
∴ \(\frac{d x}{d \theta}\) = a(2 – 2 cos 2θ)
and \(\frac{d y}{d \theta}\) = a(0 + 2 sin 2θ) = 2a sin 2θ.

Question 14.
Find f’ (x), if f(x) = (sin x)^{sin x} for all 0 < x < π. (N.C.E.R.T.)
Solution:
We have :
f(x) = (sin x)^{sin x} …(1)
Taking logs., log f(x) = log (sin x)^{sin x}
⇒ log f(x) = sin x log (sin x).
Diff. w.r.t. x,

= cos x (1 + log sin x)
⇒ f’ (x) = f(x) cos x (1 + log sin x).
Hence ,f'(x) = (sin x)^{sin x}cos x (1 + log sin x).
[Using (i)]

Question 15.
If x¹⁶ y⁹ = (x² + y)¹⁷, prove that \(\frac{d y}{d x}=\frac{2 y}{x}\) (C.B.S.E. (F) 2012)
Solution:
We have :
x¹⁶ y⁹ = (x² + y)¹⁷.
Taking logs.,
log (x¹⁶ y⁹) = log (x² + y)¹⁷
⇒ 16 log x + 9 log y = 17 log (x² + y).
Diff. w.r.t. x,

Question 16.
If y = ae^2x + be^-x, then show that \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y=0\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
Here,
y = ae^2x + be^-x ……… (1)
∴ \(\frac{d y}{d x}\) = 2ae^2x – be^-x …….. (2)
And \(\frac{d^{2} y}{d x^{2}}\) = 4ae^2x + be^-x ……….. (3)
Now, \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y\)
= [4ae^2x + be^-x] – [2ae^2x – be^-x] – 2[ae^2x + be^-x] [Using (1), (2) & (3)]
= 4ae^2x + be^-x – 2ae^2x + be^-x – 2ae^2x – 2be^2x = 0.

Question 17.
If y = log(1 + 2t² + t⁴), x = tan^-1t, find \(\frac{d^{2} y}{d x^{2}}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have : y = log(1 + 2t² + t⁴)
⇒ y = log (1 + t²)²
⇒ y = 21og (1 + t²).

Question 18.
If x sin (a + y) + sin a cos (a + y) = 0, then prove that: \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\) (A.I.C.B.S.E. 2013)
Solution:
We have :
x sin (a + y) + sin a cos (a + y) = 0 …(1)
⇒ x = \(-\frac{\sin a \cos (a+y)}{\sin (a+y)}\) …..(2)
Diff (1) w.r.t x,
x cos (a + y)(0+\(\frac{d y}{d x}\) ) + sin (a + y). 1 + sina(-sin(a+y))(0+\(\frac{d y}{d x}\)) = 0
(xcos(a + y) – sin a sin (a + y)] \(\frac{d y}{d x}\) = – sin (a + y)

⇒ – sin (a + y) [Using (2)]
⇒ -sin a[cos²(a+y)+sin²(a+y)] \(\frac{d y}{d x}\) = -sin² (a+y)
⇒ -sin a(1) \(\frac{d y}{d x}\) = = -sin² (a+y)
Hence \(\frac{d y}{d x}\) = \(\frac{\sin ^{2}(a+y)}{\sin a}\)
Which is true.

Question 19.
If sin y = x cos (a + y), then show that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\cos a}\) Also, show that \(\frac{d y}{d x}\) = cos a, when x = 0. (C.B.S.E. 2018C)
Solution:
Given, sin y = x cos (a + y)

Question 20.
Find the value of ‘c’ in Rolle’s Theorem for the function f (x) = x³ – 3x in [-√3, 0]. (A.1.C.B.S.E. 2017)
Solution:
We have : f(x) = x³ – 3x.
(i) f(x) is continuous in [-√3, 0].
[∵ f(x) is a polynomial in x]

(ii) f'(x) = 3x² – 3 …(1)
∴ f'(x) exists for each x in (-√3,0)

(iii) f(-√3) = (-√3)3 – 3(-√3)
= -3√3 + 3√3 = 0
f(0) = 0 – 0 = 0.
∴ f(-√3) =f(0).
Thus all the conditions of Rolle’s Theorem are satisified.
∴ There exists at least one number ‘c’ between – √3 and 0 such that f'(c) = 0.

But f'(c) = 3c² – 3. [Putting x – c in (1)
∴ f'(c) = 0
3c² – 3 = 0
c² = 1
c = ± 1.
c = – 1 ∈ (-√3,0).
Hence, Rolle’s Theorem is verified and c = – 1.

Question 21.
Find a point on the parabola y = (x – 3)², where the tangent is parallel to the chord joining (3, 0) and (4,1).
Solution:
We have : y = f(x) = (x – 3)².
We discuss the applicability of L.M.V. Theorem in [3, 4],
(i) fix) is continuous in [3, 4],
[ ∵ f(x) is a polynomial]

(ii) f'(x) = 2(x – 3), which exists for all x ∈ (3,4).
∴ f(x) is derivable in (3, 4).
Thus both the conditions of Lagrange’s Mean Value Theorem are satisfied.
∴ There exists at least one number c ∈ (3, 4) such that

⇒ 2(c – 3) = 1
⇒ 2c = 1
⇒ c = \(\frac{7}{2}\) ∈ (3, 4).
When x = \(\frac{7}{2}\), then y = (\(\frac{7}{2}\) – 3)² = 1/4
Hence, the required point is ( \(\frac{7}{2}, \frac{1}{4}\) )

Continuity and Differentiability Important Extra Questions Long Answer Type 1

Question 1.
Find the value of ‘a’ for which the function ‘f’ defined as :

is continuous at x =0 (CBSE 2011)
Solution:


Also f(0) = a sin π/2 (0+1)
= a sin π/2 = a(1) = a
For continuity,
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a = 1/2 = a
Hence, a = 1/2

Question 2.
Find the values of ‘p’ and ‘q’ for which :

is continuous at x = 2 (CBSE 2016)
Solution:


Also f(\(\frac{\pi}{2},\)) = p
For continuity \(\lim _{x \rightarrow \frac{\pi^{-}}{2}} f(x)=\lim _{x \rightarrow \frac{\pi^{*}}{2}} f(x)\)
= f(\(\frac{\pi}{2},\))
⇒ \(\frac{1}{2}=\frac{q}{8}\) = p
Hence p = 1/2 and q = 4

Question 3.
Find the value of ‘k’ for which

is continuous at x = 0 (A.I.C.B.S.E. 2013)
Solution:


For continuity \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ k = -1 = -1
Hence k = -1

Question 4.
For what values of ‘a’ and ‘b\ the function ‘f’ defined as :

is continuous at x = 1. (CBSE 2011)
Solution:
\(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}\) (3ax +b)
= \(\lim _{h \rightarrow 0}\) (3a (1-h) + b]
= 3a(1 – 0) + b
= 3a + b
\(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{+}}(5 a x-2 b)\)
= \(\lim _{h \rightarrow 0}\) [5a (1+h) – 2b]
= 5a (1+0) – 2b
= 5a – 2b
Also f(1) = 11
Since ‘f’ is continuous at x = 1,
∴ \(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}} f(x)\)= f(1)
⇒ 3a + b = 5a – 2b = 11.
From first and third,
3a + b = 11 …………… (1)
From last two,
5a – 2b = 11 …………… (2)
Multiplying (1) by 2,
6a + 2b = 22 ………….. (3)
Adding (2) and (3),
11a = 33
⇒ a = 3.
Putting in (1),
3(3) + b = 11
⇒ b = 11 – 9 = 2.
Hence, a = 3 and b = 2.

Question 5.
If f(x) , defined by the following is continuous at x = 0, find the values of a, b, and c.

(A.I.C.B.S.E 2011)
Solution:


Also f(0) = 2
Since f(x) is continuous at x = 0,
∴ \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a + 3 = b/2 = 2
Hence,a = -1 and b = 4.

Question 6.
Find ‘a’ and ‘b’, if the function given by :
f(x) = \(\left\{\begin{array}{ll}
a x^{2}+b, & \text { if } x<1 \\ 2 x+1, & \text { if } x \geq 1 \end{array}\right.\) is differentiable at x = 1. (C.B.S.E. Sample Paper 2018)
Solution:
Since ‘f’ is derivable at x = 1, ∴ ‘f’ is continuous at x = 1 im 33 => a + b = 2 + 1 = 3
⇒ a + b = 3 …………. (1)
Again since ‘f is differentiable at x = 1


2a = 2
Putting in (1),
1 + b = 3
⇒ b = 3 – 1
⇒ b = 2.
Hence, a = 1 and b = 2.

Question 7.
Prove that: \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]\) = \(\sqrt{a^{2}-x^{2}}\)
(C.B.S.E. (F) 2011)
Solution:

Question 8.
Differentiate \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\) w.r.t x (N.C.E.R.T)
Solution:
Let y = \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
= \(\sin ^{-1}\left(\frac{2.2^{x}}{1+\left(2^{x}\right)^{2}}\right)\)
Put 2^x = tan θ
so that θ = tan^-1(2^x) ………… (1)
Then y = \(\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ)
= 2θ = 2tan^-1(2^x).
[Using (1)]

Question 9.
If log (x² + y²) = 2 tan^-1 [ y/x] show that : \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (C.B.S.E. 2019)
Solution:

Question 10.
If y = tan^-1\(\left(\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)\), x² ≤ 1, then find \(\frac{d y}{d x}\)
We have : log (x2 + y2) = 2 tan-1 (A.I.C.B.S.E. 2015)
Solution:

Question 11.
Differentiate the following with respect to x = sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\) (A.I.C.B.S.E. 2013)
Solution:
= sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\)
= sin^-1\(\left(\frac{2.2^{x} \cdot 3^{x}}{1+(6)^{2 x}}\right)\)
= sin^-1\(\left(\frac{2.6^{x}}{1+(6)^{2 x}}\right)\)
Put 6^x = tan θ
So that θ = tan^-1(6^x) …………(1)
Then y = sin^-1( \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\) )
= sin^-1(sin 2θ)
= 2θ = 2tan^-1(6^x) [Using (1)]

Question 12.
Differentiate : tan^-1\(\left[\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\right]\) w.r.t cos^-1 x² (C.B.S.E. Outside Delhi 2019)
Solution:

Question 13.
If x^y – y^x = a^b, find \(\frac{d y}{d x}\). (Delhi 2019)
Solution:
We have : x^y – y^x = a^b
Putting x^y = u and y^x = v, we get:
u – v = a^b
so that, \(\frac{d u}{d x}-\frac{d v}{d x}\) =0 ………….(1)
Now, u = x^y
Taking logs.,
log u = log x^y
⇒ log u = y log x.
Diff. w.r.t. x,

And, v = y^x
Taking logs., log v = log y^x
⇒ log v = x log y.

Question 14.
If y = (log x)^x + x^logx, find \(\frac{d y}{d x}\) (C.B.S.E. 2019)
Solution:
Let y = (log x)^x + x^logx = u + v,
where u = (log x)^x and v = x^logx
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……….(1)
Now, u = (log x)^x
so that log u = x log (log x).
Diff. w.r.t. x,

Again, v = x^logx
so that log v = log x. log x = (logx)²
Diff w.r.t x,

Question 15.
If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\) then prove that \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\) (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\)
Putting x = sin A and y = sin B, we get:
\(\sqrt{1-\sin ^{2} \mathrm{~A}}+\sqrt{1-\sin ^{2} \mathbf{B}}=a\)= a (sin A – sin B) ⇒ cos A + cos B = a (sin A – sin B)

Question 16.
If x = a sec³ θ and y = a tan³θ, find \(\frac{d^{2} y}{d x^{2}}\)
Solution:
Given : x = a sec³ θ
y = a tan³θ

Question 17.
Find \(\frac{d y}{d x}\), if x^y. y^x = x^x. (C.B.S.E 2018C)
Solution:
We have: x^y y^x = x^x.
Taking logs.,log x^y y^x = log x^x
⇒ y log x + x log y=x log x

Question 18.
Find \(\frac{d y}{d x}\) if y^x + x^y + x^x = a^b (N.C.E.R.T. A.I.C.B.S.E.2015)
Solution:
We have: y^x + x^y + x^x
Putting y^x = u. x^y = v and x^x = w, we get:
u + y + w = a^b
Diff. w.r.t. x, \(\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\) = 0 …………… (1)
Now u = y^x ………….(2)
Taking logs., log u = log y^x
log u = x log y.
Diff. w.r.t. x,

And v = x^y
Taking logs., log v = log x^y
log v = y log x.
Diff. w.r.t. x,

[using (4)]
Lastly w = x^x
Taking logs.,
log w = xlog x
∴ \(\frac{d w}{d x}\) = x (1+log x) …………. (7)
From (1) , using (3), (5) and (7), we get:

Question 19.
If y = e^{tan-1 x}, prove that:\(\left(1+x^{2}\right) \frac{d^{2} y}{d x^{2}}+(2 x-1) \frac{d y}{d x}=0\)
(C.B.S.E. 2018C)
Solution:
Given: y = e^tan-1x,
Differentiating w.r.t. x
\(\frac{d y}{d x}=e^{\ln ^{-1} x}\left(\frac{1}{1+x^{2}}\right)=\frac{y}{1+x^{2}}\)
Agian differentiating w.r.t. x
(1 + x²)\(\frac{d y}{d x}\) = y
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + 2x \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + (2x – 1) \(\frac{d y}{d x}\) = 0

Question 20.
If x cos (a + y) = cos y, then prove that:
\(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\)
Hence show that :
sin a \(\frac{d^{2} y}{d x^{2}}\) + sin 2(a + y)\(\frac{d y}{d x}\) = 0
Solution:
We have : x cos (a + y) = cos y …………(1)
x = \(\frac{\cos y}{\cos (a+y)}\) …………..(2)
Diff. (I) w.r.t. x,
-x sin (a + y) (0 + \(\frac{d y}{d x}\) ) + cos (a + y) .1
⇒ -sin y.\(\frac{d y}{d x}\)
⇒ (xsin(a+y) – siny)\(\frac{d y}{d x}\) = cos(a +y)
⇒ (\(\frac{\cos y}{\cos (a+y)}\) sin (a+y) – sin y)\(\frac{d y}{d x}\)
⇒ cos (a + y) [Using (2)]
(sin (a + y) cos y – cos (a + y) sin y)\(\frac{d y}{d x}\)
⇒ cos² (a + y)
⇒ sin (a + y – y) \(\frac{d y}{d x}\) = cos²(a+y)
\(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
which is true.

Question 21.
If y = (sin^-1 x)², prove that:
\(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0\) (C.B.S.E. 2019)
Solution:
We have y = (sin^-1 x)²
∴ y₁ = 2(sin^-1 x). \(\frac{1}{\sqrt{1-x^{2}}}\)
⇒ \(\sqrt{1-x^{2}} \cdot y_{1}\) = 2(sin^-1 x).
Squaring, (1 – x²) y₁² = 4(sin^-1 x)²
⇒ (1 – x²) y₁² = 4y [Using (1)]
Diff. w.r.t x,
(1 – x²) 2y₁y₂ + (-2x) y₁² = 4y₁
⇒ (1 – x²) y₂ – xy₁ = 2 [Dividing by 2y₁ ]
Hence, (1-x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) – 2 = 0.

Question 22.
If y = cos (m cos^-1 x), show that
(a – x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) + m²y = 0 (C.B.S.E. Sample Paper 2018-2019)
Solution:
We have :

Question 23.
If y = sin (sin x), prove that
\(\frac{d^{2} y}{d x^{2}}\) + tanx \(\frac{d y}{d x}\) + y cos²x = 0. (C.B.S.E. 2018)
Solution:
We have :
y = sin (sin x)
∴ \(\frac{d y}{d x}\) = cos (sin x) . cos x ……(2)
and \(\frac{d^{2} y}{d x^{2}}\) = cos (sin x) (- sin x) + cos x [- sin (sin x). cos x]
= – sin x cos (sin x) – cos²x sin (sin x) …(3)
:. LHS = \(\frac{d^{2} y}{d x^{2}}\) + tan x \(\frac{d y}{d x}\) + y cos² x
⇒ – sin x cos (sin x) – cos² x sin (sin x) + tan x cos (sin x).cos x + sin (sin x) cos² x
[Using (1). (2) and (3)]
⇒ – sin x cos (sin x) – cos² x sin (sin x) + sin x cos (sin x) + cos² x sin (sin x)
⇒ – sin x cos (sin x) + sin x cos (sin x)
= 0 = RHS.

Question 24.
If x = sin t, y = sin pt, prove that:
(1 – x²)\(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) + p²y = 0
(Outside Delhi 2019)
Solution:
We have : x = sin t
and y = sin pt.
\(\frac{d y}{d x}\) = cos t
and \(\frac{d y}{d x}\) = p cos pt

which is true.

Question 25.
Find \(\frac{d y}{d x}\), if x^y.y^x = x^x. (C.B.S.E. 2019 C)
Solution:
We have: x^y.y^x = x^x
Taking logs., logx^y y^x = log x^x
⇒ y log x + x log y = x log x

Question 26.
If y = x^x, prove that
\(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}=0\) (C.B.S.E. 2016,14)
Solution:
We have : y = x^x.
Taking logs.,
log y = x log x.
Duff. w.r.t. x,
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x. \(\frac{1}{y}\) + log x.1
\(\frac{d y}{d x}\) = y(1+1ogx) ………….(1)
Again duff. w.r.t. x,

Question 27.
If x = a (cos 2θ + 2θ sin 2θ) andy = a (sin 2θ – 2θ cos 2θ), find \(\frac{d^{2} y}{d x^{2}}\) at θ = \(\frac{\pi}{8}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:
We have: x – a (cos 2θ + 2θ sin 2θ)
∴ \(\frac{d x}{d \theta}\) = a (- 2 sin 2θ + 2 sin 2θ + 4θ cos 2θ).
⇒ \(\frac{d x}{d \theta}\) = 4aθ cos 2θ ………..(1)
And y = a (sin 2θ – 2θ cos 2θ).
∴ \(\frac{d y}{d \theta}\) = a (2 cos 2θ + 4θ sin 2θ – 2 cos 2θ)
\(\frac{d y}{d \theta}\) = 4aθsin 2θ ………….. (2)

Question 28.
If x = cos t + log tan (t/2) y = sin t , then find the values of \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{4}\)
(C.B.S.E. 2019 Delhi Set-II)
Solution:
We have x = cos t log tan (t/2) and
y = sin t

Question 29.
If y = a cos (log x) + b sin (log x), show that:
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\) (C.B.S.E. 2019C)
Solution:
We have:
y = a cos (log x) + b sin (log x) …..(1)
\(\frac{d y}{d x}\) = – a sin (log x) \(\frac{1}{x}\) + b cos (log x) \(\frac{1}{x}\)
x\(\frac{d y}{d x}\) = -asin (log x) + b cos (log x).
Again diff. w.r.t.x., \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot 1\)
= – a cos (log x) . \(\frac{1}{x}\) – b sin (log x) . \(\frac{1}{x}\)
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\)
= – [a cos (log x) + b sin (log x)]
= -y. [Using (1)]
Hence, \(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\)

Question 30.
Use Lagrange’s Theorem to determine a point P on the curve f(x) = \(\sqrt{x-2}\), defined in the interval [2, 3], where the tangent is parallel to the chord joining the end points on the curve.
Solution:
We have y = f(x) = \(\sqrt{x-2}\) …….(1)
∴ f'(x) = \(\frac{1}{2 \sqrt{x-2}}\)
now f(a) = f(2) = \(\sqrt{2-2}=\sqrt{0}\) = 0
and f(b) = f(3) = \(\sqrt{3-2}=\sqrt{1}\) = 1.
By Lagrange’s Theorem, we have :

⇒ \(\frac{1}{4(x-2)}\) = 1 [Squaring both
⇒ 1 = 4x – 8
⇒ 4x = 9
⇒ x = \(\frac{9}{4}\) ∈ (2, 3).
Putting in (1), y = \(\sqrt{\frac{9}{4}-2}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
Hence, ( \(\frac{9}{4}, \frac{1}{2}\) ) is the reqd. point.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 7 Integrals. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 7 Important Extra Questions Integrals

Integrals Important Extra Questions Very Short Answer Type

Question 1.
Find \(\int \frac{3+3 \cos x}{x+\sin x} d x\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int \frac{3+3 \cos x}{x+\sin x} d x\) = 3 log lx + sin xl + c.
[∵ Num. = \(\frac{d}{d x}\) denom.]

Question 2.
Find : ∫(cos² 2x – sin² 2x)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = ∫cos 4x dx = \(\frac{\sin 4 x}{4}\)+ c.

Question 3.
Find : ∫ \(\frac{d x}{\sqrt{5-4 x-2 x^{2}}}\)   (C.B.S.E. Outside Delhi 2019)
Solution:

Question 4.
Evaluate ∫ \(\frac{x^{3}-1}{x^{2}}\) dx (N.C.E.R.T. C.B.S.E. 2010C)
Solution:

Question 5.
Find : \(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin x \cos x} d x\) (A.I.C.B.S.E. 2017)
Solution:

Question 6.
Write the value of \(\int \frac{d x}{x^{2}+16}\)
Solution:

Question 7.
Evaluate: ∫ (x³ + 1)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int_{-2}^{2} x^{3} d x+\int_{-2}^{2} 1 \cdot d x\) = I₁
⇒ 0 + \([x]_{-2}^{2}\) [∵ I₁ is an odd function] = 2 – (-2) = 4.
⇒ 2 – (-2) = 4.

Question 8.
Evaluate: \(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx. (C.B.S.E. 2014)
Solution:
\(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx
\(\int_{0}^{\pi / 2}\)e^x (-cos x + sinx)dx
|“Form: ∫e^x (f(x) + f'(x) dx”
= \(\left[e^{x}(-\cos x)\right]_{0}^{\pi / 2}\)
= -e ^π/2cos\(\frac{\pi}{2}\) + e⁰ cos 0
= -e ^π/2 (0) + (1) (1)
= -0 + 1 = 1

Question 9.
Evaluate: \(\int_{0}^{2} \sqrt{4-x^{2}} d x\). (A.I.C.B.S.E. 2014)
Solution:

= [0 + 2 sin^-1(1)] – [0 + 0]
= 2sin^-1(1)= 2(π/2) = π

Question 10.
Evaluate : If f(x) = \(\int_{0}^{x}\) t sin t dt, then write the value of f’ (x). (A.I. C.B.S.E. 2014)
Solution:
We have : f(x) = \(\int_{0}^{x}\) t sin t dt.
f'(x) = x sin x. \(\frac{d }{d x}\) (x) – 0
[Property XII ; Leibnitz’s Rule]
= x sin x . (1)
= x sin x.

Question 11.
Prove that: \(\int_{0}^{2a}\) f(x)dx = \(\int_{0}^{2a}\) f(2a-x)dx. o o
Solution:
Put x = 2a – t so that dx = – dt.
When x = 0, t – 2a. When x = 2a, t – 0.
\(\int_{0}^{2a}\) f(x)dx = \(\int_{2a}^{0}\) f(2a-t)(-dt)
=\(\int_{2a}^{0}\) f{2a-t)dt = \(\int_{0}^{2a}\) f(2a-t)dt o
[Property II]
= \(\int_{0}^{2a}\) (2a – x) dx, [Property I]
which is true.

Integrals Important Extra Questions Short Answer Type

Question 1.
Evaluate :
\(\int \frac{\cos 2 x+2 \sin ^{2} x}{\cos ^{2} x} d x\) (C.B.S.E)
Solution:

Question 2.
Find : \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Solution:
I = \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Put tan x = t so that sec² x dx = dt.
∴ I = \(\int \frac{d t}{\sqrt{t^{2}+2^{2}}}\)
= log |t + \(\sqrt{t^{2}+4}\)| + C
= log |tan x + \(\sqrt{tan^{2}+4}\)| + C

Question 3.
Find : \(\int \sqrt{1-\sin 2 x} d x, \frac{\pi}{4}<x<\frac{\pi}{2}\)
Solution:

Question 4.
Find ∫sinx . log cos x dx (C.B.S.E 2019 C)
Solution:
∫sinx . log cos x dx
Put cox x = t
so that – sin x dx = dt
i.e., sin x dx = – dt.
∴ I = -∫log t.1dt
= -[ log t.t – ∫ 1/t. t dt ]
[Integrating by parts]
= – [t log t – t] + C = f(1 – log t) + C
= cos x (1 – log (cos x)) + C.

Question 5.
Find : \(\int \frac{\left(x^{2}+\sin ^{2} x\right) \sec ^{2} x}{1+x^{2}} d x\) (CBSE Sample Paper 2018-19)
Solution:

Question 6.
Evaluate \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\) (CBSE Sample Paper 2018-19)
Solution:
I = \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\)

Question 7.
Find ∫sin^-1 (2x)dx
Solution:

Question 8.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx.
Solution:
Here, f(x)=( 1-x²) sin x cos² x.
f(x) = (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 9.
Evaluate : \(\int_{-1}^{2} \frac{|x|}{x} d x\) dx.
Solution:

Question 10.
Find \(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)   (C.B.S.E. 2018 C)
Solution:
\(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)
= 3∫sce² x dx – 5∫sec x tan x dx
= 3tan x – 5sec x + C

Question 11.
Find :
\(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:
Let I = \(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)
Put tan³ x = t
so that 3 tan² x sec² x dx = dt
i.e tan² x sec²x dx = \(\frac{d t}{3}\)

Question 12.
Find : ∫ sin x .log cos x dx.   (CBSE 2019C)
Solution:
I = ∫ sin x .log cos x dx.
Put cos x = t
i.e. sinx dx = -dt
∴ I = – ∫log t.1 dt
= -[logt.t – ∫1/t . t. dt]
[Integrating by parts]
= – [t log t – t] + C
= t(1 – log t) + C
= cos x (1 – log (cos JC)) + C.

Question 13.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx   (C.B.S.E. 2019 (Delhi))
Solution:
Here, f(x) = (1 – x²) sin x cos² x
∴ f(-x) – (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 14.
Evaluate \(\int_{-1}^{2} \frac{|x|}{x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

Question 15.
Find : \(\int_{-\pi / 4}^{0} \frac{1+\tan x}{1-\tan x} d x\)
Solution:

Integrals Important Extra Questions Long Answer Type 1

Question 1.
Evaluate : \(\int \frac{\sin ^{6} x+\cos ^{6} x}{\sin ^{2} x \cos ^{2} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

Question 2.
Integrate the function \(\frac{\cos (x+a)}{\sin (x+b)}\) w.r.t. x. (C.B.S.E. 2019 (Delhi))
Solution:

Question 3.
Evaluate : ∫ x² tan^-1 x dx. (C.B.S.E. (F) 2012)
Solution:

Question 4.
Find : ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx (N.C.E.R.T.; A.I.C.B.S.E. 2010 C)
Solution:
Let ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx
= ∫ log(log x)dx + ∫\(\frac{1}{(\log x)^{2}}\) dx …… (1)
Let I = I₁ + I₂
Now I₁ = ∫ log (log x) dx
=∫ log (log x) 1 dx
= log (log x).x – ∫ \(\frac{1}{\log x \cdot x}\)x.dx
(Integrating by parts)
= xlog(logx) – ∫ \(\frac{1}{\log x}\)dx ……….. (2)
Let I₁ = I₃ + I₄

Putting in (2),
I₁ = x log (x) – \(\frac{x}{\log x}-\int \frac{1}{(\log x)^{2}}\) dx
Putting in (1),
I = x log (log x)

Question 5.
Integrate : ∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx   (N.C.E.R.T.)
Solution:
∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx
[From ∫ e^xf(x) + f'(x) ]dx”]
= ∫ e^x tan^-1 x dx +∫ e^x \(\frac{1}{1+x^{2}}\) ) dx
= ∫ tan^-1 x. e^x dx +∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
= tan^-1 x. e^x – ∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
+∫ \(\frac{1}{1+x^{2}}\) ) e^xdx
(integrating first integral by parts)
= e^x tan^-1x + c.

Question 6.
Integrate : \(\int e^{x}\left(\frac{x^{2}+1}{(x+1)^{2}}\right) d x\) (N.C.E.R.T)
Solution:

Question 7.
Find \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\) (C.B.S.E. 2018)
Solution:
Let i = \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\)
Put sin x = t so that cos x dx = dt.

⇒ 2 ≡ A(1 + t²) + (Bt + C) (1 – t)
2 ≡ (A – B)t² + (B – C)t + (A + C).
Comparing coeffs. of t²,
A-B = 0
⇒ A = B
Comparing coeffs. of t,
0 = B – C
⇒ B = C.
Comparing constant terms,
2 = A + C.
Thus, A = B = C = 1.
∴ From (2),
\(\frac{2}{(1-t)\left(1+t^{2}\right)}=\frac{1}{1-t}+\frac{t+1}{t^{2}+1}\)
∴ From (1)

= – log |1 — t| + \(\frac { 1 }{ 2 }\) log |t² + 1| + tan^-1 t + c
= – log |1 — t| + \(\frac { 1 }{ 2 }\) log (t² + 1) + tan^-1t + c
[∵ t² ≥ 0 ⇒ t² + 1 > 0 ∴ |t² + |1 = t² + 1]
= – log |1 – sin x| + \(\frac { 1 }{ 2 }\) log (sin² x + 1) + tan^-1 (sin x) + c
= – log (1 – sin x) + \(\frac { 1 }{ 2 }\) log (1 + sin²x)
+ tan^-1 |sin x| + c.
[∵’ 1 – sin x ≥ 0 |1 – sin x| = 1 – sin x]

Question 8.
Find : \(\int \frac{3 x+5}{x^{2}+3 x-18} d x\) (C.B.S.E. 2019)
Solution:
Let 3x + 5 = A(2x + 3) + B.
Comparing,
2A = 3, 3A + B = 5

Put x2 + 3x – 18 – t
so that (2x + 3 )dx = dt.
∴ I₁ = \(\int \frac{d t}{t}\) = log |t|
= log + | x² + 3x – 18 |

Question 9.
Find: \(\int \frac{\cos x}{(1+\sin x)(2+\sin x)} d x\) 2019C)
Solution:

Question 10.
Find: \(\int \frac{x^{4}+1}{2\left(x^{2}+1\right)^{2}} d x\) (C.B.S.E. Sample Paper 2018-19)
Solution:

⇒ t² + 1 ≡ A(t + 1)² + Bdt + 1) + Ct …(2)
Comparing coeffs. of like terms, we get :
A = 1, B = 0 and C = – 2.
Putting in (1),

Question 11.
Evaluate : \(\int \frac{x+2}{\sqrt{x^{2}+5 x+6}} d x\) (A.I.C.B.S.E. 2014)
Solution:

Question 12.
Evaluate : \(\int \frac{2 x+5}{\sqrt{7-6 x-x^{2}}} d x\)
Solution:

Question 13.
Evaluate : \(\int \frac{d x}{5+4 \cos x}\)
Solution:
I = \(\int \frac{d x}{5+4 \cos x}\)
Put cos x = \(\frac{1-t^{2}}{1+t^{2}}\)
where t = tan \(\frac { x }{ 2 }\) so that dt = \(\frac { 1 }{ 2 }\) sec² \(\frac { x }{ 2 }\) dx
i.e dt = \(\frac { 1 }{ 2 }\)( 1+ tan²\(\frac { x }{ 2 }\))dx
i.e. dt = \(\frac { 1 }{ 2 }\) (1 + t2) dx i.e. dx = \(\frac{2 d t}{1+t^{2}}\)

Question 14.
Evaluate : \(\int \frac{d x}{x\left(x^{3}+1\right)}\) (A.I. C.B.S.E 2013)
Solution:
I = \(\int \frac{d x}{x\left(x^{3}+1\right)}=\int \frac{x^{2} d x}{x^{3}\left(x^{3}+1\right)}\)
[Multiplying numerator and denominator by x²]
Put x³ = t so that 3x² dx = dt
i.e , x² dx = \(\frac { 1 }{ 3 }\) dt

Question 15.
Evaluate : \(\int_{0}^{2} e^{x} d x\) as the limit of a sum. (N.C.E.R.T.)
Solution:
Here f(x) = e^x ; a = 0, b = 2.
∴ f(a) -f(0) = e° = 1
f(a + h) =f(0 + h) = e^h
f(a + 2h) =f(0 + 2h) = e^2h, …….,

where nh = b – a = 2 – 0 = 2
= \(\lim _{h \rightarrow 0}\) h[1 + e^h +e^2h +… + e^(n-1)hh]
= \(\lim _{h \rightarrow 0} h \frac{1 \cdot\left(e^{n h}-1\right)}{e^{h}-1}\)

Question 16.
Evaluate: \(\int_{-1}^{2}\) (e^3x + 7x – 5)dx as a limit of sums. (A.I.C.B.S.E. 2015)
Solution:
Here f(x) = e^3x + 7x – 5 ; a = – 1, b = 2.
f (a) = f(- 1) = e^-3 – 7 – 5 = e^-3 – 12
f (a + h) = f(-1 + h)
= e^-3(-1 + h) + 1 (-1 + h)-5

Question 17.
Evaluate: \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\). (N.C.E.R.T.)
Solution:
Let I = \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\)
Put x⁵ = t so that 5x⁴ dx = dt.
When x = – 1, t = – 1. When x = 1, t= 1.

Question 18.
Prove that:
\(\int_{0}^{a} f(x)=\int_{0}^{a} f(a-x) d x\) , hence evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E 2019C)
Solution:
(i) Put x = a – y so that dx = -dy.
When x = 0, y = a. When x = a, y = 0.
∴ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – y)(-dy)
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f{a-x)dx.

Put cos x = t
so that – sin x dx = dt
i.e. sin x dx = -dt.
When x = 0, t – cos 0=1.
When x = π, t – cos π = -1.

Question 19.
Evaluate : \(\int_{-1}^{2}\) |x³ – x | dx   (N.C.E.R.T.; C.B.S.E. 2016; A.I.C.B.S.E. 2012)
Solution:

On [- 1, 0], x³ – x ≥ 0
⇒ | x³ – x | = x³ – x;
On [0, 1], x³ – x ≤ 0
⇒ | x³ – x | = -(x³ – x) = x – x³
On [1, 2], x³ – x > 0
⇒ | x³ – x | = x³ – x

Question 20.
Solve the differential equation:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx.
Solution:
The given differential equation is:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx

Put y = vx, so that \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
∴(1) becomes:



Which is the reqd. solution.

Question 21.
Evaluate : \(\int_{-1}^{1} \frac{x+|x|+1}{x^{2}+2|x|+1} d x\) (CB.S.E. Sample Paper 2018 – 19)
Solution:

Thus f(-x) = -f(x)
⇒ f(x) is an odd function
∴ I₁ = 0 …… (2)


= 2 [log |x + 1|]\(\text { ] }_{0}^{1}\)
= 2 [log 2 – log 1]
= 2 [log 2-0]
= 2 log 2 …(3)
∴ From (1), (2) and (3), we get:
I = 2 log 2.

Question 22.
Find : \(\int \frac{4}{(x-2)\left(x^{2}+4\right)} d x\) (C.B.S.E. 2018 C)
Solution:
\(\frac{4}{(x-2)\left(x^{2}+4\right)} \equiv \frac{\mathrm{A}}{x-2}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+4}\)
4 ≡ A(x² + 4) + (Bx + C)(x-2)
By comparison,
A = \(\frac { 1 }{ 2 }\), B = –\(\frac { 1 }{ 2 }\)
and C = 1.

Integrals Important Extra Questions Long Answer Type 2

Question 1.
Evaluate : \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Solution:
Let I = \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Put tan^-1 x = t i.e, x = tan t
So that \(\frac{1}{1+x^{2}} d x\) = dt

Question 2.
Integrate : \(\int \frac{x^{3}+x}{x^{4}-9} d x\)
Solution:

Now I₁ = \(\int \frac{x^{3}}{x^{4}-9} d x\)
Put x⁴ – 9 = t so that 4x³ dx – dt
i.e x³dx = \(\frac{d t}{4}\)

Put x² = u so that 2x dx = du
i.e, xdx = \(\frac{1}{2}\) du
Putting the values of Ij and I2 in (1), we get:

Question 3.
Find : \(\int \frac{\cos \theta}{\left(4+\sin ^{2} \theta\right)\left(5-4 \cos ^{2} \theta\right)} d \theta\) (A.I.C.B.S.E. 2017)
Solution:

Question 4.
Evaluate : \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Solution:
I = \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Put sin² x = t so that 2 sin x cos x dx = dt
i.e. sin 2x dx = dt.

Question 5.
Evaluate : \(\int \frac{x^{2}-1}{x^{4}+1} d x\)
Solution:

Question 6.
Evaluate: \(\int(\sqrt{\tan x}+\sqrt{\cot x}) d x\) (N.C.E.R.T.; A.I.C.B.S.E. 2014; C.B.S.E. 2010S)
Solution:

so that sec2 x dx = 2t dt
i.e., (1 + tan² x) dx = 2t dt
⇒ (1 + f) dx = 21 dt

[Dividing Num.. & Denom. by t²]
Put t – \(\frac { 1 }{ t }\)= y so that (1 + \(\frac{1}{t^{2}}\) )dt = dy
Also t² – 2 + \(\frac{1}{t^{2}}\) = y²
t² + \(\frac{1}{t^{2}}\) = y² + 2

Question 7.
Evaluate \(\int_{0}^{\pi / 2} \frac{x+\sin x}{1+\cos x} d x\) (A.I.C.B.S.E. 2011)
Solution:


= – [log|1+0|] – [log|1+1|]
= – [0-log2] = log 2
[log|1| = log I = 0]
From (1), I = (\(\frac{\pi}{2}\)– log 2) + log 2 = \(\frac{\pi}{2}\)

Question 8.
Evaluate :
\(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\) (C.B.S.E. 2016)
Solution:
Let I = \(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\)
Put \(\frac{\pi}{4}\) + x = t
x = t – \(\frac{\pi}{4}\) so that dx = dt
when x = 0, t = \(\frac{\pi}{4}\)
when x = π, t = \(\frac{5\pi}{4}\)

Question 9.
Evaluate : \(\int_{1}^{3}\) (x² + 3x + e^x )dx, as the limit of the sum. (C.B.S.E. 2018)
Solution:
Let f (x) = x² + 3x + e^x
f(x) = f(1)
= 1² + 3(1) + e¹ = 4 + e
f(a + h) = f(1 + h.)
= (1+h)² + 3(1+h) + e^1+h
= 4 + 5 h + h² + e^1+h
f(a + 2h) = f(1 + 2h)
= (1 +2h)² + 3(1 +2h) + e^1+2h
= 4 + 10h+ 4h² + e^1+2h

Question 10.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x}{\sin x+\cos x} d x\)
Solution:

Question 11.
Evaluate : \(\int_{0}^{\pi / 2} \frac{\cos ^{2} x}{\cos ^{2} x+4 \sin ^{2} x} d x\)
Solution:


[Dividing Num. and Denom. by cos² x]
Put tan x = t so that sec² x dx = dt.
When x = \(\frac{\pi}{2}\), t = tan \(\frac{\pi}{2}\) → ∞

Question 12.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2017; A.I.C.B.S.E. 2013, 12)
Solution:

Put cos x = t so that – sin x dx = dt
i.e. sin x dx = – dt.
When x = 0, t = cos 0 = 1.
When x = π, t = cos π = – 1.

Question 13.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2018)
Solution:

Put sin x – cos x = t
so that (cos x + sin x) dx = dt.
When x = 0, t = 0 – 1 = -1.

Question 14.
Evaluate \(\int_{0}^{3 / 2}|x \sin \pi x| d x\) (C.B.S.E. 2017)
Solution:

In (0, 1), x sin πx is +ve
⇒ | x sin πx | = x sin πx.
In (0, 3/2), x sin πx is +ve
⇒ | x sin πx | = -x sin πx.

Question 15.
\(\int_{0}^{4}\) |x| + |x-2| + |x-4|)dx (C.B.S.E. 2013)
Solution:
By definition,

Now, \(\int_{0}^{4}\) (| x | + | x – 2| + | x – 4|) dx
= \(\int_{0}^{4}\) (|x| + |x-2| + |x-4|)dx
\(\int_{0}^{4}\) (| x | + | x – 2| + |x – 4| ) dx
= \(\int_{0}^{4}\) [x + (x-2)}-(x-4)]dx
= \(\int_{0}^{4}\) [(-x +6) dx + = \(\int_{0}^{4}\) (x+2)dx

= 10 +(16-6)= 10+10 = 20.

Question 16.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x \sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x\) (C.B.S.E. 2018 C)
Solution:


Let sin² x = t
⇒ sin x cos x dx = 1/2 dt
For x-0,t = sin² 0 = 0
and for x = π/2, t = sin² π/2 = 1

Question 17.
Evaluate : \(\int_{1}^{3}\)(3x² + 2x + 1)dx as the limit ofa sum. (C.B.S.E. 2018 C)
Solution:
a = 1, b = 3
and h = 2/n
nh = 2
\(\int_{1}^{3}\)(3x² + 2x + 1)dx
\(\lim _{h \rightarrow 0}\)
= lim h\f(l) +/(1 + h) +/(1 + 2h) + …
= \(\lim _{h \rightarrow 0}\) h[f(1) +f(1 + h) +f(1 + 2h) + …+ f(1 + (n — 1)h)]
= \(\lim _{h \rightarrow 0}\) h[(6+ {3(1 +h)² + 2(1 + h)+ 1} + (3(1 + 2h)² + 2(1 + 2h) + 1) + … + {3(1 +(n – 1)h)² + 2(1 +(n – 1)h)+ 1)]
= \(\lim _{h \rightarrow 0}\) h[6+ {3(1 + h² + 2h) + 2(1 +h) + 1) + {3(1 +4h² + 4h) } + 2(1 +2h)+ 1}+… + {3(1 + (n – 1)² h² + 2(n – 1)h) + 2(1 +(n—1)h)+(l +(n – 1)h}

= \(\lim _{h \rightarrow 0}\) h[(6) + (6 + 8h + 3h²) + (6 + 16h + 12h²) + … + [(6 + 3(n – 1)² h² + 8 (n —1)h}]

= \(\lim _{h \rightarrow 0}\)[6n+8h(1 + 2 +…+(n – 1))
+3h² {(1² + 2² + …+(n – 1)²}]

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 9 Differential Equations. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 9 Important Extra Questions Differential Equations

Differential Equations Important Extra Questions Very Short Answer Type

Question 1.
Find the order and the degree of the differential equation: \(x^{2} \frac{d^{2} y}{d x^{2}}=\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{4}\)
(Delhi 2019)
Solution:
Here, order = 2 and degree = 1.

Question 2
Determine the order and the degree of the differential equation:\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (C.B.S.E. 2019 C)
Solution:
Order = 2 and Degree = 1.

Question 3.
Form the differential equation representing the family of curves: y = b (x + a), where « and b are arbitrary constants. (C.B.S.E. 2019 C)
Solution:
Wehave:y= b(x + a) …(1)
Diff. w.r.t. x, b.
Again diff. w.r.t. x, \(\frac{d^{2} y}{d x^{2}}\) = 0,
which is the reqd. differential equation.

Question 4.
Write the general solution of differential equation:
\(\frac{d y}{d x}\) = e^x+y (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\frac{d y}{d x}\) = e^x+y
⇒ e^-y dy = e^x dx [Variables Separable
Integrating, \(\int e^{-y} d y+c=\int e^{x} d x\)
⇒ – e^-y + c = e^x
⇒ e^x + e^-y = c.

Question 5.
Find the integrating factor of the differential equation:
y\(\frac{d y}{d x}\) – 2x = y³e^-y
Solution:
The given equation can be written as.

Question 6.
Form the differential equation representing the family of curves y = a sin (3x – b), where a and b are arbitrary constants. (C.B.S.E. 2019C)
Solution:
We have: y – a sin (3x – b) …(1)
Diff. W.r.t y \(\frac{d y}{d x}\) = a cos (3x – b) .3
= 3a cos (3x – b)
\(\frac{d^{2} y}{d x^{2}}\) = -3a sin (3x – b) 3
= -9a sin (3x – b)
= -9y [Using (1)]
\(\frac{d^{2} y}{d x^{2}}\) + 9y = 0,m
which in the reqd. differential equation.

Differential Equations Important Extra Questions Short Answer Type

Question 1.
Determine the order and the degree of the differential equation:
\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (Outside Delhi 2019C)
Solution:
Order = 2 and Degree = 1.

Question 2.
Form the differential equation representing the family of curves: y = e^2x (a + bx), where ‘a’ and ‘h’ are arbitray constants. (Delhi 2019)
Solution:
We have : y = e^2x (a + bx) …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = e^2x (b) + 2e2x (a + bx)
⇒ \(\frac{d y}{d x}\) = be^2x + 2y ………….. (2)
Again diff. w.r.t. x,
\(\frac{d^{2} y}{d x^{2}}\) = 2be^2x + 2^2x
\(\frac{d^{2} y}{d x^{2}}\) = 2(\(\frac{d y}{d x}\) – 2y) + \(\frac{d y}{d x}\)
[Using (2)]
Hence, \(\frac{d^{2} y}{d x^{2}}\) -4 \(\frac{d y}{d x}\) + 4y = 0, which is the reqd. differential equation.

Question 3.
Solve the following differentia equation:
\(\frac{d y}{d x}\) + y = cos x – sin x (Outside Delhi 2019)
Solution:
The given differential equation is :
\(\frac{d y}{d x}\) + y = cos x – sin x dx Linear Equation
∴ I.F. = e^∫1dx = e^x
The solution is :
y.e^x = ∫ (cos x — sin x) e^x dx + C
⇒ y.e^x = e^x cos x + C
or y = cos x + C e^-x

Question 4.
Solve the following differential equation :
\(\frac{d x}{d y}\) + x = (tan y + sec²y). (Outside Delhi 2019 C)
Solution:
The given differential equation is :
\(\frac{d x}{d y}\) + x = (tany + sec²y).
Linear Equation
∵ I.F. = Jldy = ey
∴ The solution is :
x. ey = ∫ ey (tan y + sec² y)dy + c
⇒ x. ey = ey tan y + c
= x = tan y + c e-y, which is the reqd. solution.

Differential Equations Important Extra Questions Long Answer Type 1

Question 1.
Solve the differential equation
(x² – y²)dx + 2xydy = 0 (C.B.S.E. 2018)
Solution:

log x = -log (1 + v²) + log C
x(1 + v²) = C
x(1 + \(\frac{y^{2}}{x^{2}}\)) = C
x² + y² = C.

Question 2.
Find the particular solution of the differential equation (1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\), given that y = 0 when x = 1(C.B.S.E. 2018 C)
Solution:

Solution is y( 1 + x²) = \(\int \frac{1}{1+x^{2}} d x\)
= tan^-1 x + C
When y = 0,x = 1,
then 0 = \(\frac{\pi}{4}\) + C
C = \(\frac{\pi}{4}\)
∴ y(1 + x²) = tan ^-1 x – \(\frac{\pi}{4}\)
i.e, y = \(\frac{\tan ^{-1} x}{1+x^{2}}-\frac{\pi}{4\left(1+x^{2}\right)}\)

Question 3.
Find the differential equation representing the family of curves y = ae^{bx + 5}, where ‘a’and ‘A’are arbitrary constants. {C.B.S.E. 2018)
Solution:
We have: y = ae^{bx + 5} + 5 …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = ae^{bx + 5}. (b)
\(\frac{d y}{d x}\) = dy ……(2) [Using (1)]]
Again diff. w.r.t x.,
\(\frac{d^{2} y}{d x^{2}}=b \frac{d y}{d x}\) ………(3)

Dividing (3) by (2),

which is the required differential equation.

Question 4.
Find the particular solution of the differential equation x dx – ye^y \(\sqrt{1+x^{2}}\) dy = 0, given that y = 1 when x = 0. (C.B.S.E. 2019 C)
Solution:
The given differential equation is:

When x = 0,y = 1, ∴ 1 = c + c(0) ⇒ c = 1.
Putting in (2), \(\sqrt{1+x^{2}}\) = 1 + e^y(y -1),
which is the reqd. particular solution.

Question 5.
Obtain the differential equation of the family of circles, which touch the x-axis at the origin.   (N.C.E.R.T.; C.B.S.E. Sample Paper 2018)
Solution:
Let (0, α) be the centre of any member of the family of circles.

Then the equation of the family of circles is : x² + (y-α)² = α²
⇒ x² + y² – 2αy = 0 …(1)
Diff. w.r.t. x, 2x + 2y \(\frac{d y}{d x}\) 2α \(\frac{d y}{d x}\) = 0

which is the required differential equation.

Question 6.
Obtain the differential equation representing the family of parabolas having vertex at the origin and axis along the positive direction of x-axis. (N.C.E.R.T.)
Solution:
Let S (a, 0) be the focus of any member of the family of parabolas.
Then the equation of the family of curves is y² = 4 ax …………. (1)
Diff. w.r.t. x, 2y\(\frac{d y}{d x}\) = 4a ……………. (2)
Using (2) in (1), we get:
y² = (2y\(\frac{d y}{d x}\))x

y² – 2xy\(\frac{d y}{d x}\) = 0
which is the required differential equation.

Question 7.
Find the general solution of the differential equation:
(tan²x + 2 tanx + 5) \(\frac{d y}{d x}\) = 2 (1 + tanx) sec² x
Solution:
We have : (tan² x + 2 tan x + 5)\(\frac{d y}{d x}\)
= 2 (1 + tanx) sec²x
Integrating

Put t² + 2t + 5 = z
so that (2t+ 2) dt = dz.
∴ From (2),
1 = \(\int \frac{d z}{z}\) = log| z | = log |t² + 2t + 5|
= log |tan² x| + 2 tan x + 5|
From (1), y = log |tan² x| + 2 tan x + 5| + c,
which is the required general solution.

Question 8.
Solve the differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y(0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :
\(\frac{d y}{2 e^{-y}-1}=\frac{d x}{x+1}\)
| Variables Separable

Integrating, \(\int \frac{e^{y} d y}{2-e^{y}}=\int \frac{d x}{x+1}\)
⇒ – log |2 – e^y| + log |C| = log |x + 1|
⇒ (2 – e^y) (x + 1) = C.
When x = 0, y = 0, then C = 1.
Hence, the solution is (2 – e^y) (x + 1) = 1.

Question 9.
Solve: (a) (i) \(\frac{d y}{d x}\) = 1 + x + y + xy
(ii) xyy’ = 1 + x + y + xy. (N.C.E.R.T.)
(b) Find the particular solution of the differential dy
equation \(\frac{d y}{d x}\) = 1 + x + y + xy, given that y = 0 when x = 1. (A.I.C.B.S.E. 2014)
Solution:
(a), (i) The given equation is :
\(\frac{d y}{d x}\) = 1 + x + y + xy
\(\frac{d y}{d x}\) = (1 +x) (1 +y)
\(\frac{d}{1+y}\) = (1 + x)dx.
|Variables Separable

Integrating,
\(\int \frac{d y}{1+y}\) = ∫(1 + x)dx + c
⇒ log |1 + y | = x + \(\frac { 1 }{ 2 }\) x² + c,
which is the required solution.

(ii) The given equation is xyy’ = 1 + x + y + xy
⇒ xy\(\int \frac{d y}{1+y}\) = (1 + x)(1 + y)

= y – log|1 + y| = log|x|+ x + c
= x + log |x (1 + y)|+ c,
which is the required solution.

(b) From part (a) (i),
Iog|1+y| = x + \(\frac { 1 }{ 2 }\)x² + c …(1)
When x = 1, y = 0, then:
log |1+0|= 1 + \(\frac { 1 }{ 2 }\)(1)² + c
log 1 = 1 + \(\frac { 1 }{ 2 }\) + c
0 = \(\frac { 3 }{ 2 }\) + c
c = \(-\frac { 3 }{ 2 }\)
Putting in (1), log |1 + y| = x + \(\frac { 1 }{ 2 }\)x² – \(\frac { 3 }{ 2 }\)
which is the required particular solution.

Question 10.
Solve the differential equation:
\(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
given thaty = 1 when x = 0. (Outside Delhi 2019)
Solution:
The given equation is \(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
⇒ \(\frac{d y}{d x}\) = (1+x²)(1 +y²)
⇒ \(\frac{d y}{1+y^{2}}\) (x² + 1) dx
|Variables Separable

Integrating, ∫\(\frac{d y}{1+y^{2}}\) = ∫(x² + 1) dx + C
tan^-1y = \(\frac{x^{3}}{3}\) + x + C ………. (1)
Where x = 0,y = 1,
∴ tan^-1 (1) = C
C = \(\frac{\pi}{4}\)
Putting in (1),
tan^-1 y = \(\frac{x^{3}}{3}+x+\frac{\pi}{4}\)
which is the reqd. particular solution.

Question 11.
Find the particular solution of the differential equation: e^x tan y dx + (2 – e^x) sec² y dy = 0, given thaty = \(\frac{\pi}{4}\) where x = 0.
Solution:
The given differential equation is:

∴ From (1),
log C + log |e^x – 2| = log |tan y|
⇒ tany = C(e^x – 2) …(2)
When x = 0, y = y = \(\frac{\pi}{4}\)
∴ 1 = C(1 – 2)
C = -1
Putting in (2),
tan y = 2 – e^x
which is the required particular solution.

Question 12.
Find the particular solution of the following differential equation:
cosy dx + (1 + 2e^-x) siny dy = 0; y(0) = \(\frac{\pi}{4}\) .
(CBSE Sample Paper 2018 – 19)
Solution:
The given differential equation is:
cos y dx + (1 + 2e^-x) sin ydy = 0

log |e^x| – log |cos y| = log|C|
e^x + 2 = C cos y ….. (1)

Substituting, x = 0, y = \(=\frac{\pi}{4}\) in(1),we get:
1 + 2 = C cos \(=\frac{\pi}{4}\)
C = \(\frac{3}{1 / \sqrt{2}}\)
C = 3√2
Putting in (1),
e^x + 2 = 3√2 cos y
which is the required particular solution.

Question 13.
Find the particular solution of the following differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y = 0 when x = 0. (C.B.S.E. 2012)
Solution:
The given equation is (x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1

-log|2 – e^y| = log|x + 1| + log|c|,
where c’ = log |c|
⇒ log \(\left|\frac{1}{2-e^{y}}\right|\) = log |c(x + 1)|
⇒ \(\frac{1}{2-e^{y}}\) = c(x + 1)
When x = 0, y = 0;
\(\frac{1}{2-e^{0}}\) = c(0 + 1)
⇒ c = \(\frac{1}{2-1}=\frac{1}{1}\) = 1

Putting (1)
\(\frac{1}{2-e^{y}}\) = 1.(x + 1)
⇒ (x + 1)(2 – e^y) = 1
which is the required particular solution.

Question 14.
Solve the differential equation:
(1 – y²) (1 + log x)dx + 2xy dy = 0, given that when x = 1 ,y = 0.
(C.B.S.E. 2016)
Solution:
The given equation is :
(1 – y²) (1 + log x)dx + 2xy dy = 0

Putting in (1),
\(\frac{(1+\log x)^{2}}{2}\) = log|1 – y²| + 1/2
(1 + log x)² = 2 log|1 – y²| + 1
which is the required solution.

Question 15.
Solve the differential equation:
x cos x (\(\frac { y }{ x }\)) \(\frac{d y}{d x}\) = y cos(\(\frac { y }{ x }\)) = x (C.B.S.E. 2019 C)
Solution:
The given equation is:

Put \(\frac { y }{ x }\) = v i.e, y = vx so that \(\frac { dy }{ dx }\) = v + x \(\frac { dv }{ dx }\)
∴ (1) becomes:
cos v (v + x\(\frac { dv }{ dx }\)) = vcosv + 1
= v + x \(\frac { dv }{ dx }\) = v + \(\frac { 1 }{ cos v }\)
x \(\frac { dv }{ dx }\) = \(\frac { 1 }{ cos v }\)
cos v dv = \(\frac { dx }{ x }\)
[Variables Seperable]

Integrating, ∫ cos v dv = ∫ \(\frac{d x}{ x}\) + c
sin = log|x| + c
sin \(\frac{y}{ x}\) = log|x| + c,
which is the reqd. solution.

Question 16.
Find the general solution of the differential equation: \(\frac{d x}{d y}=\frac{y \tan y-x \tan y-x y}{y \tan y}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given differential equation is :

|Linear Equation
Comparing with \(\frac{d x}{d y}\) + Py = Q, we have :
‘P’ = \(\frac{1}{y}+\frac{1}{\tan y}\) and ‘Q’ = 1

∴ I.F = \(e^{\int\left(\frac{1}{y}+\frac{1}{\tan y}\right) d y}=e^{\log y+\log \sin y}\)
e^log(ysiny) = ysiny.
∴ The solution is
x x I.F. = ∫ (Q x I.F.)dy + C
⇒ x(y sin y) = ∫(1 x y sin y)dy + C
⇒ xy sin y = ∫ y sin y dy + C
⇒ xy sin y = y (- cos y) – ∫(1) -cos y)dy + C

(Integrating by Parts)
⇒ xy sin y = – y cos y + ∫ cos ydy + C
⇒ xy sin y = – y cos y + sin y + C
⇒ x = \(\frac{\sin y-y \cos y+C}{y \sin y}\)
which is the required general solution.

Question 17.
Solve the differential equation :
xdy – ydx = \(\sqrt{x^{2}+y^{2}}\) dx , given that y = 0 when x = 1. (C.B.S.E. 2019)
Solution:
The given equation can be written as :


where x = 1, y = 0
∴ 0 + \(\sqrt{1+0} \) = c(1)
⇒ c = 1
Putting in (2), y + \(\sqrt{x^{2}+y^{2}}\) = x²,
which is the reqd. solutions.

Question 18.
Solve the following differential equation:
\(x y \log \left(\frac{y}{x}\right) d x+\left(y^{2}-x^{2} \log \left(\frac{y}{x}\right)\right) d y=0\) (C.B.S.E. 2010 C)
Solution:
The given equation can be written as:

Question 19.
Solve the differential equation:
xdy-y dx= \(\sqrt{x^{2}+y^{2}}\) dx.
(iC.B.S.E. Sample Paper 2019)
Solution:
The given differential equation is:

Put y = vx, so that \(\frac{d y}{d x}\) = dv + x \(\frac{d v}{d x}\)
(1) becomes:

⇒ y+ \(\sqrt{x^{2}+y^{2}}\) = cx²,
which is the reqd. solution.

Question 20.
Prove that x² – y² = c(x² + y²)² is the general solution of the differential equation: (x³ – 3xy²)dx = (y³ – 3x²y)dy, where c is a parameter. (C.B.S.E. 2017)
Solution:
We have :(x³ – 3xy²) dx = (y³ – 3x²y)dy

∴ v³ – 3v = A(1 + v)(1 + v²) + B(1 – v) (1 + v²) + (Cv + D) (1 – v²).
Putting v= 1,
1-3 = A(2) (2)
⇒ A = -1/2

Putiing v = -1, -1 + 3 = B(2)(1 + 1)
⇒ B = 1/2

Putting v = 0
⇒ 0 = A(1)(1) + B(1)(1) + D(1)
⇒ 0 = \(-\frac{1}{2}+\frac{1}{2}\) + D
D = 0
Comparing coeff. of v³, 1 = A – B – C
⇒ C = A – B – 1 = \(-\frac{1}{2}-\frac{1}{2}\) – 1 = -2
∴ From (2),

Squaring , x² – y² = c’²(x²+ y²)²
⇒ x² – y² = c’² (x² + y² )²
where c’² = c,
which is the required solution.

Question 21.
Show that the differential equation:
2ye^x/y dx + (y – 2x e^x/y) dy = 0 is homogeneous and find the particular solution, given that x = 0 when y = 1. (C.B.S.E. 2013)
Solution:
(i) The given equation is :
2ye^x/y dx + (y – 2x e^x/y) dy = 0

Thus f(x, y) is homogeneous function of degree zero.

⇒ 2e^v = – log |y| + c
⇒ e^x/y = -log|y| + c …………….(2)

Now x = 0 when y = 1,
∴ 2(1) = -log |1| + c
⇒ 2 = – log 1 + c
⇒ 2 = —0 + c
⇒ c = 2.

Putting in (2),
2e^x/y = – log |y|+ 2,
which is the required solution.

Question 22.
Solve the differential equation:
(1 + x²)\(\frac{d y}{d x}\) + 2xy – 4x² =0, subject to the initial condition y (0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :

Multiplying (1) by (1 + x²), we get:
(1 + x²)\(\frac{d y}{d x}\) + 2xy = 4x² dx
⇒ \(\frac{d}{d x}\) y.(1 + x²) = 4x²

Integrating, y.(1 + x²) = ∫ 4x² dx = \(\frac{4 x^{3}}{3}\) + C
⇒ y(1 + x²) = \(\frac{4}{3}\) x² + C …(2)
When x = 0, y = 0,
∴ C = 0 + C
⇒ C = 0.
ry 4 T
Putting in (2), y(1 + x²) = \(\frac{4}{3}\) x³ , which is the required solution.

Question 23.
Solve the differential equation :
\(\frac{d y}{d x}-\frac{2 x}{1+x^{2}} y\) = x² + 2 (C.B.S.E. 2019)
Solution:
The given equation is :

Hence, y = (1 + x²) (x + tan^-1 x + C).

Question 24.
Find the general solution of the following differential equation:
(1 + y²) + (x – e^tan-1y)\(\frac{d y}{d x}\) (C.B.S.E. 2016)
Solution:
The given equation is:


Putting xee^tan-1y = \(\frac{1}{2}\)e^2tan-1y + c
x = \(\frac{1}{2}\)e^tan-1y + c
which is the required solution.

Question 25.
(i) Solve the differential equation:
(tan^-1 y – x)dy = (1 + y²) dx. (N.C.E.R.T.; C.B.S.E. 2015)
(ii) Find the particular solution when x = 0, y = 0. (A.I.C.B.S.E. 2013)
Solution:
(i) The given equation can be written as :
\(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) …… (1)
Comparing with \(\frac{d x}{d y}\)+ Px = Q , we have:


which is the required solution.

(ii) When
x – 0, y = 0.
0 = (tan^-10 – 1) + ce-tan^-10,
⇒ 0 – (0 – 1) + ce^-0
⇒ 0 = – 1 + c
⇒ c = 1.
Putting in (3),
x = (tan^-1 y – 1) + e^-tan-1y,
which is the required particular solution.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 11 Three Dimensional Geometry. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 11 Important Extra Questions Three Dimensional Geometry

Three Dimensional Geometry Important Extra Questions Very Short Answer Type

Question 1.
Find the acute angle which the line with direction-cosines \(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{6}}, n>\) makes with positive direction of z-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
l² + m² + n² = 1
\(\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{6}}\right)^{2}\) + n² = 1
⇒ \(\frac{1}{3}+\frac{1}{6}\) + n² = 1
n² = 1 – \(\frac{1}{2}\)
n² = \(\frac{1}{2}\)
n = \(\frac{1}{\sqrt{2}}\)
Thus, cos α = \(\frac{1}{\sqrt{2}}\)
Hence, α = 45° or \(\frac{\pi}{4}\)

Question 2.
Find the direction-cosines of the line.
\(\frac{x-1}{2}=-y=\frac{z+1}{2}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given line is \(\frac{x-1}{2}=\frac{y}{-1}=\frac{z+1}{2}\)
Its direction-ratios are <2,-1,2>.
Hence, its direction- cosine are:

Question 3.
If α, β, γ are direction-angles of a line, prove that cos 2a + cos 2P + cos 2y +1 = 0. (N.C.E.R.T.)
Solution:
Since α, β, γ are direction-angles of a line,
∴ cos² α + cos² β + cos²γ = 1

⇒ 1 + cos2α + 1 + cos2β + 1 + cos2γ = 2
⇒ cos 2α + cos 2β + cos 2γ + 1 = 0, which is true.

Question 4.
Find the length of the intercept, cut off by the plane 2x + y – z = 5 on the x-axis.   (C.B.S.E. Outside Delhi 2019)
Solution:
The given plane is2x + y – z = 5
⇒ \(\frac{x}{5 / 2}+\frac{y}{5}+\frac{z}{-5}=1\)
Its intercepts are \(\frac{x}{5 / 2}\), 5 and -5.
Hence, the length of the intercept on the x-axis is \(\frac{x}{5 / 2}\)

Question 37.
Find the length of the perpendicular drawn from the point P(3, -4,5) on the z-axis.
Solution:
Length of the perpendicular from P(3, -4,5) on the z-axis
= \(\sqrt{(3)^{2}+(-4)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5 units.

Question 5.
Find the vector equation of a plane, which is at a distance of 5 units from the origin and whose
normal vector is \(2 \hat{i}-\hat{j}+2 \hat{k}\)
Solution:
Let \(\vec{n}=2 \hat{i}-\hat{j}+2 \hat{k}\)

Question 6.
If a line makes angles 90°, 135°, 45° with the x,y and z-axes respectively, find its direction cosines.
Solution:
Direction cosines of the line are :
< cos 90°, cos 135°, cos 45° >
<0, \(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\)>

Question 7.
Find the co-ordinates of the point where the line through the points A (3,4,1) and B (5,1, 6) crosses the xy-plane.
The equations of the line through A (3,4,1) and B (5,1,6) are:

Any point on (1) is (3 + 2k,4- 3k, 1 + 5k) …………. (2)
This lies on xy-plane (z = 0).
∴ 1 + 5k = 0 ⇒ k = \(-\frac{1}{5}\)
Putting in (2), [ 3-\(\frac{2}{5}\), 4 + \(\frac{3}{5}\), 1-1)
i.e. (\(\frac{13}{5}\), \(\frac{23}{5}\), 0)
which are the reqd. co-ordinates of the point.

Question 8.
find the vector equation ofthe line which passes through the point (3,4,5) and is parallel to the vector \(2 \hat{i}+2 \hat{j}-3 \hat{k}\)
Solution:
The vector equation of the line is \(\vec{r}=\vec{a}+\lambda \vec{m}\)
i.e., \(\vec{r}=(3 \hat{i}+4 \hat{j}+5 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}-3 \hat{k})\)

Three Dimensional Geometry Important Extra Questions Short Answer Type

Question 1.
Find the acute angle between the lines whose direction-ratios are:
< 1,1,2 > and <-3, -4,1 >.
Solution:

Question 2.
Find the angle between the following pair of lines:
and
\(\frac{-x+2}{-2}=\frac{y-1}{7}=\frac{z+3}{-3}\) and \(\frac{x+2}{-1}=\frac{2 y-8}{4}=\frac{z-5}{4}\)
and check whether the lines are parallel or perpendicular. (C.B.S.E. 2011)
Solution:
The given lines can be rewritten as :
\(\frac{-x+2}{-2}=\frac{y-1}{7}=\frac{z+3}{-3}\) ………….. (1)
\(\frac{x+2}{-1}=\frac{2 y-8}{4}=\frac{z-5}{4}\) ………..(2)
Here < 2,7, – 3 > and < -1,2,4 > are direction- ratios of lines (1) and (2) respectively.

Hence, the given lines aife perpendicular.

Question 3.
Find the vector equation of the line joining (1.2.3) and (-3,4,3) and show that it is perpendicular to the z-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
Vector equation of the line passing through
(1.2.3) and(-3,4,3)is \(\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\)
where \(\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}\) and \(\vec{b}=-3 \hat{i}+4 \hat{j}+3 \hat{k}\)
⇒ \(\vec{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-4 \hat{i}+2 \hat{j})\) …(1)
Equation of z-axis is \(\vec{r}=\mu \hat{k}\) …(2)
Since \((-4 \hat{i}+2 \hat{j}) \cdot \hat{k}=0\) = 0,
∴ Line (1) is perpendicular to z-axis.

Question 4.
Find the vector equation of the plane, which is \(\frac{6}{\sqrt{29}}\) at a distance of
units from the origin and its normal vector from the origin is \(2 \hat{i}-3 \hat{j}+4 \hat{k}\) . Also, find its cartesian form. (N.C.E.R.T.)
Solution:

Question 5.
Find the direction-cosines of the unit vector perpendicular to the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) +1 = 0 through the origin. (N.C.E.R.T.)
Solution:
The given plane is \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) + 1 = 0
\(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) = 1 ………… (1)
Now \(|-6 \hat{i}+3 \hat{j}+2 \hat{k}|=\sqrt{36+9+4}\)
\(=\sqrt{49}=7\)
Dividing (1) by 7,
\(\vec{r} \cdot\left(-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\right)=\frac{1}{7}\)
which is the equation of the plane in the form \(\vec{r} \cdot \hat{n}=p\)
Thus, \(\hat{n}=-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\)
which is the unit vector perpendicular to the plane through the origin.
Hence, the direction-cosines of \(\hat{n}\) are \(<-\frac{6}{7}, \frac{3}{7}, \frac{2}{7}>\)

Question 6.
Find the acute angle between the lines
\(\frac{x-4}{3}=\frac{y+3}{4}=\frac{z+1}{5}\) and \(\frac{x-1}{4}=\frac{y+1}{-3}=\frac{z+10}{5}\)
Solution:
Vector in the direction of first line
\(\frac{x-4}{3}=\frac{y+3}{4}=\frac{z+1}{5}\) ,
\(\vec{b}=(3 \hat{i}+4 \hat{j}+5 \hat{k})\)

Vector in the direction of second line
\(\frac{x-1}{4}=\frac{y+1}{-3}=\frac{z+10}{5}\) ,
\(\vec{d}=4 \hat{i}-3 \hat{j}+5 \hat{k}\)
∴ θ, the angle between two given lines is given by:

Question 7.
Find the angle between the line:
\(\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-\hat{j}+3 \hat{k})\) and the plane \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})=4\) Also, find whether the line is parallel to the plane or not .
Solution:
The given line is :
\(\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-\hat{j}+3 \hat{k})\)
and the given plane is \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) = 4.
Now the line is parallel to 2\(\hat{i}\) – \(\hat{j}\) + 3\(\hat{k}\) and nor¬mal to the plane 2\(\hat{i}\) + \(\hat{i}\) – \(\hat{k}\)
If ‘θ’ is the angle between the line and the plane,
then \(\left(\frac{\pi}{2}-\theta\right)\) is the angle between the line and normal to the plane.
Then

Hence, the line is parallel to the plane.

Question 8.
Find the value of ‘λ’, so that the lines:
\(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2}\) and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles. Also, find whether the lines are intersecting or not
Solution:
(i) The given lines are
\(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2}\) ……………….(1)
and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) ……….. (2)
These are perpendicular if:

Hence λ = 1.

(ii) The direction cosines ofline(1) are <-3,1,2>
The direction cosines of line (2) are < -3,1, -5 >
Clearly, the lines are intersecting.

Question 9.
Find the angle between the line: \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) and the plane: 3x + 4y + z + 5 = 0.
x-2 y+1 z-3
Sol. The given line is \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) ………..(1)
and the given plane is :
3x + 4y + z + 5 = 0 …(2)
If the line (1) makes an angle ‘0’ with the plane (2), then the line (1) will make angle (90° – 0) with the normal to the plane (2).
Now direction-ratios of line (1) are:
<3, -1,-2>
and direction-ratios of normal to plane (2) are <3,4,1>.
∴ cos (90° – θ)

Question 10.
State when the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=\vec{d}\) . Show that the line \(\vec{r}=\hat{i}+\hat{j}+\lambda(\hat{2}+\hat{j}+4 \hat{k})\) is parafiel to the plane \(\vec{r} \cdot(-2 \hat{i}+\hat{k})\) = 5. Also, find the distance between the line and the plane.
Solution:
(i) A line is parallel to the plane if it is perpendicular to the normal to the plane.
The given line is \(\vec{r}=\vec{a}+\lambda \vec{b}\)
⇒ \(\vec{b}\) is parallel to the line.
The given plane is \(\vec{r} \cdot \vec{n}=\vec{d}\)

⇒ \(\vec{n}\) is normal to the plane.
Thus the line is parallel to the plane when
\(\vec{b} \cdot \vec{n}\) =0.

(ii) Here \(\vec{b}=2 \hat{i}+\hat{j}+4 \hat{k}\) and \(\vec{n}=-2 \hat{i}+\hat{k}\)
Now \(\vec{b} \cdot \vec{n}\) = (2) (- 2) + (1) (0) + (4) (1)
= -4 + 0 + 4 = 0.
Hence, the given line is parallel to the given plane.

(iii) (1,1,0) is a point on the given line.
Equation of the plane is-2x + z- 5= 0.
∴ Reqd. distance
= \(\left|\frac{-2(1)+0-5}{\sqrt{4+0+1}}\right|=\frac{7}{\sqrt{5}}=\frac{7 \sqrt{5}}{5}\)units.

Three Dimensional Geometry Important Extra Questions Very Long Answer Type 2

Question 1.
Find the shortest distance between the lines:\(\vec{r}=(4 \hat{i}-\hat{j})+\lambda(\hat{i}+{2} \hat{j}-{3} \hat{k})\) and \(\vec{r}=(\hat{i}-\hat{j}+2 \hat{k})+\mu(2 \hat{i}+4 \hat{j}-5 \hat{k})\) (C.B.S.E. 2018)
Solution:
Comparing given equations with:

Question 2.
A line makes angles α, β, γ, δ with the four diagonals of a cube, prove that:
cos² α + cos² β + cos² γ + cos² δ= \(\frac{4}{3}\). (N.C.E.R.T.)
Solution:
Let O be the origin and OA, OB, OC (each = a) be the axes.

Thus the co-ordinates of the points are :
O (0,0,0), A (a, 0,0), B (0, a, 0), C (0,0, a),
P (a, a, a), L (0, a, a), M (a, 0, a), N (a, a, 0).
Here OP, AL, BM and CN are four diagonals.
Let < l, m, n > be the direction-cosines of the given line.

Now direction-ratios of OP are:
<a-0,a-0,a-0>i.e.<a,a,a>
i.e. < 1,1,1 >,
direction-ratios of AL are:
<0-a, a-0, a-0> i.e. <-a,a,a>
i.e. <-l, 1,1 >,
direction-ratios of BM are:
<a-0,0-a, a-0>
i.e. <a,-a,a> i.e. < 1,-1, 1 >
and direction-ratios of CN are:
<a-0,a-0,0-a> i.e. <a,a,-a>
i.e. < 1,1,-1 >.

Thus the direction-cosines of OP are :
\(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
the direction-cosines of AL are:
\(<-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
the direction-cosines of BM are :
\(<\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
and the direction-cosines of CN are :
\(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}>\)
If the given line makes an angle ‘a’ with OP, then :

and cos δ = \(\frac{|l+m-n|}{\sqrt{3}}\) ………… (4)
Squaring and adding (1), (2), (3) and (4), we get:
cos² α + cos² β + cos² γ + cos²δ
= \(\frac { 1 }{ 3 }\) [(l + m + n)² + (-l + m + n)²
+ (l-m + n)² + (l + m — n)²]
= \(\frac { 1 }{ 3 }\) [4(l² + m² + n²)] = \(\frac { 1 }{ 3 }\) [4(1)].
Hence,cos² α + cos² β + cos² γ + cos²δ = \(\frac { 4 }{ 3 }\)

Question 3.
Find the equation of the plane through the line \(\frac{x-1}{3}=\frac{y-4}{2}=\frac{z-4}{-2}\) and parallel to the line:
\(\frac{x+1}{2}=\frac{1-y}{4}=\frac{z+2}{1}\)
Hence, find the shortest distance between the lines. (C.B.S.E. Sample Paper 2018-19)
Solution:
The two given lines are:
\(\frac{x-1}{3}=\frac{y-4}{2}=\frac{z-4}{-2}\) ………… (1)
and \(\frac{x+1}{2}=\frac{1-y}{4}=\frac{z+2}{1}\) ………….. (2)
Let <a, b, c> be the direction-ratios of the normal to the plane containing line (1).
∴ Equation of the plane is:
a(x- l) + b(y-4) + c(z-4) …(3),
where 3a + 2b – 2c = 0 …(4)
[∵ Reqd. plane contains line (1)] and 2a – 4b + 1.c = 0
[∵ line (1) a parallel to the reqd. plane] Solving (4) and (5),

Putting in (3),
6k(x- 1) + 7k(y – 4) + 16k(z – 4) = 0
= 6(x – 1) + 7(y – 4) + 16(z – 4) =0
[∵k ≠ 0]
⇒ 6x + 7y+ 16z-98 = 0,

which is the required equation of the plane.
Now, S.D. between two lines = perpendicular distance of (-1,1, – 2) from the plane

6(—1) + 7(1) +16(-2) – 98
V(6)2+(7)2+(16)2
-6 + 7-32-98 V36 + 49 + 256

Question 4.
Find the Vector and Cartesian equations of the plane passing through the points (2, 2, -1), (3,4,2) and (7,0,6). Also, find the vector equa¬tion of a plane passing through (4,3,1) and parallel to the plane obtained above. (C.B.S.E. 2019)
Solution:
(i) Cartesian equations
Any plane through (2,2, -1) is :
a(x – 2) + b(y- 2) + c(z + 1) = 0 … (1)
Since the plane passes through the points (3,4,2) and (7,0,6),
∴ a(3 – 2) + b(4 – 2) + c(2 +1) = 0
and a(7 – 2) + b(0 – 2) + c(6 + 1) = 0
⇒ a + 2b + 3c = 0 …(2)
and 5a – 2b + 7c = 0 …(3)
Solving (2) and (3),\(\frac{a}{14+6}=\frac{b}{15-7}=\frac{c}{-2-10}\)
⇒ \(\frac{a}{20}=\frac{b}{8}=\frac{c}{-12}\)
⇒ \(\frac{a}{5}=\frac{b}{2}=\frac{c}{-3}\) = k (say), value k ≠ 0.
∴ a = 5k,b = 2k and c = -3k,
Putting the values of a, b, c in (1), we get:
5k(x – 2) + 2k(y – 2) – 3k(z + 1) = 0
⇒ 5(x-2) + 2(y-2)-3(z+ 1) =0[∵ k ≠ 0]
=» 5x- 10 + 2y-4-3z-3 = 0
=» 5x + 2y-3z-17 = 0, …(4)
which is the reqd. Cartesian equation.
Its vector equation is \(\vec{r} \cdot(5 \hat{i}+2 \hat{j}-3 \hat{k})\) =17.

(ii) Any plane parallel to (4) is
5x + 2y – 3z + λ – 0 … (5)
Since it passes through (4, 3,1),
5(4) + 2(3) – 3(1) + λ = 0
⇒ 20 + 6 — 3 + λ = 0
⇒ λ = -23.
Putting in (5), 5x + 2y – 3z – 23 = 0, which is the reqd. equation.
Its vector equation is \(\vec{r} \cdot(5 \hat{i}+2 \hat{j}-3 \hat{k})\) = 23.

Question 5.
Find the co-ordinates of the foot of the perpendicular drawn from the point A (1,8,4) to the line joining B (0, -1,3) and C (2,-3,-1). (A.I.C.B.S.E. 2016)
Solution:
Any point on BC, which divides [BC] in the ratio k: 1,is:

This becomes M, the foot of perp. from A on BC
if AM⊥BC …(2)
But direction-ratios of BC are:
<2-0,- 3 + 1,-1 -3 > i.e. < 2,-2,-4 >
i.e, <1, -1 > -2>
and direction-ratio of AM are:
\(<\frac{2 k}{k+1}-1, \frac{-3 k-1}{k+1}-8, \frac{-k+3}{k+1}-4>\)
i.e. < k- 1,- 11k:-9, -5k— 1 >
∴ Due to (2), (1) (k- 1) + (- 1) (-1 1k-9) + (-2)(-5k- 1) = 0
⇒ k – 1 + 11k + 9 + 10k + 2 = 0
⇒ 22k + 10 = 0
⇒ k = \(-\frac{5}{11}\)
∴ From (1), the co-ordinates of M, the foot of perp. are:

Question 6.
(a) Find the image of the point (1,6,3) in the line:
\(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\)
(C.B.S.E. 2010 C)
(b) Also, write the equation of the line joining the given point and its image and find the length of the segment joining the given point and its image. (C.B.S.E. 2010 C)
Solution:
(a) Let P be the given point (1, 6, 3) and M, the foot of perpendicular from P on the given line AB:

Any point on the given line is:
(k, 1+2k, 2+3k)
For some value of k, let the point be M.
∴ Direction-ratios of PM are:
<k-1,1+2k-6, 2 + 3k – 3> i.e. .
Since PM ⊥AB ,
∴ (1) (k-1) + (2)(2k-5) + (3) (3k-1) = 0
⇒ k-l +4k – 10 + 9&-3 = 0
⇒ 14 k = 14
⇒ k = 1.

∴ Foot of perpendicular M is (1,1 + 2,2 + 3) i.e. (1,3,5).
Let P'(α, β, γ) be the image of P in the given line. Then M is the mid-point of [PP’].
∴ \(\)
⇒α + 1 = 2, β + 6 = 6, γ+3 = 10
⇒ α = 1, β = 0, γ = 7.
Hence, the reqd. image is (1,0,7).

(b) (i) The equations of the line PP’ are :

(ii) Length of segment [PP’]

Question 7.
Find the co-ordinates of the foot of perpendicu¬lar and the length of the perpendicular draw n from the point P (5,4,2) to the line:
\(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\)
Also, find the image of P in this line. (A.I.C.B.S.E. 2012)
Solution:
(i) The given line is :
\(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\)
i.e, \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) …………… (1)
The given point is P (5,4,2).

Let M be the foot of perpendicular from P on the given line AB.
Any point on (1) is (-1 + 2k, 3 +3k, l – k).
For some value of k, let the point be M.
Direction-ratios of PM are:
<-1+2k-5, 3+3k-4, 1-k-2>
i.e, <2k – 6, 3k – 1, -k – 1>
Since PM ⊥ AB ,
∴ 2(2k – 6) + 3 (3k – 1) + (-1)(-k – 1) = 0
⇒4k – 12 + 9k – 3 + k + 1 = 0
⇒14k – 14 = 0
⇒ k = 1

Foot of perpendicular M is
(-1+2, 3+3, 1,-1) i.e (1,6,0)
(ii) Length of Perpendicular
= \(\sqrt{(5-1)^{2}+(4-6)^{2}+(2-0)^{2}}\)
= \(\sqrt{16+4+4}=\sqrt{24}=2 \sqrt{6}\) units

(iii) Let P’ (α, β, γ) be the image of P in the given line.
Then M is the mid-points of [PP’].
∴ \(\frac{\alpha+5}{2}=1, \frac{\beta+4}{2}=6, \frac{\gamma+2}{2}=0\)
⇒ α+5 = 2, β + 4=12, γ+2 = 0
⇒ α = -3,β = 8,γ=-2.
Hence, the reqd. image is (-3,8, -2).

Question 8.
Find the distance between the lines L₁ and L₂ given by:
\(\vec{r}=\hat{i}+2 \hat{j}-4 \hat{k}+\lambda(2 \hat{i}+3 \hat{j}+6 \hat{k})\) and
\(\vec{r}=3 \hat{i}+3 \hat{j}-5 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+6 \hat{k})\) (N.C.E.R.T.)
Solution:
Clearly, L₁ and L₂ are parallel.
Comparing given equations with:
\(\vec{r}=\vec{a}_{1}+\lambda \vec{b}\) and \(\vec{r}=\vec{a}_{2}+\mu \vec{b}\), we have:
\(\vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k}\), so that
\(|\vec{b}|=\sqrt{4+9+36}=\sqrt{49}=7\)

∴ d, the distance between the given lines is given by:

Question 9.
Find the vector equation of the plane that contains the lines \(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+2 \hat{j}-\hat{k})\) and the points (-1, 3, -4). Also find the length of the perpendicular from the point (2,1,4) to the plane, thus obtained. (Delhi 2019)
Solution:
Let required plane be
a(x+ l) + b(y-3) + c(z + 4) = 0 …(1)

Plane contains the given line, so it will also con-tain the point (1,1,0).
So, 2a – 2b + 4c = 0
or a-b + 2c = 0
Also, a + 2b – c = 0
From (2) and (3),
\(\frac{a}{-3}=\frac{b}{3}=\frac{c}{3}\) …………(4)

From (1) and (4), required plane is
-3(x + l) + 3(y-3) + 3(z + 4) = 0
⇒ -x-l+;y-3 + z + 4 = 0
⇒ -x + y + z = 0.
Its vector equation is :
\(\vec{r} \cdot(-\hat{i}+\hat{j}+\hat{k})\) = 0.
Length of perpendicular from
\((2,1,4)=\frac{|-2+1+4|}{\sqrt{(-1)^{2}+1^{2}+1^{2}}}=\sqrt{3}\)

Question 10.
Find the vector equation of the plane which contains the line of intersection of the planes:
\(\vec{r} \cdot(\hat{i}+{2} \hat{j}+{3} \hat{k})\) – 4 = 0,
\(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) + 5 = 0
and which is perpendicular to the plane \(\vec{r} \cdot(5 \hat{i}+3 \hat{j}-6 \hat{k})\) + 8 = 0
(Outside Delhi 2019)
Solution:
Required equation of the plane is :

This is perpendicular to the plane
\(\vec{r}\) (5 \(\hat{i}\) + 3 \(\hat{j}\) — 6\(\hat{k}\)) + 8 = 0
⇒ (1+2λ) (5) + (2 + λ) (3) + (3 – λ.) (-6)=0
⇒ 5 + 10λ + 6 + 3λ – 18 + 6λ = 0 ⇒ 191 = 7
⇒19λ = 7
⇒λ = \(\frac { 7 }{ 19 }\)
Puttiong in (1),

Question 11.
Show that die line of intersection of the planes: x + 2y + 3z = 8 and 2x + 3y + 4z = 11 is coplanar with the line:
\(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z+1}{3}\)
Also, find the equation of die plane containing them. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given line is \(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z+1}{2}\) ………. (1)
This is coplanar with the line determined by the planes:
x + 2y + 3z – 8 = 0 …(2)
and 2x + 3y + 4z – 11 =0 …(3)
Here, we show that there exists a plane, which passes through the intersection of (2) and (3) and contains line (1).
Now equation of the plane through the intersection of (2) and (3) is:
(x+2y + 3z-8) + 1(2x+3y+ 4z-11) = 0 …(4)
This passes through 1, -1),
∴ (-1 -2-3-8) + k(-2-3-4-11) = 0
∴ -14-20k = 4
k = \(-\frac { 7 }{ 10 }\)
Putting in (4),
(x + 2y + 3z-8) – \(\frac { 7 }{ 10 }\)(2x + 3y + 4z – 11) = 0
=» (10x + 20y + 30z – 80)
-7 (2x + 3y + 4z – 11) = 0
⇒ 4x + y – 2z + 3 = 0 …(5)
If < a₁ , b₁ , c₁ > are direction-ratios of line (1)
and < a₂, b₂, c₂ > are direction-ratios of normal to plane (5), then
a₁a₂+ b₁b₂+ c₁ c₂ = (1) (4) + 2 (1) + 3 (-2) = 0,
which implies that line (1) lies in plane (5). Hence, the two lines are coplanar and the equation of the plane containing them is 4x + y-2z + 3=0.

Question 12.
Find the vector equation of the line passing through the point (2,3, -1) and parallel to the planes:
\(\vec{r} \cdot(3 \hat{i}+4 \hat{j}+2 \hat{k})\) = 5 andr \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}-2 \hat{k})\) = 4.
Solution:
The given planes are:
\(\vec{r} \cdot(3 \hat{i}+4 \hat{j}+2 \hat{k})\) = 5 and \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}-2 \hat{k})\) = 4
i.e. 3x + 4y + 2z = 5 and 3x- 2y – 2z = 4
⇒3x + 4y + 2z-5 = 0 ……(1)
and 3x – 2y – 2z – 4 = 0 …………. (2)
Let the line through (2,3, -1) be:
\(\frac{x-2}{a}=\frac{y-3}{b}=\frac{z+1}{c}\) …………. (3)

Since (3) is parallel to (1),
∴ a(3) + h(4) + c(2) = 0 -(3)
i.e. 3a + 4b + 2c = 0
Since (3) is parallel to (2), …(4)
∴ (a) (3) + b (-2) + c (-2) = 0 …(5)
⇒ 3a -2b -2c = 0

Question 13.
Find the equation of a plane passing through the points A (2,1,2) and B(4, – 2,1) and per-pendicular to plane \(\vec{r} \cdot(\hat{i}-2 \hat{k})\) = 5. Also, find
the coordinates of the point, where the line pass-ing through the points (3,4,1) and (5,1, 6) crosses the plane thus obtained.
Solution:
Let P(x, y, z) be any point on the plane, which
passes through A(2,1,2) and B(4, -2,1).
∴ \(\overrightarrow{\mathrm{AP}}\) and \(\overrightarrow{\mathrm{AB}}\) lie on the required plane.
Also, the required plane is perpendicular to the
given plane \(\vec{r} \cdot(\hat{i}-2 \hat{k})\) = 5.
∴ Normal to the given plane \(\overrightarrow{n_{1}}=(\hat{i}-2 \hat{k})\) lies on the required plane
⇒ \(\overrightarrow{\mathrm{AP}}\), \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{n_{1}}\) are coplanar,
where \(\overrightarrow{\mathrm{AP}}\) = (x-2) \(\hat{i}\) +(y-1)\(\hat{j}\) + (z-2)\(\hat{k}\)
and \(\overrightarrow{\mathrm{AB}}\) = 2\(\hat{i}\) – 3\(\hat{j}\) – \(\hat{k}\)

⇒ (x-2)(6-0)-(y-1)(-4 + 1) + (z-2)(0 + 3) =0
⇒ 6x – 12 + 3y -3 + 3z – 6 =0
⇒ 2x + y + z = 7 …(1)
Line passing through L(3,4,l) and M(5,1,6) is:

General point on the line is Q(2λ,+ 3, -3λ,+4, 5λ.+1).
Since the line (2) crosses plane (1),
∴ the points Q should satisfy (1).
2(2λ+3) + (-3λ+4) + (5λ,+1) = 7
⇒ 4λ + 6 – 3λ,+4 + 5λ,+ l =7
⇒ 6λ = -4
λ = \(-\frac{2}{3}\)
Hence, the point Q is (\(-\frac{4}{3}\)+3, 2+4, \(-\frac{10}{3}\)+1)
i.e, (\(-\frac{5}{3}\), 6, \(-\frac{7}{3}[latex])

Question 14.
Find the co-ordinates of the point P, where the line through A(3, -4,-5) and B (2, – 3, 1) crosses the plane passing through three points L(2,2,1), M(3,0,1) and N(4, -1,0). Also, find the ratio in which P divides the line segment AB. {C.B.S.E. 2016)
Solution:
Any plane through L(2,2,1) is:
a(x-2) + b(y-2) + c(z-1) = 0 …(1)
Since (1) passes through M(3,0,1),
∴ a(3-2) + b(0-2) + c(1 – 1) = 0
⇒ a-2b + 0 .c = 0 …(2)
Since (1) passes through N (4, – 1,0),
∴ a(4 – 2) + b(- 1 – 2) -(- c(0 – 1) – 0
⇒ 2a – 3b – c = 0 …(3)
Solving (2) and (3),
[latex]\frac{a}{2+0}=\frac{b}{0+1}=\frac{c}{-3+4}=k \text { (say) }\)
⇒ a = 2k,b = k,c = k.
Putting in (1),
2k(x-2) + k(y-2) + k(z- 1) = 0 ⇒ 2(x-2) + (y-2) + (z-l) = O[\-fc*0]
⇒ 2x + y + z-l = 0 …(4)
Now equations of AB are:

and z = -5 + 6r.
Any point on AB is
P(-r+3, r-4,6r-5) …(5)
This lies on plane (4).
∴ 2(-r + 3) + (r-4) + (6r-5)-7 = 0
⇒ 5r = 10
⇒ r= 2.
Putting in (5), the co-ordinates of P are (1,-2,7).
Let P divide the segment [AB] in the ratio of k: 1.

Comparing \(\frac{3+2 k}{k+1}\) = 1
3 + 2k = k + 1
k = -2
Hence, P divides the line segment [AB] in the ratio 2:1 externally.

Question 15.
Find the distance of the point (-1,-5, -10) from the point of intersection of the line \(\vec{r} =2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+\mathbf{1 2} \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})\) = 5. (C.B.S.E. 2018)
Solution:
The given lines is :
\(\vec{r}=2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+12 \hat{k})\)
i.e , \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}\) ……….(1)
and the given plane is r • (J — j + k) = 5
i.e. x – y + z = 5 …(2)
Any point on (1) is (2 + 3k, – 1 + 5k, 2 + 12k)
This lies on (2) if
2 + 3k + 1 – 4k + 2+12k) = 5
⇒ 11k = 0
⇒ k = 0.
Putting in (3), the point of intersection is (2,-1,2).
Its distance from (-1, -5, -10)
= \(\sqrt{(-1-2)^{2}+(-5+1)^{2}+(-10-2)^{2}}\)
= \(\sqrt{9+16+144}=\sqrt{169}\) = 13 units.

Question 16.
Find the vector equation of a line passing through the point (2,3,2) and parallel to the line:
\(\vec{r}=(-2 \hat{i}+3 \hat{j})+\lambda(\hat{2} \hat{i}-3 \hat{j}+6 \hat{k})\)
Also, find the distance between these two lines. Sol. The given line is
r = (-2i + 3j) + X{2i -3j + 6k) …(1)
The required line is :
\(\vec{r}=(2 \hat{i}+3 \hat{j}+2 \hat{k})+\mu(2 \hat{i}-3 \hat{j}+6 \hat{k})\) …(2)
Now, \(\overrightarrow{a_{1}}=-2 \hat{i}+3 \hat{j}\) , \(\overrightarrow{a_{2}}=2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(\vec{b}=2 \hat{i}-3 \hat{j}+6 \hat{k}\)
\(\vec{b}=2 \hat{i}-3 \hat{j}+6 \hat{k}\)
\(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}=4 \hat{i}+2 \hat{k}\)
Reqd. distance,

Question 17.
Find the co-ordinates of the foot of the perpendicular Q drawn from P(3,2,1) to the plane 2x – y + z + 1 = 0. Also,find the distance PQ and the image of the point P treating this plane as a mirror.
Solution:
(i) Equation of PQ is \(\frac{x-3}{2}=\frac{y-2}{-1}=\frac{z-1}{1}=\lambda\)

∴ Co-ordinates of Q are (2λ + 3, – λ + 2, λ + 1).
Since Q lies on the plane 2x-y + z+ 1=0,
4λ + 6 + λ – 2 + λ + 1 + 1 = 0
⇒ 6λ + 6 = 0
⇒ λ = – 1.
∴ Co-ordinates of Q are (- 2 + 3,1 + 2, -1 + 1)
i.e.,{ 1,3,0).

(ii) PQ = \(\sqrt{(1-3)^{2}+(3-2)^{2}+(0-1)^{2}}\)
= \(\sqrt{4+1+1}=\sqrt{6}\) units

(iii) Let P'(x’, y’, z’) be the image
∴ \(\frac{x^{\prime}+3}{2}=1, \frac{y^{\prime}+2}{2}=3, \frac{z^{\prime}+1}{2}=0\)
= x’ = -1, y’ = 4, z’ = -1.
Hence, the image of the point P is (- 1,4, – 1).

Question 18.
Find the vector equation of the plane determined by the points A(3, -1, 2), B(5, 2, 4) and C(-l, -1, 6). Hence, find the distance of the plane, thus obtained, from the origin.
Solution:
The equation of the plane is

⇒ (x-3) (12 – 0) – (y+1) (8 + 8) + (z-2) (0+12) = 0
⇒ 12(x-3)-16(y+1) +12(z-2) = 0
⇒ 3(x-3)-4(y + 1) + 3(z-2) = 0
⇒ 3x – 4y + 3z = 19.
Its vector equation is r \(\vec{r} \cdot(3 \hat{i}-4 \hat{j}+3 \hat{k})\) = 19. Distance of the plane from the origin
= \(\frac{|0-19|}{\sqrt{9+16+9}}=\frac{19}{\sqrt{34}}=\frac{19 \sqrt{34}}{34}\) = units.

Question 19.
Find the co-ordinates of the point where the line \(\frac{x-8}{4}=\frac{y-1}{1}=\frac{z-3}{8}\) intersects the plane 2x + 2y + z=3. Also, find the angle between the line and the plane.
Solution:
(i) The given line is \(\frac{x-8}{4}=\frac{y-1}{1}=\frac{z-3}{8}\)…(1)
and the given plane is2x + 2y + z- 3 = 0 …(2)
Any point on line (1) is (8 + 4-k, l + k, 3 + 8k) …(3)
This lies on plane (2).
∴ 2(8 + 4k) + 2(1 + k) + (3 + 8k) -3 = 0
16 + 8k + 2 + 2k +3 + 8 k – 3 = 0
⇒ 18k + 18 = 0 ⇒ k =-1.
Putting in (3), (4, 0, – 5), which are the required co-ordinates of the point.

(ii) If the line (1) makes an angle ‘θ’ with the plane (2), then the line (1) will make an angle of (90° – θ) with the normal to the plane (2).
Now, direction-ratios of the line (1) are <4,1, 8> and direction-ratios of the normal to the plane (2) are < 2,2,1 >.

Question 20.
Find x such that the four points:
A(5,x, 4), B(4,4,6), C(5,4, -3) and D(7,7, -2) are coplanar.
Solution:
Here,
\(\overrightarrow{\mathrm{AB}}\) = (4\(\hat{i}\) +4\(\hat{j}\) + 6\(\hat{k}\)) – (5\(\hat{i}\) +x\(\hat{j}\) + 4\(\hat{k}\))
= –\(\hat{i}\) +(4-x)\(\hat{j}\) + 2\(\hat{k}\) ,
\(\overrightarrow{\mathrm{BC}}\) = (5\(\hat{i}\) + 4\(\hat{j}\) – 3\(\hat{i}\))-(4\(\hat{i}\) + 4\(\hat{j}\) + 6\(\hat{k}\))
= \(\hat{i}\) – 9\(\hat{k}\)
and \(\overrightarrow{\mathrm{CD}}\) = (7\(\hat{i}\) + 7\(\hat{j}\) -2\(\hat{k}\))-(5\(\hat{i}\) + 4\(\hat{j}\) – 3\(\hat{k}\))
= 2\(\hat{i}\) + 3\(\hat{k}\) + \(\hat{k}\).
The four points are collinear if

⇒ (-1)(0 + 27)-(4-x)(l + 18) + 2(3-0) = 0
⇒ -27-76 + 19x +6=0
⇒ 19x=97.
Hence, x = \(\frac { 97 }{ 19 }\)

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 10 Vectors. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 10 Important Extra Questions Vectors

Vectors Important Extra Questions Very Short Answer Type

Question 1.
Classify the following measures as scalar and vector quantities:
(i) 40°
(ii) 50 watt
(iii) 10gm/cm³
(iv) 20 m/sec towards north
(v) 5 seconds. (N.C.E.R.T.)
Solution:
(i) Angle-scalar
(ii) Power-scalar
(iii) Density-scalar
(iv) Velocity-vector
(v) Time-scalar.

Question 2.
In the figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial. (N.C.E.R.T.)

Solution:
(i) \(\vec{a}, \vec{c}\) and \(\vec{a}\) are collinear vectors.
(ii) \(\vec{a}\) and \(\vec{c}\) are equal vectors.
(iii) \(\vec{b}\), \(\vec{c}\) and \(\vec{d}\) are co-initial vectors.

Question 3.
Find the sum of the vectors:
\(\vec{a}\) = \(\hat{i}-2 \hat{j}+\hat{k}\), \(\vec{a}\) = \(-2 \hat{i}+4 \vec{j}+5 \hat{k}\) and \(\vec{c}\) = \(\hat{i}-6 \hat{j}-7 \hat{k}\). (C.B.S.E. 2012)
Solution:
Sum of the vectors = \(\hat{a}+\hat{b}+\hat{c}\)

Question 4.
Find the vector joining the points P (2,3,0) and Q (-1, – 2, – 4) directed from P to Q. (N.C.E.R.T.)
Solution:
Since the vector is directed from P to Q,
∴ P is the initial point and Q is the terminal point.
∴ Reqd. vector = \(\overrightarrow{\mathrm{PQ}}\)

Question 5.
If \(\vec{a}=x \hat{i}+2 \hat{j}-z \hat{k}\) and \(\vec{b}=3 \hat{i}-y \hat{j}+\hat{k}\) are two equal vectors, then write the value of x + y + z. (C.B.S.E. 2013)
Solution:
Here
\(\vec{a}=\vec{b} \Rightarrow x \hat{i}+2 \hat{j}-z \hat{k}=3 \hat{i}-y \hat{j}+\hat{k}\)
Comparing,A: = 3,2 = -y i.e.y = -2,~z= 1 i.e. z = -1.
Hence, x + y + z = 3 – 2 – 1 = 0.

Question 6.
Find the unit vector in the direction of the sum of the vectors:
\(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}\) and \(\vec{b}=-\hat{i}+\hat{j}+3 \hat{k}\) (N.C.E.R.T.)
Solution:

Question 7.
Find the value of ‘p’ for which the vectors : \(3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel. (A.I.C.B.S.E. 2014)
Solution:
The given vectors \(3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel
If \(\frac{3}{1}=\frac{2}{-2 p}=\frac{9}{3}\) if 3 = \(\frac{1}{-p}\) = 3
if p = \(-\frac{1}{3}\)

Question 8.
If \(\vec{a}\) and \(\vec{b}\) are perpendicular vectors, \(|\vec{a}+\vec{b}|\) = 13 and \(|\vec{a}|\) =5, find the value of \(|\vec{b}|\) (A.I.C.B.S.E. 2014)
Solution:

[∵ \(\vec{a}\) and \(\vec{b}\) are perpendicular ⇒ \(\vec{a}\) \(\vec{b}\) = 0 ]

⇒ \(|\vec{b}|^{2}\) = 169 – 25 = 144.
Hence, \(|\vec{b}|\) = 12.

Question 9.
Find the magnitude of each of the two vectors \(\vec{a}\) and \(\vec{b}\) , having the same magnitude such that the angle between them is 60° and their scalar product is \(\frac { 9 }{ 2 }\) (C.B.S.E. 2018)
Solution:
By the question, \(|\vec{a}|=|\vec{b}|\) …(1)
Now \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\) cos θ
⇒ \(\frac { 9 }{ 2 }\) = \(|\vec{a}||\vec{a}|\) cos 60° [Using (1)]
⇒ \(\frac{9}{2}=|\vec{a}|^{2}\left(\frac{1}{2}\right)\)
⇒ \(|\vec{a}|^{2}\) = 9.
Hence, \(|\vec{a}|=|\vec{b}|\) = 3.

Question 10.
Find the area of the parallelogram whose diagonals are represented by the vectors: \(\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}\) and \(\vec{b}=2 \hat{i}-\hat{j}+2 \hat{k}\) (C.B.S.E. Sample Paper 2018-19)
Solution:

= \(\hat{i}\)(-6 + 4) – \(\hat{j}\)(4 – 8) + \(\hat{k}\)( – 2 + 6)
= – 2\(\hat{i}\) + 4\(\hat{j}\) + 4\(\hat{k}\).
∴ \(|\vec{a} \times \vec{b}|=\sqrt{4+16+16}=\sqrt{36}\)= 6.
∴ Area of the parallelogram = \(\frac{1}{2}|\vec{a} \times \vec{b}|\)
= \(\frac{1}{2}\) (6) = 3 sq. units.

Question 11.
Find the angle between the vectors: \(\vec{a}=\hat{i}+\hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have:\(\vec{a}=\hat{i}+\hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\)
If ‘θ’ be the angle between \(\vec{a}\) and \(\vec{b}\)

Question 12.
Find \(\vec{a} \cdot(\vec{b} \times \vec{c})\), if : \(\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}\), and \(\vec{c}=3 \hat{i}+\hat{j}+2 \hat{k}\) (A.I.C.B.S.E. 2014)
Solution:
We have:

= 2 (4 – 1) – (1) (-2 – 3) + 3 (-1 – 6)
= 6 + 5-21 = 11 – 21 = -10.

Vectors Important Extra Questions Short Answer Type

Question 1.
If θ is the angle between two vectors:
\(\hat{i}-2 \hat{j}+3 \hat{k}\) and \(3 \hat{i}-2 \hat{j}+\hat{k}\) ,find sinθ.   (C.B.S.E. 2018)
Solution:

Question 2.
X and Y are two points with position vectors \(\overrightarrow{3 a}+\vec{b}\) and \(\vec{a}-3 \vec{b}\) respectively. Write the po-sition vector of a point Z which divides the line segment XY in the ratio 2:1 externally. (C.B.S.E. Outside Delhi 2019)
Solution:
Position vector of
A = \(\frac{2(\vec{a}-3 \vec{b})-(3 \vec{a}+\vec{b})}{2-1}\) = \(-\vec{a}-7 \vec{b}\)

Question 3.
Find the unit vector perpendicular to both \(\overrightarrow{a}\) and \(\overrightarrow{b}\), where:
\(\vec{a}=4 \hat{i}-\hat{j}+8 \hat{k}\) and \(\vec{b}=-\hat{j}+\hat{k}\)
(C.B.S.E. 2019 C)
Solution:

Hence, the unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\)

Question 4.
If \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) , \(\vec{b}=-\hat{i}+{2} \hat{j}+\hat{k}\) and \(\vec{c}=3 \hat{i}+\hat{j}\) are such that \(\vec{a}+\lambda \vec{b}\) is perpendicular to \(\vec{c}\), then find the value of λ . (C.B.S.E. 2019 C)
Solution:
We have:
a = \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) and \(\vec{b}=-\hat{i}+{2} \hat{j}+\hat{k}\)
∴ \(\vec{a}+\lambda \vec{b}=(2 \hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-\hat{i}+2 \hat{j}+\hat{k})\)
= (2 – λ)\(\hat{i}\)+(2 + 2λ)\(\hat{j}\) + (3+λ)\(\hat{k}\).
Now, (\(\vec{a}+\lambda \vec{b}\)) is perpendicular to c ,
∴ \((\vec{a}+\lambda \vec{b}) \cdot \vec{c}=0\)
⇒ ((2 – λ) \(\hat{i}\) + (2 + 2λ)\(\hat{j}\) + (3 + λ\(\hat{k}\)). (3\(\hat{i}\) + \(\hat{j}\)) = 0
⇒ (2 – λ)(3) + (2 + 2λ) (1) + (3 + λ)(0) = 0
⇒ 6 – 3λ + 2 + 2λ = 0
⇒ -λ, + 8 =0.
Hence, λ,=8.

Question 5.
Let \(\vec{a}=\hat{i}+2 \hat{j}-3 \hat{k}\) and \(\vec{b}=3 \hat{i}-\hat{j}+2 \hat{k}\) be two vectors. Show that the vectors (\(\vec{a}+\vec{b}\)) and
(\(\vec{a}-\vec{b}\)) are perpendicular to each other. (C.B.S.E. Outside Delhi 2019)
Solution:
Here, \(\vec{a}+\vec{b}\) = (\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\)) + (3\(\hat{i}\) – \(\hat{j}\) + 2\(\hat{k}\))
= 4\(\hat{i}\) + \(\hat{j}\) –\(\hat{k}\)
and \(\vec{a}-\vec{b}\) = (\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\)) – (3\(\hat{i}\) – j + 2k)
= -2\(\hat{i}\) + 3\(\hat{j}\) – 5\(\hat{k}\).
Now
\(\vec{a}+\vec{b}\) . \(\vec{a}-\vec{b}\) = (4\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\))- (-2\(\hat{i}\) + 3 \(\hat{j}\) – 5\(\hat{k}\))
= (4) (- 2) + (1) (3)+(-1) (- 5)
= – 8 + 3 + 5 = 0.
Hence \(\vec{a}+\vec{b}\) is perpendicular to \(\vec{a}-\vec{b}\).

Question 6.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference
is √3 . (C.B.S.E. 2019)
Solution:

By the question,
\(|\overrightarrow{\mathrm{AB}}|=|\overrightarrow{\mathbf{B C}}|=|\overrightarrow{\mathrm{AC}}|=1\)
⇒ ΔABC is equilateral, each of its angles be¬ing 60°
⇒ ∠DAB = 2 x 60° = 120° and ∠ADB = 30°.
By Sine Formula,
\(\frac{\mathrm{DB}}{\sin \angle \mathrm{DAB}}=\frac{\mathrm{AB}}{\sin \angle \mathrm{ADB}}\)

Question 7.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|\) = 3, \(|\vec{b}|\) = 5 and \(|\vec{a}|\) = 7, then find the value of \(\overrightarrow{a} \cdot \overrightarrow{b}+\overrightarrow{b} \cdot \overrightarrow{c}+\overrightarrow{c} \cdot \overrightarrow{a}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:

Question 8.
Find \(|\vec{a}-\vec{b}|\), if two vectors a and b are such that \(|\vec{a}|\) = 2,\(|\vec{b}|\) = 3 and \(\vec{a} \cdot \vec{b}\) = 4. (N.C.E.R.T.)
Solution:

Question 9.
Find the work done by the force \(\overrightarrow{\mathbf{F}}=2 \hat{i}+\hat{j}+\hat{k}\) acting on a particle, if the particle is displaced from the point with position vector \(2 \hat{i}+\hat{j}+2 \hat{k}\) to the point with position vector \(3 \hat{i}+4 \hat{j}+5 \hat{k}\)
Solution:
Here F = 2 \(\hat{i} \)+ \(\hat{j} \) + \(\hat{k} \)
and d = (3 \(\hat{i} \) + 4\(\hat{j} \) + 5k) – (2 \(\hat{i} \) + 2\(\hat{j} \) + 2\(\hat{k} \) )
– \(\hat{i} \) +2\(\hat{j} \) + 3\(\hat{k} \) .
∴ Work done = \(\overrightarrow{\mathrm{F}} \cdot \vec{d}\)
= (2 \(\hat{i} \) + \(\hat{j} \) + \(\hat{k} \) ). ( \(\hat{i} \) + 2\(\hat{j} \) + 3\(\hat{k} \) )
= (2) (1) + (1) (2) + (1) (3)
= 2 + 2 + 3
= 7 units.

Question 10.
Find ‘λ’ if
(2\(\hat{i} \) + 6\(\hat{j} \) + 14\(\hat{k} \)) x (\(\hat{i} \) – λ\(\hat{j} \) + 7\(\hat{k} \)) = 0. (A.I.C.B.S.E. 2010)
Solution:
We have:
(2\(\hat{i}\) + 6\(\hat{j}\) + 14\(\hat{k}\)) x (\(\hat{i}\) – λ\(\hat{j}\) + 7\(\hat{k} \)) = 0
⇒ \(\hat{i} \) (42 + 14λ) – \(\hat{j}\)(14-14) + \(\hat{k}\) (-2λ – 6) = 0
⇒ 14\(\hat{i} \)(λ + 3)-2(λ + 3) ifc = o
= λ+3 = 0.
Hence, λ = -3.

Question 11.
If \(\vec{a}\) and \(\vec{b}\) are two vectors such that \(|\vec{a} \cdot \vec{b}|\)
=\(|\vec{a} \times \vec{b}|\), then what is the angle between \(\vec{a}\) and b ? (A.I.C.B.S.E. 2010)
Solution:
We have \(|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\)
⇒ \(|\vec{a}||\vec{b}| \cos \theta=|\vec{a}||\vec{b}| \sin \theta\)
⇒ cos θ = sin θ ⇒ tan θ = 1 ⇒ θ = 45°.
Hence, the angle between \(\vec{a}\) and \(\vec{a}\) = 45°.

Question 12.
If \(\vec{a}=2 \hat{i}+3 \hat{j}+\hat{k}\), b = \(\vec{b}=\hat{i}-2 \hat{j}+\hat{k}\) and \(\vec{c}=-3 \hat{i}+\hat{j}+2 \hat{k}\) ,find \([\vec{a} \vec{b} \vec{c}]\).   (C.B.S.E. 2019)
Solution:
We have : \(\vec{a}\) = 2\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\), \(\vec{b}\) = \(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\) and \(\vec{c}\) = – 3\(\hat{i}\) + \(\hat{j}\) + 2\(\hat{k}\)
∴ \([\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{rrr}
2 & 3 & 1 \\
1 & -2 & 1 \\
-3 & 1 & 2
\end{array}\right|\)
= 2 (-4-1)-3(2 + 3)+ 1.(1 -6)
= 2(-5)-3(5)+ 1(-5)
= -10-15-5 = -30.

Question 13.
For three non-zero vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\), prove that \([\vec{a}-\vec{b}, \vec{b}-\vec{c}, \vec{c}-\vec{a}]\) = 0. (C.B.S.E. 2019)
Solution:

Vectors Important Extra Questions Long Answer Type

Question 1.
Let \(\vec{a}=4 \hat{i}+5 \hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-4 \hat{j}+5 \hat{k}\) and \(\vec{c}=3 \hat{i}+\hat{j}-\hat{k}\). Find a vector \(\vec{a}\) which is perpendicular to both \(\vec{c}\) and \(\vec{b}\) and
\(\vec{d} \cdot \vec{a}\) =21. (C.B.S.E. 2018)
Solution:
Wehave: \(\vec{a}\) = 4\(\hat{i}\) + 5\(\hat{j}\) – \(\hat{k}\)
\(\vec{b}\) = \(\hat{i}\) – 4\(\hat{j}\) + 5\(\hat{k}\) and
\(\vec{c}\) = 3\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\)
Let \(\vec{d}\) = x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)

since \(\vec{d}\) is perpendicular to both \(\vec{c}\) and \(\vec{b}\)
\(\vec{d} \cdot \vec{c}\) = 0 and \(\vec{d} \cdot \vec{b}\) = 0
⇒ (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)) . (3\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\)) = 0

and (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)) . (\(\hat{i}\) -4\(\hat{j}\)+5\(\hat{j}\)) = 0
⇒ 3x + y-z = 0 …(1)
and x-4y + 5z = 0 …(2)
Also, \(\vec{d} \cdot \vec{a}\) = 21
⇒ (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)). (4\(\hat{i}\) + 5\(\hat{j}\) – \(\hat{k}\)) =21
⇒ 4x + 5y-z = 21 …(3)
Multiplying (1) by 5,
1 5x + 5y – 5z = 0 …(4)
Adding (2) and (4),
16x + y = 0 …(5)
Subtracting (1) from (3),
x + 4y = 21 …(6)
From (5),
y = -16x …(7)
Putting in (6),
x – 64x = 21
-63x: = 21
Putting in (7), y = \(-16\left(-\frac{1}{3}\right)=\frac{16}{3}\)
Putting in (1), \(3\left(-\frac{1}{3}\right)+\frac{16}{3}\) – z = 0
z = 13/3
Hence \(\vec{d}=-\frac{1}{3} \hat{i}+\frac{16}{3} \hat{j}+\frac{13}{3} \hat{k}\)

Question 2.
If \(\vec{p}=\hat{i}+\hat{j}+\hat{k}\) and \(\vec{q}=\hat{i}-2 \hat{j}+\hat{k}\) ,find a vector of magnitude 5√3 units perpendicular to the vector \(\vec{q}\). and coplanar with vector \(\vec{p}\) and \(\vec{q}\). (C.B.S.E. 2018)
Solution:
Let \(\vec{r}=a \hat{i}+b \hat{j}+c \hat{k}\) be the vector.
Since \(\vec{r} \perp \vec{q}\)
(1) (a) + (-2) (b) + 1 (c) = 0
⇒ a – 2b + c = 0
Again, \(\vec{p}\) , \(\vec{q}\) and \(\vec{r}\) and coplanar,

⇒ (1) (-2c – b) – (1) (c – a) + (1) (b + 2a) = 0
⇒ -2c-b-c + a + b + 2a = 0
⇒ 3a – 3c = 0
⇒ a – c – 0
Solving (1) and (2),

Question 3.
If \(\hat{i}+\hat{j}+\hat{k}, \quad 2 \hat{i}+5 \hat{j}, \quad 3 \hat{i}+2 \hat{j}-3 \hat{k}\) and \(\hat{i}-6 \hat{j}-\hat{k}\) respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find
whether \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{CD}}\) arecollinearornot
(C.B.S.E. 2019)
Solution:
Note : If ‘θ’ is the angle between AB and CD,
then θ is also the angle between \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C D}}\) .
Now \(\overrightarrow{\mathbf{A B}}\) = Position vector of B – Position vector of A

Since 0 ≤ θ ≤ π, it follows that θ = π. This shows that \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C D}}\) are collinear.
Alternatively, \(\overrightarrow{\mathrm{AB}}=-\frac{1}{2} \overrightarrow{\mathrm{CD}}\) which implies
that \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{CD}}\) are collinear vectors.

Question 4.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|\) = 3, \(|\vec{b}|\) = 5, and \(|\vec{c}|\) =7, find the angle between \(\vec{a}\) and \(\vec{b}\) . (C.B.S.E. 2014)
Solution:

where ‘θ’ is the angle between a and b
⇒ (3)² + (5)² + 2 (3) (5) cos θ = (7)²
⇒9 + 25 + 30 cos θ = 49
⇒ 30 cos θ = 49 – 34 ⇒ cos θ = \(\frac{1}{2}\)
⇒ θ = 60°.
Hence, the angle between \(\vec{a}\) and \(\vec{b}\) is 60°.

Question 5.
If \(\vec{a}, \vec{b}, \vec{c}\) are mutually perpendicular vectors of equal magnitude, show that \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b}\) and \(\vec{c}\) . Also, find the angle, which \(\vec{a}+\vec{b}+\vec{c}\) makes with \(\vec{a}\) or \(\vec{b}\) or \(\vec{c}\) . (C.B.S.E. 2017)
Solution:

Let α, β and γ be the angles which \(\vec{a}+\vec{b}+\vec{c}\)
makes with \(\vec{a}, \vec{b}\) and \(\vec{c}\) respectively.

From (1), (3), (4) and (5),
cos α = cos β = cos γ ⇒ α = β = γ
Hence, \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b}\) and \(\vec{b}\)

Question 6.
If with reference to a right-handed system of mutually perpendicular unit vectors
\(\hat{i}, \hat{j}, \hat{k}, \vec{\alpha}=3 \hat{i}-\hat{\jmath}\) where \(\vec{\beta}=2 \hat{i}+\hat{j}-3 \hat{k}\) then express \(\vec{\beta}\) in the form \(\vec{\beta}=\vec{\beta}_{1}+\vec{\beta}_{2}\) ,
where \(\vec{\beta}_{1}\) is parallel to \(\vec{\alpha}\) and \(\vec{\beta}_{2}\) is perpendicular to \(\vec{\alpha}\) . (N.C.E.R.T.; C.B.S.E. (F) 2013)
Solution:

Comparing co-efficients, 2 = 3λ + a₁
1= – λ + a₂ , – 3 = a3
⇒ a₁= 2 – 3λ, a₂ = 1 + λ,
a₃ = -3 …(4)
Putting in (3), 3 (2-3λ)-(1 + λ) = 0
⇒ – 10λ +5 = 0
= λ = \(\frac { 1 }{ 2 }\)
From (4) a₁ = 2 – 3\(\frac { 1 }{ 2 }\) = 2-\(\frac { 3 }{ 2 }\) = \(\frac { 1 }{ 2 }\)
and a₂ = 1 + \(1+\frac{1}{2}=\frac{3}{2}\)

Question 7.
If \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) find: \((\vec{r} \times \hat{i}) \cdot(\vec{r} \times \hat{j})+x y\) (C.B.S.E 2015)
Solution:

Question 8.
Show that the points A, B, C with position vectors \(2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) and \(3 \hat{i}-4 \hat{j}-4 \hat{k}\) respectively, are the vertices of a right angled triangle. Hence, find the area of the triangle. (A.I.C.B.S.E. 2017)
Solution:
Let(2\(\hat{i}\) – \(\hat{i}\) + \(\hat{k}\)), \(\hat{i}\) -3\(\hat{j}\) – 5\(\hat{k}\))
and (3\(\hat{i}\) -4\(\hat{j}\) -4\(\hat{k}\)) be the position vectors of the vertices A, B and C respectively.
.-. AB = (\(\hat{i}\) – 3\(\hat{j}\) – 5\(\hat{k}\)) – (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\))
= – \(\hat{i}\) – 2\(\hat{j}\) – 6\(\hat{k}\)
BC = (3\(\hat{i}\) -4\(\hat{j}\) – 4\(\hat{k}\))-(\(\hat{i}\) -3\(\hat{j}\) – 5\(\hat{k}\))
= 2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)
and = (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)) -(3\(\hat{i}\) – 4\(\hat{j}\) – 4\(\hat{k}\))
= – \(\hat{i}\) + 3 \(\hat{j}\) + 5\(\hat{k}\).
Now, \(\overrightarrow{\mathrm{BC}} \cdot \overrightarrow{\mathrm{CA}}\) = (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)). ( – \(\hat{i}\) + 3\(\hat{j}\) + 5\(\hat{k}\))
= (2)(-1) + (-1)(3) + (1)(5) = -2 -3 + 5 = 0.
Thus, \(\overrightarrow{\mathrm{BC}} \perp \overrightarrow{\mathrm{CA}}\)
⇒ ∠C = 90°.
Hence, AABC is rt. angled.

And, area of triangle = \(\frac{1}{2}|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|\) ………… (1)
But \(\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
-1 & 3 & 5 \\
-2 & 1 & -1
\end{array}\right|\)
= \(\hat{i}\)(-3-5) – \(\hat{j}\)(1 + 10) + \(\hat{k}\)(-1 + 6)
= -8\(\hat{i}\) – 11\(\hat{i}\) + 5\(\hat{i}\)
∴ \(|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|=\sqrt{64+121+25}=\sqrt{210}\)
Hence, area of triangle = \(\frac{1}{2} \sqrt{210}\) sq. units

Question 9.
Find the value of ‘λ’ if four points with position vectors \(\mathbf{3} \hat{i}+6 \hat{j}+9 \hat{k}, \hat{i}+2 \hat{j}+3 \hat{k}\), \(2 \hat{i}+3 \hat{j}+\hat{k}\) and \(4 \hat{i}+6 \hat{j}+\lambda \hat{k}\) are coplanar.   (A.I.C.B.S.E. 2017)
Solution:
Let A, B, C and D be the points with position

The four points are coplanar if \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}\) are coplanar

if – 2(λ – 1 +6) + 4(λ – 1 + 4) -6 (3 – 2) = 0
if -2λ.-10 + 4λ + 12 – 6 = 0
if 2λ,- 4 = 0 if λ = 2.
Hence, λ, = 2.

Question 10.
Let \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}\) and \(\vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\). Then :
(a) Let c₁ = 1 and c₂ = 2, find c₃ which makes \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar
(b) Let c₂ = -1 and c₃ = 1, show that no value of c₁ can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar. (C.B.S.E. 2017)
Solution:
We have : \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}\) and
\(\vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\)
(a) Here c₁ = 1 and c₂ = 2.
∴ \(\vec{c}=\hat{i}+2 \hat{j}+c_{3} \hat{k}\)
Since \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar, [Given]
∴ \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
1 & 2 & c_{3}
\end{array}\right|=0\)
⇒ (-1) [c₃ – 2] = 0
⇒ c₃ – 2 = 0
⇒ c₃ = 2.

(b) Here c₂ = -1, c₃ = 1.
∴ \(\vec{c}=c_{1} \hat{i}-\hat{j}+\hat{k}\)
Since \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar, [Given]
∴ \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
c_{1} & -1 & 1
\end{array}\right|=0\)
⇒ (-1) [1 +1] = 0
⇒ -2 = 0, which is false.
Hence, no value of c₁ can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar.

Question 11.
Show that the vectors \(\vec{a}, \vec{b} \text { and } \vec{c}\)are coplanar if \(\vec{a}+\vec{b}, \vec{b}+\vec{c}\) and \(\vec{c}+\vec{a}\) are coplanar. (N.C.E.R.T. (Supplement); (C.B.S.E. 2016)
Solution:

Question 12.
Prove that \([\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}, \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}}]=\mathbf{2}\left[\begin{array}{ccc}
\rightarrow & \overrightarrow{\mathbf{b}} & \overrightarrow{\mathbf{c}}
\end{array}\right]\)
(N.C.E.R.T. (Supplement); C.B.S.E. 2014)
Solution:

Question 13.
Show that the four points A, B, C and D with position vectors: \(\hat{i}+2 \hat{j}-\hat{k}, 3 \hat{i}-\hat{j}, 2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(4 \hat{i}+3 \hat{k}\) respectively are coplanar. (C.B.S.E. 2019 C)
Solution:

The four points A, B, C and D are coplanar ⇒ [AB,BC,CD]=O
⇒ \([\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}]=0\)
⇒ \(\left|\begin{array}{ccc}
2 & -3 & 1 \\
-1 & 4 & 2 \\
2 & -3 & 1
\end{array}\right|=0\)
⇒ 2(4 + 6) + 3 (-1 – 4) + 1.(3 – 8) = 0
⇒ 20 – 15 – 5 = 0
⇒ 0 = 0, which is true.

By going through these CBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability, students can recall all the concepts quickly.

Continuity and Differentiability Notes Class 12 Maths Chapter 5

Continuity (Definition): if f be a real-valued function on a subset of real numbers and let c be a point in its domain, then f is a continuous function at e, if

Obviously, if the left-hand limit and right-hand limit and value of the function at x = c exist and are equal to each other, i.e., if

then f is continuous at x = c.

Algebra of continuous functions:
Let f and g be two real functions, continuous at x = c, then

1. Sum of two functions is continuous at x = c, i.e., (f + g) (x), defined as f(x) + g(x), is continuous at x = c.
2. Difference of two functions is continuous at x = c, i.e., (f – g) (x), defined as f(x) – g(x), is continuous at x = c.
3. Product of two functions is continuous at x = c, i.e., (f g) (x), defined as f(x) . g(x) is continuous at x = c.
4. Quotient of two functions is continuous at x = c, (provided it is defined at x = c), i.e.,
   (\(\frac{f}{g}\))(x), defined as \(\frac{f(x)}{g(x)}\) [g(x) ≠ 0], is continuous at x = c.

However, if f(x) = λ, then
(a) λ.g, defined ty .g(x), is also continuous at x = c.
(b) Similr1y, if \(\frac{λ}{g}\) is defined as \(\frac{λ}{g}\) (x) = \(\frac{λ}{g(x)}\) , then \(\frac{λ}{g}\) is also continuous at x = c.

→ Differentiability: The concept of differentiability has been introduced in the lower class. Let us recall some important results.

→ Differentiability (Definition): Let f be a real function and c is a point in its domain. The derivative of f at c is defined as

Every differentiable function is continuous.

→ Algebra of Derivatives: Let u and v be two functions of x.

1. (u ± v)’ = u’ ± v’
2. (uv)’ = u’v + uv’
3. \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}\), where v ≠ 0.

→ Derivative of Composite Function: Let t be a real valued function which is a composite of two functions u and v, i.e., f = vou. Put u(x) = t and f= v(t).
∴ \(\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}\)

→ Chain Rule: Let/be a real valued function which is a composite fimction of u, v and w, i.e., f(wov)ou.
Put u(x) = t, v(t) = s and f = w(s). Then,
\(\frac{d f}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x}\).

→ Derivatives of Inverse Trigonometric Functions:

Functions	Domain	Derivatives
Sin-1x	[- 1, 1]	\( \frac{1}{\sqrt{1-x^{2}}} \)
Cos-1x	[- 1, 1]	\( -\frac{1}{\sqrt{1-x^{2}}} \)
tan-1x	R	\( \frac{1}{1+x^{2}} \)
Cot-1x	R	\( -\frac{1}{1+x^{2}} \)
Sec-1x	(-∞, – 1] ∪ [1, ∞)	\( \frac{1}{x \sqrt{x^{2}-1}} \)
Cosec-1x	(-∞, – 1] ∪ [1, ∞)	\( -\frac{1}{x \sqrt{x^{2}-1}} \)

Implicit Functions: An equation in form f(x, y) = 0, in which y is not expressible in terms of x, is called an implicit function of x and y.

Both sides of the equations are differentiated termwise. Then, from this equation, \(\frac{d y}{d x}\) is obtained. It may be noted that when a function of y occurs, then differentiate it w.r.t. y and multiply it by \(\frac{d y}{d x}\).

e.g., To find \(\frac{d y}{d x}\) from cos² y + sin xy = 1, we differentiate it as

Exponential Functions:

The exponential function, with positive base b > 1, is the function y = b^x.

1. The graph of y = 10^x is shown in the figure.
2. Domain = R
3. Range = R⁺
4. The point (0,1) always lies on the graph.
5. It is an increasing function, i.e., as we move from left to right, the graph rises above.
6. As x → – ∞, y → 0.
7. \(\frac{d}{dx}\) (a^x) = a^x log, a, \(\frac{d}{dx}\) e^x = e^x.

Logarithmic Functions:
Let b> 1 be a real number. b^x = a may be written as log_b a = x.

1. The graph of y = log₁₀ x is shown in the figure.
2. Domain = R⁺, Range = R.
3. It is an increasing function.
4. As x → 0, y → ∞.
5. The function y = e^x and y = log_e x are the mirror images of each other in the line y = x.
6. \(\frac{d}{dx}\) (loga x) = \(\frac{1}{x}\) l0ga e, \(\frac{d}{dx}\) loge x = \(\frac{1}{x}\)

→ Other properties of Logarithm are:

1. log_b pq = log_b p + log_b q
2. log_b \(\frac{p}{q}\) = log_a p – log_a q
3. log_b px = x log_b p – log_b q
4. log_a b = \(\frac{\log _{a} p}{\log _{b} p}\)

→ Logarithmic Differentiation:
Whenever the functions are given in the form

1. y = [u(x)]v(x) and
2. y = \(\frac{u(x) \times v(x)}{w(x)}\)

take log of both sides. Simplify and differentiate, e.g.,
Let y = (cos x)sin x, log y = sin x log cos x

Differentiating, \(\frac{1}{y}\) \(\frac{dy}{dx}\) = cos x log Cos x + sin x . – \(\frac{sin x}{cos x}\)
∴ \(\frac{dy}{dx}\) = (cos x)^{sin y} [cos x log cosx – sin x tan x].

→ Derivatives of Functions in Parametric Form: Let the given equations be x = f(t) and y = g(t), where t is the parameter. Then,

→ Second Order Derivative:
Let y = f(x), then \(\frac{dy}{dx}\) =f ‘(x).
If f ‘(x) is differentiable, then it is again differentiated.

Rolle’s Theorem:
Let f: [a, b] → R be continuous on closed interval [a, b] and differentiable on open interval (a, b) such that f(a) = f(b), where a and b are real numbers, then there exists some c ∈ (a, b) such that f ‘(c) = 0.

From the figure, we observe that f(a) = f(b). There exists a point c₁ ∈ (a, b) such that f ‘ (c) = 0, i.e., tangent at c1 is parallel to x-axis. Similarly, f(b) = f(c) → f ‘ (c₂) = 0.

→ Mean Value Theorem: Let f: [a, b] → R be a continuous function on the closed interval [a, b] and differentiable in the open interval (a, b). Then, there exists some c ∈ (a, b) such that
f ‘ (c) = \(\frac{f(b)-f(a)}{b-a}\)

Now, we know that \(\frac{f(b)-f(a)}{b-a}\) is the slope of secant drawn between A[a,f(a)] and B[b,f(b)]. We t k know that the slope of the line joining (x_1, y₁) and (x₂, y₂) is \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

The theorem states that there is a point c ∈ (a, b), where f ‘(c) is equal to the slope of AB.

In other words, there exists a point c ∈ (a, b) such that tangent at x = c is parallel to AB.

1. CONTINUITY
(i) Left Continuity. A function ‘f ’ is left-continuous at x = c if \(\lim _{x \rightarrow c^{-}}\) f (x) = f(c).

(ii) Right Continuity. A function ‘f ’ is right-continuous at x = c if \(\lim _{x \rightarrow c^{+}}\) f (x) = f(c).

(iii) Continuity at a point. A function ‘ f ’ is continuous at x = c if
\(\lim _{x \rightarrow c^{-}}\) (x) = \(\lim _{x \rightarrow c^{+}}\) f(x) = f(c).

2. (i) Polynominal functions
(ii) Rational functions
(iii) Exponential functions
(iv) Trigonometric functions are all continuous at each point of their respective domain.

3. DIFFERENTIABILITY
(i) Left Derivative. A function ‘f ’ is said to possess left derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c-h)-f(c)}{-h}\) exists finitely.

(ii) Right Derivative. A function ‘f ’ is said to possess right derivative at x = c if
\(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.
(iii) Derivative. A function is said to possess derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.

4. CONTINUITY AND DERIVABILITY
A real valued function is finitely derivable at any point of its domain, it is necessarily continuous at that point. The converse is not true.

5. STANDARD RESULTS

(i) \(\frac{d}{d x}\) (xⁿ) = nx^n-1 ∀ x ∈ R
(ii) \(\frac{d}{d x}\) ((ax + b)n = n(ax + b)^{n – 1} . a ∀ x ∈ R
(iii) \(\frac{d}{d x}(|x|)=\frac{x}{|x|}\), x ≠ 0

6. GENERAL THEOREMS
(i) The derivative of a constant is zero.
(ii) An additive constant vanishes on differentiation i.e. if f(x) = g(x) + c, where ‘c’ is any constant, then f'(x) = g'(x).
(iii) If f(x) = ag(x), then f'(x) = ag'(x), where ‘a’ is a scalar.
(iv) If f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x).

Extension.
If f(x) = a₁f₁ ± a₂f₂ ……. ± a_nf_n(x), then :
f'(x) = a₁f₁‘(x) ± a₂f₂‘(x) ± ……. ± a_nf_n‘(x)

(v) If f(x) = \(\frac{g(x)}{h(x)}\), then f'(x) = g(x)h'(x) + g'(x)h(x)
(vi) If f(x) = \(\frac{g(x)}{h(x)}\), then f ‘(x) = \(\frac{h(x) g^{\prime}(x)-g(x) h^{\prime}(x)}{(h(x))^{2}}\), h(x) ≠ 0.
(vii) If f(x) = \(\frac{1}{h(x)}\), then f'(x) = \(-\frac{h(x)}{[h(x)]^{2}}\), h'(x) ≠ 0

7. IMPORTANT RESULTS

(i) (a) \(\frac{d}{d x}\) (sinx) = cos x and \(\frac{d}{d x}\) (cos x) = – sin x ∀ x ∈ R
(b) \(\frac{d}{d x}\) (tan x) = sec² x and \(\frac{d}{d x}\) (sec x) = sec x tan x ∀ x ∈ R except odd multiples of \(\frac{\pi}{2}\)
(c) \(\frac{d}{d x}\)(cot x) = – cosec² x and \(\frac{d}{d x}\) (cosec x) = -cosec x cot x ∀ x ∈ R except even multiple of \(\frac{\pi}{2}\)

(ii)
(a) \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(b) \(\frac{d}{d x}\)(cos^-1x) = \(-\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(c) \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^{2}}\) ∀ x ∈ R
(d) \(\frac{d}{d x}\)(cot^-1x) = \(-\frac{1}{1+x^{2}}\) ∀ x ∈ R
(e) \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{|x| \sqrt{x^{2}-1}}\) x > 1 or x < -1
(f) \(\frac{d}{d x}\)cosec^-1x) = \(-\frac{1}{|x| \sqrt{x^{2}-1}}\), x > 1 or x < -1

(iii) (a) \(\frac{d}{d x}\) (a^x) = a^x log_e a, a > 0
(b) \(\frac{d}{d x}\)(e^x) = e^x
(c) \(\frac{d}{d x}\)(log_a x) = \(\frac{1}{x}\) log_a e, x > 0
(d) \(\frac{d}{d x}\) (log x) = \(\frac{1}{x}\), x>0.

8. CHAIN RULE
\(\frac{d}{d x}\) (f(g(x)) = f'(g(x)).g'(x)

9. PARAMETRIC EQUATIONS
\(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}\), \(\frac{d x}{d t}\) ≠ 0
Or \(\frac{d y}{d x}=\frac{d y}{d t} \times \frac{d t}{d x}\)

10.MORE RESULTS

(i) \(\frac{d y}{d x}=\frac{1}{\frac{d x}{d y}}\)
(ii) \(\frac{d y}{d x} \times \frac{d x}{d y}=1\)

11. ROLLE’S THEOREM
If a function f(x) is :

(i) continuous in [a, b]
(ii) derivable in (a, b)
(iii) f (a) = f (b), then there exists at least one point ‘c’ in (a, b) such that f’ (c) = 0.

12. LAGRANGE’S MEAN VALUE THEROEM (LMV THEOREM OR MV THEOREM)
If a function f(x) is :
(i) continuous in [a, b]
(ii) derivable in (a, b), then there exists at least one point ‘c’ in (a, b) such that \(\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\)

Studying from CBSE Class 12 English Flamingo Vistas Notes Summary of All Chapters in Hindi Pdf Download helps students to prepare for the exam in a well-structured and organised way. Making Flamingo Vistas Class 12 Chapters Summary saves students time during revision as they don’t have to go through the entire textbook. In CBSE Notes, students find the summary of the complete chapters in a short and concise way. Students can refer to the NCERT Solutions for Class 12 English, to get the answers to the exercise questions.

English Class 12 Notes Summary | Summary of Class 12 English Flamingo Vistas

Flamingo Class 12 Chapters Summary | Class 12 English Flamingo Summary

• The Last Lesson Summary
• Lost Spring Summary
• Deep Water Summary
• The Rattrap Summary
• Indigo Summary
• Poets and Pancakes Summary
• The Interview Summary
• Going Places Summary
• My Mother At Sixty Six Summary
• An Elementary School Classroom in a Slum Summary
• Keeping Quiet Poem Summary
• A Thing of Beauty Summary
• A Roadside Stand Summary
• Aunt Jennifer’s Tigers Summary

Vistas Class 12 Chapters Summary | Class 12 English Vistas Summary

• The Third Level Summary
• The Tiger King Summary
• Journey to The End of The Earth Summary
• The Enemy Summary
• Should Wizard Hit Mommy Summary
• On The Face of It Summary
• Evans Tries An O-Level Summary
• Memories of Childhood Summary
• Silas Marner Summary
• The Invisible Man Summary