Integrals Class 12 Important Extra Questions Maths Chapter 7

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 7 Integrals. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 7 Important Extra Questions Integrals

Integrals Important Extra Questions Very Short Answer Type

Question 1.
Find \(\int \frac{3+3 \cos x}{x+\sin x} d x\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int \frac{3+3 \cos x}{x+\sin x} d x\) = 3 log lx + sin xl + c.
[∵ Num. = \(\frac{d}{d x}\) denom.]

Question 2.
Find : ∫(cos² 2x – sin² 2x)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = ∫cos 4x dx = \(\frac{\sin 4 x}{4}\)+ c.

Question 3.
Find : ∫ \(\frac{d x}{\sqrt{5-4 x-2 x^{2}}}\)   (C.B.S.E. Outside Delhi 2019)
Solution:

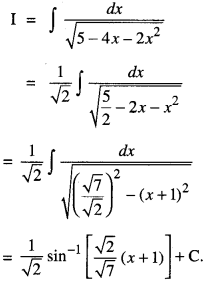
Question 4.
Evaluate ∫ \(\frac{x^{3}-1}{x^{2}}\) dx (N.C.E.R.T. C.B.S.E. 2010C)
Solution:

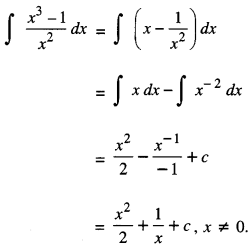
Question 5.
Find : \(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin x \cos x} d x\) (A.I.C.B.S.E. 2017)
Solution:

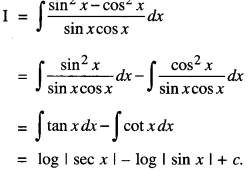
Question 6.
Write the value of \(\int \frac{d x}{x^{2}+16}\)
Solution:

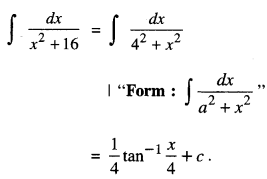
Question 7.
Evaluate: ∫ (x³ + 1)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int_{-2}^{2} x^{3} d x+\int_{-2}^{2} 1 \cdot d x\) = I₁
⇒ 0 + \([x]_{-2}^{2}\) [∵ I₁ is an odd function] = 2 – (-2) = 4.
⇒ 2 – (-2) = 4.

Question 8.
Evaluate: \(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx. (C.B.S.E. 2014)
Solution:
\(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx
\(\int_{0}^{\pi / 2}\)e^x (-cos x + sinx)dx
|“Form: ∫e^x (f(x) + f'(x) dx”
= \(\left[e^{x}(-\cos x)\right]_{0}^{\pi / 2}\)
= -e ^π/2cos\(\frac{\pi}{2}\) + e⁰ cos 0
= -e ^π/2 (0) + (1) (1)
= -0 + 1 = 1

Question 9.
Evaluate: \(\int_{0}^{2} \sqrt{4-x^{2}} d x\). (A.I.C.B.S.E. 2014)
Solution:

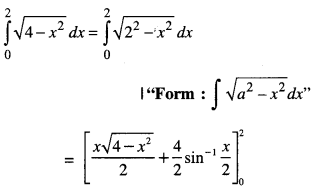
= [0 + 2 sin^-1(1)] – [0 + 0]
= 2sin^-1(1)= 2(π/2) = π

Question 10.
Evaluate : If f(x) = \(\int_{0}^{x}\) t sin t dt, then write the value of f’ (x). (A.I. C.B.S.E. 2014)
Solution:
We have : f(x) = \(\int_{0}^{x}\) t sin t dt.
f'(x) = x sin x. \(\frac{d }{d x}\) (x) – 0
[Property XII ; Leibnitz’s Rule]
= x sin x . (1)
= x sin x.

Question 11.
Prove that: \(\int_{0}^{2a}\) f(x)dx = \(\int_{0}^{2a}\) f(2a-x)dx. o o
Solution:
Put x = 2a – t so that dx = – dt.
When x = 0, t – 2a. When x = 2a, t – 0.
\(\int_{0}^{2a}\) f(x)dx = \(\int_{2a}^{0}\) f(2a-t)(-dt)
=\(\int_{2a}^{0}\) f{2a-t)dt = \(\int_{0}^{2a}\) f(2a-t)dt o
[Property II]
= \(\int_{0}^{2a}\) (2a – x) dx, [Property I]
which is true.

Integrals Important Extra Questions Short Answer Type

Question 1.
Evaluate :
\(\int \frac{\cos 2 x+2 \sin ^{2} x}{\cos ^{2} x} d x\) (C.B.S.E)
Solution:

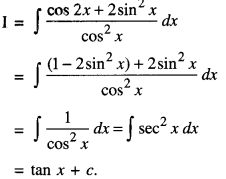
Question 2.
Find : \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Solution:
I = \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Put tan x = t so that sec² x dx = dt.
∴ I = \(\int \frac{d t}{\sqrt{t^{2}+2^{2}}}\)
= log |t + \(\sqrt{t^{2}+4}\)| + C
= log |tan x + \(\sqrt{tan^{2}+4}\)| + C

Question 3.
Find : \(\int \sqrt{1-\sin 2 x} d x, \frac{\pi}{4}<x<\frac{\pi}{2}\)
Solution:

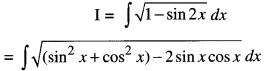
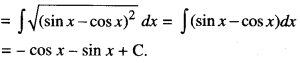
Question 4.
Find ∫sinx . log cos x dx (C.B.S.E 2019 C)
Solution:
∫sinx . log cos x dx
Put cox x = t
so that – sin x dx = dt
i.e., sin x dx = – dt.
∴ I = -∫log t.1dt
= -[ log t.t – ∫ 1/t. t dt ]
[Integrating by parts]
= – [t log t – t] + C = f(1 – log t) + C
= cos x (1 – log (cos x)) + C.

Question 5.
Find : \(\int \frac{\left(x^{2}+\sin ^{2} x\right) \sec ^{2} x}{1+x^{2}} d x\) (CBSE Sample Paper 2018-19)
Solution:

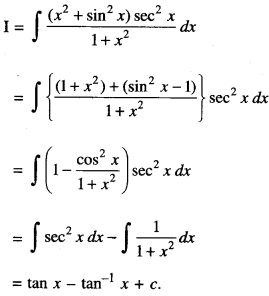
Question 6.
Evaluate \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\) (CBSE Sample Paper 2018-19)
Solution:
I = \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\)

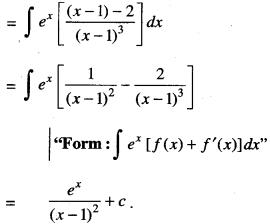
Question 7.
Find ∫sin^-1 (2x)dx
Solution:

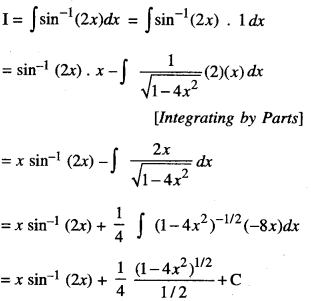
Question 8.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx.
Solution:
Here, f(x)=( 1-x²) sin x cos² x.
f(x) = (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 9.
Evaluate : \(\int_{-1}^{2} \frac{|x|}{x} d x\) dx.
Solution:

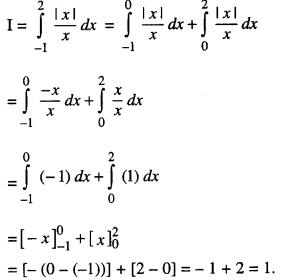
Question 10.
Find \(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)   (C.B.S.E. 2018 C)
Solution:
\(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)
= 3∫sce² x dx – 5∫sec x tan x dx
= 3tan x – 5sec x + C

Question 11.
Find :
\(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:
Let I = \(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)
Put tan³ x = t
so that 3 tan² x sec² x dx = dt
i.e tan² x sec²x dx = \(\frac{d t}{3}\)

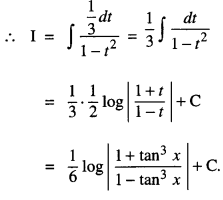
Question 12.
Find : ∫ sin x .log cos x dx.   (CBSE 2019C)
Solution:
I = ∫ sin x .log cos x dx.
Put cos x = t
i.e. sinx dx = -dt
∴ I = – ∫log t.1 dt
= -[logt.t – ∫1/t . t. dt]
[Integrating by parts]
= – [t log t – t] + C
= t(1 – log t) + C
= cos x (1 – log (cos JC)) + C.

Question 13.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx   (C.B.S.E. 2019 (Delhi))
Solution:
Here, f(x) = (1 – x²) sin x cos² x
∴ f(-x) – (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 14.
Evaluate \(\int_{-1}^{2} \frac{|x|}{x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

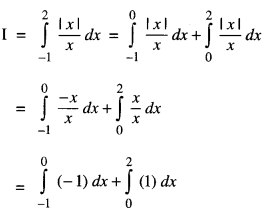
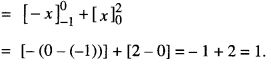
Question 15.
Find : \(\int_{-\pi / 4}^{0} \frac{1+\tan x}{1-\tan x} d x\)
Solution:

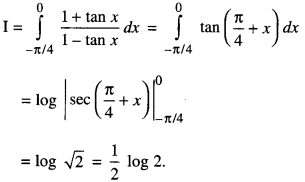
Integrals Important Extra Questions Long Answer Type 1

Question 1.
Evaluate : \(\int \frac{\sin ^{6} x+\cos ^{6} x}{\sin ^{2} x \cos ^{2} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

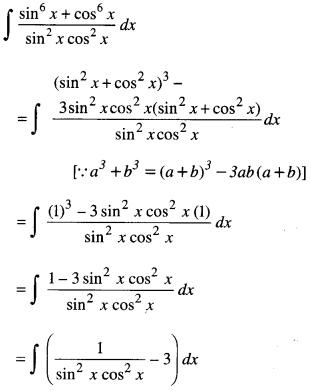
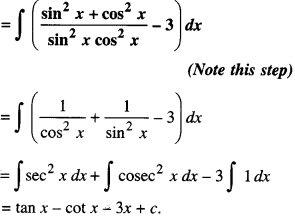
Question 2.
Integrate the function \(\frac{\cos (x+a)}{\sin (x+b)}\) w.r.t. x. (C.B.S.E. 2019 (Delhi))
Solution:

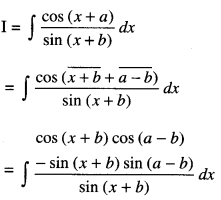
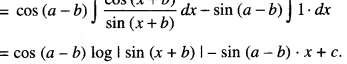
Question 3.
Evaluate : ∫ x² tan^-1 x dx. (C.B.S.E. (F) 2012)
Solution:

Question 4.
Find : ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx (N.C.E.R.T.; A.I.C.B.S.E. 2010 C)
Solution:
Let ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx
= ∫ log(log x)dx + ∫\(\frac{1}{(\log x)^{2}}\) dx …… (1)
Let I = I₁ + I₂
Now I₁ = ∫ log (log x) dx
=∫ log (log x) 1 dx
= log (log x).x – ∫ \(\frac{1}{\log x \cdot x}\)x.dx
(Integrating by parts)
= xlog(logx) – ∫ \(\frac{1}{\log x}\)dx ……….. (2)
Let I₁ = I₃ + I₄

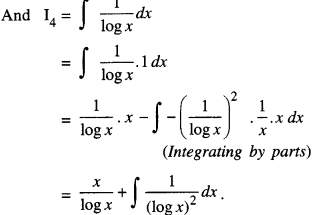
Putting in (2),
I₁ = x log (x) – \(\frac{x}{\log x}-\int \frac{1}{(\log x)^{2}}\) dx
Putting in (1),
I = x log (log x)

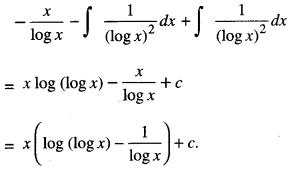
Question 5.
Integrate : ∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx   (N.C.E.R.T.)
Solution:
∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx
[From ∫ e^xf(x) + f'(x) ]dx”]
= ∫ e^x tan^-1 x dx +∫ e^x \(\frac{1}{1+x^{2}}\) ) dx
= ∫ tan^-1 x. e^x dx +∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
= tan^-1 x. e^x – ∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
+∫ \(\frac{1}{1+x^{2}}\) ) e^xdx
(integrating first integral by parts)
= e^x tan^-1x + c.

Question 6.
Integrate : \(\int e^{x}\left(\frac{x^{2}+1}{(x+1)^{2}}\right) d x\) (N.C.E.R.T)
Solution:

Question 7.
Find \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\) (C.B.S.E. 2018)
Solution:
Let i = \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\)
Put sin x = t so that cos x dx = dt.

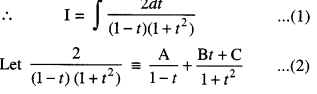
⇒ 2 ≡ A(1 + t²) + (Bt + C) (1 – t)
2 ≡ (A – B)t² + (B – C)t + (A + C).
Comparing coeffs. of t²,
A-B = 0
⇒ A = B
Comparing coeffs. of t,
0 = B – C
⇒ B = C.
Comparing constant terms,
2 = A + C.
Thus, A = B = C = 1.
∴ From (2),
\(\frac{2}{(1-t)\left(1+t^{2}\right)}=\frac{1}{1-t}+\frac{t+1}{t^{2}+1}\)
∴ From (1)

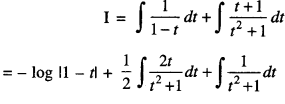
= – log |1 — t| + \(\frac { 1 }{ 2 }\) log |t² + 1| + tan^-1 t + c
= – log |1 — t| + \(\frac { 1 }{ 2 }\) log (t² + 1) + tan^-1t + c
[∵ t² ≥ 0 ⇒ t² + 1 > 0 ∴ |t² + |1 = t² + 1]
= – log |1 – sin x| + \(\frac { 1 }{ 2 }\) log (sin² x + 1) + tan^-1 (sin x) + c
= – log (1 – sin x) + \(\frac { 1 }{ 2 }\) log (1 + sin²x)
+ tan^-1 |sin x| + c.
[∵’ 1 – sin x ≥ 0 |1 – sin x| = 1 – sin x]

Question 8.
Find : \(\int \frac{3 x+5}{x^{2}+3 x-18} d x\) (C.B.S.E. 2019)
Solution:
Let 3x + 5 = A(2x + 3) + B.
Comparing,
2A = 3, 3A + B = 5

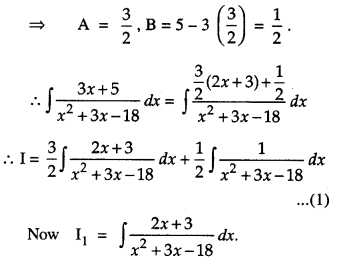
Put x2 + 3x – 18 – t
so that (2x + 3 )dx = dt.
∴ I₁ = \(\int \frac{d t}{t}\) = log |t|
= log + | x² + 3x – 18 |

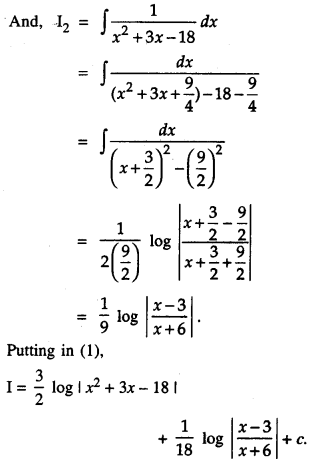
Question 9.
Find: \(\int \frac{\cos x}{(1+\sin x)(2+\sin x)} d x\) 2019C)
Solution:

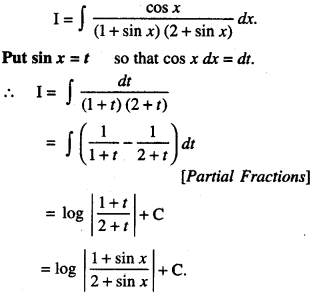
Question 10.
Find: \(\int \frac{x^{4}+1}{2\left(x^{2}+1\right)^{2}} d x\) (C.B.S.E. Sample Paper 2018-19)
Solution:

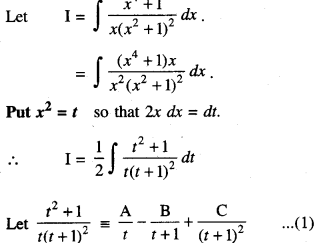
⇒ t² + 1 ≡ A(t + 1)² + Bdt + 1) + Ct …(2)
Comparing coeffs. of like terms, we get :
A = 1, B = 0 and C = – 2.
Putting in (1),

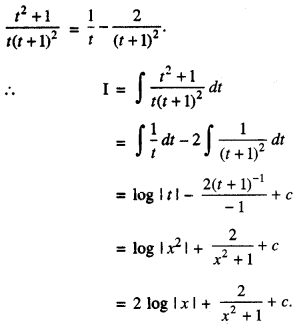
Question 11.
Evaluate : \(\int \frac{x+2}{\sqrt{x^{2}+5 x+6}} d x\) (A.I.C.B.S.E. 2014)
Solution:

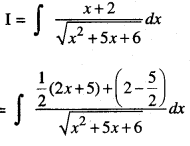
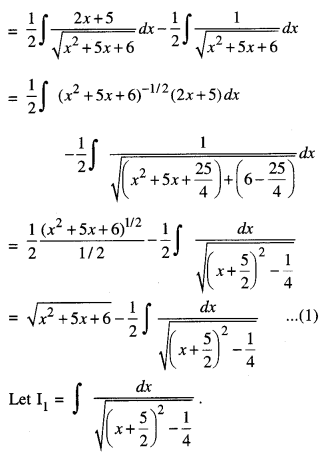
Question 12.
Evaluate : \(\int \frac{2 x+5}{\sqrt{7-6 x-x^{2}}} d x\)
Solution:

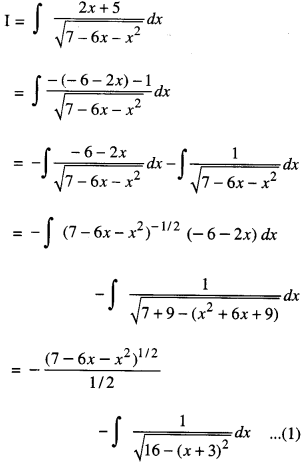
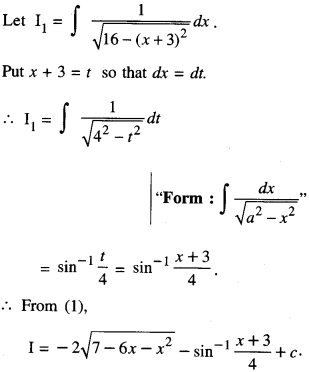
Question 13.
Evaluate : \(\int \frac{d x}{5+4 \cos x}\)
Solution:
I = \(\int \frac{d x}{5+4 \cos x}\)
Put cos x = \(\frac{1-t^{2}}{1+t^{2}}\)
where t = tan \(\frac { x }{ 2 }\) so that dt = \(\frac { 1 }{ 2 }\) sec² \(\frac { x }{ 2 }\) dx
i.e dt = \(\frac { 1 }{ 2 }\)( 1+ tan²\(\frac { x }{ 2 }\))dx
i.e. dt = \(\frac { 1 }{ 2 }\) (1 + t2) dx i.e. dx = \(\frac{2 d t}{1+t^{2}}\)

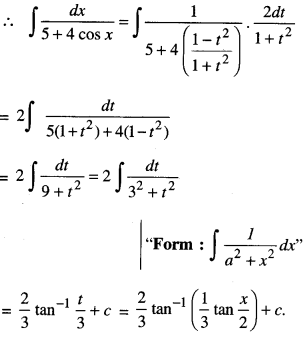
Question 14.
Evaluate : \(\int \frac{d x}{x\left(x^{3}+1\right)}\) (A.I. C.B.S.E 2013)
Solution:
I = \(\int \frac{d x}{x\left(x^{3}+1\right)}=\int \frac{x^{2} d x}{x^{3}\left(x^{3}+1\right)}\)
[Multiplying numerator and denominator by x²]
Put x³ = t so that 3x² dx = dt
i.e , x² dx = \(\frac { 1 }{ 3 }\) dt

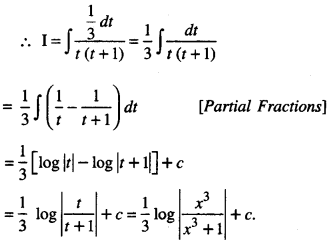
Question 15.
Evaluate : \(\int_{0}^{2} e^{x} d x\) as the limit of a sum. (N.C.E.R.T.)
Solution:
Here f(x) = e^x ; a = 0, b = 2.
∴ f(a) -f(0) = e° = 1
f(a + h) =f(0 + h) = e^h
f(a + 2h) =f(0 + 2h) = e^2h, …….,

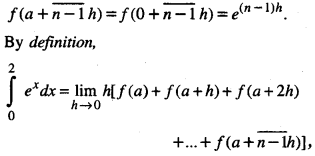
where nh = b – a = 2 – 0 = 2
= \(\lim _{h \rightarrow 0}\) h[1 + e^h +e^2h +… + e^(n-1)hh]
= \(\lim _{h \rightarrow 0} h \frac{1 \cdot\left(e^{n h}-1\right)}{e^{h}-1}\)

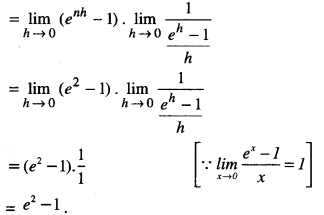
Question 16.
Evaluate: \(\int_{-1}^{2}\) (e^3x + 7x – 5)dx as a limit of sums. (A.I.C.B.S.E. 2015)
Solution:
Here f(x) = e^3x + 7x – 5 ; a = – 1, b = 2.
f (a) = f(- 1) = e^-3 – 7 – 5 = e^-3 – 12
f (a + h) = f(-1 + h)
= e^-3(-1 + h) + 1 (-1 + h)-5

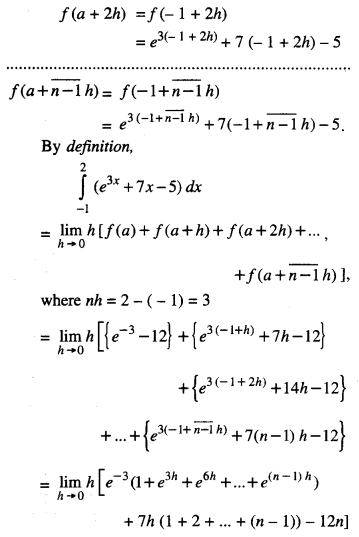
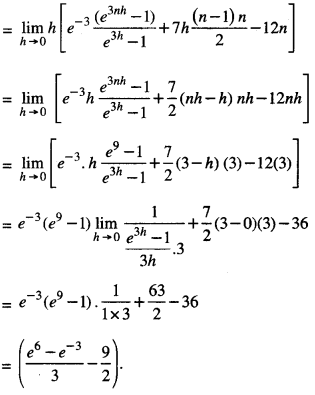
Question 17.
Evaluate: \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\). (N.C.E.R.T.)
Solution:
Let I = \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\)
Put x⁵ = t so that 5x⁴ dx = dt.
When x = – 1, t = – 1. When x = 1, t= 1.

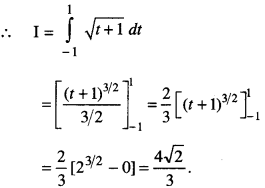
Question 18.
Prove that:
\(\int_{0}^{a} f(x)=\int_{0}^{a} f(a-x) d x\) , hence evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E 2019C)
Solution:
(i) Put x = a – y so that dx = -dy.
When x = 0, y = a. When x = a, y = 0.
∴ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – y)(-dy)
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f{a-x)dx.

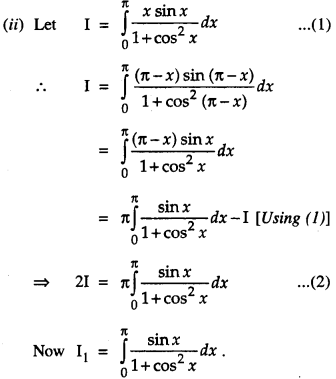
Put cos x = t
so that – sin x dx = dt
i.e. sin x dx = -dt.
When x = 0, t – cos 0=1.
When x = π, t – cos π = -1.

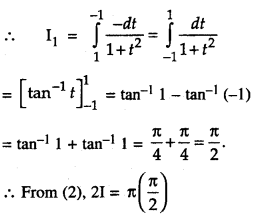
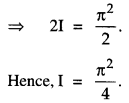
Question 19.
Evaluate : \(\int_{-1}^{2}\) |x³ – x | dx   (N.C.E.R.T.; C.B.S.E. 2016; A.I.C.B.S.E. 2012)
Solution:

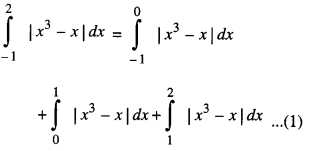
On [- 1, 0], x³ – x ≥ 0
⇒ | x³ – x | = x³ – x;
On [0, 1], x³ – x ≤ 0
⇒ | x³ – x | = -(x³ – x) = x – x³
On [1, 2], x³ – x > 0
⇒ | x³ – x | = x³ – x

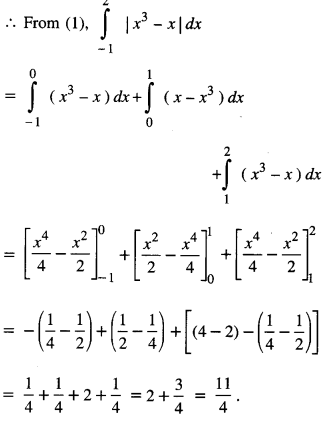
Question 20.
Solve the differential equation:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx.
Solution:
The given differential equation is:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx

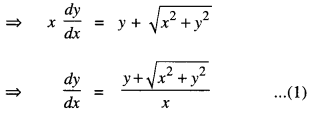
Put y = vx, so that \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
∴(1) becomes:



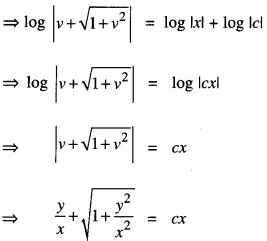
Which is the reqd. solution.

Question 21.
Evaluate : \(\int_{-1}^{1} \frac{x+|x|+1}{x^{2}+2|x|+1} d x\) (CB.S.E. Sample Paper 2018 – 19)
Solution:

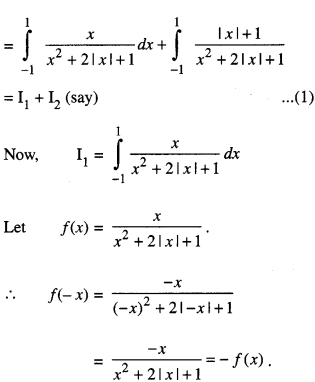
Thus f(-x) = -f(x)
⇒ f(x) is an odd function
∴ I₁ = 0 …… (2)


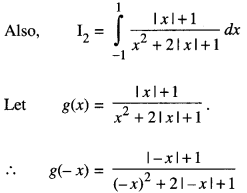
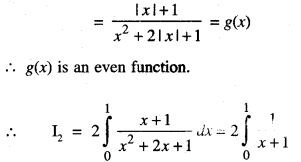
= 2 [log |x + 1|]\(\text { ] }_{0}^{1}\)
= 2 [log 2 – log 1]
= 2 [log 2-0]
= 2 log 2 …(3)
∴ From (1), (2) and (3), we get:
I = 2 log 2.

Question 22.
Find : \(\int \frac{4}{(x-2)\left(x^{2}+4\right)} d x\) (C.B.S.E. 2018 C)
Solution:
\(\frac{4}{(x-2)\left(x^{2}+4\right)} \equiv \frac{\mathrm{A}}{x-2}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+4}\)
4 ≡ A(x² + 4) + (Bx + C)(x-2)
By comparison,
A = \(\frac { 1 }{ 2 }\), B = –\(\frac { 1 }{ 2 }\)
and C = 1.

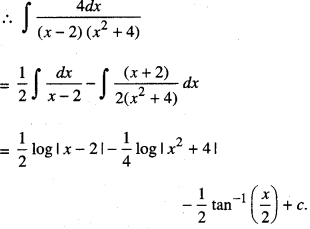
Integrals Important Extra Questions Long Answer Type 2

Question 1.
Evaluate : \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Solution:
Let I = \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Put tan^-1 x = t i.e, x = tan t
So that \(\frac{1}{1+x^{2}} d x\) = dt

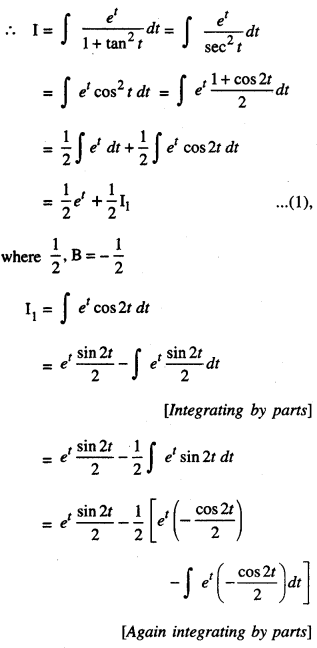
Question 2.
Integrate : \(\int \frac{x^{3}+x}{x^{4}-9} d x\)
Solution:

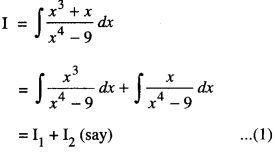
Now I₁ = \(\int \frac{x^{3}}{x^{4}-9} d x\)
Put x⁴ – 9 = t so that 4x³ dx – dt
i.e x³dx = \(\frac{d t}{4}\)

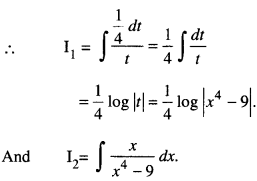
Put x² = u so that 2x dx = du
i.e, xdx = \(\frac{1}{2}\) du
Putting the values of Ij and I2 in (1), we get:

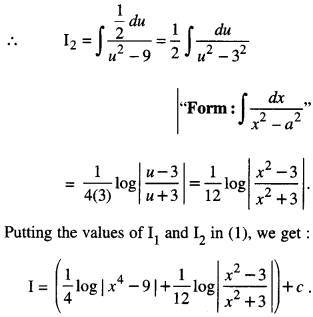
Question 3.
Find : \(\int \frac{\cos \theta}{\left(4+\sin ^{2} \theta\right)\left(5-4 \cos ^{2} \theta\right)} d \theta\) (A.I.C.B.S.E. 2017)
Solution:

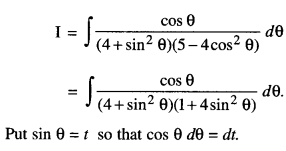
Question 4.
Evaluate : \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Solution:
I = \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Put sin² x = t so that 2 sin x cos x dx = dt
i.e. sin 2x dx = dt.

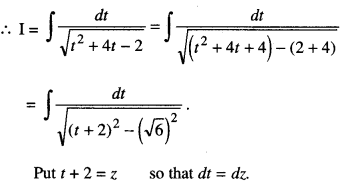
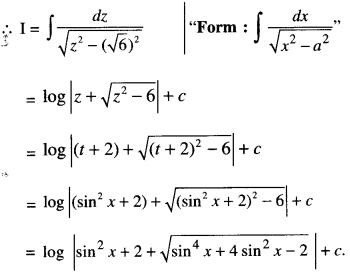
Question 5.
Evaluate : \(\int \frac{x^{2}-1}{x^{4}+1} d x\)
Solution:

Question 6.
Evaluate: \(\int(\sqrt{\tan x}+\sqrt{\cot x}) d x\) (N.C.E.R.T.; A.I.C.B.S.E. 2014; C.B.S.E. 2010S)
Solution:

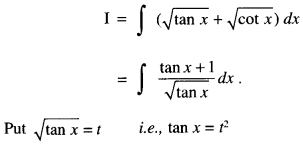
so that sec2 x dx = 2t dt
i.e., (1 + tan² x) dx = 2t dt
⇒ (1 + f) dx = 21 dt

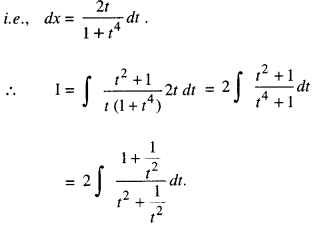
[Dividing Num.. & Denom. by t²]
Put t – \(\frac { 1 }{ t }\)= y so that (1 + \(\frac{1}{t^{2}}\) )dt = dy
Also t² – 2 + \(\frac{1}{t^{2}}\) = y²
t² + \(\frac{1}{t^{2}}\) = y² + 2

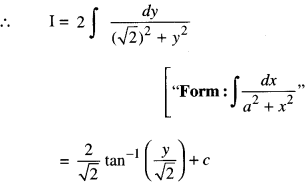
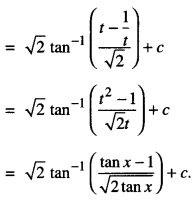
Question 7.
Evaluate \(\int_{0}^{\pi / 2} \frac{x+\sin x}{1+\cos x} d x\) (A.I.C.B.S.E. 2011)
Solution:


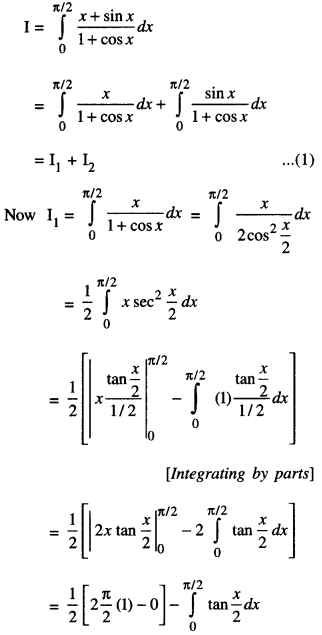
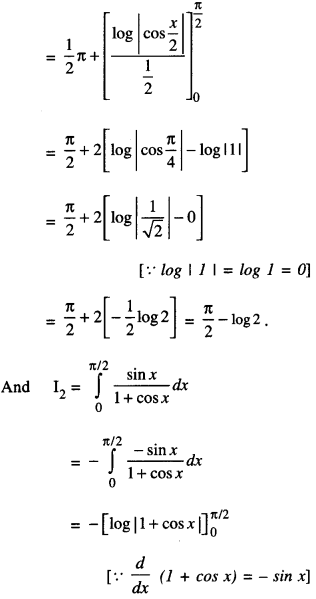
= – [log|1+0|] – [log|1+1|]
= – [0-log2] = log 2
[log|1| = log I = 0]
From (1), I = (\(\frac{\pi}{2}\)– log 2) + log 2 = \(\frac{\pi}{2}\)

Question 8.
Evaluate :
\(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\) (C.B.S.E. 2016)
Solution:
Let I = \(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\)
Put \(\frac{\pi}{4}\) + x = t
x = t – \(\frac{\pi}{4}\) so that dx = dt
when x = 0, t = \(\frac{\pi}{4}\)
when x = π, t = \(\frac{5\pi}{4}\)

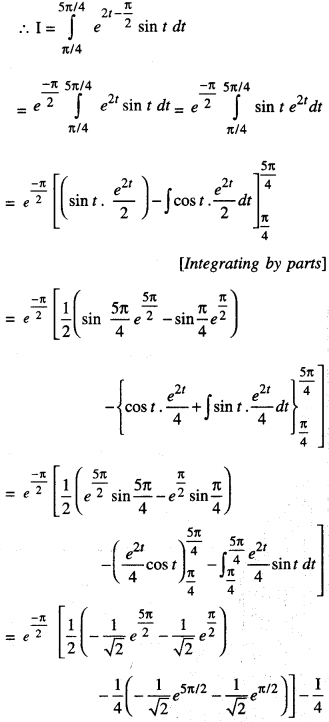
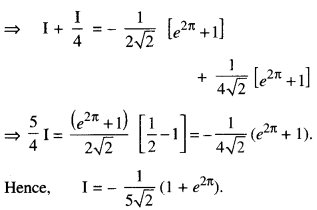
Question 9.
Evaluate : \(\int_{1}^{3}\) (x² + 3x + e^x )dx, as the limit of the sum. (C.B.S.E. 2018)
Solution:
Let f (x) = x² + 3x + e^x
f(x) = f(1)
= 1² + 3(1) + e¹ = 4 + e
f(a + h) = f(1 + h.)
= (1+h)² + 3(1+h) + e^1+h
= 4 + 5 h + h² + e^1+h
f(a + 2h) = f(1 + 2h)
= (1 +2h)² + 3(1 +2h) + e^1+2h
= 4 + 10h+ 4h² + e^1+2h

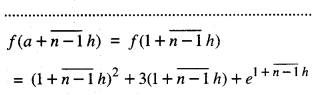
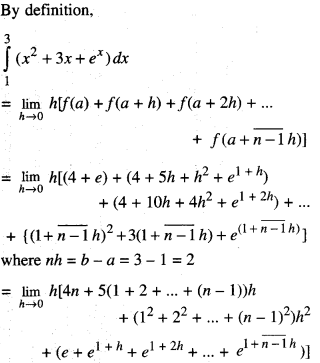
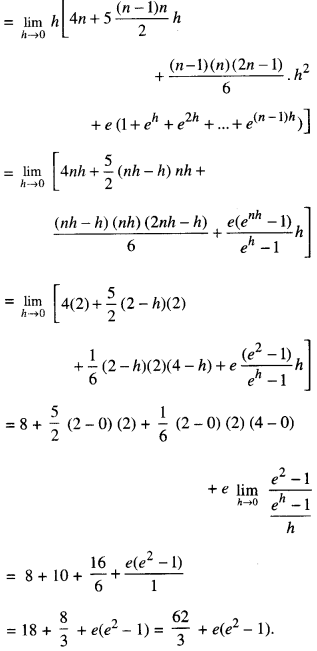
Question 10.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x}{\sin x+\cos x} d x\)
Solution:

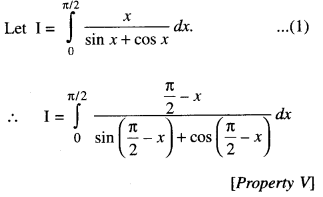
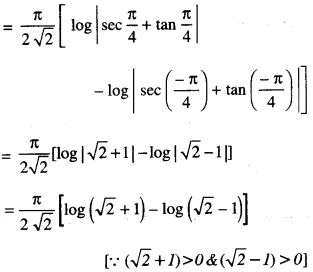
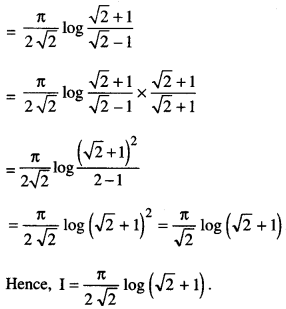
Question 11.
Evaluate : \(\int_{0}^{\pi / 2} \frac{\cos ^{2} x}{\cos ^{2} x+4 \sin ^{2} x} d x\)
Solution:


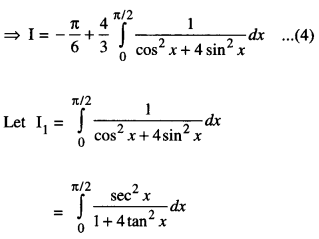
[Dividing Num. and Denom. by cos² x]
Put tan x = t so that sec² x dx = dt.
When x = \(\frac{\pi}{2}\), t = tan \(\frac{\pi}{2}\) → ∞

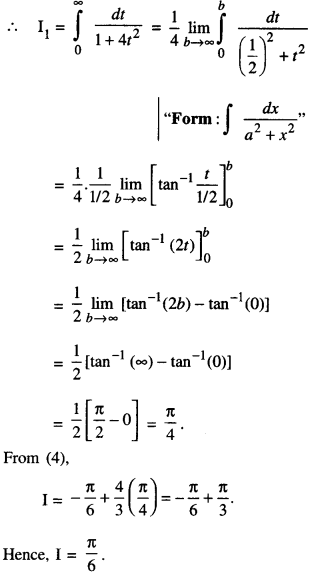
Question 12.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2017; A.I.C.B.S.E. 2013, 12)
Solution:

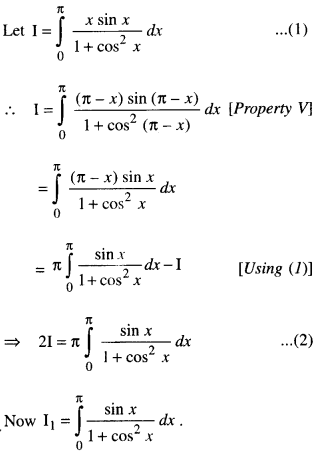
Put cos x = t so that – sin x dx = dt
i.e. sin x dx = – dt.
When x = 0, t = cos 0 = 1.
When x = π, t = cos π = – 1.

Question 13.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2018)
Solution:

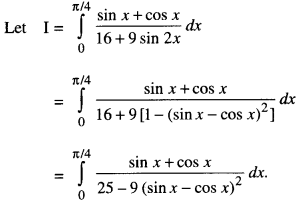
Put sin x – cos x = t
so that (cos x + sin x) dx = dt.
When x = 0, t = 0 – 1 = -1.

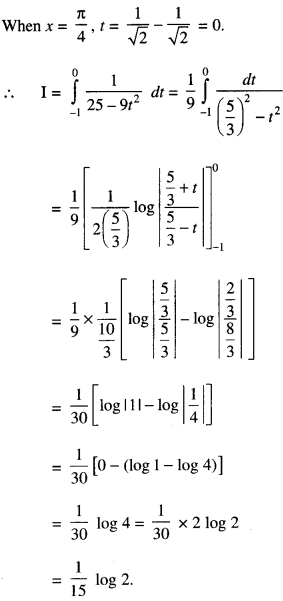
Question 14.
Evaluate \(\int_{0}^{3 / 2}|x \sin \pi x| d x\) (C.B.S.E. 2017)
Solution:

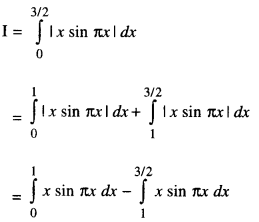
In (0, 1), x sin πx is +ve
⇒ | x sin πx | = x sin πx.
In (0, 3/2), x sin πx is +ve
⇒ | x sin πx | = -x sin πx.

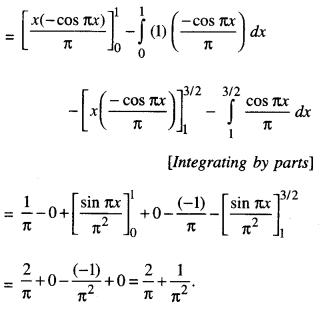
Question 15.
\(\int_{0}^{4}\) |x| + |x-2| + |x-4|)dx (C.B.S.E. 2013)
Solution:
By definition,

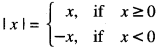
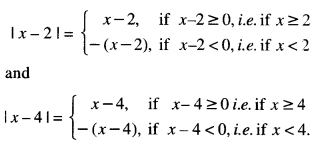
Now, \(\int_{0}^{4}\) (| x | + | x – 2| + | x – 4|) dx
= \(\int_{0}^{4}\) (|x| + |x-2| + |x-4|)dx
\(\int_{0}^{4}\) (| x | + | x – 2| + |x – 4| ) dx
= \(\int_{0}^{4}\) [x + (x-2)}-(x-4)]dx
= \(\int_{0}^{4}\) [(-x +6) dx + = \(\int_{0}^{4}\) (x+2)dx

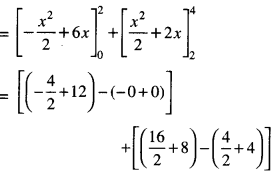
= 10 +(16-6)= 10+10 = 20.

Question 16.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x \sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x\) (C.B.S.E. 2018 C)
Solution:


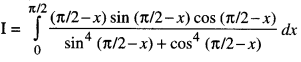
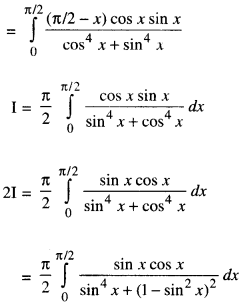
Let sin² x = t
⇒ sin x cos x dx = 1/2 dt
For x-0,t = sin² 0 = 0
and for x = π/2, t = sin² π/2 = 1

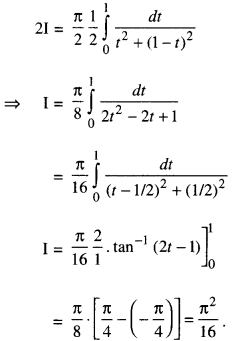
Question 17.
Evaluate : \(\int_{1}^{3}\)(3x² + 2x + 1)dx as the limit ofa sum. (C.B.S.E. 2018 C)
Solution:
a = 1, b = 3
and h = 2/n
nh = 2
\(\int_{1}^{3}\)(3x² + 2x + 1)dx
\(\lim _{h \rightarrow 0}\)
= lim h\f(l) +/(1 + h) +/(1 + 2h) + …
= \(\lim _{h \rightarrow 0}\) h[f(1) +f(1 + h) +f(1 + 2h) + …+ f(1 + (n — 1)h)]
= \(\lim _{h \rightarrow 0}\) h[(6+ {3(1 +h)² + 2(1 + h)+ 1} + (3(1 + 2h)² + 2(1 + 2h) + 1) + … + {3(1 +(n – 1)h)² + 2(1 +(n – 1)h)+ 1)]
= \(\lim _{h \rightarrow 0}\) h[6+ {3(1 + h² + 2h) + 2(1 +h) + 1) + {3(1 +4h² + 4h) } + 2(1 +2h)+ 1}+… + {3(1 + (n – 1)² h² + 2(n – 1)h) + 2(1 +(n—1)h)+(l +(n – 1)h}

= \(\lim _{h \rightarrow 0}\) h[(6) + (6 + 8h + 3h²) + (6 + 16h + 12h²) + … + [(6 + 3(n – 1)² h² + 8 (n —1)h}]

= \(\lim _{h \rightarrow 0}\)[6n+8h(1 + 2 +…+(n – 1))
+3h² {(1² + 2² + …+(n – 1)²}]