Three Dimensional Geometry Class 12 Important Extra Questions Maths Chapter 11

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 11 Three Dimensional Geometry. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 11 Important Extra Questions Three Dimensional Geometry

Three Dimensional Geometry Important Extra Questions Very Short Answer Type

Question 1.
Find the acute angle which the line with direction-cosines \(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{6}}, n>\) makes with positive direction of z-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
l² + m² + n² = 1
\(\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{6}}\right)^{2}\) + n² = 1
⇒ \(\frac{1}{3}+\frac{1}{6}\) + n² = 1
n² = 1 – \(\frac{1}{2}\)
n² = \(\frac{1}{2}\)
n = \(\frac{1}{\sqrt{2}}\)
Thus, cos α = \(\frac{1}{\sqrt{2}}\)
Hence, α = 45° or \(\frac{\pi}{4}\)

Question 2.
Find the direction-cosines of the line.
\(\frac{x-1}{2}=-y=\frac{z+1}{2}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given line is \(\frac{x-1}{2}=\frac{y}{-1}=\frac{z+1}{2}\)
Its direction-ratios are <2,-1,2>.
Hence, its direction- cosine are:

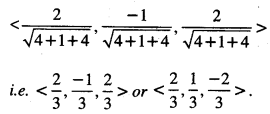
Question 3.
If α, β, γ are direction-angles of a line, prove that cos 2a + cos 2P + cos 2y +1 = 0. (N.C.E.R.T.)
Solution:
Since α, β, γ are direction-angles of a line,
∴ cos² α + cos² β + cos²γ = 1

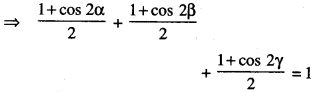
⇒ 1 + cos2α + 1 + cos2β + 1 + cos2γ = 2
⇒ cos 2α + cos 2β + cos 2γ + 1 = 0, which is true.

Question 4.
Find the length of the intercept, cut off by the plane 2x + y – z = 5 on the x-axis.   (C.B.S.E. Outside Delhi 2019)
Solution:
The given plane is2x + y – z = 5
⇒ \(\frac{x}{5 / 2}+\frac{y}{5}+\frac{z}{-5}=1\)
Its intercepts are \(\frac{x}{5 / 2}\), 5 and -5.
Hence, the length of the intercept on the x-axis is \(\frac{x}{5 / 2}\)

Question 37.
Find the length of the perpendicular drawn from the point P(3, -4,5) on the z-axis.
Solution:
Length of the perpendicular from P(3, -4,5) on the z-axis
= \(\sqrt{(3)^{2}+(-4)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5 units.

Question 5.
Find the vector equation of a plane, which is at a distance of 5 units from the origin and whose
normal vector is \(2 \hat{i}-\hat{j}+2 \hat{k}\)
Solution:
Let \(\vec{n}=2 \hat{i}-\hat{j}+2 \hat{k}\)

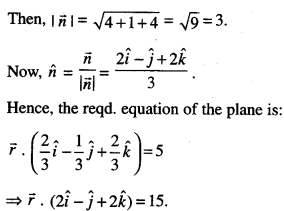
Question 6.
If a line makes angles 90°, 135°, 45° with the x,y and z-axes respectively, find its direction cosines.
Solution:
Direction cosines of the line are :
< cos 90°, cos 135°, cos 45° >
<0, \(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\)>

Question 7.
Find the co-ordinates of the point where the line through the points A (3,4,1) and B (5,1, 6) crosses the xy-plane.
The equations of the line through A (3,4,1) and B (5,1,6) are:

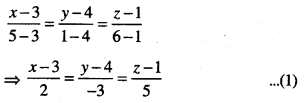
Any point on (1) is (3 + 2k,4- 3k, 1 + 5k) …………. (2)
This lies on xy-plane (z = 0).
∴ 1 + 5k = 0 ⇒ k = \(-\frac{1}{5}\)
Putting in (2), [ 3-\(\frac{2}{5}\), 4 + \(\frac{3}{5}\), 1-1)
i.e. (\(\frac{13}{5}\), \(\frac{23}{5}\), 0)
which are the reqd. co-ordinates of the point.

Question 8.
find the vector equation ofthe line which passes through the point (3,4,5) and is parallel to the vector \(2 \hat{i}+2 \hat{j}-3 \hat{k}\)
Solution:
The vector equation of the line is \(\vec{r}=\vec{a}+\lambda \vec{m}\)
i.e., \(\vec{r}=(3 \hat{i}+4 \hat{j}+5 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}-3 \hat{k})\)

Three Dimensional Geometry Important Extra Questions Short Answer Type

Question 1.
Find the acute angle between the lines whose direction-ratios are:
< 1,1,2 > and <-3, -4,1 >.
Solution:

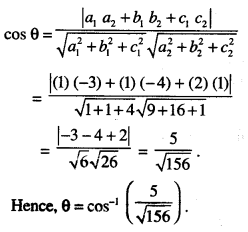
Question 2.
Find the angle between the following pair of lines:
and
\(\frac{-x+2}{-2}=\frac{y-1}{7}=\frac{z+3}{-3}\) and \(\frac{x+2}{-1}=\frac{2 y-8}{4}=\frac{z-5}{4}\)
and check whether the lines are parallel or perpendicular. (C.B.S.E. 2011)
Solution:
The given lines can be rewritten as :
\(\frac{-x+2}{-2}=\frac{y-1}{7}=\frac{z+3}{-3}\) ………….. (1)
\(\frac{x+2}{-1}=\frac{2 y-8}{4}=\frac{z-5}{4}\) ………..(2)
Here < 2,7, – 3 > and < -1,2,4 > are direction- ratios of lines (1) and (2) respectively.

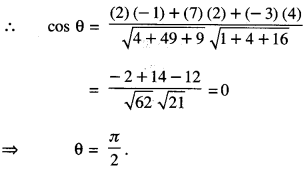
Hence, the given lines aife perpendicular.

Question 3.
Find the vector equation of the line joining (1.2.3) and (-3,4,3) and show that it is perpendicular to the z-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
Vector equation of the line passing through
(1.2.3) and(-3,4,3)is \(\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\)
where \(\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}\) and \(\vec{b}=-3 \hat{i}+4 \hat{j}+3 \hat{k}\)
⇒ \(\vec{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-4 \hat{i}+2 \hat{j})\) …(1)
Equation of z-axis is \(\vec{r}=\mu \hat{k}\) …(2)
Since \((-4 \hat{i}+2 \hat{j}) \cdot \hat{k}=0\) = 0,
∴ Line (1) is perpendicular to z-axis.

Question 4.
Find the vector equation of the plane, which is \(\frac{6}{\sqrt{29}}\) at a distance of
units from the origin and its normal vector from the origin is \(2 \hat{i}-3 \hat{j}+4 \hat{k}\) . Also, find its cartesian form. (N.C.E.R.T.)
Solution:

Question 5.
Find the direction-cosines of the unit vector perpendicular to the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) +1 = 0 through the origin. (N.C.E.R.T.)
Solution:
The given plane is \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) + 1 = 0
\(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) = 1 ………… (1)
Now \(|-6 \hat{i}+3 \hat{j}+2 \hat{k}|=\sqrt{36+9+4}\)
\(=\sqrt{49}=7\)
Dividing (1) by 7,
\(\vec{r} \cdot\left(-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\right)=\frac{1}{7}\)
which is the equation of the plane in the form \(\vec{r} \cdot \hat{n}=p\)
Thus, \(\hat{n}=-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\)
which is the unit vector perpendicular to the plane through the origin.
Hence, the direction-cosines of \(\hat{n}\) are \(<-\frac{6}{7}, \frac{3}{7}, \frac{2}{7}>\)

Question 6.
Find the acute angle between the lines
\(\frac{x-4}{3}=\frac{y+3}{4}=\frac{z+1}{5}\) and \(\frac{x-1}{4}=\frac{y+1}{-3}=\frac{z+10}{5}\)
Solution:
Vector in the direction of first line
\(\frac{x-4}{3}=\frac{y+3}{4}=\frac{z+1}{5}\) ,
\(\vec{b}=(3 \hat{i}+4 \hat{j}+5 \hat{k})\)

Vector in the direction of second line
\(\frac{x-1}{4}=\frac{y+1}{-3}=\frac{z+10}{5}\) ,
\(\vec{d}=4 \hat{i}-3 \hat{j}+5 \hat{k}\)
∴ θ, the angle between two given lines is given by:

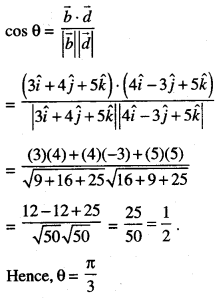
Question 7.
Find the angle between the line:
\(\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-\hat{j}+3 \hat{k})\) and the plane \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})=4\) Also, find whether the line is parallel to the plane or not .
Solution:
The given line is :
\(\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-\hat{j}+3 \hat{k})\)
and the given plane is \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) = 4.
Now the line is parallel to 2\(\hat{i}\) – \(\hat{j}\) + 3\(\hat{k}\) and nor¬mal to the plane 2\(\hat{i}\) + \(\hat{i}\) – \(\hat{k}\)
If ‘θ’ is the angle between the line and the plane,
then \(\left(\frac{\pi}{2}-\theta\right)\) is the angle between the line and normal to the plane.
Then

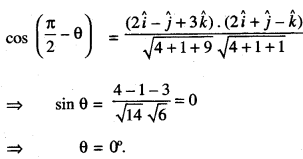
Hence, the line is parallel to the plane.

Question 8.
Find the value of ‘λ’, so that the lines:
\(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2}\) and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles. Also, find whether the lines are intersecting or not
Solution:
(i) The given lines are
\(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2}\) ……………….(1)
and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) ……….. (2)
These are perpendicular if:

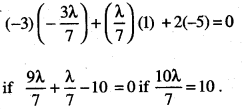
Hence λ = 1.

(ii) The direction cosines ofline(1) are <-3,1,2>
The direction cosines of line (2) are < -3,1, -5 >
Clearly, the lines are intersecting.

Question 9.
Find the angle between the line: \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) and the plane: 3x + 4y + z + 5 = 0.
x-2 y+1 z-3
Sol. The given line is \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) ………..(1)
and the given plane is :
3x + 4y + z + 5 = 0 …(2)
If the line (1) makes an angle ‘0’ with the plane (2), then the line (1) will make angle (90° – 0) with the normal to the plane (2).
Now direction-ratios of line (1) are:
<3, -1,-2>
and direction-ratios of normal to plane (2) are <3,4,1>.
∴ cos (90° – θ)

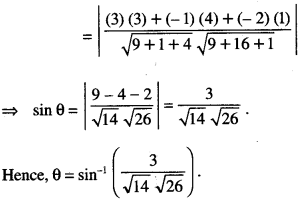
Question 10.
State when the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=\vec{d}\) . Show that the line \(\vec{r}=\hat{i}+\hat{j}+\lambda(\hat{2}+\hat{j}+4 \hat{k})\) is parafiel to the plane \(\vec{r} \cdot(-2 \hat{i}+\hat{k})\) = 5. Also, find the distance between the line and the plane.
Solution:
(i) A line is parallel to the plane if it is perpendicular to the normal to the plane.
The given line is \(\vec{r}=\vec{a}+\lambda \vec{b}\)
⇒ \(\vec{b}\) is parallel to the line.
The given plane is \(\vec{r} \cdot \vec{n}=\vec{d}\)

⇒ \(\vec{n}\) is normal to the plane.
Thus the line is parallel to the plane when
\(\vec{b} \cdot \vec{n}\) =0.

(ii) Here \(\vec{b}=2 \hat{i}+\hat{j}+4 \hat{k}\) and \(\vec{n}=-2 \hat{i}+\hat{k}\)
Now \(\vec{b} \cdot \vec{n}\) = (2) (- 2) + (1) (0) + (4) (1)
= -4 + 0 + 4 = 0.
Hence, the given line is parallel to the given plane.

(iii) (1,1,0) is a point on the given line.
Equation of the plane is-2x + z- 5= 0.
∴ Reqd. distance
= \(\left|\frac{-2(1)+0-5}{\sqrt{4+0+1}}\right|=\frac{7}{\sqrt{5}}=\frac{7 \sqrt{5}}{5}\)units.

Three Dimensional Geometry Important Extra Questions Very Long Answer Type 2

Question 1.
Find the shortest distance between the lines:\(\vec{r}=(4 \hat{i}-\hat{j})+\lambda(\hat{i}+{2} \hat{j}-{3} \hat{k})\) and \(\vec{r}=(\hat{i}-\hat{j}+2 \hat{k})+\mu(2 \hat{i}+4 \hat{j}-5 \hat{k})\) (C.B.S.E. 2018)
Solution:
Comparing given equations with:

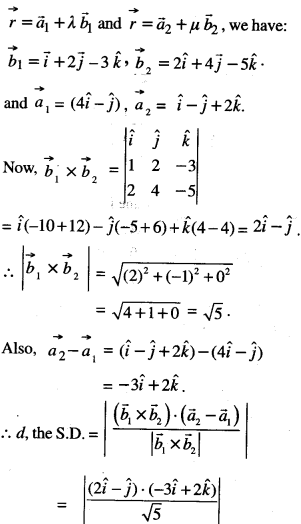
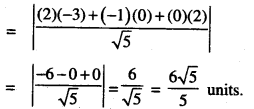
Question 2.
A line makes angles α, β, γ, δ with the four diagonals of a cube, prove that:
cos² α + cos² β + cos² γ + cos² δ= \(\frac{4}{3}\). (N.C.E.R.T.)
Solution:
Let O be the origin and OA, OB, OC (each = a) be the axes.

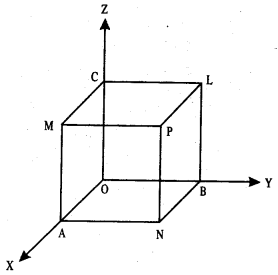
Thus the co-ordinates of the points are :
O (0,0,0), A (a, 0,0), B (0, a, 0), C (0,0, a),
P (a, a, a), L (0, a, a), M (a, 0, a), N (a, a, 0).
Here OP, AL, BM and CN are four diagonals.
Let < l, m, n > be the direction-cosines of the given line.

Now direction-ratios of OP are:
<a-0,a-0,a-0>i.e.<a,a,a>
i.e. < 1,1,1 >,
direction-ratios of AL are:
<0-a, a-0, a-0> i.e. <-a,a,a>
i.e. <-l, 1,1 >,
direction-ratios of BM are:
<a-0,0-a, a-0>
i.e. <a,-a,a> i.e. < 1,-1, 1 >
and direction-ratios of CN are:
<a-0,a-0,0-a> i.e. <a,a,-a>
i.e. < 1,1,-1 >.

Thus the direction-cosines of OP are :
\(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
the direction-cosines of AL are:
\(<-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
the direction-cosines of BM are :
\(<\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
and the direction-cosines of CN are :
\(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}>\)
If the given line makes an angle ‘a’ with OP, then :

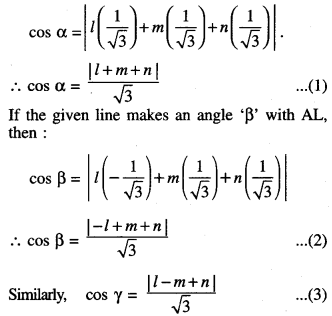
and cos δ = \(\frac{|l+m-n|}{\sqrt{3}}\) ………… (4)
Squaring and adding (1), (2), (3) and (4), we get:
cos² α + cos² β + cos² γ + cos²δ
= \(\frac { 1 }{ 3 }\) [(l + m + n)² + (-l + m + n)²
+ (l-m + n)² + (l + m — n)²]
= \(\frac { 1 }{ 3 }\) [4(l² + m² + n²)] = \(\frac { 1 }{ 3 }\) [4(1)].
Hence,cos² α + cos² β + cos² γ + cos²δ = \(\frac { 4 }{ 3 }\)

Question 3.
Find the equation of the plane through the line \(\frac{x-1}{3}=\frac{y-4}{2}=\frac{z-4}{-2}\) and parallel to the line:
\(\frac{x+1}{2}=\frac{1-y}{4}=\frac{z+2}{1}\)
Hence, find the shortest distance between the lines. (C.B.S.E. Sample Paper 2018-19)
Solution:
The two given lines are:
\(\frac{x-1}{3}=\frac{y-4}{2}=\frac{z-4}{-2}\) ………… (1)
and \(\frac{x+1}{2}=\frac{1-y}{4}=\frac{z+2}{1}\) ………….. (2)
Let <a, b, c> be the direction-ratios of the normal to the plane containing line (1).
∴ Equation of the plane is:
a(x- l) + b(y-4) + c(z-4) …(3),
where 3a + 2b – 2c = 0 …(4)
[∵ Reqd. plane contains line (1)] and 2a – 4b + 1.c = 0
[∵ line (1) a parallel to the reqd. plane] Solving (4) and (5),

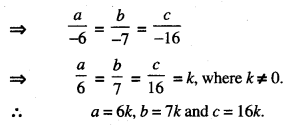
Putting in (3),
6k(x- 1) + 7k(y – 4) + 16k(z – 4) = 0
= 6(x – 1) + 7(y – 4) + 16(z – 4) =0
[∵k ≠ 0]
⇒ 6x + 7y+ 16z-98 = 0,

which is the required equation of the plane.
Now, S.D. between two lines = perpendicular distance of (-1,1, – 2) from the plane

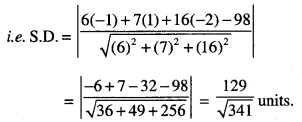
6(—1) + 7(1) +16(-2) – 98
V(6)2+(7)2+(16)2
-6 + 7-32-98 V36 + 49 + 256

Question 4.
Find the Vector and Cartesian equations of the plane passing through the points (2, 2, -1), (3,4,2) and (7,0,6). Also, find the vector equa¬tion of a plane passing through (4,3,1) and parallel to the plane obtained above. (C.B.S.E. 2019)
Solution:
(i) Cartesian equations
Any plane through (2,2, -1) is :
a(x – 2) + b(y- 2) + c(z + 1) = 0 … (1)
Since the plane passes through the points (3,4,2) and (7,0,6),
∴ a(3 – 2) + b(4 – 2) + c(2 +1) = 0
and a(7 – 2) + b(0 – 2) + c(6 + 1) = 0
⇒ a + 2b + 3c = 0 …(2)
and 5a – 2b + 7c = 0 …(3)
Solving (2) and (3),\(\frac{a}{14+6}=\frac{b}{15-7}=\frac{c}{-2-10}\)
⇒ \(\frac{a}{20}=\frac{b}{8}=\frac{c}{-12}\)
⇒ \(\frac{a}{5}=\frac{b}{2}=\frac{c}{-3}\) = k (say), value k ≠ 0.
∴ a = 5k,b = 2k and c = -3k,
Putting the values of a, b, c in (1), we get:
5k(x – 2) + 2k(y – 2) – 3k(z + 1) = 0
⇒ 5(x-2) + 2(y-2)-3(z+ 1) =0[∵ k ≠ 0]
=» 5x- 10 + 2y-4-3z-3 = 0
=» 5x + 2y-3z-17 = 0, …(4)
which is the reqd. Cartesian equation.
Its vector equation is \(\vec{r} \cdot(5 \hat{i}+2 \hat{j}-3 \hat{k})\) =17.

(ii) Any plane parallel to (4) is
5x + 2y – 3z + λ – 0 … (5)
Since it passes through (4, 3,1),
5(4) + 2(3) – 3(1) + λ = 0
⇒ 20 + 6 — 3 + λ = 0
⇒ λ = -23.
Putting in (5), 5x + 2y – 3z – 23 = 0, which is the reqd. equation.
Its vector equation is \(\vec{r} \cdot(5 \hat{i}+2 \hat{j}-3 \hat{k})\) = 23.

Question 5.
Find the co-ordinates of the foot of the perpendicular drawn from the point A (1,8,4) to the line joining B (0, -1,3) and C (2,-3,-1). (A.I.C.B.S.E. 2016)
Solution:
Any point on BC, which divides [BC] in the ratio k: 1,is:

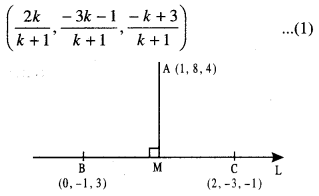
This becomes M, the foot of perp. from A on BC
if AM⊥BC …(2)
But direction-ratios of BC are:
<2-0,- 3 + 1,-1 -3 > i.e. < 2,-2,-4 >
i.e, <1, -1 > -2>
and direction-ratio of AM are:
\(<\frac{2 k}{k+1}-1, \frac{-3 k-1}{k+1}-8, \frac{-k+3}{k+1}-4>\)
i.e. < k- 1,- 11k:-9, -5k— 1 >
∴ Due to (2), (1) (k- 1) + (- 1) (-1 1k-9) + (-2)(-5k- 1) = 0
⇒ k – 1 + 11k + 9 + 10k + 2 = 0
⇒ 22k + 10 = 0
⇒ k = \(-\frac{5}{11}\)
∴ From (1), the co-ordinates of M, the foot of perp. are:

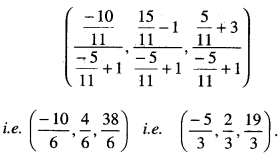
Question 6.
(a) Find the image of the point (1,6,3) in the line:
\(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\)
(C.B.S.E. 2010 C)
(b) Also, write the equation of the line joining the given point and its image and find the length of the segment joining the given point and its image. (C.B.S.E. 2010 C)
Solution:
(a) Let P be the given point (1, 6, 3) and M, the foot of perpendicular from P on the given line AB:

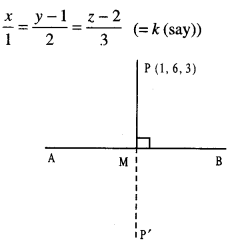
Any point on the given line is:
(k, 1+2k, 2+3k)
For some value of k, let the point be M.
∴ Direction-ratios of PM are:
<k-1,1+2k-6, 2 + 3k – 3> i.e. .
Since PM ⊥AB ,
∴ (1) (k-1) + (2)(2k-5) + (3) (3k-1) = 0
⇒ k-l +4k – 10 + 9&-3 = 0
⇒ 14 k = 14
⇒ k = 1.

∴ Foot of perpendicular M is (1,1 + 2,2 + 3) i.e. (1,3,5).
Let P'(α, β, γ) be the image of P in the given line. Then M is the mid-point of [PP’].
∴ \(\)
⇒α + 1 = 2, β + 6 = 6, γ+3 = 10
⇒ α = 1, β = 0, γ = 7.
Hence, the reqd. image is (1,0,7).

(b) (i) The equations of the line PP’ are :

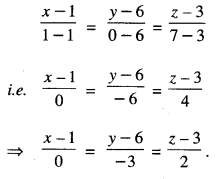
(ii) Length of segment [PP’]

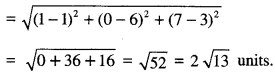
Question 7.
Find the co-ordinates of the foot of perpendicu¬lar and the length of the perpendicular draw n from the point P (5,4,2) to the line:
\(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\)
Also, find the image of P in this line. (A.I.C.B.S.E. 2012)
Solution:
(i) The given line is :
\(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\)
i.e, \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) …………… (1)
The given point is P (5,4,2).

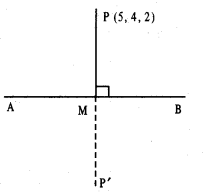
Let M be the foot of perpendicular from P on the given line AB.
Any point on (1) is (-1 + 2k, 3 +3k, l – k).
For some value of k, let the point be M.
Direction-ratios of PM are:
<-1+2k-5, 3+3k-4, 1-k-2>
i.e, <2k – 6, 3k – 1, -k – 1>
Since PM ⊥ AB ,
∴ 2(2k – 6) + 3 (3k – 1) + (-1)(-k – 1) = 0
⇒4k – 12 + 9k – 3 + k + 1 = 0
⇒14k – 14 = 0
⇒ k = 1

Foot of perpendicular M is
(-1+2, 3+3, 1,-1) i.e (1,6,0)
(ii) Length of Perpendicular
= \(\sqrt{(5-1)^{2}+(4-6)^{2}+(2-0)^{2}}\)
= \(\sqrt{16+4+4}=\sqrt{24}=2 \sqrt{6}\) units

(iii) Let P’ (α, β, γ) be the image of P in the given line.
Then M is the mid-points of [PP’].
∴ \(\frac{\alpha+5}{2}=1, \frac{\beta+4}{2}=6, \frac{\gamma+2}{2}=0\)
⇒ α+5 = 2, β + 4=12, γ+2 = 0
⇒ α = -3,β = 8,γ=-2.
Hence, the reqd. image is (-3,8, -2).

Question 8.
Find the distance between the lines L₁ and L₂ given by:
\(\vec{r}=\hat{i}+2 \hat{j}-4 \hat{k}+\lambda(2 \hat{i}+3 \hat{j}+6 \hat{k})\) and
\(\vec{r}=3 \hat{i}+3 \hat{j}-5 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+6 \hat{k})\) (N.C.E.R.T.)
Solution:
Clearly, L₁ and L₂ are parallel.
Comparing given equations with:
\(\vec{r}=\vec{a}_{1}+\lambda \vec{b}\) and \(\vec{r}=\vec{a}_{2}+\mu \vec{b}\), we have:
\(\vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k}\), so that
\(|\vec{b}|=\sqrt{4+9+36}=\sqrt{49}=7\)

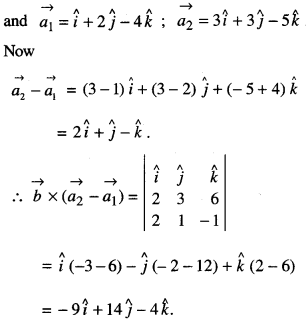
∴ d, the distance between the given lines is given by:

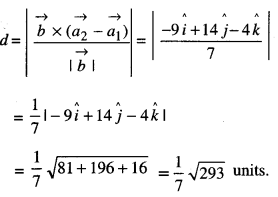
Question 9.
Find the vector equation of the plane that contains the lines \(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+2 \hat{j}-\hat{k})\) and the points (-1, 3, -4). Also find the length of the perpendicular from the point (2,1,4) to the plane, thus obtained. (Delhi 2019)
Solution:
Let required plane be
a(x+ l) + b(y-3) + c(z + 4) = 0 …(1)

Plane contains the given line, so it will also con-tain the point (1,1,0).
So, 2a – 2b + 4c = 0
or a-b + 2c = 0
Also, a + 2b – c = 0
From (2) and (3),
\(\frac{a}{-3}=\frac{b}{3}=\frac{c}{3}\) …………(4)

From (1) and (4), required plane is
-3(x + l) + 3(y-3) + 3(z + 4) = 0
⇒ -x-l+;y-3 + z + 4 = 0
⇒ -x + y + z = 0.
Its vector equation is :
\(\vec{r} \cdot(-\hat{i}+\hat{j}+\hat{k})\) = 0.
Length of perpendicular from
\((2,1,4)=\frac{|-2+1+4|}{\sqrt{(-1)^{2}+1^{2}+1^{2}}}=\sqrt{3}\)

Question 10.
Find the vector equation of the plane which contains the line of intersection of the planes:
\(\vec{r} \cdot(\hat{i}+{2} \hat{j}+{3} \hat{k})\) – 4 = 0,
\(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) + 5 = 0
and which is perpendicular to the plane \(\vec{r} \cdot(5 \hat{i}+3 \hat{j}-6 \hat{k})\) + 8 = 0
(Outside Delhi 2019)
Solution:
Required equation of the plane is :

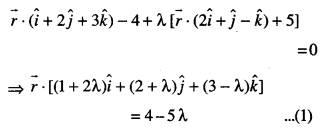
This is perpendicular to the plane
\(\vec{r}\) (5 \(\hat{i}\) + 3 \(\hat{j}\) — 6\(\hat{k}\)) + 8 = 0
⇒ (1+2λ) (5) + (2 + λ) (3) + (3 – λ.) (-6)=0
⇒ 5 + 10λ + 6 + 3λ – 18 + 6λ = 0 ⇒ 191 = 7
⇒19λ = 7
⇒λ = \(\frac { 7 }{ 19 }\)
Puttiong in (1),

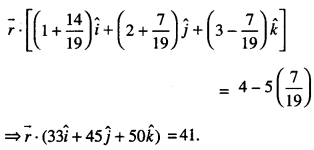
Question 11.
Show that die line of intersection of the planes: x + 2y + 3z = 8 and 2x + 3y + 4z = 11 is coplanar with the line:
\(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z+1}{3}\)
Also, find the equation of die plane containing them. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given line is \(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z+1}{2}\) ………. (1)
This is coplanar with the line determined by the planes:
x + 2y + 3z – 8 = 0 …(2)
and 2x + 3y + 4z – 11 =0 …(3)
Here, we show that there exists a plane, which passes through the intersection of (2) and (3) and contains line (1).
Now equation of the plane through the intersection of (2) and (3) is:
(x+2y + 3z-8) + 1(2x+3y+ 4z-11) = 0 …(4)
This passes through 1, -1),
∴ (-1 -2-3-8) + k(-2-3-4-11) = 0
∴ -14-20k = 4
k = \(-\frac { 7 }{ 10 }\)
Putting in (4),
(x + 2y + 3z-8) – \(\frac { 7 }{ 10 }\)(2x + 3y + 4z – 11) = 0
=» (10x + 20y + 30z – 80)
-7 (2x + 3y + 4z – 11) = 0
⇒ 4x + y – 2z + 3 = 0 …(5)
If < a₁ , b₁ , c₁ > are direction-ratios of line (1)
and < a₂, b₂, c₂ > are direction-ratios of normal to plane (5), then
a₁a₂+ b₁b₂+ c₁ c₂ = (1) (4) + 2 (1) + 3 (-2) = 0,
which implies that line (1) lies in plane (5). Hence, the two lines are coplanar and the equation of the plane containing them is 4x + y-2z + 3=0.

Question 12.
Find the vector equation of the line passing through the point (2,3, -1) and parallel to the planes:
\(\vec{r} \cdot(3 \hat{i}+4 \hat{j}+2 \hat{k})\) = 5 andr \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}-2 \hat{k})\) = 4.
Solution:
The given planes are:
\(\vec{r} \cdot(3 \hat{i}+4 \hat{j}+2 \hat{k})\) = 5 and \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}-2 \hat{k})\) = 4
i.e. 3x + 4y + 2z = 5 and 3x- 2y – 2z = 4
⇒3x + 4y + 2z-5 = 0 ……(1)
and 3x – 2y – 2z – 4 = 0 …………. (2)
Let the line through (2,3, -1) be:
\(\frac{x-2}{a}=\frac{y-3}{b}=\frac{z+1}{c}\) …………. (3)

Since (3) is parallel to (1),
∴ a(3) + h(4) + c(2) = 0 -(3)
i.e. 3a + 4b + 2c = 0
Since (3) is parallel to (2), …(4)
∴ (a) (3) + b (-2) + c (-2) = 0 …(5)
⇒ 3a -2b -2c = 0

Question 13.
Find the equation of a plane passing through the points A (2,1,2) and B(4, – 2,1) and per-pendicular to plane \(\vec{r} \cdot(\hat{i}-2 \hat{k})\) = 5. Also, find
the coordinates of the point, where the line pass-ing through the points (3,4,1) and (5,1, 6) crosses the plane thus obtained.
Solution:
Let P(x, y, z) be any point on the plane, which
passes through A(2,1,2) and B(4, -2,1).
∴ \(\overrightarrow{\mathrm{AP}}\) and \(\overrightarrow{\mathrm{AB}}\) lie on the required plane.
Also, the required plane is perpendicular to the
given plane \(\vec{r} \cdot(\hat{i}-2 \hat{k})\) = 5.
∴ Normal to the given plane \(\overrightarrow{n_{1}}=(\hat{i}-2 \hat{k})\) lies on the required plane
⇒ \(\overrightarrow{\mathrm{AP}}\), \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{n_{1}}\) are coplanar,
where \(\overrightarrow{\mathrm{AP}}\) = (x-2) \(\hat{i}\) +(y-1)\(\hat{j}\) + (z-2)\(\hat{k}\)
and \(\overrightarrow{\mathrm{AB}}\) = 2\(\hat{i}\) – 3\(\hat{j}\) – \(\hat{k}\)

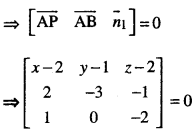
⇒ (x-2)(6-0)-(y-1)(-4 + 1) + (z-2)(0 + 3) =0
⇒ 6x – 12 + 3y -3 + 3z – 6 =0
⇒ 2x + y + z = 7 …(1)
Line passing through L(3,4,l) and M(5,1,6) is:

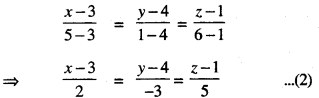
General point on the line is Q(2λ,+ 3, -3λ,+4, 5λ.+1).
Since the line (2) crosses plane (1),
∴ the points Q should satisfy (1).
2(2λ+3) + (-3λ+4) + (5λ,+1) = 7
⇒ 4λ + 6 – 3λ,+4 + 5λ,+ l =7
⇒ 6λ = -4
λ = \(-\frac{2}{3}\)
Hence, the point Q is (\(-\frac{4}{3}\)+3, 2+4, \(-\frac{10}{3}\)+1)
i.e, (\(-\frac{5}{3}\), 6, \(-\frac{7}{3}[latex])

Question 14.
Find the co-ordinates of the point P, where the line through A(3, -4,-5) and B (2, – 3, 1) crosses the plane passing through three points L(2,2,1), M(3,0,1) and N(4, -1,0). Also, find the ratio in which P divides the line segment AB. {C.B.S.E. 2016)
Solution:
Any plane through L(2,2,1) is:
a(x-2) + b(y-2) + c(z-1) = 0 …(1)
Since (1) passes through M(3,0,1),
∴ a(3-2) + b(0-2) + c(1 – 1) = 0
⇒ a-2b + 0 .c = 0 …(2)
Since (1) passes through N (4, – 1,0),
∴ a(4 – 2) + b(- 1 – 2) -(- c(0 – 1) – 0
⇒ 2a – 3b – c = 0 …(3)
Solving (2) and (3),
[latex]\frac{a}{2+0}=\frac{b}{0+1}=\frac{c}{-3+4}=k \text { (say) }\)
⇒ a = 2k,b = k,c = k.
Putting in (1),
2k(x-2) + k(y-2) + k(z- 1) = 0 ⇒ 2(x-2) + (y-2) + (z-l) = O[\-fc*0]
⇒ 2x + y + z-l = 0 …(4)
Now equations of AB are:

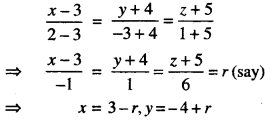
and z = -5 + 6r.
Any point on AB is
P(-r+3, r-4,6r-5) …(5)
This lies on plane (4).
∴ 2(-r + 3) + (r-4) + (6r-5)-7 = 0
⇒ 5r = 10
⇒ r= 2.
Putting in (5), the co-ordinates of P are (1,-2,7).
Let P divide the segment [AB] in the ratio of k: 1.

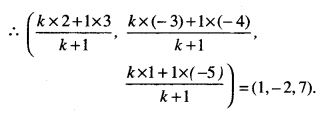
Comparing \(\frac{3+2 k}{k+1}\) = 1
3 + 2k = k + 1
k = -2
Hence, P divides the line segment [AB] in the ratio 2:1 externally.

Question 15.
Find the distance of the point (-1,-5, -10) from the point of intersection of the line \(\vec{r} =2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+\mathbf{1 2} \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})\) = 5. (C.B.S.E. 2018)
Solution:
The given lines is :
\(\vec{r}=2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+12 \hat{k})\)
i.e , \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}\) ……….(1)
and the given plane is r • (J — j + k) = 5
i.e. x – y + z = 5 …(2)
Any point on (1) is (2 + 3k, – 1 + 5k, 2 + 12k)
This lies on (2) if
2 + 3k + 1 – 4k + 2+12k) = 5
⇒ 11k = 0
⇒ k = 0.
Putting in (3), the point of intersection is (2,-1,2).
Its distance from (-1, -5, -10)
= \(\sqrt{(-1-2)^{2}+(-5+1)^{2}+(-10-2)^{2}}\)
= \(\sqrt{9+16+144}=\sqrt{169}\) = 13 units.

Question 16.
Find the vector equation of a line passing through the point (2,3,2) and parallel to the line:
\(\vec{r}=(-2 \hat{i}+3 \hat{j})+\lambda(\hat{2} \hat{i}-3 \hat{j}+6 \hat{k})\)
Also, find the distance between these two lines. Sol. The given line is
r = (-2i + 3j) + X{2i -3j + 6k) …(1)
The required line is :
\(\vec{r}=(2 \hat{i}+3 \hat{j}+2 \hat{k})+\mu(2 \hat{i}-3 \hat{j}+6 \hat{k})\) …(2)
Now, \(\overrightarrow{a_{1}}=-2 \hat{i}+3 \hat{j}\) , \(\overrightarrow{a_{2}}=2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(\vec{b}=2 \hat{i}-3 \hat{j}+6 \hat{k}\)
\(\vec{b}=2 \hat{i}-3 \hat{j}+6 \hat{k}\)
\(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}=4 \hat{i}+2 \hat{k}\)
Reqd. distance,

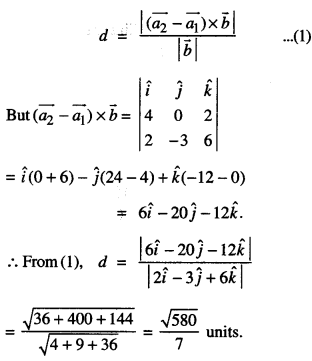
Question 17.
Find the co-ordinates of the foot of the perpendicular Q drawn from P(3,2,1) to the plane 2x – y + z + 1 = 0. Also,find the distance PQ and the image of the point P treating this plane as a mirror.
Solution:
(i) Equation of PQ is \(\frac{x-3}{2}=\frac{y-2}{-1}=\frac{z-1}{1}=\lambda\)

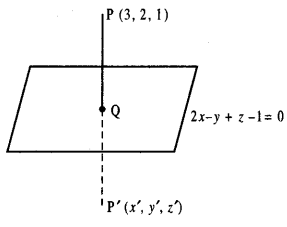
∴ Co-ordinates of Q are (2λ + 3, – λ + 2, λ + 1).
Since Q lies on the plane 2x-y + z+ 1=0,
4λ + 6 + λ – 2 + λ + 1 + 1 = 0
⇒ 6λ + 6 = 0
⇒ λ = – 1.
∴ Co-ordinates of Q are (- 2 + 3,1 + 2, -1 + 1)
i.e.,{ 1,3,0).

(ii) PQ = \(\sqrt{(1-3)^{2}+(3-2)^{2}+(0-1)^{2}}\)
= \(\sqrt{4+1+1}=\sqrt{6}\) units

(iii) Let P'(x’, y’, z’) be the image
∴ \(\frac{x^{\prime}+3}{2}=1, \frac{y^{\prime}+2}{2}=3, \frac{z^{\prime}+1}{2}=0\)
= x’ = -1, y’ = 4, z’ = -1.
Hence, the image of the point P is (- 1,4, – 1).

Question 18.
Find the vector equation of the plane determined by the points A(3, -1, 2), B(5, 2, 4) and C(-l, -1, 6). Hence, find the distance of the plane, thus obtained, from the origin.
Solution:
The equation of the plane is

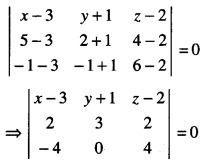
⇒ (x-3) (12 – 0) – (y+1) (8 + 8) + (z-2) (0+12) = 0
⇒ 12(x-3)-16(y+1) +12(z-2) = 0
⇒ 3(x-3)-4(y + 1) + 3(z-2) = 0
⇒ 3x – 4y + 3z = 19.
Its vector equation is r \(\vec{r} \cdot(3 \hat{i}-4 \hat{j}+3 \hat{k})\) = 19. Distance of the plane from the origin
= \(\frac{|0-19|}{\sqrt{9+16+9}}=\frac{19}{\sqrt{34}}=\frac{19 \sqrt{34}}{34}\) = units.

Question 19.
Find the co-ordinates of the point where the line \(\frac{x-8}{4}=\frac{y-1}{1}=\frac{z-3}{8}\) intersects the plane 2x + 2y + z=3. Also, find the angle between the line and the plane.
Solution:
(i) The given line is \(\frac{x-8}{4}=\frac{y-1}{1}=\frac{z-3}{8}\)…(1)
and the given plane is2x + 2y + z- 3 = 0 …(2)
Any point on line (1) is (8 + 4-k, l + k, 3 + 8k) …(3)
This lies on plane (2).
∴ 2(8 + 4k) + 2(1 + k) + (3 + 8k) -3 = 0
16 + 8k + 2 + 2k +3 + 8 k – 3 = 0
⇒ 18k + 18 = 0 ⇒ k =-1.
Putting in (3), (4, 0, – 5), which are the required co-ordinates of the point.

(ii) If the line (1) makes an angle ‘θ’ with the plane (2), then the line (1) will make an angle of (90° – θ) with the normal to the plane (2).
Now, direction-ratios of the line (1) are <4,1, 8> and direction-ratios of the normal to the plane (2) are < 2,2,1 >.

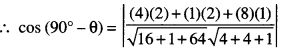
Question 20.
Find x such that the four points:
A(5,x, 4), B(4,4,6), C(5,4, -3) and D(7,7, -2) are coplanar.
Solution:
Here,
\(\overrightarrow{\mathrm{AB}}\) = (4\(\hat{i}\) +4\(\hat{j}\) + 6\(\hat{k}\)) – (5\(\hat{i}\) +x\(\hat{j}\) + 4\(\hat{k}\))
= –\(\hat{i}\) +(4-x)\(\hat{j}\) + 2\(\hat{k}\) ,
\(\overrightarrow{\mathrm{BC}}\) = (5\(\hat{i}\) + 4\(\hat{j}\) – 3\(\hat{i}\))-(4\(\hat{i}\) + 4\(\hat{j}\) + 6\(\hat{k}\))
= \(\hat{i}\) – 9\(\hat{k}\)
and \(\overrightarrow{\mathrm{CD}}\) = (7\(\hat{i}\) + 7\(\hat{j}\) -2\(\hat{k}\))-(5\(\hat{i}\) + 4\(\hat{j}\) – 3\(\hat{k}\))
= 2\(\hat{i}\) + 3\(\hat{k}\) + \(\hat{k}\).
The four points are collinear if

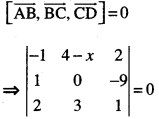
⇒ (-1)(0 + 27)-(4-x)(l + 18) + 2(3-0) = 0
⇒ -27-76 + 19x +6=0
⇒ 19x=97.
Hence, x = \(\frac { 97 }{ 19 }\)