Continuity and Differentiability Class 12 Important Extra Questions Maths Chapter 5

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 5 Continuity and Differentiability. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 5 Important Extra Questions Continuity and Differentiability

Continuity and Differentiability Important Extra Questions Very Short Answer Type

Question 1.
If y = log (cos e^x), then find \(\frac{d y}{d x}\) (Delhi 2019)
Solution:
We have :y = log (cos e^x)
∴ \(\frac{d y}{d x}=\frac{1}{\cos e^{x}}\left(-\sin e^{x}\right) \cdot e^{x}\)
= – e^x tan e^x

Question 2.
Differentiate cos {sin (x)²} w.r.t. x. (Outside Delhi 2019)
Solution:
Let y = cos {sin (x)²}.
∴ \(\frac{d y}{d x}\)= – sin {sin (x)²}. \(\frac{d y}{d x}\){sin (x)²}
= – sin {sin (x)²}. cos(x)² \(\frac{d y}{d x}\) (x²)
= – sin {sin (x)²}. cos(x)²2x
= -2x cos(x)² sin {sin(x)²}.

Question 3.
Differentiate sin²(x²) w.r.t. x².   (C.B.S.E. Sample Paper 2018-19)
Solution:
Let y = sin²(x²).
∴ \(\frac{d y}{d x}\) = 2 sin (x²) cos (x²) = sin (2x²).

Question 4.
Find \(\frac{d y}{d x}\), if y + siny = cos or.
Solution:
We have: y + sin y = cos x.
Differentiating w.r,t. x, we get:
\(\frac{d y}{d x}\) + cos y. \(\frac{d y}{d x}\) = – sin x
(1 + cos y)\(\frac{d y}{d x}\) = -sin x
Hence, \(\frac{d y}{d x}\) = \(-\frac{\sin x}{1+\cos y}\)
where y ≠ (2n + 1)π, n ∈ Z.

Question 5.
If y = \(\sin ^{-1}\left(6 x \sqrt{1-9 x^{2}}\right),-\frac{1}{3 \sqrt{2}}<x<\frac{1}{3 \sqrt{2}}\) then find \(\frac{d y}{d x}\). (C.B.S.E. 2017)
Solution:
Here y = sin^-1\(\left(6 x \sqrt{1-9 x^{2}}\right)\)
Put 3x = sin θ.
y = sin^-1 (2 sin θ cos θ)
= sin^-1 (sin 2θ) = 2θ
= 2 sin^-1 3x
\(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)

Question 6.
Is it true that x = e^logx for all real x? (N.C.E.R.T.)
Solution:
The given equation is x = e^logx
This is not true for non-positive real numbers.
[ ∵ Domain of log function is R+]
Now, let y = e^logx
If y > 0, taking logs.,
log y = log (e^logx) = log x.log e
= log x . 1 = log x
⇒ y = x.
Hence, x = e^logx is true only for positive values of x.

Question 7.
Differentiate the following w.r.t. x : 3^{x + 2}. (N.C.E.R.T.)
Solution:
Let y = 3^{x + 2}.
\(\frac{d y}{d x}\) = 3^{x + 2}.log3. \(\frac{d}{d x}\)(x + 2)
= 3^{x + 2} .log3.(1 + 0)
= 3^{x + 2}. log 3 = log 3 (3^{x + 2}).

Question 8.
Differentiate log (1 + θ) w.r.t. sin^-1θ.
Solution:
Let y = log (1 + θ) and u = sin^-1θ.

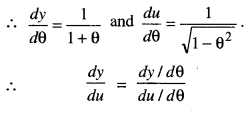
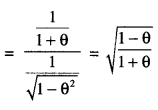
Question 9.
If y = x^x , find \(\frac{d y}{d x}\).
Solution:
Here y = x^x …(1)
Taking logs., log y = log x^x
⇒ log y = x log x.
Differentiating w.r.t. x, we get:
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x \(\frac{1}{x}\) + logx.(1)
= 1 + log x.
Hence, \(\frac{d y}{d x}\) = y (1 + log x) dx
= x^x (1 + log x). [Using (1)]

Question 10.
If y = \(\sqrt{2^{x}+\sqrt{2^{x}+\sqrt{2^{x}+\ldots \ldots+0 \infty}}}\) then prove that: (2y – 1)\(\frac{d y}{d x}\) = 2^x log 2.
Solution:
The given series can be written as :
y = \(\sqrt{2^{x}+y}\)
Squaring, y² = 2^x + y
⇒ y² – y = 2^x.
Diff. w.r.t. x, (2y -1)\(\frac{d y}{d x}\) = 2^x log 2.

Question 11.
Discuss the applicability of Rolle’s Theorem for the function f(x) = (x- 1)^2/5 in the interval [0, 3].
Solution:
Since f(x) is a polynomial in x,
∴ it is continuous in [0, 3].
And f'(x) = \(\frac { 2 }{ 5 }\)(x-1) ^-3/5 = \(\frac{2}{5} \cdot \frac{1}{(x-1)^{3 / 5}}\)
which does not exist at x = 1
⇒ f(x) is not derivable in (0, 3).
Hence, Rolle’s theorem is not applicable.

Continuity and Differentiability Important Extra Questions Short Answer Type

Question 1.
Discuss the continuity of the function : f(x) = |x| at x = 0. (N.C.E.R.T.)
Solution:

Hence ‘f’ is continuous at x = 0.

Question 2.
If f(x) = x + 1, find \(\frac{d}{d x}\)(fof)(x). (C.B.S.E. 2019)
Solution:
We have : f(x) = x + 1 …(1)
∴ fof(x) = f (f(x)) =f(x)+ 1
= (x + 1) + 1 = x + 2.
∴ \(\frac{d}{d x}\)(fof)(x).) = \(\frac{d}{d x}\)(x + 2) = 1 + 0 = 1.

Question 3.
Differentiate \(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\) with respect to x. (C.B.S.E. 2018 C)
Solution:

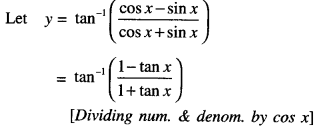
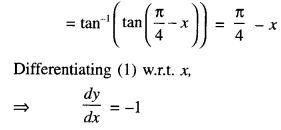
Question 4.
Differentiate: tan^-1 \(\left(\frac{1+\cos x}{\sin x}\right)\) with respect to x. (C.B.S.E. 2018)
Solution:

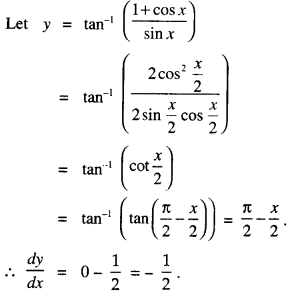
Question 5.
Write the integrating factor of the differential equation :
(tan^-1 y – x) dy = (1 + y²) dx. (C.B.S.E. 2019 (Outside Delhi))
Solution:
The given differential equation is :
(tan^-1 y – x) dy = (1 + y²) dx
⇒ \(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) Linear Equation
∴ I.F = \(e^{\int \frac{1}{1+y^{2}} d x}=e^{\tan ^{-1} y}\)

Question 6.
Find \(\frac{d y}{d x}\) if y = sin^-1\(\left[\frac{5 x+12 \sqrt{1-x^{2}}}{13}\right]\) (A.I.C.B.S.E. 2016)
Solution:

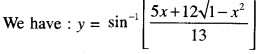
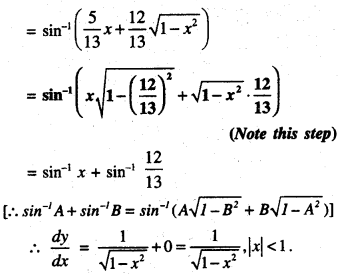
Question 7.
Find \(\frac{d y}{d x}\) if y = \(\sin ^{-1}\left[\frac{6 x-4 \sqrt{1-4 x^{2}}}{5}\right]\) (A.I.C.B.S.E. 2016)
Solution:

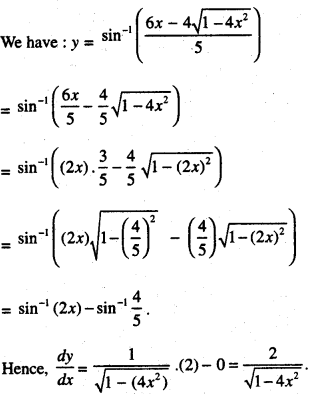
Question 8.
If y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ , prove that \(\frac{d y}{d x}=\frac{n y}{\sqrt{x^{2}+a^{2}}}\)
Solution:
y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ ……… (1)

Question 9.
The total cost C(x) associated with the production of ‘x’ units of an item is given by C(x) = 0.005x³ – 0.02x² + 30x + 5000.
Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of the total cost at any level of output. (C.B.S.E. 2018)
Solution:
We have: 0.005x³ – 0.02x² + 30x + 5000
∴ Marginal cost,
C'(x) = (0.005)(3x²) – 0.02(2x) + 30.
Hence,C'(3) = (0.005) (3×9)- (0.02) (6) + 30
= 0.135-0.12 + 30
= 30.135 – 0.12
= 30.02 units nearly

Question 10.
If (x² + y²)² = xy, find \(\frac{d y}{d x}\). (C.B.S.E. 2018)
Solution:
We have : (x² + y²)² = xy
Diff. w.r.t. x,
2(x² + y²)\(\frac{d}{d x}\)(x²+ y²) = x\(\frac{d y}{d x}\) + y(1)
2(x² + y²) [2x +2y\(\frac{d y}{d x}\) ] = x\(\frac{d y}{d x}\) + y
4x(x² + y²) – y = \(\frac{d y}{d x}\) [x – 4y(x² + y²)]
Hence \(\frac{d y}{d x}=\frac{4 x^{3}+4 x y^{2}-y}{x-4 y x^{2}-4 y^{3}}\)

Question 11.
Fing \(\frac{d y}{d x}\) if x^2/3 + y^2/3 = a^2/3 (N.C.E.R.T)
Solution:
The given equation is
if x^2/3 + y^2/3 = a^2/3
Its parametric equations are :
x = a cos³ θ,
y = a sin³ θ
[x^2/3 + y^2/3 = a^2/3 (cos²θ + sin²θ) = a^2/3(I) = a^2/3]

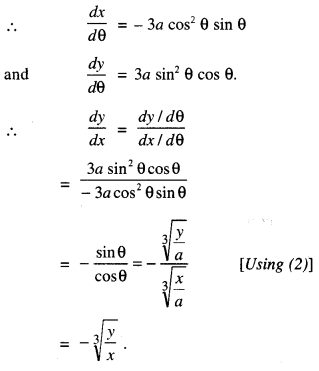
Question 12.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\), if:
x = ae^θ (sin θ – cos θ)
and y = ae^θ (sin θ + cos θ). (A.I.C.B.S.E. 2014)
Solution:
We have : x= ae^θ (sin θ – cos θ)
and y= ae^θ(sin θ + cos θ).
\(\frac{d x}{d \theta}\) = ae^θ (cos θ + sin θ) + ae^θ(sin θ – cos θ)
= 2ae^θsin θ
and \(\frac{d y}{d \theta}\) = ae^θ (cos θ – sin θ) + ae^θ(sinθ + cosθ)
= 2ae^θ cos θ

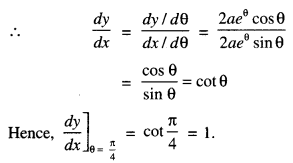
Question 13.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ), find \(\frac{d y}{d x}\) where θ = \(\frac{\pi}{3}\) (C.B.S.E 2018)
Solution:
We have :
x = a(2θ – sin 2θ)
and y = a(1 – cos 2θ).
∴ \(\frac{d x}{d \theta}\) = a(2 – 2 cos 2θ)
and \(\frac{d y}{d \theta}\) = a(0 + 2 sin 2θ) = 2a sin 2θ.

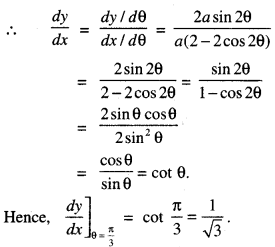
Question 14.
Find f’ (x), if f(x) = (sin x)^{sin x} for all 0 < x < π. (N.C.E.R.T.)
Solution:
We have :
f(x) = (sin x)^{sin x} …(1)
Taking logs., log f(x) = log (sin x)^{sin x}
⇒ log f(x) = sin x log (sin x).
Diff. w.r.t. x,

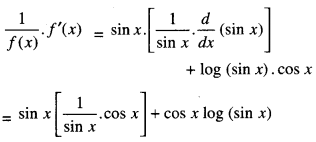
= cos x (1 + log sin x)
⇒ f’ (x) = f(x) cos x (1 + log sin x).
Hence ,f'(x) = (sin x)^{sin x}cos x (1 + log sin x).
[Using (i)]

Question 15.
If x¹⁶ y⁹ = (x² + y)¹⁷, prove that \(\frac{d y}{d x}=\frac{2 y}{x}\) (C.B.S.E. (F) 2012)
Solution:
We have :
x¹⁶ y⁹ = (x² + y)¹⁷.
Taking logs.,
log (x¹⁶ y⁹) = log (x² + y)¹⁷
⇒ 16 log x + 9 log y = 17 log (x² + y).
Diff. w.r.t. x,

Question 16.
If y = ae^2x + be^-x, then show that \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y=0\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
Here,
y = ae^2x + be^-x ……… (1)
∴ \(\frac{d y}{d x}\) = 2ae^2x – be^-x …….. (2)
And \(\frac{d^{2} y}{d x^{2}}\) = 4ae^2x + be^-x ……….. (3)
Now, \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y\)
= [4ae^2x + be^-x] – [2ae^2x – be^-x] – 2[ae^2x + be^-x] [Using (1), (2) & (3)]
= 4ae^2x + be^-x – 2ae^2x + be^-x – 2ae^2x – 2be^2x = 0.

Question 17.
If y = log(1 + 2t² + t⁴), x = tan^-1t, find \(\frac{d^{2} y}{d x^{2}}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have : y = log(1 + 2t² + t⁴)
⇒ y = log (1 + t²)²
⇒ y = 21og (1 + t²).

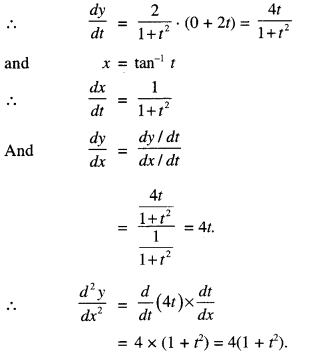
Question 18.
If x sin (a + y) + sin a cos (a + y) = 0, then prove that: \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\) (A.I.C.B.S.E. 2013)
Solution:
We have :
x sin (a + y) + sin a cos (a + y) = 0 …(1)
⇒ x = \(-\frac{\sin a \cos (a+y)}{\sin (a+y)}\) …..(2)
Diff (1) w.r.t x,
x cos (a + y)(0+\(\frac{d y}{d x}\) ) + sin (a + y). 1 + sina(-sin(a+y))(0+\(\frac{d y}{d x}\)) = 0
(xcos(a + y) – sin a sin (a + y)] \(\frac{d y}{d x}\) = – sin (a + y)

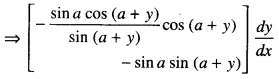
⇒ – sin (a + y) [Using (2)]
⇒ -sin a[cos²(a+y)+sin²(a+y)] \(\frac{d y}{d x}\) = -sin² (a+y)
⇒ -sin a(1) \(\frac{d y}{d x}\) = = -sin² (a+y)
Hence \(\frac{d y}{d x}\) = \(\frac{\sin ^{2}(a+y)}{\sin a}\)
Which is true.

Question 19.
If sin y = x cos (a + y), then show that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\cos a}\) Also, show that \(\frac{d y}{d x}\) = cos a, when x = 0. (C.B.S.E. 2018C)
Solution:
Given, sin y = x cos (a + y)

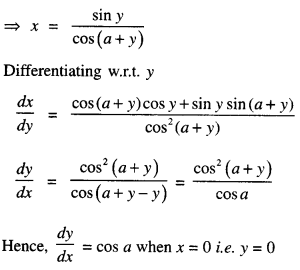
Question 20.
Find the value of ‘c’ in Rolle’s Theorem for the function f (x) = x³ – 3x in [-√3, 0]. (A.1.C.B.S.E. 2017)
Solution:
We have : f(x) = x³ – 3x.
(i) f(x) is continuous in [-√3, 0].
[∵ f(x) is a polynomial in x]

(ii) f'(x) = 3x² – 3 …(1)
∴ f'(x) exists for each x in (-√3,0)

(iii) f(-√3) = (-√3)3 – 3(-√3)
= -3√3 + 3√3 = 0
f(0) = 0 – 0 = 0.
∴ f(-√3) =f(0).
Thus all the conditions of Rolle’s Theorem are satisified.
∴ There exists at least one number ‘c’ between – √3 and 0 such that f'(c) = 0.

But f'(c) = 3c² – 3. [Putting x – c in (1)
∴ f'(c) = 0
3c² – 3 = 0
c² = 1
c = ± 1.
c = – 1 ∈ (-√3,0).
Hence, Rolle’s Theorem is verified and c = – 1.

Question 21.
Find a point on the parabola y = (x – 3)², where the tangent is parallel to the chord joining (3, 0) and (4,1).
Solution:
We have : y = f(x) = (x – 3)².
We discuss the applicability of L.M.V. Theorem in [3, 4],
(i) fix) is continuous in [3, 4],
[ ∵ f(x) is a polynomial]

(ii) f'(x) = 2(x – 3), which exists for all x ∈ (3,4).
∴ f(x) is derivable in (3, 4).
Thus both the conditions of Lagrange’s Mean Value Theorem are satisfied.
∴ There exists at least one number c ∈ (3, 4) such that

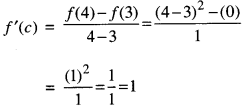
⇒ 2(c – 3) = 1
⇒ 2c = 1
⇒ c = \(\frac{7}{2}\) ∈ (3, 4).
When x = \(\frac{7}{2}\), then y = (\(\frac{7}{2}\) – 3)² = 1/4
Hence, the required point is ( \(\frac{7}{2}, \frac{1}{4}\) )

Continuity and Differentiability Important Extra Questions Long Answer Type 1

Question 1.
Find the value of ‘a’ for which the function ‘f’ defined as :

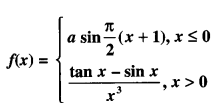
is continuous at x =0 (CBSE 2011)
Solution:


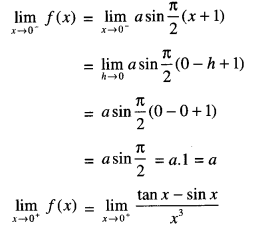
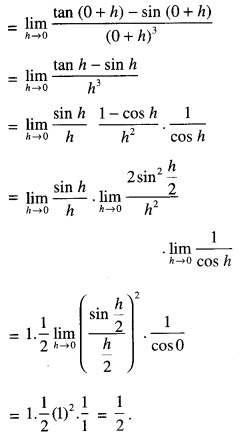
Also f(0) = a sin π/2 (0+1)
= a sin π/2 = a(1) = a
For continuity,
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a = 1/2 = a
Hence, a = 1/2

Question 2.
Find the values of ‘p’ and ‘q’ for which :

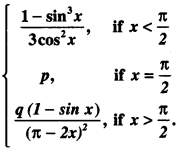
is continuous at x = 2 (CBSE 2016)
Solution:


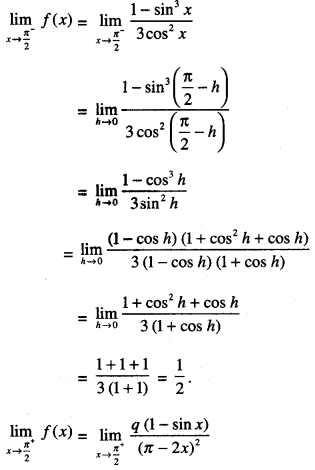
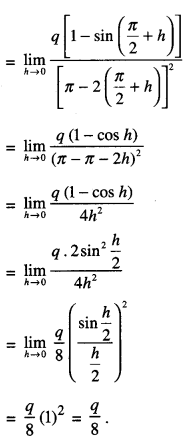
Also f(\(\frac{\pi}{2},\)) = p
For continuity \(\lim _{x \rightarrow \frac{\pi^{-}}{2}} f(x)=\lim _{x \rightarrow \frac{\pi^{*}}{2}} f(x)\)
= f(\(\frac{\pi}{2},\))
⇒ \(\frac{1}{2}=\frac{q}{8}\) = p
Hence p = 1/2 and q = 4

Question 3.
Find the value of ‘k’ for which

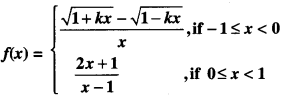
is continuous at x = 0 (A.I.C.B.S.E. 2013)
Solution:


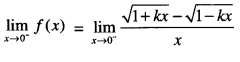
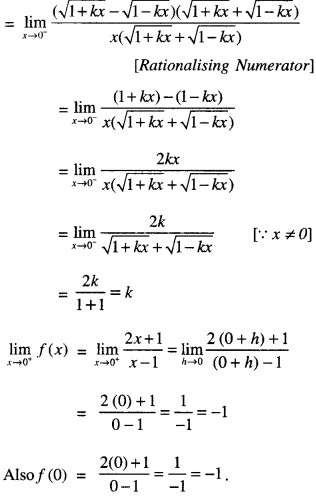
For continuity \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ k = -1 = -1
Hence k = -1

Question 4.
For what values of ‘a’ and ‘b\ the function ‘f’ defined as :

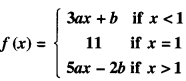
is continuous at x = 1. (CBSE 2011)
Solution:
\(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}\) (3ax +b)
= \(\lim _{h \rightarrow 0}\) (3a (1-h) + b]
= 3a(1 – 0) + b
= 3a + b
\(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{+}}(5 a x-2 b)\)
= \(\lim _{h \rightarrow 0}\) [5a (1+h) – 2b]
= 5a (1+0) – 2b
= 5a – 2b
Also f(1) = 11
Since ‘f’ is continuous at x = 1,
∴ \(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}} f(x)\)= f(1)
⇒ 3a + b = 5a – 2b = 11.
From first and third,
3a + b = 11 …………… (1)
From last two,
5a – 2b = 11 …………… (2)
Multiplying (1) by 2,
6a + 2b = 22 ………….. (3)
Adding (2) and (3),
11a = 33
⇒ a = 3.
Putting in (1),
3(3) + b = 11
⇒ b = 11 – 9 = 2.
Hence, a = 3 and b = 2.

Question 5.
If f(x) , defined by the following is continuous at x = 0, find the values of a, b, and c.

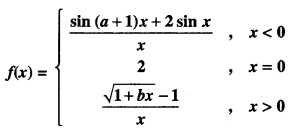
(A.I.C.B.S.E 2011)
Solution:


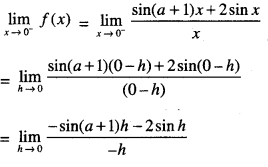
Also f(0) = 2
Since f(x) is continuous at x = 0,
∴ \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a + 3 = b/2 = 2
Hence,a = -1 and b = 4.

Question 6.
Find ‘a’ and ‘b’, if the function given by :
f(x) = \(\left\{\begin{array}{ll}
a x^{2}+b, & \text { if } x<1 \\ 2 x+1, & \text { if } x \geq 1 \end{array}\right.\) is differentiable at x = 1. (C.B.S.E. Sample Paper 2018)
Solution:
Since ‘f’ is derivable at x = 1, ∴ ‘f’ is continuous at x = 1 im 33 => a + b = 2 + 1 = 3
⇒ a + b = 3 …………. (1)
Again since ‘f is differentiable at x = 1


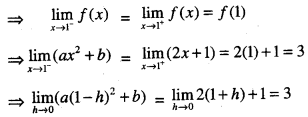
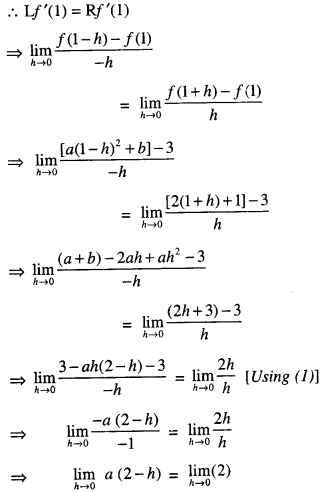
2a = 2
Putting in (1),
1 + b = 3
⇒ b = 3 – 1
⇒ b = 2.
Hence, a = 1 and b = 2.

Question 7.
Prove that: \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]\) = \(\sqrt{a^{2}-x^{2}}\)
(C.B.S.E. (F) 2011)
Solution:

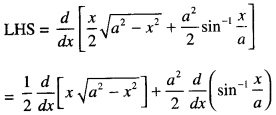
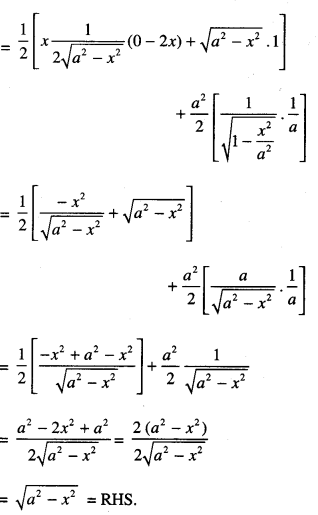
Question 8.
Differentiate \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\) w.r.t x (N.C.E.R.T)
Solution:
Let y = \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
= \(\sin ^{-1}\left(\frac{2.2^{x}}{1+\left(2^{x}\right)^{2}}\right)\)
Put 2^x = tan θ
so that θ = tan^-1(2^x) ………… (1)
Then y = \(\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ)
= 2θ = 2tan^-1(2^x).
[Using (1)]

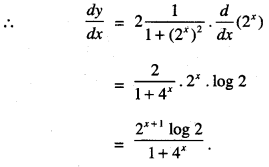
Question 9.
If log (x² + y²) = 2 tan^-1 [ y/x] show that : \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (C.B.S.E. 2019)
Solution:

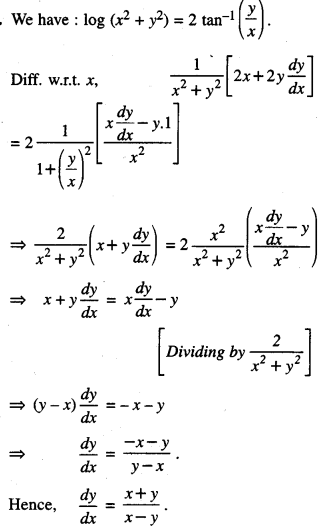
Question 10.
If y = tan^-1\(\left(\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)\), x² ≤ 1, then find \(\frac{d y}{d x}\)
We have : log (x2 + y2) = 2 tan-1 (A.I.C.B.S.E. 2015)
Solution:

Question 11.
Differentiate the following with respect to x = sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\) (A.I.C.B.S.E. 2013)
Solution:
= sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\)
= sin^-1\(\left(\frac{2.2^{x} \cdot 3^{x}}{1+(6)^{2 x}}\right)\)
= sin^-1\(\left(\frac{2.6^{x}}{1+(6)^{2 x}}\right)\)
Put 6^x = tan θ
So that θ = tan^-1(6^x) …………(1)
Then y = sin^-1( \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\) )
= sin^-1(sin 2θ)
= 2θ = 2tan^-1(6^x) [Using (1)]

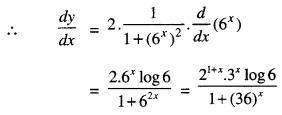
Question 12.
Differentiate : tan^-1\(\left[\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\right]\) w.r.t cos^-1 x² (C.B.S.E. Outside Delhi 2019)
Solution:

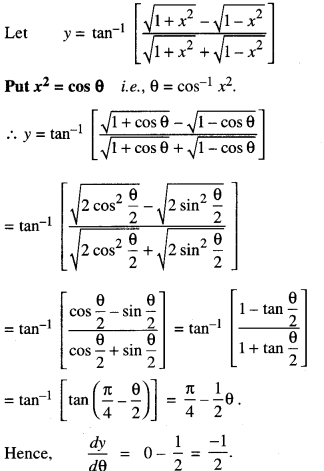
Question 13.
If x^y – y^x = a^b, find \(\frac{d y}{d x}\). (Delhi 2019)
Solution:
We have : x^y – y^x = a^b
Putting x^y = u and y^x = v, we get:
u – v = a^b
so that, \(\frac{d u}{d x}-\frac{d v}{d x}\) =0 ………….(1)
Now, u = x^y
Taking logs.,
log u = log x^y
⇒ log u = y log x.
Diff. w.r.t. x,

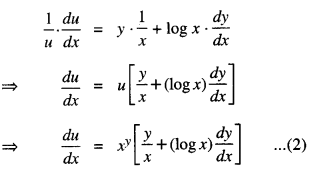
And, v = y^x
Taking logs., log v = log y^x
⇒ log v = x log y.

Question 14.
If y = (log x)^x + x^logx, find \(\frac{d y}{d x}\) (C.B.S.E. 2019)
Solution:
Let y = (log x)^x + x^logx = u + v,
where u = (log x)^x and v = x^logx
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……….(1)
Now, u = (log x)^x
so that log u = x log (log x).
Diff. w.r.t. x,

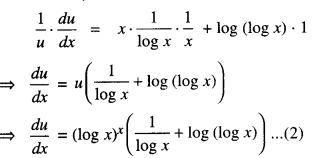
Again, v = x^logx
so that log v = log x. log x = (logx)²
Diff w.r.t x,

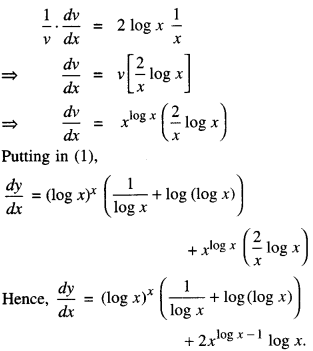
Question 15.
If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\) then prove that \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\) (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\)
Putting x = sin A and y = sin B, we get:
\(\sqrt{1-\sin ^{2} \mathrm{~A}}+\sqrt{1-\sin ^{2} \mathbf{B}}=a\)= a (sin A – sin B) ⇒ cos A + cos B = a (sin A – sin B)

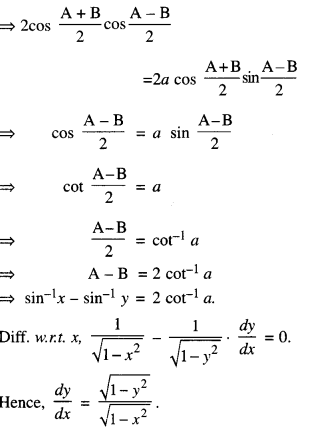
Question 16.
If x = a sec³ θ and y = a tan³θ, find \(\frac{d^{2} y}{d x^{2}}\)
Solution:
Given : x = a sec³ θ
y = a tan³θ

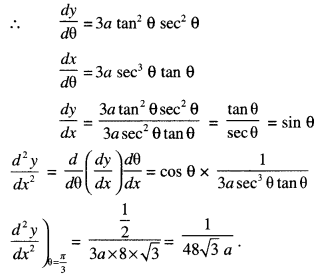
Question 17.
Find \(\frac{d y}{d x}\), if x^y. y^x = x^x. (C.B.S.E 2018C)
Solution:
We have: x^y y^x = x^x.
Taking logs.,log x^y y^x = log x^x
⇒ y log x + x log y=x log x

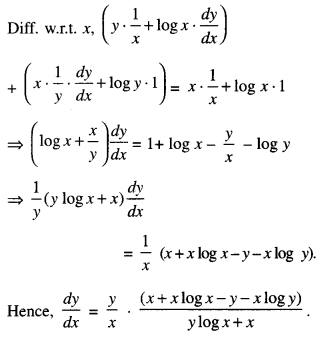
Question 18.
Find \(\frac{d y}{d x}\) if y^x + x^y + x^x = a^b (N.C.E.R.T. A.I.C.B.S.E.2015)
Solution:
We have: y^x + x^y + x^x
Putting y^x = u. x^y = v and x^x = w, we get:
u + y + w = a^b
Diff. w.r.t. x, \(\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\) = 0 …………… (1)
Now u = y^x ………….(2)
Taking logs., log u = log y^x
log u = x log y.
Diff. w.r.t. x,

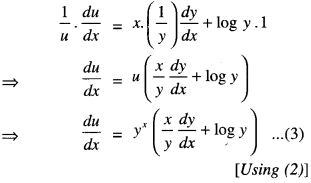
And v = x^y
Taking logs., log v = log x^y
log v = y log x.
Diff. w.r.t. x,

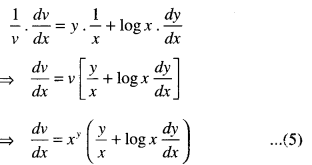
[using (4)]
Lastly w = x^x
Taking logs.,
log w = xlog x
∴ \(\frac{d w}{d x}\) = x (1+log x) …………. (7)
From (1) , using (3), (5) and (7), we get:

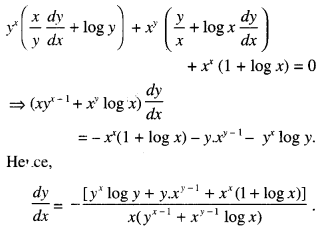
Question 19.
If y = e^{tan-1 x}, prove that:\(\left(1+x^{2}\right) \frac{d^{2} y}{d x^{2}}+(2 x-1) \frac{d y}{d x}=0\)
(C.B.S.E. 2018C)
Solution:
Given: y = e^tan-1x,
Differentiating w.r.t. x
\(\frac{d y}{d x}=e^{\ln ^{-1} x}\left(\frac{1}{1+x^{2}}\right)=\frac{y}{1+x^{2}}\)
Agian differentiating w.r.t. x
(1 + x²)\(\frac{d y}{d x}\) = y
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + 2x \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + (2x – 1) \(\frac{d y}{d x}\) = 0

Question 20.
If x cos (a + y) = cos y, then prove that:
\(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\)
Hence show that :
sin a \(\frac{d^{2} y}{d x^{2}}\) + sin 2(a + y)\(\frac{d y}{d x}\) = 0
Solution:
We have : x cos (a + y) = cos y …………(1)
x = \(\frac{\cos y}{\cos (a+y)}\) …………..(2)
Diff. (I) w.r.t. x,
-x sin (a + y) (0 + \(\frac{d y}{d x}\) ) + cos (a + y) .1
⇒ -sin y.\(\frac{d y}{d x}\)
⇒ (xsin(a+y) – siny)\(\frac{d y}{d x}\) = cos(a +y)
⇒ (\(\frac{\cos y}{\cos (a+y)}\) sin (a+y) – sin y)\(\frac{d y}{d x}\)
⇒ cos (a + y) [Using (2)]
(sin (a + y) cos y – cos (a + y) sin y)\(\frac{d y}{d x}\)
⇒ cos² (a + y)
⇒ sin (a + y – y) \(\frac{d y}{d x}\) = cos²(a+y)
\(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
which is true.

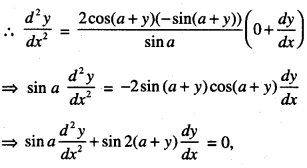
Question 21.
If y = (sin^-1 x)², prove that:
\(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0\) (C.B.S.E. 2019)
Solution:
We have y = (sin^-1 x)²
∴ y₁ = 2(sin^-1 x). \(\frac{1}{\sqrt{1-x^{2}}}\)
⇒ \(\sqrt{1-x^{2}} \cdot y_{1}\) = 2(sin^-1 x).
Squaring, (1 – x²) y₁² = 4(sin^-1 x)²
⇒ (1 – x²) y₁² = 4y [Using (1)]
Diff. w.r.t x,
(1 – x²) 2y₁y₂ + (-2x) y₁² = 4y₁
⇒ (1 – x²) y₂ – xy₁ = 2 [Dividing by 2y₁ ]
Hence, (1-x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) – 2 = 0.

Question 22.
If y = cos (m cos^-1 x), show that
(a – x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) + m²y = 0 (C.B.S.E. Sample Paper 2018-2019)
Solution:
We have :

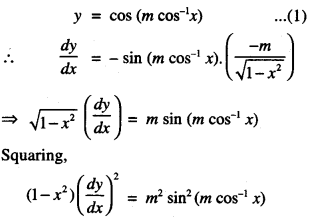
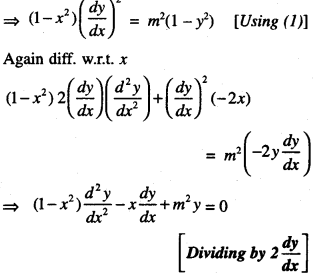
Question 23.
If y = sin (sin x), prove that
\(\frac{d^{2} y}{d x^{2}}\) + tanx \(\frac{d y}{d x}\) + y cos²x = 0. (C.B.S.E. 2018)
Solution:
We have :
y = sin (sin x)
∴ \(\frac{d y}{d x}\) = cos (sin x) . cos x ……(2)
and \(\frac{d^{2} y}{d x^{2}}\) = cos (sin x) (- sin x) + cos x [- sin (sin x). cos x]
= – sin x cos (sin x) – cos²x sin (sin x) …(3)
:. LHS = \(\frac{d^{2} y}{d x^{2}}\) + tan x \(\frac{d y}{d x}\) + y cos² x
⇒ – sin x cos (sin x) – cos² x sin (sin x) + tan x cos (sin x).cos x + sin (sin x) cos² x
[Using (1). (2) and (3)]
⇒ – sin x cos (sin x) – cos² x sin (sin x) + sin x cos (sin x) + cos² x sin (sin x)
⇒ – sin x cos (sin x) + sin x cos (sin x)
= 0 = RHS.

Question 24.
If x = sin t, y = sin pt, prove that:
(1 – x²)\(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) + p²y = 0
(Outside Delhi 2019)
Solution:
We have : x = sin t
and y = sin pt.
\(\frac{d y}{d x}\) = cos t
and \(\frac{d y}{d x}\) = p cos pt

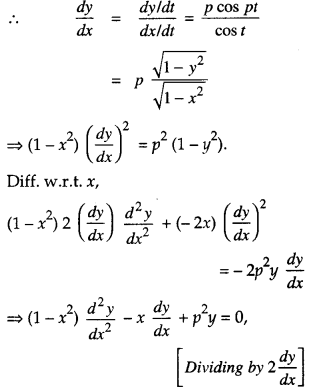
which is true.

Question 25.
Find \(\frac{d y}{d x}\), if x^y.y^x = x^x. (C.B.S.E. 2019 C)
Solution:
We have: x^y.y^x = x^x
Taking logs., logx^y y^x = log x^x
⇒ y log x + x log y = x log x

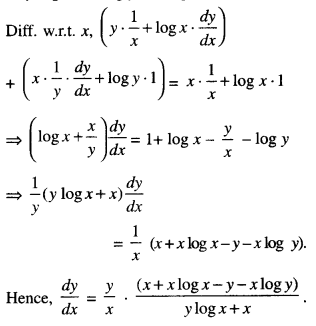
Question 26.
If y = x^x, prove that
\(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}=0\) (C.B.S.E. 2016,14)
Solution:
We have : y = x^x.
Taking logs.,
log y = x log x.
Duff. w.r.t. x,
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x. \(\frac{1}{y}\) + log x.1
\(\frac{d y}{d x}\) = y(1+1ogx) ………….(1)
Again duff. w.r.t. x,

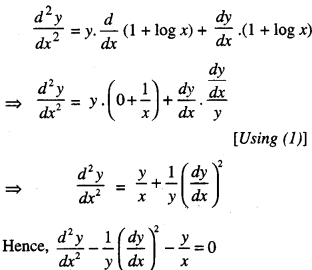
Question 27.
If x = a (cos 2θ + 2θ sin 2θ) andy = a (sin 2θ – 2θ cos 2θ), find \(\frac{d^{2} y}{d x^{2}}\) at θ = \(\frac{\pi}{8}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:
We have: x – a (cos 2θ + 2θ sin 2θ)
∴ \(\frac{d x}{d \theta}\) = a (- 2 sin 2θ + 2 sin 2θ + 4θ cos 2θ).
⇒ \(\frac{d x}{d \theta}\) = 4aθ cos 2θ ………..(1)
And y = a (sin 2θ – 2θ cos 2θ).
∴ \(\frac{d y}{d \theta}\) = a (2 cos 2θ + 4θ sin 2θ – 2 cos 2θ)
\(\frac{d y}{d \theta}\) = 4aθsin 2θ ………….. (2)

Question 28.
If x = cos t + log tan (t/2) y = sin t , then find the values of \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{4}\)
(C.B.S.E. 2019 Delhi Set-II)
Solution:
We have x = cos t log tan (t/2) and
y = sin t

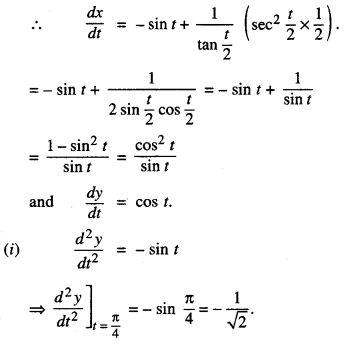
Question 29.
If y = a cos (log x) + b sin (log x), show that:
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\) (C.B.S.E. 2019C)
Solution:
We have:
y = a cos (log x) + b sin (log x) …..(1)
\(\frac{d y}{d x}\) = – a sin (log x) \(\frac{1}{x}\) + b cos (log x) \(\frac{1}{x}\)
x\(\frac{d y}{d x}\) = -asin (log x) + b cos (log x).
Again diff. w.r.t.x., \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot 1\)
= – a cos (log x) . \(\frac{1}{x}\) – b sin (log x) . \(\frac{1}{x}\)
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\)
= – [a cos (log x) + b sin (log x)]
= -y. [Using (1)]
Hence, \(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\)

Question 30.
Use Lagrange’s Theorem to determine a point P on the curve f(x) = \(\sqrt{x-2}\), defined in the interval [2, 3], where the tangent is parallel to the chord joining the end points on the curve.
Solution:
We have y = f(x) = \(\sqrt{x-2}\) …….(1)
∴ f'(x) = \(\frac{1}{2 \sqrt{x-2}}\)
now f(a) = f(2) = \(\sqrt{2-2}=\sqrt{0}\) = 0
and f(b) = f(3) = \(\sqrt{3-2}=\sqrt{1}\) = 1.
By Lagrange’s Theorem, we have :

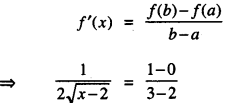
⇒ \(\frac{1}{4(x-2)}\) = 1 [Squaring both
⇒ 1 = 4x – 8
⇒ 4x = 9
⇒ x = \(\frac{9}{4}\) ∈ (2, 3).
Putting in (1), y = \(\sqrt{\frac{9}{4}-2}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
Hence, ( \(\frac{9}{4}, \frac{1}{2}\) ) is the reqd. point.