By going through these CBSE Class 11 Maths Notes Chapter 12 Introduction to three Dimensional Geometry Class 11 Notes, students can recall all the concepts quickly.
Introduction to three Dimensional Geometry Notes Class 11 Maths Chapter 12
Co-ordinates of a Point: The co-ordinates of a point are the distances from the origin of the feet of the perpendiculars from the point on the respective co-ordinate axes.
Distance Formula : The distance between the points (x1 y1, z1) and (x2, y2, z2) is given by \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\). The distance of the point (x, y, z) from the origin is given by \(\sqrt{x^{2}+y^{2}+z^{2}}\)
Section Formulae: .
(i) Section formula for internal division :
If P(x1 y1, z1) and Q(x2, y2, z2) are two points. Let R be a point on the line segment P and Q such that it divides the join of P and Q internally in the ratio m1 : m2.
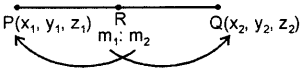
Then, the co-ordinates of R are
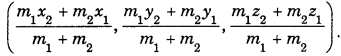
(ii) Section formula for external division :
If P(x1 y1, z1) and Q(x2, y2, z2) are two points and let R be a
point on PQ produced dividing it
externally in the ratio m1 : m2(m1 ≠ m2). Then, the co-ordinates of Rare
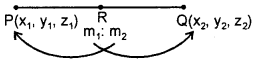
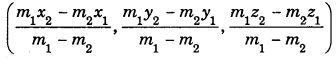
Mid-Point : The mid-point of the line segment joining (x1 y1, z1) and (x2 y2, z2) is \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right)\)
Centroid : Centroid of the triangle whose vertices are (x1 y1, z1), (x2 y2, z2) and (x3 y3, z3) is
![]()