Category: CBSE Class 11

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 6 Anatomy of Flowering Plants. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 6 Important Extra Questions Anatomy of Flowering Plants

Anatomy of Flowering Plants Important Extra Questions Very Short Answer Type

Question 1.
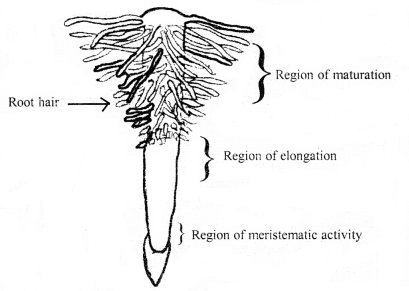
Which structure originates the lateral roots?
Answer:
Pericycle

Question 2.
What are Casparian strips?
Answer:
These are thickenings of lignin and suberin formed around the artificial walls of the endodermis to prevent plasmolysis.

Question 3.
Give an example of anomalous secondary growth.
Answer:
Bougainvillaea.

Question 4.
Name the type of wood in which vessels are absent.
Answer:
Softwood, e.g. Pinus.

Question 5.
Give an example of thick-walled parenchyma cells.
Answer:
Xylem Parenchyma in secondary tissue.

Question 6.
Which type of vascular bundles are found in Cucurbita.
Answer:
Bicollateral.

Question 7.
What are the meristematic tissues?
Answer:
They are a perpetually juvenile group of cells with the indefinite power of division.

Question 8.
What is the function of Kasparian strips?
Answer:
To prevent loss of water and minerals back to the cortex.

Question 9.
What is the function of tracheids?
Answer:
Tracheids transport water and give mechanical support to the tree.

Question 10.
What are tyloses?
Answer:
They are the vessels of hardwood containing bladder like ingrowth in the pores of lateral walls.

Question 11.
What is ring porous?
Answer:
It is a wood containing vessels of large and small sizes in distinct parts of annual rings.

Question 12.
Why do xerophytic leaves have multilayered give rise to the new plant?
Answer:
To minimize the transpiration.

Question 13.
What is diffuse-porous?
Answer:
It is a wood containing vessels of the same size in late and early.

Question 14.
What is the role of lenticel?
Answer:
It causes gaseous exchange between the atmosphere and living cells.

Question 15.
What are the functions of Tracheids?
Answer:
Tracheids transport water and give mechanical support to the tree.

Question 16.
Which tissue forms the pericycle in the dicot stem?
Answer:
Sclerenchyma tissue.

Question 17.
What is the advantage of Iigno-cellulose in the walls of the xylem?
Answer:
It provides mechanical support.

Question 18.
What uses are phloem fibres put to?
Answer:
They are used for making ropes, coarse textiles and heads.

Question 19.
Why do we notice it feasible to do grafting in monocot plants?
Answer:
Because they lack vascular cambium.

Question 20.
Name the type of plant tissue that has thin-walled cells with 12 – 140 sides and retain, the ability of division at maturity.
Answer:
Parenchyma.

Question 21.
What is phellogen?
Answer:
It is cork cambium which cuts cells upper side and lower side. The upper side cells from the phellem and lower phellogen and phelloderm constitute the periderm.

Read More:

శ్రీ శివ కవచ స్తోత్రమ్

Anatomy of Flowering Plants Biology Important Extra Questions Very Short Answer Type

Question 1.
What are tracheary elements? Of what use are these to the plants?
Answer:
These are vessels and tracheids. They are conducting cells of the xylem. The xylem vessels have perforations in their end walls while perforations are absent in tracheids, they form a continuous channel through the root, stem and leaves for the conduction of water and minerals.

Question 2.
If you are provided with microscopic preparation of transverse sections of a meristematic tissue and permanent tissue, how would you distinguish them apart?
Answer:
Meristematic tissues are composed of cells that are always in a dividing stage and divide endlessly to form new cells. These cells exist in different shapes without any intercellular spaces. These cells are thin-walled, rich in protoplasm and active with large nuclei and without vacuoles.

Permanent tissues are derived from meristematic tissue and are composed of cells, which have lost the power of division. These cells have their definite shape, size and function. These cells may be thin-walled or thick-walled.

Question 3.
What are the three basic tissues systems in Howering plants? Name the tissues under each system.
Answer:
In flowering plants, the three basic tissue systems are:
(a) DermalIt comprises the epidermis which is protective in function. During secondary growth, it is replaced by periderm.

(b) Vascular tissue system It consists of xylem and phloem and is found in the stele. In the root, the vascular bundles are renal with exarch condition whereas, in the stem, these are collateral with each condition.

(c) Ground or Fundamental Tissue It includes all the tissues except dermal and vascular, as parenchyma and sclerenchyma. It is found mainly between the epidermis and vascular cylinder and is formed of thin-walled cells with intercellular spaces in between them. Collenchyma is usually found to be thickened at the comers whereas currency nations are dead tissue and provide mechanical support.

Question 4.
Describe the structure and functions of the primary xylem.
Answer:
The primary xylem consists of tracheids vessels, xylem parenchyma and xylem fibres. The tracheids are elongated with tapering ends. They provide strength as well as help in absence of sap from roots to the leaves. The vessels are composed of a row of cells with large perforations at both ends but no bordered pits.

They help in the conduction of water and minerals and help in the storage of food. The xylem fibres are made up of sclerenchymatous cells associated with the xylem and they provide mechanical support to the plant body.

Question 5.
Why do we notice distinct rings in the tree of the temperate region while the tree of the coastal area is not distinct?
Answer:
The climatic conditions affect largely the activity of the cambium. It temperate region, the. cambium activity varies and it is not uniform throughout the year. But in coastal areas, it remains uniform throughout the year. Thus, due to the periodical activity of cambium in the temperate region, we notice distinct rings of spring and winter wood and not in the coastal area.

Question 6.
What is heartwood? Mention its any three characteristics.
Answer:
Heartwood: The hard central region of a tree trunk made up of xylem vessels that do not take part in the conduction of water.

Three characteristics of heartwood:

1. It is a non-functional and dead position.
2. It is dark coloured and filled with resins, tennis etc.

Question 7.
Point out the limitations of wood.
Answer:
Limitations of Wood:

• It does not change its physical and mechanical properties while heating.
• It cannot be changed into new shapes and forms.
• It is least resistant to infection caused by microorganisms and decay.
• It is combustible

Question 8.
What value is the study of plant anatomy?
Answer:
It helps to get the knowledge of plant structure and to solve various taxonomic problems. The determination of various adulterants in spices coffee, tea vegetable, dyes, tobacco saffron, as asafoetida is possible only when one knows about the anatomy of this substance.

Pharmacology and Pharmacology are dependent upon anatomical studies to know about the drug plants and their actions. It also helps in forming spurious materials from the standard woods. It also helps forensic experts fro solving criminal cases.

Question 9.
How is a cambial ring formed in dicotyledonous roots?
Answer:
Formation of the cambial ring in dicot roots: Perennial dicotyledonous root show secondary growth due to secondary meristems. Some parenchymatous cells in the phloem become meristematic. They divide and forms cambium strips there. External to the xylem a cambial ring is formed.

This lies on the inner side of the phloem cells and is cut off from the cambium on the inner and outer sides. Inner side cells form secondary xylem while the outer side cells of the cambium form secondary phloem. The primary phloem comes on the outside and the cambium forms a complete ring.

Question 10.
What are the permanent tissues?
Answer:
The permanent tissue is derived from meristematic tissues as the result of division and differentiation. They are composed of cells, which have lost the power of dividing. These cells have their definite shape, size and function. These cells may be thin-walled or thick-walled.

Question 11.
Are there any tissue elements of the xylem which are comparable to those of phloem? Comment.
Answer:

1. The sieve elements of the phloem are comparable to the vessel of the xylem because both lack nucleus at maturity.
2. Phloem fibre is similar to xylem fibre because both provide tensile strength to the tissue.

Phloem parenchyma and xylem parenchyma is the living components of phloem and xylem respectively.

Question 12.
Answer the following with reference to the anatomy of the monocot stem.
(i) How are the vascular bundles arranged?
Answer:
The vascular bundles are scattered in the ground tissue.

(ii) How are the xylem vessels arranged in each bundle? What do you call such an arrangement?
Answer:
Xylem vessels are ‘Y’ shaped. The big metaxylem vessels with pitted thickening from the arms, of Y. Protoxylem, occupies the lower arm of Y and is composed of spiral thickening.

But the vascular bundles are conjoint, collateral, closed and Endarch.

(iii) Vascular bundles are closed ones. What type of tissue is lacking in them?
Answer:
Cambium is absent.

Question 13.
What is phellogen? What does it produce?
Answer:
Phellogen is a cork cambium that is developed front hypodermis and epidermal cells near to the cortex. It is produced in the dicot stem during secondary growth for providing protection to the inner tissues.

It produces cork towards the outside and secondary cortex towards the inside.

Question 14.
What features make wood unique as a material?
Answer:
The following features make the wood unique as a material:

1. As it is light in weight, it can be easily transported over long distances.
2. It is a bad conductor of heat, electricity and sound.
3. It is resistant to rust.
4. It can be moulded into various desirable shapes.
5. The fluctuation in temperature does not affect largely and the volume of the wood.
6. Wood pulp is used for the synthesis of various materials like paper, plastics, rayon and transparent films.

Question 15.
List few important anatomical characteristics of the xerophytic leaf.
Answer:
The anatomical characteristics of the xerophytic leaf are:

1. The presence of a thick cuticle on both the epidermis of the leaf offers protection and reduces the rate of transpiration.
2. A multilayered epidermis is present. Its cells are elongated and lignified.
3. Stomata remain sunken in the lower epidermis. This reduces the rate of transpiration.
4. Palisade tissues are richly filled with chloroplast.
5. It also contains crystals of calcium oxalate scattered in the upper palisade tissues of leaf cells.

Question 16.
List the differences between the internal structure of the dicot stem and the Monocot stem.
Answer:

Dicot Stem	Monocot Stem
(i) Multicellular epidermal hairs are present.	(i) Epidermal hairs are generally absent.
(ii) Hypodermis is made up of collenchyma cells.	(ii) Hypodermis is made up of sclerenchyma cells.
(iii) Cortex is distinct and made up of parenchyma cells.	(iii) Cortex is not distinct but instead ground tissue is present.
(iv) Endodermis and pericycle are present.	(iv) Endodermis end pericycle are absent.
(v) A large pith is present.	(v) Pith is absent.
(vi) The prominent medullary ray between vascular bundles are present.	(vi) Medullary rays are absent.
(vii) The definite number of same size vascular bundles are arranged in a concentric ring.	(vii) The vascular bundles are of different size are found scattered in the ground tissue.
(viii) The vascular bundles are conjoint, collateral and open.	(viii) The vascular bundles are conjoint, collateral and closed.
(ix) The sheath around the vascular bundle is absent.	(ix) Bundle sheath made up of sclerenchyma cells is present around the vascular bundle.
(x) Lysigenous cavity is absent.	(x) Lysigenenous cavity is present in mature vascular bandies.
(xi) Secondary growth is present.	(xi) Secondary growth is absent.
(xii) Phloem parenchyma is present.	(xii) Phloem parenchyma is absent.

Anatomy of Flowering Plants Biology Important Extra Questions Very Short Answer Type

Question 1.
What are the characters of collenchyma tissues? Give its functions also.
Answer:
Collenchyma tissue: Collenchyma tissue cells are living isodiametric without any intercellular spaces. The comer walls are thickened by Pectinisation. They appear cylindrical in vertical section and oval or polygonal in cross-section. The nucleus in each cell lies at a comer position.

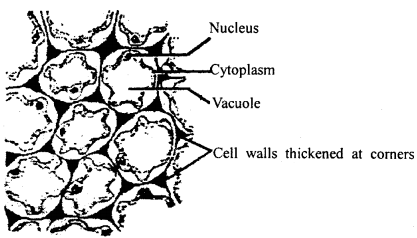
Collenchyma

They are found in the dicot stem below the epidermis and on the outer region of the leaf, midribs and pedicels. On the basis of thickening, they are of three types:

1. Lamellar,
2. Angular,
3. Lacunate

Functions: Collenchyma tissue provides mechanical function as well v as the function of photosynthesis.

Question 2.
Draw a well-labelled diagram showing the L.S.of phloem of an angiosperm with its components.
Answer:
Phloem is a food conducting tissue and it consists of:

1. Sieve, elements
2. Companion cells
3. Phloem fibres and
4. Phloem parenchyma.

1. Sieve elements: These occur as a single cell in pteridophytes and gymnosperms and longitudinal file of cells in angiosperms. The morphological specialization of sieve plates is the development of sieve area on their walls bearing sieve plates. The sieve plate bears a large number of perforations.

The protoplasmic strands maintain continuity through these perforations within the adjoining sieve tubes. In a mature sieve element there occurs a thin layer of parietal cytoplasm and a large central vacuole. The most important features of sieve elements are that they lack a nucleus at maturity.

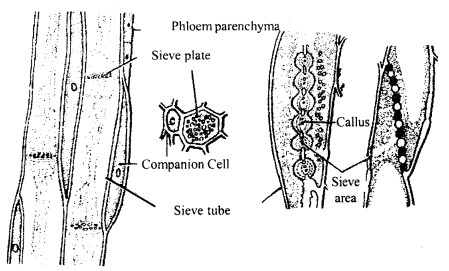
Structure of phloem (L.S)

2. Companion cells: These are thin-walled, living parenchyma narrow cells, which are closely associated with sieve tube elements. They appear rounded or polygonal with dense granular cytoplasm, « prominent nucleus and numerous small vacuoles. The companion cells lack starch.

The nuclei of the companion cells serve as the nucleus of sieve tubes as they lack them. The companion cells mainly occur in angiosperms, ac¬companying the sieve tube elements.

3. Phloem fibres: They form a prominent part of both the primary and secondary phloem. They are elongated cells with lignified walls having simple pits. They provide support and help in the transport of food material. They are used for making cords and ropes etc.

4. Phloem parenchyma: These are the living parenchyma cells associated with sieve tube cells. They are elongated with sieve tube cells. They are elongated, pointed in shape and store the starch, fat and other organic substances. The tannings and resins are also found in these cells, They are elongated like the sieve elements.

The sieve element is a living component, which lacks a nucleus at maturity.

Question 3.
Describe briefly the various types of vascular bundles.
Answer:
These are of the following types:
1. Radial The bundles in which xylem and phloem are arranged on different adulterating with each other and form the separate bundles are called radial vascular bundles as in all roots.

2. Conjoint The xylem and phloem are situated at the same radius and form a vascular bundle together.

These are divided into three types:
(a) Collateral: These are the bundles where xylem and phloem are arranged on some radius, xylem is located internally and phloem externally. These may be open when there is a patch of cambium in between the xylem and phloem e.g. Helianthus or closed when there is no cambium at all as seen in monocot stems

(b) Bicallatiral: In this vascular bundle, the phloem is found in two groups one outside the xylem elements and the other inner to them. These are always open and found in pumpkin.

(c) Concentric: The bundle in which either Phloemounds the phloem completely is known as concentric.

This exists in two forms.

1. Anphicribral: The xylem lies at the centre and is surrounded by a ring of phloem, e.g., fern.
2. Amphivaial: The phloem lies at the centre and is surrounded by the xylem e.g. Dracaena.

Question 4.
Describe briefly the internal structure of the monocot root with the help of a labelled diagram.
Answer:
A transverse section of the monocot root shows the following issues.

1. It is composed of a single layer of compactly arranged thin-walled cells without intercellular spaces and cuticle. It bears many unicellular root hair.
2. Cortex: It is present beneath the epidermis. It consists of 15-20 layers of parenchymatous cells with large intercellular spaces.
3. Endodermis: It is the innermost layer of the cortex. Its cells are barrel-shaped with Casparian strips on their anticlinal walls. The passage cells are seen just opposite the protoxylem ends.
4. Pericycle: It consists of a single layer of thin-walled parenchymatous cells.
5. Vascular bundle: The vascular bundles are radial and the xylem is exarch. The xylem and phloem bundles are always more than six.
6. Pith: It occupies the central portion of the stele and is made up of parenchymatous cells.
7. Conjunctive tissue: It consists of parenchymatous cells and is found between the xylem and phloem strands.
   
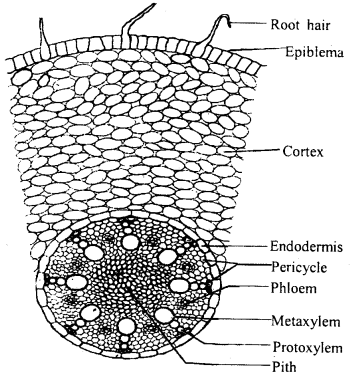
   T.S. of a typical monocot root

Question 5.
Define the following.
(i) Radial vascular bundles
Answer:
Radial vascular bundles: The bundles in which xylem and phloem are arranged in different radii alternating with each other and form the separate bundles are called radial vascular bundles as in all roots.

(ii) Collateral vascular bundles
Answer:
Collateral vascular bundles: These are the bundles where xylem and phloem are arranged not at the same radius. Xylem is located internally and phloem externally. These may be open when there is a patch of cambium in between the xylem and phloem e.g. Helianthus or closed when there is no cambium at all as seen in the monocot stem.

(iii) Exarch xylem
Answer:
Exarch xylem: It is the condition where protoxylem is located towards the periphery of axis and metaxylem inwards e.g. root.

(iv) Endarch xylem
Answer:
Endarch xylem: It is the condition where metaxylem is located towards the periphery of axis and protoxylem inwards e.g. stem.

(v) Stele
Answer:
Stele: All the tissues that lie internal to Endoolerinis are collectively called stele. The outermost layer of stell is known as the pericycle.

Question 6.
Distinguish between:
(i) Phiilem and Pheiloderm
Answer:
Phiilem: It is a dead tissue that is formed by the activity of cork cambium in the outer region of the cortex during secondary growth. It is protective in function.

Pheiloderm: It is a living tissue that is formed by the activity of cork cambium in the inner side of the cortex. It regains during secondary growth. If performs the function of storage.

(ii) Open bundle and closed bundle
Answer:
Open Bundle: Avascular bundle containing cambium between xylem and phloem is called an open bundle e.g. dicot stem.

Closed Bundle: Avascular handle lacking cambium between xylem and phloem is called a closed bundle e.g. monocot stem.

(iii) Fascicular cambium and inter fascicular cambium
Answer:
Fascicular cambium: It is a strip of cambium found between the xylem and phloem of each vascular bundle of dicot stem.

Interfascicular cambium: It is a strip of cambium that is formed from the cells of medullary rays adjoining with the fascicular cambium. It occurs dining secondary growth.

(iv) Conjoint vascular bundles and Radial vascular bundles
Answer:
Conjoint vascular bundles: Xylem and phloem lie in the same bundles. They lie on different radii alternating with each other e.g. Dicot and monocot root.

Radial vascular bundles: Xylem and phloem lie in separate bundles. They lie on different radii alternating with each other e.g. Dicot and monocot root.

(v) Periderm and Bark
Answer:
Periderm: It includes three tissue consisting of phellogen, phellem and phelloderm and is formed at the peripheral region of the axis.

Bark: It includes all the tissue external to the secondary xylem formed during secondary growth. These are cambium, secondary phloem.

Must Read:

Nifty Pivot Point

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 21 Neural Control and Coordination. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 21 Important Extra Questions Neural Control and Coordination

Neural Control and Coordination Important Extra Questions Very Short Answer Type

Question 1.
What are the major divisions of the forebrain?
Answer:
Cerebrum, Thalamus, Hypothalamus.

Question 2.
Which parts of the central nervous system constitute the grey matter?
Answer:
Areas that contain cell bodies of the neurons.

Question 3.
Name the major lobes of the cerebral hemisphere?
Answer:
Frontal, parietal, temporal and occipital.

Question 4.
What is the function of cerebral spinal fluid?
Answer:
It maintains a constant pressure inside the cranium.

Question 5.
What is the junction between two neurons known as?
Answer:
Synapse.

Question 6.
What is the polarized state of the nerve membrane?
Answer:
It is the state of the nerve membrane when its inner side is electronegative to its outer side.

Question 7.
Give two examples of unconditioned reflexes.
Answer:
(i) Salivation on tasting food.
(ii) Constriction of the pupil on the illumination of the eye.

Question 8.
Name the types of cells present in the retina.
Answer:
Rods, cones, bipolar neurons, ganglion cells, supporting cells.

Question 9.
Where is iodopsin present in the eye?
Answer:
In the cone cells of the retina

Question 10.
Where are taste buds located?
Answer:
In the mucous membrane over the papillae on the tongue.

Question 11.
Name the main parts of the human brain.
Answer:
Cerebrum, cerebellum, medulla, thalamus, and hypothalamus.

Question 12.
How many cranial nerves and spinal nerves do we possess?
Answer:
12 pairs of cranial nerves and 31 pairs of spinal nerves.

Question 13.
Which part of the brain controls posture and equilibrium?
Answer:
Cerebellum.

Question 14.
What is a polarised membrane?
Answer:
It is electrically positive outside and negative inside.

Question 15.
Compare rods and cones.
Answer:
Rods work in dim light and dark. Cones work in bright light.

Question 16.
What is the blind spot?
Answer:
The point of the retina from where the optic nerve starts and receptor cells are absent.

Neural Control and Coordination Important Extra Questions Short Answer Type

Question 1.
What are receptors?
Answer:
Receptors are peripheral nerve endings in the skin or special sense organs. They collect information from the external or internal environment of the body; transform them into electrical potential changes, which then pass along the afferent neurons to CNS.

Question 2.
Why does vitamin A deficiency produce night blindness?
Answer:
Vitamin ‘A’ is the constituent of rhodopsin, a pigment present in the photoreceptor cells of the eye. Rhodopsin breaks up into opsin and rode to visualize things in bright and dim light. There is constant consumption of vitamin A in rod cells. Deficiency of vitamin A causes impairment of synthesis of rhodopsin leading to night blindness, i.e., inability to see in the dark.

Question 3.
Why does the nerve impulse flow more rapidly in myelinated nerve fibers than in the non-myelinated fibers?
Answer:
Due to the following reasons nerve impulse flows more rapidly in myelinated nerve fibers:

1. Myelin sheath provides insulation to the nerve fibers from electrical disturbances between the neighboring fibers.
2. Myelin sheath is impermeable to free ions present in the extracellular fluid. So, it prevents the exchange of ions between the extracellular fluid and the interior of the myelinated axon.
3. The myelin sheath is absent at the Nodes of Ranvier, so, action potential jumps from one Node of Ranvier to the next. Thus, the nerve impulse flows in the form of leaps or jumps. This is known as the saltatory conduction of impulse.
4. It is more rapid than the smooth flow of impulse.

Question 4.
What is a synapse?
Answer:
It is the junction between axon terminals of a neuron and dendrites or the cell body of another neuron. There is a narrow fluid-filled space, called Synaptic Cleft separating axon terminals and dendrites at the synaptic junction. So, the two-neurons forming synapse does not form actual continuity between the neurons.

Structure of Synapse

Question 5.
Draw a labeled diagram of a section of the retina to illustrate its structure.
Answer:

Diagrammatic representation of the sectional view of the retina.

Question 6.
What functions does the hypothalamus serve in coordinating the various activities of the body?
Answer:

1. It contains nerve centers for temperature regulation, hunger, thirst, and emotional reactions.
2. It secretes neurohormones, which control the secretion of anterior pituitary hormones.
3. It synthesizes the posterior pituitary hormones and controls their release into the blood.

Question 7.
What is a nerve fiber? How is it classified according to myelin sheath?
Answer:
A nerve fiber is a long axon or dendrite of a neuron. According to the presence and absence of myelin sheath around the fibers.

These are classified as:

1. Myelinated nerve fiber (i.e., presence of myelin sheath) and
2. Non-myelinated nerve fiber (i.e., absence of myelin sheath).

Question 8.
Explain Motor-end plate.
Answer:
A Motor-end plate is a specialized structure formed by the muscle fiber at the point where the axon terminal is applied to it. The axon of the motor neuron is divided into branches near the muscle fibers. Each branch loses its myelin sheath near its termination and ends in an expanded foot-like form which is supplied closely to a muscle fiber.

There is no actual continuity between the neuron and muscle fiber. The membranes of the two are separated from each other by a narrow cleft-like fluid-filled space.

Question 9.
What are the biological functions of Dorsal and Ventral spinal nerve roots fibers?
Answer:
Dorsal spinal nerve root fibers bring impulses from the peripheral tissues, giving rise to sensations like touch, temperature, and pain, or to involuntary spontaneous activities called Reflexes.

Ventral spinal nerve root fibers: Some of the root fibers go to skeletal muscle fibers directly to stimulate or inhibit their activities; many others go to autonomic ganglia and end in them.

Question 10.
Our rods and cones evenly distributed over the entire surface of the retina? Why or not? At which point on the retina is a point-to-point image formed?
Answer:
The retina is composed of several layers of cells. First, there are the photoreceptor cells, the rods, and cones, partially embedded in the microvilli of pigmented epithelium cells of the choroids. The rod cells are present on the periphery of the retina in the human eye. The total number of rod cells has been estimated to be between 110 – 125 million. They contain a visual pigment called Rhodopsin.

The cone cells are shorter, thicker, and conical in shape. Cone cells are responsible for the perception of different colors. The total number of cone cells is 6.36 – 6.8 million. Cones are abundant on the rear wall and fovea centralis of the retina.

The point-to-point image is formed on the blind spot. From it, the optic nerve and blood vessels exit the retina and join the diencephalon of the brain.

Question 11.
Blindspot in the eye is devoid of the ability of vision. Why is it so?
Answer:
It is devoid of rods and cone cells. It is unstable to light rays.

Question 12.
If a strong odor is smelled continuously for some time, the sensation of that weakens. Justify.
Answer:
When a person continuously inhales the fumes in the air of a strong-smelling substance the sense of smell progressively and rapidly declines and finally disappears. This is because the olfactory cells get fatigued rapidly due to overstimulation. This is called olfactory adaptation, which develops from various changes in the olfactory epithelium and olfactory centers of the brain.

Question 13.
Which part of the nervous system participates in the maintenance of balance and co-ordinate body movements?
Answer:
The cerebellum process all the data and co-ordinates muscle movement in conjunction with the cortex and sends signals to the muscles to adjust.

Question 14.
What is a reflex action? What units of the nervous systems are involved with a typical vertebrate reflex arc?
Answer:
It is a spontaneous, automatic, mechanical, nerve-mediated response evoked at the unconscious level by the stimulation of any specific receptor without exercising the will of an organism.

There, are more than 200 reflexes “wired” into our nervous system all following the sequence from stimulus to reflex along the specific neural pathway that makes up the reflex arc. The simplest reflex arc involves some specific receptor, afferent sensory neuron towards an aggregation of nervous tissue which may be ganglion or the spinal cord.

Question 15.
Which nerve tract connects the right and left hemispheres of the cerebrum? Into what four lobes in each hemisphere divided?
Answer:
A longitudinal fissure splits the brain into two halves, the left, and right cerebral hemispheres. Other grooves divide the surface of each cerebral hemisphere into four lobes. The frontal lobe, temporal lobe at the front, parietal lobe, and occipital lobe at the back.

Question 16.
What is the primary function of neuroglia cells? What special structure is produced by Schwann cells?
Answer:
The neuroglia cells perform many house-keeping functions, provide nutritional support to the neurons and consume waste products. They also insulate, separating each neuron from the others.

Schwann cells, a type of neuroglial, wrap around the axon with concentric layers of the insulating plasma membrane.

Question 17.
How does a wave of depolarization spread along with a nerve fiber?
Answer:
Nerve cells have polarized membranes, having an electrical potential difference across the membrane. The trigger zone for a particular neuron is the place on the membrane where voltage-gated channels are clustered most densely. When stimulated opening of voltage-gated Na⁺ ion channel brings Na⁺ ions into the cell, a temporary, very localized, but rapid inflow of Na⁺ ions into the cells occurs, wiping out the local electrical potential difference in the immediate vicinity. This is called depolarization.

When the site of stimulation has less charge difference than the membrane surface surrounding it, this potential difference establishes a small, localized current in the immediate vicinity, which influences the nearby Na⁺ channels to open and depolarizing these cells.

The depolarization thus spreads, producing a local current, which induces passive Na⁺ channels to open and so to depolarize the near % site. In this way, initial depolarization passes outward over the membrane and spreads out in all directions along with the nerve fiber, from dendron to axon.

Question 18.
What is a synapse? How does the nerve cell across the synapse?
Answer:
A nerve signal travels from neuron to neuron all around the body. These associations are called Synapse.

There are mainly two types of synapses:

1. Electrical and
2. Chemical depending upon the nature of the transfer of information across the synapse.

In electrical synapses, cells are separated by a gap, the synaptic cleft, of only 0.2 mm. So that an action potential arriving at the presynaptic side of the cleft can sufficiently depolarize the postsynaptic membrane to directly trigger its action potential.

Chemical synapses are the common type of synapse consists of a bulbous expansion of a nerve terminal called a synaptic knob. The cytoplasm of the synaptic knob contains numerous tiny round sacs synaptic vesicles. Each vesicle contains a neurotransmitter substance responsible for the transmission of nerve impulses across the synapse.

Question 19.
What is the action potential of a neuron? Do all neurons possess the same action potential?
Answer:
Depolarisation is caused by rapid change in membrane permeability and a corresponding shift in the balance of ions. If the shift of ions and consequent shift in electrical charges is sufficient, it will trigger a wave of transient membrane depolarisation known as nerve impulse or Action potential. Different neurons possess different densities of Na⁺ ion channels, different neurons exhibit different action potentials. However, for anyone neuron, the action potential is always the same.

Question 20.
Why is the mode of conduction of electrical impulse along the myelinated neuron is advantageous to a non-myelinated neuron? What is this type of conduction called?
Answer:
The myelinated nerve fibers carry impulses nearly 20 times faster than the non-myelinated nerve fibers. These avoid the dissipation of impulses into adjacent fibers. The myelin sheath serves as a highly insulating layer that prevents the flow of ions between the fluid external to the myelin sheath and within the axon.

In non-myelinated fiber, ionic charges and depolarization are repeated over the membrane along the length of the fiber and action potential flow over the entire length of the fiber. But in myelinated fibers, ionic changes and depolarization are repeated only at the nodes. Thus the impulse is more rapid in myelinated fibers and requires less energy. This jumping of depolarization from node to node is called saltatory conduction of nerve impulse.

Saltatory conduction

Question 21.
(a) Make a clearly labeled diagram of the inner ear of a human being.
Answer:

Diagrams showing the inner ear

(b) Describe how each of the following is achieved in us
(i) hearing
(ii) balance.
Answer:

Neural Control and Coordination Important Extra Questions Long Answer Type

Question 1.
(a) Describe the reflex arc with a diagram.
Answer:
The neurons forming the pathway taken by the nerve impulses in the reflex action form the Reflex Arc.
The reflex arc consists of

1. Receptor,
2. An afferent neuron or sensory neurons from receptor to CN system,
3. The efferent neuron of motor neurons from CN system to specific muscle fibers or gland cells,
4. a number of connectors or intermediate neurons conducting impulses form the afferent to the efferent neurons.

Reflex Arc

When a specific stimulus is applied to a specific group of receptors, it stimulates the receptor to initiate a nerve impulse along the afferent neurons. This impulse travels along with the afferent connector and efferent neurons to reach an effector-muscle or gland for that reflex. Thus the flow of impulse can only be in a single direction in a reflex arc, i.e.,

Stimulus → receptor → afferent neuron → CN system efferent neuron ← (connector neuron)

(b) Distinguish between conditioned reflex and unconditioned reflex.
Answer:
Differences between conditioned reflex and unconditioned reflex:

Conditioned Reflex	Unconditioned Reflex
It is a reflex, acquired after birth by applying an indifferent stimulus before or along with the stimulus for an inborn reflex.	It is a reflex, which can be evoked even immediately after birth and needs no previous encounter with the stimulus exciting it.

Question 2.
(a) Give an account of spinal nerves in man.
Answer:
There are 31 pairs of a spinal nerve in man. From each segment of the spinal cord, there are two spinal nerves. Each spinal nerve is a mixed nerve, containing both sensory and motor nerve fibers. It runs between the spinal cord and peripheral tissue. The two roots, i.e., motor or ventral and sensory or dorsal connect the spinal nerve to the spinal cord.

The DORSAL ROOT carries sensory or afferent fiber and has a dorsal root ganglion at its middle. The VENTRAL ROOT contains a motor or efferent nerve fibers. The dorsal root fibers bring impulses from the peripheral tissue and give rise to sensations like touch, temperature, and pain.

The ventral nerve root fibers pass impulses to muscles and glands in the peripheral tissues. The spinal nerve has been named according to its relation with the vertebral column.
These are

1. Eight pairs of cervical
2. 12 pairs of thoracic
3. 5 pairs of lumber,
4. 5 pairs of sacral and
5. a pair of coccygeal or caudal.

(b) What biological functions are served by the skeletal system?
Answer:

1. The skeletal system forms the rigid structural framework of the body and supports the weight of the body along with its limbs.
2. It affords protection to the internal organs against mechanical injury by forming cage-like compartments, e.g., skull.
3. It serves as a storage depot for calcium and phosphate, which are released for a number of functions of the body.
4. It participates in movement and locomotion.

The spinal nerve in man

Question 3.
Distinguish between:
(a) Afferent neurons and efferent neurons.
Answer:
Afferent neurons and efferent neurons:
Afferent neurons: These conduct sensory impulses from the receptors present in the peripheral organs and tissues towards the central nervous system. Their bodies are called afferent neurons.

Efferent neurons: These conduct motor impulses from the central nervous system to the peripheral organs and tissues serving as effectors. Their cell bodies are called efferent neurons.

(b) Rods and cones
Answer:
Rods: Rod cells are rod-like, elongated cells, bearing long, thin cylinders, containing a visual pigment called Rhodopsin. Rod cells are present on the periphery of the retina in the human eye. These cells do not form color vision.

Cones: Cone cells are shorter, thicker, and conical in shape. These are highly sensitive to bright light and colors. They contain a violet color pigment called rhodopsin. Cone cells are responsible for the perception of different colors. Cones are abundant on the rear wall and fovea centralis of the retina.

(c) Resting membrane potential and action potential.
Answer:
Resting membrane potential: The surface of the axon carries a positive charge relative to its interior and this electrical potential difference across the plasma membrane is called resting membrane potential.

Action potential: The shift of ions and consequents shift in electrical charges is sufficient enough; it will trigger a wave of transient membrane depolarization known as nerve impulse or Action potential.

(d) Impulse conduction in myelinated nerve fiber and unmyelinated nerve fiber.
Answer:
Impulse conduction in myelinated nerve fiber: The myelinated fibers carry impulses nearly 20 times faster than the non-myelinated nerve fibers. These avoid dissipation of impulse into adjusting fibers. The myelin sheath serves as a highly insulating layer that prevents the flow of ions. Impulses are rapid.

Non-myelinated nerve fiber: Ionic changes and depolarization are repeated over the membrane all along with the fiber. Impulse requires less energy and does not need to run all along with the fiber.

(e) Aqueous humor and vitreous humor.
Answer:
Aqueous humor: The chamber between the cornea and lens is filled with a clear watery fluid, the aqueous humor.

Vitreous humor; The chamber behind the lens is filled with a semisolid gelatinous material the vitreous humor.

(f) Blindspot and yellow spot.
Answer:
Blindspot: It s a small insensitive light area of about 0.5 cm. in diameter. It is devoid of rod and cone cells. It is unable to receive light rays.
Yellow spot: A tiny circular area, about 6 mm in diameter in the retina is a yellow spot. Here the vision is sharpest. It has rod and cone cells.

(g) Cranial nerve and spinal nerves.
Answer:
Cranial nerve: There are 12 pairs of cranial nerves, 10 originate from the brain stem, but all pass through the foramina of the skull. Cranial nerves contain only sensory fibers. The remainder contains both sensory and motor fibers.

Spinal Nerve: They arise from the cord. 31 pairs of segmental spinal nerves arise from the cord. They contain both receptor neurons and effectors neurons.

Must Read:

IEX Pivot Point Calculator

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 16 Digestion and Absorption. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 16 Important Extra Questions Digestion and Absorption

Digestion and Absorption Important Extra Questions Very Short Answer Type

Question 1.
How does pepsinogen become active in the stomach?
Answer:
Due to the presence of HCI.

Question 2.
What is pancreatic amylase?
Answer:
The pancreatic juice contains a starch-digesting enzyme called pancreatic amylase.

Question 3.
Name any animal starch.
Answer:
Glycogen.

Question 4.
Name the milk-coagulating enzyme.
Answer:
Chymotrypsin.

Question 5.
Which enzyme is necessary for the digestion of fat?
Answer:
Pancreatic lipase.

Question 6.
Which part of the ruminant stomach secretes gastric juice?
Answer:
Abomasum of the ruminant stomach secretes gastric juice.

Question 7.
Name the water-soluble vitamins.
Answer:
Vitamin B-complex and vitamin C.

Question 8.
State the function of ascorbic acid.
Answer:
It is necessary for the proper development of teeth and gums.

Question 9.
Which is the largest gland in our body?
Answer:
Liver.

Question 10.
Name the cobalt-containing vitamin.
Answer:
Vitamin Bp or Cobalamine.

Question 11.
What are the finger-like projections present in small intestines called?
Answer:
Villi.

Question 12.
Name the enzyme that converts proteins into protons in the stomach.
Answer:
Pepsin.

Question 13.
Name the glands associated with digestion.
Answer:
Salivary glands, liver and pancreas.

Question 14.
Name the acid that takes part in the digestion process.
Answer:
HCI (Hydrochloric acid).

Question 15.
Write four types of teeth present in the human jaw.
Answer:

1. Incisor,
2. Canines,
3. Pre-molar
4. Molar.

Question 16.
Write two main functions of saliva.
Answer:

1. Saliva cleans the mouth cavity.
2. It makes the food soft.

Question 17.
Name the different parts of the larger intestine.
Answer:

1. Calcium,
2. Colon,
3. Rectum.

Question 18.
Name the secretion of liver and pancreatic juice.
Answer:
Bile and pancreatic juice.

Question 19.
Name the largest gland of the human body.
Answer:
Liver.

Question 20.
What is digestion?
Answer:
Digestion is the process of changing food into a simpler form so that it can be used by the body.

Digestion and Absorption Important Extra Questions Short Answer Type

Question 1.
What is the passive absorption of food?
Answer:
It is the absorption of nutrients from higher concentration to lower concentration without the expenditure of energy. This requires the nutrients to be in higher concentration in the intestinal lumen than inside the cell. The diffusion of molecules would continue as long as the concentration difference persists.

The diffusion is a slow process. Water is absorbed by osmosis from the interstitial lumen to the intestinal cells and then to blood as long as the solute concentration is higher in the blood than in the intestinal content.

Question 2.
What do you mean by incomplete and complete type of digestive tracts?
Answer:
The incomplete digestive tract has only one opening for intake of food and elimination of indigestible matter e.g. coelenterates planaria, liver fluke etc. Complete digestive tracts have a separate opening for intake of food and elimination of indigestible matter e.g. in man, frog, rabbit, etc.

Question 3.
What are wisdom teeth? Write the dental formula of permanent and milky teeth.
Answer:

• The last molar grown at maturity age in both upper and lower jaws on both sides are called wisdom teeth
• The dental formula of permanent teeth = 2, 1, 2, 3/2, 1, 2, 3 = 32; milk teeth = 2, 1, 2, 0/2, 1, 2, 0 = 20

Question 4.
What is the role of
(a) Enterogastrone
Answer:
Enterogastrone slows gastric contractions and stops the secretion of gastric juice.

(b) Cholecystokinin
Answer:
Cholecystokinin of CCK causes the release of bile from the gall bladder and the release of enzymes in pancreatic juice.

(c) Secretion
Answer:
Secretion causes the release of sodium bicarbonate in the pancreatic juice.

(d) Duocrinn
Answer:
Duocrinin causes the release of mucus from Brunner’s glands into the intestinal juice.

(e) Enterocrinin.
Answer:
Enterocrinin brings the release of enzymes from crypts of Leiberkuhn into intestinal juice.

Question 5.
Name some of the symbiotic bacteria residing in a healthy human colon. What is the role of this bacteria?
Answer:
Escherichia coli and streptococcus Faecalis, this synthesise vitamins B and K and convert bile pigment into brown pigments to impart colour to the farces; prevent the establishment of pathogenic microorganisms in the intestine.

Bile pigment contains water, mucin, lecithin, cholesterol, bile salts and bile pigments.

Question 6.
Define chemotrophs and heterotrophs?
Answer:
Organisms such as nitrifying bacteria e.g. Nitrosomonas and nitrobacteria, which capture the energy released during oxidation of inorganic chemical substances and prepare organic food with its help are called chemotrophs.

Organisms such as animal, fungi, some protestants (Trypanosoma) and any kind of bacteria which cannot utilize sun energy but use chemical bond energy in the form of organic molecules or food synthesized by other organisms in building up their own organic molecules are called Heterotro

Question 7.
How does the gastrovascular cavity in the cnidarian help in digestion?
Answer:
More organized animals, like cnidari&n (e.g. Hydra, Aurelia) have developed sac-like coelenteron or gastro Oscular cavity, which is lined by various types of endoderm cells. Gland, cells of the endoderm secrete their enzymes into the cavity and digest the food extracellularly. This kind of digestion outside cells within a cavity is extracellularly digestion. However in cnidarian, as soon as the food is, reduced to small fragments, the nutritive cells ingest them and complete the process of digestion intracellularly.

Question 8.
Crop, mid-gut-hepatic caeca, gizzard, buccal cavity, afraid gut- arrange these parts of the alimentary canal of a cockroach in proper sequence in relation to digestion.
Answer:
Buccal cavity, crop, gizzard, mid-gut, hepatic caeca, hindgut, are the parts of the alimentary canal of a cockroach.

Question 9.
Write down the human dental formula. What is meant by diphyodont?
Answer:

• The dental formula (arrangement of teeth) of human is represented as.
• 1 ²/2, C¹/1 Pm²/2, M³/3. Thus, human teeth are dissimilar or heterodont.
• Human teeth are diphyodont because milk teeth are replaced by permanent teeth in the adult.

Question 10.
What is the function of the oesophageal sphincter?
Answer:
A ring of muscle, the oesophageal sphincter, controls the opening of the oesophagus into the stomach.

Question 11.
What are microvilli? State their function.
Answer:
The finger-like projections produced by mucose, called villi. The cells that line the surface of the villi produce numerous microscopic .bristle like projections called the microvilli or brush border.

These cells mainly secrete mucus that acts as a lubricant and protects the epithelial surface from excoriation and digestion.

Question 12.
Name the cell which secretes mucus. What are the functions of mucus?
Answer:
Mucus is secreted by mucous or goblet cells.

Mucus acts as a lubricant and protects the epithelial surface from excoriation.

Question 13.
What are crypts of Leiberkuhn?
Answer:
The surface area of the gastrointestinal tract is lined by invaginations of the epithelium (pits) into the submucosa. These pits of the intestine are called the crypts of Leiberkuhn. These crypts contain specialized secretory cells.

Question 14.
Name three accessory digestive organs in a human.
Answer:

1. Tongue: It is located in the buccal cavity. Tongues are provided with gustatory receptors called taste buds.
2. Salivary glands: Humans have three pairs of salivary glands-parotid glands in the cheek, submandibular and sublingual, opening into the floor of the mouth.
3. Liver: It is situated in the right upper part of the abdomen. In an adult, the liver weighs about 1.5kg.

Question 15.
What is peristalsis how does it help in digestion?
Answer:
When food passes down into the oesophagus, a travelling wave of constrictions, which pushes the luminal contents downward is called peristalsis. Peristalsis is produced by the involuntary contraction of circular muscles. When a peristaltic wave reaches the end of the oesophagus the sphincter opens allowing the passage of bolus food to the stomach.

Question 16.
State the anatomical location of the pancreas.
Answer:
It is a soft, lobulated and elongated gland. It is the second-largest gland in the human body. It is located in the loop of the duodenum and extends up to the spleen behind the stomach. It consists of head, body and tail parts. It is a Heterocrine gland i.e. partly exocrine and partly endocrine.

The exocrine part consists of a large number of rounded glandular lobules. The endocrine part consists of a group of cells called islets of Langerhans formed of symbol cells. The alpha cells secrete glucagon hormone and symbol cells insulin hormone.

Digestion and Absorption Important Extra Questions Long Answer Type

Question 1.
What are the accessory digestive organs of a human digestive system?
Answer:
The human digestive system has many accessory organs, the tongue, which is located in the buccal cavity is a muscular organ with bony attachments with the floor of the buccal cavity. Tongues are provided with gustatory receptors called taste buds.

The accessory digestive glands include the salivary glands, the liver and the gall bladder and the pancreas. Humans have three pairs of salivary glands. Parotid glands in the cheek, submandibular and sublingual, opening into the floor of the mouth. The liver is situated in the right upper part of the abdomen. The gall bladder is a small end elongated muscular sac situated below the liver.

The pancreas is an elongated gland, situated near the junction of the stomach and the duodenum. Both the liver and pancreas act as endocrine and exocrine glands, whereas the gall bladder acts as a storing organ. The duct system of these organs is shown below diagram.

Question 2.
Discuss the five steps involved in the process of nutrition.

Digestive System
Answer:
Nutrition: Sum total of certain processes that enable a cell to utilize nutrients is called nutrition.

The entire process of nutrition includes the following steps: ingestion digestion, absorption, assimilation and egestion.
(a) Ingestion and Digestion: The process of taking in food through the mouth is called ingestion. The digestion of food starts from the mouth and ends in the intestines.
1. Mouth: The food is ingested through the mouth, carbohydrates, such as starch, are broken down or digested to form sugar. The saliva contains the enzyme salivary amylase that helps in the digestion of starch into sugar. The saliva also helps in lubricating the food and making it easier for swallowing. The tongue helps in rolling and pushing food into the oesophagus.

2. Oesophagus: TSie oesophagus or the food pipe helps in pushing the food into the stomach. The expansion and contraction of muscles of the oesophagus are called peristalsis or peristaltic movement.

3. Stomach: The stomach is a highly muscular organ. The gastric glands present in its walls secrete gastric juices and help in the digestion of food. These juices contain hydrochloric acid (HCI) and enzymes like pepsin. HCI created an acidic medium for the activation of enzymes and kills bacteria. These enzymes break down the proteins into smaller fragments called peptones. The muscles of the stomach help in churning the food so that it is properly mixed with the digestive juices.

4. Small intestine: The food moves from the stomach to the duodenum. Here emulsification of fat takes place with the help of the bile juice secreted by the liver. The bile juice is stored in the gall bladder. The pancreas secretes trypsin, amylase and lipase which are poured into the duodenum.

The food moves to the ileum, which is the lower part of the small intestine. The inner surface of the ileum contains thin finger-like projections called villi. Villi are responsible for the absorption of digested food. Blood then carries the absorbed food to a different part of the body and undigested food is pushed into the large intestine.


5. Large intestine: This part of the body absorbs water from the undigested food and solid waste is lubricated to form the faeces. The faeces pass on to the lower part of the large intestine, called the rectum, and thrown out of the body through the anus.

Question 3.
Where does the digestion of starch, proteins and fats take place and what is the role played by the associated glands?
Answer:
Starch: Digestion of starch takes place in the mouth. Carbohydrates are broken down or digested to form sugar. The saliva contains an enzyme salivary amylase that helps in the digestion of starch into sugar.

Proteins: The gastric glands present in the stomach secretes gastric juice which contains (HCI) hydrochloric acid and enzymes like pepsin. These enzymes breakdown the proteins into smaller fragments called peptones. Pepsin

Fat: Fat is digested in the duodenum (small intestine) with the help of the bile juice secreted by the liver. The bile juice is stored in the gall bladder. The pancreas secretes trypsin, amylase and lipase which are poured into the duodenum.

Must Read:

CANFINHOME Pivot Point Calculator

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 4 Animal Kingdom. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 4 Important Extra Questions Animal Kingdom

Animal Kingdom Important Extra Questions Very Short Answer Type

Question 1.
List the levels or grades of the organization
Answer:

1. Cellular level
2. Tissue level
3. Organ level
4. Organ- system level

Question 2.
Define the term incomplete digestive system.
Answer:
An incomplete digestive system has only a single opening to the outside of the body that serves as both mouth and anus.

Question 3.
Define the term complete digestive system.
Answer:
A complete digestive system has two openings, mouth, and anus.

Question 4.
Define the term open-type circulatory system.
Answer:
Open type, with the blood being pumped out of the heart and bathing the cells and tissues.

Question 5.
Define the term closed type circulatory system.
Answer:
Closed type, in which the blood is circulated through a series of tubes of varying diameters (arteries, veins, and capillaries)

Question 6.
Define radial symmetry.
Answer:
When any plane passing through the central axis of the body- divides the organism (like spokes of a bicycle wheel) into halves that approximately mirror images, it is called radial symmetry:

Question 7.
Define the bilateral symmetry
Answer:
Animals like annelids, arthropods, etc., where the body can be divided into identical left and right halves in only one plane, exhibit bilateral symmetry.

Question 8.
What is the diploblastic organization?
Answer:
Animals, in which the cells are arranged into two embryonic layers, external ectoderm and internal endoderm, are called diploblastic animals.

Question 9.
What is the triploblastic organization?
Answer:
Those animals in which the developing embryo has a third germinal layer, mesoderm, in between the ectoderm and endoderm are called triploblastic animals.

Question 10.
Define the coelom.
Answer:
The body cavity is lined by a mesoderm is called coelom.

Question 11.
Define the coelomates.
Answer:
Animals possessing coelom are called coelomates.

Question 12.
Define the acoelomates.
Answer:
The animals in which the body cavity is absent are called acoelomates.

Question 13.
What are pseudocoelomates?
Answer:
Such a body cavity is called pseudocolor and the animals possessing them are called pseudocoelomates.

Question 14.
Define metamerism.
Answer:
In some animals, the body has many segments, which show serial repetition of parts. This kind of segmentation is called metameric segmen¬tation, and the phenomenon is known as metamerism.

Question 15.
Name the major groups of the animals.
Answer:

1. Invertebrates and
2. Vertebrates

Question 16.
What are non-chordates and chordates?
Answer:
Animals are also grouped into nonchordates and chordates.

Question 17.
What are the sponges?
Answer:
Members of the Porifera phylum are commonly known as sponges.

Question 18.
Define the terms polyp and medusa.
Answer:
Cnidarians exhibit two basic body forms called polyp and medusa.

Question 19.
What is brain ganglion?
Answer:
Hooks and suckers possess a concentration of nervous tissue in the head called the brain ganglion.

Question 20.
Define the flame cells.
Answer:
Specialized cells called flame cells help in osmoregulation and excretion.

Question 21.
List the examples of Arthropoda.
Answer:
Charaxes (Butterfly), Musca (Housefly), Anax (Dragonfly), Lepisma (silverfish), Periplaneta (Cockroach) Apis (Bee), Buthus (Scorpion).

Question 22.
Give comments on Hemichordata in one sentence.
Answer:
Recently, M.J. (2005) has two placed Hemichordata as a phylum under Invertebrata.

Question 23.
Write one difference in chordates and non-chordates.
Answer:
Cordates, heart is ventral, non-chordates, heart is dorsal.

Question 24.
Give examples of Cyclostomata.
Answer:
Petromyzon (Lamprey) and Myxine (Hagfish)

Question 25.
Define colacal aperture.
Answer:
Alimentary canal, urinary and reproductive tracts open into a common chamber called the cloaca, which opens to the exterior through an aperture called cloaca! aperture.

Animal Kingdom Biology Important Extra Questions Short Answer Type

Question 1.
Discuss the level or grades of the organization.
Answer:
The kingdom Animalia includes multicellular heterotrophic animals, which exhibit different levels of organization as given below.

Cellular LevelAnimal such as sponges, which are loose associations of cells, fall into this group. Some division of labor (activities) occurs among the cells, but these cells do not organize themselves into a definite tissue.

Tissue Level Animals that have certain cells grouped together to form specific tissue are placed in this group, e.g. cnidarians and ctenophores.

Organ Level This is observed in animals that have different kinds of tissues organized into distinct organs each specialized for a particular function, e.g. some platyhelminths.

Organ-system Level Animals that have organs grouped together into functional systems, each system primarily concerned with a specific function are placed in this group, e.g., some platyhelminths, annelids, mollusks, arthropods, echinoderms, and chordates.

Question 2.
Discuss the types of patterns in the organ system.
Answer:
Various patterns of the complexity of organ systems serve as one of the useful criteria in classifying animals. For example, the digestive system may be absent, incomplete, or complete. An incomplete digestive system has only a single opening to the outside of the body that serves as both mouth and anus. A complete digestive system has two openings, mouth, and anus.

Similarly, the circulatory system may be of two types

1. Open type, with the blood being pumped out of the heart and bathing the cells and tissues directly or,
2. Closed Type, in which the blood is circulated through a series of tubes of varying diameters (arteries, veins, and capillaries).

Question 3.
Define radial symmetry and bilateral symmetry.
Answer:
Animals can be grouped into two categories based on symmetry. When any plane passing through the central axis of the body divides the organism (like spokes of a bicycle wheel) into halves that approximately mirror images, it is called radial symmetry. Cnidarians, ctenophores, and echinoderms have this kind of body plan (a).

(a) Radial symmetry

Animals like annelids, arthropods, etc (b), where the body can be divided into identical left and right halves in only one plane, exhibit bilateral symmetry.

(b) Bilateral symmetry

Question 4.
Define the diploblastic and triploblastic organization.
Answer:
Animals, in which the cells are arranged into two embryonic layers, external ectoderm and internal endoderm, are called diploblastic animals in the below figure. Those animals in which the developing embryo has a third germinal layer, mesoderm, in between the ectoderm and endoderm are called triploblastic animals.

Showing germinal layers: (a) Diplobiastic (b) Triploblastic

Question 5.
Outline the role of body cavity and coelom in animals.
Answer:
The nature of the space (body cavity) between the body wall and alimentary canal is very important in the classification. The body cavity, which is lined by mesoderm is called a column. Animals possessing coelom are called coelomates (e.g. annelids, mollusks, arthropods, echinoderms,

(a) Diagrammatic sectional view of Coelomate

(b) Diagrammatic sectional view of Pseudocoelomate

(c) Diagrammatic sectional view of Aceolomate

hemichordates and chordates) (a). The animals in which the body cavity is absent are called acoelomates (e.g., platyhelminths) (c). In some animals, the body cavity is not lined by mesoderm. Instead, the mesoderm is present as scattered pouches in between the ectoderm and endoderm. Such a body cavity is called pseudocolor and the animals possing them are called pseudocoelomates (e.g., as helminths) (b)

Question 6.
Define metamerism.
Answer:
In some animals (e.g., earthworm), the body has many segments, which show serial repetition of parts (like railway compartment). This kind of segmentation is called metameric segmentation, and the phenomenon is known as metamerism.

Question 7.
Draw the diagram broad classification of Kingdom Animalia based on common fundamental features.
Answer:

Question 8.
Describe the phylum Cnidaria.
Answer:
Cnidaria is aquatic, mostly marine, sessile, or free-swimming animals. The phylum name is derived from the stinging cells (nematocysts) or cnidoblasts present on the ectoderm of tentacles and on the body of these carnivorous animals. Cnidoblasts are used for anchorage, defense, and for capture of prey. Cnidarians exhibit tissue level of organization and exhibit radial symmetry. They are diploblastic.

The digestive system is incomplete. They have a central gastro-vascular cavity with a single opening, mouth. Digestion is extracellular and intracellular. Some of the cnidarians, e.g., corals, have skeletons composed of calcium carbonate.

Cnidarians exhibit two basic body forms called a polyp (e.g., Hydra) and medusa (e.g., Auralia). The former, a sessile and cylindrical form, whereas, the latter, umbrella-shaped and free-swimming. Those cnidarians which exist in both forms exhibit alternation of generation, i.e. polyps asexually produce medusae and medusae forming the polyps sexually (e.g., Ophelia)

Examples of cnidaria: Hydra, Porpita, Vellala, Physalia (Portuguese man-of-war), Aurelia (Jellyfish), Adamisia (Sea anemone), Pennatula (Sea- pen), Gorgonia (Sea-fan), and Meandrina (Brain coral).

Some cnidarians (a) Obelia (b) Jellyfish (c) Physalia (d) Sea anemone

Polyp and medusa body from (a) sessile poy (b) swimming medusa

Structure of Hydra

Question 9.
Distinguish between the Chordates and Non-Chordates.
Answer:

Chordates	Non-Chordates
1. Notochord present.	1. Notochord absent.
2. Central nervous system is dorsal, hollow, and single.	2. Central nervous system is ventral solid and double.
3. Pharynx perforated by gill slices	3. Gill slits are absent.
4. Heart is ventral.	4. Heart is dorsal.
5. A post-anal (tail) is present.	5. Past-anal tail is absent.

Question 10.
Explain the class amphibia.
Answer:
As their name indicates (Gr. Amphi, dual, double + bios, life), most amphibians can exist in aquatic as well as terrestrial habitats. Most of them have two pairs of limbs. The body is divisible into the head and trunk; the tail may be present in some. The amphibian skin is moist (without scales). The eyes have eyelids. A tympanum represents the ear.

The alimentary canal, urinary and reproductive tracts open into a common chamber called the cloaca, which opens to the exterior through an aperture called the cloacal aperture. Respiration may be by gills, lungs, or through the skin. The heart is three-chambered (2 auricles and 1 ventricle). These are cold-blooded animals.

Sexes are separate Fertilization is external. They are oviparous and development is direct or indirect.

Examples of Amphibia: Bufo (Toad), Rana (Frog), Hyla (Tree frog),

Salamandra (Salamander), Ichthyophis (Limbless amphibia).

Frog

Question 11.
Describe the class Reptilia.
Answer:
The class name refers to their creeping or crawling mode of locomotion. They are mostly terrestrial animals with a body covered by dry and cornified skin, epidermal scales, or scutes. They do not have external ear openings. Limbs, when present, are two pairs. The heart is usually three-chambered, but four-chambered in crocodiles, Reptiles are cold-blooded animals. The excretory organ is the kidney. Snakes and lizards shed their scales as skin cast.

Sexes are separate. Fertilization is internal. They are oviparous and development is direct.

Examples of Reptilia T Chelone (Turtle), Testudo (Tortoise), Chameleon (Tree lizard), Calotes (Garden lizard), Naja (Cobra), Crocodilus (Croco¬dile), Aligator (Alligator).

(a) Tortoise, (b) Monitor (Indian goh) (c) Naja (d) Crocodile (e) Chameleon

Question 12.
Explain the important characteristics of Mammalia.
Answer:
Mammalia is generally terrestrial, found in a variety of habitats- polar ice caps, deserts, mountains, forests, grasslands, and dark cover. Some of them have even adapted to fly or live in water. The most unique mammalian characteristic is the presence of milk-producing glands (mammary glands) by which the young ones are nourished.

Mammalia has two pairs of limbs, which are variously adapted for walking, running, climbing, burrowing, swimming, and flying. The skin of mammals is unique in possessing hairs. External ears or pinnae are present. Different types of teeth are present in the jaw. The heart is four-chambered. The lungs are well developed. Mammals show the greatest intelligence among all the animals.

Sexes are separate and fertilization is internal. They are viviparous with few exceptions and development is direct.

Some mammals:

Ornithorhynchus

Balaenoptera

Pteropus

Macropus

Question 13.
Describe the main characteristic of class-Aves.
Answer:
The characteristic features of birds are the presence of feathers and most of them can fly with few exceptions, generally called flightless birds (e.g. Ostrich). They possess beak. The forelimbs are modified into wings. The hind limbs generally have scales and are modified for walking, swimming, or clasping the tree branches. Skin is dry without glands except for the oil gland at the base of the tail. The endoskeleton is fully ossified (bony) and the long bones are hollow with air cavities.

The digestive tract of birds has additional chambers, the crop, and the gizzard. The heart is completely four-chambered. They are warm-blooded (homeotherms) animals, i.e., they are able to maintain constant body temperature. Respiration is by lungs that contain air sacs. Birds have a good sense of sight. The excretory organ is a kidney.

Sexes are separate. Fertilization is internal. They are oviparous and development is direct. Examples of Aves are Corvus (crow), Columba (pigeon), Prittacula (parrot), Struthio (Ostrich) Paver (Peacock), Aptenodytes (Penguin)

Some birds : (a) Neophron (b) Struthio (c) Psittacula (d) Pavo

Question 14.
Write some basic characterize- features of the following Phyla:
Ctenophora, Annelida, Mo.llusca, Echino Desmata and Hemichordata.
Answer:
Represents some basic characteristic features of different phyla.

Question 15.
Draw the diagram of the classification of phylum Chordata.
Answer:

Classification of phylum Chordata

Animal Kingdom Biology Important Extra Questions Long Answer Type

Question 1.
Describe the phylum Arthropods.
Answer:
The phylum Arthropoda is the largest phylum of the animal kingdom consisting of more than 900,000 species, which include many economically important insects.

1. They have an organ-system level of body organization. They are bilaterally symmetrical, triploblastic, segmented, and acoelomate animals.
2. The body of arthropods is covered by a chitinous cuticle which forms the exoskeleton. The body segments are fused to form the head, thorax, and abdomen.
3. They have jointed appendages. The appendages are variously modified to form antennae, mouthparts, pincers (chelicerae), or walking legs.
4. The digestive system is complete.
5. Respiratory organs are gills, book gills, book lungs, or tracheal system.
6. The circulatory system is open type.
7. The nervous system is almost similar to that of the annelids. Sensory organs include antennae for perceiving odor, receptors for taste, eyes (compound and simple), statocysts or balance, organs, and sound receptors.
8. Excretion takes place through green glands or malpighian tubules.
9. They are mostly dioecious. Reproduction is sexual. Fertilization is usually internal. They are mostly oviparous.

Development may be direct or indirect, passing through many larval stages. The process of transformation of a larva into an adult is called metamorphosis.

Some common arthropods (a) Centipede (b) Millipede (c) Beetle (d) Prawn (e) Spider and (f) Scorpian

Examples of Arthropoda: Araneus (Garden spides), Limulus (King crab),

Buthus (Scorpion), Scolopendra (Centipede), Cancer (Common crab), Balanus (Barnacle), Lepisma (Silverfish), Periplaneta (Cockroach), Apis (Bee) Anopheles (Mosquito), Musca (Housefly), Charaxes (Butterfly), Attelabus (Beetle), Locusta (Locust) and An ax (Dragonfly).

Question 2.
Describe the phylum Porifera.
Answer:
Members of this phylum are commonly known as sponges. They are generally marine, diploblastic bilaterally symmetrical with a significant water transport mechanism. They are considered as very primitive multi-cellular animals and have a cellular level of organization.

Water can enter through minute pores (Ostia) in the body wall directly or through the canal into a central cavity, spongocoel, from where it goes out through the osculum.

This pathway of water transport is called the canal system and is helpful in food gathering, respiratory exchange, and removal of water. Choanocytes or collar cells line the spongocoel and the canals. Digestion is intracellular. The body is supported by a skeleton made up of spicules or spongin fibers.

Sexes are not separate (monoecious/hermaphrodite/bisexual), i.e., eggs and sperm are produced by the same individual. Sponges reproduce asexually by fragmentation and sexually by the formation of gametes. Fertilization is internal and development is indirect having a larval stage that is morphologically distinct from the adult.

Examples of Porifera are Sycon (Scypha), Spongilla, Chalina, (Dead man’s finger), and Euspongia (Bath sponge)

Examples for Porifera: (a) Sycon (b) Euspongia (c) Spongilla

Read More:

Bank Nifty Pivot Point

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 18 Body Fluids and Circulation. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 18 Important Extra Questions Body Fluids and Circulation

Body Fluids and Circulation Important Extra Questions Very Short Answer Type

Question 1.
What is systole?
Answer:
The contraction phase of the cardiac chamber (s) is called systole.

Question 2.
What is diastole?
Answer:
The relaxation phase of the cardiac chamber is called diastole.

Question 3.
Where is SA-node located?
Answer:
It is located at the place of merge of sinus venous at the right wall of the right atrium.

Question 4.
In which animals we can find the sinus Venosus?
Answer:
Sinus venosus can be found in fishes, amphibians and reptiles.

Question 5.
What is the ‘lubb’ sound?
Answer:
It is the first sound produced by the heart due to the sharp closure of AV valves at the start of ventricular systole.

Question 6.
What is AV-node?
Answer:
It is a node of specialised fibres, located at the junction of the right atrium and right ventricle.

Question 7.
What is hemolymph?
Answer:
The blood of insects that lack haemoglobin is called haemolymph.

Question 8.
What is a sphygmomanometer?
Answer:
The instrument which measures blood pressure is called a sphygmomanometer.

Question 9.
What is the “dup” sound?
Answer:
It is the second sound produced by the heart due to the sharp closure of semilunar valves at the start of ventricular systole.

Question 10.
What is the role of AV-node?
Answer:
It collects the wave contraction generated by SA-node and passes down to a bundle of His and Purkinje fibres.

Question 11.
Where is RBCs (red blood cells) produced?
Answer:
RBCs are produced in the bone marrow.

Question 12.
Name different types of blood groups present in human beings.
Answer:
Types of blood group: O, A, B, AB group.

Question 13.
Name various parts of the circulation.
Answer:
Heart, blood, gases and same waste materials.

Question 14.
Name the blood vessel which carries impure blood to the heart.
Answer:
Vena cava.

Question 15.
The transport system in animals is called
Answer:
Circulatory system.

Question 16.
What is the difference between artery and vein?
Answer:

1. Artery: Thin-walled
2. Vein: thick-walled.

Question 17.
What are the different components of blood?
Answer:
Plasma, RBC, WBC, Sugar, salt, waste products.

Question 18.
What is the heartbeat rate/minute?
Answer:
72 beat/minute.

Question 19.
What are circulatory fluid and its component?
Answer:
Circulatory fluid is blood and its components are haemoglobin, RBC, WBC.

Question 20.
Give the function of blood platelets.
Answer:
They help in the clotting of blood.

Question 21.
Which blood group is known as a universal donor?
Answer:
‘O’ group is known as a universal donor.

Body Fluids and Circulation Important Extra Questions Short Answer Type

Question 1.
Why does the ventricle contract as a closed chamber in the early phase of its systole?
Answer:
In the early phases of systole the ventricle contracts as a closed chamber, so to increase the pressure in the atrium. Backflow of blood into atria is prevented by closure of AV-valves. In a closed chamber, the ventricles contract and increased pressure cause the opening of semi-lunar valves. The blood is passed into arteries with great force.

Question 2.
The blood vascular system is considered efficient than the water circulatory system in animals, why?
Answer:
The dissolved oxygen and nutrient present in water are in fewer amounts. Oxygen is supplied through oxygen carrier molecule (haemoglobin) present in plasma or cells, in higher animals. Oxygen and nutrients are supplied quickly and in fairly large amounts in animals with a blood vascular system, so considered comparatively efficient.

Question 3.
Mention, in brief, the important events that happen during the cardiac cycle.
Answer:
The cardiac cycle comprises the following three phases.
(a) Atrial systole
(b) Ventricular systole
(c) Joint diastole.

(a) Atrial systole: The atria contract from anterior to posterior and the blood is sent to respective ventricles. Time taken is 0.1 sec.
(b) Ventricular systole: The ventricles contract, deoxygenated blood is sent to lungs for oxygenation, while oxygenated blood received from lungs is sent to different parts of the body through the aortic arch. Time taken is 0.3 sec.
(c) Joint diastole: All the chambers are in systole, called joint diastole. Time taken is 0.4 sec.

Question 4
Describe in brief the types of valves present in the heart.
Answer:
Different valves present in the heart are described as under:
(a) Tricuspid valve: The valve present at the right atrioventricular aperture formed of three flaps.
(b) Bicuspid valves: The valve present at the left atrioventricular aperture, formed of two flaps, also called the mitral valve.
(c) Semi-lunar valve: Two sets of half-moon shaped (3) valves, present at openings of pulmonary aorta and aorta, present here to check backflow of blood.

Question 5.
What is hypertension? What are causative factors?
Answer:
It is a manifestation of an increase in blood pressure. A continuous or sustained rise in arterial blood pressure is known as hypertension.

The normal systolic and diastolic pressure of a healthy human is 120m and 80mm Hg respectively. Under various physiological conditions, a moderate level of fluctuation may occur and blood pressure increase. It is referred to as high blood pressure.

Question 6.
What is heart rhythm? Discuss.
Answer:
Heart muscles continuously generate impulses in a manner that causes rhythmic contraction and relaxation of the heart chambers. For the purpose of maintenance of the heart rhythm, a highly excitatory’ and conductive system is present, which includes sino-atrial node (SA) inter- nodal pathways, the atria-ventricular node (Avnode) AV bundle and the bundle of Purkinje fibres.

In normal conduction of impulse, the atrial contraction precedes that of the ventricle.

The automatic rhythmicity of the heart is its ability to contract spon¬taneously at a regular rate.

Question 7.
Define the terms:
(a) SA node,
Answer:
SA: It is a self-excitatory node that initiates excitatory waves at the highest rate. SA-node normally generates the cardiac impulse and working by knowing the rate of discharge of cardiac impulse. It can determine the rate of heartbeat. The SA-node works as the pacemaker of the heart.

(b) Systole,
Answer:
Systole: The pumping out of blood due to contraction of the heart is called systole.

(c) Diastole,
Answer:
Diastole: The relaxation of the heart is called diastole. During diastole, blood flows into the auricles to their ventricles through the open auriculoventricular valve.

(d) Pulmonary circulation.
Answer:
Pulmonary circulation: The circulatory system which is associated with the lungs through arteries and veins, is known as pulmonary circulation.

Question 8.
Fill in the blanks:
Answer:
(a) Eosinophil is a bilobed nucleus
(b) Pulmonary artery carries deoxygenated blood.
(c) Heart of cockroach is present in the pericardial sinus.
(d) Platelets helps in coagulation
(e) Haemoglobin is present in RBCs due to which its colour is red.

Question 9.
What is an artificial pacemaker? Explain.
Answer:
A pacemaker is a rhythmic centre that establishes a pace of activity. Sometimes the component of the impulse conduction system is disrupted, causing irregularity in the heart rhythm like heart failure. Such types of patients are provided with an artificial electronic device, which regularly sends a small amount of electrical charge for maintaining the rhythmicity of the heart.

The device is known as an artificial pacemaker. It is implanted subcu¬taneously in the upper thoracic region having a connection with the heart.

If patients having symptoms of ventricular escape, in which atrial impulse suddenly fails, the artificial pacemaker is connected to the right ventricle for controlling its rhythm. The artificial pacemaker consists of a pulse generator containing a cell to produce electric impulse.

Question 10.
How arteriosclerosis is different from atherosclerosis? Discuss.
Answer:
Arteriosclerosis: It is the hardening of the arteries due to deposition and thickening. In the case of arteriosclerosis, calcium salts precipitate with the cholesterol and plague. The affected artery loses the property of distension and its walls may rupture. The blood leaking from the ruptured walls may clot and block the pathway of blood flow. This may lead to a heart attack and even death.

Atherosclerosis: It is the deposition of lipids (cholesterol) on the wall lining the lumen of large and medium-sized arteries. This type of deposition is called atherosclerosis. Its formation starts with the deposition of cholesterol particles/crystals in the tunica intima and smooth muscles. This results in the reduction of the lumen size of the artery and the flow of the blood also reduce.

In extreme circumstances, these plaques may completely block the artery. The proliferation of smooth muscles occurs because these plaques provide a rough surface to the platelets causing the release of platelet, derived from growth factor (PDGF). Such plaques reduce the blood supply to the heart or may stop the supply due to complete blockage. This may result in a heart attack or stroke.

Question 11.
What is heart rhythm? Discuss.
Answer:
Heart muscles continuously generate impulses in a manner that causes rhythmic contraction and relaxation of the heart chambers. For the purpose of maintenance of the heart rhythm, a highly excitatory and conductive system is present, which includes sino-atrial node (SA) intermodal pathways, the atrioventricular node (Av node) AV bundle and the bundle of Purkinje fibres.

In normal conduction of impulse, the atrial contraction precedes that of the ventricle.

The automatic rhythmicity of the heart is its ability to contract spontaneously at a regular rate. ,

Question 12.
What is an electrocardiogram? Write about its significance.
Answer:
The passage of cardiac impulse through the heart spreads electric current into the tissues around the heart and a small portion spreads throughout the surface of the body.

These electrical changes can be recorded along the cardiac cycle. The recording of electrical potential generated by the spreading of cardiac impulse is called an electrocardiogram (ECG). The electrical activity of the heart can be graphically represented by ECG, which shows different waves.

Question 13.
Match column I with column II.

Column I	Column II
(a) Haemolymph	(i) Coagulation
(b) RBC	(ii) Immunity
(c) Antibody	(iii) Cockroach
(d) Platelets	(iv) Contraction
(e) Systole	(v) Gas transport

Answer:

Column I	Column II
(a) Haemolymph	(iii) Cockroach
(b) RBC	(v) Gas transport
(c) Antibody	(ii) Immunity
(d) Platelets	(i) Coagulation
(e) Systole	(iv) Contraction

Question 14.
What is blood? Describe its components.
Answer:
Blood is a complex connective tissue, which consists of two components:

1. Plasma: It is the extracellular fluid of blood constituting about 55% of the blood volume. Plasma contains 91 – 92% of water, 7% of proteins, 0.9% of inorganic constituents, 0.1% of glucose and the rest includes various organic and inorganic substances. Proteins are the second-largest constituents of plasma.
2. Blood corpuscles: Nearly 45% volume of blood consists of corpuscles or blood cells. Blood corpuscles are of three types: erythrocytes or red blood corpuscles (RBC), leucocytes or white blood corpuscles (WBC) and thrombocytes or blood platelets.

Question 15.
What is hypertension? What are different contributory fac¬tors?
Answer:
An abnormal rise in arterial blood pressure is called hypertension.

The contributory factors of this disease are:
(a) Hypercholesterolemia,
(b) Nervous strain,
(c) Renal disorder/impaired functioning.
(d) Arteriosclerosis.

Question 16.
What is the main advancement in avian and mammalian heart over the amphibians and reptiles heart?
Answer:
Avian and mammalian heart show complete double circulation and in them, oxygenated blood remains completely separate from deoxygenated blood. There are no accessory chambers in them. There is a single aorta in aves and mammals and double aorta in reptiles and amphibians which quickens the supply of O₂ and food to release the energy and aids in the removal of wastes from the body.

Question 17.
What is the base efficiency of the heart?
Answer:
The efficiency of the heart on beating throughout life without fatigue is based upon the principle that it rests double the time it works i.e. contraction of the heart is followed immediately by relaxation but relaxation is not followed by the next contraction. The beating of the heart is 72 times per minute. It is indicated by pulse rate per minute. The amount of blood pumped out per minutes is called heart output.

Question 18.
What does ECG stand for? Define it.
Answer:
ECG stands for electrocardiograph. It is defined as a permanent record of electrical events (depolarization and ventricles) during a cardiac cycle made on graph paper with the help of an instalment called an electrocardiogram.

It shows 5 waves i.e., P, G, R, S, T. In this P, R, T are positive waves that lie above the baseline whereas Q and S are negative waves that lie below the baseline. The part of the baseline between two deflections is called an interval.

Question 19.
What are the advantages of physical exercise?
Answer:
Any physical exercise initiates an impulse from the nervous system which causes the release of adrenaline hormone from adrenal glands into the blood.

Advantages of physical exercise:

1. Exercise increases heartbeat which reduces the workload of the heart. It increases blood circulation so that every tissue gets a supply of nutrients and oxygen.
2. It maintains normal blood pressure by lowering the chances of developing atherosclerosis- a disease, which causes narrowing of arteries.
3. Exercise increases the level of high-density lipoproteins (HDLS) which help in reducing the harmful cholesterol from arteries.
4. Exercise prevents heart attack with the development of additional or collateral blood vessels which provide alternative routes for blood supply to the muscles of the heart.
5. Exercise adds more number RBCs
6. Haemoglobin of blood increases which helps in supplying more O, to the tissues.

Question 20.
What is blood pressure? What do you mean by diastolic and systolic pressure?
Answer:
It is the pressure against the walls of blood vessels produced by the discharge of blood from the heart. It is high in arteries and Ipw in veins. It rises and falls in arteries due to heartbeat.

The temporary rise in B.P. during contraction of the heart is called systolic pressure. The temporary fall in the B.P during relaxation of the heart is called diastolic pressure.

Question 21.
What is a lymph node?
Answer:
The lymphatic vessels at intervals bear small lymph nodes which act as the filters of poisonous and foreign substances such as dust, debris, bacteria and other injurious substances. A lymph node has an inner border called the hilum. These are the masses of dense connective tissue, rich in phagocytic white corpuscles and macrophages.

Lymph nodes also produce lymphocytes, monocyte and antibodies into the lymph which are carried to the blood. These lymph nodes help in detecting and destroying cancer cells at the initial stages.

Question 22.
What is systemic circulation?
Answer:
The system of blood vessels that ensures the supply of oxygenated blood from the left ventricle to all the body organs and the return of deoxygenated blood to the right atrium is called systematic circulation.

Question 23.
Describe the importance of pulmonary circulation.
Answer:
The circulatory system associated with the lungs through arteries and veins forms the pathway of the circulatory system.

The flow of blood from the heart to the lungs and back to the heart is called pulmonary circulation. The regular oxygenated blood is returned to the heart and the pulmonary artery supplies deoxygenated blood from the right ventricle to the lungs. It is the pathway of the blood through arteries from t aorta arising from the heart and returning to the right atrium.

Question 24.
What is an electrocardiogram? Write about its significance.
Answer:
The passage of cardiac impulse .through the heart spreads electric current into the tissues around the heart and a small portion spreads throughout the surface of the body.

These electrical changes can be recorded along the cardiac cycle. The recording of electrical potential generated by the spreading of cardiac impulse is called an electrocardiogram (ECG). The electrical activity of the heart can be graphically represented by ECG, which shows different waves.

Question 25.
Write true or false:
(a) Atrio-ventricular node is the natural pacemaker of the heart.
Answer:
False

(b) Human heart has inter-auricular foramen.
Answer:
True

(c) Heart of the cockroach is segmentally arranged.
Answer:
True

(d) Right atriventricular valve is a semilunar valve
Answer:
True

(e) Normal systolic and diastolic pressure of humans is 120 and 60 mm Hg, respectively.
Answer:
False

Body Fluids and Circulation Important Extra Questions Long Answer Type

Question 1.
(a) Why is the AV bundle essential for the conduction of cardiac muscles? Explain.
Answer:
The sinoatrial node (pacemaker) of the heart spreads the cardiac impulse over the two atria to bring about their systole. It, however, cannot spread along the common cardiac muscle fibres from the atria to the ventricles. It is because, in the mammalian heart, there is no continuity between the cardiac muscle fibres of the atria and those of the ventricles.

Although the fibres of each individual chamber exist in a functional syncytium (not separatable). It is because a bond of specialized cardiac muscle fibres exists on the interatrial septum called the ATRIOVENTICULAR BUNDLE (AV bundle).

AV bundle forms the only muscular continuity between atrial and ventricular muscles. The AV bundle descends from the AV node along the interatrial septum and the interventricular septum. It branches into right and left bundle branches as it enters the ventricle.

From each AV bundle branch Purkinje which fibres spread out and connect with the common ventricular muscle fibre. Thus, the cardiac impulse spreads over the atria to reach the AV node; the AV bundle is necessary for the conductions of impulse through its two branches and the Purkinje fibres to reach the ventricular muscle fibres causing contraction of ventricles.

(b) Make a graphic representation of double circulation in the mammalian heart.
Answer:

Representation of double circulation in animals.

Question 2.
Define portal system. How is the hepatic portal system useful to our body?
Answer:
Portal system: A portal system is the circulatory system in which blood collected from one set of organs or tissues is conveyed to another organ through capillaries before entering the heart.

For example, in the hepatic portal system, blood collected from the alimentary -canal is first conveyed to the liver by the hepatic portal vein. After passing through the capillaries of the liver, it passes directly to the posterior vena cave by the hepatic vein.

Hepatic portal circulation

Use of hepatic portal system:
(i) Veins coming from the various parts of the alimentary canal carry deoxygenated and food-laden blood. Through the portal vein, it reaches the network of portal vein capillaries in the liver. The excess of food is filtered and stored in the liver as glycogen. Thus, heavily food loaded blood is not allowed to go to the heart, which may have to work more in pumping the blood.

(ii) Liver also consumes drugs and toxins present in the blood coming from the intestine. So, that heart can be saved from their harmful effects.

Question 3.
What is the lymphatic system? Discuss its importance.
Answer:
The lymphatic system consists of vessels and lymph organs, like lymph nodes, bone marrows, spleen and thymus. The fluid present in the lymphatic system is called lymph. This fluid has a composition similar to that of plasma except it is low in protein.

Fine channels present in the tissue are called lymph vessels, these are similar to veins. Besides these, a number of lymph nodes are present. The lymphatic vessels are distributed in the limbs, abdomen, thorax and neck.

The lymphatic system provides an accessory route for the flow of interstitial fluid into the blood. The lymphocytes present in the lymphatic system play important role in the defence against foreign agents or microbes.

Shows the various lymphatic organs in the human body

Question 4.
Describe the structure of the human heart.
Answer:
The human heart consists of four chambers: Two upper thin layered (Atrium) and two lower thick layered ventricles. The atria are situated at the broader end while the ventricles are situated at the lower conical end. Externally a transverse groove is present between the atria and ventricles, called the anterior interventricular sulcus and posterior intraventricular sulcus.

The right and left atria receive blood from different body parts. The right atrium receives deoxygenated blood from all parts of the body except the lungs, through the superior and inferior vena cava. Pulmonary veins bring oxygenated blood to the left atrium horn of the lungs.

Extma1 features of the human heart

The right and left atria pump their blood into the right and left ventricles. From the right ventricle, the pulmonary trunk arises which bifurcates into right and left pulmonary arteries, which supply deoxygenated blood to the lungs. The left ventricle gives rise to an ascending aorta from ‘which the oxygenated blood is supplied to the coronary- arteries and the systemic circulation of the body occurs.

Question 5.
Write the differences between
(a) Blood and haemolymph
Answer:

Blood	Haemolymph
I. It is composed of blood plasma RBCs, WBCs and platelets.	1. It is composed of watery fluid, lymphocytes. few monocytes, but no RBCs.
2. It is red in colour	2. It is a watery fluid.
3. Blood contains more plasma proteins, calcium and phosphorus ions.	3. Lymph contains fewer proteins, less calcium and phosphorus ions
4. Flow of blood is fairly rapid.	4. Haemolymph flow is very slow.
5. Blood is pumped out from the heart, flow through the arteries, capillaries and veins.	5. Haemolymph flow begins from the tissue spaces, goes to lymph capillaries.
6. Glucose concentration is comparatively low.	6. Glucose Concentration is comparatively high.

(b) Open and closed system of circulation
Answer:
Open type of circulatory System and Closed system of circulation:
Open type of circulatory System: It mainly occurs in arthropods and molluscs, such as insects, prawns, spiders, oysters, etc. In these colourless blood coming through blood vessels, flows through open spaces and channels called lacunae and sinuses.

Lacunae and sinuses together called haemocoel, which carries colourless blood called haemolymph. The oxygen-carrying pigments are generally dissolved in the plasma of blood. Deoxygenated blood from these goes to the gills for oxygenation after oxygenation blood is returned to the sinus surrounding the heart.

Closed type of circulatory system: It mainly occurs in annelids and chordates. Heart and blood vessels together constitute the closed circulatory system. The heart is a pumping organ that is provided with valves. It pumps the blood into arteries, which earn’ the blood to different organs to the body.

Question 6.
Describe the circulatory system of cockroach.
Answer:
The circulatory system is of open type. It consists of the heart and dorsal blood vessel, sinuses and haemolymph. The haemocoel is divided into three chambers or sinuses dorsal, middle and ventral. The dorsal chamber is called the pericardial sinus, the middle is the perivisceral sinus whereas the ventral is the perineural sinus. The dorsal and ventral diaphragms bear a number of pores through which haemolymph flows.

The heart of a cockroach is an elongated tubular structure, closed behind and open in front. It has thirteen funnel-shaped and segmentally arranged chambers i.e. three in the thoracic segment and ten in the abdominal segment. Valves, ensuring the unidirectional flow of blood, guard the passage of each heart chamber.

Blood flows from the posterior to the anterior end and is discharged into the tissue space of the head. Laterally each heart chamber bears a pair of apertures called Ostia which communicates with the pericardial sinus.

In each segment, a pair of triangular alary muscles is present on either side of the heart.
The blood of the cockroach is not responsible for the transportation of respiratory gases but serves for
(1) the transportation of nutrients.
(2) maintains hydrostatic pressure and
(3) acts as a reservoir of water.

The haemolymph of cockroach circulates due to contraction and relaxation of the heart and ciliary muscles,

Open type of circulatory system in cockroach

Must Read:

MUTHOOTFIN Pivot Point Calculator

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 9 Biomolecules. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 9 Important Extra Questions Biomolecules

Biomolecules Important Extra Questions Very Short Answer Type

Question 1.
What is hydrolysis?
Answer:
During the digestion of carbohydrates, the glycosidic bond between sugar residues is broken by the addition of water and this is called hydrolysis.

Question 2.
Define fatty acid.
Answer:
Fatty acids are organic acids with a hydrocarbon chain ending in a carboxyl group.

Question 3.
What are iso-enzymes?
Answer:
The enzymes possessing slightly different molecular structures but similar in their bio-catalytic action.

Question 4.
Give the names of 2 non-polar organic solvents that are used for lipid extraction from cells.
Answer:
Chloroform, Ether.

Question 5.
Name one monosaccharide sugar that is found in the blood plasma of human beings.
Answer:
Glucose.

Question 6.
What is the function of calcium in the human body?
Answer:
Calcium in bones and teeth provides strength and rigidity to them.

Question 7.
Name the bonds uniting the monosaccharide subunits.
Answer:
Monosaccharide sub-units are joined together by glycoside bonds.

Question 8.
What are lygases?
Answer:
Lygases are the enzymes that join two substrate molecules.

Question 9.
Name the ending group of fatty acids which are organic acids with a hydrocarbon chain.
Answer:
Carboxyl.

Question 10.
Which is the most common form of sugar in fruits?
Answer:
Fructose.

Question 11.
How can we overcome the deficiency of iodine?
Answer:
By using iodized common salt.

Question 12.
Names the important food storage of carbohydrates.
Answer:
Starch and Glycogen.

Question 13.
Define allosteric modulation.
Answer:
It regulates the activity of some enzymes internally.

Question 14.
Mention two functions of the sodium and potassium ions in the body.
Answer:
Functions of the sodium and potassium ions in the body are:

1. To maintain the volumes of extracellular and intracellular fluids.
2. Transmission of nerve impulses.

Question 15.
Name the small molecules of the cell.
Answer:
The small molecules of the cell are:

1. Minerals
2. Water
3. Amino acids
4. Sugars
5. Lipids
6. Nucleotides.

Biomolecules Important Extra Questions Short Answer Type

Question 1.
What are monosaccharides? Give few examples.
Answer:
Monosaccharides are the simplest carbohydrates that cannot be hydrolyzed into still smaller carbohydrates. The general formula is C_n H_2n O_n e.g. Ribose, Glucose, Fructose.

Question 2.
What is a disaccharide?
Answer:
A disaccharide is a sugar molecule composed of two monosaccharide sub-units e.g. a molecule of sucrose is formed from a molecule of glucose and a molecule of fructose by dehydration.

Question 3.
Why do fats release more energy than carbohydrates on oxidation?
Answer:
Like carbohydrates, fats are made up of C, H, and O but they contain fewer oxygen molecules than carbohydrates. On oxidation they consume more oxygen releasing more energy.

Question 4.
What is the function of calcium in our body? In what form is calcium deposited in the middle lamella?
Answer:
Calcium is impregnated in bones and teeth. It provides them with strength and rigidity.
Calcium is deposited in the middle lamella in the form of calcium pectate.

Question 5.
Define cellular pool. What are the characteristics of a small molecule in the cellular pool?
Answer:
The collection of various types of molecules in a cell is termed a cellular pool.

The characteristics of small molecules in the cellular pool are

1. Low molecular weight
2. Simple molecular conformation.
3. Higher solubility.

Question 6.
What are lipids or fats? State their characteristic. What are the functions of subcutaneous fat in our body?
Answer:
Fat or lipids are esters of glycerol and fatty acids. They are made up of C, H, and O but include proportionately less oxygen as compared to carbohydrates. They are insoluble in water and soluble in non-polar organic solvents.

Functions of subcutaneous fat are

• Storage of food (chemical form of energy).
• Shock absorption.
• Insulation.

Question 7.
How are amino acids linked to form a peptide chain?
Answer:
Amino acids are condensed together to form a peptide chain. The bond is formed between the carboxyl group of one amino acid and the amino group of adjacent amino acid. This is called a peptide bond and it is formed by dehydration.

Question 8.
What are phospholipids?
Answer:
Phospholipids are lipids containing phosphate groups e.g. phosphoglyceride. They have a hydrophilic polar head and a hydrophobic non-polar tail.

Question 9.
What are macromolecules? Give examples.
Answer:
Simple molecules assemble and form large and complex molecules called macromolecules e.g. proteins, lipids, nucleic acid, and carbohydrates.

Question 10.
Give two examples of storage polysaccharides.
Answer:
Two advantages of storing carbohydrates in the form of polysaccharides:

1. Food storage polysaccharides are starch and glycogen. Starch is found in rice, wheat, etc. Glycogen is stored in the liver. During their formation, many molecules of water are removed from monosaccharides.
2. If necessary, polysaccharides are broken down by enzymes for the release of energy.

Question 11.
What is chitin?
Answer:
Chitin: Chitin is similar to cellulose in many ways except its basic units are not glucose, but a similar molecule that contains nitrogen (N-acetyl glucosamine) and is soft as well as leathery.

Question 12.
Explain how glycosidic bonds are formed?
Answer:
Formation of Glycosidic Bonds: The aldehyde or ketone group of a monosaccharide can react and bind with an alcoholic group of another

Glycosidic bond

organic compound to join the two compounds together. This bond is known as a glycosidic bond. This bond may be hydrolyzed to give the original compounds. Monosaccharides by uniting together through glycosidic bonds give rise to compound carbohydrates.

Question 13.
Describe functions of polysaccharides in living organisms.
Answer:
Food storage polysaccharides: As the name suggests saccharides which perform the function of storing food. Examples are starch, glycogen.

Starch: It is formed as a result of photosynthesis. It is found in large quantities in rice, wheat, cereals, legumes, potato, tapioca, and bananas. It is an energy-giving substance as it stores energy.

Glycogen: It is found in the muscles and liver of mammals and stores energy. There are distinct advantages of storing carbohydrates in the form of polysaccharides

1. During the formation, many molecules of water get removed and bulk reduced
2. Polysaccharides are relatively easy to store and get broken down easily by enzymes to release energy.

Structural Polysaccharides: Examples of these are cellulose and chitin. These take part in the formation of the organism.

Cellulose: It is a plant product. It is perhaps the most abundant material found in the living world. If forms cell walls. It is a fibrous polysaccharide that has high tensile strength. Wood and cotton have large quantities of cellulose.

Chitin: Chitin is similar to cellulose in many ways except that its basic unit is not glucose, but a similar molecule that contains nitrogen (N-acetyl glucosamine). Chitin is soft and leathery, it becomes hard when it gets impregnated with calcium carbonate or certain proteins. The insolubility of these polysaccharides in water helps in retaining the particular form it also helps in strengthening the structure of organisms.

Question 14.
What is meant by the tertiary structure of proteins?
Answer:
The tertiary structure of proteins: Many amino acid units form polypeptides. The peptide bonds holding the amino acids together in a particular way constitute the primary structure of the protein. A functional protein contains one or more polypeptide chains.

Through the formation of hydrogen bonds, peptide chains assume a secondary structure. Secondary protein may be in the form of a twisted helix or pleated sheet.

When the individual peptide chains of the secondary structure of the protein are further extensively coiled and folded into sphere-like shapes with the hydrogen bonds between the amino and carboxyl group and various other kinds of bonds cross-linking on-chain to another they form tertiary structure.

The ability of proteins to carry out specific reactions is the result of their primary, secondary, and tertiary structure.

The tertiary structure (myoglobin)

Question 15.
Explain the composition of triglycerides.
Answer:
Fat is esters of fatty acids with glycerol. Each molecule of glycerol can react with 3molecules of fatty acid. On the basis of fatty acids that are attached to the glycerol molecule, the esters are called either mono, di, or triglycerides.

Triglyceride-Tripalmitin

Question 16.
Mention the difference between saturated and unsaturated fat?
Answer:
Differences between saturated and unsaturated fat:

Saturated fat	Unsaturated fat
(i) They have higher melting points	(i) lower melting points
(ii) Carbon align in the chain	(ii) Double or triple banded
(iii) Remain in solid form at 20°c but on heating become liquids	(iii) Remain in liquid form at 20°c even in water

Question 17.
Describe the structure of phospholipid. How are they arranged in the cell membrane?
Answer:
Structure of phospholipids: Phospholipids are a class of lipids that serve as the structural component of the cell membrane. Phospholipids have only 2 fatty acids attached to the glycerol while the 3rd glycerol binding site holds a phosphate group. This phosphate is bound to alcohol.

These lipids have both hydrophilic and hydrophobic pans due to a charge on the phosphoric acid/alcohol head of a molecule and lack a charge of the long tail of the molecule (made by fatty acids). When exposed to an aqueous solution the charged heads are attracted to the water phase and the non-polar tails are repelled from the water phase.

Phospholipids
When two layers of polar lipids come together to make a double layer, the outer hydrophilic face of every single layer will orient itself towards the solution, and the hydrophobic part will become immersed in the core of the bilayer.

Water acts as a solvent for polar molecules and the arrangement of phospholipids in the lipid bilayer of membranes is dependent on water.

Question 18.
Write short notes on
(i) Steroids
Answer:
Steroids: Steroids are complex compounds mostly found in animal hormones and cell membranes. The best example of steroids is cholesterol. The cell membrane of fungi contains ergosterol. The prostaglandins are fatty acid derivatives. They occur in minute amounts and function in blood clotting, smooth muscle contraction, and allergic reactions, etc.

(ii) Wax.
Answer:
Wax: Waxes are lipids. They are esters formed by the combination of a saturated long-chain fatty acid with long-chain alcohol. They play an important role in protection as tires form a water-proof covering over the root hairs and parts of the body in some organisms. Wax is soft and pliable. The paraffin is hard when cold. Fruits, feathers, leaves, the skin of man, and the exoskeleton of insects are waterproofed by the coating of wax. The bacteria causing TB and leprosy produce wax (Wax D.).

Question 19.
Describe the structure and function of ATP.
Answer:
ATP: It is a primary and universal carrier of chemical energy in the cell. Living cells capture, store and transport energy in a chemical form, largely as ATP and it is the ATP that is the carrier and intermediate source of chemical energy to those reactions in the cell which do not occur simultaneously.

These reactions can take place only if the chemical energy is released. It was Fritze Lipmann in 1941 who postulated this unifying concept and proposed the ATP cycle as given in the figure below.

Adenosine triphosphate

Question 20.
How are amino acids bonded together? Describe how these bonds are formed?
Answer:
Proteins are also formed from amino acids but they have small peptides. The two amino acids are linked by the formation of a peptide bond. Successive amino acids can be linked by peptide bonds to form a linear chain of many amino acids.

When a few amino acids are joined together, the molecule is called a peptide. Proteins are macromolecules formed from a large number of amino acids.

Peptide band

Question 21.
Draw the structure of amino acid.

(A) Acidic amino acid
Answer:
Amino acids: These are small molecules made of carbon, hydrogen, oxygen, and nitrogen, in certain cases sulfur is also found. Amino acids may be monocarboxylic or dicarboxylic acids bearing one or two amino groups.

The a-carbon is next to the carboxyl – C. The four valencies of the a-carbon of an amino acid hold respectively an amino (NH₂) group, a carboxyl (COOH) group, a hydrogen atom, and side-chain fig (B) which may be polar or non-polar.

A free amino group is basic, a free carboxyl group is acidic. Lysine and alanine are basic amino acids because they have two amino groups and one carboxyl group. Glutamic acid and aspartic acid contain one amino and two carboxyl groups each is classified as acidic amino acids.

Alanine, glycine, valine, and phenylalanine are neutral amino acids because these contain one carboxyl group. Two amino acids can be linked by the formation Of a bond called a peptide bond. With the help of peptide bonds, many amino acids form a linear chain of many amino acids.

(B) Non-polar-side chain

Question 22.
Describe the primary structure of the protein.
Answer:
Primary Structure of Protein: Proteins are made of amino acids which have carboxyl group (COOH) and amino (group) (-NH₂). The COOH end of an amino acid is joined to the -NH₂ end of the other amino acid. Many amino acids are joined by peptide bonds which held them together in a particular sequence and constitute the primary structure of proteins. The structure does not make a protein functional.

It is a linear sequence of amino acids.

Question 23.
Name different types of RNA.
Answer:
There are three types of RNA.

1. Messenger RNA (mRNA).
2. Ribosomal RNA (rRNA)
3. Transfer RNA (tRNA).

Question 24.
List the differences between DNA and RNA.
Answer:
Differences between DNA and RNA:

DNA	RNA
(1) It consists of double-helical two polynucleotide chains.	(1) It consists of only one helical of a single polynucleotide chain.
(2) Deoxyribose sugar is present in the nucleotides.	(2) Rihose sugar is present in the nucleotides.
(3) Pyrimidine bases are thymine and cytosine.	(3) Uracil base is present instead of thymine-Cytosine is the second pyrimidine base.
(4) DNA synthesizes RNA to regulate cell metabolism.	(4) RNA is synthesized by DNA and carries information from DNA to regulate cell metabolism.
(5) DNA from the main genetic material of eukaryotes.	(5) It is the genetic material of plant viruses.
(6) DNA occurs in one form only.	(6) It is the genetic material of plant viruses.
(7) It controls the transmission of hereditary characters.	(7) It controls the synthesis of proteins in the cell.

Question 25.
Distinguish between prosthetic group and co-factors.
Answer:
Differences between coenzyme, cofactor, and prosthetic groups:

Cofactor	Coenzyme	Prosthetic group
1. It is a non-protein substance or group that gets attached to an enzyme.	1. It is a non-protein group that is loosely attached to the open enzyme in a functional enzyme.	1. It is a non-protein part or group which gets attached to an open enzyme.
2. It is essential for functioning. It may be organic or inorganic or metallic co-factor	2. NAD is a coenzyme for dehydrogenases.	2. Some prosthetic groups have metals e.g. iron porphyrin of the cytochromes.

Question 26.
Explain the structure of an enzyme.
Answer:
Structure of an Enzyme: The enzymes are chemical substances. They catalyze the chemical reactions in the cells. They are secreted and synthesized by living cells. Most all the enzymes are proteinous in nature. Some enzymes contain a nonprotein part called the prosthetic group. Some p esthetic groups are metal compounds. NAD is a coenzyme. All enzymes have active sites.

1. the First carbon forms a part of the aldehyde group.	1. Second carbon forms a part of the keto group.
2. Aldoses are most commonly found in nature i.e. glucose, ribose.	2. Ketoses are less common in nature, e.g., ribulose, fructose.

Question 27.
Distinguish between Unsaturated fatty acids and Saturated fatty acid
Answer:

Unsaturated fatty acid	Saturated fatty acid
(i) Don’t have a double band between the carbon atoms.	(i) Have one or more double bonds.
(ii) High melting points	(ii) Low melting points
(iii) Can’t be synthesized in an animal body.	(iii) Can be synthesized in the animal body
(iv) Don’t cause cardiovascular diseases.	(iv) Can cause cardiovascular disease

Question 28.
Distinguish between aldose sugar and Ketose sugar
Answer:

Aldose sugar	Ketose sugar
(i) First carbon forms a part of the aldehyde group	(i) Second carbon forms a part of the Keto group
(ii) Commonly found in nature e.g. glucose, ribose.	(ii) Less common in nature, eg. ribulose, fructose.

Question 29.
Distinguish between Oil and Fat.
Answer:

Oils	Fats
1. Rich in unsaturated fats.	1. Rich in saturated fats.
2. Liquid at ordinary temperature.	2. Solid or semisolid at ordinary temperature.
3. Contains essential fatty acids.	3. Do not contain essential fatty acids.
4. Do not cause cardiovascular disorders e.g., vegetable oils.	4. Can cause cardio-vascular disorders e.g., Ghee, hydrogenated vegetable oils like Dalda.

Biomolecules Important Extra Questions Long Answer Type

Question 1.
Enlist the functions of small carbohydrates?
Answer:

1. Monosaccharides are formed during the photosynthetic pathway. They are stored in plants and are utilized by other living organisms depending on them.
2. Glucose is the blood sugar of many animals and on oxidation, it provides energy for all vital activities.
3. Nucleotides and nucleosides contain pentose sugar in the form of ribose and deoxyribose sugars. They form a part of nucleic acids.
4. Lactose of milk is formed from glucose and galactose and mammary glands of mammals.
5. Glucose is used for the synthesis of fats and amino acids.
6. Structural polysaccharides like cellulose and oligosaccharides are derived from mono-saccharides.
7. Food storage polysaccharides like starch and glycogen are derived from monosaccharides.

Question 2.
Enumerate the functions of Lipids.
Answer:

1. Lipids are storage products in plants as well as animals.
   (a) In plants, fats are stored in cotyledons or endosperm to provide nourishment to the developing embryo.
   (b) In animals fats are stored in adipocytes to be used whenever required by the body.
2. In animals, subcutaneous fats act as an insulation layer and shock \ absorber.
3. They form structural components of membranes, phospholipids, glycolipids, and sterols.
4. They take part in the synthesis of steroid hormones, vitamin D, and bile salts.
5. Act as a solvent for fat-soluble vitamins i.e., vitamin A, D, E, and K.
6. The neutral fats form a concentrated fuel producing more than twice as much energy per gram as do the carbohydrates. They thus, represent an economical food reserve in the body.
7. The wax lipids form a waterproof protective coating on animal furs, plant stem, leaves, and fruits.

Question 3.
How does water help in maintaining the constancy of the internal environment of an organism?
Answer:
Some substances, capable of neutralizing acids or bases, remain in solution in the cytoplasm as extracellular fluids, e.g., bicarbonate (HCO₃), carbonic acid, dibasic phosphate (HPO₄^-2). Acids and bases mix in the body fluids with these substances and are neutralized by them. Because of its solvent action water aids in keeping a constant pH.

Water also helps in maintaining constant body temperature by eliminating excess heat through the evaporation of sweat. Elimination of waste products through urine also helps in maintaining the constancy of the internal environment of an organism.

Question 4.
What are peroxisomes and phagosomes?
Answer:
Peroxisomes: These were for the first time observed in the kidney of rodents. They are found both in plants and animals. Their size varies from 0.5 to lp in diameter. They are delimited by a single membrane and contain a finely granular matrix. They often possess a central core called nucleoid which may consist of parallel tubules or twisted with strands. Peroxisomes are generally observed in close association with the endoplas¬mic reticulum.

Peroxisomes in different plant and animal cells differ con¬siderably in their enzymatic make-up, but they contain some peroxide-producing enzymes like urate, oxidase, D-amino acid oxidase, B-hydroxy acid oxidase, and catalase. Peroxisomes are somehow associated with some metabolic processes like photorespiration and lipid metabolism in animal cells.

Sphaerosomes: There are cell organelles bounded by a single membrane. They contain enzymes and are visible under the light microscope. These show some affinities for fat stains, including Sudan stain and sodium tetroxide.

These organelles originate from E.R. by budding. They contain enzymatic proteins which help in synthesizing oils and fats. Further devel¬opment of phagosomes takes place through an increase in the lipid content with a concomitant decrease in protein.

Question 5.
Enumerate the importance of Energy carriers.
Answer:
Energy carriers consist of nucleotides having one or two additional phosphate groups linked up at their phosphate end forming diphosphates and triphosphates. Linkage of additional phosphate groups occurs at the cost of a large amount of energy. This energy is provided by the oxidation of food mainly glucose and by photosynthesis.

Separation of the additional phosphate groups from the nucleotides by enzymatic hydrolysis releases a correspondingly large amount of energy.

Thus, ADP and ATP provide ready energy for biological activities.

The bonds joining the additional phosphate groups to the nucleotides are called high energy or energy-rich bonds, as they carry a great deal of energy. The nucleotides having more than one phosphate group are called higher nucleotides.

The energy of energy carriers, when set free is utilized for driving energy-dependent reactions in the cell and is biologically useful energy. ATP is the most common energy carrier in cells and is often called the energy currency of the cell.

Question 6.
Explain the functions of amino acids.
Answer:

1. Amino acids are the building blocks for proteins.
2. The amino acid Tyrosine takes part in the formation of the skin pigment melanin as well as hormones thyroxine and adrenaline.
3. Glycine is important for the formation of heme.
4. Tryptophan takes part in the formation of the vitamin nicotinamide.
5. In plants, tryptophan forms the growth hormone indole-3- acetic acid.
6. Amino acids are converted into glucose by deamination.
7. Histamine and other biogenic amines are formed by the removal of carboxyl groups from amino acids.

Question 7.
Give reasons for following
(i) Salts dissolve in water but oil does not
Answer:
Water molecules are hydrogen-bonded to form short-lived macromolecular aggregates. To dissolve in water, a solute molecule must form hydrogen bonds with water molecules. Salts are polar compounds, their hydrophilic polar groups form hydrogen bonds with water molecules. So they dissolve oils having hydrophobic non-polar groups that cannot join the lattice structure of water. Thus non-polar molecules of oil do not dissolve in water.

(ii) Amino acid can be basic
Answer:
A free amino group is basic and a free carboxyl group is acidic. Amino acids can be basic because they may carry two amino groups and one carboxyl group e.g., Arginine. One free amino group causes amino acids to be basic.

(iii) Phospholipids form a thin layer on the surface of an aqueous medium.
Answer:
Phospholipids form a thin layer on the surface of an aqueous medium due to the simultaneous presence of both polar and non-polar groups in the molecule. As a result, the phospholipid molecules may arrange themselves in a double-layered membrane in aqueous media.

Question 8.
Illustrate lock and key hypothesis of enzyme action?
Answer:
Mechanism of Enzyme action: The working of enzymes is a complex one. All enzymes first of all combine with the reactions they catalyze. In other words, enzymes with substrates form an intermediate complex before decomposition of the substrate can occur.

This two-way reaction can be represented as follows.
1st step: Enzyme substrate complex = Enzyme + Product.
Formation of the enzyme-substrate complex during enzyme action.

From the above, it is clear that the enzymes must combine first with substrate molecules in order to act. In order to explain the mode of action of an enzyme. Fischer proposed a lock and key theory. According to him if the right key fits in the right lock. The lock can be opened, otherwise not.

Model of enzyme activity

To explain the above in context with the enzyme action it is believed that molecules have specific configurations into which other molecules can fit. The molecules which are acted upon by the enzymes are called substrates of the enzymes. Under the above assumption, only those substrate molecules with the proper geometric shape can fit into the active site of the enzymes.

If this happens, the above molecules may compete with the substrate, and the reaction may either slow down or stop. Substances are called competitive inhibitors because they act to prevent the production of a substance.

An induced-fit model of enzyme action was given by Koshland (1959). Buttressing and catalytic are two groups of the active site of the enzyme. Their site when the substrate attaches to its bonds is broken.

Question 9.
What is the structure of DNA?
Answer:
The nucleic acids are among the largest of all molecules found in living beings. They contain three types of molecules (a) 5 carbon sugar, (b) Phosphoric acid (usually called phosphates when in chemical combi¬nation), and nitrogen-containing bases (Purines and Pyrimidines). The three join together to form a nucleotide i.e., sugar+ base + phosphate = Nucleotide. Only a few nucleotides are possible. They differ only in the kind of purines or pyrimidine (nitrogen-containing bases).

In 1953 J.D. Watson and F.H.C. Crick working in Cambridge Uni¬versity, England prepared a model of DNA molecule elucidating the struc¬ture of DNA molecule. They were awarded the Nobel Prize for this outstanding work.

Structure of DNA

Watson and Crick model of DNA: According to Watson and Crick, the DNA molecule consisted of two strands twisted around each other in the form of a helix. Each strand is made of polynucleotides, each polynucleotide consisting of many nucleotides which remain united with its complimentary’ chain with the help of bases.

Adenine always unites with thymine and cytosine with guanine. It means that one polynucleotide chain of DNA molecule is complementary to the other.

The distance between two chains of the helix is about 20 A and the helix turns over every 34 A. Each mm of the chain consists of about 10 nucleotides.

Structure of DNA

Question 10.
How does the substrate concentration affect the velocity of enzyme reaction?
Answer:
Michaelis constant or more appropriately Michaelis-Menten constant (Km) is a mathematical derivation given by Leonor Michaelis and Monde Menten in 1913 with the help of which velocity of reaction can be calculated for any substrate concentration.

Effect of substrate concentration on enzyme action

Km or Michaelis constant is the substrate concentration at which the chemical reaction attains half its maximum velocity. The constant is an inverse measure of the affinity of an enzyme for its substrate, that is the smaller the Km the greater the substrate affinity and vice versa. The value usually lies between 10⁴ – 10⁵ M

Follow For More:

NATIONALUM Pivot Point Calculator

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 1 Physical World. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 1 Important Extra Questions Physical World

Physical World Important Extra Questions Very Short Answer Type

Question 1.
Name that branch of science that deals with the study of Earth.
Answer:
Geology.

Question 2.
Name that branch of science that deals with the study of stars.
Answer:
Astronomy.

Question 3.
Name the scientist and the country of his origin whose field of work was elasticity.
Answer:
Robert Hook, England.

Question 4.
The word “Physics” comes from a Greek word. Name the word.
Answer:
The word is ‘fuses meaning ‘Nature’.

Question 5.
The word science has come from a Latin verb. Name the verb.
Answer:
The name of the Latin verb is ‘Scientia’.

Question 6.
What is the meaning of the verb ‘Scientia’?
Answer:
To ‘know’

Question 7.
Name the scientist and the country of his origin who received the Nobel Prize for his work on molecular spectra.
Answer:
C.V. Raman, India.

Question 8.
What is the most incomprehensible thing about the world?
Answer:
It is comprehensible.

Question 9.
Name a great scientist who gave the following comment on science.
“Science is not just a collection of laws, a catalog of unrelated facts. It is a creation of the human mind, with its freely invented ideas and concepts.”
Answer:
Albert Einstein.

Question 10.
Which famous philosopher gave the following comments on science?
“We know very little and yet it is astonishing that we know so much, and still more astonishing that so little knowledge of science can give so much power.”
Answer:
Bertrand Russel.

Question 11.
Who discovered the electron?
Answer:
J.J. Thomson.

Question 12.
Who discovered neutron?
Answer:
James Chadwick.

Question 13.
Who gave the general theory of relativity?
Answer:
Albert Einstein.

Question 14.
Who proposed the wave theory of light?
Answer:
Huygen.

Question 15.
Name four physics devices widely used in medical diagnosis.
Answer:

1. X-rays,
2. Ultrasound,
3. Stethoscope,
4. Microscope.

Question 16.
Name Indian-born scientist who received Nobel Prize for his discoveries in astronomy.
Answer:
S. Chandra Shekhar.

Question 17.
Metaphysics is a science that is concerned with what?
Answer:
Supernatural .events.

Question 18.
Which science is considered to be the mother of all sciences?
Answer:
Physics.

Question 19.
Name the discovery made by S.N. Bose.
Answer:
Bose-Einstein Statistics.

Question 20.
Name the scientist and the country of his origin whose field of work was ‘cosmic rays’.
Answer:
Hess, Austria.

Question 21.
What are the meaning of the Sanskrit word ‘Vijnan’ and the Arabic word ‘Ilm’?
Answer:
Knowledge.

Question 22.
Name the Sanskrit equivalent word of Physics.
Answer:
Bhautiki.

Question 23.
Name the field of Physics in which India was a leading country in the sixties.
Answer:
Cosmic rays.

Question 24.
Who discovered X-rays?
Answer:
W. Roentgen.

Question 25.
Which electronic media can help in eradicating illiteracy in India?
Answer:
Television.

Question 26.
Name the technology based on the amplification of light by population inversion?
Answer:
Laser.

Question 27.
Who discovered nuclear forces?
Answer:
H. Yukawa.

Question 28.
To which country he belonged?
Answer:
japan.

Question 29.
Who discovered Radium?
Answer:
Pierre Curie and Marie Curie.

Question 30.
Name the discovery made by W. Roentgen.
Answer:
X-rays.

Question 31.
What has been said by P.A.M. Dirac regarding physics in relation to society?
Answer:
P.A.M. Dirac said, “It is more important to have beauty in the equations of physics than to have them agree with experiments.”

Question 32.
What did Issac Newton say to measure the degree of impact of science on society?
Answer:
He said “Nature is pleased with simplicity, and affects not the pomp of superfluous causes.

Question 33.
What Neils Bohr said regarding science in relation to society?
Answer:
He said “The task of science is both to extend the range of our experience and to reduce it to order.

Question 34.
Name a few Indian physicists who have made significant contributions in the field of physics.
Answer:
C.V. Raifiaq, S. Chandra Shekhar, S.N. Bose, Homi J. Bhabha, and Meghnath Saha.

Question 35.
Name the scientific principle on which airplane works.
Answer:
Bernoulli’s theorem.

Question 36.
Name the scientific principle on which radio and T.V. works.
Answer:
Propagation of electromagnetic waves.

Question 37.
Name the scientific principle upon which laser works.
Answer:
Amplification by a process called population inversion.

Question 38.
Name the technology which works on the scientific principle “Newton’s second and third laws of motion”.
Answer:
Rocket propulsion.

Question 39.
Name the forces which are of nuclear origin.
Answer:
Strong forces.

Question 40.
What is Physics?
Answer:
It is that branch of science which deals with nature and natural phenomena.
Or
It is that branch of physical science that is to seek out and understands the basic laws of nature upon which all physical phenomena depend. It has brought to us deeper and deeper levels of understanding nature.

Question 41.
What is Science?
Answer:
It is defined as the systematic study of physical phenomena.

Question 42.
What are Biological Sciences? Give three examples.
Answer:
Those sciences which deal with living things are called Biological Sciences, e.g. Zoology, Botany, Ornithology.

Question 43.
What are Physical Sciences? Give a few examples.
Answer:
They ate defined as the sciences which deal with non-living things,
e.g. Physics, Chemistry, Astronomy, Astrology, Geology, Geography, Oceanology.

Question 44.
Define Theory.
Answer:
It is defined as the behavior of physical systems explained in terms of a set of a minimum number of laws.

Question 45.
What do you understand by the term scientific method?
Answer:
The systematic observations, logical reasoning, model-making, and theoretical prediction form the scientific method.

Question 46.
Name the scientific principle on which electric generator works.
Answer:
Electromagnetic induction (E.M.I.).

Question 47.
Name the technology which works on the scientific principle ‘Nuclear Fission’.
Answer:
Nuclear Reactor.

Question 48.
Name the technology which works on the scientific principle “Digital logic of electronic circuits”.
Answer:
Calculators and computers.

Question 49.
Name the scientific principle upon which the working of cyclotron defends.
Answer:
The motion of charged particles under electric and magnetic fields.

Question 50.
Name the. scientist and his country who discovered wireless1 telegraphy.
Answer:
G. Marconi, Italy.

Read More:

ICICIPRULI Pivot Point Calculator

Physical World Important Extra Questions Short Answer Type

Question 1.
Differentiate between Biological and Physical sciences?
Answer:

Biological Sciences	Physical Sciences
(i) They deal with living things.	(i) They deal with non-living things.
(ii) The study of the biological specimens is conducted at the molecular level.	(ii) The study of matter is conducted at atomic or ionic levels i.e. at much smaller levels.

Question 2.
What is the relation between Physics and Technology?
Answer:
Broadly speaking, physics and technology both constitute science. Physics is the heart and technology is the body of science.

The application of the principles of physics for practical purposes becomes technology, e.g.

1. Airplanes fly on the basis of Bernoulli’s theorem.
2. Rockets propulsion is based on Newton’s second and third laws of motion.
3. The generation of pow%r from the nuclear reactor is based on the phenomenon of controlled nuclear fission.
4. Lasers are based on the population inversion of electrons and so on. Thus, we can say that to some extent technology is applied to Physics.

Question 3.
What is the relation between Physics and society?
Answer:
Most of the development made in Physics has a direct impact on society, e.g.

1. Exploration of new sources of energy is of great importance to society.
2. Rapid means of transport are no less important for society.
3. society has-been enriched due to the advances in electronics, lasers, and computers.
4. The development of T.V., radio, satellites, telephone, the telegraph has revolutionized the means of communications which have a direct impact on society and so on.

Question 4.
Is Science on speaking terms with humanities?
Answer:
Yes, there is a deep relation between the development of humanity on account of science. Many socio-economic, political, and ethical problems are being tackled and solved by science. Science has greatly helped in developing art and culture. Many musical instruments have been developed due to the theories in Physics. The steam engine is inseparable from the industrial revolution which had a great impact on human civilization.

Question 5.
What is the relation between Physics and Technology?
Answer:
The interplay between physics and technology is the basic to the progress of science which is ever dynamic. Laws in waves and oscillation opened several technological fields which include telescopy, ultrasounds, microscopy, X-rays, and laser. Powerhouses, big cranes, healing devices, etc. work on the principle of electromagnetism. Atomic energy and nuclear weapons are on account of fission. Similarly, Radar, television, the internet, etc. are all based on simple laws of physics. So until there is no theory i.e. physics, there can be no experiment i.e. technology. Hence both are deeply related.

Question 6.
Is Physics more of a philosophy or more of a mathematical science?
Answer:
Physics is not a purely abstract science devoid of philosophy. Physicists are natural philosophers and Einstein is an example to quote. So Philosophy has provided the backbone to Physics.

Question 7.
Define Biophysics.
Answer:
It is defined as the understanding of biological processes based upon the principles of Physics. For example, spectroscopic techniques are used to study the constitution of biological molecules and disorders in them. Laws of thermodynamics are used to explain various biological activities of predators and also the activities of molecules.

Hence the application of Physics to bioscience is now well known to all of us.

Question 8.
Define Technology?
Answer:
It is defined as the study of newer techniques of producing machines, gadgets, etc. by using scientific discoveries and advancements. It is largely dependent on Physics.

Question 9.
Has imagination any role in Physics?
Answer:
One of the definitions of Physics says that “It is the science-based on imagination and intuition which can be tested experimentally and mathematically.” Thus, imagination has a great role in the development of physics. Schrodinger, De-Broglie, Heisenberg, and most of the other scientists who were physicists were great imaginers.

Question 10.
Name a few aspects of your daily life in which you rely on the simplicity of nature.
Answer:
Laws of Physics represent the nature in simplest form. We face nature in many ways in our daily life. For example, we work, walk, write, talk and stand on our feet, and so on. The natural way of taking bath, chewing food, etc. can easily be understood in terms of simple laws of science. Even though actions like swimming, running, and playing may be complex but the underlying laws of nature are quite simple such as Newton’s laws, friction, etc.

Question 11.
The physicists think at a level far higher than a normal individual. Explain.
Answer:
For everyone to become a leader in his field, he has to think for a higher level than an ordinary person. This is more so for the case of physicists as the technological development meant for uplifting the living condition of mankind is highly dependent on the farsightedness of the physicists in particular. He must think at a level that is philosophical and mathematically quantifying so that they can visualize the requirement of people is quite advance.

Question 12.
Name a few wartime and maritime applications of Physics.
Answer:
(a) Wartime: The wartime applications are Bombs, nuclear weapons, jet fighter bombers, missiles, ships, radar, sonar, wireless communications, transportation, and electronics.

(b) Maritime: The maritime application of physics is Navigation of ships, tankers, airplanes, T.V., radio, and music system, etc.

Question 13.
Name five Indian scientists and the field of their work.
Answer:
Following are the five Indian Scientists and the field of their work:

Name	Field of work
(1) C.V. Raman	Raman effect (Scattering of light by molecules)
(2) S. Chandrashekar	Theory of Black Hole (i.e. structure and evolution of stars)
(3) J.C. Bose	E. M. Waves
(4) S.N. Bose	Bose-Einstein statistics
(5) H.J. Bhabha	Cosmic rays

Question 14.
Who invented:
(i) Computer
Answer:
Charles Babbage

(ii) Transistor,
Answer:
J. Bardeen

(iii) Electric bulb and Telegraphy,
Answer:
A. Edison

(iv) Radar,
Answer:
Appleton

(v) Wireless telegraphy,
Answer:
Marconi

(vi) Telephone.
Answer:
Graham Bell.

Question 15.
Name the theories given by the following:
(i) Neil Bohr
Answer:
Theory of atomic structure

(ii) Lawrence,
Answer:
Cyclotron

(iii) Henry Becquerel,
Answer:
Natural radioactivity

(iv) Galileo,
Answer:
Principle of Inertia

(v) Bragg,
Answer:
Crystal structure by X- rays

(vi) Abdus Salam,
Answer:
Unified Field Theory

(vii) Millikan.
Answer:
Charge on an electron.

Question 16.
Give the nationality of the following scientists:
(i) Van der Waals,
Answer:
Dutch

(ii) Curie,
Answer:
French

(iii) Yukawa,
Answer:
Japanese

(iv) Galileo,
Answer:
Italian

(v) Michelson,
Answer:
U.S.A. (American)

(vi) Heisenberg,
Answer:
German

(vii) Archimedes,
Answer:
Greek

(viii) Maxwell,
Answer:
Scottish

(ix) Cavendish,
Answer:
English

(x) Hubble.
Answer:
Austrian.

Question 17.
List the Various gadgets you use in your house.
Answer:
The following are the gadgets commonly used in our house:

1. Pressure Cooker
2. Electric light
3. Tube light
4. Electric fan
5. Water cooler
6. Refrigerator
7. Washing machine
8. Gas stove
9. Electric iron
10. Mixi
11. Geyser
12. Electric motor.

Question 18.
Write the physical principle upon which the working of the gadgets mentioned in the above question is based.
Answer:
These are based on the following physical principles:

1. The boiling point rises with the increase in pressure.
2. Light is produced when the current is passed through a given resistor.
3. Light is emitted when an electric discharge is passed through the gas.
4. A rotating magnetic field is produced on passing current which notates the motor.
5. Due to evaporation of water, cooling in the air which is being forced out by the fan is produced.
6. On absorbing heat from the surroundings, compressed volatile liquid on sudden expansion causes cooling.
7. Current produces a rotating magnetic field that operates the motor.
8. Heat is produced due to the burning of L.P.G.
9. It works on the principle of heating effect of electric current.
10. Torque is produced on the coil due to the electric current passed through it, hence it rotates.
11. Current shows the heating effect when passed through the conductor.
12. It rotates due to the torque produced on the coil on passing an electric current through it.

Question 19.
Name one Scientist each from the following countries who have won Nobel Prize.
(a) Japan
Answer:
H. Yukawa

(b) England
Answer:
Janies Chadwick

(c) India
Answer:
C.V. Raman

(d) The U.S.A.
Answer:
K. Feynman

(e) Germany.
Answer:
Max. Plank.

Question 20.
How Darwin showed that scientific themes are at once simple even though phenomena in nature may be complex.
Answer:
Darwin found a simple basis for the origin of species and descent of man which is “Living things change producing descendants with different characteristics in a process that has been going on for as long as there has been life” by taking a large number of observations on the theory of evolution while onboard ship.

Question 21.
Illustrate by an example the beauty of a Scientific Theory.
Answer:
The theory proposed by Darwin was opposed by the church and now we have new discoveries such as selfish genes and punctuated equilibria but Darwin’s basic theory still holds. This is the beauty of Davin’s theory of evolution.

Question 22.
In science sometimes we observed certain phenomena experimentally but are unable to give a logical equation or theory for that sometimes, it also happens that we have a scientific theory supported by’ mathematical formulation yet are unable to test it immediately. Site one such example.
Answer:
Einstein worked to establish a relation between the energy and mass of the body. He was of the view that these are the two sides of the same coin or two facts of the same physical quantity. He succeeded when he gave his mass-energy equation E = mc². But its experimental verification came 40 years later in 1945 when the atomic bomb was exploded over Japan.

Question 23.
Why do we call physics an exact science? What is the aim of science?
Answer:
Physics is called exact science because it is based on the measurement of fundamental quantities.
The main aim of science is to find the truth behind the various processes taking place in the universe.

Question 24.
How science has helped in solving the food problem in several countries?
Answer:
Science has helped in solving food problem in the following ways:
(a) It has given improved and new agricultural implements.
(b) Science has improved the quality of seeds by genetic engineering.
(c) High-yielding hybrid varieties of grains have been developed. Some easily reaping varieties have also been developed and grown.
(d) Use of pesticides and insecticides has saved crops from being destroyed by insects and pests.
(e) Some new types of crops are also developed and are being developed to meet the requirement of society.

Question 25.
What is a scientific temperament and scientific way of doing things?
Answer:
A mindset molded in a particular set of thinking called the scientific way is known as scientific temperament. It is not only based on logic, facts but on reliable observations. The ultimate test of truth in science is experimental verification.

A scientific way of doing things involves the following steps:
(a) Identifying the problem or aim.
(b) Collecting all relevant information or data related to the problem.
(c) Hypothesising or proposing a possible theory.
(d) Taking experimental observation yielding consistent results.
(e) Predicting or making statements.

Question 26.
What is the scope of Physics?
Answer:
The scope of Physics is very wide i.e. the domain of Physics covers a very wide variety of natural phenomena.

For example, the range of distances we study in Physics varies from 10¹⁴ m (size of the nucleus) to 10²⁵ m (size of the universe).

Similarly, the range of masses included in the study of Physics varies from 10^-30 kg (mass of an electron) to 10⁵⁵ kg (mass of the universe). Also, the range of time i.e. time intervals of events we come across in the study of Physics varies from 10²² seconds (time taken by light to cross a nuclear distance) to 10^-8 seconds (lifetime of the sun).

Thus we see that the scope of Physics is really very wide. It includes; optics, electricity waves, and oscillations, heat and thermodynamics, magnetism, atomic and nuclear physics, computers, and electronics.

Question 27.
Physics is an exciting subject! Comment.
Answer:
The study of Physics is exciting in many ways, e g.:

1. Journey to the moon with controls from the grounds.
2. Lasers and their ever-increasing applications.
3. Live transmission of events thousands of kilometers away on the T: V.
4. The speed and memory of the fifth generation of computers.
5. Study of various types of forces in nature.
6. Technological advances in health science.
7. The use of robots is quite exciting.
8. Telephone calls over long distances and so on. Thus, Physics is exciting not only to the scientist but also to a layman, children, women, etc. The musical instruments, toy guns, toy trains, etc. all are constructed using simple principles of physics like collision, potential energy, and vibration, etc. Today the situation is that even our thought process and social values are affected by Physics. Thus, it is quite amazing.

Question 28.
Write a short note on the origin and development of Physics.
Answer:
Physics as a science took roots from the days of Copernicus, i. e., nearly four centuries ago when it was not well understood and it was considered as a part of philosophy, i.e., knowledge. Later on, with the development of knowledge about nature and its various activities, the knowledge was divided into physical and biological sciences.

Some important developments like Newton’s law of gravitation, ideas about light were developed in the 18th century. The 19th century saw some of the great discoveries in Physics and at the end f the century i.e. 1889, the electromagnetic theory was developed, Fouriuatun of Einstein’s and Plank’s ideas were laid down apart from laying the basis for the industrial revolution. Physics progressed very fast in the first quarter of the 20th century.

Atomic structure, the theory of relativity, quantum theory, nuclear physics, basics of laser theory and most of the other developments took place in this period. Then came transistors, semiconductors, television, radar, and few important discoveries during World War II.

Further development in quantum mechanics, thin-film technology, computers, lasers was developed from 1950 onward. Today we have no theoretical development beyond quantum mechanics. A unified theory is not being tried yet. This is the present status with achievements in applied fields.

Question 29.
Explain the role of science in the entertainment industry.
Answer:
Progress in science especially in physics and technology has enriched no other field as the field of entertainment. We see scientific toys like robots for children and merry-go-rounds of all sorts in amusement and entertainment parks which are not only highly entertaining but also test the endurance of an individual.

These are based on the laws of forces and the critical stages are those when a man is pitted against gravity. T.V. has invaded a large number of houses as a source of entertainment and so are the music blaring CD players. Computers have become another source of individual indoor entertainment. The use of laser beams in music and drama shows and disco dances is highly rewarding.

With the improvement in physics and technology, circus entertainment to have changed with the application of science. Thus, we conclude that the role of science and technology in the entertainment industry has increased tremendously.

Question 30.
Give some of the uses and applications of artificial satellites.
Answer:
The following are the fields where satellites are being used –
(a) Remote sensing
(b) Communication
(c) Spying
(d) Weather forecasting

(a) Remote sensing: In remote sensing, infrared photography s used from a high altitude. The technique has improved a lot and the resolution has gone down to about 5m in an area. This technique has helped in mineral and oil exploration. It has also helped in the study of forest living and crop patterns.

(b) Communication: In the field of communication, satellites have brought revolution during the last 20 years. Now new items are flashed all around the globe. Cricket matches can be seen anywhere on the globe which is played in one small part of a country. Internet, E-mail, etc. have brought people much more closer and the world has become a unified entity.

(c) Spying: In spying also use IR technology.

(d) Weather forecasting: Weather forecasting has become more reliable with the use of satellites. The rains, cyclones can now be predicted with greater accuracy 36 hours in advance or even earlier. The movement of glaciers, the position of ice and snow deposition, and the resulting flow of water in rivers is known well in advance.

Physical World Important Extra Questions Long Answer Type

Question 1.
How Physics is related to other sciences?
Answer:
Physics is so important to a branch of science that without the knowledge of Physics, other branches of science cannot make any progress.

This can be seen from the following:
(a) Physics in relation to Mathematics: The theories and concepts of Physics lead to the development of various mathematical tools like differential equations, equations of motion, etc.

(b) Physics in n .ation to Chemistry: The concept of iñteraction between various particles leads to understanding the bonding and the chemical structure of a substance. The concept of X-ray diffraction and radioactivity has helped to distinguish between the various solids and to modify the periodic table.

(c) Physics in relation to Biology: The concept of pressure and its measurement has helped us to know the blood pressure of a human being, which in turn is helpful to know the working of the heart. The discovery of X-rays has made it possible to diagnose the various diseases in the body and fracture in bones.

The optical and electron microscopes are helpful in the studies of various organisms. Skin diseases and cancer can be cured with the help of high-energy radiation like x-rays, ultraviolet rays.

(d) Physics in relation to Geology: The internal structure of various rocks can be known with the study of the crystal structure. The age of rocks and fossils can be known easily with the help of radioactivity i.e. with the help of carbon dating.

(e) Physics in relation to Astronomy: Optical telescope has made it possible to study the motion of various planets and satellites in our solar system.

The radio telescope has helped to study the structure of our galaxy and to discover pulsars and quasars (heavenly bodies having star-like structures). Pulsars are rapidly rotating neutron stars. Doppler’s effect predicted the expansion of the universe. Kepler’s laws are responsible to understand the nature of the orbits of the planets around the sun.

(f) Physics in the relation to Meteorology: The variation of pressure with temperature leads to the forecast of the weather.

(g) Physics in relation to Seismology: The movement of the earth’s crust and the types of waves produced help us in studying the earthquake and its effect.

Question 2.
Write a short note on origin and Fundamental forces in nature.
Answer:
These are the following four basic forces in nature:
(a) Gravitational forces
(b) Electromagnetic forces
(c) Weak forces
(d) Strong force or nuclear forces.

Some of the important features of these forces are discussed below:
(a) Gravitational forces: These are the forces of attraction between any two bodies in the universe due to their masses separated by a definite distance. These are governed by Newton’s law of gravitation given by
F = G \(\frac{m_{1} m_{2}}{r^{2}}\)

where m₁, m₂ are the masses of two bodies
r = distance between them
G = universal gravitational constant
= 6.67 × 10^-11 Nm²kg^-2

Characteristics of gravitational forces:

1. They are always attractive. They are never repulsive. They exist between macroscopic as well as microscopic bodies.
2. They are the weakest forces in nature.
3. They are central forces in nature i.e. they set along the line joining the centers of two bodies.
4. They are conservative forces.
5. They obey inverse square law i.e. F ∝\(\frac{1}{r^{2}}\) they vary inversely as the square of the distance between the two bodies.
6. They are long-range forces i.e. gravitational forces between any two bodies exist even when their distance of separation is quite large.
7. The field particles of gravitational forces are called gravitons. The concept of the exchange of field particles between two bodies explains how the two bodies interact from a distance.

(b) Electromagnetic forces: They include the electrostatic and magnetic forces. The electrostatic forces are the forces between two static charges while magnetic forces are the forces between two magnetic poles. The moving charges give rise to the magnetic force. The combined action of these forces is called electromagnetic forces.

Characteristics of electromagnetic forces:

1. These forces are both attractive as well as repulsive.
2. They are central forces in nature.
3. They obey inverse square law.
4. They are conservative forces in nature.
5. These forces are due to the exchange of particles known as photons which carry no charge and have zero rest mass.
6. They are 10³⁶ times stronger as compared to gravitational forces and 10¹¹ times stronger than weak forces.

(c) Strong forces: They are the forces of nuclear origin. The particles inside the nucleus are charged particles (protons) and neutral particles (neutrons) which are bonded to each other by a strong interaction called nuclear force or strong force. Hence they may be defined as the forces binding the nucleons (protons and neutrons) together in a nucleus. They are responsible for the stability of the atomic nucleus.

They are of three types:

1. n-n forces are the forces of attraction between two neutrons.
2. p-p forces are the forces of attraction between two protons.
3. n-p forces are the forces of attraction between a proton and a neutron.

Characteristics of Nuclear forces:

1. They are basically attractive in nature and become repulsive when the distance between nucleons is less than O.S fermi.
2. They obey inverse square law.
   (a) and
   (b) types are the forces that we encounter in the macroscopic world while
   (c) and
   (d) types are the forces that we encountered in the microscopic world.

(c) Weak forces: They are defined as the interactions which take, place between elementary particles during radioactive decay of a radioactive substance. In P-decay, the nucleus changes into a proton, an electron, and a particle called anti-neutrino (which is uncharged). The interaction between the electron and the anti-neutrino is known as weak interaction or weak force.

Characteristics of Weak forces:

• They are 1025 times stronger than the gravitational forces.
• They exist between leptons and leptons, leptons and mesons. etc.

Question 3.
Distinguish between the studies in the fields of science, engineering, and technology. Give an outline of the two or three industrial revolutions brought about by advancements in technology over the last twenty-five years or so.
Answer:
Science is concerned with the unfolding of the basic aspects of nature. It formulates simple laws and finds the rhythm in nature, materials, and energy. Using basic principles of science, the ways to use them for the production of different kinds of articles is called technology, i.e., it is the application of science.

The execution of the application of technology in engineering. The production of articles using machines and implements in engineering. This involves the design, development, and manufacturing of articles.

The most notable technology development in the last 25 years is in the field of information technology, computers, and electronic media. The revolution in information technology has opened up fields on the internet, satellite linking of information systems and services other peripheral developments in the industry.

Computers have changed the face of society and made life easy in several fields. It has improved work efficiency in many segments of the industry and public life. Computers have touched the lives of children playing video games and adults alike. It has helped big organizations like railways, banks, and financial institutions like the insurance sector.

India has become one of the biggest centers of software exports and a big foreign exchange earner. Advance scientific research and industrial designing are being done by computers. TV has entered most Indian houses and community centers-courtesy revolution in electronic media.

The younger generation is mad after the stereo music with CD facilities. The transistors and tape recorders are left far behind. Electronic media has changed the face of the entertainment industry as well as information dissemination. Quick transmission of news, views, and comments are accepted as natural ones by listeners and viewers.

Value-Based Type:

Question 1.
A debate was organized by a school on woman’s innate nature, capacity, and intelligence. The arguments given by the two groups were as under:
Team A: Nature makes little difference in men and women in their anatomy and feeling. So, women are not on par with men. Hence, she is inferior to men in spheres of activity like sports, scaling of mountains like the Himalayas, etc.
Team B: The students of team ‘B’ have demolished this view using scientific arguments, and by quoting examples of great women, in science and other spheres; and persuade yourself and others that, give equal opportunity, women are on par with men.
Now, Answer these questions:
(i) Which values are displayed by team ‘B’?
Answer:
The values displayed by team B are:
(a) Gender equality.
(b) Justice and support to women.
(c) Equal opportunities to women.

(ii) Do you think team B was correct? Give proper justification with examples.
Answer:
Yes, there is no difference in the capacity of women and men as far as working capacity, intelligence, decision making is concerned. It is a biological fact that the development of the human brain does not depend upon sex but on nutrition contents and heredity. If equal opportunities are afforded to both men and women, then the female mind will be as efficient as the male mind.

The list of successful women from various fields is as under Kalpana Chawala, Madame Curie, Indira Gandhi, Mother Teresa, Margaret Thatcher, etc.

Question 2.
Two friends of class XI Mohan and Raghav were discussing the role of physics in society. Mohan Said to Raghav that physics does not have any impact on our society. Since he was a student of Arts Stream. But Mohan who is a science student explained that physics and Society are directly linked because whatever is discovered in physics, it immediately affects society.

The latest technology has played an important role in the fields of communication such as radios, computers, TVs, mobile phones and connects the people with each other. Nuclear energy has brought a profound change in the thinking and living style of human beings.
(i) Which values are displayed here by Mohan?
Answer:
The values displayed by Mohan are :
(a) Intelligence
(b) Awareness
(c) Logical

(ii) Give some discoveries which have really affected society more.
Answer:
(a) Theory of relativity
(b) X-ray
(c) Radioactivity
(d) Photoelectric effect
(e) Steam engine (based on laws of thermodynamics)
(f) Computer (Based on Digital logic)
(g) Super Conductivity
(h) Radio and TVs.

Question 3.
India has had a long and unbroken tradition of great Scholarship in mathematic, astronomy, linguistics, logic, and ethics. Yet, in parallel with this, several superstitious and obscurantist attitudes and practices flourished in our society and unfortunately continue even today-among many educated people too.

A student of Class XI gave an idea to overcome this evil of our society by using scientific explanations through mass media, radio television, and newspapers.
(i) Which values are displayed by the student?
Answer:
(a) Awareness
(b) Scientific and logical ideas
(c) Concern for the upliftment of our society to eradicate the evils of society.
(d) Intelligence, Sharp mind.

(ii) How will you use your knowledge of science to develop strategies to counter these attitudes?
Solution:
Educating the common man is the only way to get rid of superstitions and obscurantist attitudes. The mass media like newspapers, magazines, radio, television, etc. Can play a vital role. School and college curriculum can be suitably developed so that there is an emphasis on these topics. Teachers can play an important role to organize the seminar and motivate them.

Question 4.
A seminar was organized to know the views of students on whether the particular application is good, bad or something that cannot be so clearly categorized:
(a) Prenatal sex determination.
(b) Development of nuclear weapons.
(c) Mass vaccination
(d) Cloning
(e) Purification of water for drinking.

Now, answers these questions:
(i) Which values arc depicted here?
Answer:
To create awareness through group activities, to develop problem-solving ability, scientific knowledge can be put to good or bad use, depending on the user.

(ii) Do you think such type of group activities are important in day-to-day life?
Answer:
Yes.

(iii) Give justification for each of the above topics from (a-e):
Answer:
(a) Bad, it leads to the practice of abortion in the case of the female fetus.
(b) Bad, because nuclear weapons may cause mass destruc¬tion of mankind.
(c) Good, because it helped to eradicate the disease.
(d) Bad, because it can destroy the normal family life.
(e) Good, because it will help to improve good health of the citizens.

Check Out:

GLENMARK Pivot Point Calculator

Studying from CBSE Class 11th Maths Revision Notes helps students to prepare for the exam in a well-structured and organised way. Making Class 11 Maths NCERT Notes saves students time during revision as they don’t have to go through the entire textbook. In CBSE Notes, students find the summary of the complete chapters in a short and concise way. Students can refer to the NCERT Solutions for Class 11 Maths, to get the answers to the exercise questions.

Class 11th Maths NCERT Notes | Maths Notes Class 11

Notes of Maths Class 11

1. Sets Class 11 Notes
2. Relations and Functions Class 11 Notes
3. Trigonometric Functions Class 11 Notes
4. Principle of Mathematical Induction Class 11 Notes
5. Complex Numbers and Quadratic Equations Class 11 Notes
6. Linear Inequalities Class 11 Notes
7. Transformations and Combinations Class 11 Notes
8. Binomial Theorem Class 11 Notes
9. Sequences and Series Class 11 Notes
10. Straight lines Class 11 Notes
11. Conic Sections Class 11 Notes
12. Introduction to three Dimensional Geometry Class 11 Notes
13. Limits and Derivatives Class 11 Notes
14. Mathematical Reasoning Class 11 Notes
15. Statistics Class 11 Notes
16. Probability Class 11 Notes

We hope students have found these Maths Notes for Class 11 NCERT useful for their studies. If you have any queries related to Maths Class 11 Notes, drop your questions below in the comment box.

Important Questions for Class 11 Maths Chapter Wise with Solutions 2020-2021: Here we are providing CBSE Important Extra Questions for Class 11 Maths with Solutions State Board Pdf download in Hindi and English Medium. Students can get Class 11 Maths NCERT Solutions, Maths Class 11 Important Extra Questions and Answers designed by subject expert teachers.

CBSE Class 11th Maths Important Extra Questions and Answers Chapter Wise Pdf

Maths Class 11 Important Questions | Important Questions of Maths Class 11

1. Sets Important Question of Maths for Class 11
2. Relations and Functions Class 11 Important Questions
3. Trigonometric Functions Class 11 Important Questions
4. Principle of Mathematical Induction Class 11 Important Questions
5. Complex Numbers and Quadratic Equations Class 11 Important Questions
6. Linear Inequalities Class 11 Important Questions
7. Permutations and Combinations Class 11 Important Questions
8. Binomial Theorem Class 11 Important Questions
9. Sequences and Series Class 11 Important Questions
10. Straight lines Class 11 Important Questions
11. Conic Sections Class 11 Important Questions
12. Introduction to three Dimensional Geometry Class 11 Important Questions
13. Limits and Derivatives Class 11 Important Questions
14. Mathematical Reasoning Class 11 Important Questions
15. Statistics Class 11 Important Questions
16. Probability Class 11 Important Questions

We hope the given CBSE Important Questions for Class 11 Maths State Board Chapter Wise Pdf download in Hindi and English Medium will help you. If you have any queries regarding NCERT Class 11 Maths Extra Important Questions and Answers, drop a comment below and we will get back to you at the earliest.

By going through these CBSE Class 11 Maths Notes Chapter 1 Sets Class 11 Notes, students can recall all the concepts quickly.

Sets Notes Class 11 Maths Chapter 1

Set: Any well-defined collection of objects, which are different from each other, and which we can see or think of is called a set.

Members of a set: The objects which belong to a set are called its members or elements.

Representation of a set: There are two ways by which the , sets can be represented :
(a) Tabular form or Roster form : Here, the elements of a
set are actually written down, separated by commas and enclosed * within braces (i.e., curly brackets). Thus,

(i) V, the set of vowels in the English alphabet = {a, e, i, o, u},
(ii) A, the set of odd natural numbers < 10 = {1, 3, 5, 7, 9),
(iii) N, the set of natural numbers = {1, 2, 3,…}.

(b) The set builder form : In this form, we list the property or properties satisfied by the elements of the set. Thus,
(i) M = {2, 3,.5, 7, 11, 13, 17, 191 = {x : x is a prime number < 20).

(ii) A = 16, 7, 8, 9, 10, 11} = {x| ∈ N, 5 < x < 12}, where ∈ stands for ‘belongs to’ and ‘ | ’ stands for ‘such that’.

It may be noted that while writing the set in roster form, an element is not generally repeated. For example, the set of letters of the word ‘SCHOOL’ is (S, C, H, O, L}.

Empty set or null set or void set : A set consisting of no element at all is called the empty set or the null set or the void | set. It is denoted by Φ (Phai). In roster form, it is written as = { }.
Examples : (i) (x : x ∈ N, 1 < x < 2} = Φ.
(ii) {x : x ∈ R, x² = – 1} = Φ.

Finite Set: A set in which the process of counting of elements surely comes to an end, is called a finite set.
Examples : ii) {x : x ∈ N, x < 500) (ii) Set of all trees on earth.

Infinite Set: A set, in which the process of counting of elements never comes to an end, is called an infinite set. Examples : (i) {x : x ∈ N, x > 50), (ii) {x : x ∈ Z, x < 1}.

Equal Sets : Two sets A and B are said to be equal, if every element of A is in B and every element of B is in A. It is written as A = B.
Examples: (i) {1, 2, 5} = {2, 1, 5} = {5, 1, 2)
(ii) {1, 2, 3, 1} = {1, 2, 3} = {1, 1, 2, 2, 3} etc.
[∵ The repetition of elements in a set is meaningless]

Equivalent Sets : Two finite sets A and B are said to be equivalent, if n(A) = n(B), where n(A) or n(B) is the number of elements in set A or B. It is written as A ↔ B.
Example: If A = {1, 2, 3} and B = {a, b, c}. Then, A ↔ B as n(A) = n(B) = 3.

Whenever A = B, then n(A) = n(B). Thus, equal sets are always equivalent. But, equivalent sets need not be equal.

Disjoint Sets : Two sets are said to be disjoint, if they have no element in common.
Example : A = {1, 3, 5} and B = {2, 4, 6) are disjoint sets.

Subset: If A and B are two sets given in such a way that every element of A is in B, then A is a subset of set B and it is written as A ⊂ B (read as ‘A is contained in B’)
If at least one element of A does not belong to B, then A is not a subset of B. It is written as A ⊄ B.
Example : If A = {1, 2, 3} and B = {3, 2, 4, 1), then A ⊂ B.

Subsets of Set of Real Numbers R :
There are many important subsets of R. Some of them are given below :
(i) The set of natural numbers = N = {1, 2, 3, 4, 5, ….)

(ii) The set of integers Z is
Z = {…., – 3, – 2, – 1, 0, 1, 2, 3, ….}

(iii) The set of rational numbers Q.
Q = {x: x = \(\frac{p}{q}\), p,q ∈ Z and q ≠ 0

(iv) Set of irrational numbers
T = {x : x e R and x ∉ Q} = R – Q.

Members of T are such as √2, √5, √7,…., π, etc.
Here, we observe that
N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, N ⊄ T.
INTERVAL AS SUBSET OF R.
Let a, b ∈ R and a < b.

Open Interval : The set of real numbers {y : a <y < b} is called an open interval and is denoted by (a, b). Here all the points between a and b belong to the open interval (a, b), but a and b do not, belong to this interval.

Closed Interval: Closed interval is defined as {a, b = [x : a ≤ x ≤ b}.
All the points between a and b and the points a and b belong to \a,b).

Closed on the left and open to right: [a, b) = {x:a ≤ x < b}.
All the points between a and b and the point a belong to fa, b) but b does not belong to this interval.

Open on the left and closed to the right:
(a, b] = {x:a < x ≤ b}.
All the points between a and b and the point b belong to (a, 6] but a does not belong to it.

Super Set: If A is subset of B, then we say that B is a super set of A and is written as B ⊃ A.’

Some results on subsets :

• Every set is a subset of itself, i.e.,A⊂A, B⊂B, etc.
• The empty set is a subset of every set, i.e., Φ ⊂ A, Φ ⊂ B, etc.
• If A = B, then A ⊂ B and B ⊂ A.
• If A ⊂ B and B ⊂ A, then A = B.
• If A contains n elements, then A has 2ⁿ subsets.

Power Set : The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set.

Proper Subset : If A is a subset of B but A ≠ B, then A is called a proper subset et P and is written as A ⊂ B. Thus, A is a proper subset of B only when every elemént of A is in B and B has at least one extra element than A.

Example: If A {1, 2. 3) and B = (1, 2, 3, 4). Then, A ⊂ B and A ≠ B. Therefore A ⊂ B.

Note : If A is a subset of B and A = B, then A is not a proper subset of B. In such a case, it is denoted as A ⊆ B.

Some results on proper subsets:

• If A ⊂ B and A ≠ B, then A ⊂ B.
• No set is a proper subset of itself.
• Φ is a proper subset of every set except itself.
• Φ has no proper subset.
• A set having n elements has (2ⁿ – 1) proper subsets.

Universal Set : If there are some sets under consideration, then there happens to be a set which is a superset of each one of the given sets. Such a set is called the universal set and it is denoted by U or ξ

Venn Diagrams : Most of the relationships between sets can be represented by means of diagrams. Figures representing sets in the form of enclosed region in the plane are called Venn diagrams. In these diagrams, the universal set is usually represented by a rectangular region and its subsets by bounded regions inside this rectangular region.

Venn Diagrams In Different Situations

1. A ⊂ U, where U is the universal set.

2. Two intersecting subsets of a universal set U.

3. Two disjoint subsets of a universal set U.

4. A⊂B⊂U, where U is the universal set.

Operation of sets : The main set operations are

1. Union of sets
2. Intersection of sets
3. Difference of sets.

Union of two sets: The union of two
sets A and B, denoted by A u B (read as A union B), is the set of all those elements which are either in A or in B or in both.

Symbolically:
A∪B = {x:x ∈ A or x ∈ B}.
Example: If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Then,
A ∪ B = {1, 2, 3, 4}∪{2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}.

Some results on union of sets :

• A⊂A⊂B and B⊂A∪B.
• If A ⊂B, then A∪B⊂B.

Intersection of sets : The intersection of two sets A and B, denoted by A ∩ B (read as A intersection B), is the set of all elements common to both A and B.

Symbolically:
A ∩ B=[x:x ∈ A and x ∈ B).
Example: If A = (1, 2, 3, 4} and B = {2, 4, 6, 8). Then,
A ∩ B = (l, 2,3, 4}∩{2, 4, 6,8} = {2, 4}.

Disjoint Sets : Two sets A and B are said to be disjoint, if A ∩ B = Φ. ,
If A ∩ B ≠ Φ, then A and B are called overlapping or intersecting sets.

Difference of two sets : The difference of two sets A a.nd B, denoted by A – B (read as A minus B), is the set of all those elements of A which are not in B.

Symbolically :
A-B = {x:x∈A and x ∉ B}.
Example: If A = {1, 2, 3, 4, 6, 12} and B = {1, 2, 4, 8, 16). Then,
A – B = {3, 6,12} and B – A = {8, 16}.
Note : In general A – B ≠ B – A.

Laws of Set Operations:

1. Commutative Laws : For any two sets A and B, we have :
(i) A∪B = B∪A (ii) A ∩ B = B ∩ A.

2. Associative Laws: For any three sets A, B and C, we have :
(i) (A∪B)∪C = A∪(B∪C), {ii) (A∩B)∩C = A∩(B∩C).

3. Distributive Laws : For any three sets A, B and C, we have:
(i) A∪(B∩C) = (A∪B)∩(A∪C).
(ii) A∩(B∪C) = (A∩B)∪(A∩C).

4. Idempotent Laws : If A is any set, then
(i) A∩A = A (ii) A∪A = A,

5. Identity Laws : If A is any subset of a universal set U and Φ is the null set, then
(i) A∩U = A (ii) A∩Φ = Φ
(iii) A∪Φ = A (iv) A∪U = U.

Complement of a set : If U be a Universal set and A is the subset of U, then complement of A with respect to U, denoted by A’ or A^c, is defined as A’ = {x 😡 ∈ U and x ∉ A}, i.e., the complement of A is the set of elements of U which are not the elements of A.

Properties of Complements:
(i) Complement Laws.
(a) A∪A’ = U (b) A∩A’ = Φ

(ii) De Morgan’s Laws.
(a) (A ∪ B)’ = A’∩ B’ (b) (A∩B)’=A’∪B’

(iii) Law of double Complementation (a)(A’)’ = A

(iv) Complement of Φ and ∪
(a) Φ’ = U (b) U’ = Φ.

Cardinal Number : n, the number of elements in a set is called the cardinal number of the set, denoted by n(A).

Example : A = {1, 2, 3, 4, 5} n(A) = 5, since A has 5 elements.

Cardinal Properties of Sets:

(а) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
If A and B are disjoint , then
n(A ∪ B) = n(A) + n(B)

(b) n[A∪B∪C] = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A ∩B ∩ C).

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 5 Morphology of Flowering Plants. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 5 Important Extra Questions Morphology of Flowering Plants

Morphology of Flowering Plants Important Extra Questions Very Short Answer Type

Question 1.
What do you mean by morphology?
Answer:
Morphology refers to external structures.

Question 2.
What are the hanging roots of a banyan tree called?
Answer:
Prop roots

Question 3.
In which type of plants, the primary root is short-lived and is replaced by a large number of roots?
Answer:
Monocotyledonous

Question 4.
Name one plant which has a fibrous root system.
Answer:
Wheat plant

Question 5.
Name one plant which has adventitious roots?
Answer:
Banyan

Question 6.
What is a root cap?
Answer:
The root is covered at the apex by a thimble-like structure called the root cap.

Question 7.
Name the region a few millimetres above the root cap?
Answer:
Region of meristematic activity.

Question 8.
What is the function of root hairs?
Answer:
To absorb water and minerals from the soil.

Question 9.
Name two plants whose taproots store food.
Answer:
Carrot and turnip

Question 10.
Name one plant whose roots come out of the ground and grow vertically upwards.
Answer:
Rhizophora.

Question 11.
What are pneumatophores?
Answer:
Roots which help to get oxygen for respiration.’

Question 12.
Which part of the plant bears nodes and internodes?
Answer:
Stem

Question 13.
Name the region of the stem where leaves are born.
Answer:
Nodes

Question 14.
What is the portion between two nodes called?
Answer:
Internode

Question 15.
Name two plants whose stems are modified to store food in them.
Answer:
Potato and ginger.

Question 16.
Name two plants whose stems are modified into woody, straight and pointed thorns.
Answer:
Citrus and Bougainvillea.

Question 17.
What is a leaf?
Answer:
The leaf is a lateral, generally flattened structure borne on the stem.

Question 18.
Name the three main parts of a leaf.
Answer:
Leaf base, Petiole and Lamina.

Question 19.
What is the relation?
Answer:
The arrangement of veins and the veinlets in the lamina of the leaf is termed venation.

Question 20.
Name the two types of compound leaves.
Answer:
(a) Pinnately compound leaf
(b) Palmately compound leaf,

Morphology of Flowering Plants Biology Important Extra Questions Short Answer Type

Question 1.
What are the functions of the root system?
Answer:
The main functions of the root system are as follows:
(a) Absorption of water and minerals from the soil.
(b) To provide a proper anchorage to the plant parts.
(c) To store reserved food material
(d) Synthesis of plant growth regulators.

Question 2.
Write a note on different types of root systems.
Answer:
(a) In most of the dicotyledonous plants, the direct elongation of the radicle leads to the formation of primary roots which grows inside the soil. The primary roots and their branches constitute the taproot system. For example-mustard plant.

(b) In monocotyledonous plants the primary root is short-lived and is replaced by a large number of roots. Their roots originate from the base of the stem and constitute the fibrous root system. For example wheat plant.

(c) In some plants, roots arise from parts of the plant other than the radicle. Such roots are called adventitious roots. For example grass, banyan tree etc.

Question 3.
Write a short note on the stem.
Answer:
The stem is the ascending part of the axis bearing branches leaves, flowers and fruits. It develops from the plumule of the embryo of a germinating seed. The stem bears nodes and internodes. The region of the stem where leaves are born is called nodes while the portion between two nodes is called an internode. The stem is generally green when young and later becomes woody and dark brown.

Question 4.
What are the main functions of the stem?
Answer:
The main functions of stem are as follows:
(a) Spreading out branches bearing leaves, flowers and fruits.
(b) To conduct water, minerals and photosynthates.
(c) Some stems perform the function of storage of food, support, protection and vegetative propagation.

Question 5.
Describe the main parts of a leaf.
Answer:
The leaf consists of three main parts-leaf base, petiole and lamina.
(a) Leaf base: The leaf is attached to the stem by the leaf base.
(b) Petiole: The petiole help hold the blade to light.
(c) Lamina: It is the green expanded part of the leaf with veins and veinlets.

Question 6.
What are the functions of petiole and lamina?
Answer:
Functions of petiole:
(a) The petiole helps hold the blade to light.
(b) It allows leaf blades to flutter in wind, thereby cooling the leaf and bringing fresh air to the leaf surface.

Functions of Lamina
(a) The veins of the lamina provide rigidity to the leaf blade
(b) It acts as channels of transport for water, minerals and food materials.

Question 7.
What do you mean by venation?
Answer:
The arrangement of veins and the veinlets in the lamina of the leaf is termed venation. The veinlets in the form of a network are termed reticulate and when the veins run parallel to each other within a lamina, the venation is termed as parallel. Dicotyledonous plants generally possess reticulate venation while monocotyledonous generally possess parallel venation.

Question 8.
Explain the two types of compound leaves.
Answer:
The two types of compound leaves are:
(a) Pinnately compound leaf: In which a number of leaflets are present on a common axis, the rachis, which represents the midrib of the leaf as in neem.
(b) Palmately compound leaves: The leaflets are attached at a common point, i.e., at the tip of the petiole, as in silk cotton.

Question 9.
What do you mean by phyllotaxy?
Answer:
The pattern of arrangement of leaves on the stem or branch is termed phyllotaxy.

It is usually of three types:
(a) Alternate: A single leaf arises at each node in an alternate manner, as in a china rose.
(b) Opposite: A pair of leaves arise at each node and lie opposite to each other as in calotropis and guava plants.
(c) Whorled: When more than two leaves arise at a node and form a whorl, as in Alstonia.

Question 10.
What are the functions of leaves?
Answer:
(a) Photosynthesis
(b) Some leaves are converted into tendrils for climbing as in peas.
(c) Some leaves are converted into spines for defence as in cacti
(d) Some leaves store food as in onion and garlic.

Question 11.
What is inflorescence? Name two types of inflorescences.
Answer:
The arrangement of flowers on the floral axis is termed an inflorescence

Types of inflorescences:
(a) Racemose: In racemose the main axis continues to grow, the flowers are borne laterally in acropetal succession.
(b) Cymose: In the cymose type of inflorescence, the main axis terminates in a flower. The flowers are borne in a basipetal order.

Question 12.
What is a flower?
Answer:
The flower is the reproductive unit in the angiosperms. It is meant for sexual reproduction. A typical flower has four different kinds of whorls arranged successively on the swollen end of the stalk or pedicel called the thalamus. The different kinds of whorls are calyx, corolla, androecium and gynoecium. The androecium and gynoecium are reproductive organs while calyx and corolla are accessory organs.

Question 13.
Write a note on the symmetry of a flower.
Answer:
The flower may be actinomorphic (radical symmetry) or zygomorphic (bilateral symmetry) in symmetry.
(a) Actinomorphic: When a flower can be divided into two equal radical halves in any radical plane passing through the centre, it is said to be actino-morphic, e.g., mustard, datura, chilli.
(b) Zygomorphic: When a flower is divided into two similar halves only in one particular vertical plane, it is said to be zygomorphic, e.g., pea, bean, cassia.

Question 14.
Write a short note on the fruit.
Answer:
Fruit is a natural or ripened ovary, developed after fertilization.

Fruit is called a parthenocarpic fruit if it is formed without fertilization of the ovary.

The fruit consists of a wall or pericarp and seeds. The pericarp may be dry or fleshy. If the pericarp is thick and fleshy, it is differentiated into the outer part called epicarp, a middle part called mesocarp and an inner part called the endocarp.

Question 15.
Write a note on the structure of a dicotyledonous seed.
Answer:
The outermost covering of a seed is called the seed coat. The seed coat has two layers, the outer testa and the inner tegmen. The developing seeds are attached to the fruit by means of a scar called the hilum, on the seed coat. A small pore called the micropyle is situated above the hilum. In the inner region of the seed coat is the embryo, consisting of an embryonal axis and two cotyledons. The cotyledons are fleshy and full of reserve food materials. At the end of the embryonal axis are present the radicle and the plumule.

Morphology of Flowering Plants Biology Important Extra Questions Long Answer Type

Question 1.
Write a note on the regions of the root.
Answer:
At the apex, the root is covered by a thimble-like structure called the root cap. The root cap protects the tender apex of the root as it penetrates the soil. A few millimetres above the root cap is the region of meristematic activity. The cells present in this region are very small, thin-walled and with dense protoplasm.

The cells proximal to this region undergo rapid elongation and enlargement and are also responsible for the growth of the root in length. This region is called the region of elongation. The cells of this region gradually differentiate and mature. This zone proximal to the region of elongation is called the region of maturation. Some epidermal cells, from this region, form very fine and delicate, thread-like structures called root hairs. The functions of these root hairs are to absorb water and minerals from the soil.

The regions of the root-tip

Question 2.
Write a note of different types of leaves and phyllotaxy.
Answer:
When the lamina of the leaf is entire or incised and the incisions do not touch the midrib, the leaf is said to be simple. A leaf is said to be compound when the incisions of the lamina reach up. to the midrib breaking it into a number of leaflets. In both simple and compound leaves a bud is present in the axil of the petiole. However, a bud is not present in the axil of leaflets of the compound leaf.

There are two types of compound leaves:
(a) Pinnately compound leaf
(b) Palmately compound leaf

In a pinnately compound leaf, a number of leaflets are present on a common axis, the rachis, which represents the midrib of the leaf. However in palmately compound leaves, the leaflets are attached at a common point,
i. e, the tip of the petiole.

Phyllotaxy refers to the pattern of arrangement of leaves on the stem or branch. Phyllotaxy is of three types alternate, opposite and whorled. A single leaf that arises at each node in an alternate manner is called alternate phyllotaxy, for example, as in china rose. When a pair of leaves arise at each node and lie opposite to each other it is called opposite phyllotaxy, for example in calotropis. If more than two leaves arise at a node and form a whorl it is called whorled phyllotaxy, as in Alstonia.

Different types of phyllotaxy: (a) Alternate (b) Opposite(c) Whorled

Question 3.
Write in details about a flower.
Answer:
A flower is a reproductive unit in the angiosperms. It is meant for sexual reproduction. Four different kinds of whorls are found in a flower. These are arranged successively on the swollen end of the stalk or pedicel, called the thalamus or receptacle.

These are calyx, corolla, androecium and gynoecium.
(a) Calyx: It is the outermost whorl of the flower and its members are called sepals. Mostly the sepals are green in colour, leaf-like and protect the flower in the bud stage. The calyx may be gamosepalous (in which sepals are united or polysepalous (in which sepals are free).

(b) Corolla: It is composed of petals that are usually brightly coloured to attract insects for pollination. The shape of the corolla may be tubular, bell-shaped, funnel-shaped or wheel-shaped.

(c) Aestivation: The pattern of arrangement of sepals or petals in the floral bud with respect to the other members of the same whorl is known as aestivation. The main types of aestivation are valvate, twisted, imbricate and vexillary.

Types of aestivation in corolla: (a) Valvate (b) Twisted (c) Imbricate (d) Vexillary

(d) Androecium: It is composed of stamens which are male reproductive organs of a flower. Each stamen consists of a stalk or a filament and an anther. Each anther is usually bilobed. There are two chambers (pollen sacs) in each lobe. The pollen grains are produced in pollen sacs.

Position of floral parts on thalamus : (a) Hypogynous (b) and (c) Perigynous (d) Epigynous

(e) Gynoecium: It is the female reproductive part of the flower. It is made up of one or more carpels. A carpel consists of three parts ovary, stigma and style. The stigma is at the tip of the style and is the receptive surface for pollen grains. The ovary is an enlarged basal part. The style connects the ovary to the stigma. Each ovary bears one or more ovules attached to a flattened, cushion-like placenta.

A flower may be trimerous tetramerous or pentamerous when the floral appendages are in multiples of 3, 4 and 5 respectively.

The flowers are described as hypogynous perigynous and epigynous based on the position of calyx, corolla and androecium in respect of the ovary on the thalamus.