By going through these CBSE Class 11 Maths Notes Chapter 10 Straight lines Class 11 Notes, students can recall all the concepts quickly.
Straight lines Notes Class 11 Maths Chapter 10
Co-ordinate Geometry: The branch of Mathematics in which geometrical problem are solved through algebra by using the co-ordinate system, is known as co-ordinate geometry or analytical geometry.
Algebrical Representation of a Point: It is done by means of two numbers defined in a particular way called co-ordinates of the point.
Co-ordinate Axes : Let X’OX and Y’OY, be two mutually perpendicular lines taken as axes whose positive directions are shown by arrows on the axes. Let these axes intersect at O. Then, point O is called origin and the axes taken are called co¬ordinate axes.
(i) X’OX is called axis of x or x-axis.
(ii) Y’OY is called axis of y or y-axis.
Since the axes taken are mutually at right angles, they are called rectangular axes.
Quadrants : The co-ordinate axes divide the plane into four parts called quadrants.
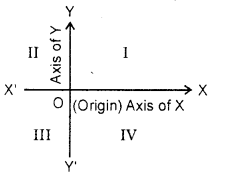
XOY, YOX’, XOY’ and Y’OX are called first, second, third and fourth quadrants respectively. The names of the quadrants as I, II, III and IV are fixed once for all.
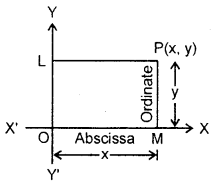
Co-ordinates : Let P be any point in the plane of axes. From P, draw PL, PM ⊥ on y-axis and x-axis respectively. Then, length LP is called the x-coordinate or the abscissa of point P and MP is called the y-co-ordinate or the ordinate of point P. Point whose abscissa is x and ordinate is y, is called the point (x, y).
Signs of Co-ordinates : The co-ordinates of point lying in the first, second, third and fourth quadrants are as (+, +), (-, +), (-, -) and (+, -) respectively.
Note :
- Co-ordinates of orgin are (0, 0).
- Ordinate of every point on the x-axis is zero.
- Abscissa of every point on the y-axis is zero.
Distance Between Two Points : The distance between two
points P(x1, y1) and Q(x2,y2) is given by PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Note : 1. When the line PQ is parallel to they-axis, the abscissa of points P and Q will be equal, i.e., x1 = x2. Therefore, PQ = |y2 – y1|
2. When the line PQ is parallel to the x-axis, the ordinate of points P and Q wll be equal i.e.,y1= y2. Therefore, PQ = |x2 – x1 |.
3. The distance of a point P(x, y) from the origin (0, 0) is given
by OP = \(\sqrt{x^{2}+y^{2}}\)
Tests : In questions relating to geometrical figures such as triangle, quadrilateral, etc., take the given vertices in the given order.
(i) For an isosceles triangle : At least two sides are equal.
(ii) For an equilateral triangle : Three sides are equal.
(iii) For a right angled triangle : Sum of the squares of two sides is equal to the square of the third side.
(iv) For collinear points : Sum of the distances between two point-pairs is equal to the distance between the third point pair.
(v) For a square : Four sides are equal, two diagonals are
equal.
(vi) For a rhombus : Four sides are equal and there is no need to prove that two diagonals are unequal as a square is also a rhombus.
(vii) For a rectangle : Opposite sides are equal and two diagonals are equal.
(viii) For a parallelogram: Opposite sides are equal and there is no need to prove that two diagonals are unequal as a rectangle is also a parallelogram.
Internal Division : A point R between the points P and Q on the line segment PQ is said to divide PQ internally in the ratio m1 : m2,
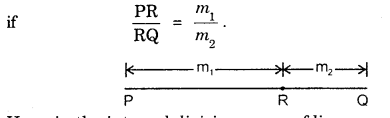
Here, in the internal division, sense of line segments PR and RQ is same.
∴ m1 and m2 are both positive.
External Division : A point R on the part of the line segment PQ produced or QP produced is said to divide PQ externally in the ratio m1 : m2
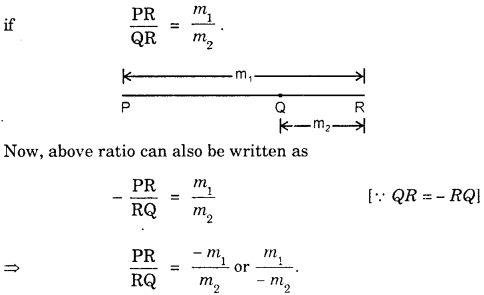
Hence, if a point R divides PQ externally in ratio m1 : m2, then we can say that R divides internally in the ratio – m1 : m2 or m1: – m2.
Section Formula (Internal division) : The co-ordinates of the point R(x, y) which divides internally the straight line segment joining points P(x1, y1) and Q(x2, y2) in the ratio m1: m2 is given by
\(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)
How to remember: To find the x-co-ordinate of R, multiply m1 with the x-coordinate of the point remote from m1 and m2 by the x co-ordinate of the point remote from m2 and add these product, and divide the sum by m1 + m2. Similarly, findy.
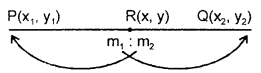
Note : 1. The co-ordinates of the mid-point of the line segment joining( the points P(x1 y1) and Q(x2, y2) are given by
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
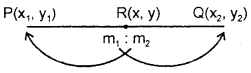
2. If a point R divides the line segment joining the points P(x1 y1) and Q(x2, y2) in the ratio k : 1, then the co-ordinates of R are given by \(\left(\frac{k x_{2}+x_{1}}{k+1}, \frac{k y_{2}+y_{1}}{k+1}\right)\)
3. If R divides PQ externally in the ratio m1 : m2
divides PQ internally in the ratio m1: -m2.
∴ The co-ordinates of R are given by
\(\left(\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}, \frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}\right)\)
Area of a Triangle : The area of the triangle having vertices
as (x1, y1), (x2, y2) and (x3, y3) is given by \(\frac { 1 }{ 2 }\) [(x1y2 – x2y1 + (x2y3 – x3y2 + (x3y1 – x1y3)]
or
\(\frac { 1 }{ 2 }\) [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]
How to remember : Result of area can be written down in a simpler way as in the figure given :
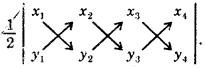
Numbers to be multiplied are shown by arrows. All the products with arrow downwards are of positive sign and are added to the products with arrow upwards with negative sign.
Condition of Collinearity of Three Points : Three points A(x1, y1), B(x2, y2) and C(x3, y3) will be collinear, if and only if the area of the triangle ABC is zero. That is,
(x1y2 – x2y1) + (x2y3 – x3y2) + (x3y1 – x1y3) = 0.
or x1(y2-y3) + x2(y3-y1) + x3(y1-y2) = 0.
Slope of a Line : The slope (or gradient) of a line is the tangent of the angle which the part of the line above the x-axis makes with the positive direction of the x-axis.
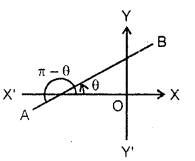
Note : 1. The slope of the line is independent of the sense of line. Consider sense AB. Then slope = tan θ and on cosidering sense BA, the slope = tan (π + θ) = tan θ. Thus, it is same for both senses of the line.
2. The slope of a line is denoted by m, i.e., m = tan θ, where θ is the angle which the line makes with the positive direction ofx-axis.
3. Slope of a line is not defined, when θ = 90°, as tan 90° is not defined.
4. The slope of a line equally inclined to axes is ± 1.
[∵ tan 45° = 1, tan 135° = – 1]
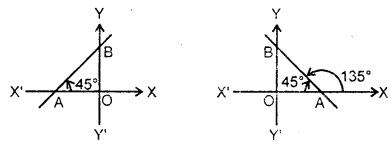
5. If a line is parallel to the x-axis, θ = 0 and its slope m = tan 0° = 0.
Slope of a Line Joining Two Points : The slope of the line joining points (x1,y1) and (x2 , y2) is given by \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Condition of Parallelism and Perpendicularity :
(i) The two lines are parallel, if their slopes are equal, i.e., m1 = m2.
(ii) The two lines are perpendicular, if the product of their slopes = – 1, i.e., m1m2 = -1
Or the slope of one line is the negative reciprocal of the other.
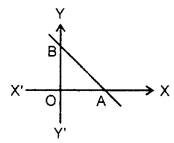
Intercepts : Let a straight line AB meet the axes in A and B. Then,
(i) OA is called the intercept of the line on x-axis or x-intercept.
(ii) OB is called the intercept of the line ony-axis or y-intercept.
(iii) AB is called the portion of the line intercepted between the axes.
Rule for Signs of Intercepts: (i) The intercept on the x-axis is positive, if measured to the right of the origin and negative, if measured to the left.
(ii) The intercept on the y-axis is positive, if it is measured above the origin, and negative, if measured below.
Locus of a point: Locus of a point is the path traced by a moving point when it moves under some given geometrical conditions.
Method to Find Locus of Moving Point:
Step 1 : Suppose the co-ordinates of moving point as (x, y).
Step 2 : Write down the given condition under which the point moves.
Step 3 : Express the geometrical condition in step 2 in terms of x and y, i.e., co-ordinates of the moving point.
Step 4 : Simplify, if required, the result in step 3. Equation so obtained, will be the equation of the locus.
Equation of Straight Lines Parallel to Co-ordinate Axes
(i) Equation of a straight line parallel to x-axis and at a distance of ‘b’ from it is y = b.
(ii) Equation of x-axis is y = 0.
(iii) Equation of a straight line parallel to y-axis and at a distance of ‘a’ from it is x = a.
(iv) Equation of y-axis is x – 0.
A Line Through The Origin : The equation of a straight line passing through the origin and making an angle θ with the positive direction of the x-axis is y = mx, where m = tanθ.
Slope-Intercept Form: (i) The equation of straight line which cuts off a given intercept ‘c’ on they-axis and is inclined at a given angle ‘θ’ to the x-axis is y = mx + c, where m = tan θ.
(ii) The equation of a line whose slope is m and the x-intercept is d, which is y = m(x – d).
Intercept Form : The equation of a straight line which cuts off given intercepts a and b from the axes is \(\frac{x}{b}+\frac{y}{b}\) = 1.
Normal Form : The equation of a straight line in terms of the length of the perpendicular p from the origin upon it and the angle a which this perpendicular makes with the x-axis is x cos α+y sin α = P
Point-Slope Form : The equation of a straight line drawn through a given point (x1,y1) making an angle 0 with x-axis is y – y1 = m(x – x1), where m = tan θ.
Two-Point Form : The equation of a straight line passing through, two given points (x1, y1) and (x2, y2) is y – y1 =\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)(x-x1).
Distance Form : The equation of a straight line in the form x – x y – y
\(\frac{x-x_{1}}{\cos \theta}=\frac{y-y_{1}}{\sin \theta}\) = r. where (x1, y1) is a point on the line, r the distance between the points (x, y) and (x1, y1), θ is the angle which the line makes with the x-axis.
General Equation of a Straight Line : Any equation of the first degree in x and y represents a straight line, such as
Ax + By + C = 0 …(1)
Some Cases :
(i) If A = 0, B ≠ 0, then (1) reduces to By + C = 0
⇒ y = \(-\frac{\mathrm{C}}{\mathrm{B}}\) which is the equation of horizontal line ii.e. parallel to x axis)
(ii) If A = C = 0, B ≠ 0, then (1) reduces to y = 0, which is the equation of x-axis.
(iii) If A ≠ 0, B = 0, then (1) reduces to Ax + C = 0 ⇒ x = \(-\frac{\mathrm{C}}{\mathrm{A}}\) , which is the equation of a vertical line (i.e., parallel to y-axis).
(iv) If B = C = 0, A ≠ 0, then (1) reduces x = 0, which is the equation of y-axis.
(v) If A ≠ 0, B ≠ 0, C = 0, then (1) reduces to Ax + By = 0 ⇒ y = \(-\frac{\mathrm{A}}{\mathrm{B}} x\) , which is the equation of a straight line passing through the origin.
Rule to Find the Intercepts of a Line on the Axes : In the equation of the line. Puty = 0, and find x. This gives the intercept on the x-axis. Again, put x = 0, and findy. This is intercept on the v- axis.
Rule to Reduce the General Equation to the Normal Form:
In the given equation :
Divide both sides by \(\sqrt{(\text { coeff. of } x)^{2}+\left(\text { coeff. of } y^{2}\right)^{2}}\)
Transpose the constant term to R.H.S. and make it positive (by changing the signs throughout, if necessary).
Identical Lines : If equations ax + by + c = C and a’x + b’y + c’ = 0 represent the same straight line, then \(\frac{a}{a^{\prime}}=\frac{b}{b^{\prime}}=\frac{c}{c^{\prime}}\)
Point of Intersection of Two Lines : Let equation of the lines be
a1x + b1y + c1= 0
and a2c + b2y + c2 = 0
The point of intersection can be obtained by solving these equations by cross-multiplication.
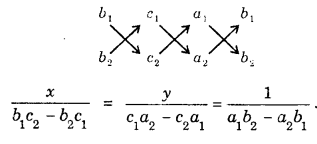
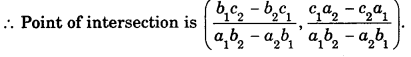
Test for Concurrence of Three Lines : If the equations of three lines are a1x + b1y + c1= 0, a2c + b2y + c2 = 0, a3x + b3y + c3= 0 and if three constants l, m, n can be found such that l(a1x + b1y + c1) + m(a2x + b2y + c2) + n(a1x + b3y + c3 = 0 identically (i.e., = 0, for all values of x and y), then the three straight lines meet in a point.
Angle between Two Lines: (i) The angle θ between two lines y = m1x + c1 and y = m2x + c2 is given by tan θ = ±\(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\) .
Condition of Parallelism : If lines are parallel, then θ, the angle between them = 0.
⇒ tan θ = tan 0° = 0
⇒ \(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\)= 0
⇒ m1 – m2 = 0
⇒ m1 = m2.
Thus, the two lines are parallel, if their slopes are equal.
Condition of perpendicularity : If lines are perpendicular to each other, then 0, the angle between them = 90°.
⇒ tan θ = tan 90° = ∞
⇒ \(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\) = ∞
⇒ The denominator, 1 + m1m2 = 0.
⇒ m1 m2 = – 1 or m2 = \(-\frac{1}{m_{1}}\)
Hence, the two lines are perpendicular to each other, if the product of their slopes = – 1, or the slopes of one line is the negative reciprocal of the other.
Note : 1. Angle between the two lines means the acutal angle between the lines Hence, for finding the angle between the two lines, we shall be rejecting the negative values of tan 0.
2. The complete angle formula is used, when the angle between the lines is given.
(ii) The angle θ between the lines Ax + By + C = 0 and A’x + By + C’ = 0 is given by tan θ = .
\(\frac{\mathbf{A}^{\prime} \mathbf{B}-\mathbf{A B}^{\prime}}{\mathbf{A A}^{\prime}+\mathbf{B B}^{\prime}}\)
Condition of parallelism : If the lines are parallel, then θ =
⇒ tan θ = tan 0° = 0.
⇒ \(\frac{\mathrm{A}^{\prime} \mathrm{B}-\mathrm{AB}^{\prime}}{\mathrm{AA}^{\prime}+\mathrm{BB}^{\prime}}\) = 0
⇒ A’B-AB’ = 0
⇒ \(\frac{\mathrm{A}}{\mathrm{A}^{\prime}}=\frac{\mathrm{B}}{\mathrm{B}^{\prime}}\)
Thus, if two lines (equations in the general form) are parallel, then the ratio of the coeff. of x = ratio of the coeff. of y.
Condition of perpendicularity : If lines are perpendicular to each other, then θ = 90°.
tan θ = tan 90° = ∞
⇒ \(\frac{A^{\prime} B-A B^{\prime}}{A A^{\prime}+B B^{\prime}}\) = ∞
⇒ AA’ + BB’ = 0.
Hence, if two lines (equation in the general form) are perpendicular to each other, then the product of the coeffs. of x + product of the coeffs. of y = 0.
Perpendicular Distance Formula : (i) The perpendicular distance of the point (x1, yx) from the line xcos a + ysin a = p is ± (x1cos α+ y1sin α – p).
(ii) The perpendicular distance of the point (x1 y1) from the line ax + by + c = 0is ± \(\frac{a x_{1}+b y_{1}+c}{\sqrt{a^{2}+b^{2}}}\)
Distance Between the Parallel Lines: The distance between parallel lines ax + by + c = 0 and ax + by + c is \(\frac{c-c^{\prime}}{\sqrt{a^{2}+b^{2}}}\)