By going through these CBSE Class 11 Maths Notes Chapter 2 Relations and Functions Class 11 Notes, students can recall all the concepts quickly.
Relations and Functions Notes Class 11 Maths Chapter 2
Ordered Pair: Two elements a and b, listed in a specific order, form an ordered pair, denoted by (a,b).
In general, (a,b) ≠ (b, a) and (a1 b1) = (a2, b2) ⇔ a1 = a2 and b1 = b2.
Cartesian Product of Sets : If A and B are two non-empty sets, then the set of all ordered pairs (a, b) such that a ∈ A and b ∈ B, is called the cartesian product of A and B, to be denoted by A x B.
Thus, A x B = {(a, b): a e A and b ∈ B)
Remarks : (i) If A = Φ or B = Φ, then A x B = Φ
(ii) If A ≠ Φ and B ≠ Φ, then A x B ≠ Φ.
(iii) A x B ≠ B x A, in general.
(.iv) If A and B are finite sets, then n(A x B) = n(A).n(B).
(v) If either A or B is an infinite set, then A x B is an infinite set.
(vi) If A = B, then A x B is expressed as A2.
(vii) In general, if A1 A2 ………. An are n sets, then (a1, a2,…, an) is called an ra-tuple, where ai = Ai, i = 1,2,…, n and the set of all such n-tuples, is called the cartesian product of A1, A2,…, An. It is denoted by x A1 x A2 x …, x An = ( a1, a2,…, an): ai ∈ Ai, 1 ≤ i ≤ n).
Relation :
(i) Definition : A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A x B. The subset is derived by describing a relationship between the first element and the second element of the ordered pair in A x B.
(ii) Image : The second element of each ordered pair of the relation R is called the image of the first element.
(iii) Domain : The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R.
(iv) Co-domain : The set B is known as the co-domain of relation R.
Note that range ⊆ co-domain.
Functions : Let X and Y be two non-empty sets. A function or mapping ‘f’ from X into Y written as f: X → F is a rule by which each element x ∈ X is associated to a unique element y ∈ Y. We then say that f is a mapping of X into Y or f is a function of X to Y.
Element y ∈ Y to which the element x ∈ X is associated is called f-image of x or image of x or the value of the function at x and x is called pre-image of y. The set X is called domain and Y is called the co-domain of the function. The set formed by all the f – images of the elements of Y is called the range of the function and is denoted by f(X) or {f(X)}. Clearly, range is the subset of Y.
The numbers x and y, where y is an image ofx are also denoted by ordered pair ix,y) or [x, fix)).
Some Functions With Graphs
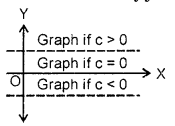
1. Constant function : The constant function is defined by y = f(x) = c, where c is a real number.
The graph of this function is set of all points (x, c) i.e., the straight line parallel to x-axis.
Domain = All reals
Range = {c}.
2. Absolute value function : The absolute value function is defined as y = f(x) = | x |. This function can also be written as
|x| = \(\left\{\begin{array}{ll}
x, & \text { if } x \geq 0 \\
-x, & \text { if } x<0 \end{array}\right.\)
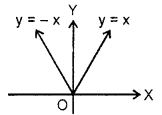
The graph of this function is set of all points of the form (x, |x |). Domain = All reals. Range = All non-negative reals.
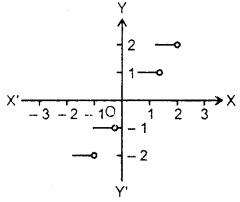
3. The greatest integer function : The greatest integer function is defined as y = f(x) = [x]. [x] means the greatest integer n such that n ≤ x. For example : [3.5] = 3, [4] = 4, [-5.1] =-6. The graph of [x] gives Domain = Set of ail reals Range = Set of integers.
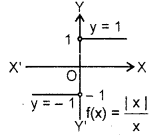
4. Signum function : Let R be the set of real numbers. Then, the function f: R → R defined by f(x) = \(\left\{\begin{array}{ll} 1, & \text { if } x>0 \\
0, & \text { if } x=0 \\
-1, & \text { if } x<0
\end{array}\right.\) is known as signum function.
Domain of f = R.
Range of f = {- 1, 0, 1}.
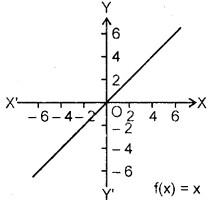
5. Identity function : Let R be the set of real numbers. A real valued function f is defined as f: R → R by y = f(x) = x for each value of x e R. Such a function is called the identity function.
Domain of f = R.
Range of f = R.
6. Polynomial function: A function f: R → R is said to be the polynomial function, if for each x ∈ R, y = f(x) = a0 + a1x + a2x2 + … + anxnanxn, where n is non-negative integer and a0, a1, a2,…, an ∈ R.
7. Rational functions : These functions are of type \(\frac{f(x)}{g(x)}\), where f(x) and g(x) are polynomial functions of* defined in a domain where g(x) ≠ 0.
Algebra Of Real Functions
(i) Addition of two real functions : Let f: X → R and g : X→ R be any two real functions, where X ⊂ R. Then, we define(f+g):X ⊂ R by (f+g)(x) = f(x)+g(x) for all x ∈ X.
(ii) Subtraction of a real function from another : Let f: X → R and g: X → R be two real functions, where X ⊂ R. Then, we define (f -g)x: x → R by (f-g)x – f(x)-g(x) for all x ∈ X.
(iii) Multiplication by Scalar: Let f: R → R be a real valued function and c be a scalar, where c is real number. Then, the product cf is a function from X to R defined by (f)(x) = cf(x), x ∈ X.
(iv) Multiplication of two real functions : The product of two real functions, f: x → R and g : x → R is a function fg : X → R defined by (fg){x) = f(x)g(x), for all x ∈ X.
(v) Quotient of two real functions: Let fandg be two real functions defined from X → R, where X⊂R. The quotient of f by g is function defined by \(\left[\frac{f}{g}\right][x]=\frac{f(x)}{g(x)}\), for all x ∈ X such that g(x) ≠ 0.