Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C

Question 1.
Given a triangle ABC in which A = (4, -4), B (0, 5) and C = (5, 10). A point P lies on BC such that BP : PC = 3 : 2. Find the length of line segment AP.
Solution:
B (0, 5), C (5, 10) and BP : PC = 3 : 2 Co-ordinates of P will be

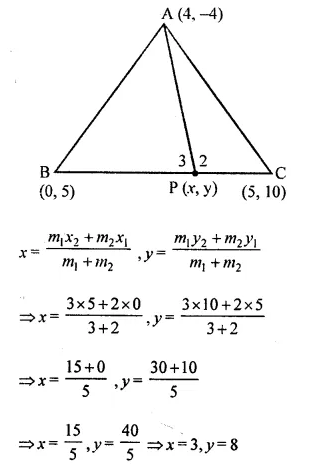
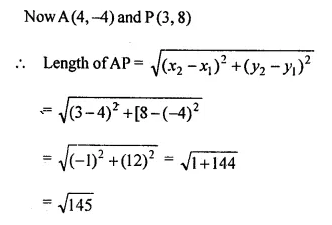
Question 2.
A (20, 0) and B (10, – 20) are two fixed points, find the co-ordinates of the point P in AB such that 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that AB = 6AQ.
Solution:
(i) A (20, 0), B (10, – 20)

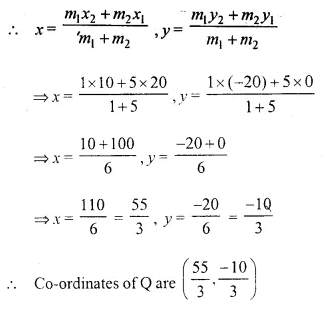
Question 3.
A (-8, 0), B (0, 16) and C (0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP : PB = 3 : 5 and AQ : QC = 3 : 5. Show that: PQ = \(\frac { 3 }{ 8 }\) BC.
Solution:

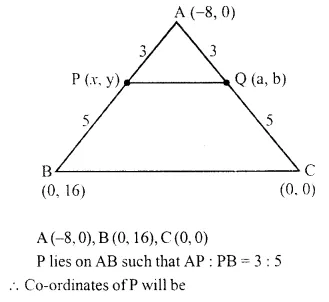
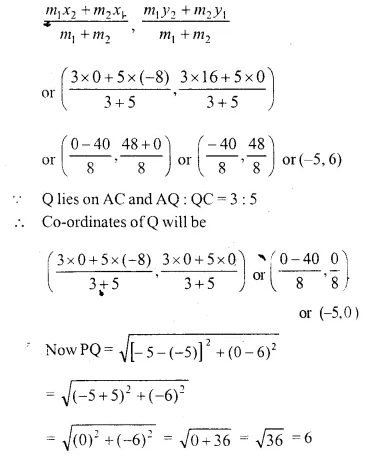
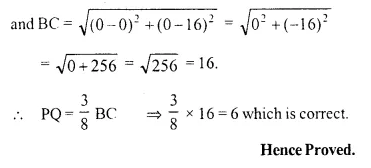
Question 4.
Find the co-ordinates of points of trisection of the line segment joining the points (6, -9) and the origin.
Solution:
Points are A (6, -9) and O (0,0) let P and Q are points, which trisect AO

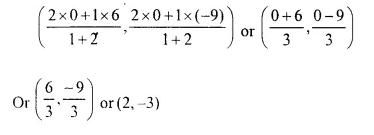
Question 5.
A line segment joining A (-1, \(\frac { 5 }{ 3 }\)) and B (a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.
(i) Calculate the value of ‘a’.
(ii) Calculate the co-ordinates of ‘P’. (1994)
Solution:

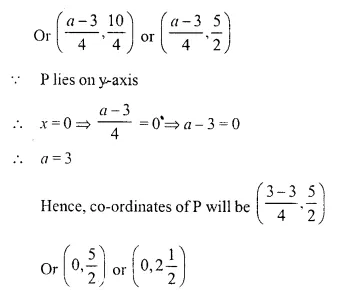
Question 6.
In what ratio is the line joining A (0, 3) and B (4, -1), divided by the x-axis ? Write the co-ordinates of the point where AB intersects the x-axis. [1993]
Solution:
Let the ratio be m₁ : m₂ when the x-axis intersects the line AB at P.

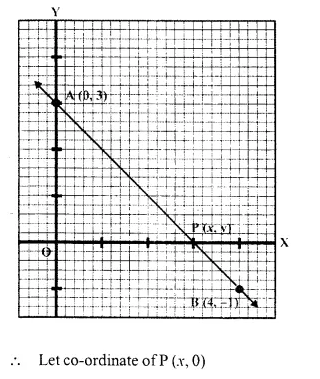
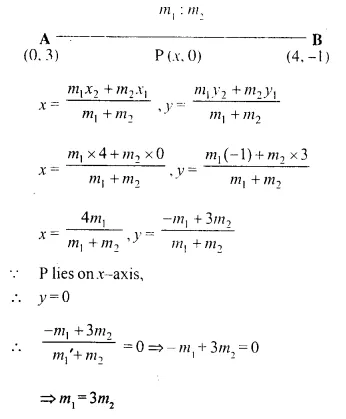
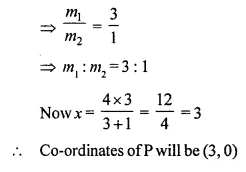
Question 7.
The mid point of the segment AB, as shown in diagram, is C (4, -3). Write down the co-ordinates of A and B. (1996)

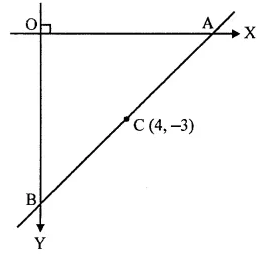
Solution:
Let co-ordinates of A (x, 0) and B (0, y) and C (4, -3) the mid point of AB.

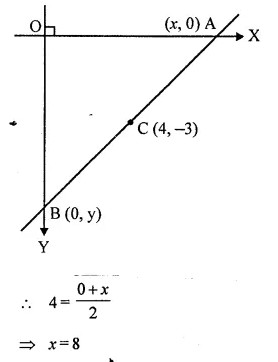
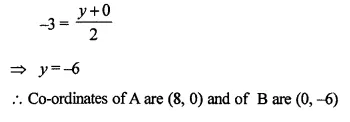
Question 8.
AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
(i) the length of radius AC
(ii) the coordinates of B.
Solution:

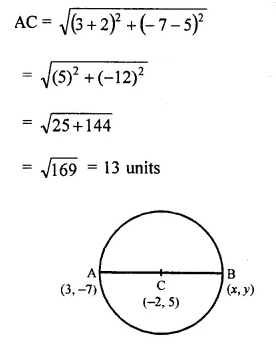
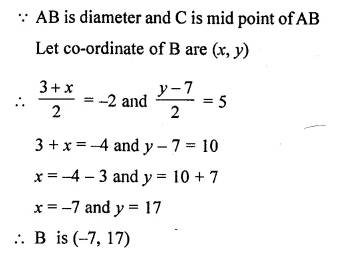
Question 9.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are A (- 1, 3), B (1, – 1) and C (5, 1)
Solution:

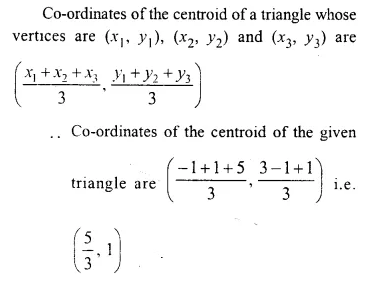
Question 10.
The mid-point of the line segment joining (4a, 2b – 3) and (-4, 3b) is (2, -2a). Find the values of a and b.
Solution:
Let A and B are two points and P is its mid point then A is (4a, 2b -3), B(-4, 2b) and P is (2, -2a)

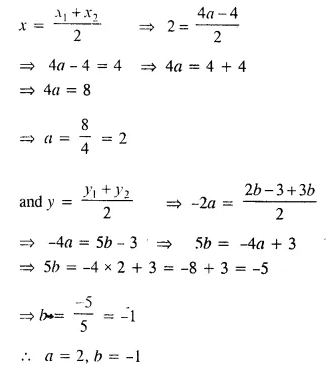
Question 11.
The mid point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the value of a and b.
Solution:
The midpoint of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1)

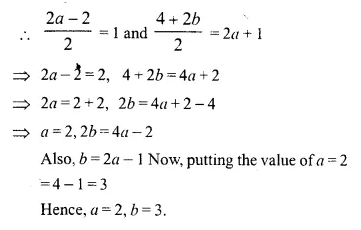
Question 12.
(i) Write down the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP, where O is the origin.
(iii) In what ratio does the y-axis divide the line AB ? [ICSE 1995]
Solution:
Point P, divides a line segment giving the points A (-4, 1) and B (17, 10) is the ratio 1 : 2.

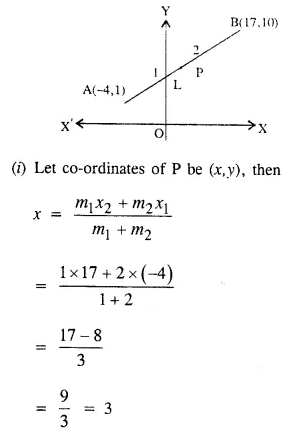
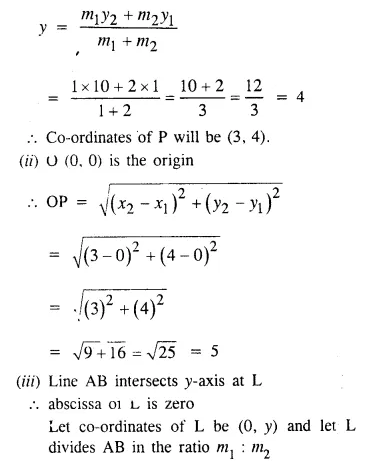
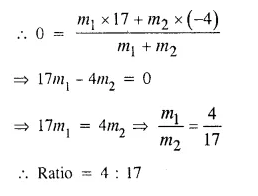
Question 13.
Prove that the points A(-5, 4); B (-1, -2) and C (5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D. So that ABCD is a square. [1992]
Solution:
In ABC, the co-ordinates of A, B and C are (-5, 4), B(-1, -2) and C (5, 2) respectively.

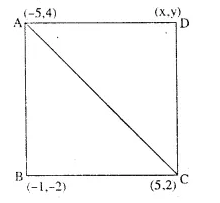
ABC is also a right-angled triangle.
Hence ABC is an isosceles right angled triangle,
Let D be the fourth vertex of square ABCD and co-ordinates of D be (x,y)
Since the diagonals of a square bisect each other and let O be the point of intersection of AC and BD.
O is mid-point of AC as well as BD.

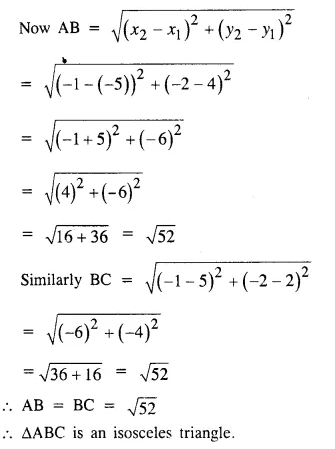
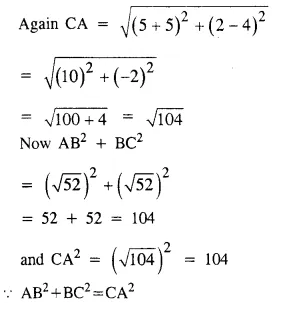
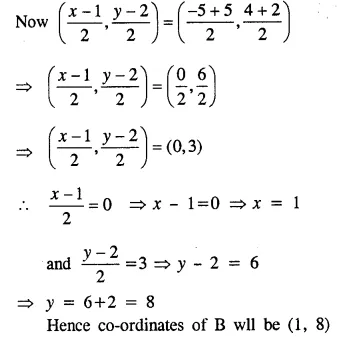
Question 14.
M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1). Find the co-ordinates of point M. Further, if R (2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.
Solution:
Two points are given A (-3, 7) and B (9, -1)
M is the mid-point of line joining AB.
Co-ordinates of M wll be

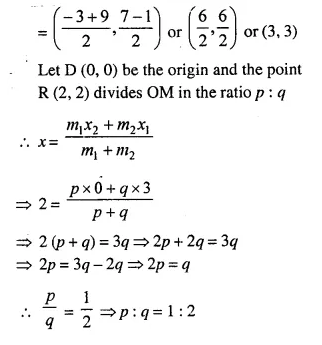
Question 15.
Calculate the ratio in which the line joining A (-4, 2) and B (3, 6) is divided by point P (x, 3). Also find
(i) x
(ii) Length of AP. (2014)
Solution:
Let ratio = k : 1

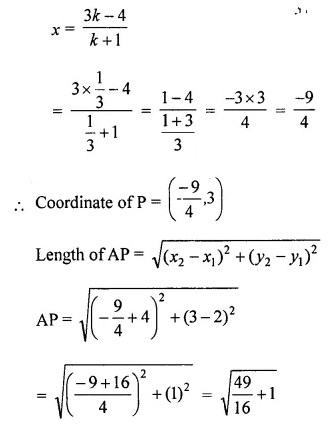
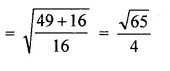
Question 16.
Find the ratio in which the line 2x + y = 4 divides the line segment joining the points P (2, -2) and Q (3, 7).
Solution:
Let the given line 2x + y = 4 divides the line segment joining the points P (2, -2) and Q (3,7) in the ratio k : 1 at a point (x, y) on it.

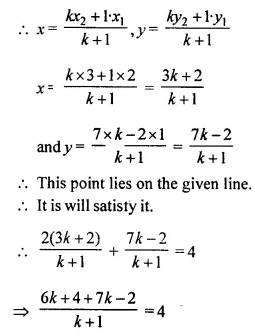
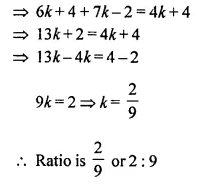
Question 17.
If the abscissa of a point P is 2. Find the ratio in which this point divides the line segment joining the points (-4, 3) and (6, 3). Also, find the co-ordinate of point P.
Solution:
Abscissa of a point P is 2
Let co-ordinates of point P be (2, y)
Let point P (2, y) divides the line segment joining the points (-4, 3) and (6, 3) in the ratio k : 1

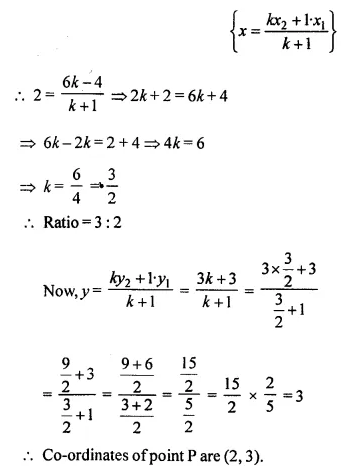
Question 18.
The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x – y + k = 0, find the value of k, Also, find the co-ordinates of point Q.
Solution:
A line joining the points (2, 1) and (5, -8) is trisector at P and Q.

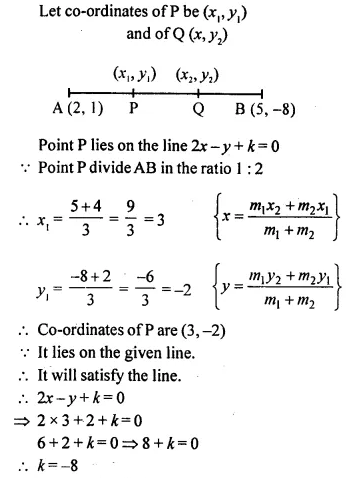
Question 19.
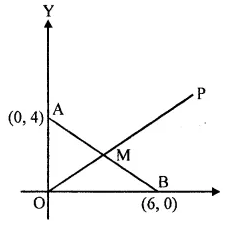
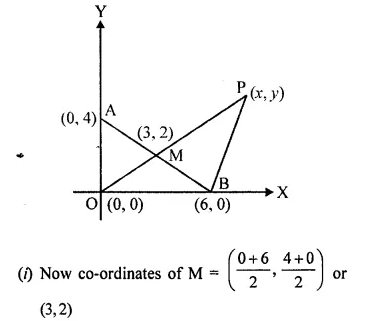
M is the mid-point of the line segment joining the points A (0, 4) and B (6, 0). M also divides the line segment OP in the ratio 1 : 3. Find:
(i) co-ordinates of M
(ii) co-ordinates of P
(iii) length of BP

Solution:
M is mid point of the line segment joining the points A (0, 4) and B (6, 0)
M divides the line segment OP in the ratio 1 : 3

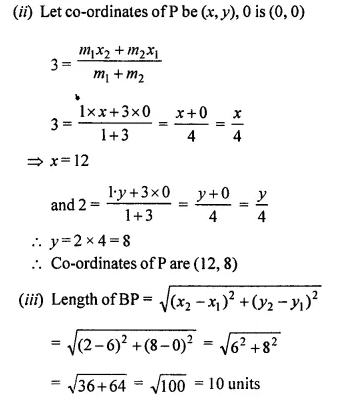
Question 20.
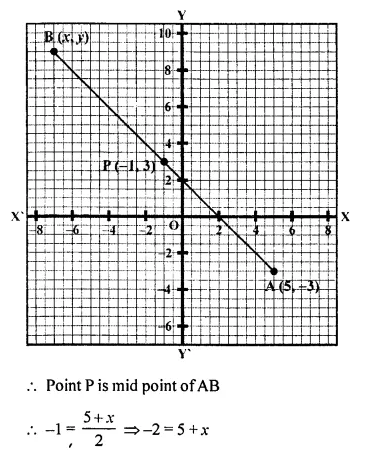
Find the image of the point A (5, -3) under reflection in the point P (-1, 3).
Solution:
Image of the point A (5, -3) under reflection in the point P (-1, 3)
Let B (x, y) be the point of reflection of A (5, -3) under P(-1, 3)

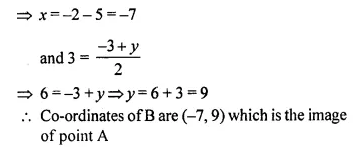
Question 21.
A (-4, 2), B (0, 2) and C (-2, -4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of PQR is the same as the centroid of ABC.
Solution:
A (-4, 2), B (0, 2) and C (-2, -4) are the vertices of ABC.
P, Q and R are the mid-points of the sides BC, CA and AB respectively.
G is the centroid of medians AP, BQ and CR.
Co-ordinates of G are

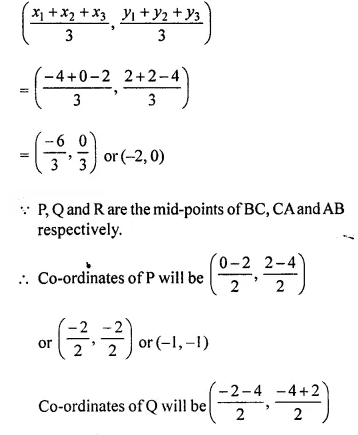
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.