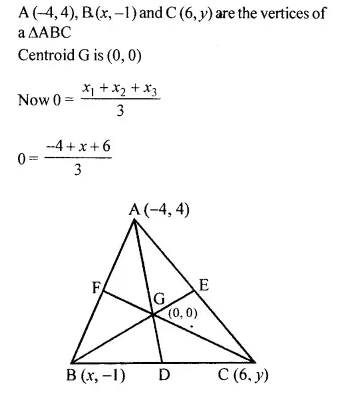
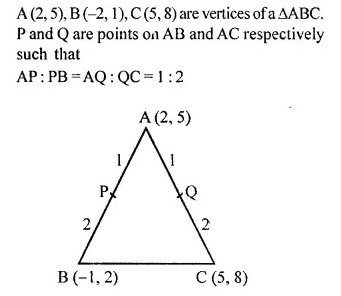
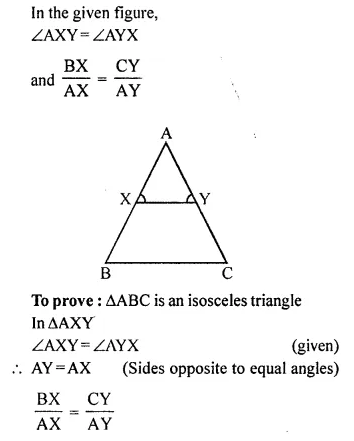
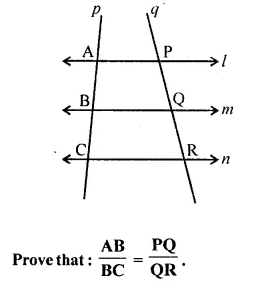
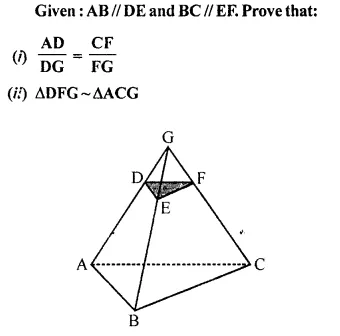
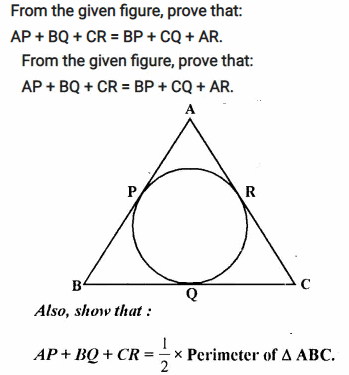
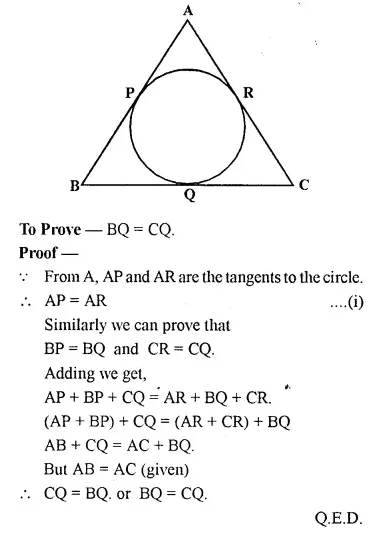
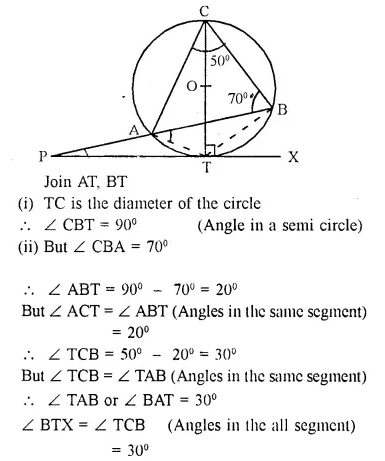
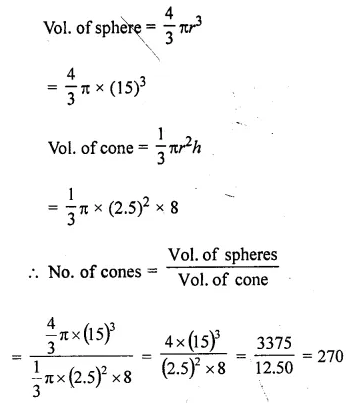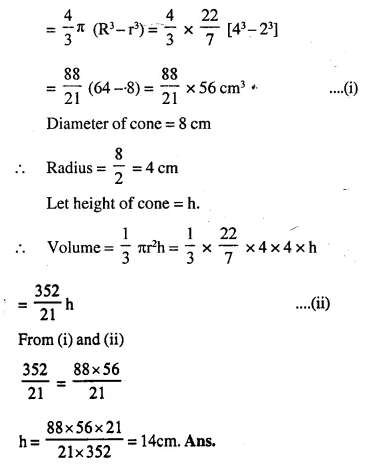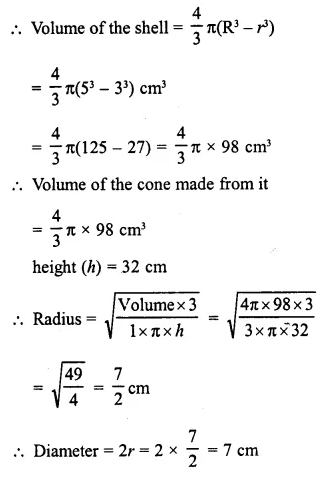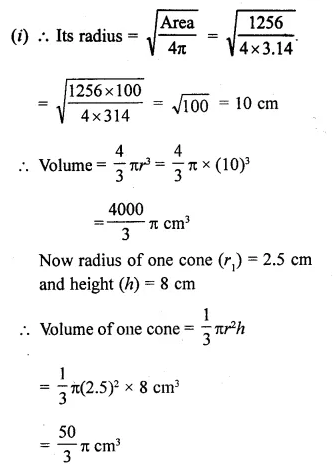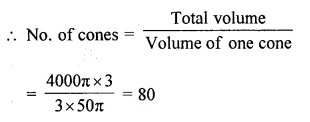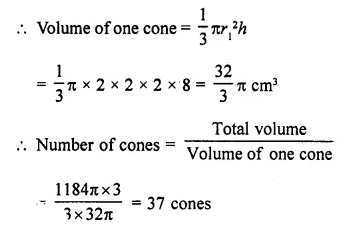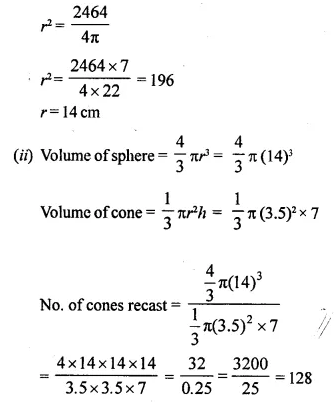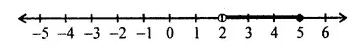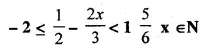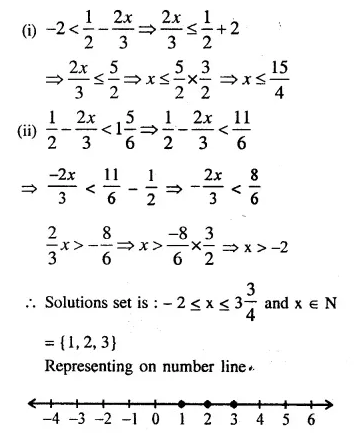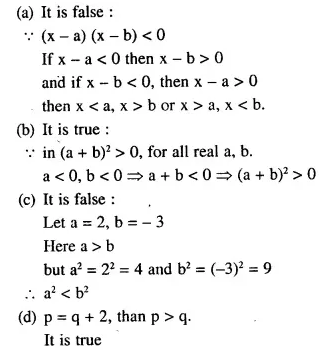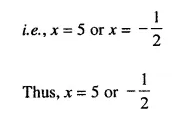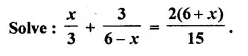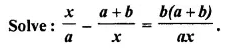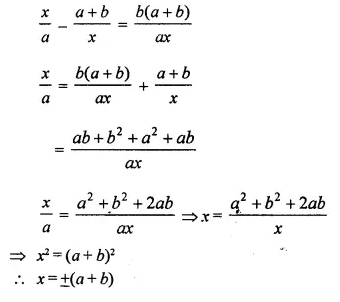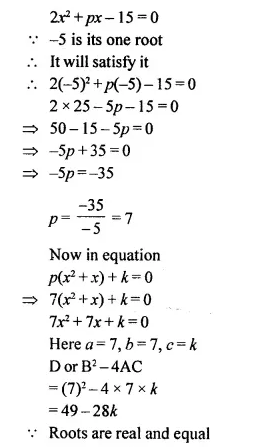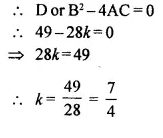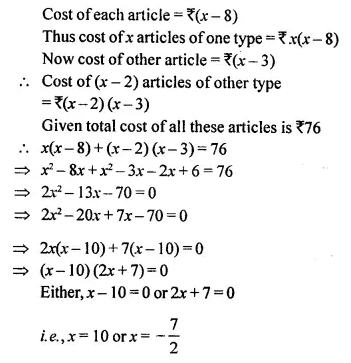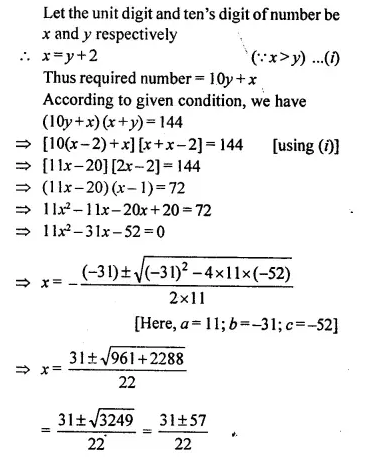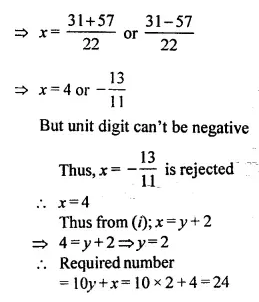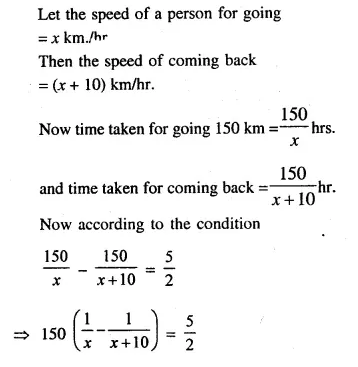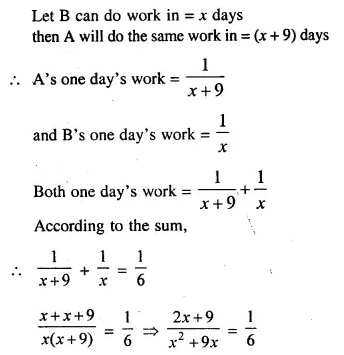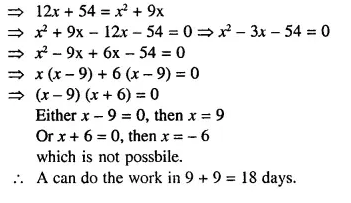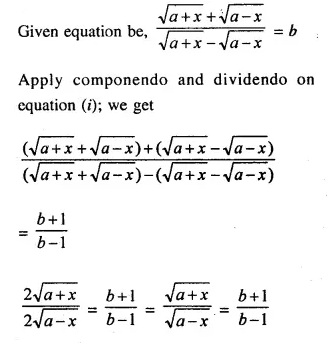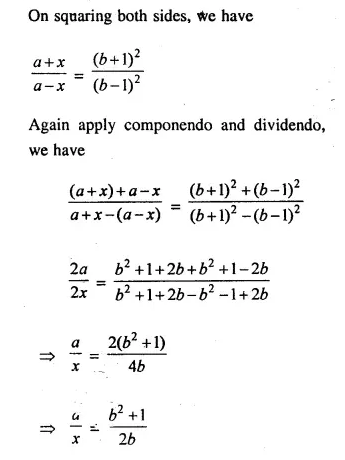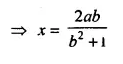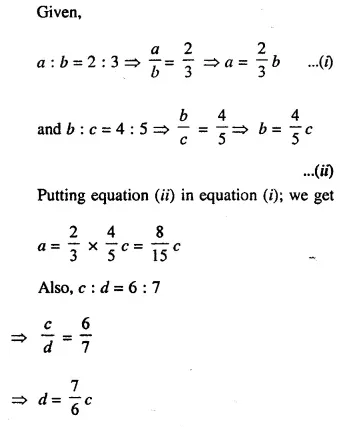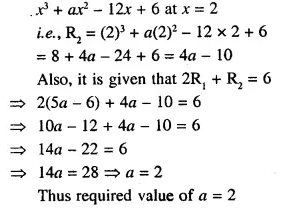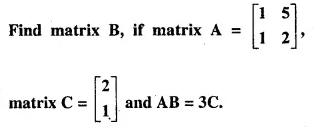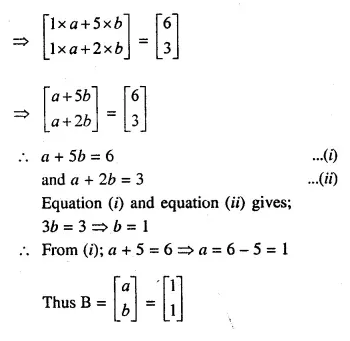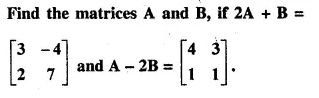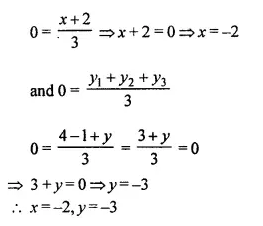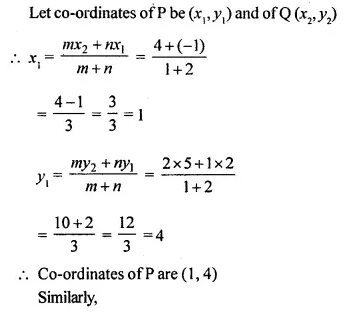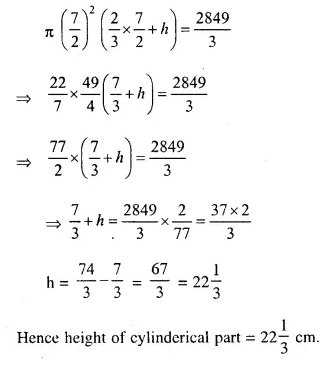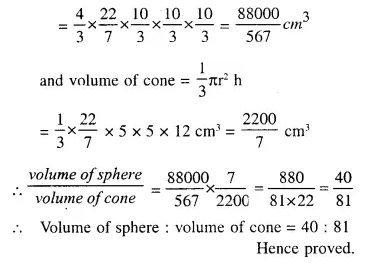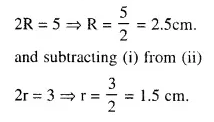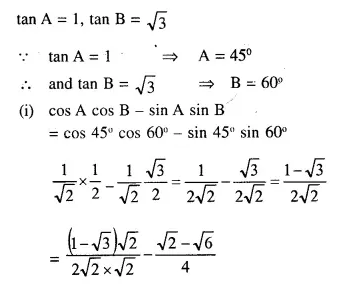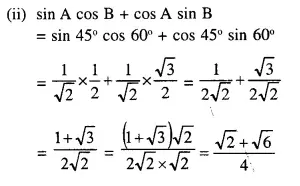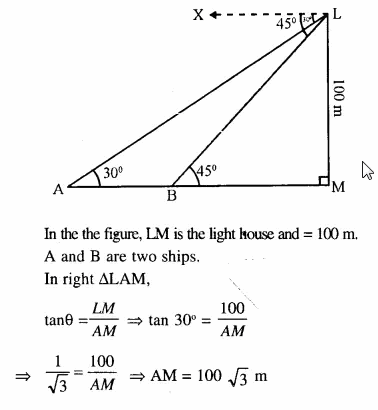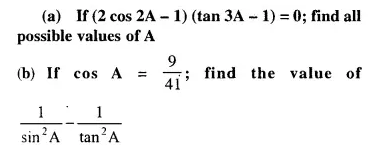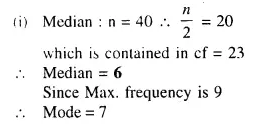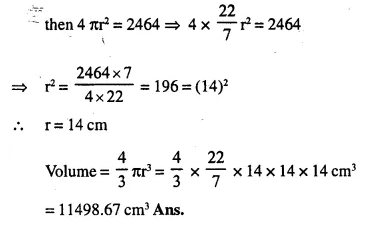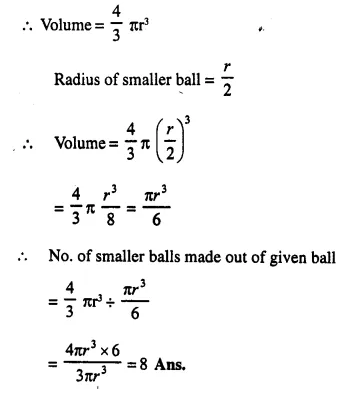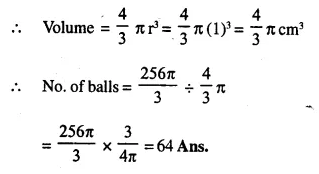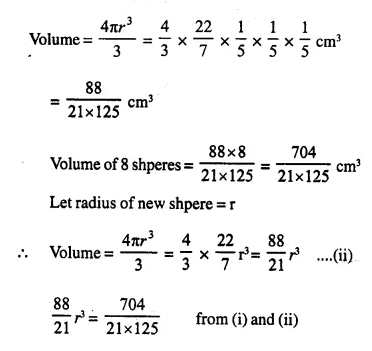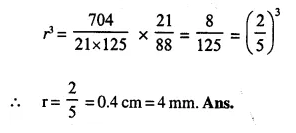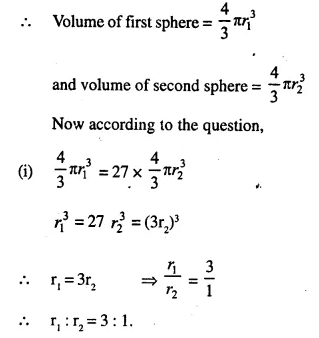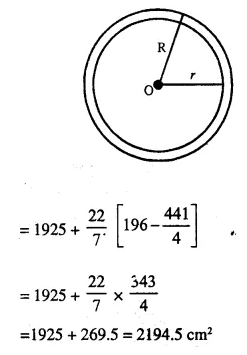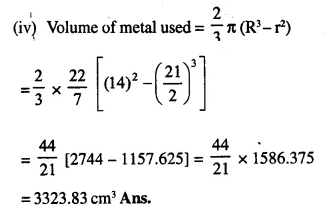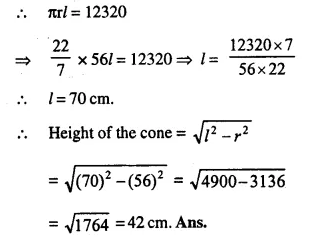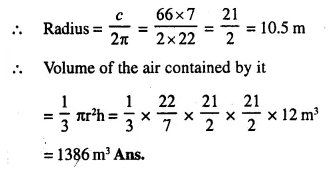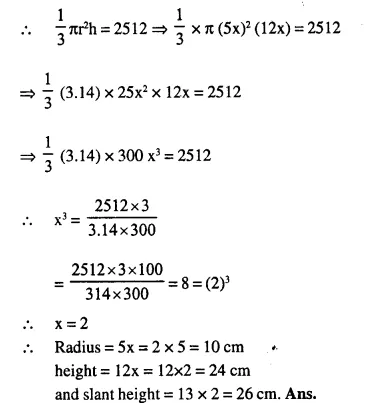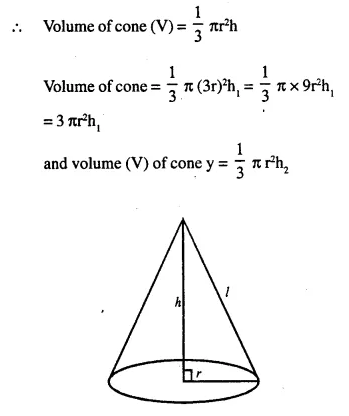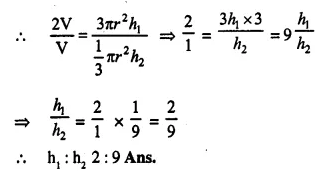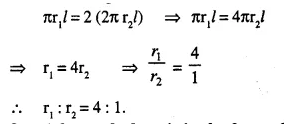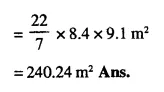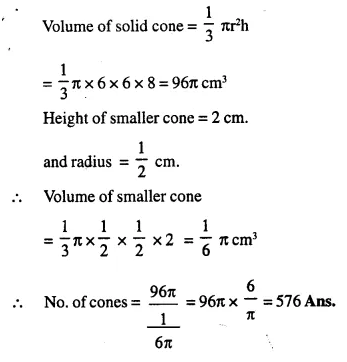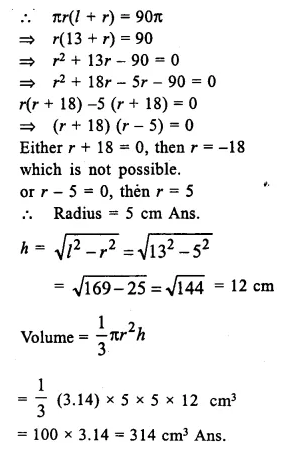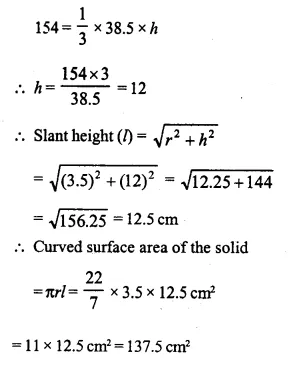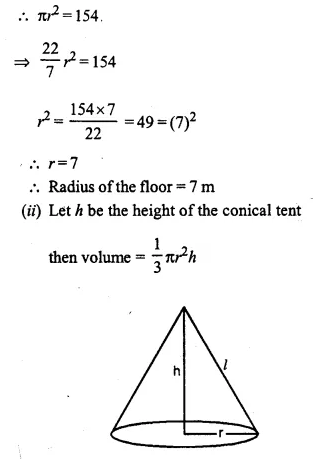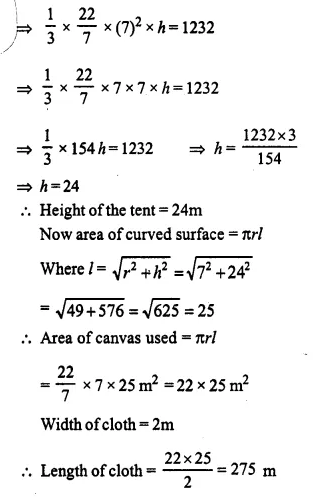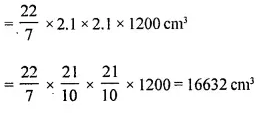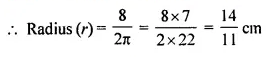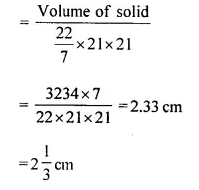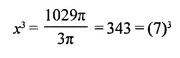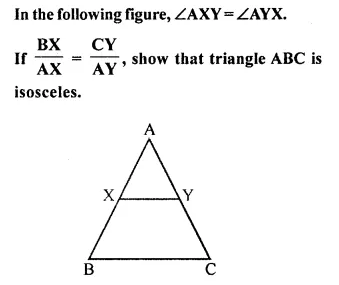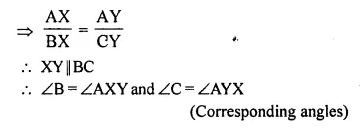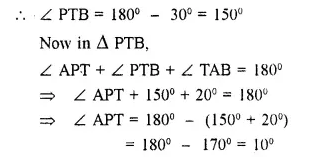Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20E
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G
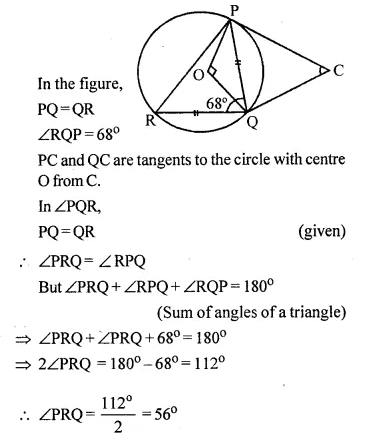
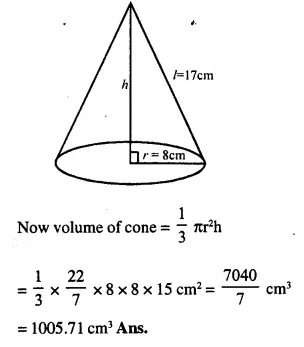
Question 1.
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
Solution:
Height of cone = 15 cm
and radius of base = \(\frac { 7 }{ 2 }\)cm.
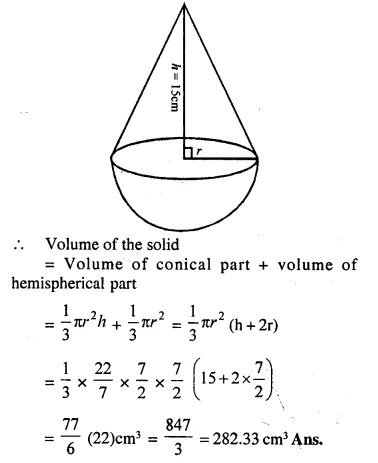
Question 2.
A buoy is made in the form of hemisphere surmounted by a right, cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-thirds of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
Solution:
Radius of hemispherical part (r)
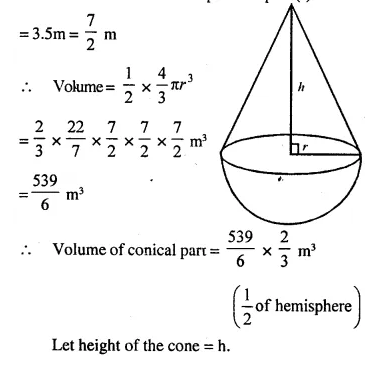
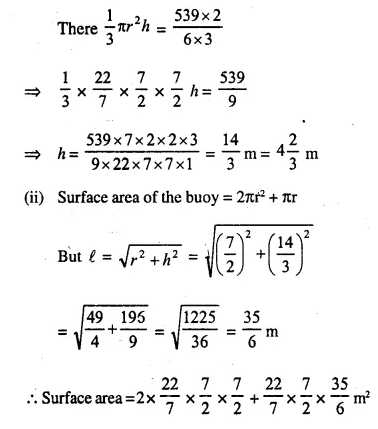
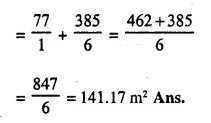
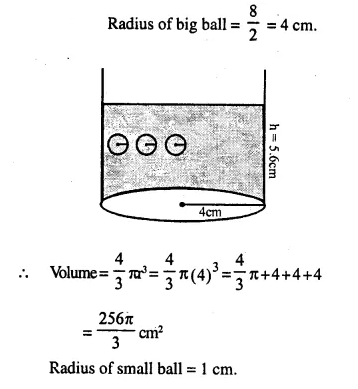
Question 3.
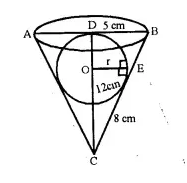
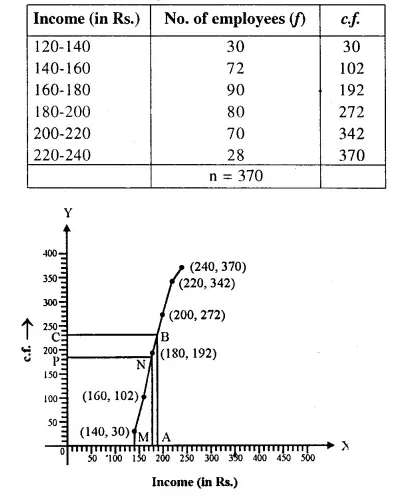
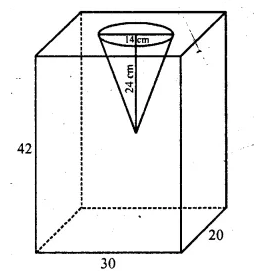
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find:
(i) the surface area of remaining solid,
(ii) the volume of remaining solid,
(iii) the weight of the material drilled out if it weighs 7 gm per cm3.
Solution:
Length of rectangular solid (l) = 30 cm
Breadth (b) = 20 cm
and height (h) = 42 cm
Diameter of the cone = 14 cm
(i) Surface area of remaining solid Surface area of rectangular solid + Surface area of curved surface of cone – Surface area of the base of the cone
= 2 (lb + bh + hl) + πrl – πr2
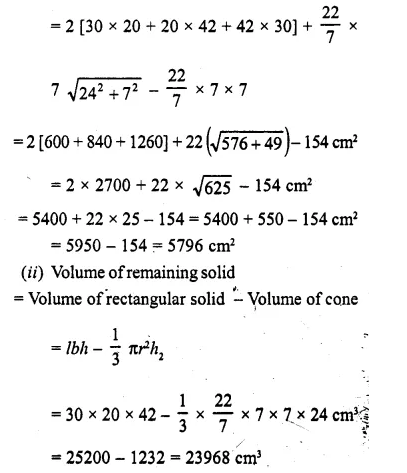
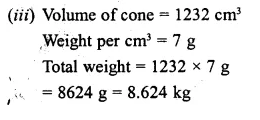
Question 4.
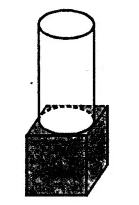
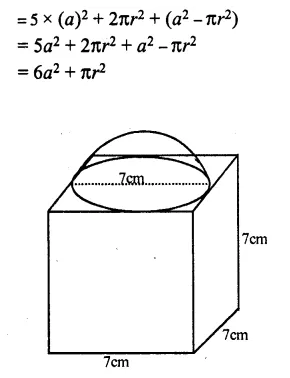
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
Solution:
Side of a cubical block = 7 cm
Radius of the hemisphere = \(\frac { 7 }{ 2 }\)cm
Now total surface area of the block
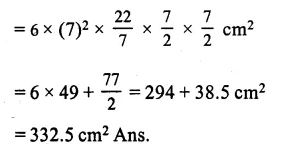
Question 5.
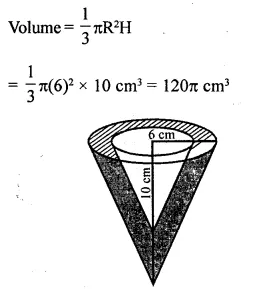
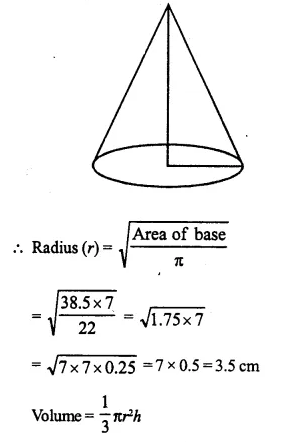
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the rim. When lead shots each of which is a sphere of radius 0.5 cm are dropped into the vessel, one- fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Solution:
Radius of conical vessel (R) = 5 cm
and height (h) = 8 cm
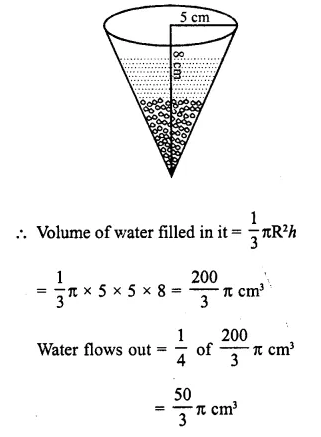

Question 6.
A hemi-spherical bowl has neligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
Solution:
Upper circumference of the hemi-spherical bowl = 198 cm

Question 7.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Solution:
Radius of solid hemisphere = r
Radius of the cone carved out of the hemisphere = r
and height (h) = r
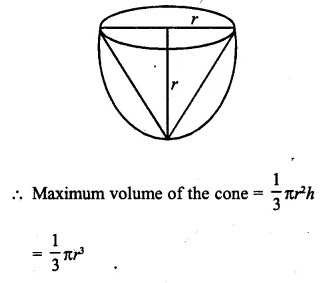
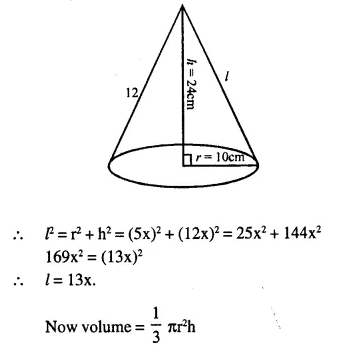
Question 8.
The radii of the bases of two solid right circular cones of same height are r1 and r2 The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms of r1, r2 • and R.
Solution:

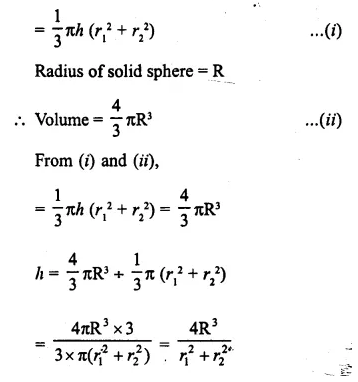
Question 9.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number * of cones so formed.
Solution:
Diameter of solid hemisphere = 28 cm
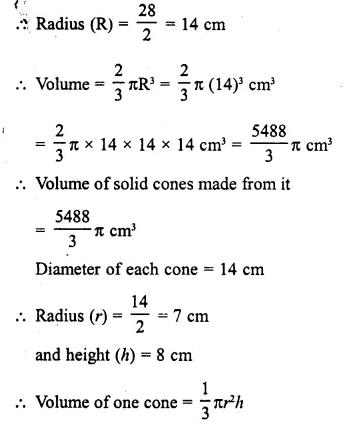
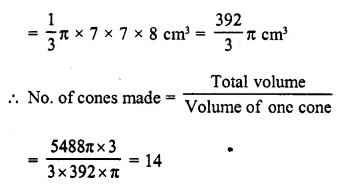
Question 10.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Solution:
Let radius of the base of cone = r
and height = h
Then radius of hemisphere = r
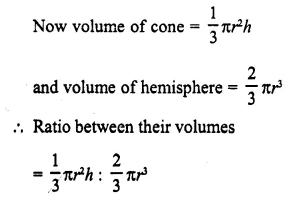
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.