Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B 

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B 

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18C

Question 1.
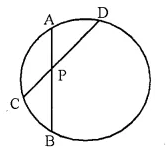
(i) In the given figure 3 x CP = PD = 9 cm and AP = 4.5 cm. Find BP.

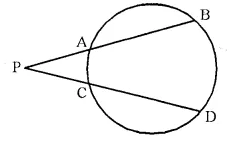
(ii) In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4 cm. Find CD.

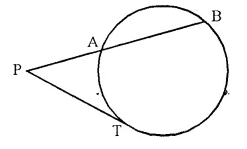
(iii) In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.

Solution:

Question 2.
In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
(i) AB.
(ii) the length of tangent PT. (2014)

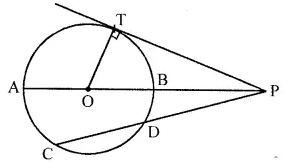
Solution:
PT is tangent and PDC is secant out to the circle
∴ PT² = PC x PD
PT² = (5 + 7.8) x 5 = 12.8 x 5
PT² = 64 ⇒ PT = 8 cm
In ΔOTP
PT² + OT² = OP²
8²+x² = (x + 4)²
⇒ 64 +x² = x² + 16 + 8x
64- 16 = 8x
⇒ 48 = 8x
x = \(\frac { 48 }{ 8 }\) = 6 cm
∴ Radius = 6 cm
AB = 2 x 6 = 12 cm

Question 3.
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60°, calculate
(i) ∠ QAB
(ii) ∠ PAD
(iii) ∠ CDB.

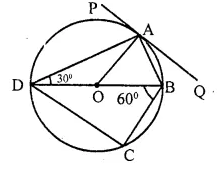
Solution:
(i) PAQ is a tangent and AB is the chord, ∠ QAB = ∠ ADB (Angles in the alternate segment)
= 30°
(ii) OA = OD (Radii of the same circle)
∴ ∠ OAD = ∠ ODA = 30°
But OA ⊥ PQ
∴ ∠ PAD = ∠ OAP – ∠OAD = 90° – 30° = 60°
(iii) BD is diameter
∴ ∠ BCD = 90° (Angle in semi circle)
Now in ∆ BCD,
∠ CDB + ∠ CBD + ∠ BCD = 180°
⇒ ∠ CDB + 60° + 90° = 180°
⇒ ∠ CDB = 180°- (60° + 90°) = 180° – 150° = 30°

Question 4.
If PQ is a tangent to the circle at R; calculate:
(i) ∠ PRS
(ii) ∠ ROT.
Given O is the centre of the circle and angle TRQ = 30°.
Solution:

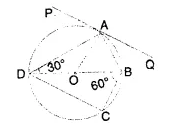
PQ is tangent and OR is the radius
∴ OR ⊥ PQ
∴ ∠ORT = 90° =
∠TRQ = 90° – 30° = 60°
But in ∆ OTR, OT = OR (Radii of the circle)
∴ ∠ OTR = 60° or ∠STR = 60°
But ∠PRS = ∠STR (Angles in the alternate segment) = 60°
In ∆ ORT, ∠ OTR = 60°, ∠ TOR = 60°
∴ ∠ROT= 180°-(60°+ 60°)= 180°-120° = 60°

Question 5.
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersect AB produced in D. Show that BC = BD.
Solution:


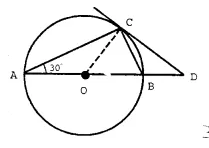
Given: In a circle, O is the centre,
AB is the diameter, a chord AC such that ∠ BAC = 30°
and a tangent from C, meets AB in D on producing. BC is joined.
To Prove: BC = BD
Construction: Join OC
Proof : ∠ BCD = ∠ BAC =30°(Angle in alternate segment)
Arc BC subtends ∠ DOC at the centre of the circle and ∠ BAC at the remaining part of the circle.
∴ ∠ BOC = 2 ∠ BAC = 2 x 30° = 60°
Now in ∆ OCD,
∠ BOC or ∠ DOC = 60° (Proved)
∠ OCD = 90° (∵ OC ⊥ CD)
∴ ∠ DOC + ∠ ODC = 90°
⇒ 60° + ∠ ODC = 90°
∴ ∠ ODC = 90°- 60° = 30°
Now in ∆BCD,
∵∠ ODC or ∠ BDC = ∠ BCD (Each = 30°)
∴ BC = BD Q.E.D.

Question 6.
Tangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR, show that ∆PQR is isosceles.
Solution:

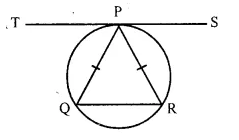
In a circumcircle of ∆PQR, a tangent TPS is drawn through P which is parallel to QR
To prove : ∆PQR is an isosceles triangle.
Proof:
∵ TS \(\parallel\) QR
∠TPQ = ∠PQR (Alternate angles) ….(i)
∵ TS is tangent and PQ is the chord of the circle
∴ ∠TPQ = ∠RP (Angles in the alternate segment) ….(ii)
From (i) and (ii),
∠PQR = ∠QRP
∴ PQ = PR (Opposite sides of equal angles)
∴ ∆PQR is an isosceles triangle
Hence proved

Question 7.
Two circles with centres O and O’ are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O’ at A. Prove that OA bisects angle BAC.

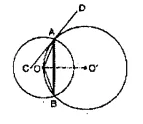
Solution:

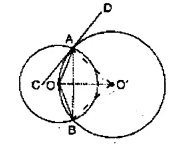
Given: Two circles with centre O and O’ intersect each other at A and B, O lies on the circumference, of the other circle. CD is a tangent at A to the second circle. AB, OA are joined.
To Prove: OA bisects ∠ BAC.
Construction: Join OB, O’A, O’B and OO’
Proof: CD is the tangent and AO is the chord
∠ OAC = ∠ OBA …(i)
(Angles in alt. segment)
In ∆ OAB, OA = OB (Radii of the same circle)
∴ ∠ OAB = ∠ OBA ….(ii)
From (i) and (ii),
∠ OAC = ∠ OAB
∴ OA is the bisector of ∠ BAC Q.E.D.

Question 8.
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that: ∠ CPA = ∠DPB.

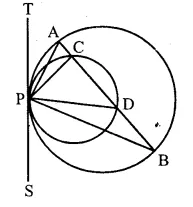
Solution:
Given:Two circles touch each other internally at P. A chord AB of the bigger circle intersects the smaller circle at C and D. AP, BP, CP and DP are joined.
To Prove: ∠ CPA = ∠ DPB
Construction: Draw a tangent TS at P to the circles given.
Proof:
∵ TPS is the tangent, PD is the chord.
∴ ∠ PAB = ∠ BPS …(i) ( Angles in alt. segment)
Similarly we can prove that
∠ PCD = ∠ DPS …(ii)
Subtracting (i) from (ii), we gel
∠ PCD – ∠ PAB = ∠ DPS – ∠ BPS
But in ∆ PAC,
Ext. ∠ PCD = ∠ PAB + ∠ CPA
∴ ∠ PAB + ∠ CPA – ∠ PAB = ∠ DPS – ∠ BPS
∠ CPA = ∠ DPB           Q.E.D.

Question 9.
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Solution:

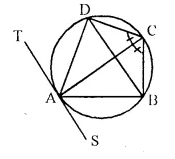
Given: ABCD is a cyclic quadrilateral and diagonal AC bisects ∠ BCD. AT A. a tangent TAS is drawn. BD is joined.
To Prove: TS || BD.
Proof: ∠ ADB = ∠ ACB …….(i) (Angles in the same segment)
Similarly ∠ ABD = ∠ ACD ……..(ii)
But ∠ ACB = ∠ ACD (AC is the bisector of ∠ BCD)
∴ ∠ ADB = ∠ ABD |From (i) and (ii)]
TAS is a tangent and AB is chord
∴ ∠ BAS = ∠ ADB (Angles in all segment)
But ∠ ADB = ∠ ABD (Proved)
∴ ∠ BAS = ∠ ABD
But these are alternate angles.
∴ TS || BD.      Q.E.D.

Question 10.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠ BCG = 108° and O is the centre of the circle,
Find:
(i) angle BCT
(ii) angle DOC

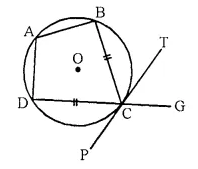
Solution:

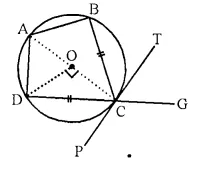
Join OC, OD and AC.
(i) ∠ BCG + ∠ BCD = 180° (Linear pair)
⇒ 108° + ∠ BCD = 180°
(∵∠ BCG = 108° given)
∴∠ BCD = 180° – 108° = 72°
BC = CD (given)
∴ ∠ DCP = ∠ BCT
But ∠ BCT + ∠ BCD + ∠ DCP = 180°
∴∠ BCT + ∠ BCT + 72° = 180°
(∵∠ DCP = ∠ BCT)
2 ∠ BCT = 180° – 72° = 108°
∴∠ BCT = \(\frac { { 108 }^{ \circ } }{ 2 }\) = 54°
(ii) PCT is the tangent and CA is chord
∴ ∠ CAD = ∠ BCT = 54°
But arc DC subtends ∠ DOC at the centre and
∠ CAD at the remaining part of the circle
∴ ∠ DOC = 2 ∠ CAD = 2 x 54° = 108°.

Question 11.
Two circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T; show that the points P, B, Q and T arc concyclic.
Solution:
Given: Two circles intersect each other at point A and B. PAQ is a line which intersects circles at P, A and Q. At P and Q, tangents are drawn to the circles which meet at T.
To Prove: P, B, Q, T are concyclic.

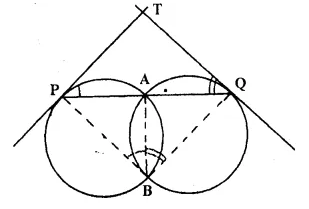
Construction: Join AB, BP and BQ.
Proof: TP is the tangent and PA. a chord
∴ ∠ TPA = ∠ ABP
(angles in alt. segment)
Similarly we can prove that
∠ TQA = ∠ ABQ …,(ii)
Adding (i) and (ii), we get
∠ TPA + ∠ TQA = ∠ ABP + ∠ ABQ
But in ∆ PTQ,
∠ TPA + ∠ TQA + ∠ PTQ = 180°
⇒ ∠ TPA + ∠ TQA = 180° – ∠ PTQ
⇒ ∠ PBQ = 180°- ∠ PTQ
⇒ ∠ PBQ + ∠PTQ = 180°
But there are the opposite angles of the quadrilateral
∴ Quad. PBQT is a cyclic
Hence P, B. Q and T are concyclic     Q.E.D.

Question 12.
In the figure; PA is a tangent to the circle. PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also shaw that:

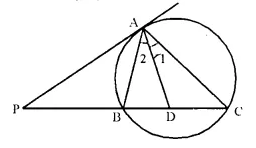
Solution:
Given: In a circle PA is the tangent, PBC is the secant and AD is the bisector of ∠BAC which meets the secant at D.
To Prove:
(i) ∆ PAD is an isosceles triangle.
(ii) ∠CAD = \(\frac { 1 }{ 2 }\) [(∠PBA – ∠PAB)]
Proof:
(i) PA is the tangent and AB is chord.
∠PAB = ∠C ….(i)
(Angles in the alt. segment)
AD is the bisector is ∠BAC
∴ ∠1 = ∠2 ….(ii)
In ∆ ADC,
Ext. ∠ADP = ∠C + ∠1
= ∠PAB + ∠2 = ∠PAD
∴ ∆ PAD is an isosceles triangle.
(ii) In A ABC,
Ext. ∠PBA = ∠C + ∠BAC
∴∠BAC = ∠PBA – ∠C
⇒ ∠1 + ∠2 = ∠PBA – ∠PAB [from (i)]
⇒ 2 ∠1 = ∠PBA – ∠PAB
⇒ ∠1 = – [∠PBA – ∠PAB]
⇒ ∠CAD = – [∠PBA – ∠PAB] Q.E.D.

Question 13.
Two circles intersect each other at points A and B. Their common tangent touches the circles v at points P and Q as shown in the figure . Show that the angles PAQ and PBQ arc supplementary. [2000]

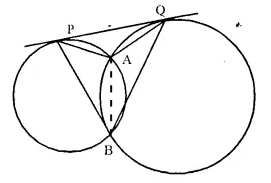
Solution:
Given: Two circles intersect each other at A and
B. A common tangent touches the circles at P and
Q. PA. PB, QA and QB are joined.
To Prove: ∠ PAQ + ∠ PBQ = 180°
or ∠ PAQ and ∠ PBQ are supplementary.
Construction: Join AB.
Proof: PQ is the tangent and AB is the chord
∴ ∠ QPA = ∠ PBA (alternate segment) ,…(i)
Similarly we can prove that
∠ PQA = ∠ QBA ,…(ii)
Adding (i) and (ii), we get
∠ QPA + ∠ PQA = ∠ PBA + ∠ QBA
But ∠ QPA + ∠ PQA = 180° – ∠ PAQ ,…(iii) (In ∆ PAQ)
and ∠ PBA + ∠ QBA = ∠ PBQ ,…(iv)
from (iii) and (iv)
∠ PBQ = 180° – ∠ PAQ
⇒ ∠ PBQ + ∠ PAQ = 180°
= ∠ PAQ + ∠ PBQ = 180°
Hence ∠ PAQ and ∠ PBQ arc supplementary Q.E.D.

Question 14.
In the figure, chords AE and BC intersect each other at point D.
(i) If ∠ CDE = 90°.
AB = 5 cm, BD = 4 cm and CD 9 cm;
Find DE.
(ii) If AD = BD, show that AE = BC.

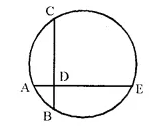
Solution:

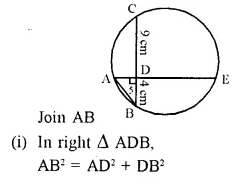
Question 15.
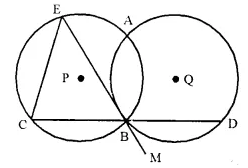
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles arc congruent; show that CE = BD.

Solution:

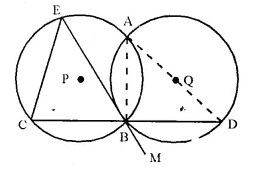
Given: Two circles with centre P and Q intersect each other at A and B. CBD is a line segment and EBM is tangent to the circle with centre Q, at B. Radii of the cirlces are equal.
To Prove: CE = BD
Construction: Join AB and AD.
Proof: EBM is the tangent and BD is the chord
∴ ∠ DBM = ∠ BAD (Anglesi in alt. segment)
But ∠ DBM = ∠ CBE (Vertically opposite angles)
∴ ∠ BAD = ∠ CBE
∵ In the same circle or congruent circles, if angles are equal, then chords opposite to them are also equal.
∴ CE = BD Q.E.D.

Question 16.
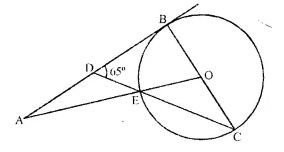
In the following figure O is the centre of ti.e circle and AB is a tangent to it at point B. ∠BDC = 65°, Find ∠BAO

Solution:
Given: ∠BDC = 65° and AB is tangent to circle with centre O.
∵ OB is radius
⇒ OB ⊥ AB
In ∆BDC
∠DBC + ∠BDC + ∠B CD = 180°
90° + 65° + ∠BCD =180°
⇒ ∠BCD = 25°
∵ OE = OC = radius
⇒ ∠OEC = ∠OCE
⇒ ∠OEC = 25°
Also, ∠BOE = ∠OEC + ∠OCE
[Exterior angle = sum of opposite interior angles in a ∆]
⇒ ∠BOE = 25°+ 25°
⇒∠BOE = 50°
⇒ ∠BOA = 50°
In ∆AOB
∠AOB + ∠BAO + ∠OBA = 180°
50° + ∠BAO + 90° = 180°
⇒ ∠BAO = 40°

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B  are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.