Selina Concise Mathematics Class 10 ICSE Solutions Chapter 19 Constructions (Circles) Ex 19
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 19 Constructions (Circles) Ex 19
Question 1.
Draw a circle of radius 3 cm. Mark a point P at a distance of 5cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Solution:
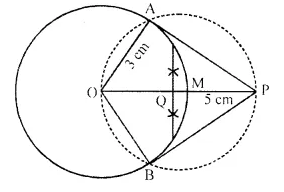
Steps of Construction:
(i) Draw a circle with centre O and radius 3 cm.
(ii) From O, take a point P such that OP = 5 cm.
(iii) Draw the bisector of OP which intersects OP at M.
(iv) With centre M, and radius OM. draw’ a circle which intersects the given circle at A and B.
(v) Join AP and BP.
AP and BP are the required tangents.
On measuring them, AP = BP = 4 cm.
Question 2.
Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Solution:
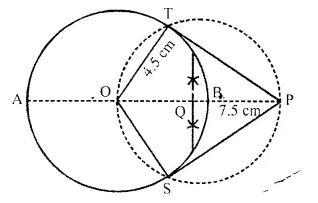
Steps of Construction:
(i) Draw a line segment AB = 9 cm.
(ii) Draw a circle with centre O and AB as diameter.
(iii) Take a point P from the centre at a distance of 7.5 cm.
(iv) Draw an other circle OP as diameter which intersects the given circle at T and S.
(v) Join TP and SP.
TP and SP are are required tangents.
On measuring their lengths, TP = SP = 6 cm.
Question 3.
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45°.
Solution:
Steps of Construction:
(i) Draw a circle with centre O and radius 5 cm.
(ii) Draw two arcs making an angle of 180° – 45° = 135°
so that ∠AOB = 135°.
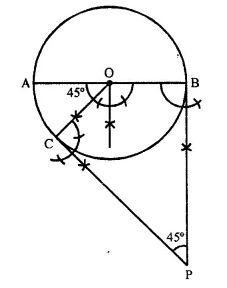
(iii) At A and B, draw two rays making an angle of 90° at each point which meet each other at P, out side the circle.
Then AP and BP are the required tangents which make an angle of 45° at P.
Question 4.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Solution:
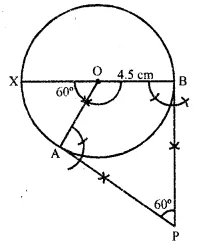
Steps of Construction:
(i) Draw a circle with centre O and radius 4.5 cm.
(ii) Draw two arcs making an angle of 180° – 60° = 120° i.e. ∠AOB = 120°.
(iii) At A and B draw rays making an angle of 90° at each point which meet each other at P outside the circle.
AP and BP are the required tangents which makes an angle of 60° at P.
Question 5.
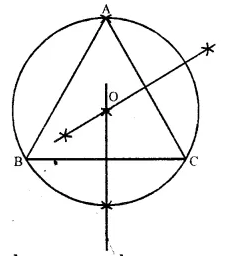
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Solution:
Steps of Construction:
(i) Draw a line segment BC = 4.5 cm.
(ii) With centres B and C, draw two arcs of radius 4.5 cm. which intersect each other at A.
(iii) Join AB and AC,
(iv) Draw the perpendicular bisectors of AB and BC intersecting each other at O.
(v) With centre O, and radius OA or OB or OC draw a circle which will passes through A, B and C.
This is the required circumcircle of ∆ ABC.
Measuring OA = 2.6 cm
Question 6.
Construct triangle ABC, having given = 7 cm, AB – AC = 1 cm and ∠ABC = 45°.
(ii) Inscribe a circle in the ∆ ABC constructed in (i) above,
Solution:
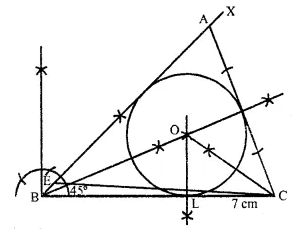
Steps of Construction:
(i) Draw a line segment BC = 7 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = AB – AC = 1 cm.
(iii) Join EC and draw the perpendicular bisector of EC intersecting BX at A.
(iv) Join AC
∆ ABC is the required triangle.
(v) Draw angle bisectors of ∠ABC and ∠ACB intersecting each other at O.
(vi) From O, draw perpendicular OL to BC.
(vii) O as centre and OL as radius draw circle which touches the sides of the A ABC. This is the required in-circle of ∆ ABC.
On measuring radius OL = 1.8 cm (approx.).
Question 7.
Using ruler and compasses only, draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the circle.
Solution:
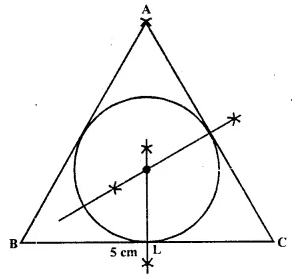
Steps of Construction:
(i) Draw a line segment BC = 5 cm.
(ii) With centre B and C, draw two arcs of 5 cm radius each which intersect each other at A.
(iii) Join AB and AC.
(iv) Draw angle bisectors of ∠B and ∠C intersecting each other at O.
(v) From O, draw OL ⊥ BC.
(vi) Now with centre O and radius OL, draw a circle which will touch the sides of the ∆ ABC. Measuring OL =1.4 cm. (approx.).
Question 8.
Using ruler and compasses only,
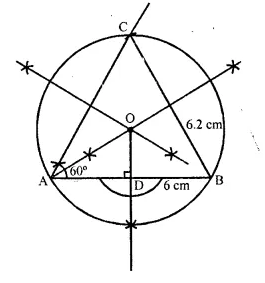
(i) Construct a triangle ABC with the following data:
Base AB = 6 cm, BC = 6.2 cm and ∠CAB = 60°.
(ii) In the same diagram, draw a circle which passes through the points A, B and C and mark its centre O.
(iii) Draw a perpendicular from O to AB which meets AB in D.
(iv) Prove that AD = BD.
Solution:
Steps of Construction:
(i) Draw a line segment AB = 6 cm.
(ii) At A, draw a ray making an angle of 60° with BC.
(iii) B as centre and 6.2 cm as radius draw an arc which intersect the AX rays at C.
(iv) Join CB.
∆ ABC is the required triangle.
(v) Draw the perpendicular bisectors of AB and AC intersecting each other at O.
(vi) With centre O, and radius as OA or OB or OC, draw a circle which will pass through A, B and C.
(vii) From O, draw OD ⊥ AB.
Proof: In right ∆ OAD and ∆ ODB
Hyp, OA = OB (radii of the saine circle)
Side OD = OD (Common)
∴ OAD ≅ OBD (R.H.S.)
∴ AD = BD (C.P.C.T.)
Question 9.
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC and measure its radius.
Solution:
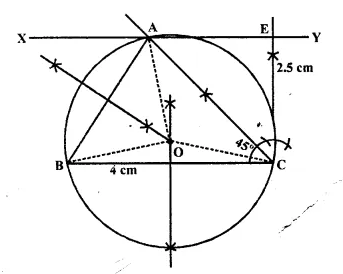
Steps of Construction:
(i) Draw a line segment BC = 4 cm.
(ii) At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm.
(iii) From E, draw another perpendicular line EY.
(iv) From C, draw a ray making an angle of 45° with CB, which intersects EY at A.
(v) JoinAB.
∆ ABC is the required triangle.
(vi) Draw perpendicular bisectors of sides AB and BC intersecting each other at O.
(vii) With centre O, and radius OB, draw a circle which passes through A, B and C.
Measuring the radius OB = OC = OA = 2 cm
Question 10.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
(i) What do you call the point O ?
(ii) What is the relation between the distances OA, OB and OC?
(iii) Does the perpendicular bisector of BC pass through O ?
Solution:
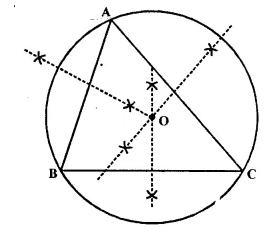
(i) Perpendicular bisectors of sides AB and AC intersect each other at O.
(ii) O is called the circum centre of circumcircle of ∆ ABC.
(iii) OA, OB and OC are the radii of the circumcircle.
(iv) Yes, the perpendicular bisector of BC will also pass through O.
Question 11.
The bisectors of angles A and B of a scalene triangle ABC meet at O.
(i) What is the point O called ?
(ii) OR ancLOQ are drawn perpendiculars to AB and CA respectively. What is the relation between OR and OQ ?
(iii) What is the relation between angle ACO and angle BCO ?
Solution:
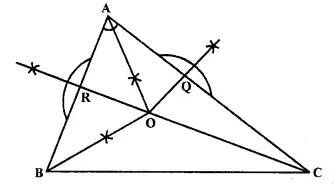
(i) ∆ ABC is a scalene triangle.
(ii) Angle bisectors of ∠A and ∠B intersect each other at O. O is called the incentre of the incircle of ∆ ABC.
(iii) Through O, draw perpendiculars to AB and AC which meet AB and AC at R and Q respectively.
(iv) OR and OQ are the radii of the in circle and OR =OQ.
(v) OC is the bisector of ∠C
∴∠ACO = ∠BCO
Question 12.
(i) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
(ii) Find its incentre and mark it I.
(iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle. What is the length of the radius of this circle.
Solution:
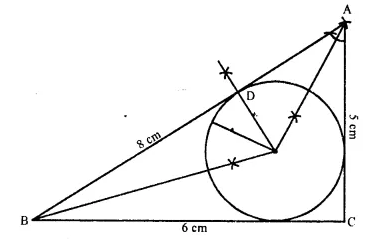
Steps of Construction:
(i) Draw a line segment BC = 6 cm.
(ii) With centre B and radius 8 cm draw ah arc.
(iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
(iv) Join AB and AC.
∆ ABC is the given triangle.
(v) Draw the angle bisectors of ∠B and ∠A intersecting each other at I.
Then I is the incentre of incircle of ∆ ABC.
(vi) Through I, draw ID ⊥ AB.
(vii) Now from D, cut off DP = DQ = \(\frac { 2 }{ 2 }\) = 1 cm.
(viii) With centre I, and radius IP or IQ, draw a circle which will intersect each side of ∆ ABC cuting chords of 2 cm each.
Question 13.
Construct an equilateral triangle ABC with side 6cm. Draw a circle circumscribing the triangle ABC.
Solution:
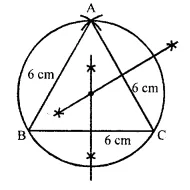
Steps of construction:
(i) Draw a line segment BC = 6cm.
(ii) With centre B and C, draw arcs with radius 6 cm each which intersect each other at A.
(iii) Join AB and AC,
then ∆ABC is the equilateral triangle.
(iv) Draw the perpendicular bisectors of BC and AB which intersect each other at O.
(v) Join OB and OC and OA.
(vi) With centre O, and radius OA or OB or OC, draw a circle which will pass through A, B and C.
This is the required circle.
Question 14.
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Solution:
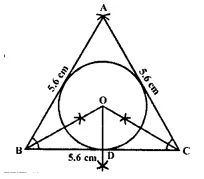
Steps of construction:
(i) Draw a line segment BC = 5.6 cm
(ii) With centre B and C,
draw two arcs of radius 5.6cm each which intersect each other at A.
(iii) Join AB and AC, then ∆ABC is an equilateral triangle.
(iv) Draw the angle bisectors of ∠B and ∠C which intersect each other at I.
(v) From I, draw ID ⊥ BC.
(vi) With centre I and radius ID, draw circle which touches the sides of the ∆ABC. This is the required circle.
Question 15.
Draw a circle circumscribing a regular hexagon of side 5cm.
Solution:
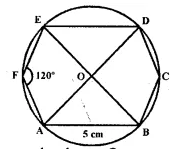
Steps of construction:
(i) Draw a regular hexagon ABCDEF whose each side is 5cm.
(ii) Join its diagonals AD, BE and CF intersecting each other at O.
(iii) With centre O and radius OA, draw a circle which will pass through the vertices of the hexagon A, B, C, D, E and F. This is the required circle.
Question 16.
Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Solution:
Steps of construction:
(i) Draw a line segment AB = 5.8cm.
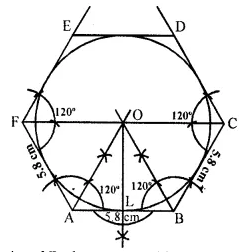
(ii) At A and B, draw rays making an angle of 120° each and cut off AF = BC = 5.8 cm.
(iii) Again at F and C, draw rays making an angle of 120° each and cut off FE = CD = 5.8 cm.
(iv) JoinDE. Then ABCDEF is the regular hexagon.
(v) Draw the bisectors of ∠A and ∠B intersecting each other at O.
(vi) From O, draw OL J. AB.
(vii) With centre O and radius OL, draw a circle which touches the sides of the hexagon. This is the required incircle of the hexagon.
Question 17.
Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
Solution:
Steps of construction:
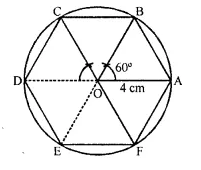
(i) Draw a circle of radius 4 cm with centre O.
(ii) Since regular hexagon \(\frac { { 360 }^{ \circ } }{ 6 }\) = 60°, draw radii
OA and OB, such that ∠AOB = 60°.
(iii) Cut off arcs BC, CD, DE, EF and each equal to arc AB on given circle.
(iv) Join AB, BC, CD, DE, EF, FA to get required regular hexagon ABCDEF in a given circle.
Question 18.
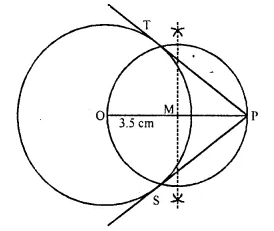
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent (2011).
Solution:
Steps of construction:
(i) Draw a line segment OP = 6 cm
(ii) With centre O and radius 3.5 cm, draw a circle
(iii) Draw the mid point of OP.
(iv) With centre M and diameter OP, draw a circle which intersect the circle at T and S.
(v) Join PT and PS.
PT and PS are the required tangent on measuring the length of PT = PS = 4.8 cm
Question 19.
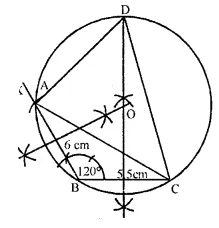
Construct a triangle ABC in which base BC=5.5 cm,AB = 6cmand ∠ABC = 120°.
(i) Construct a circle circumscribing the triangle ABC.
(ii) Draw- a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Solution:
Steps of construction:
(i) Draw BC = 6 cm. x
(ii) At B, draw ∠XBC= 120°.
(iii) From BX, cut off AB = 6 cm.
(iv) Join AC to get ∆ ABC.
(v) Draw the perpendicular bisector of BC and AB. These bisectors meet at O. With O as centre and radius equal tb OA, draw a circle, which passes through A, B and C. This is the required circumcircle of ∆ABC.
(vi) Produce the perpendicular bisector of BC so that it meets the circle at D. Join CD and AD to _ get the required cyclic quadrilateral ABCD.
Question 20.
Using a ruler and compasses only :
(i) Construct a triangle ABC with the following data : AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠BCP
Solution:
Steps of construction:
(i) Draw AB = 3.5
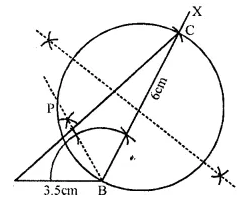
(ii) At B, draw ∠ABX = 120°.
(iii) With B as center draw an arc of radii 6 cm at C.
(iv) Join A and C.
(v) Draw the perpendicular bisector of line BC and draw a circle with BC as diameter.
(vi) Draw angle bisector of ∠B.
Meets the circle at P
∴ P is the required point ∠BCP = 30°
Question 21.
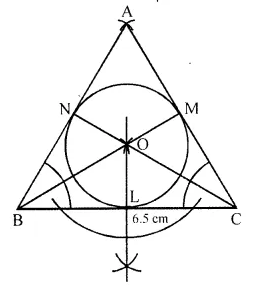
Construct a ∆ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle. (2014)
Solution:
Steps of construction:
(i) Draw a line segment BC = 6.5 cm.
(ii) From B, draw an arc of radius of 5.5 cm and from C, another arc of 5 cm radius which intersect each other at A.
(iii) Join AB and AC.
∆ABC is required triangle.
(iv) Draw the angle bisectors of ∠B and ∠C which intersect each other at O.
(v) Through O, draw OL ⊥ BC.
(vi) With centre O and radius OL, draw a circle which touches the sides of ∆ABC.
(vii) On measuring, OL = r = 1.5 cm.
Question 22.
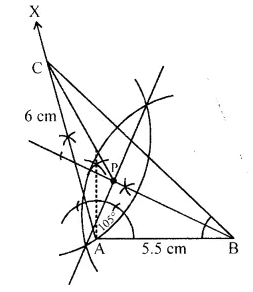
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC. (2015)
Solution:
Steps of construction:
(i) Draw a line segment AB = 5.5 cm.
(ii) At A, draw a ray AX making an angle of 105°.
(iii) Cut off AC from AX =6 cm.
(iv) JoinCB.
∆ABC is required triangle.
(v) Draw angle bisector CX of ∠C.
CX is the locus of points equidistant from BA and BC.
(vi) Draw the perpendicular bisector of BC which is the locus of points equidistant from the points B and C.
These two loci intersect each other at P.
Join PC and on measuring it, it is 4.8 cm (approx).
Question 23.
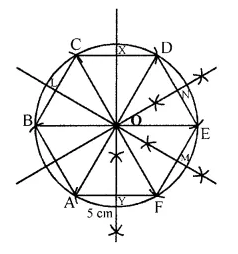
Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them. (2016)
Solution:
Steps of construction :
(i) Draw AF measuring 5 cm using a ruler.
(ii) With A as the centre and radius equal to AF, draw an arc above AF.
(iii) With F as the centre, and same radius cut the previous arc at O.
(iv) With O as the centre, and same radius draw a circle passing through A and F.
(v) With A as the centre and same radius, draw an arc to cut the circle above AF at B.
(vi) With B as the centre and same radius, draw an arc to cut the circle at C.
(vii) Repeat this process to get remaining vertices of the hexagon at D and E
(viii) Join consecutive arcs on the circle to form the hexagon.
(ix) Draw the perpendicular bisectors of AF, EF and DE.
(x) Extend the bisectors of AF, EF and DE to meet CD, BC and AB at X, L and O respectively.
(xi) Join AD, CF and EB.
(xii) These are the 6 lines of symmetry of the regular hexagon.
Question 24.
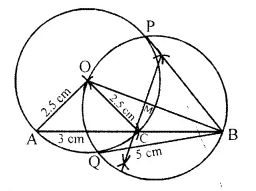
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct:
(i) A circle of radius 2.5 cm, passing through A and C.
(ii) Construct two tangents to the circle from the external point B. Measure and record the length of the tangents. (2016)
Solution:
Steps of construction :
(i) Draw AB = 5 cm using a ruler.
(ii) With A as the centre cut an arc of 3 cm on AB to obtain C.
(iii) With A as the centre and radius 2.5 cm, draw an arc above AB.
(iv) With same radius, and C as the centre draw an arc to cut the previous arc and mark the intersection as O.
(v) With O as the centre and radius 2.5 cm, draw a circle so that points A and C lie on the circle formed
(vi) Join OB.
(vii) Draw the perpendicular bisector of OB to obtain the mid-point of OB, M.
(viii) With M as the centre and radius equal to OM, draw a circle to cut the previous circle at points P and Q.
(ix) Join PB and QB. PB and QB are the required tangents to the given circle from exterior point B.
QB = PB = 3 cm
That is, length of the tangents i.e. 3.2 cm.
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 19 Constructions (Circles) Ex 19 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.