Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
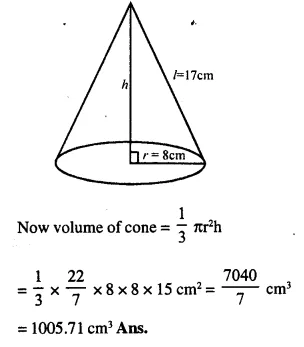
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
Solution:
Slant height (L) = 17 cm
Radius (r) = 8cm
But l²= r² + h²
⇒  h² = l²-r² = 17² – 8²
⇒ h² = 289 – 64 = 225 = (15)²
∴   h=15 cm.

Question 2.
The curved suface area of a cone is 12320 cm². If the radius of its base is 56 cm, find its height.
Solution:
Curved surface area = 12320 cm²
Radius of base (r) = 56 cm.
Let slant height = l.

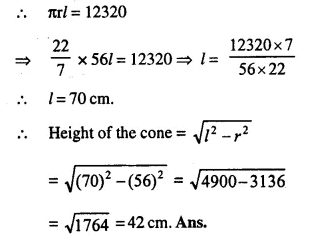
Question 3.
The circumference of the base of a 12 m high conical tent is 66m. Find the volume of the air contained in it.
Solution:
Circumference of conical tent = 66 m
and height (h) = 12 m.

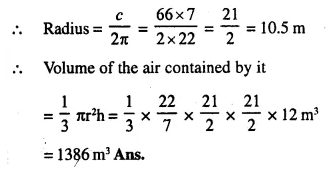
Question 4.
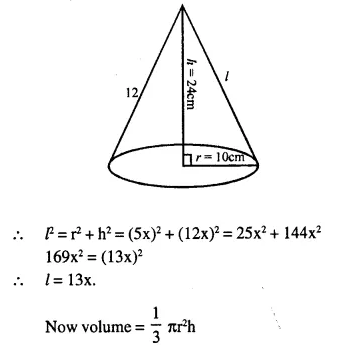
The radius and the height of a right circular cone are in the ratio 5 :12 and its volume is 2512 cubic Cm. Find the radius and slant height of the cone. (Take π = 3.14)
Solution:
The ratio between radius and height = 5 : 12
Volume =2512 cm³
Let radius (r) = 5x and
height (h) = 12x
and slant height = l

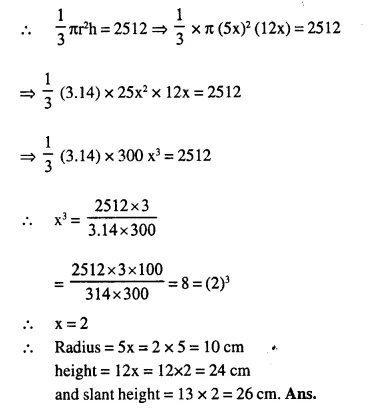
Question 5.
Two right circular cones x and y are made, x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
Solution:
Let radius of cone y = r
∴ radius of cone x = 3r
Let volume of cone y = V
Then volume of x = 2V
Let h₁ be the height of x and h₂ be the height of y.

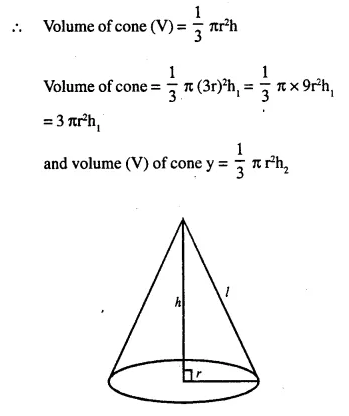
Question 6.
The diameters of two cones are equal, if their slant heights are in the ratio of 5:4, find the ratio of their curved surface area.
Solution:
Let radius of each one = r
and ratio between their slant heights =5:4
Let slant height of the first cone = 5x
and slant height of second = 4 x
∴  Curved surface area of the first cone
= πr = πr x 5x = 5πrx.
and curved suface area of second cone
= πr x 4x = 4πrx
∴ Ratio between them = 5 πrx : 4 πrx
= 5:4

Question 7.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Solution:
Let the slant height of first cone = l
then slant height of the second cone = 2l
and let r₁  be the radius of the first cone and r₂ be the radius of the second cone.
Then curved surface area of the first cone = πr₁l
and that of second cone = πr₂2l= 2πr₂l.
According to the condition,

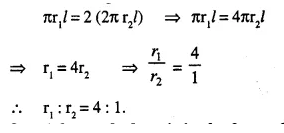
Question 8.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5m. Find its volume. How much cloth is required to just cover the heap?
Solution:

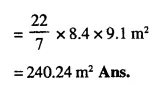
Question 9.
Find what length of canvas, 1.5m in width, is required to make a conical tent 48 m in diameter and 7m in height Given that 10% of the canvas is used in folds and stritchings. Also, find the cost of the canvas at the rate of ₹24 per metre.
Solution:

Question 10.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
Solution:
Height of solid cone (h) = 8 cm.
Radius (r) = 6 cm.

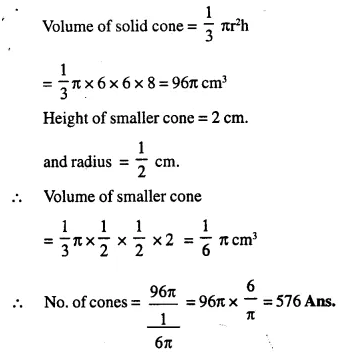
Question 11.
The total surface area of a right circular cone of slant height 13 cm is 90π cm². Calculate:
(i) its radius in cm
(ii) its volume in cm³. [Take π = 3.14]
Solution:
Total surface area of cone = 90π cm²
slaint height (l) = 13 cm
Let r be its radius, then
Total surface area = πrl + πr² = πr (l + r)

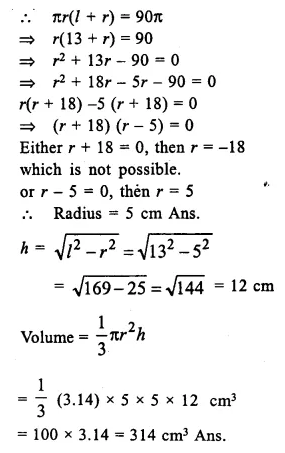
Question 12.
The area of the base of a conical solid is 38.5 cm² and its volume is 154 cm³. Find curved surface area of the solid.
Solution:
Area of base of a solid cone = 38.5 cm²
and volume  = 154 cm³

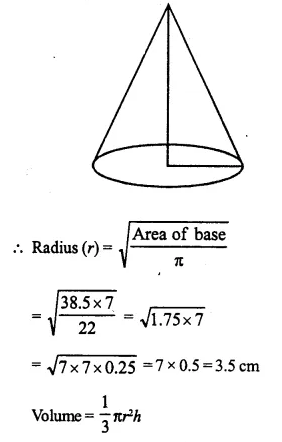
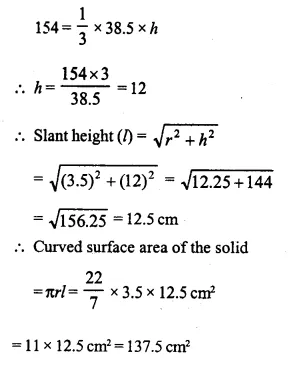
Question 13.
A vessel, in the form of an invested cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged ?
Solution:
Diameter of the base of cone = 25.2 cm

Question 14.
The volume of a conical tent is 1232 m³ and the area of the base floor is 154 m². Calculate the:
(i) radius of the floor.
(ii) height of the tent.
(iii) length of the canvas required to cover this conical tent if its width is 2 m. (2008)
Solution:
Volume of conical tent = 1232 m³
Area of base floor = 154 m²
(i)  Let r be the radius of the floor

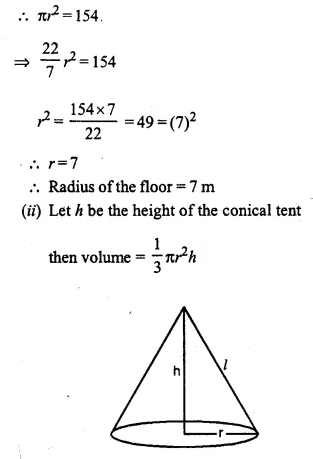
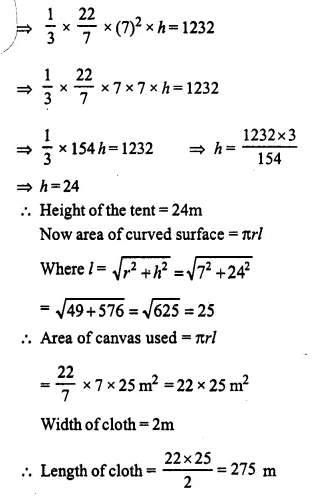
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.