Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

Question 1.
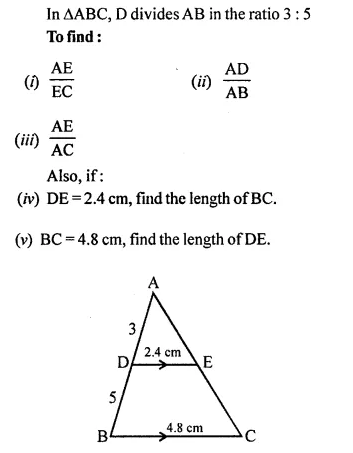
In the following figure, point D divides AB in the ratio 3 : 5. Find:

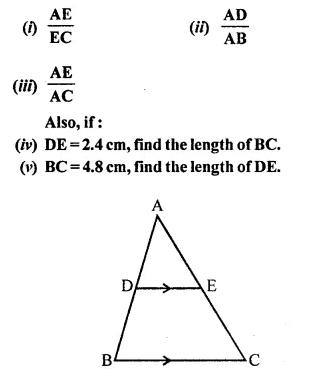
Solution:

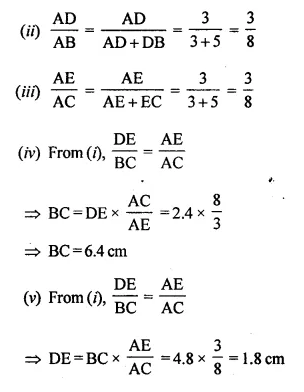
Question 2.
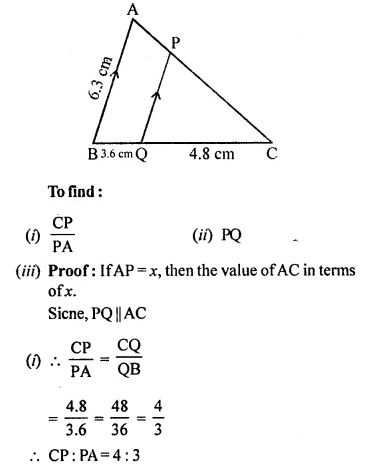
In the given figure, PQ // AB;
CQ = 4.8 cm, QB = 3.6 cm and AB = 6.3 cm. Find:
(i) \(\frac { CP }{ PA }\)
(ii) PQ
(iii) If AP = x, then the value of AC in terms of x.

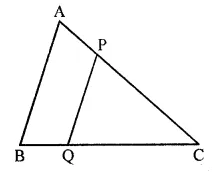
Solution:
In the given figure,
PQ || AB
CQ = 4.8 cm, QB = 3.6 cm, AB = 6.3 cm

Question 3.
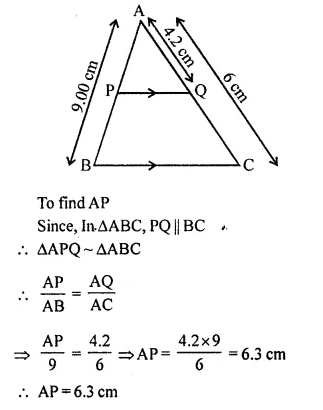
A line PQ is drawn parallel tp the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
Solution:
In ΔABC, PQ || BC
AB = 9.0 cm, CA = 6 cm, AQ = 4.2 cm

Question 4.
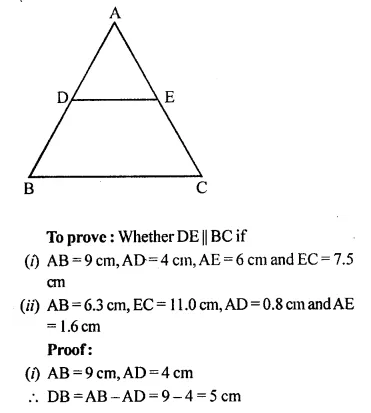
In ΔABC, D and E are the points on sides AB and AC respectively.
Find whether DE // BC, if:
(i) AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm
(ii) AB = 63 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Solution:
In ΔABC, D and E are the points on sides AB and AC respectively.

Question 5.
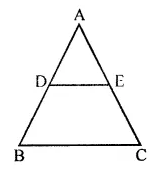
In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If ‘x’ be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of ‘x’.

Solution:
In the given figure,

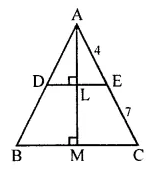
ΔABC ~ ΔADE
AE : EC = 4 : 7, DE = 6.6 cm, BC = ?
Draw AL ⊥ DE and AM ⊥ BC and AL = x cm
Find AM in terms of x
ΔADE ~ ΔABC

Question 6.
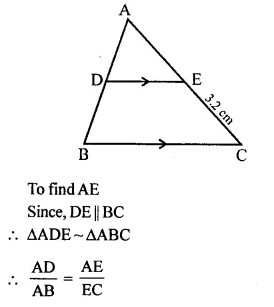
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC = 3.2 cm, find the length of AE.
Solution:
In ΔABC DE || BC
AB = 5 BD, EC = 3.2 cm

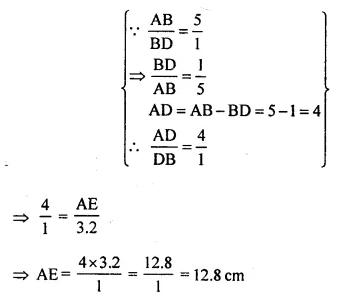
Question 7.
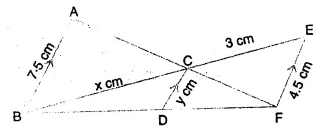
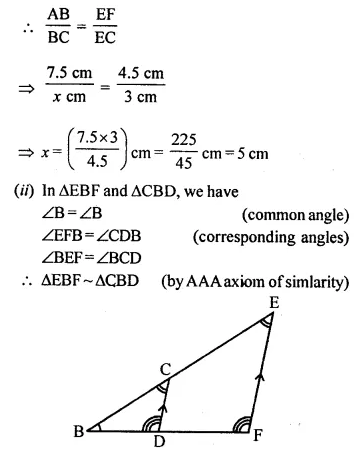
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

Solution:
(i) In ΔACB and ΔFCE, we have
∠ACB = ∠FCE (vertically opposite angles)
∠CBA = ∠CEF (alternate angles)
ΔACB ~ ΔFCE (AA Axiom of similarity)
Thus their corresponding sides are proportional.

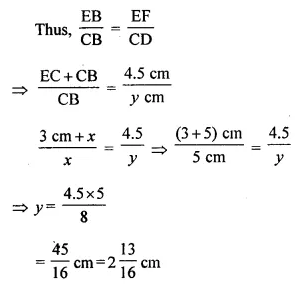
Question 8.
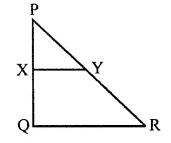
In the figure, given below, PQR is a right angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

Solution:
Given, PQ = 6 cm; PY = 4 cm;
PX : XQ = 1 : 2
Since a line drawn || to one side of triangle divide the other two sides proportionally.

Question 9.
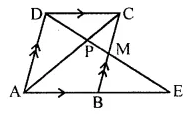
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that: PE = 2PD.

Solution:
In the given figure, ABCD is a ||gm
AB || CD, AD || BC
M is mid point of BC
DM intersect AB produced at E and AC at P
To prove: PE = 2PD
Proof: In ΔDEA,
AD || BC (Opposite sides of || gm)
M is mid-point of CB B is mid-point of AE
AB = BE ⇒ AE = 2AB or 2CD
In ΔPAE and ΔPCD
∠APE = ∠CPD (Vertically opposite angles)
∠PAE = ∠PCD (Alternate angles)
ΔPAE ~ ΔPCD

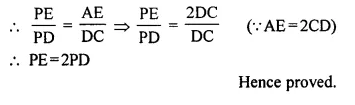
Question 10.
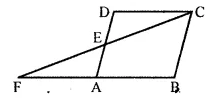
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

Solution:
In the given figure, ABCD is a ||gm E is a point on AD
CE is produced to meet BA produced at point F
AE = 4 cm, AF = 8 cm, AB = 12 cm
To find the perimeter of ||gm ABCD
In ΔFBC,
AD or AE || BC (Opposite sides of ||gm)

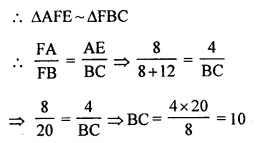
Perimeter of ||gm ABCD = 2 (AB + BC) = 2 (12 + 10) cm = 2 x 22 = 44 cm

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.