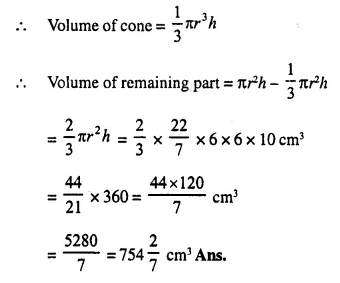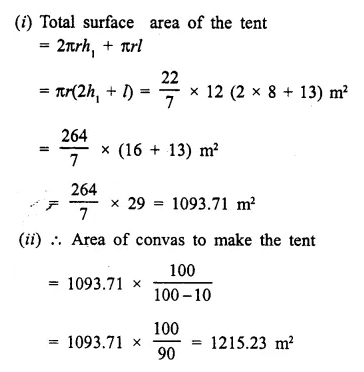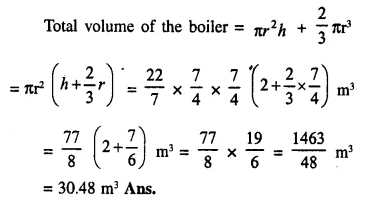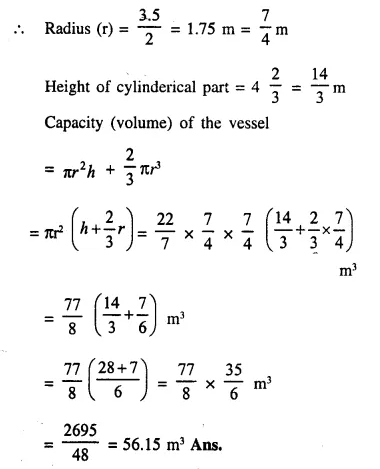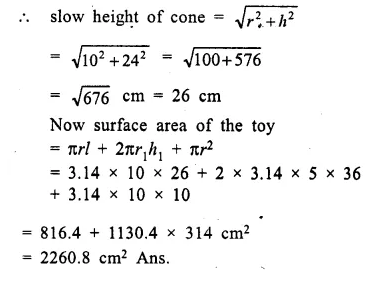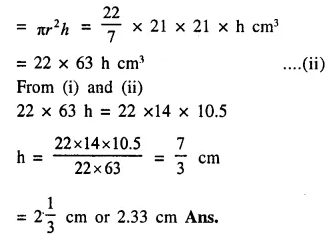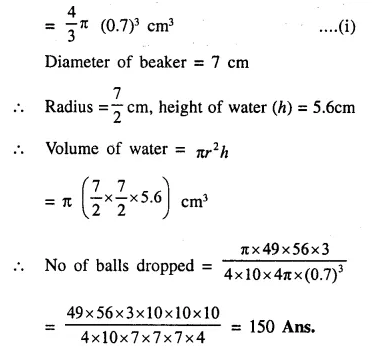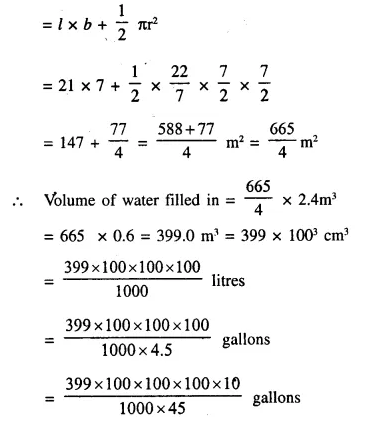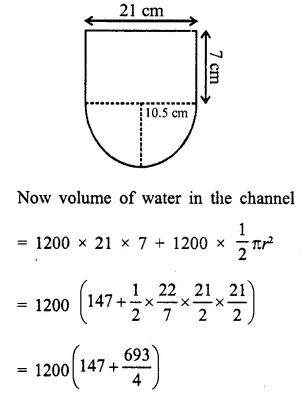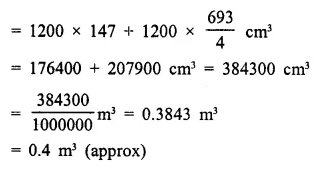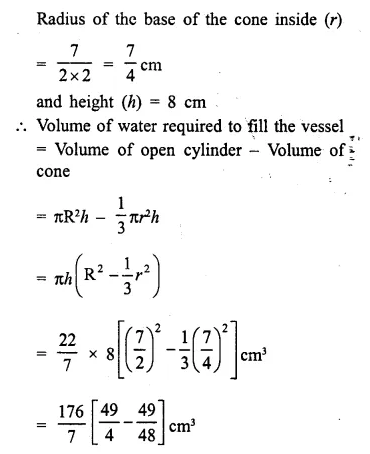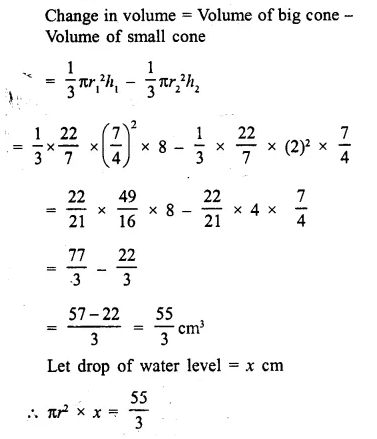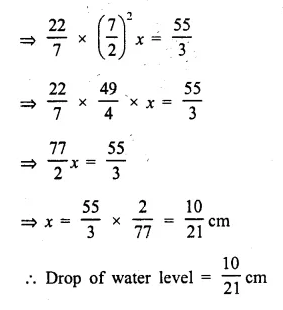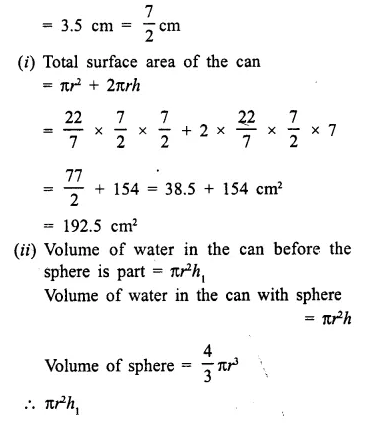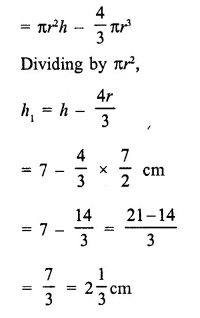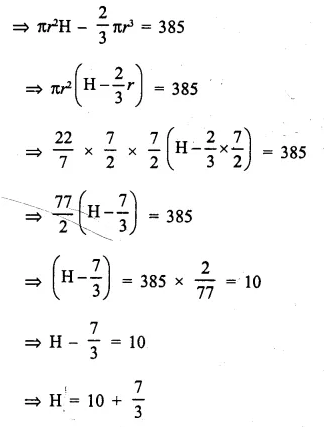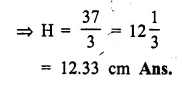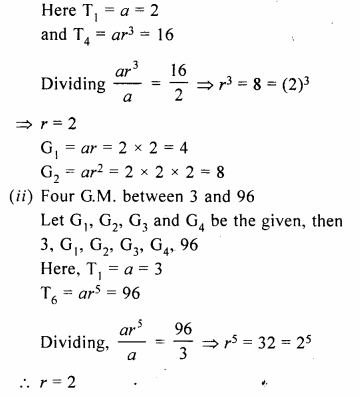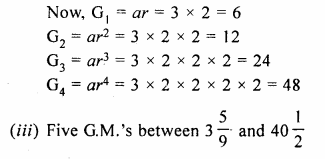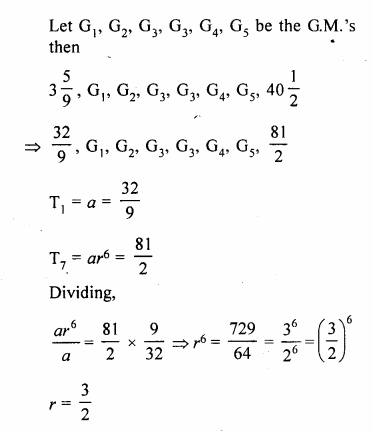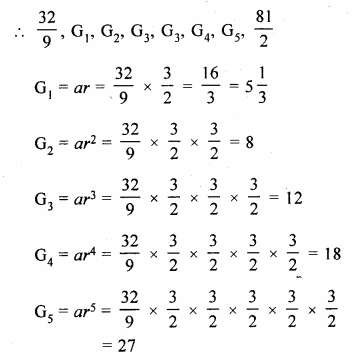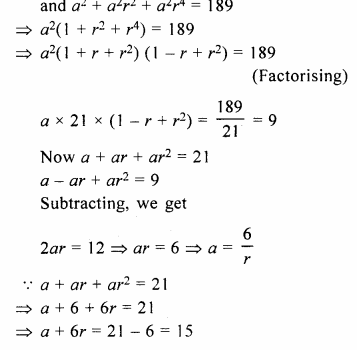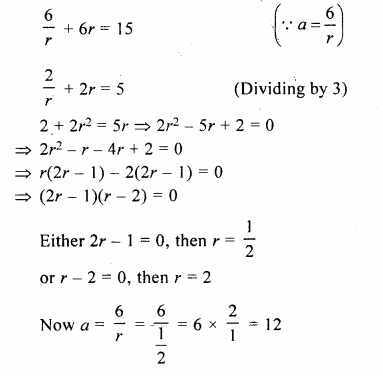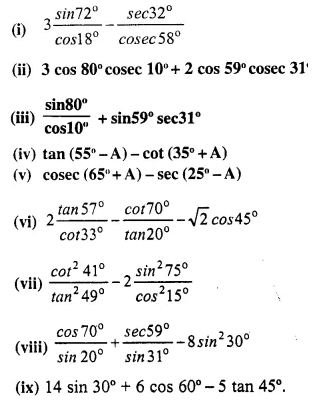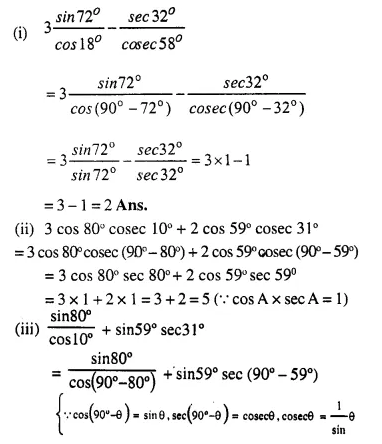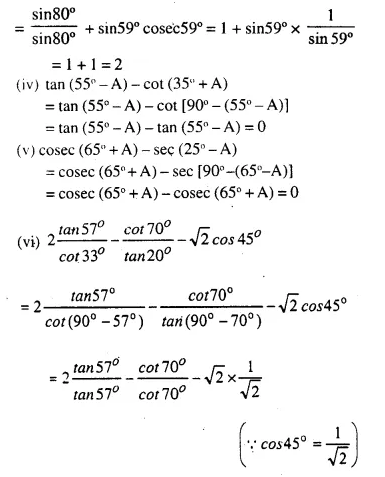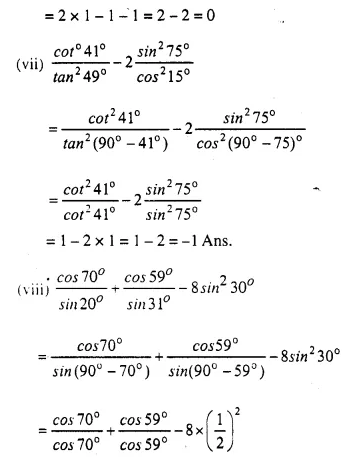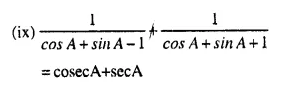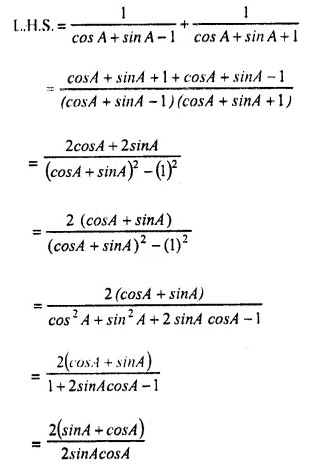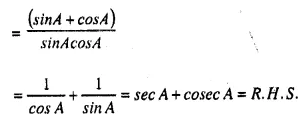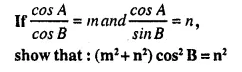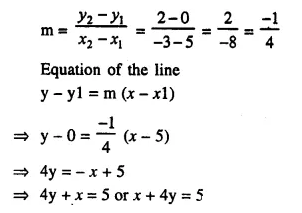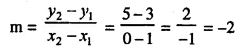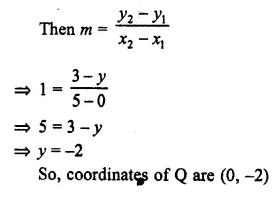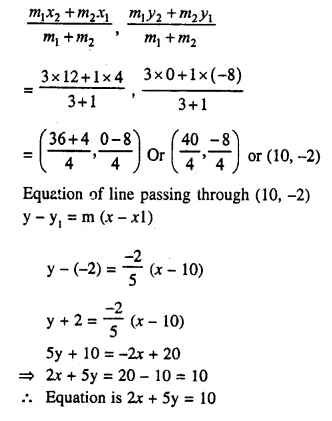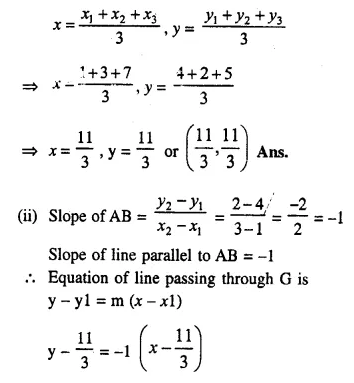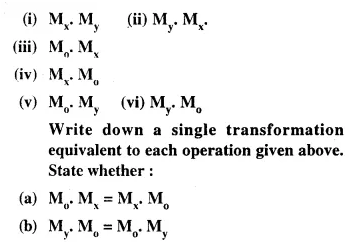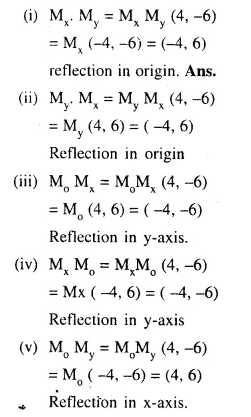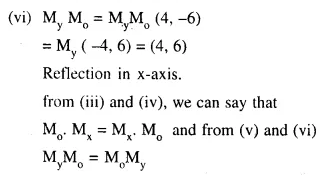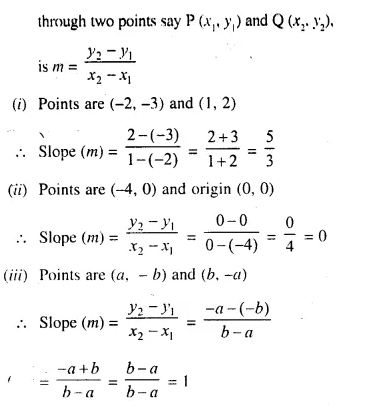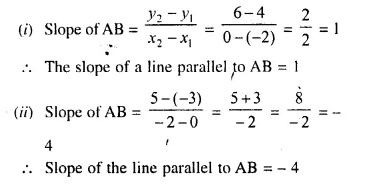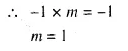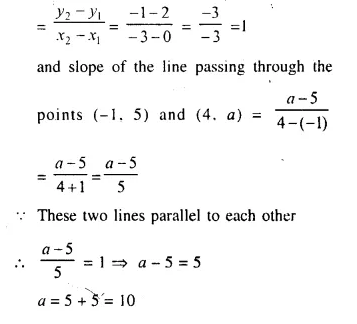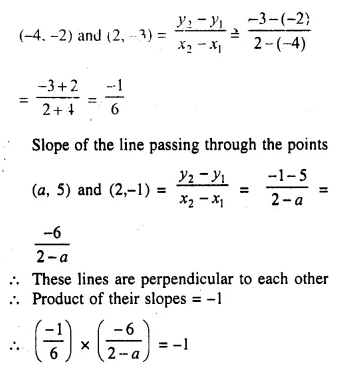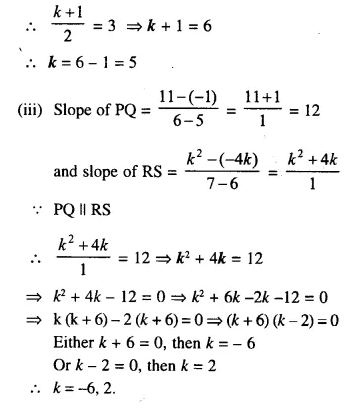Tag: Selina Publishers Mathematics for Class 10

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20G

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 20G.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

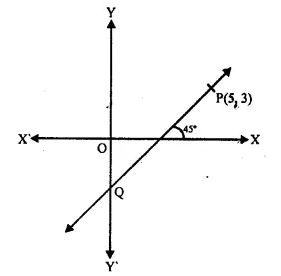
Question 1.
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter 12 cm ?
Solution:
Diameter of cone = 12cm
∴ Radius (r₁) = \(\frac { 12 }{ 2 }\)= 6cm
Height (A) = 45 cm
∴  Volume = \(\frac { 1 }{ 3 }\)πR²h
= \(\frac { 1 }{ 3 }\) x π x 6 x 6 x 45 cm³
= 540 π cm²
∴ Volume of solid spheres = 540 π cm³
Diameter of one sphere = 6cm
∴  Radius = \(\frac { 6 }{ 2 }\) = 3 cm
∴ Volume of one spherical ball

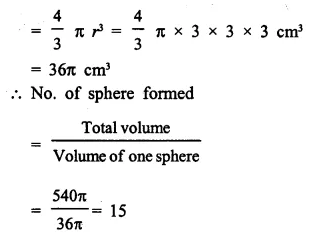
Question 2.
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere. (Answer correct to the nearest integer).
Solution:
Radius of cylinder = 7 cm
and height 14 cm
By carving a largest sphere from it,
the radius of the sphere will be = 7 cm

Question 3.
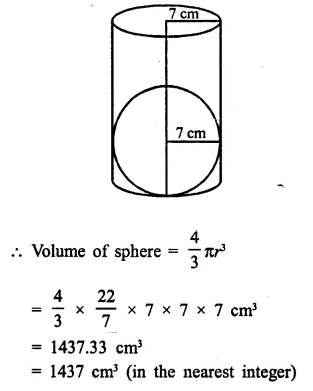
A right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled in identical cones of height 12 cm and diameter 6 cm having a hemi­spherical shape on the top. Find the number of cones  required.
Solution:
Diameter of cylinder = 12 cm
∴ Radius (r) = \(\frac { 12 }{ 2 }\) = 6 cm
Height (h) = 15 cm
Volume of ice-cream in cylinder = πr²h = π x 6 x 6 x 15 = 540π cm³
∴  Volume of ice-cream = 540π cm³
Now diameter of cone = 6 cm

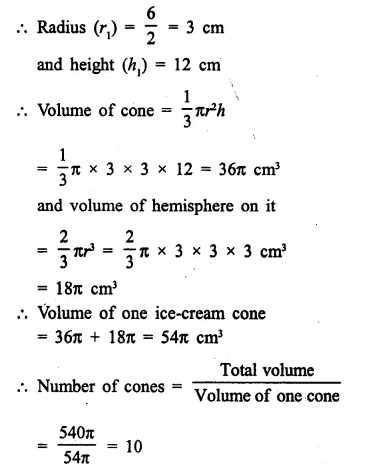
Question 4.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π , the volume of the solid.
Solution:
Radius of each cone and hemi-sphere (r) = 8 cm
Height of cone (h) = r = 8 cm

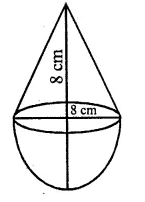
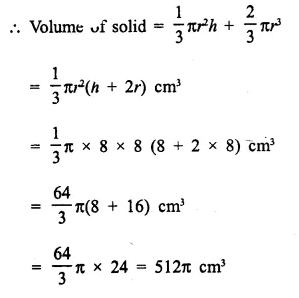
Question 5.
The diameter of sphere is 6 It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Solution:
Diameter of a sphere = 6 cm.
∴ Radius = \(\frac { 6 }{ 2 }\) = 3 cm.

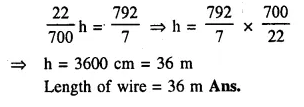
Question 6.
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
Solution:
Let edge of the cube = a
∴ Volume of cube = a x a x a = a³
The sphere, which exactly fits in the cube, has radius = \(\frac { a }{ 2 }\)

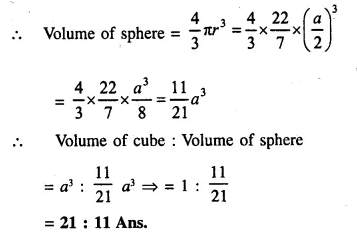
Question 7.
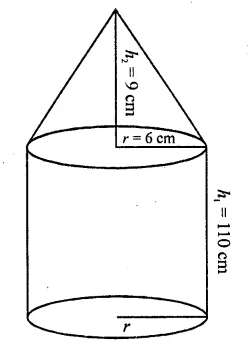
An iron pole consisting of a cylindrical por­tion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1cm³ of iron has 8 gm of mass (approx).

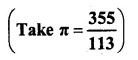
Solution:
Radius of the base of poles (r) = \(\frac { 12 }{ 2 }\) = 6cm.

P.Q.
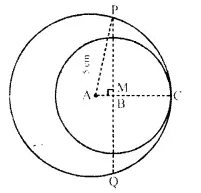
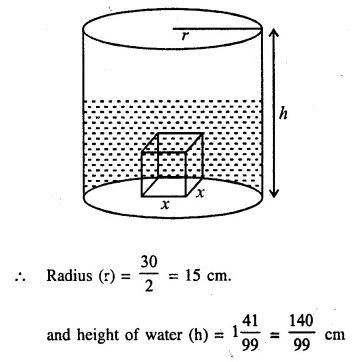
When a metal cube is completely submerged in water contained in a cylindrical vessel with diameter 30 cm, the level of water rises by 1 \(\frac { 41 }{ 99 }\) cm. Find:
(i) the length of the edge of the cube.
(ii) the total surface area of the cube.
Solution:
Diameter of cylinderical vessel = 30 cm

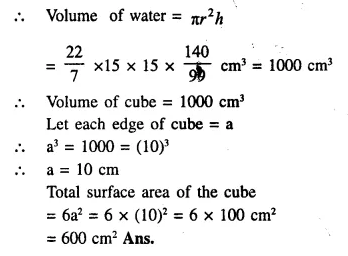
Question 8.
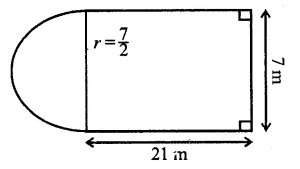
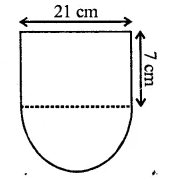
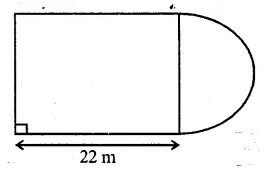
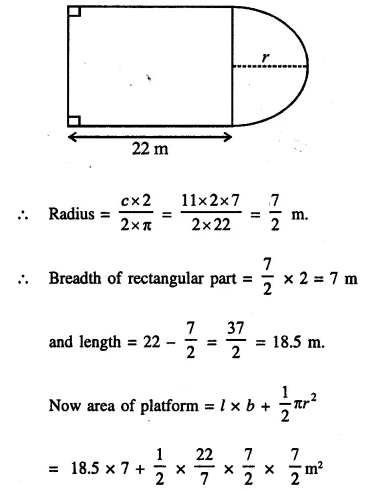
In the following diagram a rectangular plat­form with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.

Solution:
Length of platform = 22m
Circumference of semicircle = 11m

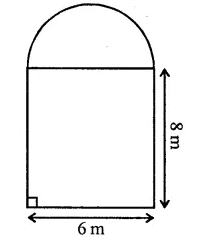
Question 9.
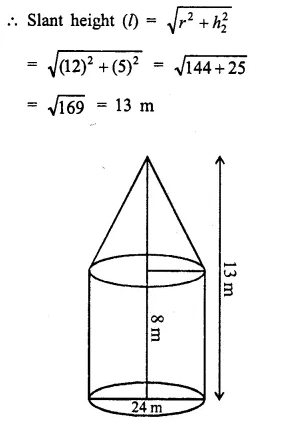
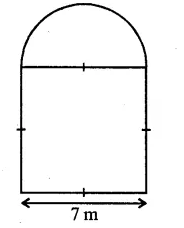
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the following figure. The tunnel is 80 m long. Calculate :
(i) Its volume
(ii) The surface area of the tunnel (excluding the floor) and
(iii) its floor area.

Solution:
Side of square = 7m
Radius of semicircle = \(\frac { 7 }{ 2 }\) m
Length of tunnel = 80 m.

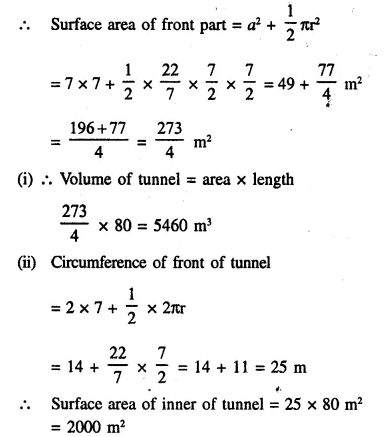
Question 10.
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diam­eter 7 cm through which water flows at the rate of 4 ms^-1. Calculate, in minutes, the time it takes to fill the tank.
Solution:
Diameter of cylindrical tank = 2.8 m 2.8
∴ Radius (r) = \(\frac { 2.8 }{ 2 }\) = 1.4 m
and height (h) = 4.2 m
Volume of water filled in it = πr²h

Question 11.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm². If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
Solution:
Rate of flow of water = 9km / hr
∴ Water flow in 1 hr 15 minutes i.e. in \(\frac { 5 }{ 4 }\)  hr

Question 12.
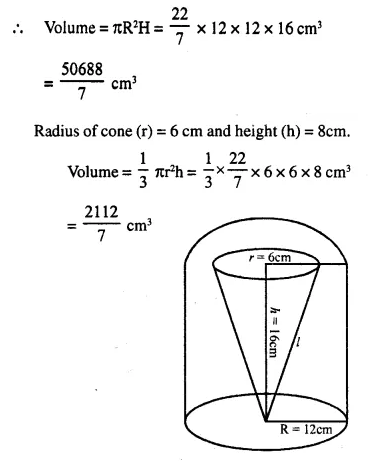
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm, and the other dimensions are as shown. Calculate :
(a) the total surface area,
(b) the total volume of the solid and
(c) the density of the material if its total weight is 1.7 kg.

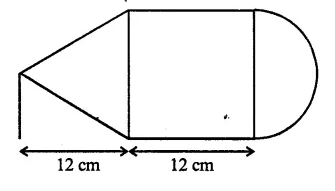
Solution:
Diameter = 10 cm
∴  Radius (r) =  \(\frac { 10 }{ 2 }\)   = 5 cm

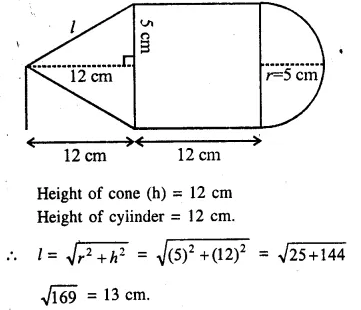
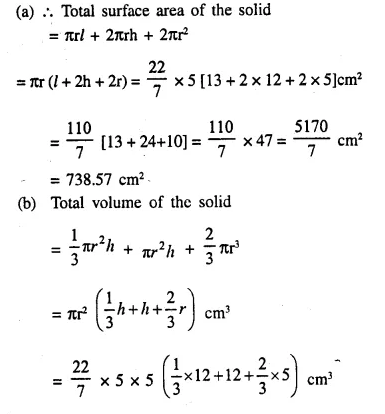
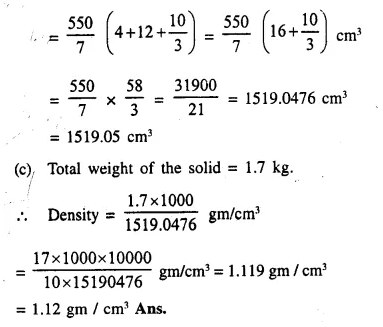
Question 13.
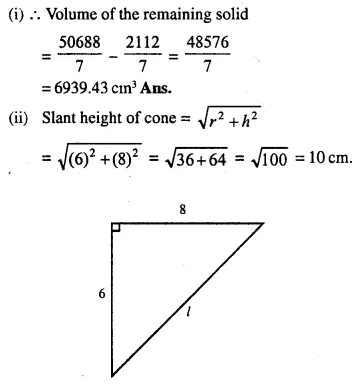
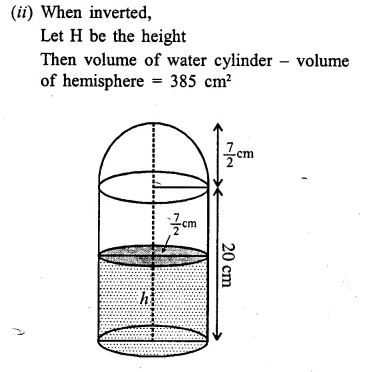
A solid, consisting of a right circular cone, standing on a hemisphere, is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimetre. [1998]
Solution:
Radius of cylinder = 3 cm
and height = 6 cm
Radius of hemisphere = 2 cm
and height of cone = 4 cm

Volume of water in the cylinder when it is full
= πr²h = π x (3)² x 6 cm³ = 54π cm³
Volume of water displaced = Volume of cone + volume of hemisphere

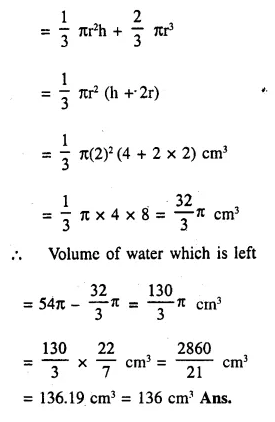
Question 14.
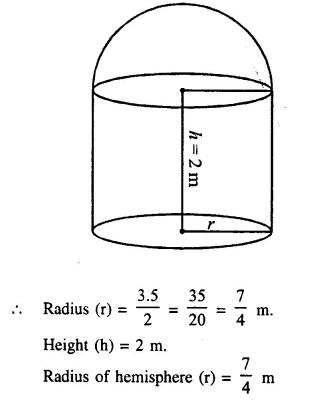
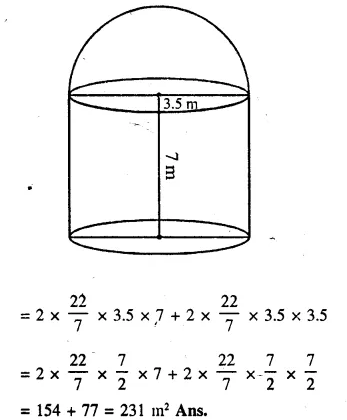
A metal container in the form of a cylinder is surmounted by a hemi-sphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate
(i) he total area of the internal surface, exclud­ing the base;
(ii) the internal volume of the container in m³ [1999]
Solution:
Radius of cylinder = 3.5 m
and height = 7 m.
(i) Total surface area of container excluding the base = curved surface area of cylinder + area of hemisphere = 2πrh + 2πr²

Question 15.
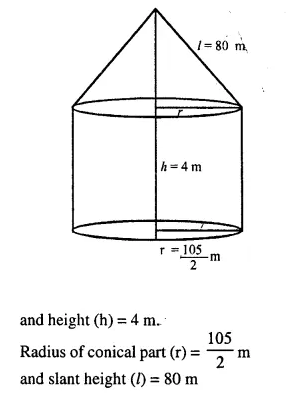
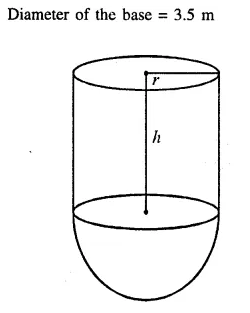
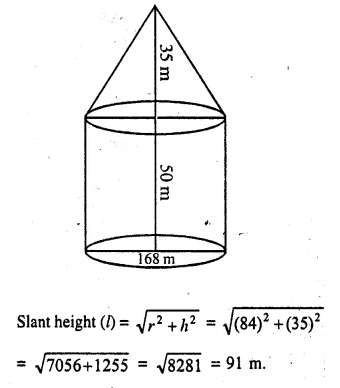
An exhibition tent is in the form of a cylin­der surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m².     [2001]
Solution:
Total height of the tent = 85 m.
Daimeter of the base = 168 m.
∴ Radius (r) = \(\frac { 168 }{ 2 }\) = 84 m
Height of cylindrical part = 50 m
Then height of conical part (h) = 85 – 50 = 35 m

P.Q.
The total surface area of a hollow cylinder, which is open from both sides is 3575 cm²; area of the base ring is 357.5 cm² and height is 14 cm. Find the thickness of the cylinder.
Solution:
Total surface area of a hollow cylinder = 3575 cm²
Area of base ring = 357.5 cm²
Height = 14 cm.
Let external radius = R
and internal radius = r
and let thickness of cylinder = (R – r) = d
∴  Total surface area = 2πRh + 2πrh + 2π (R²– r²)
= 2πh (R + r) + 2π (R + r) (R – r)
= 2π (R + r) [h + R – r]
= 2π (R + r) (h + d)
= 2π (R + r) (14 + d)
But 2π (R + r) (14 + d) = 3575                  ….(i)
and area of the base = π (R² – r²) = 357.5
⇒  π (R + r) ( R – r) = 357.5
⇒ π (R + r)d = 357.5                                 ….(ii)

Question 16.
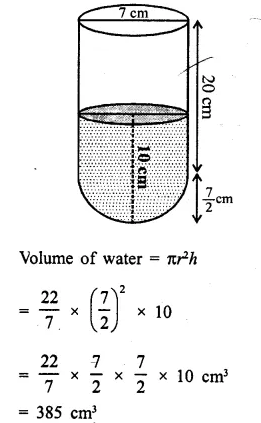
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube  is \(\frac { 5159 }{ 6 }\)cm³, and \(\frac { 4235 }{ 6 }\) cm³ of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
Solution:

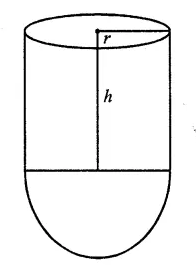
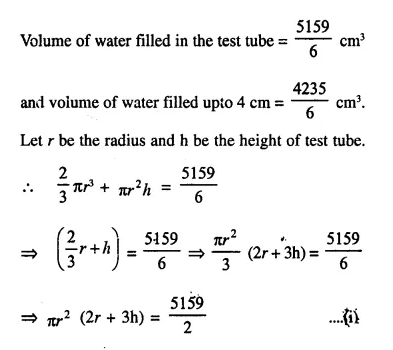
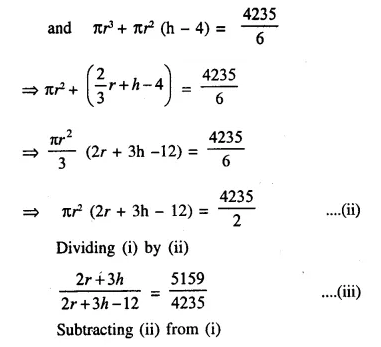
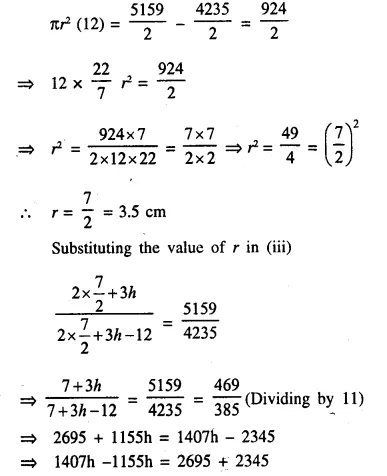
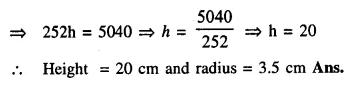
Question 17.
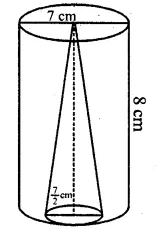
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7cm and its height is 8cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10cm. How much water, in cm³, will be required to fill the vessel completely.
Solution:
Diameter of hemisphere = 7cm
Diameter of the base of a cone = 7cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\) cm = 3.5 cm
Height (h) = 8cm.

Question 18.
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.   (2015)
Solution:
Radius of first sphere = 2 cm

Question 19.
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used.             (2016)
Solution:
Let the number of cones be n,
Let radius of the sphere be r_s, radius of a cone be r_c and h be the height of the cone.
Volume of sphere = n(Volume of a metallic cone)

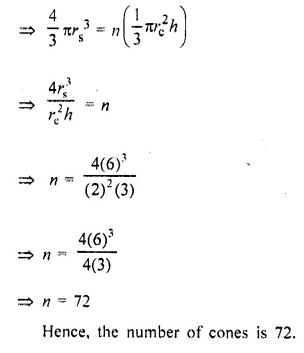
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

Question 1.
In the given circle with diameter AB, find the value of x. (2003)

Solution:

∠ABD = ∠ACD = 30° (Angle in the same segment)
Now in ∆ ADB,
∠BAD + ∠ADB + ∠DBA = 180° (Angles of a ∆)
But ∠ADB = 90° (Angle in a semi-circle)
∴ x + 90° + 30° = 180°
⇒ x + 120° = 180°
∴ x = 180°- 120° = 60°

Question 2.
In the given figure, O is the centre of the circle with radius 5 cm, OP and OQ are perpendiculars to AB and CD respectively. AB = 8cm and CD = 6cm. Determine the length of PQ.

Solution:

Radius of the circle whose centre is O = 5 cm
OP ⊥ AB and OQ ⊥ CD, AB = 8 cm and CD = 6 cm.
Join OA and OC, then OA = OC=5cm.
∴ OP ⊥ AB
∴ P is the mid-point of AB.
Similarly, Q is the mid-point of CD.
In right ∆OAP,
OA² = OP² + AP² (Pythagorous theoram)
⇒ (5)² =OP² +(4)² ( ∵ AP = AB = \(\frac { 1 }{ 2 }\) x 8 = 4cm)
⇒ 25 = OP² + 16
⇒ OP³ = 25 – 16 = 9 = (3)²
∵ OP = 3 cm
Similarly, in right ∆ OCQ,
OC² = OQ² + CQ²
⇒ (5)² =OQ²+(3)² (∵ CQ = CD = \(\frac { 1 }{ 2 }\) x 6 = 3cm)
⇒ 25 = OQ² + 9
⇒ OQ³ = 25 – 9 = 16 = (4)²
∴ OQ = 4 cm
Hence, PQ = OP + OQ = 3-4 = 7 cm.

Question 3.
The given figure shows two circles with centres A and B; and radii 5cm and 3cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

Solution:

Join AP and produce AB to meet the bigger circle at C.
AB = AC – BC = 5 cm – 3 cm = 2 cm.
But, M is the mid-point of AB
∴ AM = \(\frac { 2 }{ 2 }\) = 1cm.
Now in right ∆APM,
AP2 = MP2 + AM2 (Pythagorous theorem)
⇒ (5)² = MP² -1- (1 )²
⇒ 25 = MP: + 1
⇒ MP: = 25 – 1 = 24

Question 4.
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.

Solution:

Given: In the figure ABC is a triangle in winch ∠A = 30°
To Prove: BC is the radius of circumcircle of ∆ABC whose O is the centre.
Const: Join OB and OC.
Proof: ∠BOC is at the centre and ∠BAC is at the remaining part of the circle
∴ ∠BOC = 2 ∠BAC = 2 x 30° = 60°
Now in ∆OBC,
OB = OC (Radii of the same circle)
∴ ∠OBC = ∠OCB
But ∠OBC + ∠OCB + ∠BOC – 180°
∠OBC + ∠OBC + 60°- 180°
⇒ 2 ∠OBC = 180°- 60° = 120°
⇒ ∠OBC = \(\frac { { 120 }^{ circ } }{ 2 }\) = 60°
∴ ∆OBC is an equilateral triangle.
∴ BC = OB = OC
But OB and OC are the radii of the circumcircle
∴ BC is also the radius of the circumcircle.

Question 5.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Solution:

Given: In ∆ABC, AB-AC and a circle with AB as diameter is drawn which intersects the side BC and D.
To Prove: D is the mid point of BC.
Const: Join AD.
Proof: ∠ 1 = 90° (Angle in a semi-circle)
But ∠ 1 + ∠ 2 – 180° (Linear pair)
∴ ∠ 2 = 90°
Now, in right ∆ ABD and ∆ ACD,
Hyp. AB – Hyp. AC (Given)
Side AD – AD (Common)
∴ ∆ABD = ∆ACD (RHS criterion of congruency)
∴ BD = DC (c.p.c.t.)
Hence D is he mid point of BC. Q.E.D.

Question 6.
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.

Solution:
Join OE,
Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∴ ∠EOC = 2 ∠EBC = 2 x 65° = 130°
Now, in ∆OEC, OE = OC (radii of the same circle)
∴ ∠OEC = ∠OCE
But ∠ OEC + ∠ OCE + ∠ EOC = 180°
⇒ ∠ OCE + ∠ OCE + ∠ EOC = 180°

Question 7.
Chords AB and CD of a circle intersect each other at point P, such that AP = CP. S.how that AB = CD.

Solution:
Given: Two chords AB and CD intersect each other at P inside the circle with centre O and AP = CP.

To Prove: AB = CD.
Proof: ∵ Two chords AB and CD intersect each other inside the circle at P.
∴ AP x PB = CP x PD ⇒ \(\frac { AP}{ CP }\) = \(\frac { AD }{ PB }\)
But AP = CP ….(i) (given)
∴ PD = PB or PB = PD …,(ii)
Adding (i) and (ii),
AP + PB = CP + PD
⇒ AB = CD Q.E.D.

Question 8.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Solution:
Given: ABCD is a cyclic quadrilateral and PRQS is a quadrilateral formed by the angle bisectors of angle ∠A, ∠B, ∠C and ∠D.
To Prove: PRQS is a cyclic quadrilateral.
Proof: In ∆APD,

∠1 +∠2 + ∠P= 180° ,…(i)
Similarly, in ∆BQC.
∠3 + ∠4 + ∠Q= 180° ….(ii)
Adding (i) and (ii), we get:
∠1 + ∠2 + ∠P + ∠3 + ∠4 ∠Q = 180° + 180° = 360°
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠P + ∠Q = 360° ..(iii)
But ∠1+∠2+∠3+∠4 = \(\frac { 1 }{ 2 }\) (∠A+∠B+∠C+∠D)
= \(\frac { 1 }{ 2 }\) x 360°= 180°
∴ ∠P + ∠Q = 360° – 180° = 180° [From (iii)]
But these are the sum of opposite angles of quadrilateral PRQS
∴ Quad. PRQS is a cyclic quadrilateral. Q.E.D.

Question 9.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate:
(I) ∠BDC
(ii) ∠BEC
(iii) ∠BAC (2014)

Solution:
∠DBC = 58°
BD is diameter
∴ ∠DCB=90° (Angle in semi circle)

(i) In ∆BDC
∠BDC + ∠DCB + ∠CBD = 180°
∠BDC = 180°- 90° – 58° = 32°
(ii) ∠BEC =180°-32°
(opp. angle of cyclic quadrilateral)
= 148°
(iii) ∠BAC = ∠BDC = 32°
(Angles in same segment)

Question 10.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Solution:

Given: In ∆ABC, AB = AC and D and E are points on AB and AC such that AD = AE, DE is joined.
To Prove: B,C,E,D. are concyclic.
Proof: In ∆ABC, AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides)
Similarly in ∆ADE, AD = AE (given)
∴ ∠ADE = ∠AED
In ∆ABC,
∵ \(\frac { AP }{ AB }\) = \(\frac { AE }{ AC }\)
∴ DE || BC.
∴ ∠ADE = ∠B (Corresponding angles)
But ∠B = ∠C (Proved)
∴ Ext. ∠ADE = its interior opposite ∠C.
∴ BCED is a cyclic quadrilateral.
Hence B,C, E and D are concyclic.

Question 11.
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE’= 20°; determine ∠BCD. Give reason in support of your answer.

Solution:

In cyclic quad. ABCD,
AF || CB and DA is produced to E such that
∠ADC = 92° and ∠FAE – 20°
Now, we have to find the measure of ∠BCD In cyclic quad. ABCD,
∠B – ∠D = 180° ⇒ ∠B + 92° = 180″
⇒∠B = 180°-92° = 88°
∵ AF || CB.
∴∠FAB = ∠B = 88°
But ∠FAE – 20° (Given)
Ext. ∠BAE – ∠BAF + ∠FAE
= 88° + 20° = 108°
But Ext. ∠BAE – ∠BCD
∴ ∠BCD = 108°

Question 12.
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC – 80°, calculate
(i) ∠DBC,
(ii) ∠IBC,
(iii) ∠BIC.

Solution:

Join DB and DC, IB and IC.
∠BAC = 66°, ∠ABC = 80°. I is the incentre of the ∆ABC.
(i) ∵ ∠DBC and ∠DAC are in the same segment
∴ ∠DBC – ∠DAC.
But ∠DAC = \(\frac { 1 }{ 2 }\)∠BAC = \(\frac { 1 }{ 2 }\) x 66° = 33°
∴ ∠DBC = 33°.
(ii) ∵ I is the incentre of ∆ABC.
∴ IB bisect ∠ABC
∴ ∠ IBC = \(\frac { 1 }{ 2 }\) ∠ABC = \(\frac { 1 }{ 2 }\) x 80° = 40°.
(iii) ∴∠BAC = 66° ∠ABC = 80°
∴ In ∆ABC,
∠ACB = 180° – (∠ABC + ∠CAB)
= 180°-(80°+ 66°)= 180°- 156° = 34°
∵ IC bisects the ∠C
∴ ∠ ICB = \(\frac { 1 }{ 2 }\) ∠C = \(\frac { 1 }{ 2 }\) x 34° = 17°.
Now in ∆IBC,
∠ IBC + ∠ ICB + ∠ BIC = 180°
⇒ 40° + 17° + ∠BIC = 180°
⇒ ∠ BIC = 180° – (40° + 17°) = 180° – 57°
= 123°

Question 13.
In the given figure, AB = AD = DC= PB and ∠DBC = x°. Determine in terms of x :
(i) ∠ABD
(ii) ∠APB

Hence or otherwise prove that AP is parallel to DB.
Solution:
Given: In figure, AB = AD = DC = PB.
∠DBC = x. Join AC and BD.
To Find : the measure of ∠ABD and ∠APB.
Proof: ∠DAC=∠DBC= x(angles in the same segment)
But ∠DCA = ∠DAC (∵ AD = DC)
= x
But ∠ABD = ∠DAC (Angles in the same segment)
In ∆ABP, ext. ∠ABC = ∠BAP + ∠APB
But ∠ BAP = ∠APB (∵ AB = BP)
2 x x = ∠APB + ∠APB = 2∠APB
∴ 2∠APB = 2x
⇒ ∠APB = x
∵ ∠APB = ∠DBC = x
But these are corresponding angles
∴ AP || DB. Q.E.D.

Question 14.
In the given figure, ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.

Solution:
Given: In the figure, ABC, AEQ and CEP are straight lines.
To prove: ∠APE + ∠CQE = 180°.
Const: Join EB.
Proof: In cyclic quad. ABEP,
∠APE+ ∠ABE= 180° ….(i)
Similarly in cyclic quad. BCQE

∠CQE +∠CBE = 180° ….(ii)
Adding (i) and (ii),
∠APE +∠ABE + ∠CQE +∠CBE = 180° + 180° = 360°
⇒ ∠APE + ∠CQE + ∠ABE + ∠CBE = 360°
But ∠ABE + ∠CBE = 180° (Linear pair)
∴ ∠APE + ∠CQE + 180° = 360°
⇒ ∠APE + ∠CQE = 360° – 180° = 180°
Hence ∠APE and ∠CQE are supplementary. Q.E.D.

Question 15.
In the given figure, AB is the diameter of the circle with centre O.

If ∠ADC = 32°, find angle BOC.
Solution:
Arc AC subtends ∠AOC at the centre and ∠ ADC at the remaining part of the circle

∴ ∠AOC = 2 ∠ADC
= 2 x 32° = 64°
∵ ∠AOC + ∠ BOC = 180° (Linear pair)
⇒ 64° + ∠ BOC = 180°
⇒ ∠ BOC=180° – 64° =116° .

Question 16.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A : whereas sides PQ and SR produced meet at point B.
If ∠ A : ∠ B = 2 : 1 ; find angles A and B.
Solution:
PQRS is a cyclic-quadrilateral in which ∠ PQR =135°
Sides SP and RQ are produced to meet at A and sides PQ and SR are produced to meet at B.

Question 17.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA. If AC produced and BD produced meet at point P ; show that ∠ APB = 60°.

Solution:
Given : In the figure, AB is the diameter of the circle with centre O.
CD is the chord with length equal to the radius OA.
AC and BD are produced to meet at P.
To prove : ∠ APB = 60°
Const : Join OC and OD
Proof : ∵ CD = OC = OD (Given)
∴ ∆OCD is an equilateral triangle
∴ ∠ OCD = ∠ ODC = ∠ COD = 60°
In ∆ AOC, OA = OC (Radii of the same circle)
∴ ∠ A = ∠ 1
Similarly, in ∆ BOD,
OB = OD
∴∠2= ∠B
Now in cyclic quadrilateral ACDB,
∠ A CD + ∠B = 180°

∠60°+ ∠ 1 + ∠B = 180°
= ∠ 1 + ∠B = 180° – 60°
⇒∠ 1 + ∠B = 120°
But ∠ 1 = ∠ A
∴ ∠ A + ∠B = 120° …(i)
Now, in ∆ APB,
∠ P + ∠ A + ∠ B = 180° (Sum of angles of a triangle)
⇒ ∠P+120°=180° [From (i)]
⇒ ∠P = 180°- 120°= 60°
Hence ∠ P = 60° or ∠ APB = 60° Hence proved.

Question 18.
In the following figure,

ABCD is a cyclic quadrilateral in which AD is parallel to BC.
If the bisector of angle A meets BC at point E and the given circle at point F, prove that :
(i) EF = FC
(ii) BF = DF
Solution:

Given : ABCD is a cyclic quadrilateral in which AD || BC.
Bisector of ∠ A meets BC at E and the given circle at F. DF and BF are joined.
To prove :
(i) EF = FC
(ii) BF = DF
Proof : ∵ ABCD is a cyclic -quadrilateral and AD || BC
∵ AF is the bisector of ∠ A
∴ ∠ BAF = ∠ DAF
∴ Arc BF = Arc DF (equal arcs subtends equal angles)
⇒ BF = DF(equal arcs have equal chords)
Hence proved

Question 19.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E ; whereas sides BC and AD produced meet at point F. If ∠ DCF : ∠ F : ∠ E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Solution:
Given : In a circle, ABCD is a cyclic quadrilateral AB and DC are produce to meet at E and BC and AD are produced to meet at F.

Question 20.
The following figure shows a circle with PR as its diameter.

If PQ = 7 cm, QR = 3 cm, RS = 6 cm. find the perimeter of the cyclic quadrilateral PQRS. (1992)
Solution:
In the figure, PQRS is a cyclic quadrilateral in which PR is a diameter
PQ = 7 cm,
QR = 3 RS = 6cm
∴ 3 RS = 6cm
and RS = \(\frac { 6 }{ 3 }\) = 2cm
Now in ∆ PQR,
∠ Q = 90° (Angle in a semi-circle)
∴ PR² = PQ² + QR² (Pythagoras theorem)
= (7)² + (6)² = 49 + 36 = 85
Again, in right ∆ PSQ, PR² = PS² + RS²
⇒ 85 = PS² + (2)²
⇒ 85 = PS² + 4
⇒ PS² = 85 – 4 = 81 = (9)²
∴ PS = 9cm
Now, perimeter of quad. PQRS = PQ + QR + RS + SP = (7 + 9 + 2 + 6) cm = 24cm

Question 21.
In the following figure, AB is the diameter of a circle with centre O.

If chord AC = chord AD, prove that :
(i)arc BC = arc DB
(ii) AB is bisector of ∠ CAD. Further, if the length of arc AC is twice the length of arc BC, find :
(a) ∠ BAC
(b) ∠ ABC
Solution:
Given : In a circle with centre O, AB is the diameter and AC and AD are two chords such that AC = AD.
To prove : (i) arc BC = arc DB
(ii) AB is the bisector of ∠CAD
(iii) If arc AC = 2 arc BC, then find
(a) ∠BAC (b) ∠ABC

Construction: Join BC and BD.
Proof : In right angled A ABC and A ABD
Side AC = AD (Given)
Hyp. AB = AB (Common)
∴ ∆ ABC ≅ ∆ ABD (R.H.S. axiom)
(i) ∴ BC = BD (C.P.C.T)
∴ Arc BC = Arc BD (equal chords have equal arcs)
(ii) ∠ BAC = ∠ BAD (C.P.C.T)
∴ AB is the bisector of ∠CAD.
(iii) If arc AC = 2 arc B
Then ∠ABC = 2 ∠BAC
But ∠ABC – 2 ∠BAC = 90°
∴ 2 ∠BAC + ∠BAC = 90°
⇒ 3 ∠BAC = 90° ⇒ ∠BAC = 30°
and ∠ABC = 2 ∠BAC = 2 * 30° = 60°

Question 22.
In cyclic-quadrilateral ABCD ; AD = BC,
∠ BAC = 30° and ∠ CBD = 70°, find:
(i) ∠ BCD
(ii) ∠ BCA
(iii) ∠ ABC
(iv) ∠ ADC
Solution:
ABCD is a cyclic-quadrilateral and AD = BC
∠ BAC = 30°, ∠ CBD = 70°
∠ DAC = ∠ CBD , (Angles in the same segment)

But ∠ CBD = 70°
∴ ∠ DAC = 70°
⇒ ∠ BAD = ∠ BAC + ∠ DAC = 30° + 70° = 100°
But ∠ BAD + ∠ BCD = 180°
(Sum of opposite angles of a cyclic quad.)
⇒100°+ ∠ BCD=180° ⇒ ∠ BCD=180° – 100° = 80°
∴ ∠ BCD = 80°
∵ AD = BC (Given)
∴ ∠ ACD = ∠ BDC
(Equal chords subtends equal angles)
But ∠ ACB = ∠ ADB
(Angles in the same segment)
∴ ∠ ACD + ∠ ACB = ∠ BDC + ∠ ADB
⇒ ∠ BCD = ∠ ADC = 80° (∵ ∠ BCD = 80°)
∴ ∠ ADC = 80°
But in ∆ BCD,
∠ CBD + ∠ BCD + ∠ BDC = 180° (Angles of a triangle)
⇒ 70° + 80° + ∠ BDC = ∠ 180°
⇒ 150°+ ∠ BDC = 180°
∴ ∠ BDC = 180° – 150° = 30°
⇒ ∠ ACD = 30° (∵ ∠ ACD = ∠ BDC)
∴ ∠ BCA = ∠ BCD – ∠ ACD = 80° – 30° = 50°
∠ ADC + ∠ABC = 180°
(Sum of opp. angles of a cyclic quadrilateral)
⇒ 80°+ABC = 180°
⇒ ∠ ABC=180°-80° = 100°

Question 23.
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the values of a, b and c.

Solution:
Now, ∠ ACE = 43° and ∠ CAF = 62° (given)
In ∆ AEC,

∠ ACE + ∠ CAE + ∠ AEC = 180°
∴ 43° + 62° + ∠ AEC = 180°
105° + ∠ AEC = 180°
⇒ ∠ AEC = 180°- 105° = 75°
Now, ∠ ABD + ∠AED=180°
(Opposite ∠ s of a cyclic quad, and ∠ AED = ∠ AEC)
⇒ 0 + 75°= 180° a = 180° – 75° = 105°
∠ EDF = ∠ BAE (Angles in the alternate segments)
∴ c = 62°
In ∆BAF, ∠a + 62° + ∠b = 180°
⇒ 105°+ 62°+ ∠b= 180°
⇒ 167° + ∠6 = 180°
⇒ ∠b= 180°-167°= 13°
Hence, a= 105°, 6=13° and c = 62°.

Question 24.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25° .

Find:
(i) ∠CAD
(ii)∠CBD
(iii) ∠ADC
Solution:

In the given figure,
ABCD is a cyclic quad, in which AB || DC
∴ ABCD is an isosceles trapezium AD = BC
(i) Join BD
and Ext. ∠BCE = ∠BAD
{ Ext. angle of a cyclic quad, is equal to interior opposite angle}
∴ ∠BAD = 80° (∵ ∠BCE = 80°)
But ∠BAC = 25°
∴ ∠CAD = ∠BAD – ∠BAC = 80° – 25° = 55°
(ii) ∠CBD = ∠CAD (Angles in the same segment)
= 55°
(iii) ∠ADC = ∠BCD (Angles of the isosceles trapezium)
= 180°- ∠BCE =180°- 80° = 100°

Question 25.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AJD and BC produced meet at P, show that ∠APB = 60°.
Solution:

Given : In a circle, ABCD is a cyclic quadrilateral in which AB is the diameter and chord CD is equal to the radius of the circle
To prove: ∠APB = 60°
Construction : Join OC and OD
Proof: ∵ chord CD = CO = DO (radii of the circle)
∴ ∆DOC is an equilateral triangle
∠DOC = ∠ODC = ∠OCD – 60°
Let ∠A = x and ∠B = y
∵ OA = OD = OC = OB (radii of the same circle)
∴ ∠ODA = ∠OAD = x and ∠OCB = ∠OBC =y
∴∠AOD = 180° – 2x and ∠BOC = 180° – 2y
But AOB is a straight line
∴ ∠AOD + ∠BOC + ∠COD = 180°
180°- 2x + 180° -2y + 60° = 180°
⇒ 2x + 2y = 240°
⇒ x + y = 120°
But ∠A + ∠B + ∠P = 180° (Angles of a triangle)
⇒ 120° + ∠P = 180°
⇒ ∠P = 180° – 120° = 60°
Hence ∠APB = 60°

Question 26.
In the figure, given alongside, CP bisects angle ACB. Show that DP bisects angle ADB.

Solution:
Given : In the figure,
CP is the bisector of ∠ACB
To prove : DP is the bisector of ∠ADB
Proof: ∵ CP is the bisector of
∴ ∠ACB ∠ACP = ∠BCP
But ∠ACP = ∠ADP {Angles in the same segment of the circle}
and ∠BCP = ∠BDP
But ∠ACP = ∠BCP
∴ ∠ADP = ∠BDP
∴ DP is the bisector of ∠ADB

Question 27.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

Solution:
In the figure,
ABCD is a cyclic quadrilateral
AC and BD are its diagonals
∠BAC = 30° and ∠CBD = 70°
Now we have to find the measures of ∠BCD, ∠BCA, ∠ABC and ∠ADB
∠CAD = ∠CBD = 70°
(Angles in the same segment)
Similarly ∠BAC = ∠BDC = 30°
∴ ∠BAD = ∠BAC + ∠CAD = 30° + 70° = 100°
(i) Now ∠BCD + ∠BAD = 180° (opposite angles of cyclic quad.)
⇒ ∠BCD + 100°= 180°
⇒ ∠BCD = 180°-100° = 80°
(ii) ∵ AD = BC (given)
∴ ∠ABCD is an isosceles trapezium
and AB || DC
∴ ∠BAC = ∠DCA (alternate angles)
⇒ ∠DCA = 30°
∠ABD = ∠D AC = 30° (Angles in the same segment)
∴ ∠BCA = ∠BCD – ∠DAC = 80° – 30° = 50°
(iii) ∠ABC = ∠ABD + ∠CBD = 30° + 70° = 100°
(iv) ∠ADB = ∠BCA = 50° (Angles in the same segment)

P.Q.
In the given below figure AB and CD are parallel chords and O is the centre.
If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.

Solution:
Given : AB = 24 cm, CD = 18 cm
⇒AM = 12 cm, CN = 9 cm
Also, OA = OC = 15 cm
Let MO = y cm, and ON = x cm
In right angled ∆AMO

(OA)² = (AM)² + (OM)²
(15)² = (12)² + (y²
⇒ (15)²-(12)²
⇒ y² = 225-144
⇒ y² = 81 = 9 cm
In right angled ∆CON
(OC)² = (ON)² + (CN)²
⇒(15 )²= x2 + (9)²
⇒ x² = 225-81
⇒x²= 144
⇒ x = 12 cm
Now, MN = MO + ON =y + x = 9 cm + 12 cm = 21 cm

Question 28.
In the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED (2016)
Solution:

(i) AD is parallel to BC, that is, OD is parallel to BC and BD is transversal.
∴ ∠ODB = ∠CBD = 32° (Alternate angles)
In ∆OBD,
OD = OB (Radii of the same circle)
⇒ ∠ODB = ∠OBD = 32°
(ii) AD is parallel to BC, that is, AO is parallel to BC and OB is transversal.
∴∠AOB = ∠OBC (Alternate angles)
∠OBC = ∠OBD + ∠DBC
⇒ ∠OBC = 32° + 32°
⇒ ∠OBC = 64°
∴ ∠AOB = 64°
(iii) In AOAB,
OA = OB(Radii of the same circle)
∴ ∠OAB = ∠OBA = x (say)
∠OAB + ∠OBA + ∠AOB = 180°
⇒ x + x + 64° = 180°
⇒ 2x = 180° – 64°
⇒ 2x= 116°
⇒ x = 58°
∴ ∠OAB = 58°
That is ∠DAB = 58°
∴ ∠DAB = ∠BED = 58°
(Angles inscribed in the same arc are equal)

Question 29.
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T.

(i) Prove ∆TPS ~ ∆TRQ
(ii) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm.
(iii) Find area of quadrilateral PQRS if area of ∆PTS = 27 cm2.(2016)
Solution:
(i) Since PQRS is a cyclic quadrilateral ∠RSP + ∠RQP = 180°
(Since sum of the opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠RQP = 180° – ∠RSP …(i)
∠RQT + ∠RQP = 180°
(Since angles from a linear pair)
⇒ ∠RQP = 180° – ∠RQT …(ii)
From (i) and (ii),
180° – ∠RSP = 180° – ∠RQT
⇒ ∠RSP = ∠RQT …(iii)
In ∆TPS and ∆TRQ,
∠PTS = ∠RTQ (common angle)
∠RSP = ∠RQT [From (iii)]
∴ ATPS ~ ATRQ (AA similarity criterion)
(ii) Since ∆TPS ~ ∆TRQ implies that corresponding sides are proportional that

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere (Surface Area and Volume) Ex 20F

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21F

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20G

Question 1.
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the ramaining solid.
Solution:
Height of the cylinder (h) = 10 cm
and radius of base (r) = 6 cm.
∴ Volume of cylinder = πr²h
Height of cone = 10 cm
and radius of base of cone = 6 cm

Question 2.
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out Find the volume and total surface area of the remaining solid.
Solution:
Radius of solid cylinder (R) = 12 cm
and height (H) = 16 cm.

Question 3.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs. 15 per metre if the width is 1.5 m.
Solution:
Radius of the cylindrical part of tent (r) = \(\frac { 105 }{ 2 }\)m

Question 4.
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate:
(i) total surface area .of the tent,
(ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Solution:
Total height = 13 m
Diameter of base of the tent = 24 m
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Height of cylindrical part h₁ = 8 m
and height of conical part (h₂) = 13 – 8 = 5 m

Question 5.
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemi-spherical lid. Find the volume of its interior, including the part covered by the lid.
Solution:
Diameter of cylinderical boiler = 3.5 m

Question 6.
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is 4 \(\frac { 2 }{ 3 }\) m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
Solution:

Question 7.
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.

If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm ; find the total surface area of the toy.  [Take π = 3.14]
Solution:
Height of the conical part (h₁)= 24 cm
total height of the toy = 60 cm
∴ Height of cylinderical part (h) = 60-24 = 36 cm
Radius of the cone (r) = twice the radius of the cylinder = 10 cm
∴ Radius of cylinder (r₁) = 5 cm

Question 8.
A cylindrical container with diameter of base 42 cm contains sufficient water to sub­merge a rectangular solid of iron with dimensions 22 cm x 14 cm x 10.5 cm. Find the rise in level of the water when the solid is submerged.
Solution:
Diameter of cylinderical container = 42cm
∴  Radius (r) = \(\frac { 42 }{ 2 }\) = 21 cm.
Dimension of a rectangular solid = 22 cm x 14cm x 10.5 cm
∴ Volume of solid
= 22 x 14 x 10.5 cm³        ….(i)
Let the height of water = h
∴ Volume of water in the container

Question 9.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
Solution:
Diameter of spherical marble = 1.4 cm.
∴ Radius = \(\frac { 1.4 }{ 2 }\) = 0.7 cm.
Volume of one ball = \(\frac { 4 }{ 3 }\) πr³

Question 10.
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tun­nel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m².

Solution:
Breadth of’tunnel = 6 m
and height = 8m
Length of tunnel = 35 m
Radius of semicircle = \(\frac { 6 }{ 2 }\) = 3 m.
Circumference of semicircle = πr = \(\frac { 22 }{ 7 }\) x 3 = \(\frac { 66 }{ 7 }\) m
∴ Internal surface area of the tunnel

Question 11.
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.


(Given : 1 gallon = 4.5 litres)
Solution:
Length = 21m
breadth = 7 m
Depth of water = 2.4 m
∴ Radius of semicircle = \(\frac { 7 }{ 2 }\) m.
Area of the cross section = Area of rectangle + area of semicircle

Question 12.
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.

Solution:
Rate of water flow = 20 cm/sec.
Period = 1 min. = 60 sec.
Radius of semi-circular part (r) = \(\frac { 21 }{ 2 }\)  cm
Height of channel (h) = 7 cm
Length of channel = 20 x 60 = 1200 cm

Question 13.
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is 3 \(\frac { 1 }{ 2 }\) cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is 1 \(\frac { 3 }{ 4 }\) cm and the radius of whose base is 2 cm, find the drop in the water level.  [1993]
Solution:
Diameter of cylinder = 7 cm
∴ Radius (R) = \(\frac { 7 }{ 2 }\) cm
Height (h) = 8 cm

Question 14.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
(i) the total surface area of the can in contact with water when the sphere is in it;
(ii) the depth of water in the can before the sphere was put into the can. [1997]
Solution:
Radius of the cylindrical can = 3.5 cm
∴  Radius of the sphere which fits in it

Question 15.
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level’of water, when it is inverted upside down, common diameter is 7 cm and height of the cylinder is 20  cm.
Solution:
(i) Diameter of the cylinder = 7 cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\) cm

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 20 Cylinder, Cone and Sphere Ex 20F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Question 1.
Find the sum of n terms of the series :
(i) 4 + 44 + 444 + ….
(ii) 0.8 + 0.88 + 0.888 + ….
Solution:
(i) 4 + 44 + 444 + ….
= \(=\frac { 4 }{ 9 } \left[ 9+99+999+…. \right] \)

Question 2.
Find the sum of infinite terms of each of the following geometric progression:
(i)\(1+\frac { 1 }{ 3 } +\frac { 1 }{ 9 } +\frac { 1 }{ 27 } +…\)
(ii)\(1-\frac { 1 }{ 2 } +\frac { 1 }{ 4 } -\frac { 1 }{ 8 } +…\)
(iii)\(\frac { 1 }{ 3 } +\frac { 1 }{ { 3 }^{ 2 } } -\frac { 1 }{ { 3 }^{ 3 } } +…\)
(iv)\(\sqrt { 2 } -\frac { 1 }{ \sqrt { 2 } } +\frac { 1 }{ 2\sqrt { 2 } } -\frac { 1 }{ 4\sqrt { 2 } } +…\)
(v)\(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +\frac { 1 }{ 9\sqrt { 3 } } +… \)
Solution:
(i)\(1+\frac { 1 }{ 3 } +\frac { 1 }{ 9 } +\frac { 1 }{ 27 } +…\) upto infinity
S_n = \(\\ \frac { a }{ 1-r } \)

Question 3.
The second term of a G.P. is 9 and sum of its infinite terms is 48. Find its first three terms.
Solution:
In a G.P.
T₂ = 9, sum of infinite terms = 48
Let a be the first term and r be the common ratio, therefore,
S_∞ = \(\\ \frac { a }{ 1-r } \)

Question 4.
Find three geometric means between \(\\ \frac { 1 }{ 3 } \) and 432.
Solution:
Let G₁, G₂ and G₃ be three means between
\(\\ \frac { 1 }{ 3 } \) and 432, then

Question 5.
Find :
(i) two geometric means between 2 and 16
(ii) four geometric means between 3 and 96.
(iii) five geometric means between \(3 \frac { 5 }{ 9 } \) and \(40 \frac { 1 }{ 2 } \).
Solution:
(i) Two G.M. between 2 and 16
Let G₁ , and G₁ be the G.M.,
then 2, G₁, G₂, 16

Question 6.
The sum of three numbers in G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find numbers
Solution:
Sum of three numbers in G.P = \(\\ \frac { 39 }{ 10 } \)
and their product = 1

Question 7.
Find the numbers in G.P. whose sum is 52 and the sum of whose product in pairs is 624.
Solution:
Sum of 3 numbers in G.P. = 52
and their product in pairs = 624
Let numbers be a, ar, ar²

Question 8.
The sum of three numbers in G.P. is 21 and the sum of their squares is 189. Find the numbers.
Solution:
Sum of three numbers in G.P. = 21
Sum of their squares = 189
Let three numbers be a, ar, ar², then
a + ar + ar² = 21
=> a( 1 + r + r²) = 21….(i)

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

Question 1.
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.

Solution:

In circle with centre O, ∠BAO = 30°, ∠BCO = 40°.
Join BO.
OA = OB = OC (Radii of the circle)
∠OBA = ∠OAB = 30° and ∠OBC = ∠OCB = 40°
∠ABC = 30° + 40° = 70°
Now, AOC is at the centre and ∠ABC is on the remaining part of the circle.
∠AOC = 2 ∠ABC = 2 x 70° = 140°.

Question 2.
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.

Solution:

(i) In ΔABD
65° + 70° + ∠ADB = 180°
∠ADB = 180° – 65° – 70° = 45°
∠ADC = 45° + 45° = 90°
AC is diameter [Angle in semi circle is 90°]
(ii) ∠ACB = ∠ADB = 45° [angle in same segment]

Question 3.
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
(i) ∠OCA,
(ii) ∠OAC.

Solution:

O is the centre of the circle,
∠AOB = 70°
arc AB subtends ∠AOB at the centre
and ∠ OCA is at the remaining part of circle
∠AOB = 2 ∠OCA
or ∠OCA = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 70° = 35°
In ΔOAC,
OC = OA (Radii of the same circle)
∠OAC = ∠OCA = 35°

Question 4.
In each of the following figures, O is the centre of the circle. Find the values of a, b, and c.

Solution:

(i) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part
∠AOB = 2 ∠ACB
or ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 130° = 65°
or b = 65°
But a + b = 180° (Opposite angles of a cyclic quad.)
a = 180° – b = 180° – 65° = 115°
a = 115°, b = 65°
(ii) Arc AB subtends ∠ AOB at the centre and ∠ACB at the remaining part.

Reflex ∠AOB = 2 ∠ACB
or ∠ACB = \(\frac { 1 }{ 2 }\) (reflex ∠AOB) = \(\frac { 1 }{ 2 }\) [360°- 112°]
= \(\frac { 1 }{ 2 }\) x 248° = 124°
Hence, c = 124°.

Question 5.
In each of the following figures, O is the centre of the circle. Find the value of a, b, c and d.

Solution:
(i) BOD is a diameter

∠BAD = 90° (Angle in a semi-circle)
∠ADB = 180° – (90° + 35°) = 180° – 125° = 55°
But ∠ACB = ∠ADB = 55° (Angles in the same segment)
a = 55°.
(ii) In ΔEBC.

Ext. 120° = 25° + ∠BCE
∠BCE = 120° – 25° = 95°
But ∠ADB = ∠ACB = 95° (Angles in the same segment)
b = 95°.
(iii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part,

∠ AOB = 2 ∠ ACB = 2 x 50° = 100°
In ΔAOB,
OA = OB (Radii of the same circle)
∠OAB = ∠OBA
But ∠OAB + ∠OBA = 180° – 100° = 80°
c = ∠OAB = ~ x 80° = 40°.
(iv) In the given figure, O is the centre of the circle.
AOB is its diameter and ∠ABP = 45°
Q is any point and BQ, PQ are joined

In ΔABP,
∠APB = 90° (Angle in a semicircle)
∠PAB + ∠PBA = 90°
⇒ ∠PAB + 45° = 90°
⇒ ∠PAB = 90° – 45°
⇒ ∠PAB = 45°
Now ∠PAB = ∠PQB (Angle in the same segment)
BPQB = 45°
⇒ d = 45°

Question 6.
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O1 and 02 are the centres of two circles.

Solution:

Given- Two circles with centre O1 and O2 intersect each other at A and B.
AC and AD are the diameters of the circles.
To Prove- D, B, C are in the same straight line.
Construction- Join AB.
Proof- AO1C is diameter.
∠ABC = 90°. (Angle in a semi-circle)
Similarly ∠ABD = 90°,
Adding, we get:
∠ABC + ∠ABD = 90° + 90° = 180°
DBC is a straight line.
or D, B, C are in the same line.

Question 7.
In the figure given beow, find :
(i) ∠BCD,
(ii) ∠ADC,
(iii) ∠ABC.

Show steps of your workng.
Solution:

ABCD is a cyclic quadrilateral
∠A + ∠C = 180°.
∠C = 180° – ∠A = 180° – 105° = 75°
or ∠BCD = 75°
DC || AB
∠ADC + ∠DAB = 180° (Angles on the same side of the transversal of || lines)
∠ADC = 180° – ∠DAB = 180° – 105° = 75°
But ∠ADC + ∠ABC = 180° (opposite angles of a cyclic quad.)
∠ABC = 180° – ∠ADC = 180° – 75° = 105°

Question 8.
In the given figure, O is centre of the circle. If ∠ AOB = 140° and ∠ OAC = 50°; find :
(i) ∠ ACB,
(ii) ∠OBC,
(iii) ∠OAB,
(iv) ∠CBA

Solution:

O is the centre of circle ∠AOB = 140° and ∠OAC = 50°.
AB is joined
Reflex ∠AOB = 360° – 140° = 220°
But ∠ACB = \(\frac { 1 }{ 2 }\) Reflex ∠AOB = \(\frac { 1 }{ 2 }\) x 220° = 110°
In quad. OACB,
∠AOB + ∠OAC + ∠ACB + ∠OBC = 360°
⇒ 140° + 50° + 110° + ∠OBC = 360°
⇒ 300° + ∠OBC = 360°
⇒ ∠OBC = 360° – 300° = 60°
In ∆OAB,
∠AOB + ∠OAB + ∠OBA = 180°
But ∠OBA = ∠OAB (Angles opposite to equal sides)
140° + ∠OAB + ∠OAB = 180°
2 ∠OAB = 180° – 140° = 40°
∠OAB = \(\frac { 40 }{ 2 }\) = 20°
∠OAB = ∠OBA = 20°.
⇒ ∠OBC = ∠CBA + ∠ABO
⇒ 60° = ∠CBA + 20°
⇒ ∠CBA = 40°

Question 9.
Calculate :
(i) ∠ CDB,
(ii) ∠ ABC,
(iii) ∠ ACB.

Solution:
∠CDB = ∠BAC (Angles is the same segment) = 49°
∠ABC = ∠ADC (Angles in the same segment) = 43°
∠ADB = ∠ADC + ∠BDC = 43° + 49° = 92°
and ∠ADB + ∠ACB = 180° (opposite angles of a cyclic quad.)
∠ACB = 180° – ∠ADB = 180° – 92° = 88°.

Question 10.
In the figure given below, ABCD is a eyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
(i) ∠BDC,
(ii) ∠BCD,
(iii) ∠BCA.

Solution:
In cyclic quad. ABCD,
∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°.
∠A + ∠C = 180° (opposite angles of a cyclic quad.)
∠C = 180° – ∠A = 180° – 75° = 105° or ∠BCD = 105°
In ΔABD,
∠BAD + ∠ABD + ∠ADB = 180°
⇒ 75° + 58° + ∠ ADB = 180°

⇒ 133° + ∠ADB = 180°
⇒ ∠ADB = 180° – 133° = 47°
∠BDC = 77° – ∠ADB = 77° – 47° = 30°
But ∠BCA = ∠BDA (Angles in the same) = 47°

Question 11.
In the following figure, O is centre of the circle and ΔABC is equilateral. Find :
(i) ∠ADB
(ii) ∠AEB

Solution:

∠ACB and ∠ADB are in the same segment.
∠ADB = ∠ACB. = 60°. (Angle of an equilateral triangle)
AEBD is a cyclic quadrilateral
∠AEB + ∠ADB = 180°
⇒ ∠AEB + 60° = 180°
⇒ ∠AEB = 180° – 60° = 120°.

Question 12.
Given- ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD

Solution:

In ΔABC, ∠CBA = 50°, ∠CAB = 75°,
∠ACB = 180° – (∠CBA + ∠CAB) = 180° – (50° = 75°) = 180° – 125° = 55°
Bui ∠ADB = ∠ACB = 55° (Angles in the same segment)
Now in ΔABD,
∠DAB + ∠ABD + ∠ADB = 180°.
⇒ ∠DAB + ∠ABD + 55° = 180°
⇒ ∠DAB + ∠ABD = 180° – 55° = 125°.

Question 13.
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

Solution:

ABCD is a cyclic quadrilateral and ∠ADC = 130°
O is centre of the circle, AOB is diameter.
∠ABC = 180° – 130° = 50°.
In ΔABC,
∠ACB = 90° (angle in semicircle)
∠BAC + ∠CBA = 90°.
∠BAC + 50° = 90°
∠BAC = 90° – 50° = 40°.

Question 14.
In the figure given below, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.

Solution:

∠AOC + ∠COB = 180° (Linear pair)
∠COB = 180° – ∠AOC = 180° – 110° = 70°
Arc BC subtends ∠COB at the centre and x at the remaining part of circle
∠COB = 2x
⇒ x = \(\frac { 1 }{ 2 }\) ∠COB = \(\frac { 1 }{ 2 }\) x 70° = 35°

Question 15.
In the following figure, O is centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

Solution:

Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of circle,
∠AOB = 2 ∠ACB
or ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 60° = 30°
Now in ΔDBC,
∠DBC + ∠ACB + ∠BDC = 180°
⇒ ∠DBC + 30° + 100° = 180°
⇒ ∠DBC = 180° – 130° = 50°
or ∠OBC = 50°.

Question 16.
ABCD is a cyclic quadrilateral in which ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate :
(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB.

Solution:

(i) ∠ CBD = ∠ DAC = 27° (Angles in the same segment)
(ii) In ΔADB,
∠ABD + ∠BAD + ∠BDA = 180°.
⇒ 50° + ∠BAD + 33° = 180°
⇒ ∠BAD + 83° = 180°
⇒ ∠BAD = 180° – 83° = 97°
In cyclic quad. ABCD,
∠BAD + ∠DCB = 180°
⇒ 97° + ∠DCB = 180°
⇒ ∠DCB = 180°- 97° = 83°
(iii) ∠BAD = 97°
⇒ ∠BAC + ∠CAD = 97°
⇒ ∠BAC + 27° = 97°
⇒ ∠BAC = 97° – 27° = 70°
∠CAB = 70°.

Question 17.
In the figure given below, AB is diameter of the circle whose centre is O. Given that:
∠ECD = ∠EDC = 32°. Show that ∠COF = ∠CEF.

Solution:

Given- AB is the diameter of a circle with centre O
and ∠ECD = ∠EDC = 32°
To Prove- ∠COF = ∠CEF
Proof- Arc CF subtends ∠COF at the centre and ∠CDF at the remaining part of the circle.
∠COF = 2 ∠CDF = 2 x ∠EDC = 2 x 32° = 64° ….. (i)
In ΔCED,
Ext. ∠CEF = ∠CDF + ∠DCE = ∠EDC + ∠ECD = 32° + 32° = 64° ….(ii)
from (i) and (ii)
∠CDF = ∠CEF

Question 18.
In the figure given below, AB and CD arc straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in:
(i) ∠DCE,
(ii) ∠ABC.

Solution:

In circle, COD is the diameter.
∠CED = 90° (Angle in a semi circle)
In right A CDE,
∠ DCE + ∠ EDC = 90°
⇒ ∠ DCE + 40° = 90°
∠ DCE = 90° – 40° = 50°
In ΔOBC.
Ext. ∠COA = ∠OBC + ∠OCB
⇒ 80° = ∠OBC + 50°
⇒ ∠OBC = 80° – 50° = 30°
or ∠ABC = 30°

Question 19.
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that AB = BE.

Solution:
Given- AC is a diameter of a circle with centre O.
AE is a chord which intersects the smaller circle with AO as diameter at B.

To Prove- AB = BE.
Construction- Join OB.
Proof- ∠ABO = 90° (Angle in a semi circle)
OB ⊥ AE
OB bisects chord AE
Hence, AB = BE.

Question 20.
In the following figure,
(i) if ∠ BAD = 96°, find ∠BCD and ∠BFE,
(ii) Prove that AD is parallel to FE.

Solution:
Given- In the figure, ∠BAD = 96°
To Prove-
(i) Find ∠BCD and ∠BFE
(ii) AD || EF
Proof- ABCD is a cyclic quadrilateral.
∠BAD + ∠BCD = 180°
⇒ 96° + ∠BCD = 180°
⇒ ∠BCD = 180° – 96° = 84°
Again BCEF is a cyclic quadrilateral,
Ext. ∠BCD = Int. opposite ∠BFE
∠BFE = 84°.
∠BAD + ∠BFE = 96° + 84° = 180°
But these are on same side of the transversal.
AD || FE.

Question 21.
Prove that
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
Solution:

(i) ABCD is a parallelogram in a circle with centre O.
To Prove- ABCD is a rectangle.
Proof- ABCD is a cyclic parallelogram.
∠A + ∠C = 180°.
But ∠A = ∠C (opposite angles of a ||gm)
∠A = ∠C = 90°
Similarly we can prove that
∠B = ∠D = 90°
Each angle of a ||gm is right angle
Hence ABCD is a rectangle.
(ii) Given- ABCD is a cyclic rhombus.
To Prove- ABCD is a square.
Proof- ABCD is cyclic rhombus
∠A + ∠C = 180°
But ∠A = ∠C (opposite angles of rhombus)
∠A = ∠C = 90°
Similarly we can prove that ∠B = ∠D = 90°
Each angle of a rhombus is a right angle
ABCD is a square.

Question 22.
In the following figure, AB = AC. Prove that DECB is an isosceles trapezium.

Solution:
Given- In the figure, AB = AC.
To Prove- DECB is an isosceles trape∠ium.
Proof- In ∆ABC,
AB = AC
∠B = ∠C
DECB is a cyclic quadrilateral.
∠B + ∠DEC = 180°
∠C + ∠DEC = 180°
But this is the sum of interior angles on one side of a transversal.
DE || BC ….(i)
But ∠ADE = ∠B
and ∠AED = ∠C (Corresponding angles)
∠ADE = ∠AED (∠B = ∠C)
AD = AE (Opposite to equafangles)
But AB = AC (Given)
AB – AD = AC – AE
⇒ DB = EC ….(ii)
From (i) and (ii)
DECB is an isosceles trape∠ium.

Question 23.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are draw n. Show that the points A, Q and B are collinear.
Solution:

Given- Two circles with centres O and O’ intersect each other at P and Q.
From P, PA and PB are two diameters are drawn.
To Prove- A, Q and B are collinear.
Construction-
Join PQ, AQ and BQ.
Proof- In first circle.
∠PAQ = 90° (Angle in a semi circle) ….(i)
Similarly, in second circle, ∠PBQ = 90° ….(ii)
Adding (i) and (ii).
∠PAQ + ∠PBQ = 90° + 90° = 180°
But, there are adjacent angles
AQB is a straight line.
Hence A, Q and B are collinear.
Hence proved.

Question 24.
ABCD is a quadrilateral inscribed in a circle, having ∠A = 60°; O is the centre of the circle. Show that:
∠OBD + ∠ODB = ∠CBD + ∠CDB.
Solution:
Given- ABCD is a cyclic quadrilateral in which ∠A = 60°
and O is the centre of the circle.
BD, OB and OD are joined.
To Prove- ∠OBD + ∠ODB = ∠CBD + ∠CDB
Proof- Arc BCD subtends ∠BOD at the centre and ∠BAD at remaining part of the circle.

∠BOD = 2 ∠BAD = 2 x 60° = 120°
In ∆BOD,
∠BOD = 120°
∠OBD + ∠ ODB = 180° – 120° = 60° …. (i)
ABCD is a cyclic quadrilateral
∠A + ∠C = 180°
⇒ 60° + ∠C = 180°
⇒ ∠C = 180° – 60° = 120°
In ∆BCD,
∠CBD + ∠CDB + ∠ C = 180°.
∠CBD + ∠CDB + 120° = 180°
∠CBD + ∠CDB = 180° – 120° = 60° ….(ii)
From (i) and (ii),
∠OBD + ∠ODB = ∠CBD + ∠CDB

Question 25.
The figure given below, shows a circle with centre O.
Given- ∠AOC = a and ∠ABC = b.
(i) Find the relationship between a and b. :
(ii) Find the measure of angle OAB, if OABC is a parallelogram.

Solution:

(i) ∠AOC = a, ∠ABC = b
Reflex ∠AOC = 360° – a
Now arc AC subtends reflex ∠AOC at the centre and ∠ABC at the remaining part of the circle
∠ABC = \(\frac { 1 }{ 2 }\) ref. ∠AOC
b = \(\frac { 1 }{ 2 }\) (360° – a)
⇒ 2b = 360° – a
⇒ a + 2b = 360° ….(i)
(ii) If OABC is a || gm,
then ∠AOC = ∠ABC
⇒ a = b
Substituting the value of a, in ….(i)
b + 2b = 360°
⇒ 3b = 360°
⇒ b = 120°
But ∠OAB + ∠ABC = 180° (Angles in a || gm)
⇒ ∠OAB + b = 180°
⇒ ∠OAB + 120° = 180°
⇒ ∠OAB = 180° – 120° = 60°.

Question 26.
Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.
Solution:
Given- Two chords AB and CD intersect each other at P inside the circle, OA, OB, OC and OD are joined.
To Prove- ∠AOC + ∠BOD = 2 ∠APC.
Construction- Join AD
Proof- Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining pari of the circle
∠AOC = 2 ∠ADC ….(i)
Similarly, ∠BOD = 2 ∠BAD ….(ii)
Adding (i) and (ii),

∠AOC + ∠BOD = 2 ∠ADC
⇒ 2 ∠ BAD = 2 (∠ADC + ∠BAD) ….(iii)
But in ∆PAD,
Ext. ∠APC = ∠PAD + ∠ADC = ∠ADC + ∠BAD …(iv)
from (iii) and (iv)
∠AOC + ∠BOD = 2 ∠APC

Question 27.
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°.
Calculate:
(i) ∠RNM,
(ii) ∠NRM.

Solution:

Join RN and MS. .
(i) RS is the diameter
∠RMS = 90° (Angle in semi circle)
∠RSM + ∠MRS = 90°
∠RSM = 90° – 29° = 61°
But ∠RSM + ∠RNM = 180° (Angles in a cyclic quad.)
61° + ∠RNM = 180°
⇒ ∠RNM = 180° – 61 = 119°
NM || RS
∠NMR = ∠MRS = 29° (Alt. angles)
In ∆RNM,
∠NRM + ∠RNM + ∠NMR = 180°
⇒ ∠NRM + 119° + 29° = 180°
⇒ ∠NRM + 148° = 180°
⇒ ∠NRM = 180° – 148° = 32°.

Question 28.
In the figure given alongside, AB // CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Solution:

AB || CD.
∠BAD = ∠ADC (Alternate angles) = 25° (∠ADC = 25° given)
Join AC and BD.
∠CAD = 90° (Angle in semi circle)
∠CAB = ∠CAD + ∠DAB = 90° + 25° = 115°
Now in cyclic quad. CABD.
∠CAB + ∠BDC = 180°
⇒ ∠CAB + ∠BDA + ∠ADC = 180°
⇒ 115° + ∠BDA + 25° = 180°
⇒ ∠BDA + 140° = 180°
⇒ ∠BDA = 180° – 140° = 40°
∠AEB and ∠BDA are in tire same segment of a circle
∠AEB = ∠BDA = 40° (proved)
Hence ∠AEB = 40°.

Question 29.
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight fine is drawn to meet the circles at C and D. Prove that AC is || to BD.

Solution:
Given- Two circles intersect each other at P and Q. Through P, a line APB is drawn to meet the circles in A and B. Through Q, another straight line CQD is drawn meeting the circles in C and D.
AC, BD are joined.
To Prove- AC || BD.
Construction- Join PQ
Proof- APQC is a cyclic quadrilateral.

∠A + ∠PQC = 180° …… (i)
In cyclic quad. PBDQ,
Ext. ∠PQC = ∠ B …… (ii)
from (i),
∠A + ∠B = 180°.
But these are interior angles on the same side of a transversal.
AC || BD.

Question 30.
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
Solution:

Given- The sides AB and DC of a cyclic quad. ABCD are produced to meet at P and PA = PD.
To Prove- AD || BC
Proof- In ∆PAD,
PA = PD (given)
∠A = ∠D (angles opposite to equal sides)
ADCB is a cyclic quad.
Ext. ∠PCB = ∠A = ∠D
But these are corresponding angles. ,
BC || AD or AD || BC.

Question 31.
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find:
(i) ∠PRB,
(ii) ∠ PBR,
(iii) ∠ BPR.

Solution:
∠PRB = ∠BAP (Angles in the same segment)
∠PRB = 35°

In ∆ABP,
∠APB = 90° (Angle in semi circle)
∠BPQ = 90°.
In ∆PQR,
∠R + ∠Q + ∠RPQ = 180°
⇒ 35° + 25° + ∠RPQ = 180°
⇒ ∠RPQ = 180° – 60° = 120°
⇒ ∠BPR = ∠RPQ – ∠BPQ = 120° – 90° = 30°
In ∆PBR,
∠PBR = 180° – (∠R + ∠BPR) = 180° – (35° + 30°) = 180° – 65° = 115°

Question 32.
In the given figure SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = SR.

Solution:
Given- SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral.

To Prove SQ = SR.
Proof- In cyclic quad. PQRS,
Ext. ∠SPT = ∠QRS
But ∠RPS = ∠SPT (PS is the bisector of ∠RPT)
∠QRS = ∠RPS ….(i)
But ∠RPS = ∠RQS (Angles in the same segment)
∠QRS = ∠RQS
Now in ∆QRS,
∠QRS = ∠RQS (proved)
SQ = SR (Sides opposite to equal angles)

Question 33.
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the si∠es of the angles CEB and OCE.

Solution:

In the figure, ∠AOE = 150°, ∠DAO = 51°
Now in cyclic quad. ADEB,
Ext. ∠CEB = Int. Opp ∠DAO = 51°.
In ∆OEB,
Ext. ∠AOE = ∠OBE + ∠OEB
= ∠OBE + ∠OBE (OB = OE) = 2 ∠OBE
2 ∠OBE = 150°
⇒ ∠ OBE = 75°
∠EBC = 180° – 75° = 105°
Now in ∆EBC,
∠CEB + ∠OCE + ∠EBC = 180°
⇒ 51° + ∠OCE + 105° = 180°
⇒ ∠OCE + 156° = 180°
⇒ ∠OCE = 180° – 156° = 24°.

Question 34.
In the figure, given below, P and Q arc the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.

Solution:

In circle with centre P,
Arc AB subtends ∠APB at the centre and ∠ACB at the remaining part of the circle.
∠APB = 2 ∠ACB
⇒ ∠ACB = \(\frac { 1 }{ 2 }\) ∠APB = \(\frac { 1 }{ 2 }\) x 150° = 75°
But ∠ACB + ∠DCB = 180° (Linear pair)
∠DCB = 180° – ∠ACB = 180° – 75° = 105°
In circle with centre O,
Arc BD subtends ∠ BQD at the centre and ∠ DCB at the remaining part of the circle
∠BQD = 2 ∠DCB = 2 x 105° = 210°
But x + ∠BQD = 360° (Angles at a point)
⇒ x + 210° = 360°
⇒ x = 360° – 210° = 150°.

Question 35.
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given ∠APB = a°. Calculate, in terms of a°, the value of :
(i) obtuse ∠AOB,
(ii) ∠ACB,
(iii) ∠ADB.

Give reasons for your answers clearly.
Solution:

Arc AB in small circle subtends ∠AOB at the centre and ∠APB at the remaining part of the circle.
(i) ∠AOB = 2 ∠APB = 2a° (∠APB = a°)
∠APB = (2a)°
(ii) In larger circle, AOBC is a cyclic quad.
∠AOB + ∠ACB = 180°.
⇒ 2a° + ∠ACB = 180°
∠ACB = 180° – 2a° = (180° – 2a°)
(iii) But ∠ ACB and ∠ ADB are in the same segment
∠ADB = ∠ ACB = (180° – 2a°)

Question 36.
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.

Solution:
In ∆OBC,
OB = OC (radii of the same circle)
∠OBC = ∠BCO or ∠ABC = ∠BCO
∠BCO = ∠ABC = 55°
Now in ∆OBC,
Ext. AOC = ∠OBC + ∠BCO = 55° + 55° = 110°
x = 110°

Now in cyclic quad, ABCD,
∠ADC + ∠ABC = 180°
⇒ y + 55° = 180°
⇒ y = 180° – 55° = 125°

Question 37.
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that: ∠BCD = 2 ∠ABE.

Solution:
Given- A is the centre of the circle and ABCD is a parallelogram.
CDE is a straight line.
To Prove- ∠BCD = 2 ∠ABE.

Proof- AB || DC (opposite sides of a || gm)
∠ABE = ∠BED (Alternate angles) ….(i)
ABCD is a || gm (given)
∠BAD = ∠BCD (opposite angles of a ||gm) ….(ii)
Now arc BD subtends ∠BAD at the centre and ∠BED at the remaining part of the circle
∠BAD = 2 ∠BED
from (i) and (ii)
∠BCD = 2 ∠ABE

Question 38.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
(i) ∠DAB,
(ii) ∠BDC.

Solution:

∠DAB and ∠BED are in the same segment of the circle.
∠DAB = ∠BED = 65° (∠BED = 65° given)
DC || AB (Given)
∠BDC = ∠DBA (Alternate angles)
In ∆ADB,
AOB is the diameter
∠ADB = 90° (Angle in semi circle)
∠DAB + ∠DBA = 90°
⇒ 65° + ∠DBA = 90°
⇒ ∠DBA = 90° – 65° = 25°
But ∠DBA = ∠BDC (proved)
∠BDC = 25°

Question 39.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate:
(i) ∠EBA,
(ii) ∠BCD.

Solution:

AOB is the diameter,
∠AEB = 90°
and ∠EAB + ∠EBA = 90°
⇒ 63° + ∠EBA = 90°
⇒ ∠EBA = 90° – 63° = 27°
ED || AB (given)
∠DEB = ∠EBA (Alternate angles) = 27°
In cyclic quad. EBCD,
∠DEB + ∠BCD = 180° (opposite angles of a cyclic quad.)
⇒ 27° + ∠BCD = 180°
⇒ ∠BCD = 180° – 27° = 153°.

Question 40.
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB arc produced to meet at F. If ∠BEG = 42° and ∠BAD = 98°; calculate :
(i) ∠AFB,
(ii) ∠ADC.

Solution:

In ∆AED,
∠ADE + ∠AED + ∠EAD = 180° (Angles of a triangle)
⇒ ∠ADE + 42° + 98° = 180°
⇒ ∠ADE + 140° = 180°
⇒ ∠ ADE = 180° – 140° = 40° or ∠ADC = 40°
In cyclic quad. ABCD.
∠BAD + ∠BCD = 180°
⇒ 98° + ∠BCD = 180°
⇒ ∠BCD = 180° – 98° = 82°
Now in ∆FCD,
∠DFC + ∠FDC + ∠FCD = 180°
⇒ ∠AFB + ∠ADC + ∠BCD = 180°
⇒ ∠AFB + 40° + 82° = 180°
⇒ ∠AFB + 122° = 180°
⇒ ∠AFB = 180° – 122° = 58°

Question 41.
In the following figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°. Calculate :
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC. Also, show that the ∆AOD is an equilateral triangle.

Solution:

(i) ABCD is a cyclic quadrilateral,
∠DCB + ∠DAB = 180°
⇒ 120° + ∠DAB = 180°
∠DAB =180° – 120° = 60°
(ii) AOB is a diameter.
∠ADB = 90° (Angle in a semi circle)
∠ DAB + ∠DBA = 90°
60° + ∠ DBA = 90°
∠DBA = 90° – 60° = 30°
(iii) In ∆OBD,
OD = OB (radii of the same circle)
∠ ODB = ∠ OBD
or ∠ABD = 30° (from ii)
But DO || CB (given)
∠ODB = ∠DBC (Alternate angles)
⇒ 30° = ∠DBC or ∠DBC = 30°
(iv) ∠ABD + ∠DBC = 30° + 30° = 60°
⇒ ∠ABC = 60°
Again in cyclic quad. ABCD,
∠ADC + ∠ABC = 180°
∠ADC + 60° = 180°
∠ ADC = 180° – 60° = 120°
In ∆AOD,
OA = OD (radii of the same circle)
∠ AOD = ∠ DAO or ∠ DAB = 60° (proved in (i))
∠ADO = 60° (Third angle)
∠ADO = ∠AOD = ∠DAO = 60°
∆AOD is an equilateral triangle.

Question 42.
In the given figure, I is the incentre of ∆ABC. BI when produced meets the circum circle of ∆ABC at D.
Given ∠BAC = 55° and ∠ACB = 65°; calculate:
(i) ∠DCA,
(ii) ∠DAC,
(iii) ∠DCI,
(iv) ∠AIC

Solution:

Join AD, DC, AI and Cl,
In ∆ABC,
∠BAC = 55°, ∠ACB = 65°
∠ABC = 180° – (∠BAC + ∠ACB) = 180°- (55° + 65°) = 180° – 120° = 60°
In cyclic quad. ABCD,
∠ABC + ∠ADC = 180°
⇒ 60° + ∠ADC = 180°
∠ADC = 180° – 60°= 120°
In ∆ADC,
∠ DAC + ∠ DCA + ∠ ADC = 180°
⇒ ∠ DAC+ ∠ DCA + 120° = 180°
⇒ ∠ DAC+ ∠ DCA = 180° – 120° = 60°
But ∠ DAC = ∠ DCA (I lies on the bisector of ∠ ABC)
∠ DAC = ∠ DCA = 30°
DI is perpendicular bisector of AC
∠ AIC = ∠ ADC= 120°
IC is the bisector of ∠ ACB
∠ ICA = \(\frac { 65 }{ 2 }\) = 32.5°
∠DCI = ∠DCA + ∠ACI = 30° + 32.5° = 62.5° = (62.5)° = 60° 30′.

Question 43.
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circum circle of the triangle at points P, Q and R respectively. Prove that:
(i) ∠ ABC = 2 ∠ APQ,
(ii) ∠ ACB = 2 ∠ APR,
(iii) ∠ QPR = 90° – \(\frac { 1 }{ 2 }\) ∠BAC.

Solution:
Given- ∆ABC is inscribed in a circle. Bisectors of ∠BAC, ∠ABCand ∠ACB meet the circumcircle of the∆ABC at P, Q and R respectively.

To Prove-
(i) ∠ ABC = 2 ∠APQ.
(ii) ∠ ACB = 2 ∠ APR.
(iii) ∠ QPR = 90° – \(\frac { 1 }{ 2 }\) ∠BAC.
Construction-
Join PQ and PR.
Proof- ∠ABQ and ∠APQ are in the same segment of the circle.
∠ ABQ = ∠ APQ
But ∠ ABQ = – ∠ ABC (BQ is the angle bisector of ∠ ABC)
\(\frac { 1 }{ 2 }\) ∠ ABC = ∠ APQ
Or ∠ ABC = 2 ∠APQ …,(i)
Similarly, ∠ APR and ∠ ACR are in the same segment of the circle.
∠ APR = ∠ ACR
But ∠ ACR = \(\frac { 1 }{ 2 }\) ∠ ACB (CR is the angles bisector of ∠ ACB)
\(\frac { 1 }{ 2 }\) ∠ ACB = ∠ APR
Or ∠ ACB = 2 ∠ APR ….(ii)
Adding (i) and (ii)
∠ ABC + ∠ ACB = 2 ∠ APQ + 2∠ APR = 2 (∠ APQ + ∠ APR) = 2 ∠ PQR
Or 2 ∠ PQR = ∠ ABC + ∠ ACB
∠ PQR = \(\frac { 1 }{ 2 }\) (∠ ABC + ∠ ACB) ….(iii)
But ∠ ABC + ∠ ACB + ∠ BAC = 180° (Angles of a triangle)
∠ ABC + ∠ ACB = 180° – ∠ BAC ….(iv)
from (iii) and (iv) we get,
∠ PQR = \(\frac { 1 }{ 2 }\) (180° – ∠ BAC) = 90° – \(\frac { 1 }{ 2 }\) ∠ BAC

Question 44.
Calculate the angles x, y and z if :

Solution:

Ext. ∠ ADC = x + z ….(i)
and in ΔBPC,
Ext. ∠ ABC = y + x ….(ii)
(∠ BCP = ∠ DCQ = x vertically opposite angles)

Adding (i) and (ii),
x + z + y + x = ∠ ADC + ∠ ABC.
But ∠ ADC + ∠ ABC = 180° (opposite angles of a cyclic quad)
2x + y + z = 180°
⇒ 2 x 3k + 4k + 5k = 180°
⇒ 6k + 4k + 5k = 180°
⇒ 15k = 180°
⇒ k = 12°
x = 3k = 3 x 12° = 36°= x = 36°
y = 4k = 4 x 12° = 48°= y = 48°
z = 5k = 5 x 12° = 60° = z = 60°

Question 45.
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
(i) Angle ABC
(ii) Angle BEC [1995]

Solution:
In the figure, AB = AC = CD, ∠ ADC = 38°
BE is joined.
In ΔACD, AC = CD
∠CAD = ∠CDA = 38°
Ext. ∠ ACB = ∠ CAD + ∠ CDA = 38° + 38° = 76°

But in ΔABC,
AB = AC (given)
∠ ABC = ∠ ACB = 76°
and ∠ BAC =180° – (76° + 76°) = 180° – 152° = 28°

But ∠ BEC = ∠ BAC (Angles in the same segment)
∠BEC = 28°.

Question 46.
In the given figure. AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x. [1996]

Solution:
Arc subtends ∠ AOB at the centre and ∠ACB at the remaining part of the circle.
∠ AOB = 2 ∠ ACB
⇒ x = 2q ⇒ q = \(\frac { x }{ 2 }\)
But ∠ ADB and ∠ ACB are in the same segment
∠ ADB = ∠ ACB – q
Now in ΔAED,
p + q + 90° = 180° (sum of angles of a Δ)
⇒ p + q = 90°
⇒ p = 90° – q
⇒ p = 90° – \(\frac { x }{ 2 }\)
Arc BC subtends ∠ BOC at the centre and ∠ ADC at the remaining part of the circle
∠BOC = 2 ∠BDC = 2r.
r = \(\frac { 1 }{ 2 }\) ∠ BOC = \(\frac { 1 }{ 2 }\) (180° – x)
(∠ AOB + ∠ BOC = 180°)
r = 90° – \(\frac { 1 }{ 2 }\) x. = 90° – \(\frac { x }{ 2 }\)

Question 47.
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠ AOB = 80° and ∠ ACE = 10°. Calculate:
(i) Angle BEC,
(ii) Angle BCD,
(iii) Angle CED. [1998]

Solution:
Arc AB subtends ∠ AOB at the centre and ∠ACB at the remaining part of the circle.
∠ ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 80° = 40°
But ∠ BOC + ∠ AOB = 180° (A linear pair)
∠ BOC + 80° = 180°
⇒ ∠ BOC = 180° – 80° = 100°
(i) Arc BC subtends ∠ BOC at the centre and ∠ BEC at the remaining part of the circle
∠ BEC = \(\frac { 1 }{ 2 }\) ∠ BOC = \(\frac { 1 }{ 2 }\) x 100° = 50°
(ii) EB || DC
∠ DCE = ∠ BEC (Alternate angles) = 50°
∠ BCD = ∠ BCA + ∠ ACE + ∠ ECD = 40° + 10° + 50° = 100°
(iii) In cyclic quad. CDE,
∠ BED + ∠ BCD = 180°
⇒ ∠ BEC + ∠ CED + ∠ BCD = 180°
⇒ 50° + ∠ CED + 100° = 180° (Proved in (i) and (ii))
⇒ ∠ CEb + 150° = 180°
∠ CED = 180° – 150° = 30°.

Question 48.
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ ABC + ∠ CDE. Give reasons for your answer. [1998]

Solution:

Join OA, OB, OC, OD.
In ΔOAB,
OA = OB (Radii of the same circle)
∠ 1 = ∠ 2
Similarly we can prove that
∠3 = ∠4,
∠5 = ∠6,
∠7 = ∠8
In A OAB,
∠1 + ∠2 + ∠a = 180° (Angles of a triangle)
Similarly ∠3 + ∠4 + ∠b = 180°
∠5 + ∠6 + ∠c = 180°
∠7 + ∠8 + ∠d = 180°
Adding we get
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 + ∠a + ∠b + ∠c + ∠d = 4 x 180° = 720°
⇒∠2 + ∠2 + ∠3 + ∠3 + ∠6 + ∠6+ ∠ 7 + ∠7 + ∠a + ∠b + ∠c + ∠d = 720°
⇒ 2 ∠2 + 2 ∠3 + 2 ∠6 + 2 ∠7 + ∠a + ∠ b + ∠ c + ∠ d = 720°
⇒ 2 [∠2 + ∠3] + 2 [∠6 + ∠7| + 180° = 720° ( ∠a + ∠b + ∠c + ∠d = 180°)
⇒ 2 ∠ ABC + 2 ∠ CDE = 720° – 180° = 540°
⇒ 2 (∠ ABC + ∠ CDE) = 540°
⇒ ∠ ABC + ∠ CDE = 270°

Question 49.
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠ CBE = 64°, calculate ∠ DEC. [1991]

Solution:
Join AB.
AOC is the diameter
∠ ABC = 90° (Angle in a semi circle)
⇒ ∠ ABE + ∠ CBE = 90°
⇒ ∠ ABE + 64° = 90°
∠ ABE = 90° – 64° = 26° …(i)
AC || ED
∠ DEC = ∠ ACE (alternate angles)
But ∠ ACE = ∠ ABE (Angles in the same segment)
∠ DEC = ∠ ABE = 26° [from (i)]

Question 50.
Use the given figure to find :
(i) ∠ BAD,
(ii) ∠ DQB. [1987]

Solution:
In ΔAPD,
∠ ADP + ∠ DPA + ∠ PAD = 180°
85° + 40° + ∠ PAD = 180°
∠ PAD = 180° – (85° + 40°) = 180° – 125° = 55° or ∠ BAD = 55°
In cyclic quad. ABCD,
∠ ADC + ∠ ABC = 180°
85° + ∠ ABC = 180°
∠ ABC = 180° – 85° = 95°
Now, in ΔAQB,
∠ QAB + ∠ ABC + ∠ BQA = 180°
⇒ 55° + 95° + ∠ BQA = 180°
⇒ 150° + ∠ BQA = 180°
⇒ ∠DQB = ∠ BQA = 180° – 150° = 30°

Question 51.
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = x°; find (in terms of x) the values of:
(i) ∠ COB,
(ii) ∠DOC,
(iii) ∠DAC,
(iv) ∠ADC. [1991]

Solution:
Join CB.
In ΔAOC,
OA = OC (radii of the same circle)
∠ OCA = 4 OAC = x
Ext. ∠ COB = ∠ OAC + ∠ OCA = x + x = 2x
In ΔACB, ∠ ACB = 90° (Angle in semi circle)
∠ OBC = 90° – ∠ OAC = 90° – x
In cyclic quad. ABCD,
∠ ABC + ∠ ADC = 180°
⇒ ∠OBC + ∠ADC =180°
⇒ (90 – x) + 4 ADC = 180°
∠ADC = 180° – 90° + x = 90° + x
DC || AB
∠ DCO = ∠ COB = 2x (alternate angle)
And ∠ DCA = ∠ CAB = x (alternate angles)
In ΔADC,
∠ DAC + ∠ DCA + ∠ ADC = 180°
∠ DAC + x + 90 + x = 180°
2x + 90° + ∠ DAC = 180°
∠ DAC = 180° – 90° – 2x = 90° – 2x
In ΔOCD,
∠ DOC + ∠ OCD + ∠ CDO = 180°
∠ DOC + 2x + 2x = 180°
∠ DOC = 180° – 4x
Hence ∠ COB = 2x,
∠ DOC = 180° – 4x
∠ DAC = 90° – 2x
and ∠ ADC = 90° + x

Question 52.
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find :
(i) ∠DAB
(ii) ∠DBA

Solution:
Join DB
(i) ∠DAB + ∠DCB = 180° [Opposite angles of a cyclic quadrilateral are supplementary]
∠DAB = 180° – 130° = 50°

(ii) In ΔADB,
∠ADB = 90° [Angle in a semi-circle is 90°]
So, ∠DBA = 180° – (∠DAB + ∠ADB) = 180° – (50° + 90°) = 40°

Question 53.
In the given figure, PQ is a diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS. [1992]

Solution:
In ΔOPR, OR = OP (radii of the same circle)
∠ OPR = ∠ ORP = x (Say)
∠POR = 180° – 2x
Similarly in ΔOQS,
OS = OQ
∠ OSQ = ∠ SQO = y (say)
∠ SOQ = 180° – 2y
POQ is a straight line,
∠ POR + ∠ ROS + ∠ SOQ = 180°
⇒ 180° – 2x + 42° + 180° – 2y = 180°
⇒ 222° – 2x – 2y = 0
⇒ 2 (x + y) = 222°
x + y = 111° ….(i)
In. ΔPQT,
⇒ ∠P + ∠Q + ∠T = 180°
⇒ ∠ OPR + ∠ SQO + ∠ RTS = 180°
⇒ x + y + ∠RTS = 180°
⇒ ∠ RTS = 180° – (x + y) = 180° – 1110 [From(i)] = 69°

Question 54.
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠ PQR = 58°, Calculate:
(i) ∠RPQ,
(ii) ∠STP. [1989]

Solution:

Join PR,
In ΔPQR,
∠ PRQ = 90° (Angle in a semi-circle)
∠ RPQ + ∠ RQP = 90°
⇒ ∠RPQ + 58° = 90°
⇒ ∠RPQ = 90° – 58° = 32°
SR || PQ (given)
∠ SRP = ∠ RPQ (Alternate angles) = 32° [from(i)]
Now, in cyclic quad. PRST,
∠ STP + ∠ SRP = 180°
⇒ ∠STP + 32° = 180°
⇒ ∠STP = 180° – 32° = 148°

Question 55.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60°. Calculate the numerical values of: [1987]
(i) ∠ ABD
(ii) ∠ DBC
(iii) ∠ ADC

Solution:

Join BD,
Arc AD, subtends ∠ AOD at the centre and ∠ ABD at the remaining part of the circle
∠ ABD = \(\frac { 1 }{ 2 }\) ∠ AOD = \(\frac { 1 }{ 2 }\) x 60° = 30°
In ΔOBD,
OB = OD (Radii of the same circle)
∠ ODB = ∠ OBD = ∠ ABD = 30°
OD||BC (given)
∠ ODB = ∠ DBC (Alternate angles)
∠ DBC = ∠ ODB = 30° .
Again OD || BC
∠ AOD = ∠ OBC (Corresponding angles)
⇒ ∠ OBC = ∠ AOD = 60°
Now, in cyclic quad. ABCD,
∠ ADC+ ∠ ABC = 180°
⇒ ∠ ADC + 60° = 180°
⇒ ∠ ADC = 180° – 60° = 120°

Question 56.
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠ APB = 75° and ∠ BCD = 40°. find:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB. [1984]

Solution:

Join AB, AD.
(i) Arc AB of the smaller circle subtends ∠ AOB at the centre and ∠ APB at the remaining part of the circle.
∠ AOB = 2 ∠ APB = 2 x 75° = 150°
(ii) OACB is a cyclic quad.
∠AOB + ∠ACB = 180°
⇒ 150° + ∠ACB = 180°
⇒ ∠ACB = 180° – 150° = 30°
(in) Again, ABDC is a cyclic quad,
∠ ABD + ∠ ACD = 180°
⇒ ∠ABD + (30° + 40°) = 180° (∠ ACD = ∠ ACB + ∠ BCD)
⇒ ∠ ABD + 70° = 180°
⇒ ∠ ABD = 180° – 70° = 110°
(iv) ∠ ACB and ∠ADB are in the same segment
∠ ADB = ∠ ACB = 30°

Question 57.
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find :
(i) ∠BCD
(ii) ∠ACB
Hence, show that AC is a diameter.

Solution:
In circle ABCD is a cyclic quadrilateral AC andBD are joined.
∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°
ABCD is a cyclic quadrilateral
65° + ∠BCD = 180°
⇒ ∠BCD = 180° – 65° = 115°
Arc AB subtends ∠ABD and ∠ACD in the same segment
∠ACD = ∠ABD = 70° (∠ABD = 70°)
∠ACB = ∠BCD – ∠ACD = 115° – 70° = 45°
But arc AB subtends ∠ADB and ∠ACD in the same segment
∠ADB = ∠ACB = 45°
∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°
Now in segment ADC,
∠ADC = 90°
Segment ADC is a semi-circle
Hence AC is the diameter of the circle.
Hence proved.

Question 58.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
Solution:
In a cyclic quadrilateral ABCD,
∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5
Let ∠A = 3x, ∠C = x,
But ∠A + ∠C = 180° (Opposite angles of a cyclic quadrilateral)
⇒ 3x + x = 180°
⇒ 4x = 180°
⇒ x = 45°
∠A = 3x = 3 x 45° = 135°
∠C = x = 45°
∠B = ∠D = 1 : 5
Similarly, Let ∠B = y and ∠D = 5y
But ∠B + ∠D = 180°
y + 5y = 180°
⇒ 6y = 180°
⇒ y = 30°
∠B = y = 30°
and ∠D = 5y = 5 x 30° = 150°
Hence ∠A = 135°, ∠B = 30°, ∠C = 45° and ∠D = 150°
Hence Proved.

Question 59.
The given figure shows a circle with centre O and ∠ABP = 42°. Calculate the measure of:
(i) ∠PQB
(ii) ∠QPB + ∠PBQ

Solution:
In the figure
∠ABP = 42°.
Join PO, QO
Arc PA subtends ∠POA at the centre and ∠PBA at the remaining part.
∠POA = 2 ∠PBA = 2 x 42° = 84°
But ∠AOP + ∠BOP = 180° (Linear pair)
⇒ ∠POA+ ∠POB = 180°
⇒ 84° + ∠POB = 180°
⇒ POB = 180° – 84° = 96°
Similarly, arc BP subtends ∠BOP on the centre and ∠PQB at the remaining part of the circle
∠PQB = \(\frac { 1 }{ 2 }\) ∠POB = \(\frac { 1 }{ 2 }\) x 96° = 48°
But in ΔPBQ,
∠QPB + ∠PBQ + ∠PQB = 180° (Angles of a triangle)
∠QPB + ∠PBQ + 48° =180°
⇒ ∠QPB + ∠PBQ = 180°
⇒ ∠QPB + ∠PBQ = 180° – 48° = 132
Hence (i) PQB = 48° and
(ii) ∠QPB + ∠PBQ = 132°

Question 60.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y:

(i) express ∠AMD in terms of x.
(ii) express ∠ABD in terms of y.
(iii) prove that: x = y.
Solution:
In the figure, M is the centre of the circle chords AB and CD are perpendicular to each other at L.
∠MAD = x and ∠BAC = y
(i) In ΔAMD,
AM = DM (Radii of the same circle)
∠MDA = ∠MAD (Angles opposite to equal sides) = x
But, in ΔAMD,
∠MAD + ∠MDA + ∠AMD = 180° (Sum of angles of a triangle)
⇒ x + x + ∠AMD = 180°
⇒ 2x + ∠AMD = 180°
⇒ ∠AMD = 180°
∠AMD = 180° – 2x
(ii) Arc AD subtends ∠AMD at the circle and ∠ABD at the remaining part of the circle
∠AMD = 2∠ABD
⇒ ∠ABD = \(\frac { 1 }{ 2 }\) ∠ABD = \(\frac { 1 }{ 2 }\) [180°- 2x] = 90° – x
AB ⊥s CD
∠ALC = 90°
In ΔALC,
∠LAC + ∠LCA = 90°
⇒ ∠BAC + ∠DAC = 90°
⇒ y = ∠DAC = 90°
⇒ ∠DAC = 90° – y
But ∠DAC ∠ABD (Angles in the same segment)
∠ABD = 90° – y
But ∠ABD = 90° – x, Proved
90°- x = 90°- y
⇒ ∠x = yHence proved.

Question 61.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
Solution:
Given : In circle with centre O,
ABCD is cyclic quadrilateral in which CD is equal radius of the circle and AB is diameter.
CD = \(\frac { 1 }{ 2 }\) AB
AD and BC are produced to meet at P.
To prove: ∠APB = 60°
Construction : Join DO, CO and PB
In ΔDOC,
DO = CO = DC (Radii of the circle)
ΔDOC is an equilateral triangle
∠DOC = 60° ….(i)
Now, arc DC subtends ∠DOC at the centre arc ∠DBC at the remaining part of the circle
∠DBC = \(\frac { 1 }{ 2 }\) ∠DOC = \(\frac { 1 }{ 2 }\) x 60° = 30° …(ii)
But ∠ADB = 90° (Angle in a semi-circle)
∠PDB = 90° (∠PDB x ∠ADB = 180°, Linear pair)
Now in ΔPDB,
∠PDB = 90° (Proved)
⇒ ∠DPB = ∠DBC = 90°
⇒ ∠DPB + 30° = 90°
⇒ ∠DPB = 90° – 30° = 60°
⇒ APB = 60°
Hence proved.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Show that:
(i) tan 10° tan 15° tan 75° tan 80° = 1
(ii) sin 42° sec 48°+cos 42° cosec 48°= 2

Solution:
(i) tan 10° tan 15° tan 75° tan 80°= 1
L.H.S. = tan 10° tan 15° tan 75° tan 80°
= tan (90° – 80°) tan (90° – 75°) tan 75° tan 80°
= cot 80° cot 75° tan 75° tan 80°
= tan 80° cot 80° x tan 75° cot 75°
= 1 x 1 = 1= R.H.S. (∵ tan A cot A = 1)
(ii) sin 42° sec 48°+ cos 42° cosec 48°= 2
L.H.S. = sin 42° sec 48°+ cos 42° cosec 48°
= sin 42° sec (90° – 42°) + cos 42° cosec (90° – 42°)
= sin 42° cosec 42°+ cos 42° sec 42°
=1 + 1=2 R.H.S. (∵ sin A cosec A=1, cos A sec A=1)

Question 2.
Express each of the following in terms of angles between 0°and 45°.
(i) sin 59° + tan 63°
(ii) cosec 68° + cot 72°
(iii) cos 74° + sec 67°
Solution:
(i) sin 59° + tan 63°
= sin (90° – 31°) + tan (90° – 27°)
= cos 31°+ cot 27°
(ii) cosec 68° + cot 72°
= cosec (90° – 22°) + cot (90° – 18°)
= sec 22°+ tan 18°
(iii) cos 74°+ sec 67°
= cos (90° – 16°) + sec (90° – 23°)
= sin 16°+ cosec 23°

Question 3.
Show that:

Solution:

Question 4.
For triangle ABC, Show that:

Solution:

Question 5.
Evaluate:

Solution:

Question 6.

Solution:

Question 7.
Find (in each case, given below) the value of x, if:
(i) sin x = sin 60° cos 30° – cos 60° sin 30°
(ii) sin x = sin 60° cos 30° + cos 60° sin 30°
(iii) cos x = cos 60° cos 30° – sin 60° sin 30°

(v) sin 2x = 2 sin 45° cos 45° 
(vi) sin 3x = 2 sin 30° cos 30°
(vii) cos (2x – 6°) = cos² 30° – cos² 60°
Solution:

Question 8.
In each case, given below, find the value of angle A, where 0° ≤ A ≤ 90°.
(i) sin (90° – 3A). cosec 42° = 1
(ii) cos (90° – A). sec 77° = 1
Solution:

Question 9.
Prove that:

Solution:

Question 10.
Evaluate:

Solution:

Question 11.
Without using trigonometric tables, evaluate sin² 34° + sin² 56° + 2 tan 18° tan 72° – cot² 30°.
Solution:

Question 12.
Without using trigonometrical tables, evaluate: cosec² 57° – tan² 33° + cos 44° cosec 46° – \( \sqrt{2} \) cos45°- tan² 60°
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Prove that: 

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Question 2.
If xcosA + ysinA = m and xsinA-ycosA = n, then prove that: x²+y² = m² + n²
Solution:
x cos A + y sin A = m    …(i)
x sin A – y cos A = n     ….(ii)
squaring (i) and (ii)
x² cos² A + y² sin² A + 2 xy cosA sinA = m²
x² sin² A + y² cos² A – 2 xy cos A sin A = n²
Adding we get,
x² (sin² A + cos² A) + y² (sin² A + cos² A) = m²+n²
∴ x²+y² = m² + n²(∵ sin²A + cos²A= 1)
Hence proved.

Question 3.
If m = a sec A +b tan A and n=atanA + bsecA, then prove that: m²-n² = a²-b²
Solution:
m = asec A + btan A         ……(i)
n = a tan A + b sec A       …..(ii)
squaring (i) and (ii)
m² = a² sec² A + b² tan² A + 2ab sec A tan A
n² = a² tan² A + b² sec² A + 2 ab tan A sec A
Subtracting, we get
m² – n² = a² (sec² A – tan² A) + b² (tan² A – sec² A)
= a²x 1 +b²(-1) = a²-b² ( ∵ sec²A-tan²A= 1)  .
Henceproved

Question 4.
If x = r sin A cos B, y = r sin A sin B and z = r cos A, then prove that: x² + y² + z² = r.
Solution:
x = r sin A cos B      ….(i)
y = r sin A sin B      ….(ii)
z = r cosA               …….(iii)
Squaring, (i), (ii) & (iii)
x²=r² sin² A cos² B,
y² = r²sin²Asin²B,
z² = r²cos²A
Adding, we get,
x²+y² + z²=r² (sin²A cos²E + sin² A sin² B+cos²A)
= r[sin²A (cos² B + sin²B) + cos²A]
= r [sin² A x 1 + cos² A]
= r² [sin² A + cos² A] = r² x 1  = r²        ( ∵ sin² A + cos² A = 1)
Hence proved.

Question 5.
If sin A + cos A = m and sec A + cosec A=n, show that n (m²-1) = 2m
Solution:

Question 6.
If x = r cos A cos B, y = r cos A sin B and z = r sin A, show that x² + y² + z² = r²
Solution:
x = r cosAcosB              ….(i)
y = r cosAsinB             ….(ii)
z = r sinA                 ….(iii)
Squaring (i), (ii), (iii)
x² = r² cos² A cos² B, y² = r² cos² A sin²B
z² = r²sin²A
Adding, we get
x² + y² + z² = r² (cos² A cos²B + cos² A sin² B + sin² A)
= r² [cos² A (cos² B + sin²B) + sin² A]
= r²[cos²Ax 1+sin²A]
= r² (1) = r^{2    `}Hence proved.

Question 7.

Solution:

P.Q.

Solution:

P.Q.
Evaluate:

Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

Question 1.
Find the equation of line whose :
(i) y-intercept = 2 and slope = 3,
(ii) y-intercept = -1 and slope = \(\frac { -3 }{ 4 }\)
Solution:
(i) The point whose y-intercept = 2 will be (0, 2) and slope (m) = 3.
Equation of line will be

Question 2.
Find the equation of a line whose :
(i) y-intercept = -1 and inclination = 45°
(ii) y-intercept = 3 and inclination = 30°
Solution:
(i) The point whose y-intercept is -1, will be (0, -1) and inclination = 45°
Slope (m) = tan 45° = 1
Equation will be

Question 3.
Find the equation of the line whose slope is \(\frac { -4 }{ 3 }\) and which passes through (-3, 4).
Solution:
Slope of the line (m) = \(\frac { -4 }{ 3 }\)
The point from which the line passes (-3, 4)
Equation of line will be y – y₁ = m (x – x₁)

Question 4.
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
Solution:
The line passes through the point (5, 4) and angle of inclination = 60°
slope (m) = tan 60° = √3
Equation of line
y – y₁ = m (x – x₁)
⇒ y – 4 = √3 (x – 5)
⇒ y – 4 = √3 x – 5√3
⇒ y = √3 x + 4 – 5√3

Question 5.
Find the equation of the line passing through:
(i) (0, 1) and (1, 2)
(ii) (-1, -4) and (3, 0)
(iii) (4, -2) and (5, 2)
Solution:
Two given points are (0, 1) and (1, 2)
Slope of the line passing through these two

Question 6.
The co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
(i) The gradient of PQ
(ii) The equation of PQ,
(iii) The co-ordinates of the point where PQ intersects the x-axis.
Solution:
Two points P (2,-6) and Q (-3, 5) are given.

⇒ 5y – 30 = x – 2
⇒ 5y = x – 2 + 30
⇒ 5y = x + 28 ….(i)
(iii) Co-ordinates of the point where PQ intersects x-axis will be = 0
substituting, the value of y in (i)
5 x 0 = x + 28 ⇒ x + 28 = 0 ⇒ x = -28
Co-ordinates of point are (-28, 0)

Question 7.
The co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
(i) the equation of AB
(ii) the co-ordinates of the point where the line AB intersects they- axis.
Solution:
Slope of the line passing through two points A (-3, 4) and B (2, -1) will be :

Its abscissa = 0
substituting, the value of x = 0 in (i)
0 + y = 1
y = 1
Co-ordinates of point = (0, 1)

Question 8.
The figure given below shows two straight lines AB and CD intersecting each other at point P (3, 4). Find the equations of AB and CD.

Solution:
Two lines AB and CD intersect each other at P (3, 4)
AB inclined at angle of 45° and CD at angle of 60° with the x-axis.
Slope of AB = tan 45° = 1
and slope of CD = tan 60° = √3
Now, equation of line AB will be
y – y₁ = m (x – x₁)
⇒ y – 4 = 1 (x – 3)
⇒ y – 4 = x – 3
⇒ y = x – 3 + 4
⇒ y = x + 1
(ii) Equation of CD will be :
y – y₁ = m (x – x₁)
⇒ y – 4 = √3 (x – 3)
⇒ y – 4 = √3 x – 3√3
⇒ y = √3 x – 3√3 + 4
⇒ y = √3 x + 4 – 3√3

Question 9.
In ΔABC, A (3, 5), B (7, 8) and C (1, -10). Find the equation of the median through A.
Solution:
AD is median
D is mid point of BC


Equation of AD
y – y₁ = m (x – x₁)
⇒ y + 1 = -6 (x – 4)
⇒ y + 1 = -6x + 24
⇒ y + 6x = -1 + 24
⇒ 6x + y = 23

Question 10.
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex, C = (7, 5). Find the equations of BC and CD.

Solution:

ABCD is a ||gm in which AB = CD || x-axis
∠A = 60° and C (7, 5)
(i) CD || AB || x-axis ,
Equation of CD will be
y – y₁ = m (x – x₁)
⇒ y – 5 = 0 (x – 7)
⇒ y – 5 = 0
⇒ y = 5
BC || AD
Slope of BC = tan 60° = √3
Equation of BC will be
y – y₁ = m (x – x₁)
⇒ y – 6 = √3 (x – 7)
⇒ y – 6 = √3 x – 7√3
⇒ y = √3 x + 6 – 7√3

Question 11.
Find the equation of the straight line passing through origin and the point of intersection of the lines x + 2y = 7 and x – y = 4.
Solution:
Point of intersection of two lines
x + 2y = 7 ….(i)
x – y = 4 ….(ii)
Subtracting, we get
3y = 3
y =1
Substituting, the value of y in (ii)
x – 1 = 4
⇒ x = 4 + 1 = 5
Point of intersection is (5, 1)
Slope of the line passing through origin (0, 0) and (5, 1)

Equation of line will be
y – y₁ = m (x – x₁)
⇒ y – 5 = \(\frac { 1 }{ 2 }\) (x – 1)
⇒ 5y – 25 = x – 1
⇒ 5y = x – 1 + 25 = x + 24
⇒ 5y = x + 24

Question 12.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
Solution:

Question 13.
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Solution:

Slope of line through A, perpendicular to BC = -(-1) = 1
Now, the equation of line through A (0, 3) is
y – y₁ = m (x – x₁)
y – 3 = 1 (x – 0)
⇒ y – 3 = x
⇒ y = x + 3

Question 14.
Find the equation of the perpendicular dropped from the point (-1, 2) onto the line joining the points (1, 4) and (2, 3).
Solution:
Slope of the line joining the points (1, 4) and (2, 3)

Slope of line perpendicular to the above line = 1
Equation of line passing through (-1, 2)
y – y₁ = m (x – x₁)
⇒ y – 2 = 1 [x -(-1)]
⇒ y – 2 = x + 1
⇒ y = x + 1 + 2
⇒ y = x + 3

Question 15.
Find the equation of the line, whose :
(i) x-intercept = 5 and y-intercept = 3
(ii) x-intercept = -4 and y-intercept = 6
(iii) x-intercept = -8 and y-intercept = -4
(iv) x-intercept = 3 and y-intercept = -6
Solution:
(i) When x-intercept = 5, then point will be (5, 0)
and when y-intercept = 3, then point will be (0, 3)
Slope of the line passing through these points

Question 16.
Find the equation of the line whose slope is \(\frac { -5 }{ 6 }\) and x-intercept is 6.
Solution:

Question 17.
Find the equation of the line with x-intercept 5 and a point on it (-3, 2).
Solution:
x-intercept of the line = 5
Point = (5, 0)
Slope of the line passing through the point (-3, 2)

Question 18.
Find the equation of the line through (1, 3) and making an intercept of 5 on the y- axis.
Solution:
The line makes y-intercept = 5
Point = (0, 5)
Slope of the line passing through the point (1, 3) and (0, 5)

Equation of the line
y – y₁ = m (x – x₁)
⇒ y – 3 = -2 (x – 1)
⇒ y – 3 = -2x + 2
⇒ 2x + y = 2 + 3
⇒ 2x + y = 5

Question 19.
Find the equations of the lines passing through point (-2, 0) and equally inclined to the co-ordinate axes.


Solution:
(i) Slope of line AB = tan 45° = 1
Equation passing through the point (-2, 0)
y – y₁ = m (x – x₁)
⇒ y – 0 = 1 (x + 2)
⇒ y = x + 2
⇒ x – y + 2 = 0
(ii) Slope of line CD = tan (-45°) = -1
Equation passing through the point (-2, 0)
y – y₁ = m (x – x₁)
⇒ y – 0 = -1 (x + 2)
⇒ y = -x – 2
⇒ y + x + 2 = 0
⇒ x + y + 2 = 0

Question 20.
The line through P (5, 3) intersects y axis at Q.

(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the co-ordinates of Q.
Solution:
(i) Here θ = 45°
So, slope of the line = tanθ = tan 45° = 1
(ii) Equation of the line through P and Q is
y – 3 = 1 (x – 5)
⇒ y – x + 2 = 0
(iii) Let the coordinates of Q be (0, y)

Question 21.
Write down the equation of the line whose gradient is \(\frac { -2 }{ 5 }\) and which passes through point P, where P divides the line segment joining A (4, -8) and B (12, 0) in the ratio 3 : 1.
Solution:
Slope of the line m = \(\frac { -2 }{ 5 }\)
P divides the line AB, whose co-ordinates are (4, -8) and (12, 0) in the ratio of 3 : 1
Co-ordinates of P be

Question 22.
A (1, 4), B (3, 2) and C (7, 5) are vertices of a triangle ABC. Find :
(i) the co-ordinates of the centroid of ΔABC.
(ii) the equation of a line, through the centroid and parallel to AB. [2002]
Solution:
(i) Co-ordinates of vertices of ΔABC are A (1, 4), B (3, 2), C (7, 5)
and let G be the centroid of ΔABC.
Co-ordinates of G are

Question 23.
A (7, -1), B (4, 1) and C (-3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point F in AC; such that AP : CP = 2 : 3.
Solution:
P divides AC in the ratio of 2 : 3

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points) Ex 12B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B

Question 1.
Attempt this question on graph paper.
(a) Plot A (3, 2) and B (5, 4) on graph paper. Take 2cm = 1 unit on both the axes.
(b) Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
(c) Write down:
(i) The geometrical name of the figure ABB’A’;
(ii) The measure of angle ABB’ ;
(iii) The image A” of A, when A is reflected in the origin.
(d) The single transformation that maps A’ to A”. [1995]
Solution:
From the graph, we can say that
(iii) (a) an isosceles trapezium
(b) 45°
(c) ( -3, -2)
(d) reflection in y-axis

Question 2.
Points (3,0) and (-1,0) are invariant points under reflection in the line L1; points (0, -3) and (0, 1) are invariant points on reflection in line L2
(a) Name or write equations for the lines L1 and L2 .
(b) Write down the images of points P (3, 4) and Q ( -5, -2) on reflection in L. Name the images as P’ and Q’ respectively.
(c) Write down the images of P and Q on re-flection in L,. Name the images as P” and Q” respectively.
(d) State or describe a single transformation that maps P’ onto P”. [1996]
Solution:

(a) Points (3, 0) and (-1, 0) are invariant points under reflection L .
Here the ordinates of both points are 0 It is x-axis or y = 0.
Again points (0, -3) and (0, 1) are invariant- points on reflection in line L2
Here the abscissas are 0 in both points.
It is y-axis or x = 0.
(b) The co-ordinates of the images of points P (3, 4) and Q (-5, -2) on reflection in L, will be P (3, -4) and Q'(-5, 2)
(c) The co-ordinate of images of points P (3, 4) and Q (-5, -2) on reflection in L2 will be P’ (-3, 4) and Q’ (5, -2)
(d) Reflection is in origin because the co-ordinates of P’ and P” have opposite signs.

Question 3.
(a) Point P (a, b) is reflected in the x-axis to P’ (5, -2), write down the values of a and b.
(b) P” is the image of P when reflected in y- axis, write down the co-ordinates of P”.
(c) Name a single transformation that maps P’ to P”. (1997):
Solution:
(a) P (a, b) is reflected in x-axis to P’ (5, -2). the co-ordinates of P will be (5, 2)
a = 5, b = 2
(b) P” is the image of P when reflected is y-axis.
Co-ordinates of P” will be ( -5, 2)
(c) Reflection is in origin.

Question 4.
The point (-2, 0) on reflection in a line is mapped to (2, 0) and the point (5, -6) on reflection in the same line is mapped to (-5, -6).
(a) State the name of the mirror line and write its equation.
(b) State the co-ordinates of the image of (-8, -5) in the mirror line.
Solution:
Point (-2, 0) is mapped to (2, 0) to a certain line and point (5, -6) is also mapped to (-5, -6) to the same line.
(a) We see that sign of x-coordinate is changed.
The required line is y-axis whose equation will be x = 0.
(b) The co-ordinates of the image of the point (-8, -5) in the same mirror line will be (8, -5).

Question 5.
The points P (4, 1) and Q (-2, 4) are reflected in line y = 3, Find the co-ordinates of P’, the image of P and Q’, the image of Q.
Solution:
Co-ordinates of P and Q are (4, 1) and ( -2, 4) respectively.

The co-ordinates of image of P which is P’ are (4, 5) reflection in the line y = 3
and co-ordinates of image of Q when is Q’ are ( -2, 2) reflection is the line y = 3 as shown in the graph.

Question 6.
A point P (-2, 3) is reflected in the line x = 2 to point P’. Find the co-ordinates of P’.
Solution:
The image of P ( -2, 3) is P’ which is reflected in the line x = 2. The co-ordinates of P’ will be (6, 3) as shown in the graph.

Question 7.
A point P (a, b) is reflected in the x-axis to P’ (2, -3). Write down the values of a and b. P” is the image of P, reflected in the y- axis. Write down the co-ordinates of P”. Find the co-ordinates of P'”, when P is reflected in the line, parallel to y-axis, such that x = 4. [1998]
Solution:

(i) A point P (a, b) is reflected in v-axis to P’ (2, -3)
Co-ordinates of P will be (2, 3) a = 2, b = 3.
(ii) P” is the image of P, when reflected in the y- axis
Co-ordinates of P” will be ( -2, 3)
(iii) The image of P is P'” reflected in a line parallel to y-axis i.e. x = 4.
Co-ordinates of P”‘ will be (6, 3)

Question 8.
Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
(a) A’ of A under reflection in the x-axis.
(b) B’ of B under reflection in the line AA’.
(c) A” of A under reflection in the y-axis.
(d) B” of B under reflection in the line AA”.
Solution:
Co-ordinates of A are (3, 4) and co-ordinates of B are (0, 2)
(a) Co-ordinates, of A’ of A under reflection in the v-axis are (3, -4)
(b) Co-ordinates of B’ of B under reflection in the line AA’ are (6, 2)
(c) Co-ordinates of A” of A under reflection in y-axis are (-3, 4)
(d) Co-ordinates of B” of B under reflection in the line A A” are (0, 8).

Question 9.
(a) Plot the points A(3, 5) and B(-2, -4). Use 1 cm = 1 unit on both the axes.
(b) A’ is the image of A when reflected in the v-axis. Write down the co-ordinates of A’ and plot it on the graph paper.
(c) B’ is the image of B when reflected in the y-axis, followed by reflection in the origin.
Write down the co-ordinates of B’ and plot it on the graph paper.
(d) Write down the geometrical name of the figure AA’ BB’.
(e) Name two invariant points under reflection in the x-axis. [1999]
Solution:
(a) The points A (3, 5) and B(-2, -4) have been plotted on the graph.
(b) A’ is the image of A when reflected in the x-axis

Co-ordinates of A’ will be (3, -5)
(c) B’ is the image of B when reflected in y- axis, followed by reflection in the origin.
Co-ordinates will be (-2, 4)
Images A’ and B’ have also been plotted.
(d) Join AA’, A’B, BB’ and B’A the quadrilateral so joined is an isosceles trapezium.
(e) The points C and D whose co-ordinates ! are (3,0) and (-2, 0) are invariant points under reflection in the x-axis.

Question 10.
The point P (5,3) was reflected in the origin to get the image P’.
(a) Write down the co-ordinates of P’.
(b) If M is the foot of the perpendicular from P to the x-axis, find the co-ordinates of M.
(c) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(d) Name the figure PM P’ N.
(e) Find the area of the figure PM P’ N.
Solution:
(a) Points P(5, 3) is reflected to P’ in the origin.
Co-ordinates of P’ will be (-5, -3).
(b) PM ⊥ on x-axis.
Co-ordinates of P’ will be (5, 0)
(c) P’N X on x-axis
Coordinates of N will be (-5, 0).
(d) PM, MP’ P’N and N. P are joined which form a parallelogram PMP’N.
(e) Area of || gm PMP’N = 2 (Area of ∆PMN)
= 2 (\(\frac { 1 }{ 2 }\) x 10 x 3) Sq. cm
= 30 Sq. cm

Question 11.
The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write :
(i) the co-ordinates of P’ and O’,
(ii) the length of the segments PP’ and OO’,
(iii) the perimeter of the quadrilateral POP’O’.
(iv) the geometrical name of the figure POP’O’.
Solution:

(i) Point P (3, 4) is reflected to P’ in x-axis and then its co-ordinates will be (3, -4) again O’ is the image of O (0, 0) reflected in PP’, then co-ordinates of O’ will be (6, 0)
(ii) Length of PP’ = 4 + 4 = 8 units and OO’ = 3 + 3 = 6 units
(iii) Diagonals of OPO’P’ bisect each other at right angles at M.
OPO’P’ is a rhombus.
(iv) The perimeter of quadrilateral OPO’P’ = 5 x 4 = 20 units
(v) The quadrilateral OPO’P’ is a rhombus as rhombus shown on the graph paper.

Question 12.
A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear? (2004)
Solution:
On the given graph, plot the points A(1, 1), B(5, 1). C(4, 2) and D(2, 2) Join AB, BC, CD and DA.

The quadrilateral is of trapezium in shape.
Now points A, B, C and D are reflected in the origin on to A’, B’, C and D’ respectively.
Co-ordinates of A’ are (-1, -1), of B’ are (-5, -1), of C are (-4, -2) and of D’ are (-2, -2).
A’ B, B’C’, CD’ and D’A’ are joined.
Yes, we see that DA A’D’ are collinear.

Question 13.
P and Q have co-ordinates (0, 5) and (-2, 4).
(a) P is invariant when reflected in an axis, Name the axis.
(b) Find the image of Q on reflection in the axis found in fa)
(c) (0, k) on reflection in the origin is invariant. Write the value of k.
(d) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:
Co-ordinates of the given points P and Q, are (0, 5) and (-2, 4) and have been plotted on the graph.

(a) P is invariant in y-axis
(b) Image of Q(-2, 4) is Q’ in years and its Co-ordinates will be (2, 4)
(c) (0, k) on reflections in we origin is also invariant
Co-ordinates will be (0, 0) k = 0
(d) Let Q” be image of Q reflection in his origin.
Again Q” is reflected in x-axis and its image will be Q’ (2, 4)

Question 14.
(a) The point P (2, -4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(b) The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(c) Name the figure PQR.
(d) Find the area of figure PQR.
Solution:


The graph of the solution set is shown by the thick portion of the number line. The solid circle at -3 indicates that the number – 3 is included among the solutions whereas the open circle at 3 indicates that 3 is not included among the solutions.
(c) (i) Since the point Q is the reflection of the point P (2, – 4) in the line x = 0, the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line x = 0, the co-ordinates of R are (- 2, 4).
(iii) Figure PQR is the right angled triangle PQR.
(d) Area of ∆PQR = \(\frac { 1 }{ 2 }\) x QR x PQ = \(\frac { 1 }{ 2 }\) x 4 x 8 = 16 sq. units.

Question 15.
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’ B’
(iv) Find its perimeter.
Solution:

Question 16.
Use graph paper for this question. (Take 2 cm = 1 unit along both x and y axis.
Plot the points O (0, 0), A (-4, 4), B (-3, 0) and C (0, -3)
(i) Reflect points A and B on the y-axis and name them A’ and B’ respectively. Write down their coordinates. k
(ii) Name the figure OABCB’A’.
(iii) State the line of symmetry of this figure. (2016)
Solution:


(ii) The figure OABCB’A’ is similar to arrow headed.
(iii) The y-axis is the line of symmetry of figure OABCB’A’.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points) Ex 12A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B

Question 1.
Complete the following table.

Solution:
We can complete the blanks as under
(a) Reflection in origin
(b) (4, -2)
(c) (0, 6)
(d) Reflection in origin
(e) Reflection in y-axis.

Question 2.
A point P is its own image under the reflection in a line l. Describe the position of the point P with respect to the line l.
Solution:

The image of the point is itself the point P with respect to a line l, Then the point lies in the line l.

Question 3.
State the co-ordinates of the following points under reflection in x-axis:
(i) (3, 2)
(ii) (-5, 4)
(iii) (0, 0)
Solution:
The co-ordinates of the given points under reflection in x-axis are as under :
(i) (3, -2)
(ii) (-5, -4)
(iii) (0, 0).

Question 4.
State the co-ordinates of the following points under reflection in y-axis :
(i) (6, -3)
(ii) (-1, 0)
(iii) (-8, -2)
Solution:
The co-ordinates of the points under reflection in y-axis are :
(i) (-6, -3)
(ii) (1, 0)
(iii) (8, -2)

Question 5.
State the co-ordinates of the following points under reflection in origin :
(i) (-2, -4)
(ii) (- 2, 7)
(iii) (0, 0)
Solution:
The co-ordinates of the points under reflection in origin are :
(i) (2, 4)
(ii) (2, -7)
(iii) (0, 0)

Question 6.
State the co-ordinates of the following points under reflection in the line x = 0 :
(i) ( -6, 4)
(ii) (0, 5)
(iii) (3, -4)
Solution:
The co-ordinates of the points under reflection in the line x = 0, or y-axis are :
(i) (6, 4)
(ii) (0, 5)
(iii) ( -3, -4)

Question 7.
State the co-ordinates of the following points under reflection in the line y = 0;
(i) (-3, 0)
(ii) (8, -5)
(iii) (-1, -3)
Solution:
The co-ordinates of the points under reflection in the line y = 0 or x-axis are :
(i) (-3, 0)
(ii) (8, 5)
(iii) (-1, 3)

Question 8.
A point P is reflected in the x-axis. Co-ordinates of its image are (- 4, 5).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
(i) The co-ordinates of a point P in the x-axis are (-4, 5).
the co-ordinates of P will be (-4, -5)
(ii) Now the co-ordinates of the image of P under reflection in the y-axis will be (4, -5).

Question 9.
A point P is reflected in the origin. Co-ordinates of its image are ( -2, 7).
(i) Find the co-ordinate of P.
(ii) Find the co-ordinates of the image of P under reflection in the x-axis.
Solution:
The co-ordinates of a point P in the origin are (-2, 7)
The co-ordinates of P will be (2, -7)
(ii) and the co-ordinate of the image of P under the reflection in the x-axis will be (2, 7)

Question 10.
The point P (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6) evaluate a and b.
Solution:
The co-ordinates of P reflected in the origin will be P ( -a, -b).
Again the co-ordinates of image of P’ under reflection in the y-axis is rule be (a, -b).
But the co-ordinates of P’ are given as (4, 6)
a = 4, -b = 6 ⇒ b = -6

Question 11.
The point P (x, y) is first reflected in the x- axis and then reflected in the origin to P’. If P’ has co-ordinates ( -8, 5); evaluate x and y.
Solution:
The co-ordinates of P reflected to the x-axis will be (x, -y)
and its coordinate will be reflected in the origin P (-x, y).
But the co-ordinates of P’ are (-8, 5)
-x = -8 => x = 8
y = 5

Question 12.
The point A ( -3, 2) is reflected in the x- axis to the point A’. Point A’ is then reflected in the origin to point A’.
(a) Write down the co-ordinates of A’
(b) Write down a single transformation that maps A onto A’
Solution:
(a) The co-ordinates of A’, the reflected point in x-axis will be ( -3, -2).
(i) the co-ordinates of A’, the reflected points of A’ in the origin will be (3, 2).
(b) The reflection is in y-axis.

Question 13.
The point A (4, 6) is first reflected in the origin to point A’. Point A’ is then reflected in the y-axis to point A’.
(i) Write down the co-ordinates of A’.
(ii) Write down a single transformation that maps A onto A’.
Solution:
Co-ordinates of point A are (4, 6). The co-ordinate of A’, the image of A as reflected in the origin will be ( -4, -6).
(i) Again the co-ordinates of A’, the image of A’ as reflected in the y-axis will be (4, -6).
(ii) The reflection is in x-axis.

Question 14.
The triangle ABC, where A is (2, 6). B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A’B’C’. Triangle A’B’C’ is then reflected in the origin to triangle A”B”C”.
(i) Write down the co-ordinates of A”. B” and C”.
(ii) Write down a single transformation that maps triangle ABC onto triangle A”B”C”.
Solution:
In ∆ABC. co-ordinates of vertices.
A are (2. 6), B ( -3. 5) and C (4, 7).
Then the co-ordinates of vertices of ∆A’B’C’ when reflected in the y-axis will be A’ ( -2, 6). B’ (3, 5) and C’ ( -4, 7).
Again the co-ordinates of vertices of ∆A”B”C” when reflected in the origin will be A” (2, -6), B” ( -3, -5) and C”(4, -7).
(ii) The reflection of ∆ABC is in x-axis.

Question 15.
P and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P’ and Q in the y-axis to Q’. State the co-ordinates of P’ and Q’.
Solution:
Co-ordinates of P is ( -2, 3) and co-ordinates of Q (5, 4).
Then the co-ordinates of P’ when reflected in x-axis will be (-2, -3)
and the co-ordinates of Q’ when reflected in y-axis will be (-5, 4)

Question 16.
On a graph paper, plot the triangle ABC whose vertices are at the points A (3,1), B (5,0) and C (7,4). On the same diagram, draw the image of the triangle ABC under reflection in the origin 0 (0, 0).
Solution:
∆ABC whose vertices are A (3, 1), B (5, 0) and C (7, 4).
Now the image of ∆ABC is ∆A’B’C’ under reflection in the origin O (0, 0).
The co-ordinates of the vertice A’, B’ and C’ will be A’ ( -3, -1), B’ (- 5, 0) and C’ ( -7, -4) as shown on the graph.

Question 17.
Find the image of point (4, -6) under the following operations :

Solution:
Since the co-ordinates of a given point are (4, -6), then

Question 18.
Point A (4, -1) is reflected as A’ in the y- axis. Point B on reflection in the x-axis is mapped as B’ ( -2, 5). Write the co-ordinates of A’ and B.
Solution:
A’ is the reflection of point A (4, -1) in the y-axis and its co-ordinates will be (-4, -1)
Co-ordinates of B’, the image of point B are ( -2, 5) in the x-axis.
Co-ordinates of B will be ( -2, -5)

Question 19.
The point (-5, 0) on reflection in a line is mapped as (5, 0) and the point (-2, -6) on reflection in the same line is mapped as (2, -6).
(a) Name the line of reflection.
(b) Write the co-ordinates of the image of (5, -8) in the line obtained in (a).
Solution:
(a) The point (-5, 0) is reflected in a line as (5, 0)
Here, x is mapped as -x
Again point (-2, -6) is mapped in the reflection of the same line as (2, -6)
Here x is mapped as -x
The line of reflection will be y-axis
(b) Now the co-ordinates of the image of the point (5, -8) in the same line will be (-5, -8)

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

Question 1.
Find the slope of the line whose inclination is :
(i) 0°
(ii) 30°
(iii) 72° 30′
(iv) 46°
Solution:
(i) Slope of line whose inclination is 0° = tanθ = tan 0° = 0
(ii) Slope of line whose inclination is 30° = tan 30° = \(\frac { 1 }{ \surd 3 }\)
(iii) Slope of line whose inclination is 72° 30′ = tan 72°30’ = 3. 1716 (Using tables)
(iv) Slope of line whose inclination is 46° = tan 46° = 1.0355 (Using tables)

Question 2.
Find the inclination of the line whose slope is:
(i) 0
(ii) √3
(iii) 0.7646
(iv) 1.0875
Solution:
Slope of a line = tanθ. Where θ is the inclination
(i) When slope is θ. then tanθ = 0 ⇒ θ = 0°
(ii) When slope is θ, then tanθ = √3 ⇒ θ = 60°
(iii) When slope is 0.7646, then tanθ = 0.7646 ⇒ θ = 37°24′ (Using tables)
(iv) When slope is 1.0875, then tanθ = 1.0875 ⇒ θ = 47°24′ (Using tables)

Question 3.
Find the slope of the line passing through the following pairs of points :
(i) (-2, -3) and (1, 2)
(ii) (-4, 0) and origin
(iii) (a, -b ) and (b, -a)
Solution:
We know that, slope of a line which passes

Question 4.
Find the slope of the line parallel to AB if:
(i) A = (-2, 4) and B = (0, 6)
(ii) A = (0, -3) and B = (-2, 5)
Solution:

Question 5.
Find the slope of the line perpendicular to AB if:
(i) A = (0, -5) and B = (-2, 4)
(ii) A = (3, -2) and B = (-1, 2)
Solution:

Question 6.
The line passing through (0, 2) and (-3, -1) is parallel to the line passing through (-1, 5) and (4, a). Find a.
Solution:
Slope of the line passing through two points (0, 2) and (-3, -1)

Question 7.
The line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1). Find a.
Solution:
Slope of the line passing through the points

Question 8.
Without using the distance formula, show that the point A (4, -2), B (-4, 4) and C (10, 6) are the vertices of a right-angled triangle.
Solution:


AB and CA are perpendicular to each other
Hence, ΔABC is a right-angled triangle.

Question 9.
Without using the distance formula, show that the points A (4, 5), B (1, 2), C (4, 3) and D (7, 6) are the vertices of a parallelogram.
Solution:


Slopes of AB and DC are equal
AB || DC Similarly slope of BC and slope of DA are equal.
BC || DA
Hence ABCD is a parallelogram.

Question 10.
(-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the – quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
Solution:





QR || PS.
Hence PQRS is a parallelogram.

Question 11.
Show that the points P (a, b + c), Q (b, c + a) and R (c, a + b) are collinear.
Solution:
The given points are P (a, b + c), Q (b, c + a) and R (c, a + b)
We know that, these points P, Q, R are collinear if Slope of PQ = Slope of QR

Slope of PQ = Slope of QR
P, Q and R are collinear.

Question 12.
Find x, if the slope of the line joining (x, 2) and (8, -11) is \(\frac { -3 }{ 4 }\).
Solution:
Slope of line joining (x, 2) and (8, -11) is

Question 13.
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.

Solution:
ΔABC is an equilateral

Each angle is equal to 60°
Side AB is parallel to x-axis
Slope of AB = slope of x-axis = 0.
Slope of AC = tan A = tan 60° = √3
Slope of CB = tan B = tan 120° = tan (180°- 60°) = – tan 60° = -√3
Slopes of AB, BC and CA are 0, -√3, √3

Question 14.
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also, find :
(i) the slope of the diagonal AC
(ii) the slope of the diagonal BD.

Solution:

ABCD is a square in which AB || DC || x-axis.
AD || BC || y-axis
Slope of AB and DC = 0
and slope of AD and BC = not defined (tan90° is not defined)
AC and BD are the diagonals of square ABCD.
Now slope of AC = tan 45° = 1
and slope of BD = tan 135° = tan (180° – 45°) = – tan 45° = -1

Question 15.
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find :
(i) the slope of the altitude of AB
(ii) the slope of the median AD and
(iii) the slope of the line parallel to AC.
Solution:
Vertices of ΔABC are A (5, 4), B (-3, -2), and C (1, -8)

Question 16.
The slope of the side BC of a rectangle ABCD is \(\frac { 2 }{ 3 }\). Find
(i) The slope of the side AB,
(ii) the slope of the side AD.
Solution:
ABCD is a rectangle in which

Question 17.
Find the slope and the inclination of the line AB if
(i) A = (-3, -2) and B = (1, 2)
(ii) A = (0, -√3) and B = (3, 0)
(iii) A = (-1, 2√3) and B = (-2, √3)
Solution:

Question 18.
The points (-3, 2), (2, -1) and (a, 4) are collinear, Find ‘a’.
Solution:
Points are collinear.
Slope of (-3, 2) and (2, -1) = Slope of (2, -1) and (a, 4)
Now, Slope of (-3, 2) and (2, -1) will be

Question 19.
The points (k, 3), (2, -4) and (-k + 1, -2) are collinear. Find k.
Solution:
Points (k, 3), (2, -4) and (-k + 1, -2) are collinear
Slope of (k, 3) and (2, -4) = slope of (2, -4) and (-k + 1, -2)
Now, slope of (k, 3) and (2, -4)

Question 20.
Plot the points A (1, 1), B (4, 7) and C (4, 10) on a graph paper. Connect A and B, and also A and C.
Which segment appears to have the steeper slope, AB or AC ?
Justify your conclusion by calculating the slopes of AB and AC.
Solution:

Question 21.
Find the value(s) of k so that PQ will be parallel to RS. Given :
(i) P (2, 4), Q (3, 6), R (8, 1) and S (10, k)
(ii) P (3, -1), Q (7, 11), R (-1, -1) and S (1, k)
(iii) P (5, -1), Q (6, 11), R (6, -4k) and S (7, k²)
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.