Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

Question 1.
Find the slope of the line whose inclination is :
(i) 0°
(ii) 30°
(iii) 72° 30′
(iv) 46°
Solution:
(i) Slope of line whose inclination is 0° = tanθ = tan 0° = 0
(ii) Slope of line whose inclination is 30° = tan 30° = \(\frac { 1 }{ \surd 3 }\)
(iii) Slope of line whose inclination is 72° 30′ = tan 72°30’ = 3. 1716 (Using tables)
(iv) Slope of line whose inclination is 46° = tan 46° = 1.0355 (Using tables)

Question 2.
Find the inclination of the line whose slope is:
(i) 0
(ii) √3
(iii) 0.7646
(iv) 1.0875
Solution:
Slope of a line = tanθ. Where θ is the inclination
(i) When slope is θ. then tanθ = 0 ⇒ θ = 0°
(ii) When slope is θ, then tanθ = √3 ⇒ θ = 60°
(iii) When slope is 0.7646, then tanθ = 0.7646 ⇒ θ = 37°24′ (Using tables)
(iv) When slope is 1.0875, then tanθ = 1.0875 ⇒ θ = 47°24′ (Using tables)

Question 3.
Find the slope of the line passing through the following pairs of points :
(i) (-2, -3) and (1, 2)
(ii) (-4, 0) and origin
(iii) (a, -b ) and (b, -a)
Solution:
We know that, slope of a line which passes

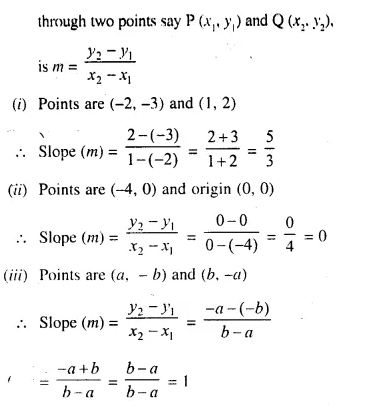
Question 4.
Find the slope of the line parallel to AB if:
(i) A = (-2, 4) and B = (0, 6)
(ii) A = (0, -3) and B = (-2, 5)
Solution:

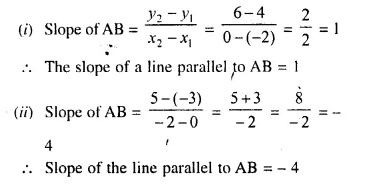
Question 5.
Find the slope of the line perpendicular to AB if:
(i) A = (0, -5) and B = (-2, 4)
(ii) A = (3, -2) and B = (-1, 2)
Solution:

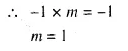
Question 6.
The line passing through (0, 2) and (-3, -1) is parallel to the line passing through (-1, 5) and (4, a). Find a.
Solution:
Slope of the line passing through two points (0, 2) and (-3, -1)

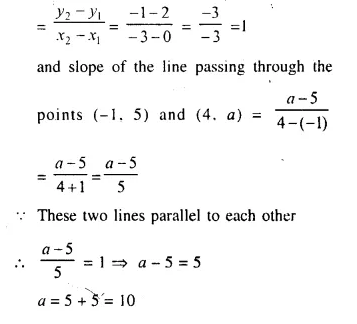
Question 7.
The line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1). Find a.
Solution:
Slope of the line passing through the points

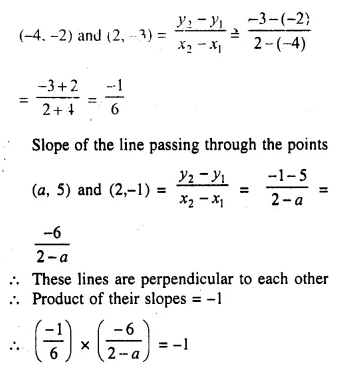
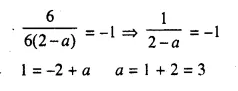
Question 8.
Without using the distance formula, show that the point A (4, -2), B (-4, 4) and C (10, 6) are the vertices of a right-angled triangle.
Solution:


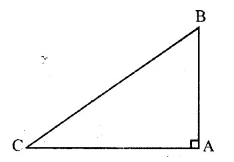
AB and CA are perpendicular to each other
Hence, ΔABC is a right-angled triangle.

Question 9.
Without using the distance formula, show that the points A (4, 5), B (1, 2), C (4, 3) and D (7, 6) are the vertices of a parallelogram.
Solution:


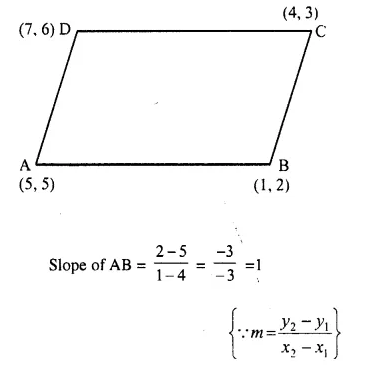
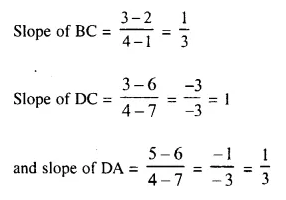
Slopes of AB and DC are equal
AB || DC Similarly slope of BC and slope of DA are equal.
BC || DA
Hence ABCD is a parallelogram.

Question 10.
(-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the – quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
Solution:





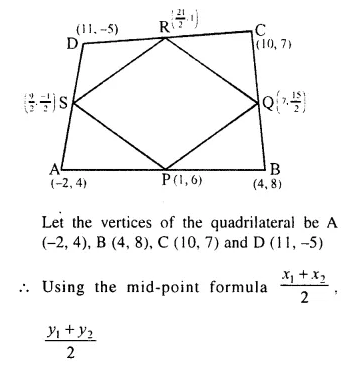
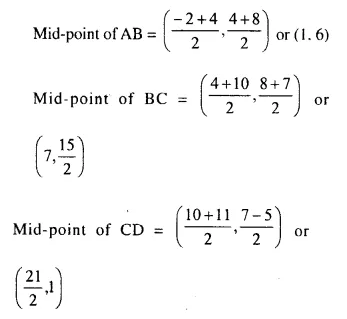
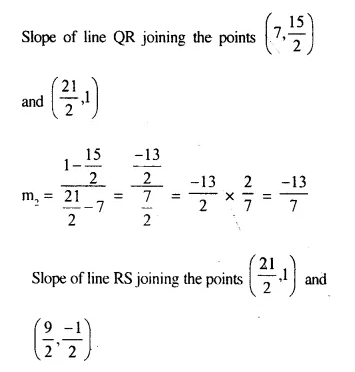
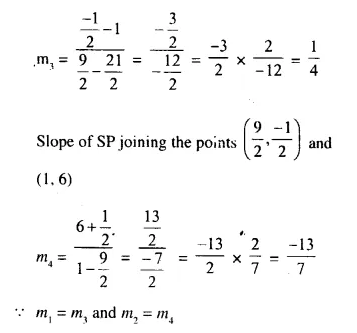
QR || PS.
Hence PQRS is a parallelogram.

Question 11.
Show that the points P (a, b + c), Q (b, c + a) and R (c, a + b) are collinear.
Solution:
The given points are P (a, b + c), Q (b, c + a) and R (c, a + b)
We know that, these points P, Q, R are collinear if Slope of PQ = Slope of QR

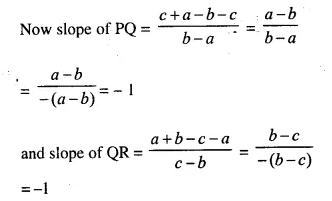
Slope of PQ = Slope of QR
P, Q and R are collinear.

Question 12.
Find x, if the slope of the line joining (x, 2) and (8, -11) is \(\frac { -3 }{ 4 }\).
Solution:
Slope of line joining (x, 2) and (8, -11) is

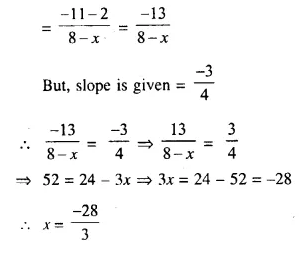
Question 13.
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.

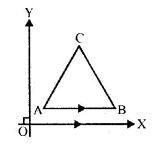
Solution:
ΔABC is an equilateral

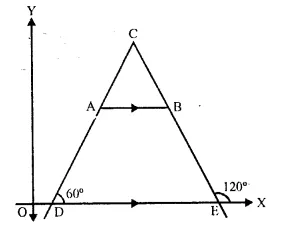
Each angle is equal to 60°
Side AB is parallel to x-axis
Slope of AB = slope of x-axis = 0.
Slope of AC = tan A = tan 60° = √3
Slope of CB = tan B = tan 120° = tan (180°- 60°) = – tan 60° = -√3
Slopes of AB, BC and CA are 0, -√3, √3

Question 14.
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also, find :
(i) the slope of the diagonal AC
(ii) the slope of the diagonal BD.

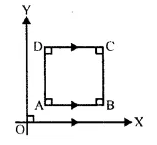
Solution:

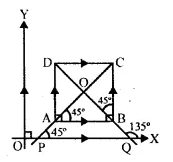
ABCD is a square in which AB || DC || x-axis.
AD || BC || y-axis
Slope of AB and DC = 0
and slope of AD and BC = not defined (tan90° is not defined)
AC and BD are the diagonals of square ABCD.
Now slope of AC = tan 45° = 1
and slope of BD = tan 135° = tan (180° – 45°) = – tan 45° = -1

Question 15.
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find :
(i) the slope of the altitude of AB
(ii) the slope of the median AD and
(iii) the slope of the line parallel to AC.
Solution:
Vertices of ΔABC are A (5, 4), B (-3, -2), and C (1, -8)

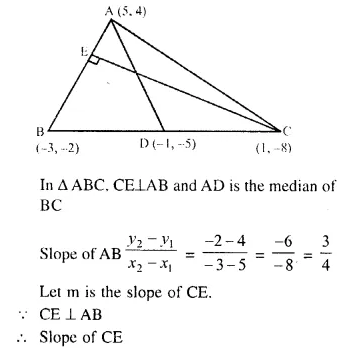
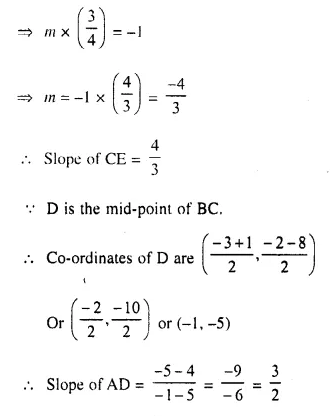
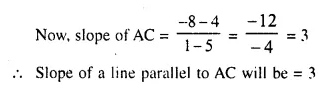
Question 16.
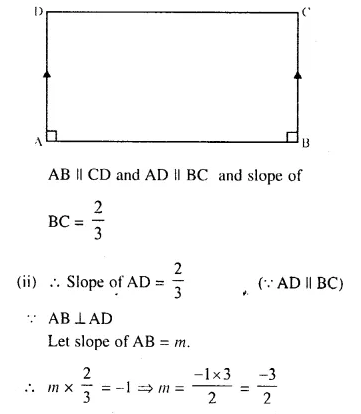
The slope of the side BC of a rectangle ABCD is \(\frac { 2 }{ 3 }\). Find
(i) The slope of the side AB,
(ii) the slope of the side AD.
Solution:
ABCD is a rectangle in which

Question 17.
Find the slope and the inclination of the line AB if
(i) A = (-3, -2) and B = (1, 2)
(ii) A = (0, -√3) and B = (3, 0)
(iii) A = (-1, 2√3) and B = (-2, √3)
Solution:

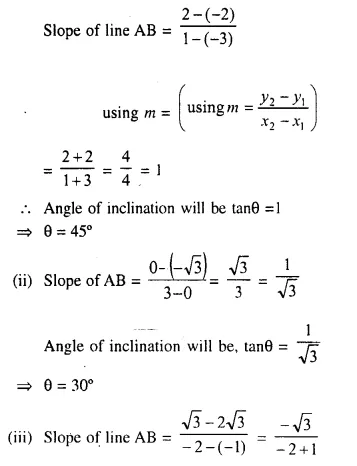
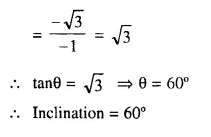
Question 18.
The points (-3, 2), (2, -1) and (a, 4) are collinear, Find ‘a’.
Solution:
Points are collinear.
Slope of (-3, 2) and (2, -1) = Slope of (2, -1) and (a, 4)
Now, Slope of (-3, 2) and (2, -1) will be

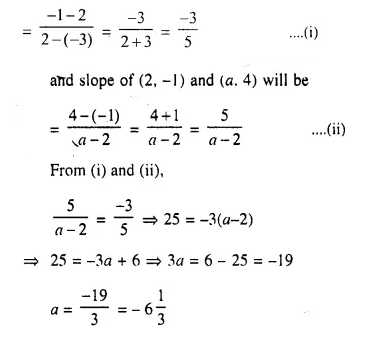
Question 19.
The points (k, 3), (2, -4) and (-k + 1, -2) are collinear. Find k.
Solution:
Points (k, 3), (2, -4) and (-k + 1, -2) are collinear
Slope of (k, 3) and (2, -4) = slope of (2, -4) and (-k + 1, -2)
Now, slope of (k, 3) and (2, -4)

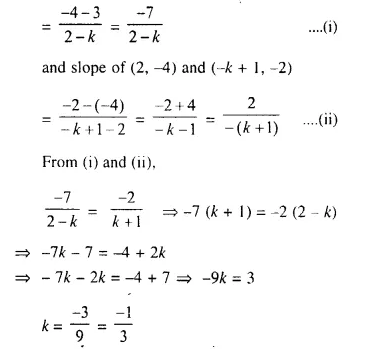
Question 20.
Plot the points A (1, 1), B (4, 7) and C (4, 10) on a graph paper. Connect A and B, and also A and C.
Which segment appears to have the steeper slope, AB or AC ?
Justify your conclusion by calculating the slopes of AB and AC.
Solution:

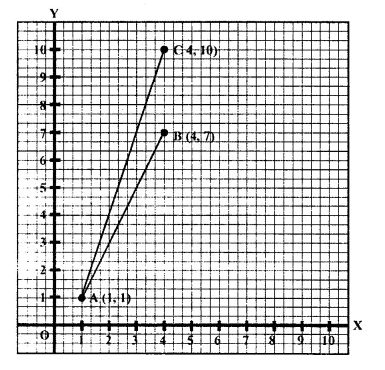
Question 21.
Find the value(s) of k so that PQ will be parallel to RS. Given :
(i) P (2, 4), Q (3, 6), R (8, 1) and S (10, k)
(ii) P (3, -1), Q (7, 11), R (-1, -1) and S (1, k)
(iii) P (5, -1), Q (6, 11), R (6, -4k) and S (7, k²)
Solution:

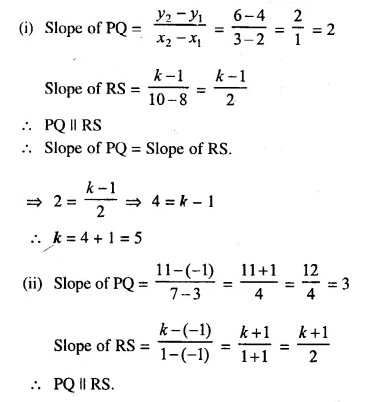
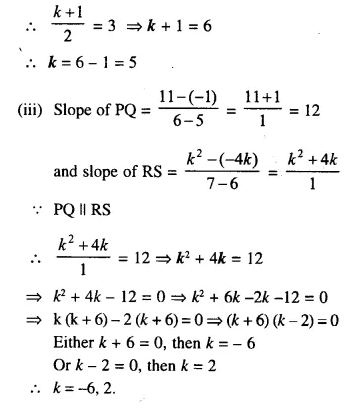
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.