Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Question 1.
Which term of the G.P. :
– 10, \(\frac { 5 }{ \surd 3 } ,-\frac { 5 }{ 6 } ,….-\frac { 5 }{ 72 } ? \)
Solution:
– 10, \(\frac { 5 }{ \surd 3 } ,-\frac { 5 }{ 6 } ,….\)
Here a = – 10
r = \(\frac { 5 }{ \surd 3 } \div \left( -10 \right) \)

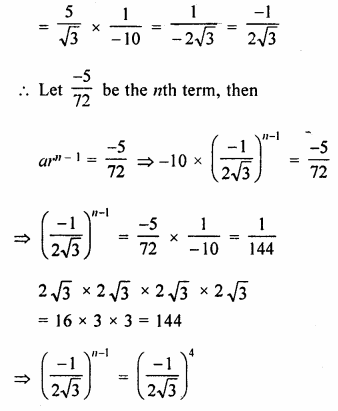
n – 1 = 4
=> n = 4 + 1 = 5
It is 5th term

Question 2.
The fifth term of a G.P. is 81 and its second term is 24. Find the geometric progression.
Solution:
In a G.P.
T₅ = ar⁴ = 81
T₂ = ar = 24

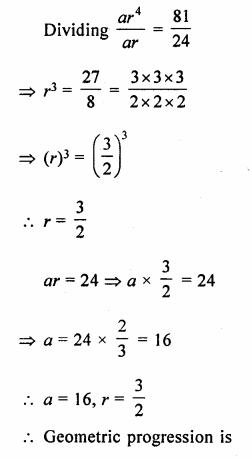
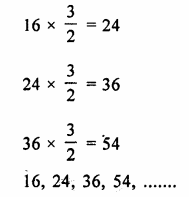
Question 3.
Fourth and seventh terms of a G.P. \(\\ \frac { 1 }{ 18 } \) are \(– \frac { 1 }{ 486 } \) respectively. Find the GP.
Solution:
In a G.P.

Question 4.
If the first and the third terms of a G.P. are 2 and 8 respectively, find its second term
Solution:
In a G.P.
T₁ = 2, and T₃ = 8
=>a = 2 and ar² = 8
Dividing, we get
r² = \(\\ \frac { 8 }{ 2 } \) = 4 = (2)²
r = 2
Second term = ar = 2 x 2 = 4

Question 5.
The product of 3rd and 8th terms of a G.P. is 243. If its 4th term is 3, find its 7th term.
Solution:
Let a be first term and r be common ratio, then
T₃ = ar²
T₈ = ar⁷
T₃ x T₈ = ar² x ar⁷
= 243

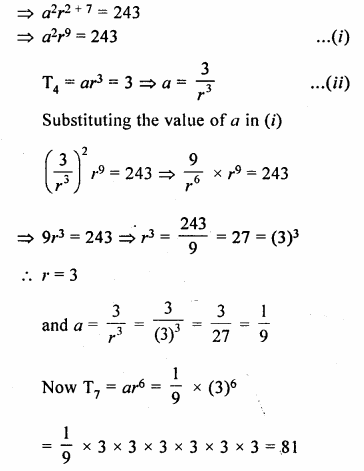
Question 6.
Find the geometric progression with 4th term = 54 and 7th term = 1458.
Solution:
In a G.P.
T₄ = 54 and T₇ = 1458
Let a be the first term and r be the common
ratio, then

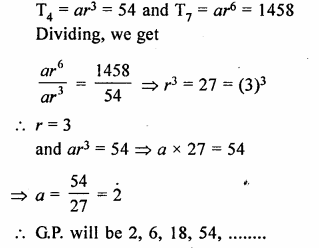
Question 7.
Second term of a geometric progression is 6 and its fifth term is 9 times of its third term. Find the geometric progression. Consider that each term of the G.P. is positive.
Solution:
In a G.P.
T₂ = 6,
T₅ = 9 x T₃
Let a be the first term and r be the common ratio

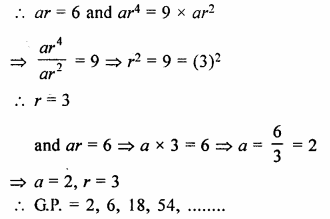
Question 8.
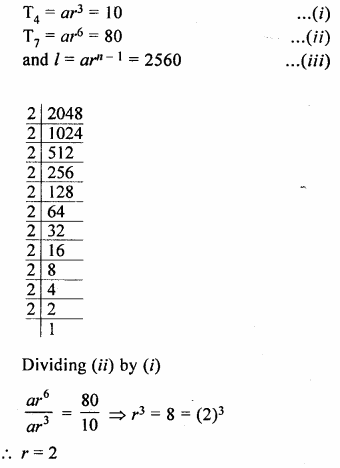
The fourth term, the seventh term and the last term of a geometric progression are 10, 80 and 2560 respectively. Find its first term, common ratio and number of terms.
Solution:
In a G.P.
T₄= 10,
T₇ = 80 and l = 2560
Let a be the first term and r be the common ratio. Therefore

Question 9.
If the 4th and 9th terms of a G.P. are 54 and 13122 respectively, find the GP. Also, find its general term.
Solution:
In a G.P.
T₄ = 54 and T₉ = 13122
Let a be the first term and r be the common ratio

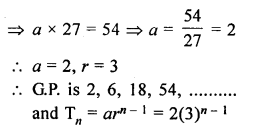
Question 10.
The fifth, eight and eleventh terms of a geometric progression are p, q and r respectively. Show that : q² = pr.
Solution:
In a G.P.
T₅ = p,
T₈ = q and T₁₁ = r
To show that q² = pr
Let a be the first term and r be the common ratio, therefore
ar⁴ = p, ar⁷ = q and ar¹⁰ = r
Squaring the ar⁷ = q

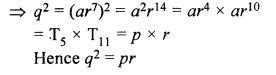
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.