Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions

Question 1.
Find the sum of n terms of the series :
(i) 4 + 44 + 444 + ….
(ii) 0.8 + 0.88 + 0.888 + ….
Solution:
(i) 4 + 44 + 444 + ….
= \(=\frac { 4 }{ 9 } \left[ 9+99+999+…. \right] \)

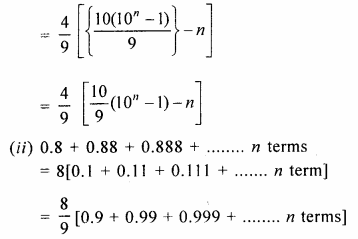
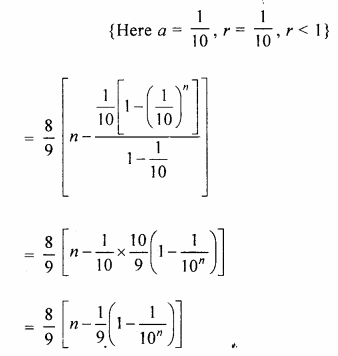
Question 2.
Find the sum of infinite terms of each of the following geometric progression:
(i)\(1+\frac { 1 }{ 3 } +\frac { 1 }{ 9 } +\frac { 1 }{ 27 } +…\)
(ii)\(1-\frac { 1 }{ 2 } +\frac { 1 }{ 4 } -\frac { 1 }{ 8 } +…\)
(iii)\(\frac { 1 }{ 3 } +\frac { 1 }{ { 3 }^{ 2 } } -\frac { 1 }{ { 3 }^{ 3 } } +…\)
(iv)\(\sqrt { 2 } -\frac { 1 }{ \sqrt { 2 } } +\frac { 1 }{ 2\sqrt { 2 } } -\frac { 1 }{ 4\sqrt { 2 } } +…\)
(v)\(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +\frac { 1 }{ 9\sqrt { 3 } } +… \)
Solution:
(i)\(1+\frac { 1 }{ 3 } +\frac { 1 }{ 9 } +\frac { 1 }{ 27 } +…\) upto infinity
S_n = \(\\ \frac { a }{ 1-r } \)

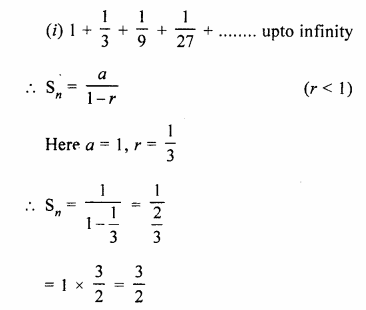
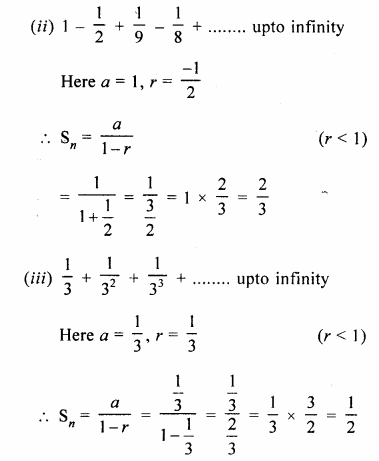
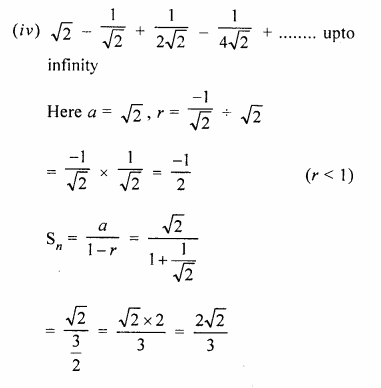
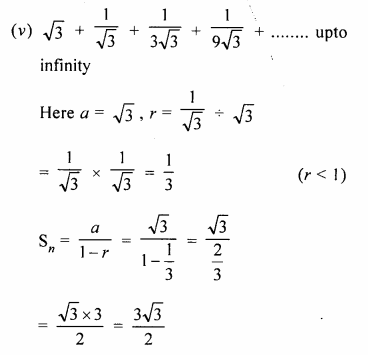
Question 3.
The second term of a G.P. is 9 and sum of its infinite terms is 48. Find its first three terms.
Solution:
In a G.P.
T₂ = 9, sum of infinite terms = 48
Let a be the first term and r be the common ratio, therefore,
S_∞ = \(\\ \frac { a }{ 1-r } \)

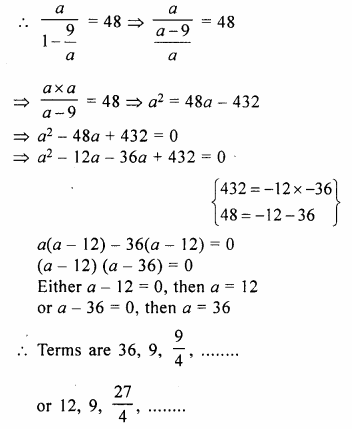
Question 4.
Find three geometric means between \(\\ \frac { 1 }{ 3 } \) and 432.
Solution:
Let G₁, G₂ and G₃ be three means between
\(\\ \frac { 1 }{ 3 } \) and 432, then

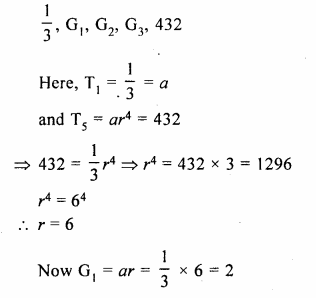
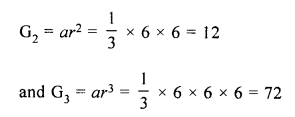
Question 5.
Find :
(i) two geometric means between 2 and 16
(ii) four geometric means between 3 and 96.
(iii) five geometric means between \(3 \frac { 5 }{ 9 } \) and \(40 \frac { 1 }{ 2 } \).
Solution:
(i) Two G.M. between 2 and 16
Let G₁ , and G₁ be the G.M.,
then 2, G₁, G₂, 16

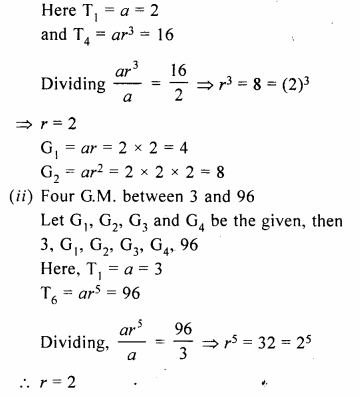
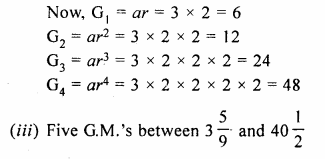
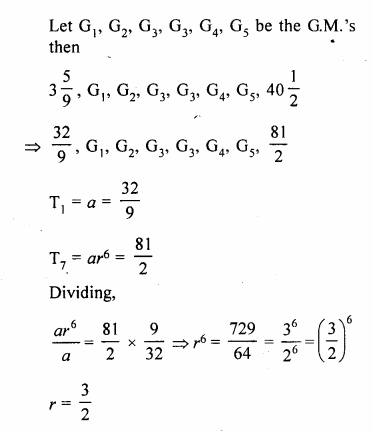
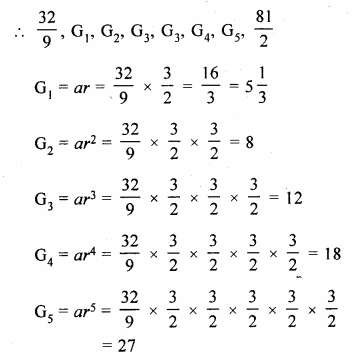
Question 6.
The sum of three numbers in G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find numbers
Solution:
Sum of three numbers in G.P = \(\\ \frac { 39 }{ 10 } \)
and their product = 1

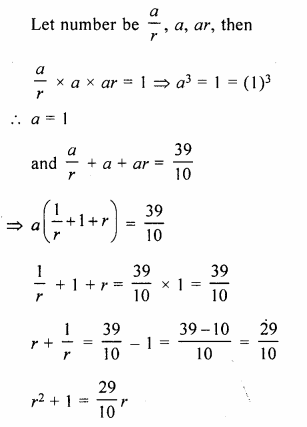
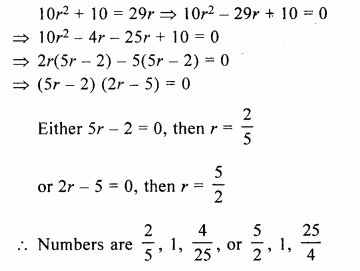
Question 7.
Find the numbers in G.P. whose sum is 52 and the sum of whose product in pairs is 624.
Solution:
Sum of 3 numbers in G.P. = 52
and their product in pairs = 624
Let numbers be a, ar, ar²

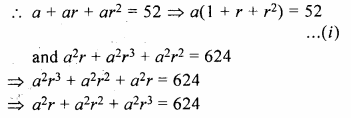
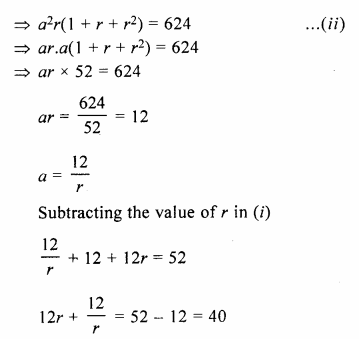
Question 8.
The sum of three numbers in G.P. is 21 and the sum of their squares is 189. Find the numbers.
Solution:
Sum of three numbers in G.P. = 21
Sum of their squares = 189
Let three numbers be a, ar, ar², then
a + ar + ar² = 21
=> a( 1 + r + r²) = 21….(i)

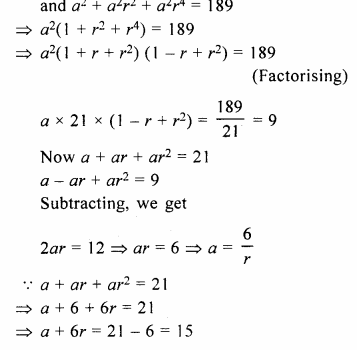
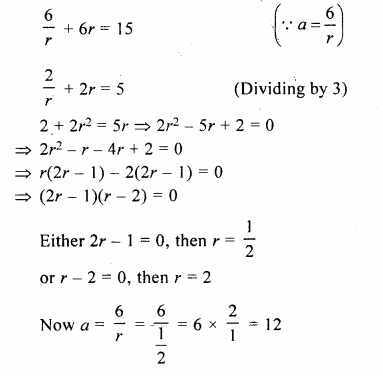
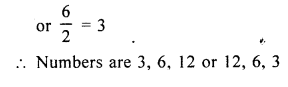
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.