Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

Question 1.
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.

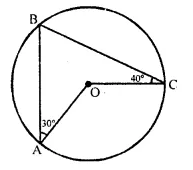
Solution:

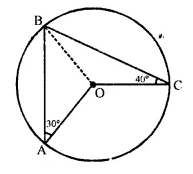
In circle with centre O, ∠BAO = 30°, ∠BCO = 40°.
Join BO.
OA = OB = OC (Radii of the circle)
∠OBA = ∠OAB = 30° and ∠OBC = ∠OCB = 40°
∠ABC = 30° + 40° = 70°
Now, AOC is at the centre and ∠ABC is on the remaining part of the circle.
∠AOC = 2 ∠ABC = 2 x 70° = 140°.

Question 2.
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.

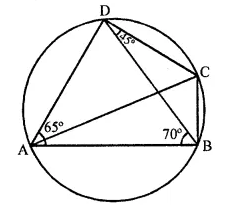
Solution:

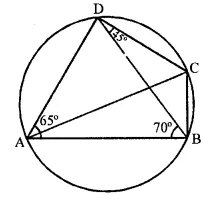
(i) In ΔABD
65° + 70° + ∠ADB = 180°
∠ADB = 180° – 65° – 70° = 45°
∠ADC = 45° + 45° = 90°
AC is diameter [Angle in semi circle is 90°]
(ii) ∠ACB = ∠ADB = 45° [angle in same segment]

Question 3.
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
(i) ∠OCA,
(ii) ∠OAC.

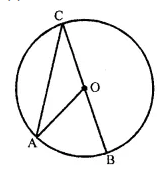
Solution:

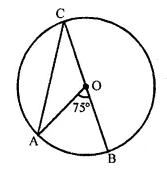
O is the centre of the circle,
∠AOB = 70°
arc AB subtends ∠AOB at the centre
and ∠ OCA is at the remaining part of circle
∠AOB = 2 ∠OCA
or ∠OCA = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 70° = 35°
In ΔOAC,
OC = OA (Radii of the same circle)
∠OAC = ∠OCA = 35°

Question 4.
In each of the following figures, O is the centre of the circle. Find the values of a, b, and c.

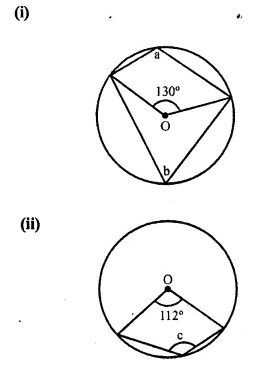
Solution:

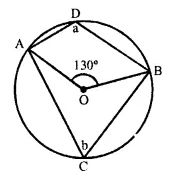
(i) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part
∠AOB = 2 ∠ACB
or ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 130° = 65°
or b = 65°
But a + b = 180° (Opposite angles of a cyclic quad.)
a = 180° – b = 180° – 65° = 115°
a = 115°, b = 65°
(ii) Arc AB subtends ∠ AOB at the centre and ∠ACB at the remaining part.

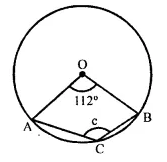
Reflex ∠AOB = 2 ∠ACB
or ∠ACB = \(\frac { 1 }{ 2 }\) (reflex ∠AOB) = \(\frac { 1 }{ 2 }\) [360°- 112°]
= \(\frac { 1 }{ 2 }\) x 248° = 124°
Hence, c = 124°.

Question 5.
In each of the following figures, O is the centre of the circle. Find the value of a, b, c and d.

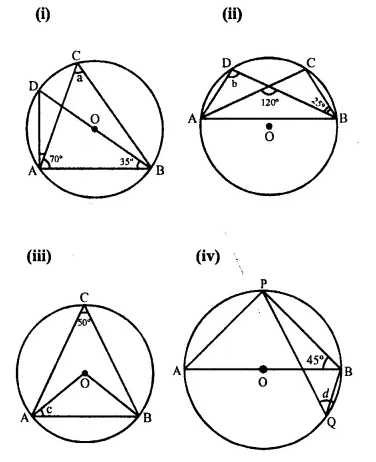
Solution:
(i) BOD is a diameter

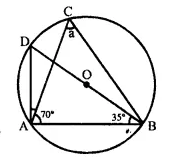
∠BAD = 90° (Angle in a semi-circle)
∠ADB = 180° – (90° + 35°) = 180° – 125° = 55°
But ∠ACB = ∠ADB = 55° (Angles in the same segment)
a = 55°.
(ii) In ΔEBC.

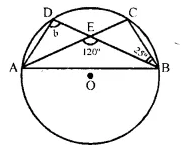
Ext. 120° = 25° + ∠BCE
∠BCE = 120° – 25° = 95°
But ∠ADB = ∠ACB = 95° (Angles in the same segment)
b = 95°.
(iii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part,

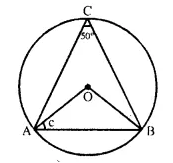
∠ AOB = 2 ∠ ACB = 2 x 50° = 100°
In ΔAOB,
OA = OB (Radii of the same circle)
∠OAB = ∠OBA
But ∠OAB + ∠OBA = 180° – 100° = 80°
c = ∠OAB = ~ x 80° = 40°.
(iv) In the given figure, O is the centre of the circle.
AOB is its diameter and ∠ABP = 45°
Q is any point and BQ, PQ are joined

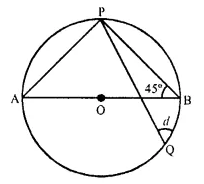
In ΔABP,
∠APB = 90° (Angle in a semicircle)
∠PAB + ∠PBA = 90°
⇒ ∠PAB + 45° = 90°
⇒ ∠PAB = 90° – 45°
⇒ ∠PAB = 45°
Now ∠PAB = ∠PQB (Angle in the same segment)
BPQB = 45°
⇒ d = 45°

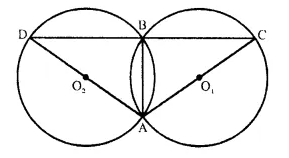
Question 6.
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O1 and 02 are the centres of two circles.

Solution:

Given- Two circles with centre O1 and O2 intersect each other at A and B.
AC and AD are the diameters of the circles.
To Prove- D, B, C are in the same straight line.
Construction- Join AB.
Proof- AO1C is diameter.
∠ABC = 90°. (Angle in a semi-circle)
Similarly ∠ABD = 90°,
Adding, we get:
∠ABC + ∠ABD = 90° + 90° = 180°
DBC is a straight line.
or D, B, C are in the same line.

Question 7.
In the figure given beow, find :
(i) ∠BCD,
(ii) ∠ADC,
(iii) ∠ABC.

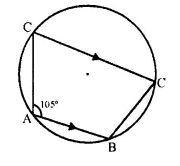
Show steps of your workng.
Solution:

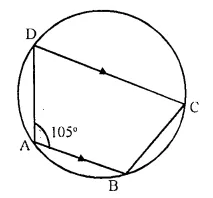
ABCD is a cyclic quadrilateral
∠A + ∠C = 180°.
∠C = 180° – ∠A = 180° – 105° = 75°
or ∠BCD = 75°
DC || AB
∠ADC + ∠DAB = 180° (Angles on the same side of the transversal of || lines)
∠ADC = 180° – ∠DAB = 180° – 105° = 75°
But ∠ADC + ∠ABC = 180° (opposite angles of a cyclic quad.)
∠ABC = 180° – ∠ADC = 180° – 75° = 105°

Question 8.
In the given figure, O is centre of the circle. If ∠ AOB = 140° and ∠ OAC = 50°; find :
(i) ∠ ACB,
(ii) ∠OBC,
(iii) ∠OAB,
(iv) ∠CBA

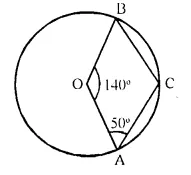
Solution:

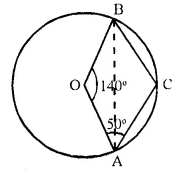
O is the centre of circle ∠AOB = 140° and ∠OAC = 50°.
AB is joined
Reflex ∠AOB = 360° – 140° = 220°
But ∠ACB = \(\frac { 1 }{ 2 }\) Reflex ∠AOB = \(\frac { 1 }{ 2 }\) x 220° = 110°
In quad. OACB,
∠AOB + ∠OAC + ∠ACB + ∠OBC = 360°
⇒ 140° + 50° + 110° + ∠OBC = 360°
⇒ 300° + ∠OBC = 360°
⇒ ∠OBC = 360° – 300° = 60°
In ∆OAB,
∠AOB + ∠OAB + ∠OBA = 180°
But ∠OBA = ∠OAB (Angles opposite to equal sides)
140° + ∠OAB + ∠OAB = 180°
2 ∠OAB = 180° – 140° = 40°
∠OAB = \(\frac { 40 }{ 2 }\) = 20°
∠OAB = ∠OBA = 20°.
⇒ ∠OBC = ∠CBA + ∠ABO
⇒ 60° = ∠CBA + 20°
⇒ ∠CBA = 40°

Question 9.
Calculate :
(i) ∠ CDB,
(ii) ∠ ABC,
(iii) ∠ ACB.

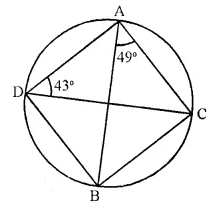
Solution:
∠CDB = ∠BAC (Angles is the same segment) = 49°
∠ABC = ∠ADC (Angles in the same segment) = 43°
∠ADB = ∠ADC + ∠BDC = 43° + 49° = 92°
and ∠ADB + ∠ACB = 180° (opposite angles of a cyclic quad.)
∠ACB = 180° – ∠ADB = 180° – 92° = 88°.

Question 10.
In the figure given below, ABCD is a eyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
(i) ∠BDC,
(ii) ∠BCD,
(iii) ∠BCA.

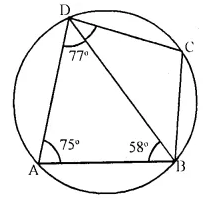
Solution:
In cyclic quad. ABCD,
∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°.
∠A + ∠C = 180° (opposite angles of a cyclic quad.)
∠C = 180° – ∠A = 180° – 75° = 105° or ∠BCD = 105°
In ΔABD,
∠BAD + ∠ABD + ∠ADB = 180°
⇒ 75° + 58° + ∠ ADB = 180°

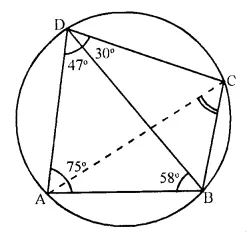
⇒ 133° + ∠ADB = 180°
⇒ ∠ADB = 180° – 133° = 47°
∠BDC = 77° – ∠ADB = 77° – 47° = 30°
But ∠BCA = ∠BDA (Angles in the same) = 47°

Question 11.
In the following figure, O is centre of the circle and ΔABC is equilateral. Find :
(i) ∠ADB
(ii) ∠AEB

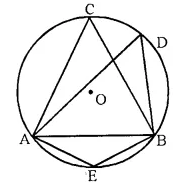
Solution:

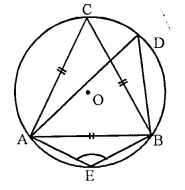
∠ACB and ∠ADB are in the same segment.
∠ADB = ∠ACB. = 60°. (Angle of an equilateral triangle)
AEBD is a cyclic quadrilateral
∠AEB + ∠ADB = 180°
⇒ ∠AEB + 60° = 180°
⇒ ∠AEB = 180° – 60° = 120°.

Question 12.
Given- ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD

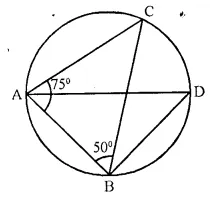
Solution:

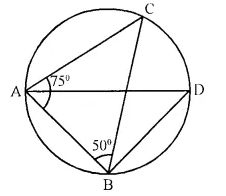
In ΔABC, ∠CBA = 50°, ∠CAB = 75°,
∠ACB = 180° – (∠CBA + ∠CAB) = 180° – (50° = 75°) = 180° – 125° = 55°
Bui ∠ADB = ∠ACB = 55° (Angles in the same segment)
Now in ΔABD,
∠DAB + ∠ABD + ∠ADB = 180°.
⇒ ∠DAB + ∠ABD + 55° = 180°
⇒ ∠DAB + ∠ABD = 180° – 55° = 125°.

Question 13.
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

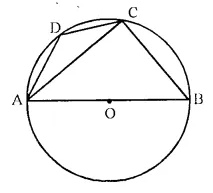
Solution:

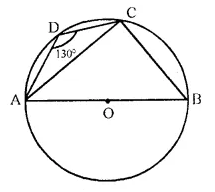
ABCD is a cyclic quadrilateral and ∠ADC = 130°
O is centre of the circle, AOB is diameter.
∠ABC = 180° – 130° = 50°.
In ΔABC,
∠ACB = 90° (angle in semicircle)
∠BAC + ∠CBA = 90°.
∠BAC + 50° = 90°
∠BAC = 90° – 50° = 40°.

Question 14.
In the figure given below, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.

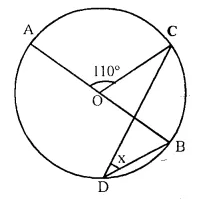
Solution:

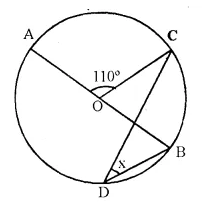
∠AOC + ∠COB = 180° (Linear pair)
∠COB = 180° – ∠AOC = 180° – 110° = 70°
Arc BC subtends ∠COB at the centre and x at the remaining part of circle
∠COB = 2x
⇒ x = \(\frac { 1 }{ 2 }\) ∠COB = \(\frac { 1 }{ 2 }\) x 70° = 35°

Question 15.
In the following figure, O is centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

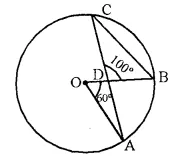
Solution:

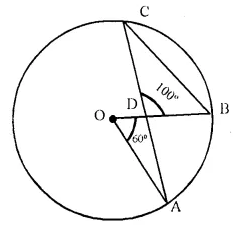
Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of circle,
∠AOB = 2 ∠ACB
or ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 60° = 30°
Now in ΔDBC,
∠DBC + ∠ACB + ∠BDC = 180°
⇒ ∠DBC + 30° + 100° = 180°
⇒ ∠DBC = 180° – 130° = 50°
or ∠OBC = 50°.

Question 16.
ABCD is a cyclic quadrilateral in which ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate :
(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB.

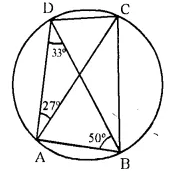
Solution:

(i) ∠ CBD = ∠ DAC = 27° (Angles in the same segment)
(ii) In ΔADB,
∠ABD + ∠BAD + ∠BDA = 180°.
⇒ 50° + ∠BAD + 33° = 180°
⇒ ∠BAD + 83° = 180°
⇒ ∠BAD = 180° – 83° = 97°
In cyclic quad. ABCD,
∠BAD + ∠DCB = 180°
⇒ 97° + ∠DCB = 180°
⇒ ∠DCB = 180°- 97° = 83°
(iii) ∠BAD = 97°
⇒ ∠BAC + ∠CAD = 97°
⇒ ∠BAC + 27° = 97°
⇒ ∠BAC = 97° – 27° = 70°
∠CAB = 70°.

Question 17.
In the figure given below, AB is diameter of the circle whose centre is O. Given that:
∠ECD = ∠EDC = 32°. Show that ∠COF = ∠CEF.

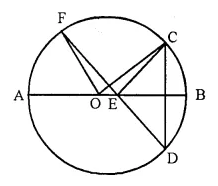
Solution:

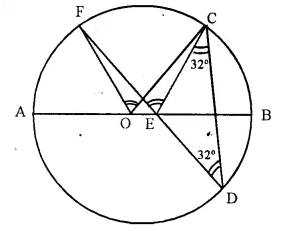
Given- AB is the diameter of a circle with centre O
and ∠ECD = ∠EDC = 32°
To Prove- ∠COF = ∠CEF
Proof- Arc CF subtends ∠COF at the centre and ∠CDF at the remaining part of the circle.
∠COF = 2 ∠CDF = 2 x ∠EDC = 2 x 32° = 64° ….. (i)
In ΔCED,
Ext. ∠CEF = ∠CDF + ∠DCE = ∠EDC + ∠ECD = 32° + 32° = 64° ….(ii)
from (i) and (ii)
∠CDF = ∠CEF

Question 18.
In the figure given below, AB and CD arc straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in:
(i) ∠DCE,
(ii) ∠ABC.

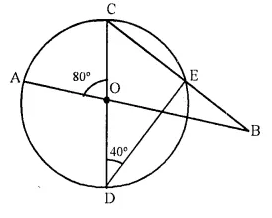
Solution:

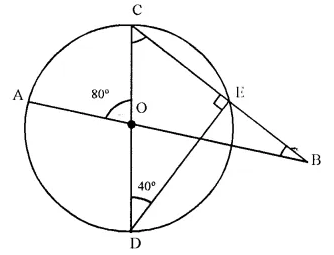
In circle, COD is the diameter.
∠CED = 90° (Angle in a semi circle)
In right A CDE,
∠ DCE + ∠ EDC = 90°
⇒ ∠ DCE + 40° = 90°
∠ DCE = 90° – 40° = 50°
In ΔOBC.
Ext. ∠COA = ∠OBC + ∠OCB
⇒ 80° = ∠OBC + 50°
⇒ ∠OBC = 80° – 50° = 30°
or ∠ABC = 30°

Question 19.
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that AB = BE.

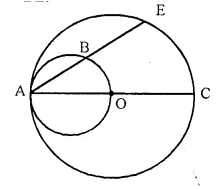
Solution:
Given- AC is a diameter of a circle with centre O.
AE is a chord which intersects the smaller circle with AO as diameter at B.

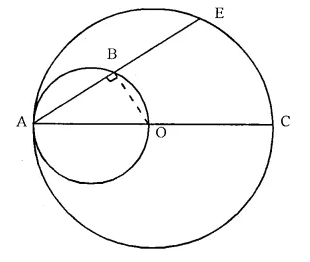
To Prove- AB = BE.
Construction- Join OB.
Proof- ∠ABO = 90° (Angle in a semi circle)
OB ⊥ AE
OB bisects chord AE
Hence, AB = BE.

Question 20.
In the following figure,
(i) if ∠ BAD = 96°, find ∠BCD and ∠BFE,
(ii) Prove that AD is parallel to FE.

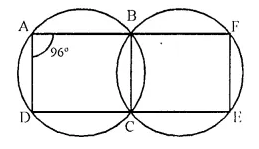
Solution:
Given- In the figure, ∠BAD = 96°
To Prove-
(i) Find ∠BCD and ∠BFE
(ii) AD || EF
Proof- ABCD is a cyclic quadrilateral.
∠BAD + ∠BCD = 180°
⇒ 96° + ∠BCD = 180°
⇒ ∠BCD = 180° – 96° = 84°
Again BCEF is a cyclic quadrilateral,
Ext. ∠BCD = Int. opposite ∠BFE
∠BFE = 84°.
∠BAD + ∠BFE = 96° + 84° = 180°
But these are on same side of the transversal.
AD || FE.

Question 21.
Prove that
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
Solution:

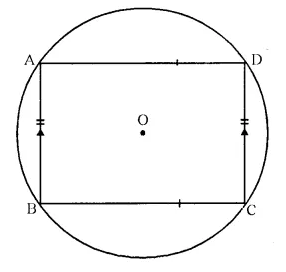
(i) ABCD is a parallelogram in a circle with centre O.
To Prove- ABCD is a rectangle.
Proof- ABCD is a cyclic parallelogram.
∠A + ∠C = 180°.
But ∠A = ∠C (opposite angles of a ||gm)
∠A = ∠C = 90°
Similarly we can prove that
∠B = ∠D = 90°
Each angle of a ||gm is right angle
Hence ABCD is a rectangle.
(ii) Given- ABCD is a cyclic rhombus.
To Prove- ABCD is a square.
Proof- ABCD is cyclic rhombus
∠A + ∠C = 180°
But ∠A = ∠C (opposite angles of rhombus)
∠A = ∠C = 90°
Similarly we can prove that ∠B = ∠D = 90°
Each angle of a rhombus is a right angle
ABCD is a square.

Question 22.
In the following figure, AB = AC. Prove that DECB is an isosceles trapezium.

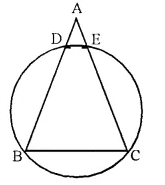
Solution:
Given- In the figure, AB = AC.
To Prove- DECB is an isosceles trape∠ium.
Proof- In ∆ABC,
AB = AC
∠B = ∠C
DECB is a cyclic quadrilateral.
∠B + ∠DEC = 180°
∠C + ∠DEC = 180°
But this is the sum of interior angles on one side of a transversal.
DE || BC ….(i)
But ∠ADE = ∠B
and ∠AED = ∠C (Corresponding angles)
∠ADE = ∠AED (∠B = ∠C)
AD = AE (Opposite to equafangles)
But AB = AC (Given)
AB – AD = AC – AE
⇒ DB = EC ….(ii)
From (i) and (ii)
DECB is an isosceles trape∠ium.

Question 23.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are draw n. Show that the points A, Q and B are collinear.
Solution:

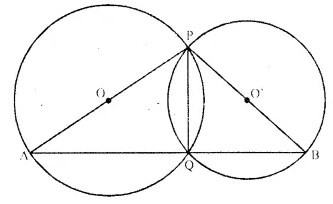
Given- Two circles with centres O and O’ intersect each other at P and Q.
From P, PA and PB are two diameters are drawn.
To Prove- A, Q and B are collinear.
Construction-
Join PQ, AQ and BQ.
Proof- In first circle.
∠PAQ = 90° (Angle in a semi circle) ….(i)
Similarly, in second circle, ∠PBQ = 90° ….(ii)
Adding (i) and (ii).
∠PAQ + ∠PBQ = 90° + 90° = 180°
But, there are adjacent angles
AQB is a straight line.
Hence A, Q and B are collinear.
Hence proved.

Question 24.
ABCD is a quadrilateral inscribed in a circle, having ∠A = 60°; O is the centre of the circle. Show that:
∠OBD + ∠ODB = ∠CBD + ∠CDB.
Solution:
Given- ABCD is a cyclic quadrilateral in which ∠A = 60°
and O is the centre of the circle.
BD, OB and OD are joined.
To Prove- ∠OBD + ∠ODB = ∠CBD + ∠CDB
Proof- Arc BCD subtends ∠BOD at the centre and ∠BAD at remaining part of the circle.

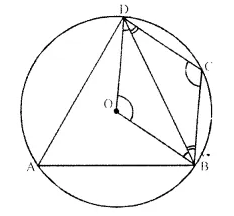
∠BOD = 2 ∠BAD = 2 x 60° = 120°
In ∆BOD,
∠BOD = 120°
∠OBD + ∠ ODB = 180° – 120° = 60° …. (i)
ABCD is a cyclic quadrilateral
∠A + ∠C = 180°
⇒ 60° + ∠C = 180°
⇒ ∠C = 180° – 60° = 120°
In ∆BCD,
∠CBD + ∠CDB + ∠ C = 180°.
∠CBD + ∠CDB + 120° = 180°
∠CBD + ∠CDB = 180° – 120° = 60° ….(ii)
From (i) and (ii),
∠OBD + ∠ODB = ∠CBD + ∠CDB

Question 25.
The figure given below, shows a circle with centre O.
Given- ∠AOC = a and ∠ABC = b.
(i) Find the relationship between a and b. :
(ii) Find the measure of angle OAB, if OABC is a parallelogram.

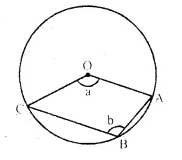
Solution:

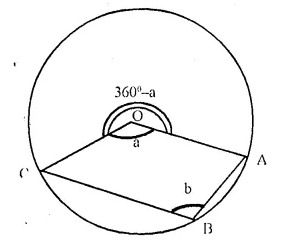
(i) ∠AOC = a, ∠ABC = b
Reflex ∠AOC = 360° – a
Now arc AC subtends reflex ∠AOC at the centre and ∠ABC at the remaining part of the circle
∠ABC = \(\frac { 1 }{ 2 }\) ref. ∠AOC
b = \(\frac { 1 }{ 2 }\) (360° – a)
⇒ 2b = 360° – a
⇒ a + 2b = 360° ….(i)
(ii) If OABC is a || gm,
then ∠AOC = ∠ABC
⇒ a = b
Substituting the value of a, in ….(i)
b + 2b = 360°
⇒ 3b = 360°
⇒ b = 120°
But ∠OAB + ∠ABC = 180° (Angles in a || gm)
⇒ ∠OAB + b = 180°
⇒ ∠OAB + 120° = 180°
⇒ ∠OAB = 180° – 120° = 60°.

Question 26.
Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.
Solution:
Given- Two chords AB and CD intersect each other at P inside the circle, OA, OB, OC and OD are joined.
To Prove- ∠AOC + ∠BOD = 2 ∠APC.
Construction- Join AD
Proof- Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining pari of the circle
∠AOC = 2 ∠ADC ….(i)
Similarly, ∠BOD = 2 ∠BAD ….(ii)
Adding (i) and (ii),

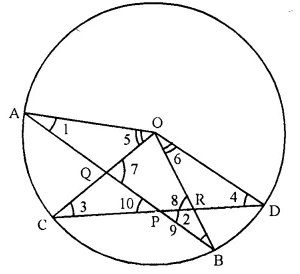
∠AOC + ∠BOD = 2 ∠ADC
⇒ 2 ∠ BAD = 2 (∠ADC + ∠BAD) ….(iii)
But in ∆PAD,
Ext. ∠APC = ∠PAD + ∠ADC = ∠ADC + ∠BAD …(iv)
from (iii) and (iv)
∠AOC + ∠BOD = 2 ∠APC

Question 27.
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°.
Calculate:
(i) ∠RNM,
(ii) ∠NRM.

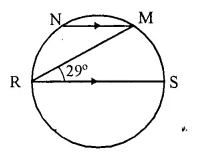
Solution:

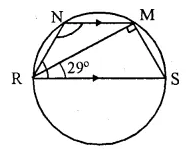
Join RN and MS. .
(i) RS is the diameter
∠RMS = 90° (Angle in semi circle)
∠RSM + ∠MRS = 90°
∠RSM = 90° – 29° = 61°
But ∠RSM + ∠RNM = 180° (Angles in a cyclic quad.)
61° + ∠RNM = 180°
⇒ ∠RNM = 180° – 61 = 119°
NM || RS
∠NMR = ∠MRS = 29° (Alt. angles)
In ∆RNM,
∠NRM + ∠RNM + ∠NMR = 180°
⇒ ∠NRM + 119° + 29° = 180°
⇒ ∠NRM + 148° = 180°
⇒ ∠NRM = 180° – 148° = 32°.

Question 28.
In the figure given alongside, AB // CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

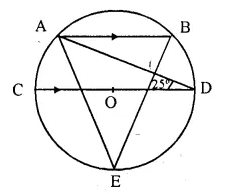
Solution:

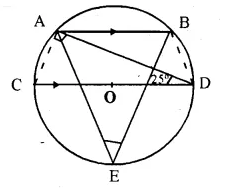
AB || CD.
∠BAD = ∠ADC (Alternate angles) = 25° (∠ADC = 25° given)
Join AC and BD.
∠CAD = 90° (Angle in semi circle)
∠CAB = ∠CAD + ∠DAB = 90° + 25° = 115°
Now in cyclic quad. CABD.
∠CAB + ∠BDC = 180°
⇒ ∠CAB + ∠BDA + ∠ADC = 180°
⇒ 115° + ∠BDA + 25° = 180°
⇒ ∠BDA + 140° = 180°
⇒ ∠BDA = 180° – 140° = 40°
∠AEB and ∠BDA are in tire same segment of a circle
∠AEB = ∠BDA = 40° (proved)
Hence ∠AEB = 40°.

Question 29.
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight fine is drawn to meet the circles at C and D. Prove that AC is || to BD.

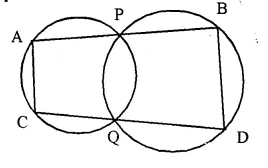
Solution:
Given- Two circles intersect each other at P and Q. Through P, a line APB is drawn to meet the circles in A and B. Through Q, another straight line CQD is drawn meeting the circles in C and D.
AC, BD are joined.
To Prove- AC || BD.
Construction- Join PQ
Proof- APQC is a cyclic quadrilateral.

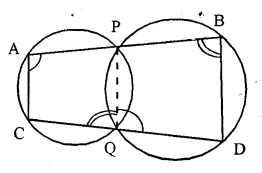
∠A + ∠PQC = 180° …… (i)
In cyclic quad. PBDQ,
Ext. ∠PQC = ∠ B …… (ii)
from (i),
∠A + ∠B = 180°.
But these are interior angles on the same side of a transversal.
AC || BD.

Question 30.
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
Solution:

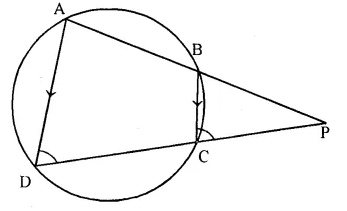
Given- The sides AB and DC of a cyclic quad. ABCD are produced to meet at P and PA = PD.
To Prove- AD || BC
Proof- In ∆PAD,
PA = PD (given)
∠A = ∠D (angles opposite to equal sides)
ADCB is a cyclic quad.
Ext. ∠PCB = ∠A = ∠D
But these are corresponding angles. ,
BC || AD or AD || BC.

Question 31.
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find:
(i) ∠PRB,
(ii) ∠ PBR,
(iii) ∠ BPR.

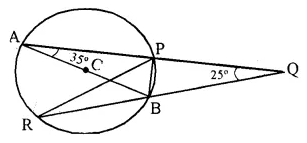
Solution:
∠PRB = ∠BAP (Angles in the same segment)
∠PRB = 35°

In ∆ABP,
∠APB = 90° (Angle in semi circle)
∠BPQ = 90°.
In ∆PQR,
∠R + ∠Q + ∠RPQ = 180°
⇒ 35° + 25° + ∠RPQ = 180°
⇒ ∠RPQ = 180° – 60° = 120°
⇒ ∠BPR = ∠RPQ – ∠BPQ = 120° – 90° = 30°
In ∆PBR,
∠PBR = 180° – (∠R + ∠BPR) = 180° – (35° + 30°) = 180° – 65° = 115°

Question 32.
In the given figure SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = SR.

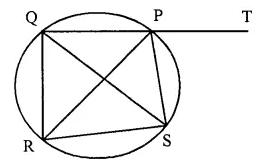
Solution:
Given- SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral.

To Prove SQ = SR.
Proof- In cyclic quad. PQRS,
Ext. ∠SPT = ∠QRS
But ∠RPS = ∠SPT (PS is the bisector of ∠RPT)
∠QRS = ∠RPS ….(i)
But ∠RPS = ∠RQS (Angles in the same segment)
∠QRS = ∠RQS
Now in ∆QRS,
∠QRS = ∠RQS (proved)
SQ = SR (Sides opposite to equal angles)

Question 33.
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the si∠es of the angles CEB and OCE.

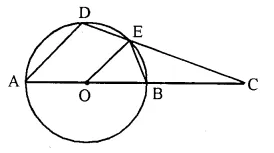
Solution:

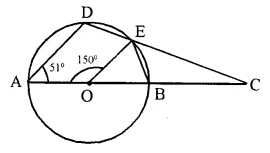
In the figure, ∠AOE = 150°, ∠DAO = 51°
Now in cyclic quad. ADEB,
Ext. ∠CEB = Int. Opp ∠DAO = 51°.
In ∆OEB,
Ext. ∠AOE = ∠OBE + ∠OEB
= ∠OBE + ∠OBE (OB = OE) = 2 ∠OBE
2 ∠OBE = 150°
⇒ ∠ OBE = 75°
∠EBC = 180° – 75° = 105°
Now in ∆EBC,
∠CEB + ∠OCE + ∠EBC = 180°
⇒ 51° + ∠OCE + 105° = 180°
⇒ ∠OCE + 156° = 180°
⇒ ∠OCE = 180° – 156° = 24°.

Question 34.
In the figure, given below, P and Q arc the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.

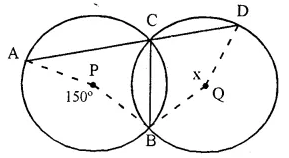
Solution:

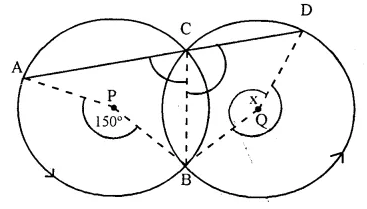
In circle with centre P,
Arc AB subtends ∠APB at the centre and ∠ACB at the remaining part of the circle.
∠APB = 2 ∠ACB
⇒ ∠ACB = \(\frac { 1 }{ 2 }\) ∠APB = \(\frac { 1 }{ 2 }\) x 150° = 75°
But ∠ACB + ∠DCB = 180° (Linear pair)
∠DCB = 180° – ∠ACB = 180° – 75° = 105°
In circle with centre O,
Arc BD subtends ∠ BQD at the centre and ∠ DCB at the remaining part of the circle
∠BQD = 2 ∠DCB = 2 x 105° = 210°
But x + ∠BQD = 360° (Angles at a point)
⇒ x + 210° = 360°
⇒ x = 360° – 210° = 150°.

Question 35.
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given ∠APB = a°. Calculate, in terms of a°, the value of :
(i) obtuse ∠AOB,
(ii) ∠ACB,
(iii) ∠ADB.

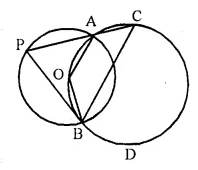
Give reasons for your answers clearly.
Solution:

Arc AB in small circle subtends ∠AOB at the centre and ∠APB at the remaining part of the circle.
(i) ∠AOB = 2 ∠APB = 2a° (∠APB = a°)
∠APB = (2a)°
(ii) In larger circle, AOBC is a cyclic quad.
∠AOB + ∠ACB = 180°.
⇒ 2a° + ∠ACB = 180°
∠ACB = 180° – 2a° = (180° – 2a°)
(iii) But ∠ ACB and ∠ ADB are in the same segment
∠ADB = ∠ ACB = (180° – 2a°)

Question 36.
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.

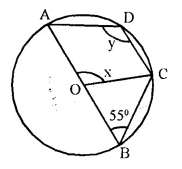
Solution:
In ∆OBC,
OB = OC (radii of the same circle)
∠OBC = ∠BCO or ∠ABC = ∠BCO
∠BCO = ∠ABC = 55°
Now in ∆OBC,
Ext. AOC = ∠OBC + ∠BCO = 55° + 55° = 110°
x = 110°

Now in cyclic quad, ABCD,
∠ADC + ∠ABC = 180°
⇒ y + 55° = 180°
⇒ y = 180° – 55° = 125°

Question 37.
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that: ∠BCD = 2 ∠ABE.

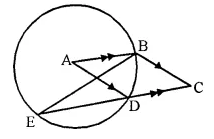
Solution:
Given- A is the centre of the circle and ABCD is a parallelogram.
CDE is a straight line.
To Prove- ∠BCD = 2 ∠ABE.

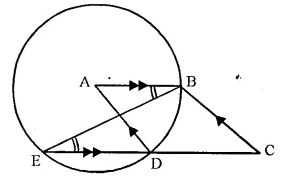
Proof- AB || DC (opposite sides of a || gm)
∠ABE = ∠BED (Alternate angles) ….(i)
ABCD is a || gm (given)
∠BAD = ∠BCD (opposite angles of a ||gm) ….(ii)
Now arc BD subtends ∠BAD at the centre and ∠BED at the remaining part of the circle
∠BAD = 2 ∠BED
from (i) and (ii)
∠BCD = 2 ∠ABE

Question 38.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
(i) ∠DAB,
(ii) ∠BDC.

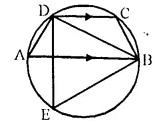
Solution:

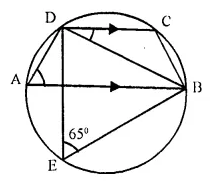
∠DAB and ∠BED are in the same segment of the circle.
∠DAB = ∠BED = 65° (∠BED = 65° given)
DC || AB (Given)
∠BDC = ∠DBA (Alternate angles)
In ∆ADB,
AOB is the diameter
∠ADB = 90° (Angle in semi circle)
∠DAB + ∠DBA = 90°
⇒ 65° + ∠DBA = 90°
⇒ ∠DBA = 90° – 65° = 25°
But ∠DBA = ∠BDC (proved)
∠BDC = 25°

Question 39.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate:
(i) ∠EBA,
(ii) ∠BCD.

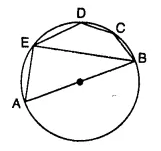
Solution:

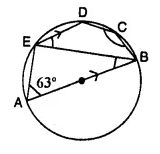
AOB is the diameter,
∠AEB = 90°
and ∠EAB + ∠EBA = 90°
⇒ 63° + ∠EBA = 90°
⇒ ∠EBA = 90° – 63° = 27°
ED || AB (given)
∠DEB = ∠EBA (Alternate angles) = 27°
In cyclic quad. EBCD,
∠DEB + ∠BCD = 180° (opposite angles of a cyclic quad.)
⇒ 27° + ∠BCD = 180°
⇒ ∠BCD = 180° – 27° = 153°.

Question 40.
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB arc produced to meet at F. If ∠BEG = 42° and ∠BAD = 98°; calculate :
(i) ∠AFB,
(ii) ∠ADC.

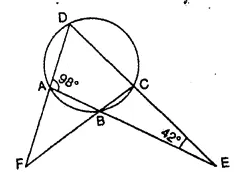
Solution:

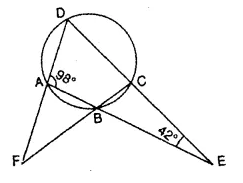
In ∆AED,
∠ADE + ∠AED + ∠EAD = 180° (Angles of a triangle)
⇒ ∠ADE + 42° + 98° = 180°
⇒ ∠ADE + 140° = 180°
⇒ ∠ ADE = 180° – 140° = 40° or ∠ADC = 40°
In cyclic quad. ABCD.
∠BAD + ∠BCD = 180°
⇒ 98° + ∠BCD = 180°
⇒ ∠BCD = 180° – 98° = 82°
Now in ∆FCD,
∠DFC + ∠FDC + ∠FCD = 180°
⇒ ∠AFB + ∠ADC + ∠BCD = 180°
⇒ ∠AFB + 40° + 82° = 180°
⇒ ∠AFB + 122° = 180°
⇒ ∠AFB = 180° – 122° = 58°

Question 41.
In the following figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°. Calculate :
(i) ∠DAB,
(ii) ∠DBA,
(iii) ∠DBC,
(iv) ∠ADC. Also, show that the ∆AOD is an equilateral triangle.

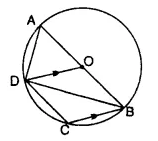
Solution:

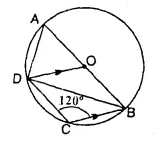
(i) ABCD is a cyclic quadrilateral,
∠DCB + ∠DAB = 180°
⇒ 120° + ∠DAB = 180°
∠DAB =180° – 120° = 60°
(ii) AOB is a diameter.
∠ADB = 90° (Angle in a semi circle)
∠ DAB + ∠DBA = 90°
60° + ∠ DBA = 90°
∠DBA = 90° – 60° = 30°
(iii) In ∆OBD,
OD = OB (radii of the same circle)
∠ ODB = ∠ OBD
or ∠ABD = 30° (from ii)
But DO || CB (given)
∠ODB = ∠DBC (Alternate angles)
⇒ 30° = ∠DBC or ∠DBC = 30°
(iv) ∠ABD + ∠DBC = 30° + 30° = 60°
⇒ ∠ABC = 60°
Again in cyclic quad. ABCD,
∠ADC + ∠ABC = 180°
∠ADC + 60° = 180°
∠ ADC = 180° – 60° = 120°
In ∆AOD,
OA = OD (radii of the same circle)
∠ AOD = ∠ DAO or ∠ DAB = 60° (proved in (i))
∠ADO = 60° (Third angle)
∠ADO = ∠AOD = ∠DAO = 60°
∆AOD is an equilateral triangle.

Question 42.
In the given figure, I is the incentre of ∆ABC. BI when produced meets the circum circle of ∆ABC at D.
Given ∠BAC = 55° and ∠ACB = 65°; calculate:
(i) ∠DCA,
(ii) ∠DAC,
(iii) ∠DCI,
(iv) ∠AIC

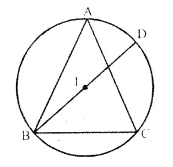
Solution:

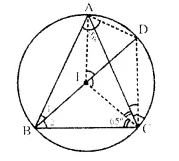
Join AD, DC, AI and Cl,
In ∆ABC,
∠BAC = 55°, ∠ACB = 65°
∠ABC = 180° – (∠BAC + ∠ACB) = 180°- (55° + 65°) = 180° – 120° = 60°
In cyclic quad. ABCD,
∠ABC + ∠ADC = 180°
⇒ 60° + ∠ADC = 180°
∠ADC = 180° – 60°= 120°
In ∆ADC,
∠ DAC + ∠ DCA + ∠ ADC = 180°
⇒ ∠ DAC+ ∠ DCA + 120° = 180°
⇒ ∠ DAC+ ∠ DCA = 180° – 120° = 60°
But ∠ DAC = ∠ DCA (I lies on the bisector of ∠ ABC)
∠ DAC = ∠ DCA = 30°
DI is perpendicular bisector of AC
∠ AIC = ∠ ADC= 120°
IC is the bisector of ∠ ACB
∠ ICA = \(\frac { 65 }{ 2 }\) = 32.5°
∠DCI = ∠DCA + ∠ACI = 30° + 32.5° = 62.5° = (62.5)° = 60° 30′.

Question 43.
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circum circle of the triangle at points P, Q and R respectively. Prove that:
(i) ∠ ABC = 2 ∠ APQ,
(ii) ∠ ACB = 2 ∠ APR,
(iii) ∠ QPR = 90° – \(\frac { 1 }{ 2 }\) ∠BAC.

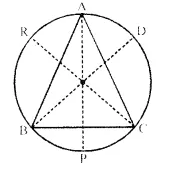
Solution:
Given- ∆ABC is inscribed in a circle. Bisectors of ∠BAC, ∠ABCand ∠ACB meet the circumcircle of the∆ABC at P, Q and R respectively.

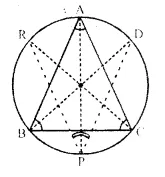
To Prove-
(i) ∠ ABC = 2 ∠APQ.
(ii) ∠ ACB = 2 ∠ APR.
(iii) ∠ QPR = 90° – \(\frac { 1 }{ 2 }\) ∠BAC.
Construction-
Join PQ and PR.
Proof- ∠ABQ and ∠APQ are in the same segment of the circle.
∠ ABQ = ∠ APQ
But ∠ ABQ = – ∠ ABC (BQ is the angle bisector of ∠ ABC)
\(\frac { 1 }{ 2 }\) ∠ ABC = ∠ APQ
Or ∠ ABC = 2 ∠APQ …,(i)
Similarly, ∠ APR and ∠ ACR are in the same segment of the circle.
∠ APR = ∠ ACR
But ∠ ACR = \(\frac { 1 }{ 2 }\) ∠ ACB (CR is the angles bisector of ∠ ACB)
\(\frac { 1 }{ 2 }\) ∠ ACB = ∠ APR
Or ∠ ACB = 2 ∠ APR ….(ii)
Adding (i) and (ii)
∠ ABC + ∠ ACB = 2 ∠ APQ + 2∠ APR = 2 (∠ APQ + ∠ APR) = 2 ∠ PQR
Or 2 ∠ PQR = ∠ ABC + ∠ ACB
∠ PQR = \(\frac { 1 }{ 2 }\) (∠ ABC + ∠ ACB) ….(iii)
But ∠ ABC + ∠ ACB + ∠ BAC = 180° (Angles of a triangle)
∠ ABC + ∠ ACB = 180° – ∠ BAC ….(iv)
from (iii) and (iv) we get,
∠ PQR = \(\frac { 1 }{ 2 }\) (180° – ∠ BAC) = 90° – \(\frac { 1 }{ 2 }\) ∠ BAC

Question 44.
Calculate the angles x, y and z if :

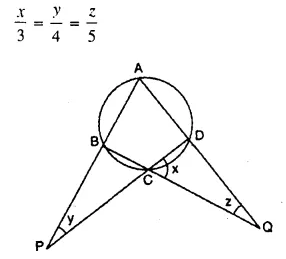
Solution:

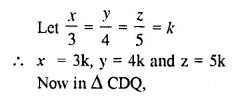
Ext. ∠ ADC = x + z ….(i)
and in ΔBPC,
Ext. ∠ ABC = y + x ….(ii)
(∠ BCP = ∠ DCQ = x vertically opposite angles)

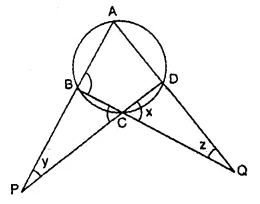
Adding (i) and (ii),
x + z + y + x = ∠ ADC + ∠ ABC.
But ∠ ADC + ∠ ABC = 180° (opposite angles of a cyclic quad)
2x + y + z = 180°
⇒ 2 x 3k + 4k + 5k = 180°
⇒ 6k + 4k + 5k = 180°
⇒ 15k = 180°
⇒ k = 12°
x = 3k = 3 x 12° = 36°= x = 36°
y = 4k = 4 x 12° = 48°= y = 48°
z = 5k = 5 x 12° = 60° = z = 60°

Question 45.
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
(i) Angle ABC
(ii) Angle BEC [1995]

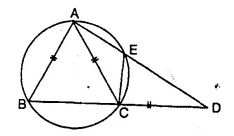
Solution:
In the figure, AB = AC = CD, ∠ ADC = 38°
BE is joined.
In ΔACD, AC = CD
∠CAD = ∠CDA = 38°
Ext. ∠ ACB = ∠ CAD + ∠ CDA = 38° + 38° = 76°

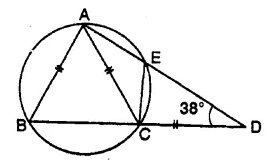
But in ΔABC,
AB = AC (given)
∠ ABC = ∠ ACB = 76°
and ∠ BAC =180° – (76° + 76°) = 180° – 152° = 28°

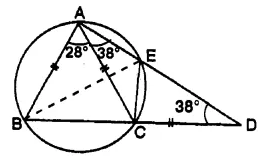
But ∠ BEC = ∠ BAC (Angles in the same segment)
∠BEC = 28°.

Question 46.
In the given figure. AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x. [1996]

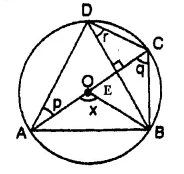
Solution:
Arc subtends ∠ AOB at the centre and ∠ACB at the remaining part of the circle.
∠ AOB = 2 ∠ ACB
⇒ x = 2q ⇒ q = \(\frac { x }{ 2 }\)
But ∠ ADB and ∠ ACB are in the same segment
∠ ADB = ∠ ACB – q
Now in ΔAED,
p + q + 90° = 180° (sum of angles of a Δ)
⇒ p + q = 90°
⇒ p = 90° – q
⇒ p = 90° – \(\frac { x }{ 2 }\)
Arc BC subtends ∠ BOC at the centre and ∠ ADC at the remaining part of the circle
∠BOC = 2 ∠BDC = 2r.
r = \(\frac { 1 }{ 2 }\) ∠ BOC = \(\frac { 1 }{ 2 }\) (180° – x)
(∠ AOB + ∠ BOC = 180°)
r = 90° – \(\frac { 1 }{ 2 }\) x. = 90° – \(\frac { x }{ 2 }\)

Question 47.
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠ AOB = 80° and ∠ ACE = 10°. Calculate:
(i) Angle BEC,
(ii) Angle BCD,
(iii) Angle CED. [1998]

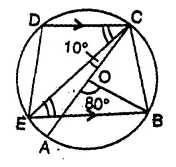
Solution:
Arc AB subtends ∠ AOB at the centre and ∠ACB at the remaining part of the circle.
∠ ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 80° = 40°
But ∠ BOC + ∠ AOB = 180° (A linear pair)
∠ BOC + 80° = 180°
⇒ ∠ BOC = 180° – 80° = 100°
(i) Arc BC subtends ∠ BOC at the centre and ∠ BEC at the remaining part of the circle
∠ BEC = \(\frac { 1 }{ 2 }\) ∠ BOC = \(\frac { 1 }{ 2 }\) x 100° = 50°
(ii) EB || DC
∠ DCE = ∠ BEC (Alternate angles) = 50°
∠ BCD = ∠ BCA + ∠ ACE + ∠ ECD = 40° + 10° + 50° = 100°
(iii) In cyclic quad. CDE,
∠ BED + ∠ BCD = 180°
⇒ ∠ BEC + ∠ CED + ∠ BCD = 180°
⇒ 50° + ∠ CED + 100° = 180° (Proved in (i) and (ii))
⇒ ∠ CEb + 150° = 180°
∠ CED = 180° – 150° = 30°.

Question 48.
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ ABC + ∠ CDE. Give reasons for your answer. [1998]

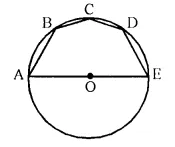
Solution:

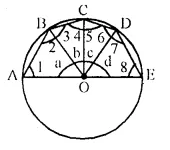
Join OA, OB, OC, OD.
In ΔOAB,
OA = OB (Radii of the same circle)
∠ 1 = ∠ 2
Similarly we can prove that
∠3 = ∠4,
∠5 = ∠6,
∠7 = ∠8
In A OAB,
∠1 + ∠2 + ∠a = 180° (Angles of a triangle)
Similarly ∠3 + ∠4 + ∠b = 180°
∠5 + ∠6 + ∠c = 180°
∠7 + ∠8 + ∠d = 180°
Adding we get
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 + ∠a + ∠b + ∠c + ∠d = 4 x 180° = 720°
⇒∠2 + ∠2 + ∠3 + ∠3 + ∠6 + ∠6+ ∠ 7 + ∠7 + ∠a + ∠b + ∠c + ∠d = 720°
⇒ 2 ∠2 + 2 ∠3 + 2 ∠6 + 2 ∠7 + ∠a + ∠ b + ∠ c + ∠ d = 720°
⇒ 2 [∠2 + ∠3] + 2 [∠6 + ∠7| + 180° = 720° ( ∠a + ∠b + ∠c + ∠d = 180°)
⇒ 2 ∠ ABC + 2 ∠ CDE = 720° – 180° = 540°
⇒ 2 (∠ ABC + ∠ CDE) = 540°
⇒ ∠ ABC + ∠ CDE = 270°

Question 49.
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠ CBE = 64°, calculate ∠ DEC. [1991]

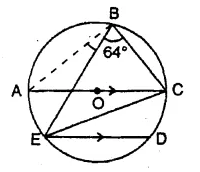
Solution:
Join AB.
AOC is the diameter
∠ ABC = 90° (Angle in a semi circle)
⇒ ∠ ABE + ∠ CBE = 90°
⇒ ∠ ABE + 64° = 90°
∠ ABE = 90° – 64° = 26° …(i)
AC || ED
∠ DEC = ∠ ACE (alternate angles)
But ∠ ACE = ∠ ABE (Angles in the same segment)
∠ DEC = ∠ ABE = 26° [from (i)]

Question 50.
Use the given figure to find :
(i) ∠ BAD,
(ii) ∠ DQB. [1987]

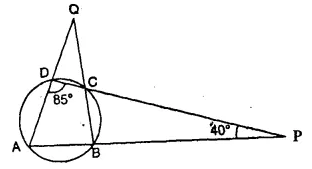
Solution:
In ΔAPD,
∠ ADP + ∠ DPA + ∠ PAD = 180°
85° + 40° + ∠ PAD = 180°
∠ PAD = 180° – (85° + 40°) = 180° – 125° = 55° or ∠ BAD = 55°
In cyclic quad. ABCD,
∠ ADC + ∠ ABC = 180°
85° + ∠ ABC = 180°
∠ ABC = 180° – 85° = 95°
Now, in ΔAQB,
∠ QAB + ∠ ABC + ∠ BQA = 180°
⇒ 55° + 95° + ∠ BQA = 180°
⇒ 150° + ∠ BQA = 180°
⇒ ∠DQB = ∠ BQA = 180° – 150° = 30°

Question 51.
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = x°; find (in terms of x) the values of:
(i) ∠ COB,
(ii) ∠DOC,
(iii) ∠DAC,
(iv) ∠ADC. [1991]

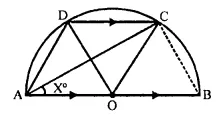
Solution:
Join CB.
In ΔAOC,
OA = OC (radii of the same circle)
∠ OCA = 4 OAC = x
Ext. ∠ COB = ∠ OAC + ∠ OCA = x + x = 2x
In ΔACB, ∠ ACB = 90° (Angle in semi circle)
∠ OBC = 90° – ∠ OAC = 90° – x
In cyclic quad. ABCD,
∠ ABC + ∠ ADC = 180°
⇒ ∠OBC + ∠ADC =180°
⇒ (90 – x) + 4 ADC = 180°
∠ADC = 180° – 90° + x = 90° + x
DC || AB
∠ DCO = ∠ COB = 2x (alternate angle)
And ∠ DCA = ∠ CAB = x (alternate angles)
In ΔADC,
∠ DAC + ∠ DCA + ∠ ADC = 180°
∠ DAC + x + 90 + x = 180°
2x + 90° + ∠ DAC = 180°
∠ DAC = 180° – 90° – 2x = 90° – 2x
In ΔOCD,
∠ DOC + ∠ OCD + ∠ CDO = 180°
∠ DOC + 2x + 2x = 180°
∠ DOC = 180° – 4x
Hence ∠ COB = 2x,
∠ DOC = 180° – 4x
∠ DAC = 90° – 2x
and ∠ ADC = 90° + x

Question 52.
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find :
(i) ∠DAB
(ii) ∠DBA

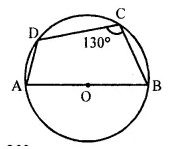
Solution:
Join DB
(i) ∠DAB + ∠DCB = 180° [Opposite angles of a cyclic quadrilateral are supplementary]
∠DAB = 180° – 130° = 50°

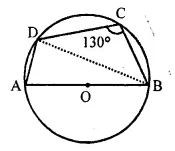
(ii) In ΔADB,
∠ADB = 90° [Angle in a semi-circle is 90°]
So, ∠DBA = 180° – (∠DAB + ∠ADB) = 180° – (50° + 90°) = 40°

Question 53.
In the given figure, PQ is a diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS. [1992]

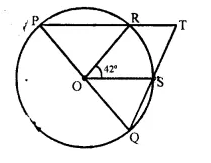
Solution:
In ΔOPR, OR = OP (radii of the same circle)
∠ OPR = ∠ ORP = x (Say)
∠POR = 180° – 2x
Similarly in ΔOQS,
OS = OQ
∠ OSQ = ∠ SQO = y (say)
∠ SOQ = 180° – 2y
POQ is a straight line,
∠ POR + ∠ ROS + ∠ SOQ = 180°
⇒ 180° – 2x + 42° + 180° – 2y = 180°
⇒ 222° – 2x – 2y = 0
⇒ 2 (x + y) = 222°
x + y = 111° ….(i)
In. ΔPQT,
⇒ ∠P + ∠Q + ∠T = 180°
⇒ ∠ OPR + ∠ SQO + ∠ RTS = 180°
⇒ x + y + ∠RTS = 180°
⇒ ∠ RTS = 180° – (x + y) = 180° – 1110 [From(i)] = 69°

Question 54.
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠ PQR = 58°, Calculate:
(i) ∠RPQ,
(ii) ∠STP. [1989]

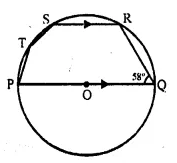
Solution:

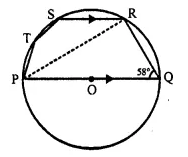
Join PR,
In ΔPQR,
∠ PRQ = 90° (Angle in a semi-circle)
∠ RPQ + ∠ RQP = 90°
⇒ ∠RPQ + 58° = 90°
⇒ ∠RPQ = 90° – 58° = 32°
SR || PQ (given)
∠ SRP = ∠ RPQ (Alternate angles) = 32° [from(i)]
Now, in cyclic quad. PRST,
∠ STP + ∠ SRP = 180°
⇒ ∠STP + 32° = 180°
⇒ ∠STP = 180° – 32° = 148°

Question 55.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60°. Calculate the numerical values of: [1987]
(i) ∠ ABD
(ii) ∠ DBC
(iii) ∠ ADC

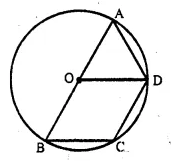
Solution:

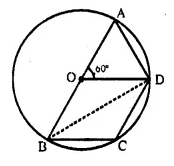
Join BD,
Arc AD, subtends ∠ AOD at the centre and ∠ ABD at the remaining part of the circle
∠ ABD = \(\frac { 1 }{ 2 }\) ∠ AOD = \(\frac { 1 }{ 2 }\) x 60° = 30°
In ΔOBD,
OB = OD (Radii of the same circle)
∠ ODB = ∠ OBD = ∠ ABD = 30°
OD||BC (given)
∠ ODB = ∠ DBC (Alternate angles)
∠ DBC = ∠ ODB = 30° .
Again OD || BC
∠ AOD = ∠ OBC (Corresponding angles)
⇒ ∠ OBC = ∠ AOD = 60°
Now, in cyclic quad. ABCD,
∠ ADC+ ∠ ABC = 180°
⇒ ∠ ADC + 60° = 180°
⇒ ∠ ADC = 180° – 60° = 120°

Question 56.
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠ APB = 75° and ∠ BCD = 40°. find:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB. [1984]

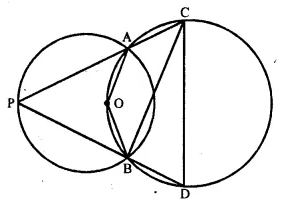
Solution:

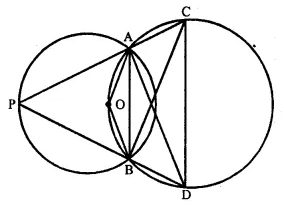
Join AB, AD.
(i) Arc AB of the smaller circle subtends ∠ AOB at the centre and ∠ APB at the remaining part of the circle.
∠ AOB = 2 ∠ APB = 2 x 75° = 150°
(ii) OACB is a cyclic quad.
∠AOB + ∠ACB = 180°
⇒ 150° + ∠ACB = 180°
⇒ ∠ACB = 180° – 150° = 30°
(in) Again, ABDC is a cyclic quad,
∠ ABD + ∠ ACD = 180°
⇒ ∠ABD + (30° + 40°) = 180° (∠ ACD = ∠ ACB + ∠ BCD)
⇒ ∠ ABD + 70° = 180°
⇒ ∠ ABD = 180° – 70° = 110°
(iv) ∠ ACB and ∠ADB are in the same segment
∠ ADB = ∠ ACB = 30°

Question 57.
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find :
(i) ∠BCD
(ii) ∠ACB
Hence, show that AC is a diameter.

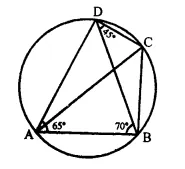
Solution:
In circle ABCD is a cyclic quadrilateral AC andBD are joined.
∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°
ABCD is a cyclic quadrilateral
65° + ∠BCD = 180°
⇒ ∠BCD = 180° – 65° = 115°
Arc AB subtends ∠ABD and ∠ACD in the same segment
∠ACD = ∠ABD = 70° (∠ABD = 70°)
∠ACB = ∠BCD – ∠ACD = 115° – 70° = 45°
But arc AB subtends ∠ADB and ∠ACD in the same segment
∠ADB = ∠ACB = 45°
∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°
Now in segment ADC,
∠ADC = 90°
Segment ADC is a semi-circle
Hence AC is the diameter of the circle.
Hence proved.

Question 58.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
Solution:
In a cyclic quadrilateral ABCD,
∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5
Let ∠A = 3x, ∠C = x,
But ∠A + ∠C = 180° (Opposite angles of a cyclic quadrilateral)
⇒ 3x + x = 180°
⇒ 4x = 180°
⇒ x = 45°
∠A = 3x = 3 x 45° = 135°
∠C = x = 45°
∠B = ∠D = 1 : 5
Similarly, Let ∠B = y and ∠D = 5y
But ∠B + ∠D = 180°
y + 5y = 180°
⇒ 6y = 180°
⇒ y = 30°
∠B = y = 30°
and ∠D = 5y = 5 x 30° = 150°
Hence ∠A = 135°, ∠B = 30°, ∠C = 45° and ∠D = 150°
Hence Proved.

Question 59.
The given figure shows a circle with centre O and ∠ABP = 42°. Calculate the measure of:
(i) ∠PQB
(ii) ∠QPB + ∠PBQ

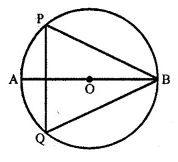
Solution:
In the figure
∠ABP = 42°.
Join PO, QO
Arc PA subtends ∠POA at the centre and ∠PBA at the remaining part.
∠POA = 2 ∠PBA = 2 x 42° = 84°
But ∠AOP + ∠BOP = 180° (Linear pair)
⇒ ∠POA+ ∠POB = 180°
⇒ 84° + ∠POB = 180°
⇒ POB = 180° – 84° = 96°
Similarly, arc BP subtends ∠BOP on the centre and ∠PQB at the remaining part of the circle
∠PQB = \(\frac { 1 }{ 2 }\) ∠POB = \(\frac { 1 }{ 2 }\) x 96° = 48°
But in ΔPBQ,
∠QPB + ∠PBQ + ∠PQB = 180° (Angles of a triangle)
∠QPB + ∠PBQ + 48° =180°
⇒ ∠QPB + ∠PBQ = 180°
⇒ ∠QPB + ∠PBQ = 180° – 48° = 132
Hence (i) PQB = 48° and
(ii) ∠QPB + ∠PBQ = 132°

Question 60.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y:

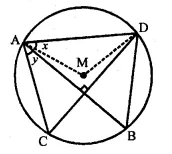
(i) express ∠AMD in terms of x.
(ii) express ∠ABD in terms of y.
(iii) prove that: x = y.
Solution:
In the figure, M is the centre of the circle chords AB and CD are perpendicular to each other at L.
∠MAD = x and ∠BAC = y
(i) In ΔAMD,
AM = DM (Radii of the same circle)
∠MDA = ∠MAD (Angles opposite to equal sides) = x
But, in ΔAMD,
∠MAD + ∠MDA + ∠AMD = 180° (Sum of angles of a triangle)
⇒ x + x + ∠AMD = 180°
⇒ 2x + ∠AMD = 180°
⇒ ∠AMD = 180°
∠AMD = 180° – 2x
(ii) Arc AD subtends ∠AMD at the circle and ∠ABD at the remaining part of the circle
∠AMD = 2∠ABD
⇒ ∠ABD = \(\frac { 1 }{ 2 }\) ∠ABD = \(\frac { 1 }{ 2 }\) [180°- 2x] = 90° – x
AB ⊥s CD
∠ALC = 90°
In ΔALC,
∠LAC + ∠LCA = 90°
⇒ ∠BAC + ∠DAC = 90°
⇒ y = ∠DAC = 90°
⇒ ∠DAC = 90° – y
But ∠DAC ∠ABD (Angles in the same segment)
∠ABD = 90° – y
But ∠ABD = 90° – x, Proved
90°- x = 90°- y
⇒ ∠x = yHence proved.

Question 61.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
Solution:
Given : In circle with centre O,
ABCD is cyclic quadrilateral in which CD is equal radius of the circle and AB is diameter.
CD = \(\frac { 1 }{ 2 }\) AB
AD and BC are produced to meet at P.
To prove: ∠APB = 60°
Construction : Join DO, CO and PB
In ΔDOC,
DO = CO = DC (Radii of the circle)
ΔDOC is an equilateral triangle
∠DOC = 60° ….(i)
Now, arc DC subtends ∠DOC at the centre arc ∠DBC at the remaining part of the circle
∠DBC = \(\frac { 1 }{ 2 }\) ∠DOC = \(\frac { 1 }{ 2 }\) x 60° = 30° …(ii)
But ∠ADB = 90° (Angle in a semi-circle)
∠PDB = 90° (∠PDB x ∠ADB = 180°, Linear pair)
Now in ΔPDB,
∠PDB = 90° (Proved)
⇒ ∠DPB = ∠DBC = 90°
⇒ ∠DPB + 30° = 90°
⇒ ∠DPB = 90° – 30° = 60°
⇒ APB = 60°
Hence proved.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.