Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

Question 1.
In the given circle with diameter AB, find the value of x. (2003)

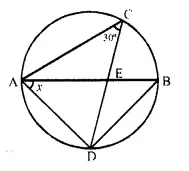
Solution:

∠ABD = ∠ACD = 30° (Angle in the same segment)
Now in ∆ ADB,
∠BAD + ∠ADB + ∠DBA = 180° (Angles of a ∆)
But ∠ADB = 90° (Angle in a semi-circle)
∴ x + 90° + 30° = 180°
⇒ x + 120° = 180°
∴ x = 180°- 120° = 60°

Question 2.
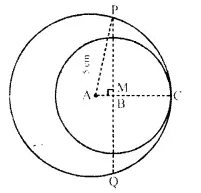
In the given figure, O is the centre of the circle with radius 5 cm, OP and OQ are perpendiculars to AB and CD respectively. AB = 8cm and CD = 6cm. Determine the length of PQ.

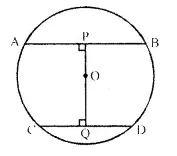
Solution:

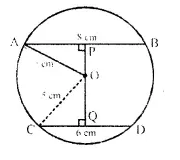
Radius of the circle whose centre is O = 5 cm
OP ⊥ AB and OQ ⊥ CD, AB = 8 cm and CD = 6 cm.
Join OA and OC, then OA = OC=5cm.
∴ OP ⊥ AB
∴ P is the mid-point of AB.
Similarly, Q is the mid-point of CD.
In right ∆OAP,
OA² = OP² + AP² (Pythagorous theoram)
⇒ (5)² =OP² +(4)² ( ∵ AP = AB = \(\frac { 1 }{ 2 }\) x 8 = 4cm)
⇒ 25 = OP² + 16
⇒ OP³ = 25 – 16 = 9 = (3)²
∵ OP = 3 cm
Similarly, in right ∆ OCQ,
OC² = OQ² + CQ²
⇒ (5)² =OQ²+(3)² (∵ CQ = CD = \(\frac { 1 }{ 2 }\) x 6 = 3cm)
⇒ 25 = OQ² + 9
⇒ OQ³ = 25 – 9 = 16 = (4)²
∴ OQ = 4 cm
Hence, PQ = OP + OQ = 3-4 = 7 cm.

Question 3.
The given figure shows two circles with centres A and B; and radii 5cm and 3cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

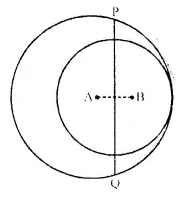
Solution:

Join AP and produce AB to meet the bigger circle at C.
AB = AC – BC = 5 cm – 3 cm = 2 cm.
But, M is the mid-point of AB
∴ AM = \(\frac { 2 }{ 2 }\) = 1cm.
Now in right ∆APM,
AP2 = MP2 + AM2 (Pythagorous theorem)
⇒ (5)² = MP² -1- (1 )²
⇒ 25 = MP: + 1
⇒ MP: = 25 – 1 = 24

Question 4.
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.

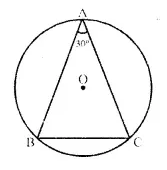
Solution:

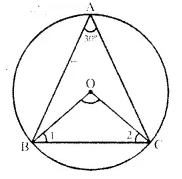
Given: In the figure ABC is a triangle in winch ∠A = 30°
To Prove: BC is the radius of circumcircle of ∆ABC whose O is the centre.
Const: Join OB and OC.
Proof: ∠BOC is at the centre and ∠BAC is at the remaining part of the circle
∴ ∠BOC = 2 ∠BAC = 2 x 30° = 60°
Now in ∆OBC,
OB = OC (Radii of the same circle)
∴ ∠OBC = ∠OCB
But ∠OBC + ∠OCB + ∠BOC – 180°
∠OBC + ∠OBC + 60°- 180°
⇒ 2 ∠OBC = 180°- 60° = 120°
⇒ ∠OBC = \(\frac { { 120 }^{ circ } }{ 2 }\) = 60°
∴ ∆OBC is an equilateral triangle.
∴ BC = OB = OC
But OB and OC are the radii of the circumcircle
∴ BC is also the radius of the circumcircle.

Question 5.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Solution:

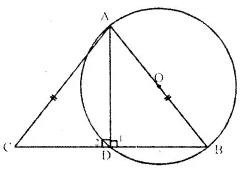
Given: In ∆ABC, AB-AC and a circle with AB as diameter is drawn which intersects the side BC and D.
To Prove: D is the mid point of BC.
Const: Join AD.
Proof: ∠ 1 = 90° (Angle in a semi-circle)
But ∠ 1 + ∠ 2 – 180° (Linear pair)
∴ ∠ 2 = 90°
Now, in right ∆ ABD and ∆ ACD,
Hyp. AB – Hyp. AC (Given)
Side AD – AD (Common)
∴ ∆ABD = ∆ACD (RHS criterion of congruency)
∴ BD = DC (c.p.c.t.)
Hence D is he mid point of BC. Q.E.D.

Question 6.
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.

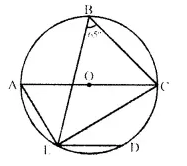
Solution:
Join OE,
Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∴ ∠EOC = 2 ∠EBC = 2 x 65° = 130°
Now, in ∆OEC, OE = OC (radii of the same circle)
∴ ∠OEC = ∠OCE
But ∠ OEC + ∠ OCE + ∠ EOC = 180°
⇒ ∠ OCE + ∠ OCE + ∠ EOC = 180°

Question 7.
Chords AB and CD of a circle intersect each other at point P, such that AP = CP. S.how that AB = CD.

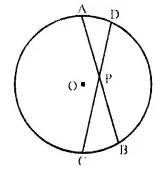
Solution:
Given: Two chords AB and CD intersect each other at P inside the circle with centre O and AP = CP.

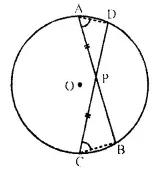
To Prove: AB = CD.
Proof: ∵ Two chords AB and CD intersect each other inside the circle at P.
∴ AP x PB = CP x PD ⇒ \(\frac { AP}{ CP }\) = \(\frac { AD }{ PB }\)
But AP = CP ….(i) (given)
∴ PD = PB or PB = PD …,(ii)
Adding (i) and (ii),
AP + PB = CP + PD
⇒ AB = CD Q.E.D.

Question 8.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Solution:
Given: ABCD is a cyclic quadrilateral and PRQS is a quadrilateral formed by the angle bisectors of angle ∠A, ∠B, ∠C and ∠D.
To Prove: PRQS is a cyclic quadrilateral.
Proof: In ∆APD,

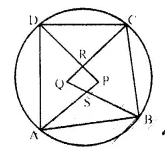
∠1 +∠2 + ∠P= 180° ,…(i)
Similarly, in ∆BQC.
∠3 + ∠4 + ∠Q= 180° ….(ii)
Adding (i) and (ii), we get:
∠1 + ∠2 + ∠P + ∠3 + ∠4 ∠Q = 180° + 180° = 360°
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠P + ∠Q = 360° ..(iii)
But ∠1+∠2+∠3+∠4 = \(\frac { 1 }{ 2 }\) (∠A+∠B+∠C+∠D)
= \(\frac { 1 }{ 2 }\) x 360°= 180°
∴ ∠P + ∠Q = 360° – 180° = 180° [From (iii)]
But these are the sum of opposite angles of quadrilateral PRQS
∴ Quad. PRQS is a cyclic quadrilateral. Q.E.D.

Question 9.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate:
(I) ∠BDC
(ii) ∠BEC
(iii) ∠BAC (2014)

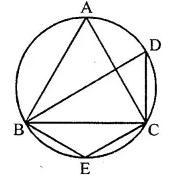
Solution:
∠DBC = 58°
BD is diameter
∴ ∠DCB=90° (Angle in semi circle)

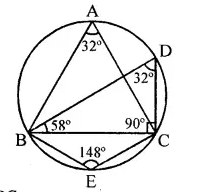
(i) In ∆BDC
∠BDC + ∠DCB + ∠CBD = 180°
∠BDC = 180°- 90° – 58° = 32°
(ii) ∠BEC =180°-32°
(opp. angle of cyclic quadrilateral)
= 148°
(iii) ∠BAC = ∠BDC = 32°
(Angles in same segment)

Question 10.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Solution:

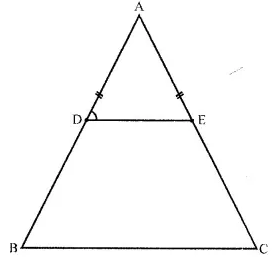
Given: In ∆ABC, AB = AC and D and E are points on AB and AC such that AD = AE, DE is joined.
To Prove: B,C,E,D. are concyclic.
Proof: In ∆ABC, AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides)
Similarly in ∆ADE, AD = AE (given)
∴ ∠ADE = ∠AED
In ∆ABC,
∵ \(\frac { AP }{ AB }\) = \(\frac { AE }{ AC }\)
∴ DE || BC.
∴ ∠ADE = ∠B (Corresponding angles)
But ∠B = ∠C (Proved)
∴ Ext. ∠ADE = its interior opposite ∠C.
∴ BCED is a cyclic quadrilateral.
Hence B,C, E and D are concyclic.

Question 11.
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE’= 20°; determine ∠BCD. Give reason in support of your answer.

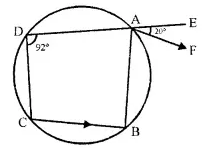
Solution:

In cyclic quad. ABCD,
AF || CB and DA is produced to E such that
∠ADC = 92° and ∠FAE – 20°
Now, we have to find the measure of ∠BCD In cyclic quad. ABCD,
∠B – ∠D = 180° ⇒ ∠B + 92° = 180″
⇒∠B = 180°-92° = 88°
∵ AF || CB.
∴∠FAB = ∠B = 88°
But ∠FAE – 20° (Given)
Ext. ∠BAE – ∠BAF + ∠FAE
= 88° + 20° = 108°
But Ext. ∠BAE – ∠BCD
∴ ∠BCD = 108°

Question 12.
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC – 80°, calculate
(i) ∠DBC,
(ii) ∠IBC,
(iii) ∠BIC.

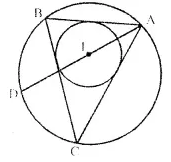
Solution:

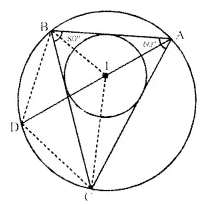
Join DB and DC, IB and IC.
∠BAC = 66°, ∠ABC = 80°. I is the incentre of the ∆ABC.
(i) ∵ ∠DBC and ∠DAC are in the same segment
∴ ∠DBC – ∠DAC.
But ∠DAC = \(\frac { 1 }{ 2 }\)∠BAC = \(\frac { 1 }{ 2 }\) x 66° = 33°
∴ ∠DBC = 33°.
(ii) ∵ I is the incentre of ∆ABC.
∴ IB bisect ∠ABC
∴ ∠ IBC = \(\frac { 1 }{ 2 }\) ∠ABC = \(\frac { 1 }{ 2 }\) x 80° = 40°.
(iii) ∴∠BAC = 66° ∠ABC = 80°
∴ In ∆ABC,
∠ACB = 180° – (∠ABC + ∠CAB)
= 180°-(80°+ 66°)= 180°- 156° = 34°
∵ IC bisects the ∠C
∴ ∠ ICB = \(\frac { 1 }{ 2 }\) ∠C = \(\frac { 1 }{ 2 }\) x 34° = 17°.
Now in ∆IBC,
∠ IBC + ∠ ICB + ∠ BIC = 180°
⇒ 40° + 17° + ∠BIC = 180°
⇒ ∠ BIC = 180° – (40° + 17°) = 180° – 57°
= 123°

Question 13.
In the given figure, AB = AD = DC= PB and ∠DBC = x°. Determine in terms of x :
(i) ∠ABD
(ii) ∠APB

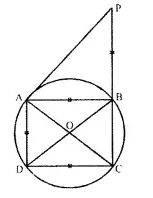
Hence or otherwise prove that AP is parallel to DB.
Solution:
Given: In figure, AB = AD = DC = PB.
∠DBC = x. Join AC and BD.
To Find : the measure of ∠ABD and ∠APB.
Proof: ∠DAC=∠DBC= x(angles in the same segment)
But ∠DCA = ∠DAC (∵ AD = DC)
= x
But ∠ABD = ∠DAC (Angles in the same segment)
In ∆ABP, ext. ∠ABC = ∠BAP + ∠APB
But ∠ BAP = ∠APB (∵ AB = BP)
2 x x = ∠APB + ∠APB = 2∠APB
∴ 2∠APB = 2x
⇒ ∠APB = x
∵ ∠APB = ∠DBC = x
But these are corresponding angles
∴ AP || DB. Q.E.D.

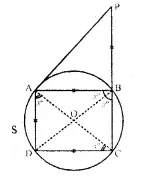
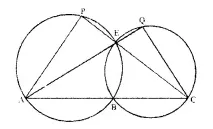
Question 14.
In the given figure, ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.

Solution:
Given: In the figure, ABC, AEQ and CEP are straight lines.
To prove: ∠APE + ∠CQE = 180°.
Const: Join EB.
Proof: In cyclic quad. ABEP,
∠APE+ ∠ABE= 180° ….(i)
Similarly in cyclic quad. BCQE

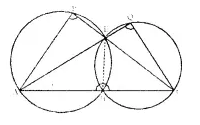
∠CQE +∠CBE = 180° ….(ii)
Adding (i) and (ii),
∠APE +∠ABE + ∠CQE +∠CBE = 180° + 180° = 360°
⇒ ∠APE + ∠CQE + ∠ABE + ∠CBE = 360°
But ∠ABE + ∠CBE = 180° (Linear pair)
∴ ∠APE + ∠CQE + 180° = 360°
⇒ ∠APE + ∠CQE = 360° – 180° = 180°
Hence ∠APE and ∠CQE are supplementary. Q.E.D.

Question 15.
In the given figure, AB is the diameter of the circle with centre O.

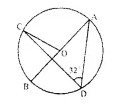
If ∠ADC = 32°, find angle BOC.
Solution:
Arc AC subtends ∠AOC at the centre and ∠ ADC at the remaining part of the circle

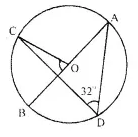
∴ ∠AOC = 2 ∠ADC
= 2 x 32° = 64°
∵ ∠AOC + ∠ BOC = 180° (Linear pair)
⇒ 64° + ∠ BOC = 180°
⇒ ∠ BOC=180° – 64° =116° .

Question 16.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A : whereas sides PQ and SR produced meet at point B.
If ∠ A : ∠ B = 2 : 1 ; find angles A and B.
Solution:
PQRS is a cyclic-quadrilateral in which ∠ PQR =135°
Sides SP and RQ are produced to meet at A and sides PQ and SR are produced to meet at B.

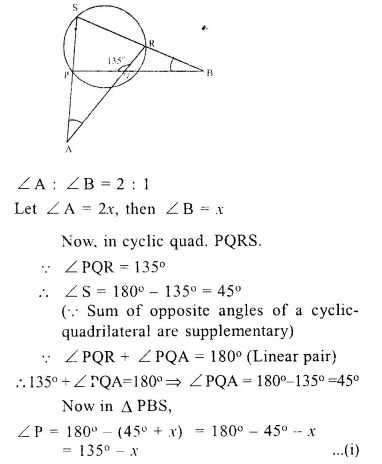
Question 17.
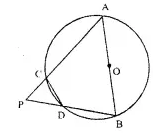
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA. If AC produced and BD produced meet at point P ; show that ∠ APB = 60°.

Solution:
Given : In the figure, AB is the diameter of the circle with centre O.
CD is the chord with length equal to the radius OA.
AC and BD are produced to meet at P.
To prove : ∠ APB = 60°
Const : Join OC and OD
Proof : ∵ CD = OC = OD (Given)
∴ ∆OCD is an equilateral triangle
∴ ∠ OCD = ∠ ODC = ∠ COD = 60°
In ∆ AOC, OA = OC (Radii of the same circle)
∴ ∠ A = ∠ 1
Similarly, in ∆ BOD,
OB = OD
∴∠2= ∠B
Now in cyclic quadrilateral ACDB,
∠ A CD + ∠B = 180°

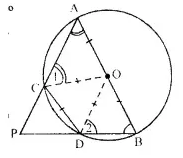
∠60°+ ∠ 1 + ∠B = 180°
= ∠ 1 + ∠B = 180° – 60°
⇒∠ 1 + ∠B = 120°
But ∠ 1 = ∠ A
∴ ∠ A + ∠B = 120° …(i)
Now, in ∆ APB,
∠ P + ∠ A + ∠ B = 180° (Sum of angles of a triangle)
⇒ ∠P+120°=180° [From (i)]
⇒ ∠P = 180°- 120°= 60°
Hence ∠ P = 60° or ∠ APB = 60° Hence proved.

Question 18.
In the following figure,

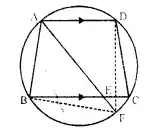
ABCD is a cyclic quadrilateral in which AD is parallel to BC.
If the bisector of angle A meets BC at point E and the given circle at point F, prove that :
(i) EF = FC
(ii) BF = DF
Solution:

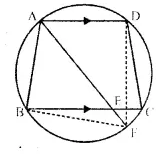
Given : ABCD is a cyclic quadrilateral in which AD || BC.
Bisector of ∠ A meets BC at E and the given circle at F. DF and BF are joined.
To prove :
(i) EF = FC
(ii) BF = DF
Proof : ∵ ABCD is a cyclic -quadrilateral and AD || BC
∵ AF is the bisector of ∠ A
∴ ∠ BAF = ∠ DAF
∴ Arc BF = Arc DF (equal arcs subtends equal angles)
⇒ BF = DF(equal arcs have equal chords)
Hence proved

Question 19.
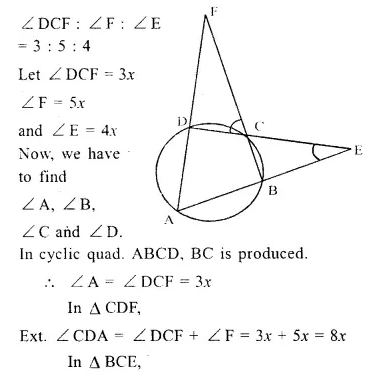
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E ; whereas sides BC and AD produced meet at point F. If ∠ DCF : ∠ F : ∠ E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Solution:
Given : In a circle, ABCD is a cyclic quadrilateral AB and DC are produce to meet at E and BC and AD are produced to meet at F.

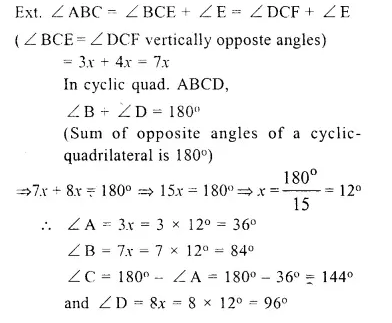
Question 20.
The following figure shows a circle with PR as its diameter.

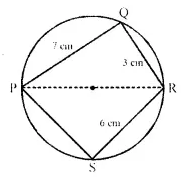
If PQ = 7 cm, QR = 3 cm, RS = 6 cm. find the perimeter of the cyclic quadrilateral PQRS. (1992)
Solution:
In the figure, PQRS is a cyclic quadrilateral in which PR is a diameter
PQ = 7 cm,
QR = 3 RS = 6cm
∴ 3 RS = 6cm
and RS = \(\frac { 6 }{ 3 }\) = 2cm
Now in ∆ PQR,
∠ Q = 90° (Angle in a semi-circle)
∴ PR² = PQ² + QR² (Pythagoras theorem)
= (7)² + (6)² = 49 + 36 = 85
Again, in right ∆ PSQ, PR² = PS² + RS²
⇒ 85 = PS² + (2)²
⇒ 85 = PS² + 4
⇒ PS² = 85 – 4 = 81 = (9)²
∴ PS = 9cm
Now, perimeter of quad. PQRS = PQ + QR + RS + SP = (7 + 9 + 2 + 6) cm = 24cm

Question 21.
In the following figure, AB is the diameter of a circle with centre O.

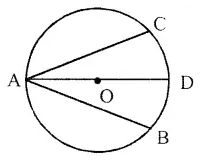
If chord AC = chord AD, prove that :
(i)arc BC = arc DB
(ii) AB is bisector of ∠ CAD. Further, if the length of arc AC is twice the length of arc BC, find :
(a) ∠ BAC
(b) ∠ ABC
Solution:
Given : In a circle with centre O, AB is the diameter and AC and AD are two chords such that AC = AD.
To prove : (i) arc BC = arc DB
(ii) AB is the bisector of ∠CAD
(iii) If arc AC = 2 arc BC, then find
(a) ∠BAC (b) ∠ABC

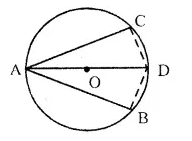
Construction: Join BC and BD.
Proof : In right angled A ABC and A ABD
Side AC = AD (Given)
Hyp. AB = AB (Common)
∴ ∆ ABC ≅ ∆ ABD (R.H.S. axiom)
(i) ∴ BC = BD (C.P.C.T)
∴ Arc BC = Arc BD (equal chords have equal arcs)
(ii) ∠ BAC = ∠ BAD (C.P.C.T)
∴ AB is the bisector of ∠CAD.
(iii) If arc AC = 2 arc B
Then ∠ABC = 2 ∠BAC
But ∠ABC – 2 ∠BAC = 90°
∴ 2 ∠BAC + ∠BAC = 90°
⇒ 3 ∠BAC = 90° ⇒ ∠BAC = 30°
and ∠ABC = 2 ∠BAC = 2 * 30° = 60°

Question 22.
In cyclic-quadrilateral ABCD ; AD = BC,
∠ BAC = 30° and ∠ CBD = 70°, find:
(i) ∠ BCD
(ii) ∠ BCA
(iii) ∠ ABC
(iv) ∠ ADC
Solution:
ABCD is a cyclic-quadrilateral and AD = BC
∠ BAC = 30°, ∠ CBD = 70°
∠ DAC = ∠ CBD , (Angles in the same segment)

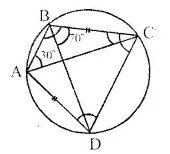
But ∠ CBD = 70°
∴ ∠ DAC = 70°
⇒ ∠ BAD = ∠ BAC + ∠ DAC = 30° + 70° = 100°
But ∠ BAD + ∠ BCD = 180°
(Sum of opposite angles of a cyclic quad.)
⇒100°+ ∠ BCD=180° ⇒ ∠ BCD=180° – 100° = 80°
∴ ∠ BCD = 80°
∵ AD = BC (Given)
∴ ∠ ACD = ∠ BDC
(Equal chords subtends equal angles)
But ∠ ACB = ∠ ADB
(Angles in the same segment)
∴ ∠ ACD + ∠ ACB = ∠ BDC + ∠ ADB
⇒ ∠ BCD = ∠ ADC = 80° (∵ ∠ BCD = 80°)
∴ ∠ ADC = 80°
But in ∆ BCD,
∠ CBD + ∠ BCD + ∠ BDC = 180° (Angles of a triangle)
⇒ 70° + 80° + ∠ BDC = ∠ 180°
⇒ 150°+ ∠ BDC = 180°
∴ ∠ BDC = 180° – 150° = 30°
⇒ ∠ ACD = 30° (∵ ∠ ACD = ∠ BDC)
∴ ∠ BCA = ∠ BCD – ∠ ACD = 80° – 30° = 50°
∠ ADC + ∠ABC = 180°
(Sum of opp. angles of a cyclic quadrilateral)
⇒ 80°+ABC = 180°
⇒ ∠ ABC=180°-80° = 100°

Question 23.
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the values of a, b and c.

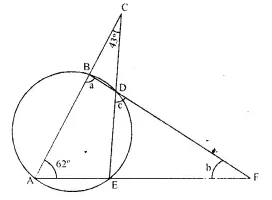
Solution:
Now, ∠ ACE = 43° and ∠ CAF = 62° (given)
In ∆ AEC,

∠ ACE + ∠ CAE + ∠ AEC = 180°
∴ 43° + 62° + ∠ AEC = 180°
105° + ∠ AEC = 180°
⇒ ∠ AEC = 180°- 105° = 75°
Now, ∠ ABD + ∠AED=180°
(Opposite ∠ s of a cyclic quad, and ∠ AED = ∠ AEC)
⇒ 0 + 75°= 180° a = 180° – 75° = 105°
∠ EDF = ∠ BAE (Angles in the alternate segments)
∴ c = 62°
In ∆BAF, ∠a + 62° + ∠b = 180°
⇒ 105°+ 62°+ ∠b= 180°
⇒ 167° + ∠6 = 180°
⇒ ∠b= 180°-167°= 13°
Hence, a= 105°, 6=13° and c = 62°.

Question 24.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25° .

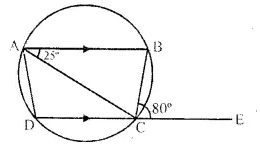
Find:
(i) ∠CAD
(ii)∠CBD
(iii) ∠ADC
Solution:

In the given figure,
ABCD is a cyclic quad, in which AB || DC
∴ ABCD is an isosceles trapezium AD = BC
(i) Join BD
and Ext. ∠BCE = ∠BAD
{ Ext. angle of a cyclic quad, is equal to interior opposite angle}
∴ ∠BAD = 80° (∵ ∠BCE = 80°)
But ∠BAC = 25°
∴ ∠CAD = ∠BAD – ∠BAC = 80° – 25° = 55°
(ii) ∠CBD = ∠CAD (Angles in the same segment)
= 55°
(iii) ∠ADC = ∠BCD (Angles of the isosceles trapezium)
= 180°- ∠BCE =180°- 80° = 100°

Question 25.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AJD and BC produced meet at P, show that ∠APB = 60°.
Solution:

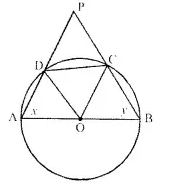
Given : In a circle, ABCD is a cyclic quadrilateral in which AB is the diameter and chord CD is equal to the radius of the circle
To prove: ∠APB = 60°
Construction : Join OC and OD
Proof: ∵ chord CD = CO = DO (radii of the circle)
∴ ∆DOC is an equilateral triangle
∠DOC = ∠ODC = ∠OCD – 60°
Let ∠A = x and ∠B = y
∵ OA = OD = OC = OB (radii of the same circle)
∴ ∠ODA = ∠OAD = x and ∠OCB = ∠OBC =y
∴∠AOD = 180° – 2x and ∠BOC = 180° – 2y
But AOB is a straight line
∴ ∠AOD + ∠BOC + ∠COD = 180°
180°- 2x + 180° -2y + 60° = 180°
⇒ 2x + 2y = 240°
⇒ x + y = 120°
But ∠A + ∠B + ∠P = 180° (Angles of a triangle)
⇒ 120° + ∠P = 180°
⇒ ∠P = 180° – 120° = 60°
Hence ∠APB = 60°

Question 26.
In the figure, given alongside, CP bisects angle ACB. Show that DP bisects angle ADB.

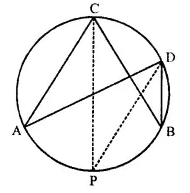
Solution:
Given : In the figure,
CP is the bisector of ∠ACB
To prove : DP is the bisector of ∠ADB
Proof: ∵ CP is the bisector of
∴ ∠ACB ∠ACP = ∠BCP
But ∠ACP = ∠ADP {Angles in the same segment of the circle}
and ∠BCP = ∠BDP
But ∠ACP = ∠BCP
∴ ∠ADP = ∠BDP
∴ DP is the bisector of ∠ADB

Question 27.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

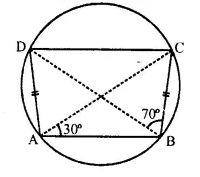
Solution:
In the figure,
ABCD is a cyclic quadrilateral
AC and BD are its diagonals
∠BAC = 30° and ∠CBD = 70°
Now we have to find the measures of ∠BCD, ∠BCA, ∠ABC and ∠ADB
∠CAD = ∠CBD = 70°
(Angles in the same segment)
Similarly ∠BAC = ∠BDC = 30°
∴ ∠BAD = ∠BAC + ∠CAD = 30° + 70° = 100°
(i) Now ∠BCD + ∠BAD = 180° (opposite angles of cyclic quad.)
⇒ ∠BCD + 100°= 180°
⇒ ∠BCD = 180°-100° = 80°
(ii) ∵ AD = BC (given)
∴ ∠ABCD is an isosceles trapezium
and AB || DC
∴ ∠BAC = ∠DCA (alternate angles)
⇒ ∠DCA = 30°
∠ABD = ∠D AC = 30° (Angles in the same segment)
∴ ∠BCA = ∠BCD – ∠DAC = 80° – 30° = 50°
(iii) ∠ABC = ∠ABD + ∠CBD = 30° + 70° = 100°
(iv) ∠ADB = ∠BCA = 50° (Angles in the same segment)

P.Q.
In the given below figure AB and CD are parallel chords and O is the centre.
If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.

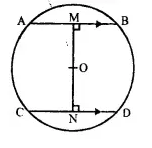
Solution:
Given : AB = 24 cm, CD = 18 cm
⇒AM = 12 cm, CN = 9 cm
Also, OA = OC = 15 cm
Let MO = y cm, and ON = x cm
In right angled ∆AMO

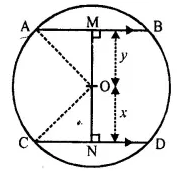
(OA)² = (AM)² + (OM)²
(15)² = (12)² + (y²
⇒ (15)²-(12)²
⇒ y² = 225-144
⇒ y² = 81 = 9 cm
In right angled ∆CON
(OC)² = (ON)² + (CN)²
⇒(15 )²= x2 + (9)²
⇒ x² = 225-81
⇒x²= 144
⇒ x = 12 cm
Now, MN = MO + ON =y + x = 9 cm + 12 cm = 21 cm

Question 28.
In the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED (2016)
Solution:

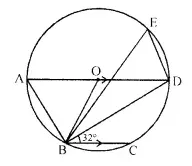
(i) AD is parallel to BC, that is, OD is parallel to BC and BD is transversal.
∴ ∠ODB = ∠CBD = 32° (Alternate angles)
In ∆OBD,
OD = OB (Radii of the same circle)
⇒ ∠ODB = ∠OBD = 32°
(ii) AD is parallel to BC, that is, AO is parallel to BC and OB is transversal.
∴∠AOB = ∠OBC (Alternate angles)
∠OBC = ∠OBD + ∠DBC
⇒ ∠OBC = 32° + 32°
⇒ ∠OBC = 64°
∴ ∠AOB = 64°
(iii) In AOAB,
OA = OB(Radii of the same circle)
∴ ∠OAB = ∠OBA = x (say)
∠OAB + ∠OBA + ∠AOB = 180°
⇒ x + x + 64° = 180°
⇒ 2x = 180° – 64°
⇒ 2x= 116°
⇒ x = 58°
∴ ∠OAB = 58°
That is ∠DAB = 58°
∴ ∠DAB = ∠BED = 58°
(Angles inscribed in the same arc are equal)

Question 29.
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T.

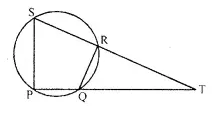
(i) Prove ∆TPS ~ ∆TRQ
(ii) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm.
(iii) Find area of quadrilateral PQRS if area of ∆PTS = 27 cm2.(2016)
Solution:
(i) Since PQRS is a cyclic quadrilateral ∠RSP + ∠RQP = 180°
(Since sum of the opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠RQP = 180° – ∠RSP …(i)
∠RQT + ∠RQP = 180°
(Since angles from a linear pair)
⇒ ∠RQP = 180° – ∠RQT …(ii)
From (i) and (ii),
180° – ∠RSP = 180° – ∠RQT
⇒ ∠RSP = ∠RQT …(iii)
In ∆TPS and ∆TRQ,
∠PTS = ∠RTQ (common angle)
∠RSP = ∠RQT [From (iii)]
∴ ATPS ~ ATRQ (AA similarity criterion)
(ii) Since ∆TPS ~ ∆TRQ implies that corresponding sides are proportional that

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.