Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17C

P.Q.
In the given diagram, chord AB = chord BC.

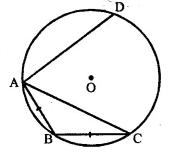
(i) What is the relation between arcs AB and BC?
(ii) What is the relation between ∠AOB and ∠BOC?
(iii) If arc AD is greater than arc ABC, then what is the relation between chords AD and AC?
(iv) If ∠AOB = 50°, find the measure of angle BAC.
Solution:

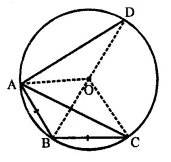
Join OA, OB, OC and OD,
(i) Arc AB = Arc BC (∵ Equal chords subtends equal arcs)
(ii) ∠AOB = ∠BOC (∵ Equal arcs subtends equal angles at the centre)
(iii) If arc AD > arc ABC, then chord AD > AC.
(iv) ∠AOB = 50°
But ∠ BOC = ∠AOB (ftom (ii) above)
∴ ∠BOC = 50°
Now, arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.
∴ ∠BOC = \(\frac { 1 }{ 2 }\)∠BOC = \(\frac { 1 }{ 2 }\) x 50°= 25°

Question P.Q.
In ∆ ABC, the perpendiculars from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively.
Prove that: arc CD = arc CE.
Solution:
Given: In ∆ ABC, perpendiculars from A and B are drawn on their opposite sides BC and AC at L and M respectively and meets the circumcircle of ∆ ABC at D and E respectively on producing.
To Prove: Arc CD = Arc CE
Construction: Join CE and CD
Proof: In ∆ APM and ∆ BPL,
∠AMP = ∠BLP (Each = 90°)
∠1 = ∠2 (Vertically opposite angles)

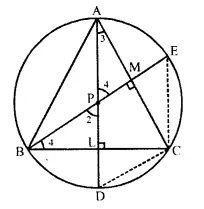
∴ ∆ APM ~ ∆ BPL (AA postulate)
∴ Third angle = Third angle
∴ ∠3 = ∠4
∵ Arc which subtends equal angle at the circumference of the circle, are also equal.
∴ Arc CD = Arc CE Q.E.D

Question 1.
In a cyclic-trape∠ium, the non-parallel sides are equal and the diagonals are also equal. Prove it.

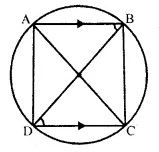
Solution:
Given: A cyclic-trape∠ium ABCD in which AB || DC and AC and BD are joined
To Prove:
(i) AD = BC
(ii) AC = BD
Proof:
∵AB || DC (given)
∴ ∠ABD = ∠BDC (Alternate angles)
∵ Chord AD subtends ∠ABD and chord BC subtends ∠BDC at the circumference of the circle
But ∠ABD = ∠BDC (Proved)
∴ Chord AD = Chord BC
⇒ AD = BC
Now in ∆ADC and ∆BDC
DC = DC (common)
AD = BC (proved)
and ∠CAD = ∠CBD (Angle in the same segment)
∴ ∆ADC ≅ ∆BDC (ASS axiom)
∴ AC = BD (c.p.c.t.)

Question 2.
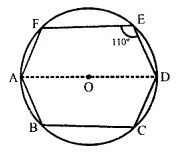
In the following figure, AD is the diameter of the circle with centre Q. Chords AB, BC and CD are equal. If ∠ DEF = 110°, calculate:
(i) ∠AEF,
(ii) ∠FAB.

Solution:

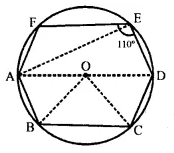
Join AE, OB and OC
(i) ∵ AOD is the diameter
∴ ∠AED = 90° (AngIe in a semi-circle)
But ∠DEF = 110° (given)
∴ ∠AEF = ∠DEF – ∠AED =110° – 90° = 20°
(ii) ∵ Chord AB = Chord BC = Chord CD (given)
∴ ∠AOB = ∠BOC = ∠COD (Equal chords subtends equal angles at the centre)
But ∠AOB + ∠BOC + ∠COD = 180° (AOD is a straight line)
∴ ∠AOB – ∠BOC = ∠COD = 60°
In ∆ OAB, OA = OB (Radii of the same cirlce)
∴ ∠OAB = ∠OBA
But ∠OAB + ∠OBA = 180° – ∠AOB
= 180° – 60°= 120″
∴ ∠OAB = ∠OBA = 60°
In cyclic quad. ADEF,
∴ ∠DEF + ∠DAFJ= 180°
⇒ 110° + ∠DAF = 180°
∴ ∠DAF = 180° – 110° = 70°
Now, ∠FAB = ∠DAF + ∠OAB = 70° + 6Q° = 130°

Question P.Q.
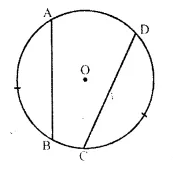
In the given figure, if arc AB = arc CD, then prove that the quardrilateral ABCD is an isosceles-trapezium (O is the centre of the circle).

Solution:
Given: In the figure, O is the centre of a circle and arc AB = arc CD

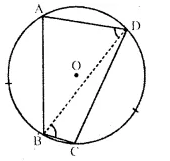
To Prove: ABCD is an isosceles trapezium.
Construction: Join BD, AD and BC.
Proof: Since, equal arcs subtends equal angles at the circumference of a circle.
∴ ∠ADB = ∠DBC ( ∵ arc AB = arc dD)
But, these are alternate angles.
∴ AD || BC.
∴ ABCD is a trapezium.
∵ Arc AB = Arc CD (Given)
∴ Chord AB = Chord CD
∴ ABCD is an isosceles trapezium. Q.E.D.

Question P.Q.
In the given figure, ABC is an isosceles triangle and O is the centre of its circumcirclc. Prove that AP bisects angle BPC.

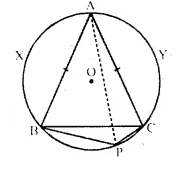
Solution:
Given: ∆ ABC is an isosceles triangle in * which AB = AC and O is the centre of the circumcircle.
To Prove: AP bisects ∠BPC

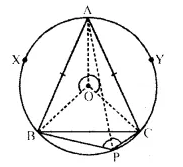
Proof: Chord AB subtends ∠APB and hord AC subtends ∠APC at the circumference of the circle.
But chord AB = chord AC.
∴ ∠APB ∠APC x
∴ AP is the bisector of ∠BPC Q.E.D.

Question 3.
If two sides of a cyclic-quadrilateral are parallel; prove that:
(i) its other two sides are equal.
(ii) its diagonals are equal.
Solution:

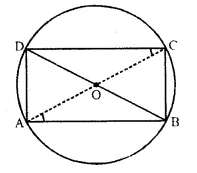
Given: ABCD is a cyclic quadrilateral in whicnAB || DC. AC and BD are its diagonals.
To Prove:
(i) AD = BC, (ii) AC = BD.
Proof: AP || CD.
∴ ∠DCA = ∠CAB (Alternate angles)
Now, chord AD subtends ∠DCA and chord BC subtends ∠CAB at the circumference of the circle.
∵∠DCA = ∠CAB (Proved)
∴ Chord AD = chord BC or AD = BC.
Now, in A ACB and A ADB,
AB = AB (Common),
BC = AD (Proved)
∠ACB = ∠ADB (Angles in the same segment)
∆ ACB ≅ ∆ ADB (SAA postulate)
∴ AC = BT (C. P. C. T) Q.E.D.

Question 4.
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠ PTS = 75°.
Calculate:
(i) ∠POS,
(ii) ∠QOR,
(iii) ∠ PQR

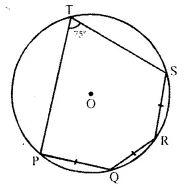
Solution:

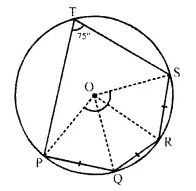
Join OP, OQ, OR and OS.
∵ PQ = QR = RS.
∴ ∠POQ = ∠QOR = ∠ROS
(Equal chords subtends equal angles at the centre)
Arc PQRS subtends ∠POS at the centre and ∠PTS at the remaining part of the circle
∴ ∠POS = 2 ∠PTR = 2 x 75° = 150°
⇒ ∠POQ + ∠QOR + ∠ROS = 150°

Question 5.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
(i) ∠ AOB,
(ii) ∠ ACB,
(iii) ∠ ABC.

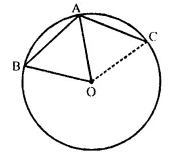
Solution:
Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.

Question 6.
In a regular pentagon ABODE, inscribed in a circle; find ratio between angle EDA and angle ADC. [1990]
Solution:

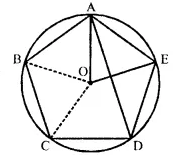
Arc AE subtends ∠AOE at the centre and ∠ADE at the centre and ∠ADE at the remaining part of the circumference.

Question 7.
In the given figure, AB = BC = CD and ∠ ABC = 132°. Calculate :
(i) ∠AEB,
(ii) ∠AED,
(iii) ∠ COD. [1993]

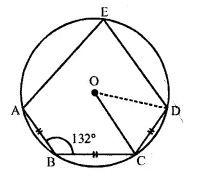
Solution:
In the figure, O is the centre of circle AB = BC = CD and ∠ABC = 132°
Join BE and CE
(i) In cyclic quadrilateral ABCE ∠ABC + ∠AEC = 180°
(sum of opposite angles)

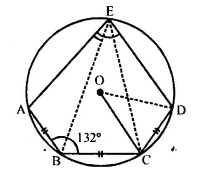
⇒ 132° + ∠AEC = 180°
⇒ ∠AEC = 180° – 132° = 48°
∵ AB = BC (given)
∴ ∠AEB = ∠BEC
(equal chords subtends equal angles)

Question 8.
In the figure, O is centre of the circle and the length Of arc AB is twice the length of arc BC. if angle AOB = 108°, find :
(i) ∠ CAB,
(ii)∠ADB. [1996]

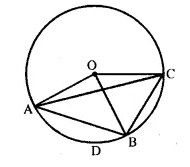
Solution:
(i) Join AD and DB.
∵ Arc AB = 2 arc BC. and ∠ AOB = 108° 1 1
∴ ∠ BOC = \(\frac { 1 }{ 2 }\) ∠ AOB = \(\frac { 1 }{ 2 }\) x 108° = 54°

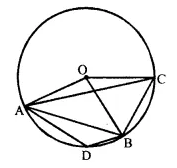
Now, arc BC subtends ∠ BOC at the centre and ∠CAB at the remaining part of die circle.
∴ ∠CAB = \(\frac { 1 }{ 2 }\) ∠BOC = \(\frac { 1 }{ 2 }\) x 54° = 27°
(ii) Again arc AB subtends ∠ AOB at the centre and ∠ ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 108° = 54°
In cyclic quad. ADBC,
∠ ADB + ∠ ACB = 180°
⇒ ∠ ADB+ 54° =180°
∴ ∠ ADB = 180° – 54° = 126°

Question 9.
The figure shows a circle with centre O, AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.

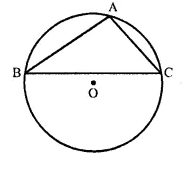
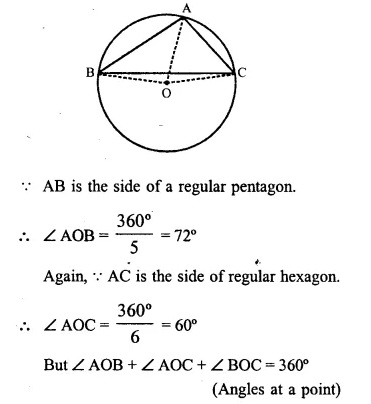
Solution:
Join OA, OB and OC.

Question 10.
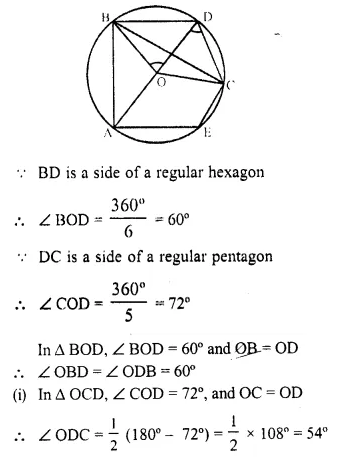
In the given figure, BD is a side ol’ a regular hexagon, DC is a side of a regular pentagon, and AD is a diameter. Calculate :
(i) ∠ ADC,
(ii) ∠ BDA,
(iii) ∠ ABC,
(iv) ∠AEC. [1984]

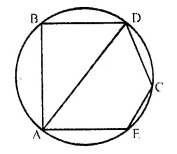
Solution:
Join BC, BO, CO, and EO.

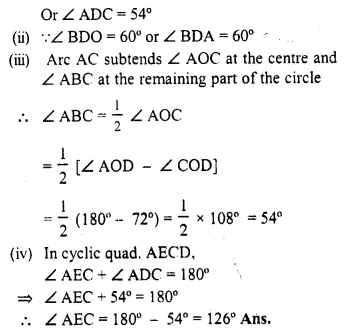
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles Ex 17B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.