Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points) Ex 12B
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B
Question 1.
Attempt this question on graph paper.
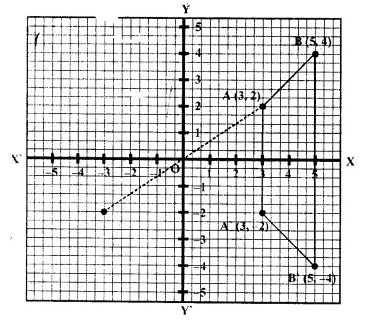
(a) Plot A (3, 2) and B (5, 4) on graph paper. Take 2cm = 1 unit on both the axes.
(b) Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
(c) Write down:
(i) The geometrical name of the figure ABB’A’;
(ii) The measure of angle ABB’ ;
(iii) The image A” of A, when A is reflected in the origin.
(d) The single transformation that maps A’ to A”. [1995]
Solution:
From the graph, we can say that
(iii) (a) an isosceles trapezium
(b) 45°
(c) ( -3, -2)
(d) reflection in y-axis
Question 2.
Points (3,0) and (-1,0) are invariant points under reflection in the line L1; points (0, -3) and (0, 1) are invariant points on reflection in line L2
(a) Name or write equations for the lines L1 and L2 .
(b) Write down the images of points P (3, 4) and Q ( -5, -2) on reflection in L. Name the images as P’ and Q’ respectively.
(c) Write down the images of P and Q on re-flection in L,. Name the images as P” and Q” respectively.
(d) State or describe a single transformation that maps P’ onto P”. [1996]
Solution:
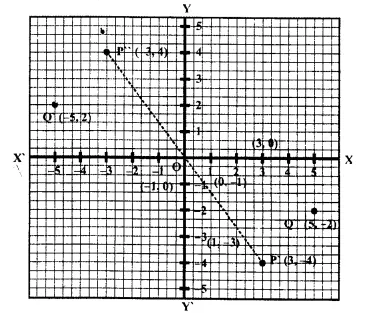
(a) Points (3, 0) and (-1, 0) are invariant points under reflection L .
Here the ordinates of both points are 0 It is x-axis or y = 0.
Again points (0, -3) and (0, 1) are invariant- points on reflection in line L2
Here the abscissas are 0 in both points.
It is y-axis or x = 0.
(b) The co-ordinates of the images of points P (3, 4) and Q (-5, -2) on reflection in L, will be P (3, -4) and Q'(-5, 2)
(c) The co-ordinate of images of points P (3, 4) and Q (-5, -2) on reflection in L2 will be P’ (-3, 4) and Q’ (5, -2)
(d) Reflection is in origin because the co-ordinates of P’ and P” have opposite signs.
Question 3.
(a) Point P (a, b) is reflected in the x-axis to P’ (5, -2), write down the values of a and b.
(b) P” is the image of P when reflected in y- axis, write down the co-ordinates of P”.
(c) Name a single transformation that maps P’ to P”. (1997):
Solution:
(a) P (a, b) is reflected in x-axis to P’ (5, -2). the co-ordinates of P will be (5, 2)
a = 5, b = 2
(b) P” is the image of P when reflected is y-axis.
Co-ordinates of P” will be ( -5, 2)
(c) Reflection is in origin.
Question 4.
The point (-2, 0) on reflection in a line is mapped to (2, 0) and the point (5, -6) on reflection in the same line is mapped to (-5, -6).
(a) State the name of the mirror line and write its equation.
(b) State the co-ordinates of the image of (-8, -5) in the mirror line.
Solution:
Point (-2, 0) is mapped to (2, 0) to a certain line and point (5, -6) is also mapped to (-5, -6) to the same line.
(a) We see that sign of x-coordinate is changed.
The required line is y-axis whose equation will be x = 0.
(b) The co-ordinates of the image of the point (-8, -5) in the same mirror line will be (8, -5).
Question 5.
The points P (4, 1) and Q (-2, 4) are reflected in line y = 3, Find the co-ordinates of P’, the image of P and Q’, the image of Q.
Solution:
Co-ordinates of P and Q are (4, 1) and ( -2, 4) respectively.
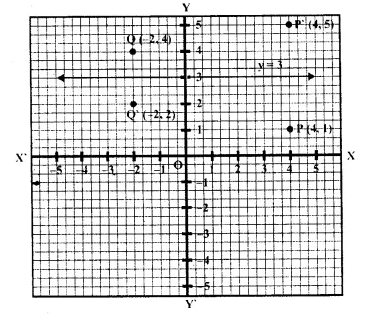
The co-ordinates of image of P which is P’ are (4, 5) reflection in the line y = 3
and co-ordinates of image of Q when is Q’ are ( -2, 2) reflection is the line y = 3 as shown in the graph.
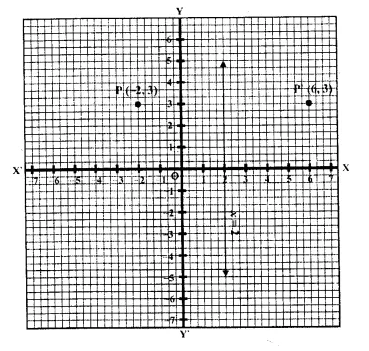
Question 6.
A point P (-2, 3) is reflected in the line x = 2 to point P’. Find the co-ordinates of P’.
Solution:
The image of P ( -2, 3) is P’ which is reflected in the line x = 2. The co-ordinates of P’ will be (6, 3) as shown in the graph.
Question 7.
A point P (a, b) is reflected in the x-axis to P’ (2, -3). Write down the values of a and b. P” is the image of P, reflected in the y- axis. Write down the co-ordinates of P”. Find the co-ordinates of P'”, when P is reflected in the line, parallel to y-axis, such that x = 4. [1998]
Solution:
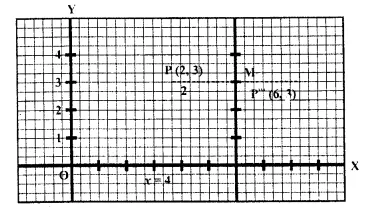
(i) A point P (a, b) is reflected in v-axis to P’ (2, -3)
Co-ordinates of P will be (2, 3) a = 2, b = 3.
(ii) P” is the image of P, when reflected in the y- axis
Co-ordinates of P” will be ( -2, 3)
(iii) The image of P is P'” reflected in a line parallel to y-axis i.e. x = 4.
Co-ordinates of P”‘ will be (6, 3)
Question 8.
Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
(a) A’ of A under reflection in the x-axis.
(b) B’ of B under reflection in the line AA’.
(c) A” of A under reflection in the y-axis.
(d) B” of B under reflection in the line AA”.
Solution:
Co-ordinates of A are (3, 4) and co-ordinates of B are (0, 2)
(a) Co-ordinates, of A’ of A under reflection in the v-axis are (3, -4)
(b) Co-ordinates of B’ of B under reflection in the line AA’ are (6, 2)
(c) Co-ordinates of A” of A under reflection in y-axis are (-3, 4)
(d) Co-ordinates of B” of B under reflection in the line A A” are (0, 8).
Question 9.
(a) Plot the points A(3, 5) and B(-2, -4). Use 1 cm = 1 unit on both the axes.
(b) A’ is the image of A when reflected in the v-axis. Write down the co-ordinates of A’ and plot it on the graph paper.
(c) B’ is the image of B when reflected in the y-axis, followed by reflection in the origin.
Write down the co-ordinates of B’ and plot it on the graph paper.
(d) Write down the geometrical name of the figure AA’ BB’.
(e) Name two invariant points under reflection in the x-axis. [1999]
Solution:
(a) The points A (3, 5) and B(-2, -4) have been plotted on the graph.
(b) A’ is the image of A when reflected in the x-axis
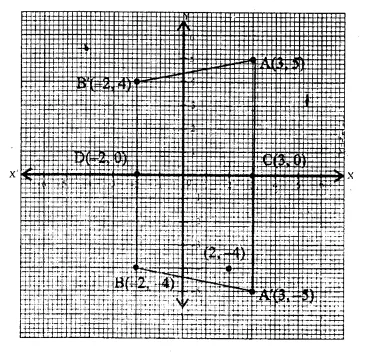
Co-ordinates of A’ will be (3, -5)
(c) B’ is the image of B when reflected in y- axis, followed by reflection in the origin.
Co-ordinates will be (-2, 4)
Images A’ and B’ have also been plotted.
(d) Join AA’, A’B, BB’ and B’A the quadrilateral so joined is an isosceles trapezium.
(e) The points C and D whose co-ordinates ! are (3,0) and (-2, 0) are invariant points under reflection in the x-axis.
Question 10.
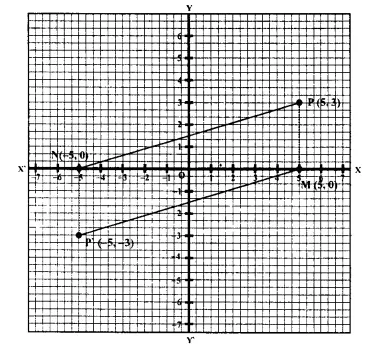
The point P (5,3) was reflected in the origin to get the image P’.
(a) Write down the co-ordinates of P’.
(b) If M is the foot of the perpendicular from P to the x-axis, find the co-ordinates of M.
(c) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(d) Name the figure PM P’ N.
(e) Find the area of the figure PM P’ N.
Solution:
(a) Points P(5, 3) is reflected to P’ in the origin.
Co-ordinates of P’ will be (-5, -3).
(b) PM ⊥ on x-axis.
Co-ordinates of P’ will be (5, 0)
(c) P’N X on x-axis
Coordinates of N will be (-5, 0).
(d) PM, MP’ P’N and N. P are joined which form a parallelogram PMP’N.
(e) Area of || gm PMP’N = 2 (Area of ∆PMN)
= 2 (\(\frac { 1 }{ 2 }\) x 10 x 3) Sq. cm
= 30 Sq. cm
Question 11.
The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write :
(i) the co-ordinates of P’ and O’,
(ii) the length of the segments PP’ and OO’,
(iii) the perimeter of the quadrilateral POP’O’.
(iv) the geometrical name of the figure POP’O’.
Solution:
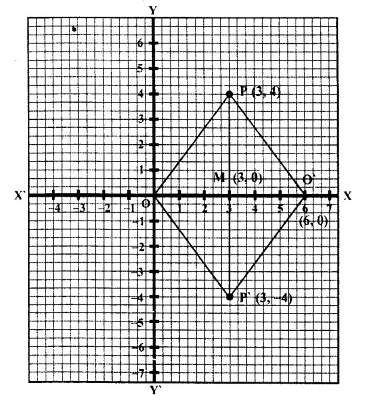
(i) Point P (3, 4) is reflected to P’ in x-axis and then its co-ordinates will be (3, -4) again O’ is the image of O (0, 0) reflected in PP’, then co-ordinates of O’ will be (6, 0)
(ii) Length of PP’ = 4 + 4 = 8 units and OO’ = 3 + 3 = 6 units
(iii) Diagonals of OPO’P’ bisect each other at right angles at M.
OPO’P’ is a rhombus.
(iv) The perimeter of quadrilateral OPO’P’ = 5 x 4 = 20 units
(v) The quadrilateral OPO’P’ is a rhombus as rhombus shown on the graph paper.
Question 12.
A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A’, B’, C’ and D’ respectively. Locate A’, B’, C’ and D’ on the graph sheet and write their co-ordinates. Are D, A, A’ and D’ collinear? (2004)
Solution:
On the given graph, plot the points A(1, 1), B(5, 1). C(4, 2) and D(2, 2) Join AB, BC, CD and DA.
The quadrilateral is of trapezium in shape.
Now points A, B, C and D are reflected in the origin on to A’, B’, C and D’ respectively.
Co-ordinates of A’ are (-1, -1), of B’ are (-5, -1), of C are (-4, -2) and of D’ are (-2, -2).
A’ B, B’C’, CD’ and D’A’ are joined.
Yes, we see that DA A’D’ are collinear.
Question 13.
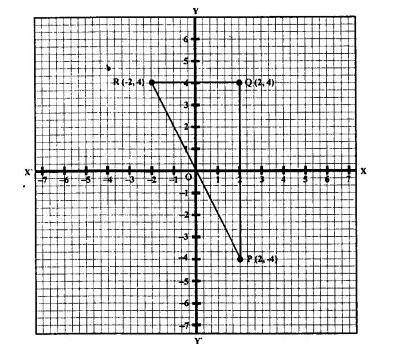
P and Q have co-ordinates (0, 5) and (-2, 4).
(a) P is invariant when reflected in an axis, Name the axis.
(b) Find the image of Q on reflection in the axis found in fa)
(c) (0, k) on reflection in the origin is invariant. Write the value of k.
(d) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:
Co-ordinates of the given points P and Q, are (0, 5) and (-2, 4) and have been plotted on the graph.
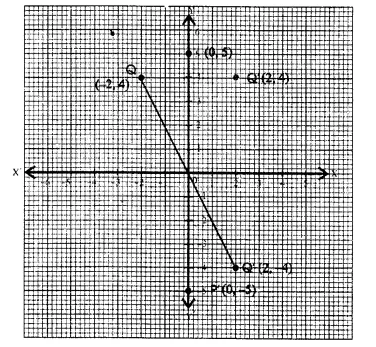
(a) P is invariant in y-axis
(b) Image of Q(-2, 4) is Q’ in years and its Co-ordinates will be (2, 4)
(c) (0, k) on reflections in we origin is also invariant
Co-ordinates will be (0, 0) k = 0
(d) Let Q” be image of Q reflection in his origin.
Again Q” is reflected in x-axis and its image will be Q’ (2, 4)
Question 14.
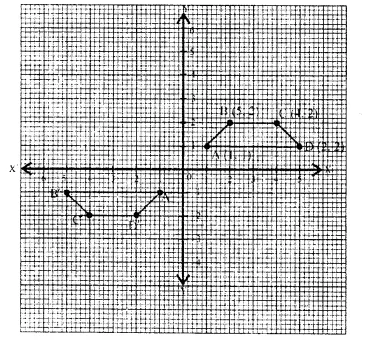
(a) The point P (2, -4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(b) The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(c) Name the figure PQR.
(d) Find the area of figure PQR.
Solution:

The graph of the solution set is shown by the thick portion of the number line. The solid circle at -3 indicates that the number – 3 is included among the solutions whereas the open circle at 3 indicates that 3 is not included among the solutions.
(c) (i) Since the point Q is the reflection of the point P (2, – 4) in the line x = 0, the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line x = 0, the co-ordinates of R are (- 2, 4).
(iii) Figure PQR is the right angled triangle PQR.
(d) Area of ∆PQR = \(\frac { 1 }{ 2 }\) x QR x PQ = \(\frac { 1 }{ 2 }\) x 4 x 8 = 16 sq. units.
Question 15.
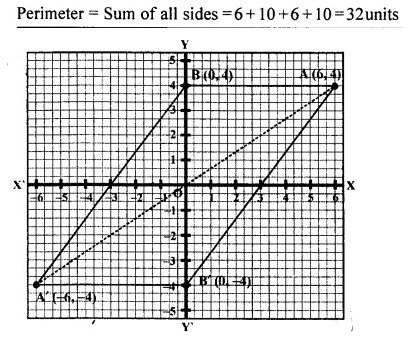
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’ B’
(iv) Find its perimeter.
Solution:
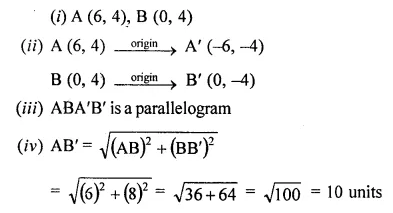
Question 16.
Use graph paper for this question. (Take 2 cm = 1 unit along both x and y axis.
Plot the points O (0, 0), A (-4, 4), B (-3, 0) and C (0, -3)
(i) Reflect points A and B on the y-axis and name them A’ and B’ respectively. Write down their coordinates. k
(ii) Name the figure OABCB’A’.
(iii) State the line of symmetry of this figure. (2016)
Solution:
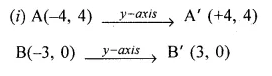
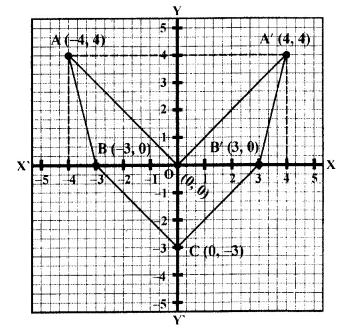
(ii) The figure OABCB’A’ is similar to arrow headed.
(iii) The y-axis is the line of symmetry of figure OABCB’A’.
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 12 Reflection Ex 12B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.