Equilibrium Class 11 Notes Chemistry Chapter 7

By going through these CBSE Class 11 Chemistry Notes Chapter 7 Equilibrium, students can recall all the concepts quickly.

Equilibrium Notes Class 11 Chemistry Chapter 7

Chemical equilibria are important in numerous biological and environmental processes. For example, equilibria involving O₂ molecules and the protein hemoglobin play a crucial role in the transport and delivery of O₂ from our lungs to our muscles. Similarly, equilibria involving CO molecules and hemoglobin account for the toxicity of CO.

In the case of evaporation of water in a closed vessel, the no, of molecules leaving the surface of water equals the no. of molecules of H₂O returning to liquid state from the vapor state. This is an equilibrium state. However, this equilibrium state is not static. It is Dynamic equilibrium. Thus at equilibrium, the rate of evaporation is equal to the rate of condensation. It may be represented by
H₂O (l) ⇌ H₂O (vap)

The mixture of reactants and products in the equilibrium state is called an equilibrium mixture.

The state of chemical equilibrium in a chemical reaction may be classified into three groups characterized by the extent to which the reactions proceed.

1. The reactions proceed nearly to completion and only negligible concentrations of the reactants are left.
2. The reactions in which only some amount of products are formed and most of the reactants remain unchanged at equilibrium stage.
3. The reactions in which concentrations of the reactants and products are comparable when the system is at equilibrium.

Equilibrium in Physical processes
1. Solid-Liquid Equilibrium: For example
ice ⇌ water
i.e. H₂O(s) ⇌ H₂O(l)
At equilibrium, rate of melting = rate of freezing.

The temperature at which the solid and liquid forms of any substance coexist is called the melting point.
2. Liquid-Vapour Equilibrium: For example
H₂O(l) ⇌ H₂O(g)
At equilibrium: rate of evaporation = rate of condensation.

3. Equilibrium involving dissolution of solids of gases in liquids: Different solids dissolve in any solvent to different extents. Certain solids dissolve more, while many others dissolve less.

The maximum mass (in grams) of a solute which can be dissolved in 100 g of a solvent at any temperature and pressure is called its solubility at that temperature and pressure,
(a) Solids in liquids: When a small quantity of sugar is added to some water (say 100 mL) it gets dissolved. When a little more sugar is added, it also gets dissolved. If the addition of sugar is continued, then a stage comes when no more sugar dissolves, and the added sugar settles down.

The solution at this stage contains the maximum amount of sugar the solution can have at that temperature. This solution is called a saturated solution of sugar. In a saturated solution
Sugar (s) N ⇌ Sugar (aq)
of sugar in contact with solid sugar, a dynamic equilibrium is established. At the equilibrium state, the number of sugar molecules going into the solution from the solid sugar is equal to the number of molecules precipitating out from the solution at a given temperature. Thus at equilibrium.

Rate of dissolution of solid sugar = Rate of precipitation of sugar from the solution.

(b) Gases in Liquids: Gases dissolve in liquids. The solubility of a gas in any liquid depends upon.

• nature of the gas and that of the liquid.
• the temperature of the liquid
• pressure of the gas over the surface of the solution.

The effect of pressure on the solubility of a gas in a liquid is described by Henry’s Law.

Henry law states that,
“At a certain temperature, the mass of a gas which dissolves in a definite volume of a liquid is proportional to the pressure of the gas over the solution.”

If p is the pressure of the gas over the solution, m is the mass of the gas dissolved in one unit volume of the liquid.
Then, according to Henry’s law
m ∝ p
or
m = kp
where k is the proportionality- constantly called Henry’s Law constant.

equilibrium concentration calculator quantity for each species from the initial quantity and the change.

4. General Characteristics of Equilibria involving Physical Processes:
It has been noted that
(a) for liquid-vapor equilibrium, the vapor pressure is constant at t given temperature.
(b) for solid-liquid equilibrium, there is only one temperature (melting point) at 1 atm at which the two phases can coexist. If there is no exchange of heat with the surroundings, the mass of the two phases remains constant.
(c) for dissolution of solids in liquids the solubility is constant at a given temperature.
(d) for dissolution of gases in liquids, the concentration of a gas in a liquid is proportional to the pressure (concentration)! of the gas over the liquid.

Table: Some Features of Physical Equilibria

Process	Conclusion
Liquid ⇌ Vapour H2O (l)   ⇌ H2O (g)	PH2O constant at a given temperature.
Solid ⇌ Liquid H2O (s)  ⇌ H2O (l)	The melting point is fixed at constant pressure.
Solute (s) ⇌ Solute solution) Sugar (s) ⇌ Sugar (solution)	The concentration of solute in a solution is constant at a given temperature.
Gas (g) ⇌ gas (aq) For’example, CO2 (g) ⇌ CO2 (acl)	[gas (aq)]/[gas (g)] is constant at a given temperature. [CO2 (aq)] /[CO2 (g)] is constant at a given temperature.

For the physical processes discussed above following characteristics are common to the system of equilibrium.

1. Equilibrium is possible only in a closed system at a given temperature.
2. Both the opposing processes occur at the same rate and there is a dynamic but stable condition. ,
3. All measurable properties of the system remain constant.
4. When equilibrium is attained for a physical process, it is characterized by the constant value of one of its parameters at a given temperature.
5. The magnitude of such quantities at any stage indicates the extent to which the physical process has proceeded before reaching equilibrium.

Equilibrium in Chemical Processes-Dynamic Equilibrium
Similar to physical systems, chemical reactions also attain a state of equilibrium. These reactions can proceed both in the forward direction as well as backward direction. When rates in both directions become equal, the concentrations of reactants and products remain constant. This is the stage of chemical equilibrium.

Let there be a reversible reaction
A + B ⇌ C + D
With time, concentrations of A and B decrease, and those of C and D increase. This leads to a decrease in the rate of forwarding direction and increases in the rate of backward direction. When both the rates become equal, the system reaches a state of equilibrium.

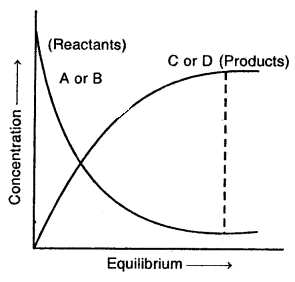
Characteristic of Chemical Equilibrium:

1. The equilibrium state is reached only if the process is carried out in a closed vessel.
2. It is dynamic equilibrium, i.e., at this stage the reaction, although appears to be stopped, actually takes place in both directions with the same speed.
3. An equilibrium state can be approached from both sides.
4. At equilibrium state/composition of the reactants and products remain constant.

3. Law of Chemical Equilibrium and Equilibrium Constant: Goldberg and Waage proposed that for a general reversible reaction
A + B ⇌ C + D

the following Equilibrium equation holds:
KC = \(\frac{[\mathrm{C}] \times[\mathrm{D}]}{[\mathrm{A}] \times[\mathrm{B}]}\)
where Kc is called equilibrium constant and the expression on the right side is called equilibrium constant expression.

The above equation is also called the Law of Mass Action because concentration was earlier referred to as active mass.

→ Law of mass action: It states that under a given set of conditions, the rate of a chemical reaction is directly proportional to the product of the concentration (active mass) of the reacting substances.
Active mass (Molar concentration) = \(\frac{\text { No. of moles }}{\text { Vol. in litres }}\)

The active mass of a gas or liquid means its molar concentration, while the active mass of a solid is always taken as unity, irrespective of the quantity.

The Law of mass action is applicable only to reversible reactions.
Let us consider a general reversible reaction
aA + bB ⇌ cC + dD
The rate of forwarding reaction = K_f [A]^a[B]^b
Similarly, the rate of backward reaction = K_f [C]^c[D]^d
where and K_f and K_b be the respective rate constants.

Since at equilibrium, the rate of both reactions are equal
K_f[A]^a[B]^b = K_f[C]^c[D]^d
\(\frac{\mathrm{K}_{f}}{\mathrm{~K}_{b}}=\frac{\left[\mathrm { C } \left[^{c}[\mathrm{D}]^{d}\right.\right.}{[\mathrm{A}]^{a}[\mathrm{~B}]^{b}}\)
or
K = \(\frac{[\mathrm{C}]^{\mathrm{c}}[\mathrm{D}]^{d}}{[\mathrm{~A}]^{a}[\mathrm{~B}]^{b}}\)
where K is.called equilibrium constant.

Characteristics of the equilibrium constant:
1. Its value is independent
(a) of the original concentration of the reactants.
(b) of volume.
(c) of the presence of inert materials.
(e) of the direction from which equilibrium is attained.
(f) of the nature and number of steps in the reaction as long as stoichiometry is not changed.

2. It has a definite value at a given temperature and changes with temperature.

For a reversible reaction at equilibrium; the ratio of the product of concentrations of the products to the product of concentrations of the reactants when each concentration term is raised to a power equal to the corresponding stoichiometric coefficient in the balanced chemical equation at a constant temperature is constant. This constant is called the Equilibrium Constant.

For a homogeneous chemical reaction aA + bB ⇌ cD + dD
when concentrations of reactants and products are expressed in moles per liter units represented by [ A], |B], [Cl, [D] (their active masses), the equilibrium constant is written as K_C and is given by
K_C = \(\frac{[C]^{c} \times[D]^{d}}{[A]^{a} \times[B]^{b}}\)

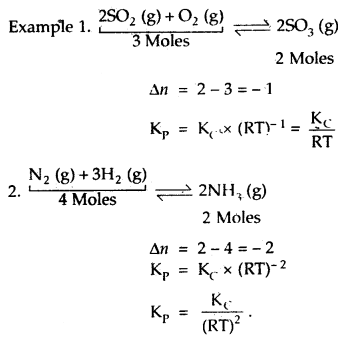
Further, if the reaction is a homogeneous gas-phase reaction then the molar concentration of a substance is directly proportional to K_p
K_p = K_c × (RT)^Δn
If Δn = 1,then K_p = K_c × RT

(c) If Δn < 0, i.e. when the no. of moles of reactants is more than that of products or when the reaction proceeds with a decrease in the no. of moles

→ Units of Equilibrium Constant: The unit of K depends upon the number of moles of reactants and products involved in the reaction.
1. When a total number of moles of products is equal to the number of moles of reactants, K has no units. For example.
N₂ (g) + O₂ (g) ⇌ 2NO (g)
K = \(\frac{[\mathrm{NO}(\mathrm{g})]^{2}}{\left[\mathrm{~N}_{2}(\mathrm{~g})\right]\left[\mathrm{O}_{2}(\mathrm{~g})\right]}\)

= \(\frac{[\mathrm{mol} / \mathrm{L}]^{2}}{[\mathrm{~mol} / \mathrm{L}][\mathrm{mol} / \mathrm{L}]}\) = no units.

2. When/ the total number of moles of products is different than the total number of moles of reactants. In such reactions, K has units. For example,
N₂ (g) + 3H₂ (g) ⇌ 2NH₃ (g)

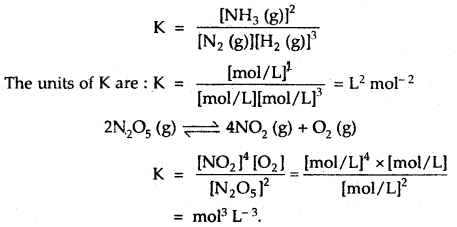
Value of K_p for Some reactions

→ Homogeneous Equilibrium: A reversible reaction in which all the reactants and products at equilibrium are in the same phase is called a homogeneous equilibrium.
(a) In the gas phase

(b) In the liquid phase: Here, all the reactants and products are liquids that are miscible in one another. They may take place in an open or closed vessel.
CH₃COOH (l) + C₂H₅OH (l) ⇌ CH₃COOC₂H₅ (l) + H₂O (l)
KC = \(\frac{\left[\mathrm{CH}_{3} \mathrm{COOC}_{2} \mathrm{H}_{5}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}(\mathrm{l})\right]\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}(1)\right]}\)

(c) In the solution phase: Here the reactants and products are present in a solution. The choice of the solvent depends upon the nature of the reaction.
I₂ (aq) + r^– (aq) ⇌ I₃ (aq)
iodine iodine ion tri iodide ion
2H₂O (l) ⇌ H₃⁺O (aq) + OH^– (aq)
Fe³⁺ (aq) + SCN^– (aq) ⇌ [Fe(SCN)]²⁺ (aq)

Heterogeneous Equilibrium: A reversible reaction involving equilibrium between various chemical species present in two or more phases is said to be a heterogeneous chemical equilibrium. It may be noted here that all solids constitute separate phases.
Examples:

and [CaO] are both constants.

Here CaCO₃ and CaO are in solid phases and CO₂ is in the gaseous phase; [CaCO₃] = 1 and [CaO] = 1
(b) 3Fe (s) + 4H₂O (g) ⇌ Fe₃O₄ (s) + 4H₂ (g)

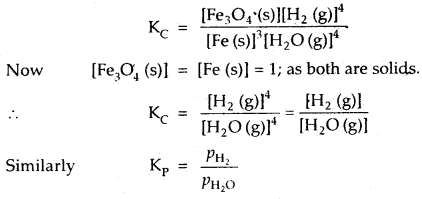
where PH₂ and PH₂O are the partial pressures of H₂ (g) and H₂O (g) at eqbm.

(c) Pb²⁺ (aq) + CrO₂^4- (aq) ⇌ PbCrO₄ (s)

(d) 2Hg (s)+ O₂ (g) ⇌ 2HgO (s)

(e) for the reaction
Ni (s) + 4CO (g) ⇌ Ni(CO)₄ (g)
K_C = \(\frac{\left[\mathrm{Ni}(\mathrm{CO})_{4}\right]}{[\mathrm{CO}]^{4}}\)

(f) Ag₂O (s) + 2HNO₃ (aq) ⇌ 2AgNO₃ (aq) + H₂O (l)
K_C = \(\frac{\left[\mathrm{Ag} \mathrm{NO}_{3}\right]^{2}}{\left[\mathrm{H} \mathrm{NO}_{3}\right]^{2}}\)

Applications of Equilibrium constants:
1. Predicting the direction and extent of reaction from the magnitude of the equilibrium constant: The magnitude of the equilibrium constant K of a reaction indicates how far a reaction can go and in which direction.

For example aA + bB ⇌ cC + dD is given by
K = [C]^c × [D]^d /[A]^a[B]^b
where all concentrations are at equilibrium. It is dear that the larger the value of K, the greater will be the equilibrium concentration of- the components on the R.H.S. of the reaction (products) relative to those on the L.H.S. (reactants).

Thus the value of K provides information about the extent and direction of the reaction.
(a) When K > > 1: When the value of K is very high such as; 10⁷ – 10¹⁵ or more, the reactions proceed to almost completion. In such reactions, almost the whole of the reacting substances gets converted into products.

(b) When K > 1: When the value of K is greater than one (but not too large), the reaction in the forward direction is favored more than the reaction in the backward direction. In such cases, the equilibrium concentration of products is higher than that of the reactants.

(c) When K = 1: When the value of K is equal to one, both the direction of the reaction are almost equally favored. In such cases the equilibrium concentrations of reactants and products are comparable.

(d) When K < 1: When the value of K is smaller than one, the reaction in the backward direction is favored. In such cases, the equilibrium concentrations of reactants will be much higher than the concentration of the products.

2. Calculating Equilibrium Concentrations: Once the value of the equilibrium constant for a reaction is known, we can use it to calculate the concentration of a substance (reactant or product) in the equilibrium mixture.

Relationship between Equilibrium Constant K, Reaction Quotient Q, and Gibbs Energy G

The value of K_C for a reaction does not depend upon the rate of the reaction. It is directly related to the thermodynamics of the reaction and in particular to the change in Gibbs energy, ΔG. If,

1. ΔG is negative, the reaction is spontaneous and proceeds in the forwarding direction. ’
2. ΔG is positive, the reaction is non-spontaneous. Instead, the products of the forward reaction shall be converted to the reactants, as ΔG will have a negative value for the reverse direction.
3. ΔG is 0, the reaction has achieved equilibrium, at this point, there is no longer any free energy left to drive the reaction.

Mathematically
ΔG = ΔG° + RT InQ, where G° is standard Gibbs energy
At equilibrium, when ΔG = 0 and Q = K_C, the above equation becomes
ΔG = ΔG° + RT InK = 0
or ΔG° = – RT InK.
InK = – ΔG°/RT

Taking antilog
K = e^-ΔG°/RT … (1)

Hence using the equation (1), the reaction spontaneity can be interpreted in terms of the value of ΔG°
1. If ΔG° < 0, then – ΔG/RT is positive and e^-ΔG°/RT > 1 making K > 1. It implies a reaction in the forward direction or a spontaneous reaction.

2. If ΔG° > 0, then – ΔG°/RT is negative and e^-ΔG°/RT < 1, that is K < 1 which implies a non-spontaneous reaction or a reaction which proceeds in the forward direction to such a small degree that only a very minute quantity of product is formed.

Factors affecting Equilibria:
1. Let Chatelier’s principle: “Whenever a system in equilibrium is subjected to a change in temperature,, pressure or composition, the equilibrium shifts in a direction so as to undo the effect of the change applied”.

2. Effect of concentration change: If a system is at equilibrium and the concentration of one of the species involved in the reaction is increased then the system will readjust so as decrease the concentration of that species. Thus/if the concentration of substance involved in the equilibrium is increased, the increased concentration, Similarly, if the concentration of some substances is decreased, the reaction will proceed so as to make up the loss in the concentration.

Let us consider the-reaction
aA + bB ⇌ cC + dD

At equilibrium, the concentration of A, B, C, and D are constant. If to this reaction at equilibrium, a small amount of the substance A is added, then according to Le Chatelier’s principle, the equilibrium shifts in a direction so as to undo the effect of the increased concentration of A. That is, the reaction proceeds in the d.rection so as to decrease the concentration of A.

This can be done only by making more A react with B to form more products. That is, an increase in the concentration of A (or any reactant) will shift the equilibrium towards the right, (products side). On the other hand, when the concentration of C (or any other product) is increased, the reaction will shift towards the left (reactant side).

Thus, in general, an increase in the concentration of any of the substances on one side of the equilibrium shifts the equilibrium to produce more of the substances on the other side of it.

3. Effect of Pressure Change: Change of pressure has no significant effect on the following equilibria:
(a) The equilibria involving only solids are not affected by a change of pressure because there is virtually no change in volume due to a change in pressure.

(b) The equilibria involving liquids and/or gases where the number of moles before and after the attainment of equilibrium remains the same, i.e., when Δn = 0, also are not affected by a change of pressure. When the pressure on a reaction involving gases (where Δn ≠ 0) is changed, the equilibrium will shift in a direction so as to undo the effect of change in pressure. For example, an increase in pressure will cause a decrease in volume.

So, an increase of pressure on a gaseous system will shift the equilibrium in a direction of a decrease in volume, and vice versa. Therefore, in a reaction which proceeds with a decrease in volume (Δn = -ve), the equilibrium will shift in the forward direction by increasing pressure.

On the other, hand, in a reaction which proceeds with an increase – in volume (Δn = +ve), the equilibrium will shift towards the right by decreasing the pressure.

4. Effect of Temperature Change: According to the Le Chatelier principle when the temperature of a system at equilibrium is increased, i.e., the heat is supplied to the system, the system should move in a direction so that the added heat is absorbed. So, an increase in the temperature of a chemical system at equilibrium favors the reaction that proceeds with the absorption of heat, i.e., an endothermic reaction is favored.

On the other hand, if the temperature of the system is decreased under constant pressure and volume conditions, the equilibrium – will shift in such a way so as to produce some heat. Thus, a decrease in the temperature of a system at equilibrium favors the reaction which proceeds with the evolution of heat, i.e., an exothermic reaction is favored.

For example, the reaction
N₂ (g) + 3H₂ (g) ⇌ 2NH₃ (g); ΔH = – 93.6 kj is exothermic in the forward direction and endothermic in the backward direction.

Let the temperature of the system at equilibrium be increased. Then, according to Le Chatelier’s principle, the equilibrium will shift in a direction heat is absorbed, i.e., in the endothermic direction. Therefore, on increasing temperature, the reaction will shift towards the left (reactant side). Thus, an increase in the temperature of this reaction will result in the formation of a lesser amount of ammonia.

On the other hand, a decrease in the temperature of this system will favor the endothermic direction of the equilibrium. Thus, when the temperature of this system is lowered, the equilibrium will shift in the forward direction, i.e., more ammonia will be produced.

5. Effect of a Catalyst: Catalyst has no effect on the equilibrium concentrations of the reactants and products. In fact, a catalyst accelerates the forward and the backward reactions to the same extent and therefore, simply helps’1 in the. attainment of the equilibrium state faster.

Inert gas added keeping the pressure of the system constant: In this gas, the addition of an inert gas increases the volume of the system, which in turn, causes the equilibrium position of the system to move in the direction of a large number of gaseous molecules. Thus, we will have

→ Inert gas added keeping the volume of the system constant: Addition of inert gas into a system at equilibrium under constant volume causes

1. an increase in the pressure of the system
2. an increase in the total number of moles in the system.

The total pressure of a system is therefore given by
P_total V = n_total RT
or
\(\frac{n_{\text {total }}}{P_{\text {total }}}=\frac{V}{R T}\)

Under constant-volume at any temperature, the ratio total/Ptotal remains constant even on the addition of inert gas. As a result, there is no change in any of the variables and the amounts of the substances at equilibrium remain unaffected by the addition of inert gas, i.e., the equilibrium position of the reaction remains unaffected.

Concentration Quotient or Reaction Quotient and predicting the direction of reaction:
For the reaction aA + bB ⇌ cC + dD at any stage of the reaction, other than the stage of chemical equilibrium, concentration ratio [C]^c[D]^d / [A]^a[B]^b is called concentration quotient or reaction quotient.

It is usually represented by Q_c or Q. Thus concentration quotient Q_c = [C]^c × [D]^d/[A]^a[B]^b

1. If Q = K, the reaction is in equilibrium.
2. If Q > K, Q will tend to decrease so as to become equal to K. As a result the reaction will proceed in the Backward direction.
3. If Q < K, Q will tend to increase. As a result, the reaction will proceed in the forward direction.

Consider the gaseous reaction of H2 and I2,
H₂ (g) + I₂ (g) ⇌ 2HI (g) K_c = 57.0 at 700 K.

Suppose we have molar concentrations
[H₂]_t = 0.10 M, [I₂]_t = 0.2 M and [HI]_t = 0.40 M.
(the subscript t on the concentration symbols means that the concentrations were measured at some arbitrary time t, not necessarily at equilibrium).

Thus, the reaction quotient; Qt at this stage of the reaction is given by,
Q_t = [HI]^t₂/|H₂]_t[I₂]_t = (0.40)²/(0.10) × (0.20) = 8.0.

Now, in this case, Q_c(8.0), does not equal K_c (57.0), so the mixture of H₂ (g), I₂ (g), and HI (g) is most at equilibrium; that is, more H₂ (g) and I₂ (g) will react to form more HI (g) and their concentrations will decrease till Q_c = K_c.

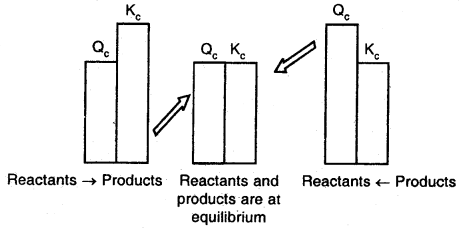
Predicting the direction of the reaction

The reaction quotient, Q_f is useful, we can predict the direction of reaction by comparing the values of Q_c and K_c
Thus, we can make the following generalizations concerning the direction of the reaction:

• If Q_r < K_t. net reaction goes from left to right.
• If Q_r > K_c, the net reaction goes from right to left.
• If Q_r = K_f, no net reaction occurs.

Problem (1)
The value of ΔG° for the phosphorylation of glucose in glycolysis is 13.8 kJ/mol. Find the value of at 298 K?
Solution: ΔG° = 13.8 kJ/mol = 13.8 × 103 J/mol
Also, ΔG° = – RT InK_c.

Hence, InK_c = – 13.8 × 10³ J/mol/8.31 Jmol^-1 × 298 K
InK_c = – 5.569
K_c = e – 5.569
K_c = 3.81 × 10^-3

Problem (2)
Hydrolysis of sucrose gives,
Sucrose + H₂O ⇌ Glucose + Fructose
Equilibrium constant K_c for the reaction is 2 × 1013 at 300 K. Calculate ΔG° at 300 K?
Answer:
ΔG° = – RT ln K_f
ΔG° = – 8.314 J mol^-1 K^-1 × 300 K × In (2 × 10¹³)
ΔG° = – 7.64 × 10⁴ J mol^-1

→ Ionic Equilibrium: There are substances that conduct electricity in their molten states or in the form of their aqueous solutions. These are called electrolytes. On the other hand, there are substances that do not conduct electricity in the molten states or in the form of their aqueous solutions and these are called non-electrolytes.

→ Strong and Weak Electrolytes: Depending upon the extent of ionization, the electrolytes may be divided into two classes: strong electrolytes and weak electrolytes.
1. Strong electrolytes: The substance which ionizes almost completely into ions in an aqueous solution are called strong electrolytes.

For example, HCl, H₂SO₄ HNO₃ NaOH, KOH, NaCl, KNO₃, etc. are strong electrolytes.
HCl + H₂O → H₃O+ + Cl^–
HNO₃ + H₂O → H₃O⁺ + NO₃^–

(ii) Weak electrolytes: The substances which ionize to a small extent in an aqueous solution are called weak electrolytes. For example, CH₃COOH, NH₄OH, (NH₄)₂ CO₃, HCN, etc. are weak electrolytes.
CH₃COOH + H₂O ⇌ H₃O+ + CH₃COO^–
NH₃ + H₂O ⇌ NH₄⁺ + OH^–

Ionization of weak electrolytes: Weak electrolytes are only partially ionized and a dynamic equilibrium is established between the ions and the unionized molecules. The equilibrium which is established between the unionized molecules and the ions in the solution of weak electrolytes is called ionic equilibrium,

The fraction of the total number of molecules of an electrolyte which \ ionizes into ions is called the degree of ionization or degree of dissociation.

It is denoted by the symbol an (alpha).
Degree of ionisation,
α = \(\frac{\text { Number of molecules of the electrolyte which ionise }}{\text { Total number of molecules of the electrolyte }}\)

Dissociation or Ionisation Constant for Weak Electrolytes: Consider a weak electrolyte CH3COOH in equilibrium with its ions when dissolved in water as
CH₃COOH (aq) + H₂O (l) ⇌ CH₃COO^– (aq) + H₃O⁺ (aq)

The equilibrium constant K, is
K_a = \(\frac{c \alpha^{2}}{1-\alpha}\)

Since the degree of dissociation of a weak acid is very small as compared to 1, then 1 – α may be taken approximately equal to 1.
K = cα²
α = \(\)\sqrt{\frac{\mathrm{K}_{a}}{c}} ∴ [H₃O⁺] = ca = \(\sqrt{\mathrm{K}_{a} c}\)

Thus, knowing the ionisation the ionisation constant K_a, degree of ionisation can be calculated.

Similarly, for a weak base, if the ionisation constant is K_b, c is the concentration and α is the degree of ionisation, then
K_b = \(\frac{c \alpha^{2}}{1-\alpha}\)
or
α = \(\sqrt{\frac{K_{b}}{c}}\)(1 – α) ≈ 1

Acids, Eases and Salts:
1. Arrhenius Acids and Bases: Arrhenius defined acids as substances that produce hydrogen ions in water and bases that produce hydroxyl ions. Thus, according to the Arrhenius concept, hydrogen chloride, acetic acid, and sulphuric acid, are acids because all these compounds give free H⁺ ions in an aqueous solution.
HCl (g) + H₂O (excess) ⇌ H⁺ (aq) + Cl^– (aq)
H₂SO₄ + H₂O (excess) ⇌ 2H⁺ (aq) + SO₂^-4 (aq)
CH₃COOH + H₂O (excess) ⇌ H⁺ (aq) + CH₃COO^– (aq)

The compounds such as NaOH and NH4OH are bases because these compounds give free OH- ions in aqueous solutions.
NaOH + H₂O (excess) ⇌ Na⁺ (aq) + OH^– (aq)
NH₄OH + H₂O (excess) ⇌ NH₄⁺ (aq) + OH^– (aq)

Ionization of Acids and Bases
→ The Bronsted-Lowry Acids and Bases: Any hydrogen-containing species (a molecule, a cation, or an anion) which is capable of donating one or more protons to any other substance is called an acid.

Any species (molecule, cation, or anion) which is capable of accepting one or more protons from acid is called a base.
Thus, according to the Bronsted-Lowry concept, an acid is a proton donor, and. a base is a proton acceptor.

Let us consider the dissolution of hydrogen chloride (HCl) in water described by the reaction
HCl (aq) + H₂O (1) ⇌ H₃O⁺ (aq) + Cl^– (aq)

In this reaction, HCl donates its one proton to become Cl^– and H₂O accepts one proton to become H₃O⁺. Thus, HCl is a Bronsted acid and H₂O is a Bronsted base.

Every acid must form a base on donating its proton and every base must form an acid on accepting a proton.

Conjugate Acid-Base Pairs: Consider the reaction between an acid and a base

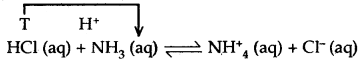
In this reaction, HCl donates a proton (acts as an acid) and forms Cl^– ion which has a tendency to accept a proton (can act as a base). Similarly, NH₃ accepts a proton and acts as a base but it forms an NH₄⁺ ion which has a tendency to behave as an acid. In other words, an acid donates a proton .and becomes a base and a base accepts a proton and becomes an acid.

The base formed from acid is referred to as the conjugate base of the acid. Similarly’ the acid formed from a base is called the conjugate acid of the base. Thus, in the above example, Cl^– is the conjugate base of acid HCl arid NH₄⁺ is the conjugate acid of the base NH₃.

The pairs of acids and bases are formed from each other by the gain or loss of a proton are called conjugate acid-base pairs.

Thus, each acid-base reaction involves two pairs of conjugate acids and bases. These are labeled as 1 and 2 as shown below:

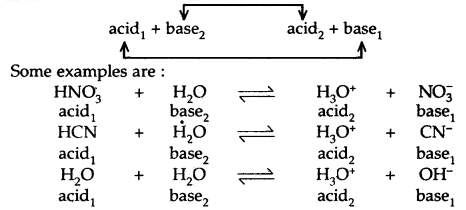
It may be noted that the conjugate base of a strong acid is a weak base and the conjugate base of a weak acid is a strong base. Strong acids like HCl, HNO₃ have weak bases like Cl^– and NO₃ and vice versa.

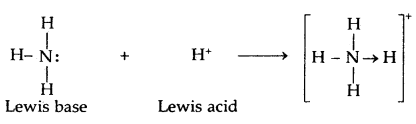
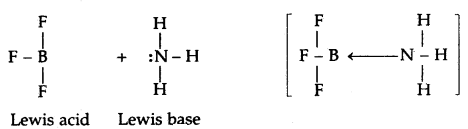
Lewis’s concept of Acids and Bases: G.N. Lewis (1923) proposed a more general and broader concept of acids and bases. According to this concept, an acid is a substance (molecule or ion) that can accept a pair of electrons while a base is a substance (molecule or ion) that can donate a pair of electrons. Some examples of Lewis acids and bases are

Lewis bases

1. Neutral species having at least one lone pair of electrons, e.g. NH₃, -NH₂, ROH
2. Negatively charged ions e.g., CN^–, Cl^–, OH^–.

Lewis acids

1. Molecules in which the central atom has incomplete octet e.g., AlCl₃, BF₃, FeCl₃, etc,
2. Simple cations act as Lewis acids, e.g., Ag⁺, H⁺, etc.
3. Molecules having empty d-orbitals in the central atom, e.g., SiF₄, SnCl₄, PF₅.
4. Molecules in which atoms of dissimilar electronegativities are joined by multiple bonds, e.g., CO₂, SO₂, etc.

The acid-base reaction may be written as:


Problem. Classify the following species into Lewis acids and Lewis bases and show how these act as such:

Answer:
This ion acts as a Lewis base as it can donate any one of its four electron pairs.

(b) OH^–
Answer:
OH^– is a lewis base as it can donate an electron lone pair.

(c) H⁺
Answer:
H⁺ A proton is a lewis acid as it can accept a lone pair of electrons from bases like OH^– and F^– ions.

(d) BCl₃^–
Answer:
BCl₃^– acts as a lewis acid as it can accept a lone pair from species like ammonia or amine molecules.

Ionization of water-ionic product of water
Water is a weak electrolyte and it undergoes self ionization as
H₂O + H₂O ⇌ H₃O⁺ + OH^–

Applying the law of chemical equilibrium
K = \(\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{O}\right]^{2}}\)

Since the dissociation of water takes place to a small extent, the concentration of the undissociated water is nearly constant. Therefore,
K = \(\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\text {Constant }}\)
K × Constant = [H₃O⁺][OH^–]
or
K_w = [H₃O⁺][OH^–]

where is a constant and is known as ionic product of water. Its value is constant at a particular temperature. At 298 K, the value of K_w is 1.008 × 10^-14mol2 L^-2. That is,
K_w = [H₃O+][OH-] = 1.008 × 10^-14 at 298 K

It is quite evident that the concentrations of H3O+ and OH- ions are equal in pure water so that
[H₃O⁺] = [OH^–] = 1.0 × 10^-7 mol L^-1

It may be remembered that
if [H₃O⁺] = [OH^–]: the solution is neutral
[H₃O⁺] > [OH^–]: the solution is acidic
[H₃O⁺] < [OH^–]: the solution is basic.

In a basic or acidic solution, the concentration of H3O+ or OH- may be calculated as
[H₃O⁺] = \(\frac{\mathrm{K}_{w}}{\left[\mathrm{OH}^{-}\right]}\)[OH~] = \(\frac{\mathrm{K}_{w}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\)

pH scale
The pH of a solution may be defined as the negative logarithm of the H₃O⁺ ion concentration in moles per liter. Mathematically, it may be expressed as
pH = – log [H₃O⁺]
or
log [H₃O⁺]

For neutral solution, pH = – log [1.0 × 10^-7] = 7
In a similar way, by substituting different values of [H₃O⁺] in the above relation, it can be seen that

• For acidic solution pH <7
• For basic solution pH >7
• For neutral solution pH = 7

To express the acidic or basic character of a solution, a scale has been proposed from pH 1 to 14. This scale is known as the pH scale.

It may be noted that solutions having pH between 0 to 2 are strongly acidic, those with pH between 2 to 4 are moderately acidic while the others having pH between 4 to 7 are weakly acidic. Similarly, the solutions having pH values between 7 to 10 are weakly basic, those having pH 10 to 12 are moderately basic whereas the others which haying a pH range between 12 to 14 are strongly basic.

p^OH scale Like p^H, p^OH may be defined as
p^OH = – log [OH^–]

At 298K p^H + p^OH = pK° = – logK_w = – log 10^-14
∴ p^H + p^OH= 14

At 298 K, Ionic product of water =1.0 × 10^-14
[precisely = 1.08 × 10^-14 mol² L^-2]

The value of K_w goes on increasing as the temperature increases.

It is because with the increase in temperature, the degree of ionization of water into H⁺ ions and OH^– ions increases.
But since pH = – log [H⁺]
∴ the p^H of water decreases with an increase in temperature.

The ionization of Bases
The bases in their aqueous solutions furnish OH^– (hydroxyl) ions.
For example
NaOH + H₂O (excess) → Na⁺ (aq) + OH^– (aq)
NH₃ + H₂O (excess) ⇌ NH₄OH (aq) ⇌ NH₄⁺ (aq) + OH^– (aq)

Strong bases like NaOH and KOH are completely dissociated into their constituent ions in dilute solutions.

Weak Bases like NH₄OH, AgOH are ionized in an aqueous solution to a small extent only. The ionization of a base is characterized by an equilibrium constant called base dissociation constant (K_b), for example for a base like MOH
MOH + H₂O (excess) ⇌ M⁺ (aq) + OH^– (aq)
K_b = \(\frac{\left[\mathrm{M}^{+}(\mathrm{aq})\right] \times\left[\mathrm{OH}^{-}(\mathrm{aq})\right]}{[\mathrm{M}(\mathrm{OH})]}\)

If n moles of a base is dissolved in V liters of the solution and a is the degree of dissociation of the base, then the amounts of various species at equilibrium present are

• No. of moles of MOH = n(1 – α)
• No. of moles of OH^– = nα
• No. of moles of M⁺ = nα

The corresponding concentrations in moles per litre are
[MOH] = n(1 – α)/V mol L^-1 = C(1 – α) mol L^-1
[OH^–] = nα/V mol L^-1 = Cα mol L^-1
[M⁺] = na/V mol^-1 = Cα mol L^-1.

Thus, the ionisation constant of the base is given by
K_b = \(\frac{\left[\mathrm{M}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{MOH}]}=\frac{\mathrm{C} \alpha \cdot \mathrm{C} \alpha}{\mathrm{C}(1-\alpha)}=\frac{\mathrm{C} \alpha^{2}}{(1-\alpha)}\)

where C is the molar concentration of the base in solution.
If α is small (i.e., the base is fairly weak) then a can be ignored in comparison to 1. Then
K_b = Cα²
or
α = \(\sqrt{\frac{\mathrm{K}_{b}}{\mathrm{C}}}=\sqrt{\mathrm{K}_{b} \mathrm{~V}}\) ……..(1)

where V is the volume of the solution in liters containing one mole of the base MOH. From equation (1), it is apparent that the degree of ionization of the base increases with dilution.

The hydroxide ion concentration in the solution is given by,
[OH] = Cα = C × \(\sqrt{\frac{\mathrm{K}_{b}}{\mathrm{C}}}=\sqrt{\mathrm{K}_{b} \mathrm{C}}\).

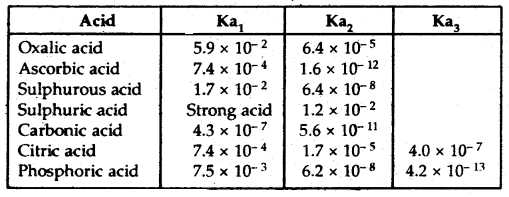
→ Di and Polybasic Acids and Di-and Polyacidic Bases: Some of the acids like oxalic acid, sulphuric acid, and phosphoric acids have more than one ionizable proton per molecule of the acid. Such acids are known as polybasic or polyprotic acids. The ionization reactions for example of a dibasic acid H₂X, are represented by the equations:
H₂X (aq) ⇌ H⁺ (aq) + HX^– (aq)
HX^– (aq) ⇌ H⁺(aq) + X₂^–(aq)

And the corresponding equilibrium constants are given below:
K_a1 = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{HX}^{-}\right]}{\left[\mathrm{H}_{2} \mathrm{X}\right]}\) and
K_a2 = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{2-}\right]}{\left[\mathrm{HX}^{-}\right]}\)

Here K_a1 and K_a2 are called the first and second ionization constants respectively of the acid H₂X. Similarly for tribasic acid like H₃PO₄ we have three ionization constants.

Similarly, expressions can be written for di and poly acidic bases

Table: The ionization constants of some common polyprotic acids (298 K)

→ Common ion effect in the ionization of Acids and Bases: The products of ionization of acid are hydrogen ions and the corresponding anion. If any one of the products is added to the acid solution then the acid is ionized to a lesser extent in agreement with Le Chatelier’s principle. Let us consider the example of acetic acid whose dissociation may be represented by its dissociation equilibria.
HAc (aq) ⇌ H⁺ (aq) + Ac^– (Aq) .
K_a = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A} c^{-}\right]}{[\mathrm{HAc}]}\)

If hydrogen ion is provided from any other source, it will combine with the acetate ion and reduce the degree of ionization of acetic acid. Similar will be the effect when the anion is added to the equilibrium mixture from an external source.

Hydrolysis of salts and the pH of their solutions: Salt hydrolysis describes the interaction of water and the cation/anion or both of a salt. The pH of the solution gets affected by this interaction. The cations (e.g., Na⁺, Rb⁺, Ca²⁺, Ba²⁺, etc.) of the strong Bases and, Anions (e.e. Cl^–, Br^–, I^–, NO₃^– etc.) of strong acids do not hydrolyze and therefore the solutions of salts formed by strong acids and bases are neutral i.e., their pH is 7. On the other hand, the solutions of salts formed from strong bases and weak acids are alkaline i.e., their pH is greater than 7. While the solutions of strong acids and weak bases are acidic i.e., their pH is less than 7.

→ The salts of strong bases and weak acids: Consider the solution of salts like MX formed by a strong base MOH and a weak acid HX. The salt is a strong electrolyte and is completely dissociated into M⁺ and X^– ions.
MX (s) + H₂O (l) → M⁺ (aq) + X^– (aq)

If the concentration of the salt is ‘C‘, then the concentration of M⁺ and X^– is also C. M⁺ is the cation of a strong base and therefore it remains as such but the anion X^– reacts with a water molecule to give unionized acid. This process is known as hydrolysis.
X^– (aq) + H₂O (l) ⇌ HX (aq) + OH^– (aq)

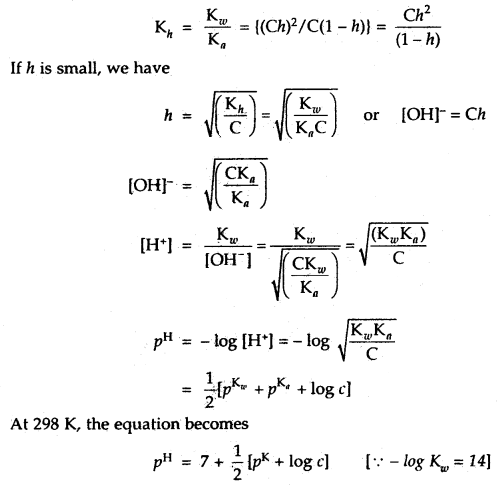
If ‘h’ is the degree of hydrolysis indicating the extent to which the anion is hydrolyzed and C is the concentration of MX or X^–, and further assuming that the concentration of water remains constant, the equilibrium constant for the reaction called the hydrolysis constant, K_h is given by the equation
K_h = \(\frac{[\mathrm{HX}]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{X}^{-}\right]}\)

Multiplying the numerator and the denominator of the right-hand side of the above equation by [H⁺], we obtain
K_h = \(\frac{[\mathrm{HX}]\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{X}^{-}\right]\left[\mathrm{H}^{+}\right]}=\frac{\mathrm{K}_{w}}{\mathrm{~K}_{a}}\)

If ‘C’ is the concentration of the salt in the solution and ‘h’ is the degree of hydrolysis, then after the equilibrium is established the concentration of various species in the solutions are given by the equations:
[X^–] = C(1 -h) and [OH^–] = [HX] = Ch

We then have the quadratic equation

→ The salts of strong acids and weak bases: The salt MX formed by a strong acid HX and a weak base MOH when dissolved in water dissociated into cations M⁺ and anions X^–. The cation undergoes hydrolysis represented by the reaction

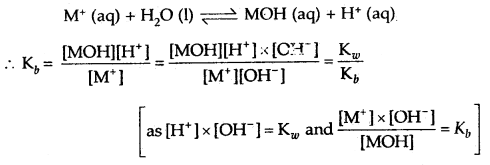
If ‘C is the concentration of the salt in the solution, h is its degree of hydrolysis, then equilibrium concentrations of various species are given by the equation.
[MOH] = [H⁺] = Ch and [M⁺] = C(1 – h)
K_h = Hydrolysis constt. = \(\frac{\mathrm{K}_{w}}{\mathrm{~K}_{b}}\)
= \(\frac{(C h)^{2}}{C(1-h)}=\frac{C h^{2}}{1-h}\)

If h = degree of hydrolysis is small
1 -h ≈ 1
∴ K_h = Ch²

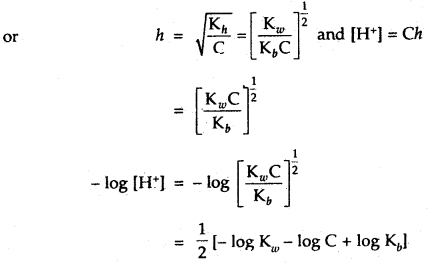
pH = \(\frac{1}{2}\)[p^K_w – p^K_b – log C]

At 298 K, the equation becomes
pH = 7 – \(\frac{1}{2}\)[p^K_b + logC]

→ The salts of weak bases and weak acids: Consider a salt MX formed by the weak base MOH and the weak acid MX. The salt in the aqueous solution is completely dissociated into the ions and both of these now ionize in water by the reaction
M⁺ (aq) + X^– (aq) + H₂O (l) ⇌ MOH (aq) + HX (aq)

Assuming that in dilute solution the concentration of water remains constant, the hydrolysis constant is given by the equation:
K_h = \(\frac{[\mathrm{MOH}][\mathrm{HX}]}{\left[\mathrm{M}^{+}\right]\left[\mathrm{X}^{-}\right]}\)

Multiplying the right hand side both in the numerator and the denominator by [H+][OH_], we get
K_h = \(\frac{[\mathrm{MOH}][\mathrm{HX}]}{\left[\mathrm{M}^{+}\right]\left[\mathrm{OH}^{-}\right]} \cdot \frac{[\mathrm{HX}]}{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right]}\) × [H+][OH-]

= \(\frac{K_{a}}{\left(K_{b} \times K_{a}\right)}\)

If ‘C’ the concentration of the salt and ‘h’ the degree of hydrolysis, then at equilibrium, the concentrations of various species are given by the relations
[MOH] = [HX] = Ch and [M⁺] = [X-] = C(1 – h) and
we have now
K_b = \(\frac{(\mathrm{C}) n^{2}}{\left[\mathrm{C}(1-h)^{2}\right]}=\frac{h}{(1-h)^{2}}\)
or
\(\frac{h}{1-h}\) = (K_h)^1/2

The concentration of the hydrogen ion can be calculated using the equation for the ionization constant of the acid, HX
K_a = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right]}{[\mathrm{HX}]}\)

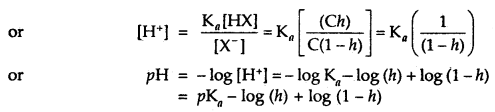
If K_h is small then ‘h’ is also small and we have h = K1/2 and (1 – h) = 1 and we have
pH = p^K_a – log (h) = p^K_a – [(log (K^_b)^1/2]
= \(\frac{1}{2}\)[p^K_w + p^K_a – p^K_b]
and at 298 K, we have pH = 7 + \(\frac{1}{2}\)(p^K_a – p^K_b).

→ Problem: The p^K_a of acetic acid and p^K_b of ammonium hydroxide are respectively 4.76 and 4.75. Calculate the pH of ammonium acetate solution.
Answer:
pH = 7 + \(\frac{1}{2}\)(p^K_a – p^K_b) = 7 + \(\frac{1}{2}\)(7.46 – 4.75)
= 7 + \(\frac{1}{2}\)(0.01) = 7.005.

→ Buffer Solutions: Many-body fluids e.g. blood and urine have definite pH and any deviation in their pH indicates malfunctioning of the body. The control of pH is very important in chemical and biochemical processes.

The solutions which resist change in their pH on dilution or on the addition of a small amount of acid or base are called buffer solutions.

Solubility Equilibria of Sparingly Soluble Salts The solubility of a substance depends on a number of factors. They are the lattice enthalpy of the salt and the solvation enthalpy of the ion. For salt to dissolve in a solvent the strong forces of attraction between the ions (lattice energy) must be overcome by the ion solvent its solvation enthalpy must be greater than its lattice enthalpy. On the basis of their solubility, the salts can be classified into 3 categories.

Category I:	Soluble	Solubility > 0.1 M
Category II:	Slightly	soluble 0.01 < solubility < 0.1 M
Category III:	Sparingly	soluble Solubility < 0.01 M.

Solubility Product Constant
Whenever a sparingly soluble ionic substance like AgCl, AgBr, Agl, BaSO₄, PbCrO₄, etc. is placed in a polar solvent like water, it dissolves to a very limited extent to produce ions in the solution. After a little while, an equilibrium between the solid phase and the ions in the solution is established. For example, for an ionic substance AB, the equilibrium is

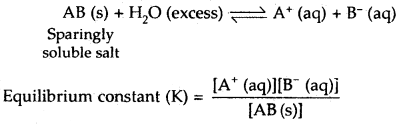
Since the concentration of the solid substances, AB at any temperature is constant, hence the above equilibrium (between ions and solid substance) can be described by a new constant K.
K_sp = [A⁺(aq)][B^–(aq)]

K_sp is called the solubility product constant or simply as solubility product of the salt concerned

K_sp for a salt of the type AB₂: For a sparingly soluble ionic salt of type AB₂, the dissolution leads to the equilibrium AB₂ (S) + H₂O (excess) ⇌ [A²⁺ (aq) + 2B^– (aq)]
K_sp = [A²⁺ (aq)][B^– (aq)]²

→ K_sp for a salt of the type A_mB_n: For a salt of the type A_mB_n (s), dissolution leads to dissociation according to the reaction.
A_mB_n (s) + H₂O (excess) ⇌ mA^p+ (aq) + nB^q- (aq)
where m^p+ = n^q-

The solubility product constant for the salt AmBn is then expressed as ‘
K_sp = [A^p+ (aq)]m [B^q- (aq)]n

Thus, the solubility product constant (Ksp) of a sparingly soluble salt is defined as the product of the molar concentrations of the ions in its saturated solution each raised to the power equal to the stoichiometric coefficient of the species in the balanced chemical equation.

Common ion effect on the solubility of ionic salts: A shift in the position of the equilibrium involving molecular and ionic forms of an electrolyte, by adding a strong electrolyte having one ion common to it is called common ion effect.

The solubility of a sparingly soluble salt decreases when a highly soluble salt having one ion common to the sparingly soluble salt is added to the solution due to the common ion effect. For example,

The solubility of AgCl (sparingly soluble salt) in water decreases when a small amount of KCl or NaCl is added to the solution. This is because KCl or NaCl dissociate completely in solution to produce more Cl^– ions.
KCl → K⁺ + Cl_^–

This increase in the concentration of Cl^– ion shifts the equilibrium.
AgCl (s) ⇌ Ag⁺(aq) + Cl^–(aq)

towards left. This causes more precipitation of AgCl (s). As a result, the solubility of AgCl in the solution decreases.

Table: The solubility product constants, K_sp of some common ionic salts at 298 K


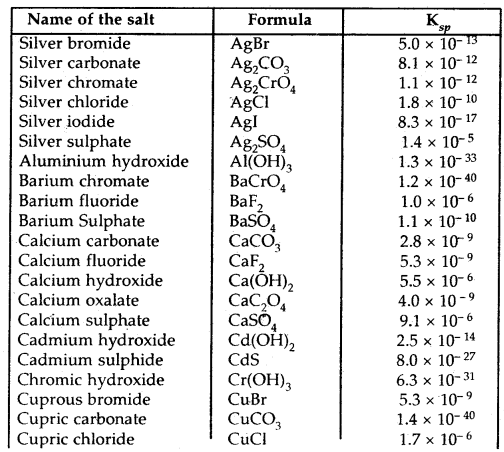
→ Equilibrium: It represents the state of a process in which the properties like the temperature, pressure, and concentration of the system do not show any change with the passage of time.

→ Equilibrium Mixture: The mixture of reactants and products in the equilibrium state is called an Equilibrium mixture.

Henry’s Law: The mass of a gas dissolved in a given mass of a solvent at any temperature is directly proportional to the pressure of the gas above the solvent.
i.e., m ∝ p
or
m = kp
where k is a constant of proportionality and is called Henry’s Constant. Its value depends upon the nature of the gas, the nature of the liquid, and the temperature.

Dynamic Equilibrium in Chemical Reactions The chemical reactions reach a state of dynamic equilibrium in which the rates of forward and reverse reactions are equal and there is no net change in composition.

Law of Chemical Equilibrium and Equilibrium Constant At a given temperature, the product of concentrations of the reaction products raised to the respective stoichiometric coefficient in the balanced chemical equation divided by the product of concentrations of the reactants raised to their individual stoichiometric coefficients has a constant value. This constant value is called the Equilibrium Constant.

The equilibrium constant for a general reaction
a A + bB ⇌ cD + dD
is expressed by KC = \(\frac{[\mathrm{C}]^{c} \times[\mathrm{D}]^{d}}{[\mathrm{~A}]^{a} \times[\mathrm{B}]^{b}}\).
where [A], [B], [C], [D] are the equilibrium concentrations of the reactants and products.

If the equilibrium constant for the reaction
H₂ (g) + I₂ (g) ⇌ 2HI (g) is K_c = [HI]²/[H₂][I₂]

the equilibrium constant for the reverse reaction
2HI (g) ⇌ H₂ (g) + I₂ (g) at the same temp, is
K_c = [H₂][I₂]/[HI]² = \(\frac{1}{x}=\frac{1}{\mathrm{~K}_{\mathrm{C}}}\)

Thus K_C = \(\frac{1}{\mathrm{~K}_{\mathrm{C}}}\)

→ Homogeneous Equilibrium: When the reactants and products of a chemical reaction are in the same state, the system is said to have a homogeneous equilibrium.

→ Heterogeneous Equilibrium: Equilibrium in a system having more than one phase is called heterogeneous equilibrium.

Predicting the direction of the reaction For a general reaction
aA + bB ⇌ cD + dD
Q_c = [C]^c × [D]^d/[A]^a × [B]^b then

• If Q_c > K_c, the reaction will proceed in the direction of reactants (reverse reaction).
• If Q_c < K_c, the reaction will proceed in the direction of the products (forward reaction).
• If Q_c = K_c, the reaction mixture is already in equilibrium.

That is, no net reaction occurs.
Relationship between Equilibrium Constant K, Reaction Quotient Q, and Gibbs Energy G

• If ΔG is negative, the reaction is spontaneous and proceeds in the forward direction.
• If ΔG is positive, the reaction is non-spontaneous.
• If ΔG = 0, the reaction has achieved equilibrium.

Mathematically,
ΔG – ΔG° + RT InQ.
where G° is standard Gibbs energy.
At equilibrium, when ΔG = 0 and Q = K_c

The above equation becomes
ΔG = ΔG° + RT InK .
ΔG° = – RT InK.
InK = – ΔG°/RT

Taking antilogs
K = e^{-ΔG /RT}

Thus if ΔG° < 0 then – ΔG°/RT is positive and e^{-ΔG /RT} > 1 making K > 1 which implies a spontaneous reaction.

If ΔG° > 0; then – ΔG°/RT is negative and e-ΔG /RT < 1, that is Kc < 1, which implies a non-spontaneous reaction.

For a general reaction
aA + bB ⇌ cD + dD

If p_A, p_B p_C and p_D indicate their partial pressures and [A], [B], [C] and [D] indicate their molar concentrations,

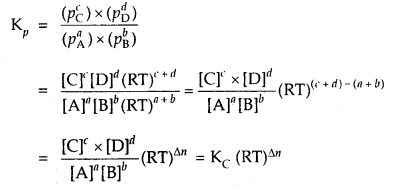
where Δn = (number of moles of gaseous products) – (number of moles of gaseous reactants) in the balanced chemical equation.

→ Le-Chatelier’s Principle: When a system in equilibrium is subjected to a change of temperature, pressure, or concentration the equilibrium shifts in a direction so as to undo the effect of the change applied.

This is applicable to all chemical and physical equilibria.

Arrhenius Concept of Acids and Bases.
→ Acids: are hydrogen-containing substances that dissociate in water to give hydrogen ions H⁺ (aq).

→ Bases: Bases are substances that produce hydroxyl ions OH^– (aq) on dissociation in water.

Bronsted-Lowry Concept of Acids and Bases
→ Acid: Acid is a substance that is capable of donating a hydrogen – ion H⁺. It is a Proton-donor.

→ Base: It is a substance that is capable of accepting a hydrogen ion H⁺. It is a Proton-acceptor.

Conjugate Acid-base Pair: The acid-base pair which differs only by one proton is called a conjugate acid-base pair.
HCl is an acid whose conjugate base is Cl^–.
NH₃ is a base whose conjugate acid is NH₄⁺.
OH^– is called the conjugate base of an acid H₂O.

If Bronsted acid is a strong acid, then its conjugate base is a weak base and vice-versa,

Lewis Concept of Acids and Bases
→ Acid: It is species which accepts electron pair.

→ Base: It is a species that donates an electron pair.

Thus in the reaction
BF₃ + :NH₃ ⇌ BF3 :NH₃
BF₃ is an acid and: NH₃ is a base.

The Ionisation Constant of Water and its Ionic Product
K_w which is = [H⁺] × [OH^–] is called an Ionic product of water

At 298 K, concentration to H⁺ = 1.0 × 10^-7 M
∴ Concentration of [OH-] is also = 1.0 × 10^-7 M
K_w = [H⁺] × [OH^–] = [H₃O⁺] × [OH-]
= 1.0 × 10^-14M²

The value of Ka is temperature-dependent.
Acidic substance [H₃O⁺] > [OH^–]
Neutral substance [H₃O⁺] = [OH^–]
Basic substance [H₃P⁺] < [OH^–]

The pH scale
PH = – log a_H⁺
where a_H⁺ is hydrogen ion activity

Hence pH of pure water = – log [10^-7] = 7.
Acidic solution has pH < 7.
Basic solution has pH > 7
Pure water or Neutral solution has pH = 7
K_w = [H₃O⁺] × [OH^–] – 10^-14
– log K_w = – log {[H₃O⁺] × OH^–]} = – log 10^-14
– log K_w = – log [H₃O⁺] – log [OH^–] = – log 10^-14
or
p^K_w = p^H + p^OH = 14

→ p^H meter: It is a device that measures the p^H-dependent electrical potential of the test solution within 0.001 precission

Ionization constants of weak acids
For a weak acid HX

HX (aq) + H₂O (I) ⇌ H₃O⁺ (aq) + X^– (aq)
K_a = [H₃O⁺][X^–]/[HX]
where K_a is called the dissociation or ionization constant of acid HX.

At a given temperature, the value of K_a is a measure of the strength of the acid HX. K_a is a dimensionless quantity.
Ionization of weak bases:
For a weak base MOH
MOH (aq) ⇌ M⁺ (aq) + OH^– (aq)
K_b = [M⁺] × [OH^–]/[MOH] is called base ionisation constant.

The value of K_b is a measure of the strength of a base.
K_a + K_b = K_w for a conjugate acid-base pair
or
p^K_a + p^K_b = p^K_w = 14 at 298 K

Note 1. For a polybasic acid, if K_a1, K_a2… are successive dissociation constants, then
K_a1 > K_a2 >K_a3

Similarly, H₂ S is a stronger acid than H₂O.

Note 3. In HA, H-A bond polarity becomes the deciding factor for determining the acid strength. As the electronegativity of A increases, the strength of the acid also increases.

→ Common-Ion Effect: The suppression of the degree of dissociation of a weak acid or a weak base on the addition of a common ion is called Common-Ion Effect.

Thus the degree of dissociation of a weak base NH₄OH is suppressed on the addition of common ion NH₄⁺ by adding NH₄Cl which is a strong base.

Hydrolysis of Salts

1. Salts of strong acids and strong bases like NaCl, KCl, NaNO₃ KNO₃/ K₂SO₄, Na₂SO₄ do not undergo hydrolysis. Their solutions in water are neutral.
2. Salts of strong acids and weak bases like NH₄Cl, CuSO₄ yield acidic solutions in water.
3. Salts of weak acids and strong bases on hydrolysis like CH₃COONa, Na₂CO₃ yield basic solutions in water.
4. Salts of weak acids and weak bases undergo hydrolysis.
   e.g. CH₃COONH₄. Their acidic or basic nature depends upon the comparative strength of the acid/base.

Buffer Solutions: The solution which resists a change in pH value on dilution or with the addition of small amounts of acid or alkali is called Buffer solutions.