RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS

RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS
• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS

Answer each of the following questions either in one word or one sentence or per requirement of the questions :
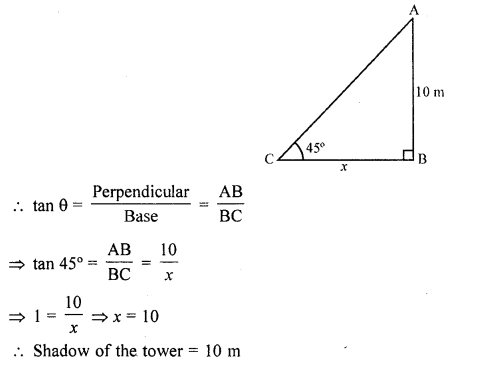
Question 1.
The height of a tower is 10 m. What is the length of its shadow when Sun’s altitude is 45° ?
Solution:
Let AB be the tower and BC is its shadow
Height of AB = 10 m
Let length of BC = x
Angle of elevation of A at C is 45°

Question 2.
If the ratio of the height of a angle tower and the length of 7 its shadow is \(\sqrt { 3 } \) : 1, what is the of elevation of the Sun?
Solution:
Ratio in the height of a tower and its shadow = \(\sqrt { 3 } \) : 1

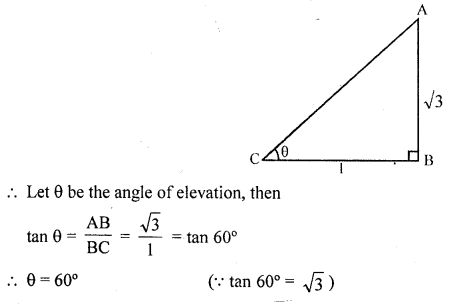
Question 3.
What is the angle of elevation of the Sun when the length of the shadow of a vertical pole is equal to its height ?
Solution:
Let height of a vertical pole = h
Then its shadow = x

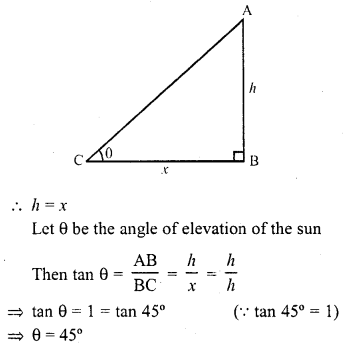
Question 4.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle of elevation of the top of the tower is 60°, what is the height of the tower ?
Solution:
Let AB be the tower and the angles of elevation of its top from a point C on the ground is 60° and BC = 20 m
Let height of the tower AB = h

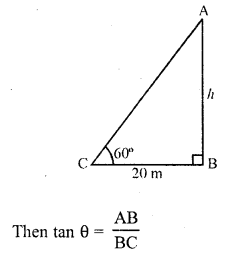
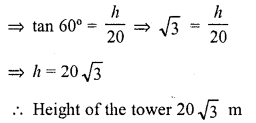
Question 5.
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line, with it are complementary, find the height of the tower.
Solution:
Let CD be the tower and let the angles of elevation of the top C of the tower from two points A and B are θ and (90° – θ) as the angles are complementary

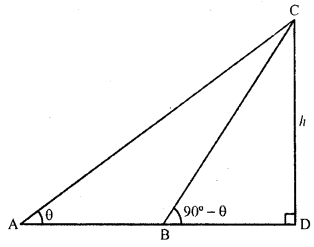
Let height of the tower CD = h
and AD = 9 m, BD = 4 m

Question 6.
In the figure, what are the angles of depression from the observing positions O₁ and O₂ of the object at A ?
Solution:
In the given figure, draw XY || ABC from O₁,O₂ (by joinging them)
∵∠AO₁C = 60°
∠AO₁O₂ = 90° – 60° = 30°
Similarly,
∵∠O₂ AB = 45°
∠XO₂A = ∠O₂AB = 45° (alternate angles)
Hence angles of depression are 30° and 45°

Question 7.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x : y. [CBSE2015]
Solution:
Let AB and CD be two towers which are apart from each other at a distance of BD and M is mid point of BD.
Angles of elevation are 30° and 60°

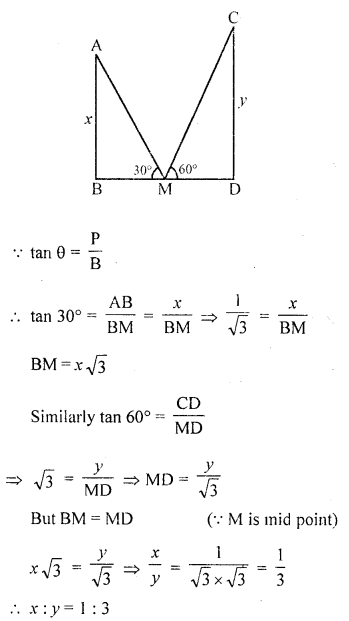
Question 8.
The angle of elevation of the top of a tower at a point on the ground is 30°. What will be the angle of elevation, if the height of the tower is tripled?     [CBSE 2015]
Solution:
Let AB be the tower and apgle of elevation of A at C is 30°

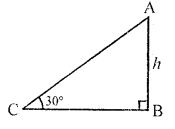
Question 9.
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 60° to the horizontal and reaches upto a point D of pole. If AD = 2.54 m, find the length of the ladder. (Use \(\sqrt { 3 } \)  = 1.73)       [CBSE 2016]
Solution:
BD = AB – AD = 6 – 2.54 = 3.46 m

Question 10.
An observer, 1.7 m tall, is 20\(\sqrt { 3 } \) m away from a tower. The angle of elevation from the eye of an observer to the top of tower is 30°. Find the height of the tower. [CBSE 2016]
Solution:

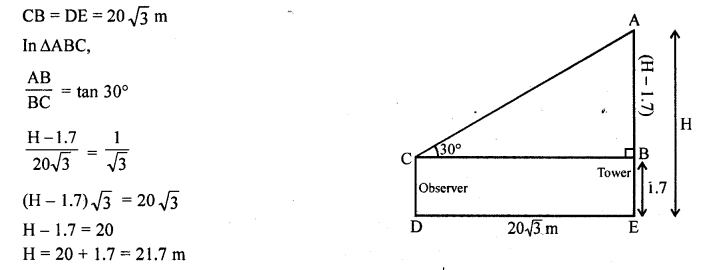
Question 11.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top-of the tower from the eye of the observer. [CBSE 2017]
Solution:

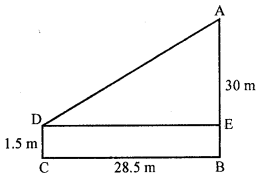
Here, AE = 28.5 m
ED = BC = 28.5 m
In ΔADE,
tan ∠ADE = \(\frac { 28.5 }{ 28.5 }\)
= ∠ADE = tan^-1(1) – 45°
∴ The angle of elevation at the top of the tower from the eye of the observer is 45°.

Hope given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.