ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test
Question 1.
(i)\(\begin{bmatrix} 2 & -1 \\ 5 & 1 \end{bmatrix}\)
(ii)[2 3 – 7]
(iii)\(\left[ \begin{matrix} 3 \\ 0 \\ -1 \end{matrix} \right] \)
(iv)\(\left[ \begin{matrix} \begin{matrix} 2 \\ 0 \\ 1 \end{matrix} & \begin{matrix} -4 \\ 0 \\ 7 \end{matrix} \end{matrix} \right] \)
(v)\(\left[ \begin{matrix} \begin{matrix} 2 & 7 & 8 \end{matrix} \\ \begin{matrix} -1 & \sqrt { 2 } & 0 \end{matrix} \end{matrix} \right] \)
(vi)\(\left[ \begin{matrix} \begin{matrix} 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \end{matrix} \right] \)
Solution:
(i) It is square matrix of order 2
(ii) It is row matrix of order 1 × 3
(iii) It is column matrix of order 3 × 1
(iv) It is matrix of order 3 × 2
(v) It is matrix of order 2 × 3
(vi) It is zero matrix of order 2 × 3
Question 2.
(i) If a matrix has 4 elements, what are the possible order it can have ?
(ii) If a matrix has 8 elements, what are the possible order it can have ?
Solution:
(i) It can have 1 × 4, 4 × 1 or 2 × 2 order
(ii) It can have 1 × 8, 8 × 1,2 × 4 or 4 × 2 order
Question 3.
Construct a 2 x 2 matrix whose elements aij are given by
(i) aij = 2i – j
(ii) aij = i.j
Solution:
(i) It can be \(\begin{bmatrix} 1 & 0 \\ 3 & 2 \end{bmatrix}\)
(ii) It can be \(\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}\)
Question 4.
Find the values of x and y if : \(\left[ \begin{matrix} 2x+y \\ 3x-2y \end{matrix} \right] =\left[ \begin{matrix} 5 \\ 4 \end{matrix} \right] \)
Solution:
Comparing corresponding elements,
2x + y = 5 …(i)
3x – 2y = 4 …(ii)
Multiply (i) by 2 and (ii) by ‘1’ we get
4x + 2y = 10, 3x – 2y = 4
Adding we get, 7x = 14 ⇒ x = 2
Substituting the value of x in (i)
2 x 2 + y = 5 ⇒ 4 + y = 5
y = 5 – 4 = 1
Hence x = 2, y = 1
Question 5.
Find the value of x if \(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Solution:
\(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Comparing the corresponding terms, we get.
-y = 2
⇒ y = -2
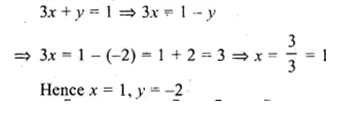
Question 6.
If \(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) ,find values of x and y
Solution:
\(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing the corresponding terms, we get.
x + 3 = 5
⇒ x = 5 – 3 = 2
⇒ y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7
Question 7.
Find the values of x, y and z if
\(\left[ \begin{matrix} \begin{matrix} x+2 & \quad \quad 6 \end{matrix} \\ \begin{matrix} 3 & \quad \quad \quad 5z \end{matrix} \end{matrix} \right] =\begin{bmatrix} -5 & \quad { y }^{ 2 }+y \\ 3 & -20 \end{bmatrix}\)
Solution:
Comparing the corresponding elements of equal determinents,
x + 2 = -5
⇒ x = -5 – 2 = -7
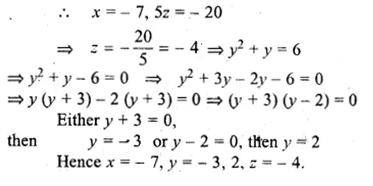
Question 8.
Find the values of x, y, a and b if
\(\begin{bmatrix} x-2 & y \\ a+2b & 3a-b \end{bmatrix}=\begin{bmatrix} 3 & 1 \\ 5 & 1 \end{bmatrix}\)
Solution:
Comparing corresponding elements
x – 2 = 3, y = 1
x = 3 + 2 = 5
a + 2b = 5 ……(i)
3a – b = 1 ……..(ii)
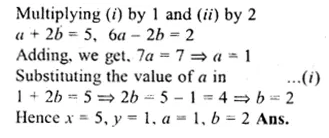
Question 9.
Find the values of a, b, c and d if
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Solution:
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Comparing the corresponding terms, we get.
3 = d ⇒ d = 3
⇒ 5 + c = – 1
⇒ c = -1 – 5
⇒ c = -6
a + b = 6 and ab = 8
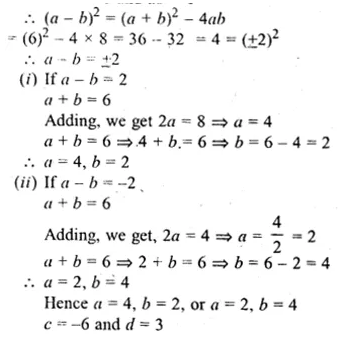
Question 10.
Find the values of x, y, a and b, if
\(\left[ \begin{matrix} \begin{matrix} 3x+4y & 2 & x-2y \end{matrix} \\ \begin{matrix} a+b & 2a-b & -1 \end{matrix} \end{matrix} \right] =\left[ \begin{matrix} \begin{matrix} 2 & \quad 2\quad & 4 \end{matrix} \\ \begin{matrix} 5 & -5 & -1 \end{matrix} \end{matrix} \right] \)
Solution:
Comparing the corresponding terms, we get.
3x + 4y = 2 ……(i)
x – 2y = 4 …….(ii)
Multiplying (i) by 1 and (ii) by 2
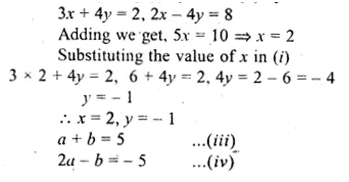
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.