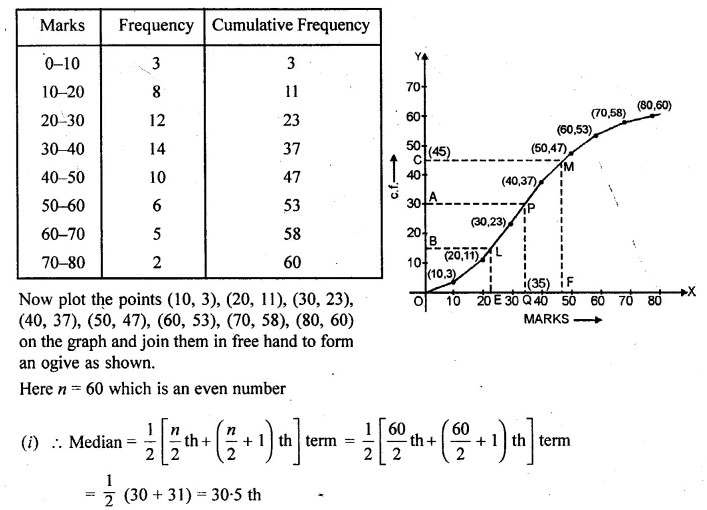
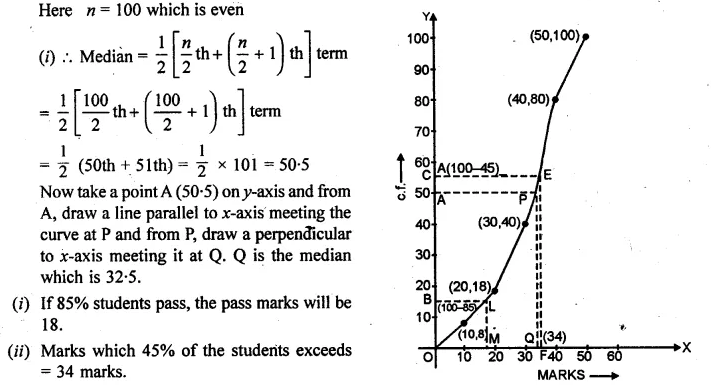
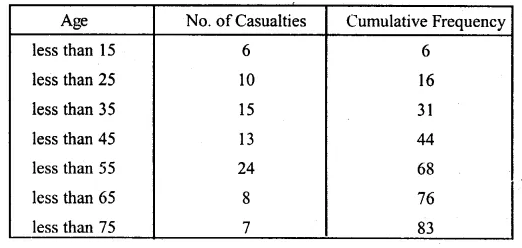
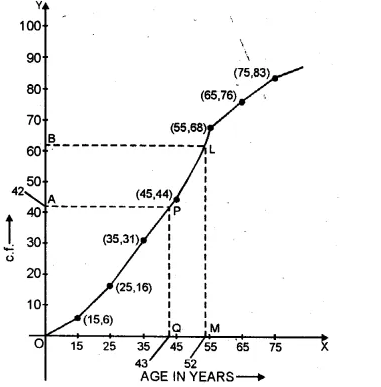
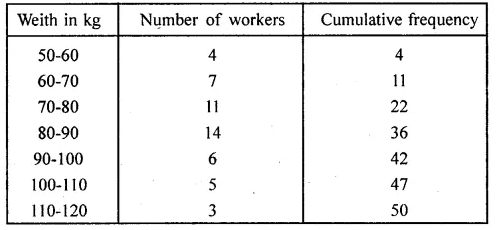
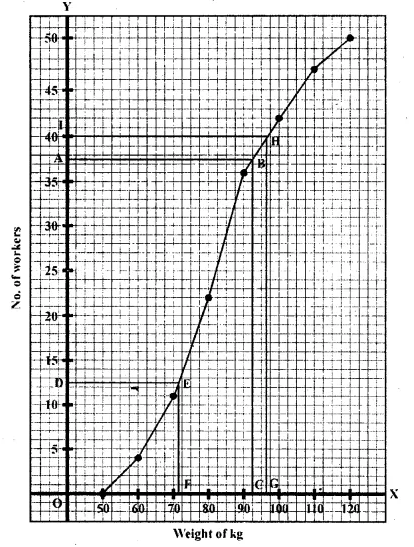
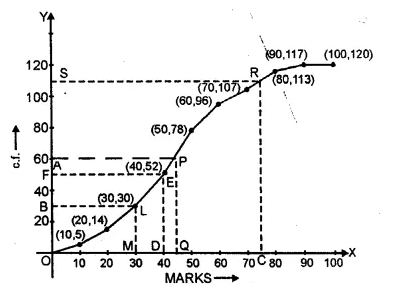
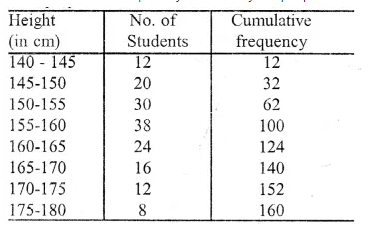
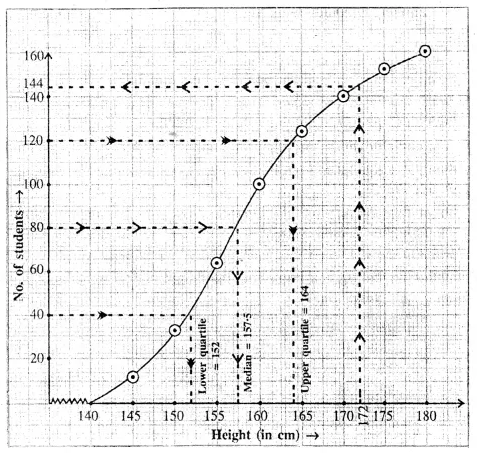
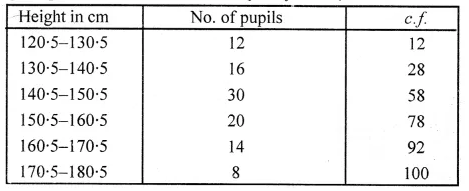
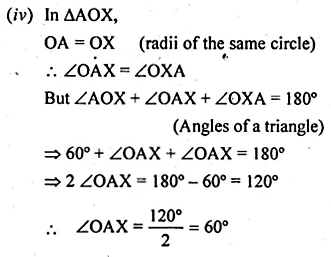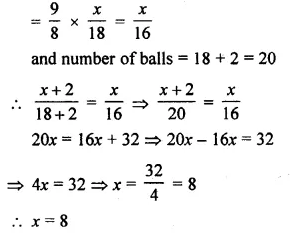ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test
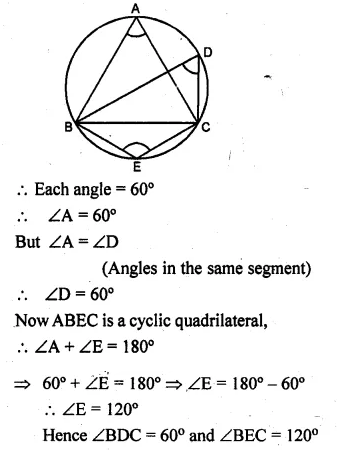
Question 1.
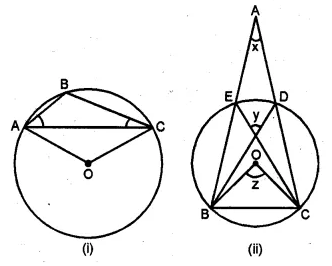
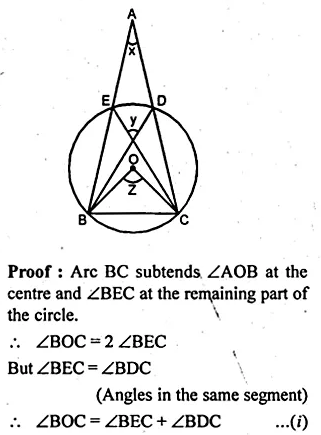
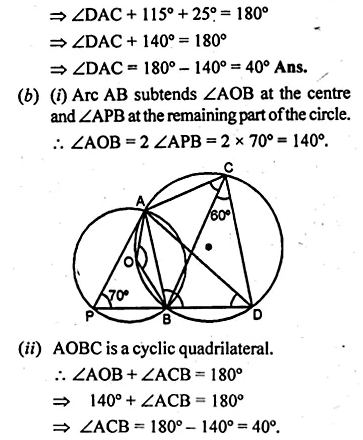
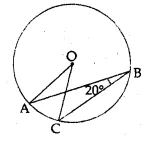
In the given figure, O is the centre of the circle. If ∠ABC = 20°, then ∠AOC is equal to
(a) 20°
(b) 40°
(c) 60°
(d) 10°
Solution:
In the given figure,
Arc AC subtends ∠AOC at the centre
and ∠ABC at the remaining part of the circle
∠AOC = 2∠ABC = 2 × 20° = 40° (b)
Question 2.
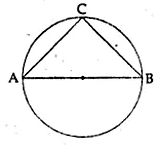
In the given figure, AB is a diameter of the circle. If AC = BC, then ∠CAB is. equal to
(a) 30°
(b) 60°
(c) 90°
(d) 45°
Solution:
In the given figure,
AB is the diameter of the circle and AC = BC
∠ACB = 90° (angle in a semi-circle)
AC = BC
Question 3.
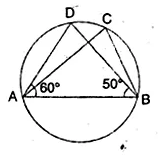
In the given figure, if ∠DAB = 60° and ∠ABD = 50° then ∠ACB is equal to
(a) 60°
(b) 50°
(c) 70°
(d) 80°
Solution:
In the given figure,
∠DAB = 60°, ∠ABD = 50°
In ∆ADB, ∆ADB = 180° – (60° + 50°)
= 180° – 110° = 70°
∠ACB = ∠ADB
(angles in the same segment) = 70° (c)
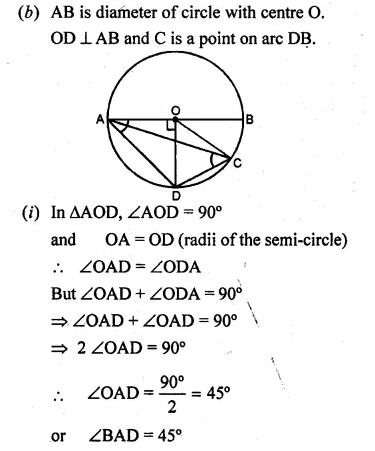
Question 4.
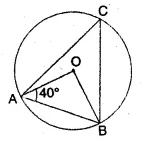
In the given figure, O is the centre of the circle. If ∠OAB = 40°, then ∠ACB is equal to
(a) 50°
(b) 40°
(c) 60°
(d) 70°
Solution:
In the given figure, O is the centre of the circle.
In ∆OAB,
∠OAB = 40°
But ∠OBA = ∠OAB = 40°
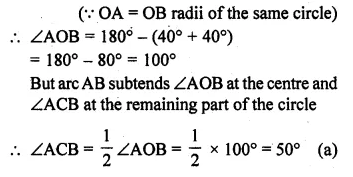
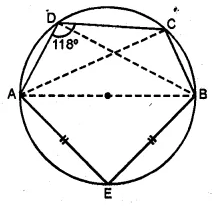
Question 5.
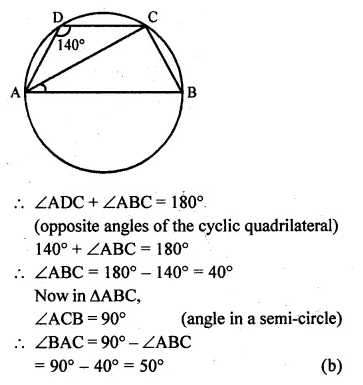
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to
(a) 80°
(b) 50°
(c) 40°
(d) 30°
Solution:
ABCD is a cyclic quadrilateral,
AB is the diameter of the circle circumscribing it
∠ADC = 140°, ∠BAC = Join AC
Question 6.
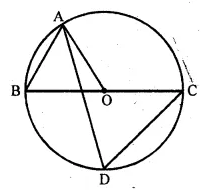
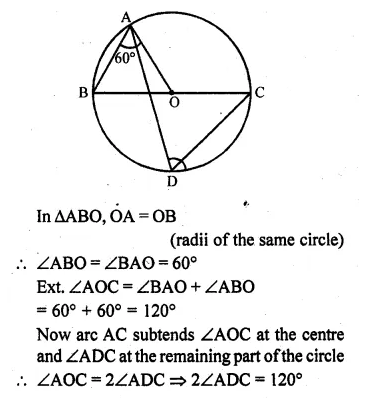
In the given figure, O is the centre of the circle. If ∠BAO = 60°, then ∠ADC is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 120°
Solution:
In the given figure, O is the centre of the circle ∠BAO = 60°

Question 7.
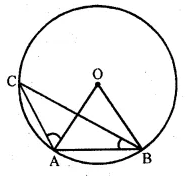
In the given figure, O is the centre of the circle. If ∠AOB = 90° and ∠ABC = 30°, then ∠CAO is equal to
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Solution:
In the given figure, O is the centre of the circle
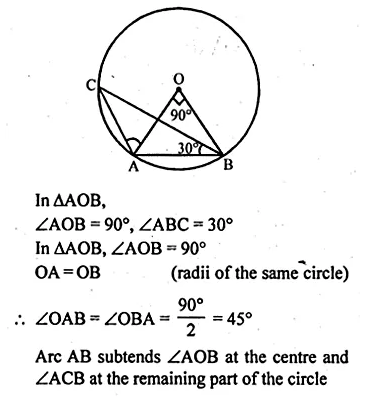
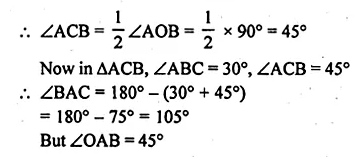
∠CAO = 105° – 45° = 60° (d)
Question 8.
In the given figure, O is the centre of a circle. If the length of chord PQ is equal to the radius of the circle, then ∠PRQ is
(a) 60°
(b) 45°
(c) 30°
(d) 15°
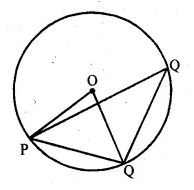
Solution:
In the given figure, O is the centre of the circle
Chord PQ = radius of the circle
∆OPQ is an equilateral triangle
∴∠POQ = 60°
Arc PQ subtends ∠POQ at the centre and
∴∠PRQ at the remaining part of the circle
∴∠PRQ = \(\\ \frac { 1 }{ 2 } \) ∠POQ = \(\\ \frac { 1 }{ 2 } \) x 60° = 30° (c)
Question 9.
In the given figure, if O is the centre of the circle then the value of x is
(a) 18°
(b) 20°
(c) 24°
(d) 36°
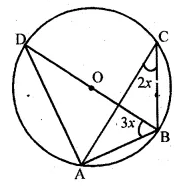
Solution:
In the given figure, O is the centre of the circle.
Join OA.
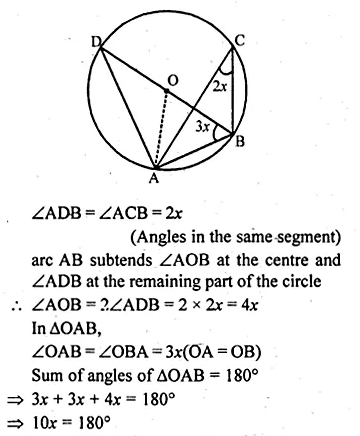
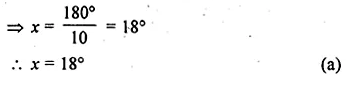
Question 10.
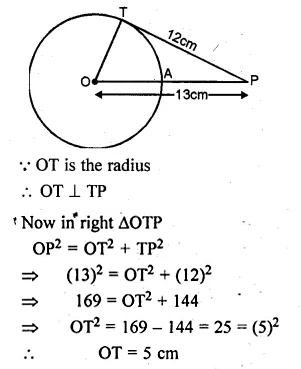
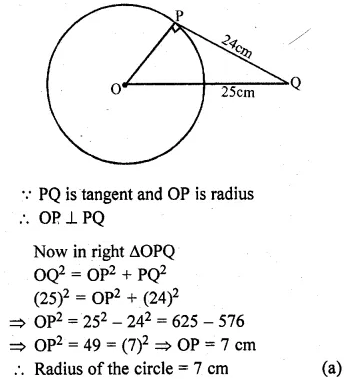
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
From Q, length of tangent PQ to the circle = 24 cm
and QO = 25 cm
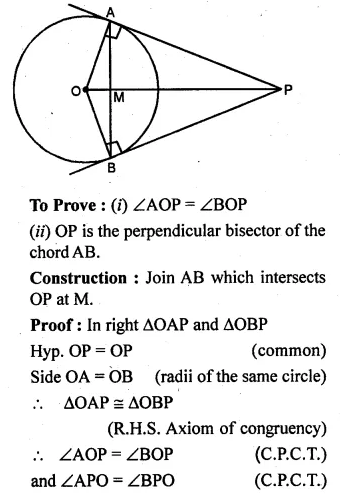
Question 11.
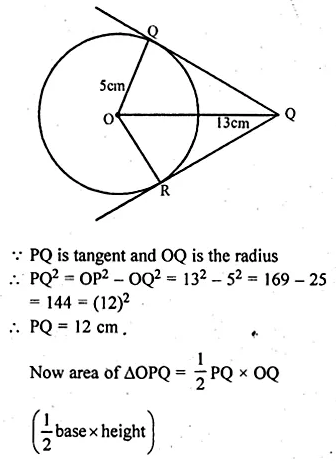
From a point which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm²
(b) 65 cm²
(c) 30 cm²
(d) 32.5 cm²
Solution:
Let point P is 13 cm from O, the centre of the circle
Radius of the circle (OQ) = 5 cm
PQ and PR are tangents from P to the circle
Join OQ and OR
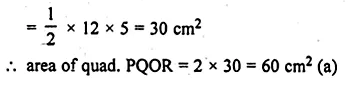
Question 12.
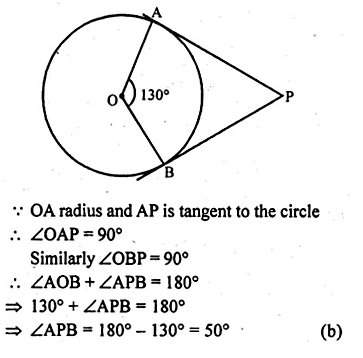
If angle between two radii of a circle is 130°, the angle between the tangents at the ends of the radii is
(a) 90°
(b) 50°
(c) 70°
(d) 40°
Solution:
Angles between two radii OA and OB = 130°
From A and B, tangents are drawn which meet at P
Question 13.
In the given figure, PQ and PR are tangents from P to a circle with centre O. If ∠POR = 55°, then ∠QPR is
(a) 35°
(b) 55°
(c) 70°
(d) 80°
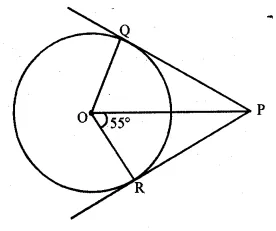
Solution:
In the given figure,
PQ and PR are the tangents to the circle from a point P outside it

Question 14.
If tangents PA and PB from an exterior point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 100°
Solution:
Length of tangents PA and PB to the circle from a point P
outside the circle with centre O, and inclined an angle of 80°
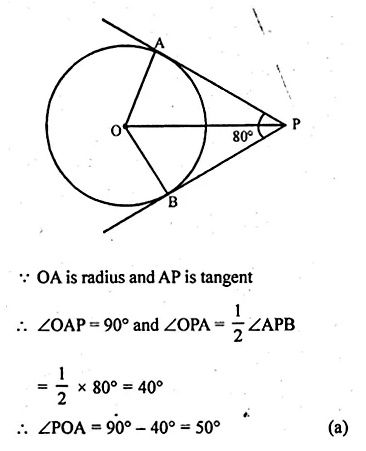
Question 15.
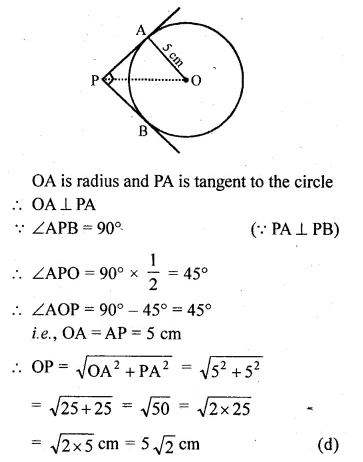
In the given figure, PA and PB are tangents from point P to a circle with centre O. If the radius of the circle is 5 cm and PA ⊥ PB, then the length OP is equal to
(a) 5 cm
(b) 10 cm
(c) 7.5 cm
(d) 5√2 cm
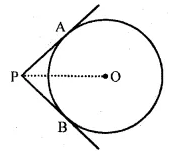
Solution:
In the given figure,
PA and PB are tangents to the circle with centre O.
Radius of the circle is 5 cm, PA ⊥ PB.
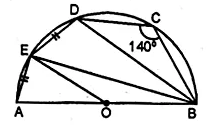
Question 16.
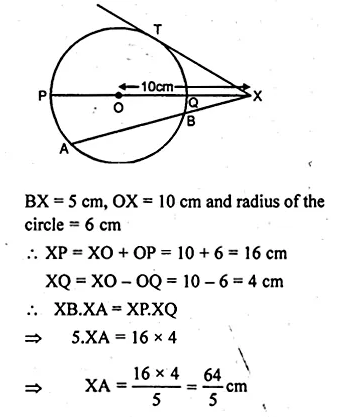
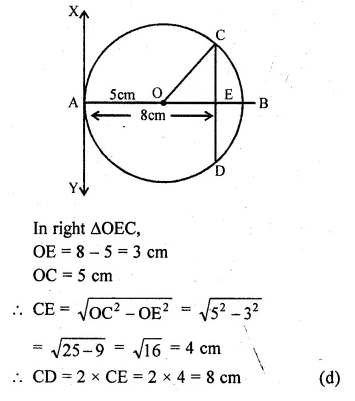
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:
AB is the diameter of a circle with radius 5 cm
At A, XAY is a tangent to the circle
CD || XAY at a distance of 8 cm from A
Join OC
Question 17.
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other is
(a) 3 cm
(b) 6 cm
(c) 9 cm
(d) 1 cm
Solution:
Radii of two concentric circles are 4 cm and 5 cm
AB is a chord of the bigger circle
which is tangent to the smaller circle at C.
Join OA, OC
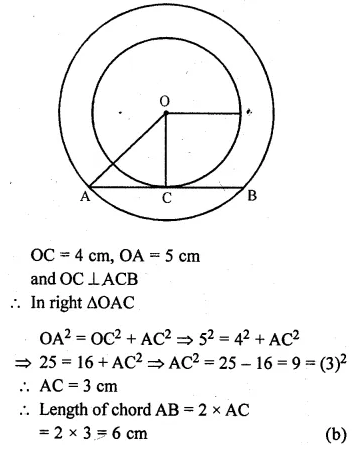
Question 18.
In the given figure, AB is a chord of the circle such that ∠ACB = 50°. If AT is tangent to the circle at the point A, then ∠BAT is equal to
(a) 65°
(b) 60°
(c) 50°
(d) 40°
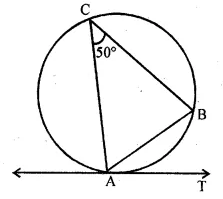
Solution:
In the given figure, AB is a chord of the circle
such that ∠ACB = 50°
AT is tangent to the circle at A
AT is tangent and AB is a chord
∠ACB = ∠BAT = 50°
(Angles in the alternate segments) (c)
Question 19.
In the given figure, O is the centre of a circle and PQ is a chord. If the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is
(a) 100°
(b) 80°
(c) 90°
(d) 75°
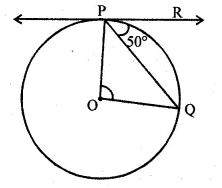
Solution:
In the given figure, O is the centre of the circle.
PR is tangent and PQ is chord ∠RPQ = 50°
OP is radius and PR is tangent to the circle

Question 20.
In the given figure, PA and PB are tangents to a circle with centre O. If ∠APB = 50°, then ∠OAB is equal to
(a) 25°
(b) 30°
(c) 40°
(d) 50°
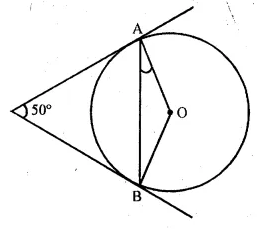
Solution:
In the given figure,
PA and PB are tangents to the circle with centre O.
∠APB = 50°
But ∠AOB + ∠APB = 180°
∠AOB + 50° = 180°
⇒ ∠AOB = 180° – 50° = 130°
In ∆OAB,
OA = OB (radii of the same circle)
∠OAB = ∠OBA
But ∠OAB + ∠OBA = 180° – ∠AOB
= 180° – 130° = 50°
∠OAB = \(\frac { { 50 }^{ 0 } }{ 2 } \) = 25° (a)
Question 21.
In the given figure, sides BC, CA and AB of ∆ABC touch a circle at point D, E and F respectively. If BD = 4 cm, DC = 3 cm and CA = 8 cm, then the length of side AB is
(a) 12 cm
(b) 11 cm
(c) 10 cm
(d) 9 cm
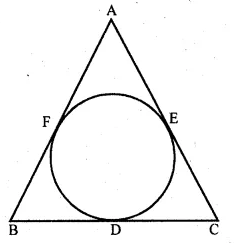
Solution:
In the given figure,
sides BC, CA and AB of ∆ABC touch a circle at D, E and F respectively.
BD = 4 cm, DC = 3 cm and CA = 8 cm
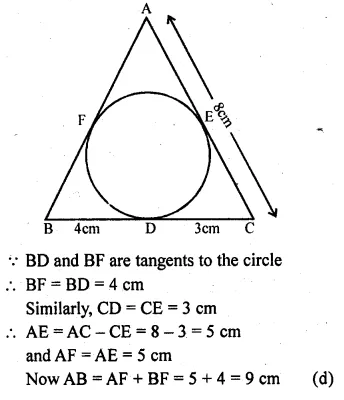
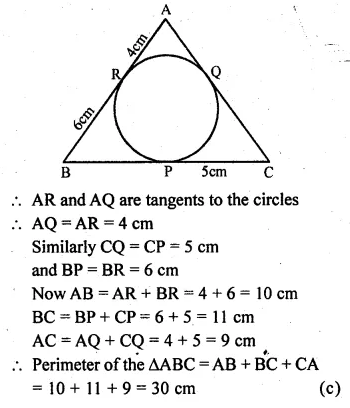
Question 22.
In the given figure, sides BC, CA and AB of ∆ABC touch a circle at the points P, Q and R respectively. If PC = 5 cm, AR = 4 cm and RB = 6 cm, then the perimeter of ∆ABC is
(a) 60 cm
(b) 45 cm
(c) 30 cm
(d) 15 cm
Solution:
In the given figure, sides BC, CA and AB of ∆ABC
touch a circle at P, Q and R respectively
PC = 5 cm, AR = 4 cm, RB = 6 cm
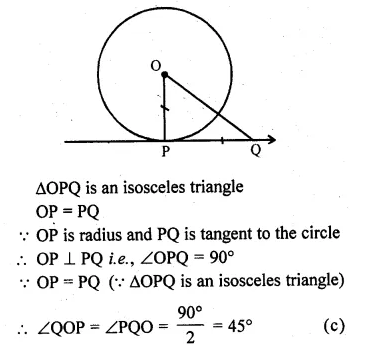
Question 23.
PQ is a tangent to a circle at point P. Centre of circle is O. If ∆OPQ is an isosceles triangle, then ∠QOP is equal to
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Solution:
PQ is tangent to the circle at point P centre of the circle is O.
Question 24.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then the value of x is
(a) 25°
(b) 65°
(c) 115°
(d) 90°
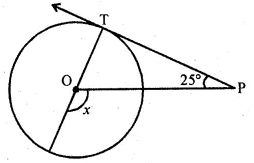
Solution:
In the given figure, PT is the tangent at T to the circle with centre O.
∠TPO = 25°
OT is the radius and TP is the tangent

Question 25.
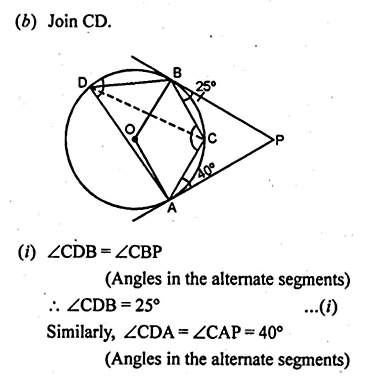
In the given figure, PA and PB are tangents at ponits A and B respectively to a circle with centre O. If C is a point on the circle and ∠APB = 40°, then ∠ACB is equal to
(a) 80°
(b) 70°
(c) 90°
(d) 140°
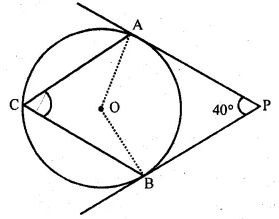
Solution:
In the given figure,
PA and PB are tangents to the circle at A and B respectively
C is a point on the circle and ∠APB = 40°
But ∠APB + ∠AOB = 180°
Question 26.
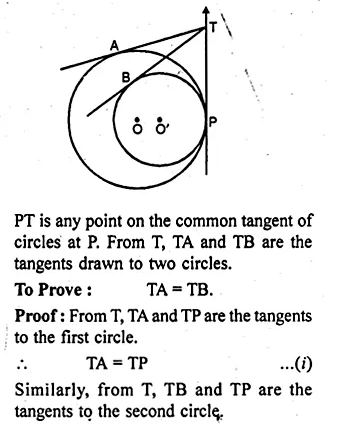
In the given figure, two circles touch each other at A. BC and AP are common tangents to these circles. If BP = 3.8 cm, then the length of BC is equal to
(a) 7.6 cm
(b) 1.9 cm
(c) 11.4 cm
(d) 5.7 cm
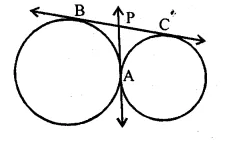
Solution:
In the given figure, two circles touch each other at A.
BC and AP are common tangents to these circles
BP = 3.8 cm

Question 27.
In the given figure, if sides PQ, QR, RS and SP of a quadrilateral PQRS touch a circle at points A, B, C and D respectively, then PD + BQ is equal to
(a) PQ
(b) QR
(c) PS
(d) SR
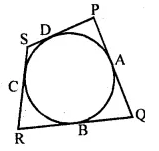
Solution:
In the given figure,
sides PQ, QR, RS and SP of a quadrilateral PQRS
touch a circle at the points A, B, C and D respectively
PD and PA are the tangents to the circle
∴ PA = PD …(i)
Similarly, QA and QB are the tangents
∴ QA = QB …(ii)
Now PD + BQ = PA + QA = PQ (a)
[From (i) and (ii)]
Question 28.
In the given figure, PQR is a tangent at Q to a circle. If AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
(a) 20°
(b) 40°
(b) 35°
(d) 45°
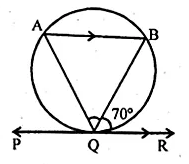
Solution:
In the given figure, PQR is a tangent at Q to a circle.
Chord AB || PR and ∠BQR = 70°
BQ is chord and PQR is a tangent
∠BQR = ∠A

Question 29.
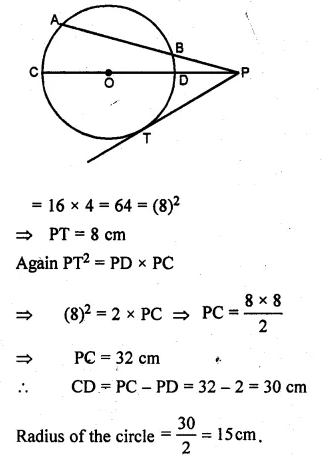
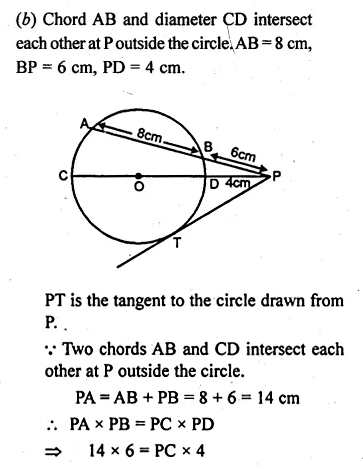
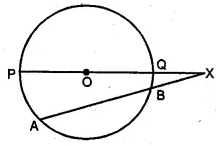
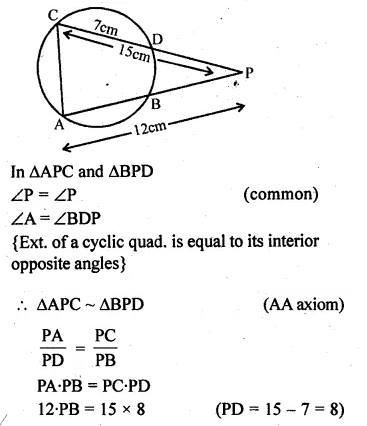
Two chords AB and CD of a circle intersect externally at a point P. If PC = 15 cm, CD = 7 cm and AP = 12 cm, then AB is
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) none of these
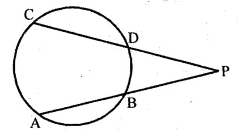
Solution:
In the given figure,
two chords AB and CD of a circle intersect externally at P.
PC = 15 cm, CD = 7 cm, AP = 12 cm
Join AC and BD
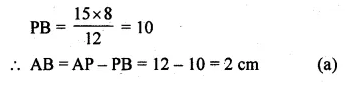
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.