ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Find the mode of the following sets of numbers ;
(i) 3, 2, 0, 1, 2, 3, 5, 3
(ii) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(iii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Solution:
(i) ∵ The number 3 occurs maximum times
Mode = 3
(ii) ∵ The number 8 occurs maximum times
Mode = 8
(iii) ∵ The number 5, occurs maximum times
Mode = 5

Question 2.
Calculate the mean, the median and the mode of the numbers : 3, 2, 6, 3, 3, 1, 1, 2
Solution:
Arranging in ascending order 1, 1, 2, 2, 3, 3, 3, 6
(i) Mean = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\frac { 1+1+2+2+3+3+3+6 }{ 8 } \)
= \(\\ \frac { 21 }{ 8 } \)
= 2.625
(ii) Here n = 8 which is even

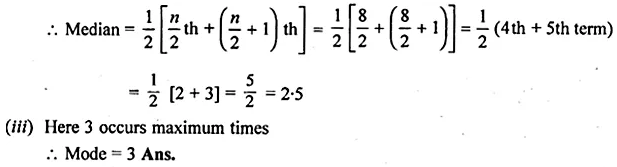
Question 3.
Find the mean, median and mode of the following distribution : 8, 10, 7, 6, 10, 11, 6, 13, 10
Solution:
Mean = \(\\ \frac { 8+10+7+6+10+11+6+13+10 }{ 2 } \)
= \(\\ \frac { 81 }{ 9 } \) = 9
Given nos. in ascending order are as follows:
6, 6, 7, 8, 10, 10, 10, 11, 13
Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = 5th term = 10
Mode = 10 (having highest frequency 3 times)

Question 4.
Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2
Solution:
Arranging in ascending order 1, 2, 3, 3, 3, 4, 5, 5, 6, 7
(i) Mean = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\frac { 1+2+3+3+3+4+5+5+6+7 }{ 8 } \)
= \(\\ \frac { 39 }{ 10 } \)
= 3.9

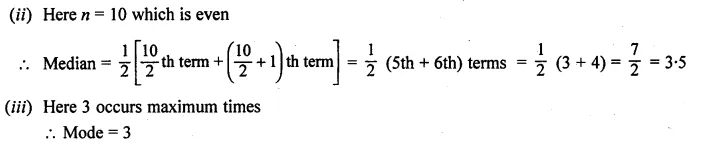
Question 5.
The marks of 10 students of a class in an examination arranged in ascending order are as follows: 13, 35, 43, 46, x, x +4, 55, 61,71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data. (2017)
Solution:
Given marks are 13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
n = 10 (even), median = 48

Question 6.
A boy scored the following marks in various class tests during a term each test being marked out of 20: 15, 17, 16, 7, 10, 12, 14, 16, 19, 12, 16
(i) What are his modal marks ?
(ii) What are his median marks ?
(iii) What are his mean marks ?
Solution:
Arranging in ascending order 7, 10, 12, 12, 14, 15, 16, 16, 16, 17, 19
(ii) Here n = 11 which is odd

Question 7.
Find the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks : 0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8
Solution:
Here, n = 16

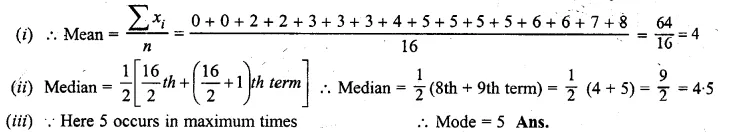
Question 8.
Find the mode and median of the following frequency distribution :

Solution:

Question 9.
The marks obtained by 30 students in a class assessment of 5 marks is given below:

Calculate the mean, median and mode of the above distribution.
Solution:

Question 10.
The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.

Solution:

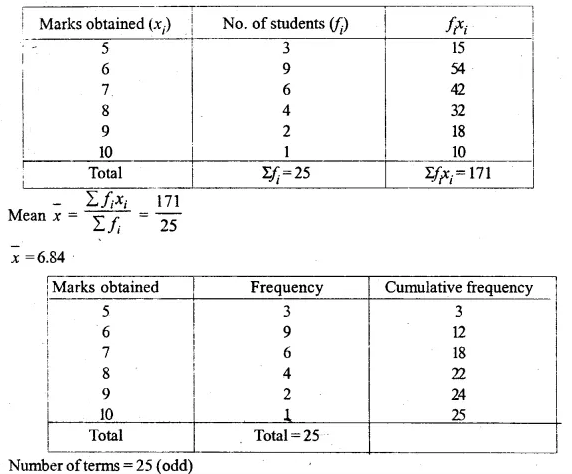
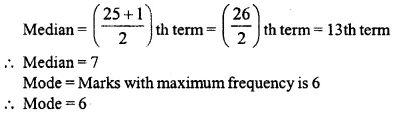
Question 11.
At a shooting competition, the scores of a competitor were as given below :

(i) What was his modal score ?
(ii) What was his median score ?
(iii) What was his total score ?
(iv) What was his mean ?
Solution:
Writing the given distribution in cumulative frequency distribution:

Question 12.
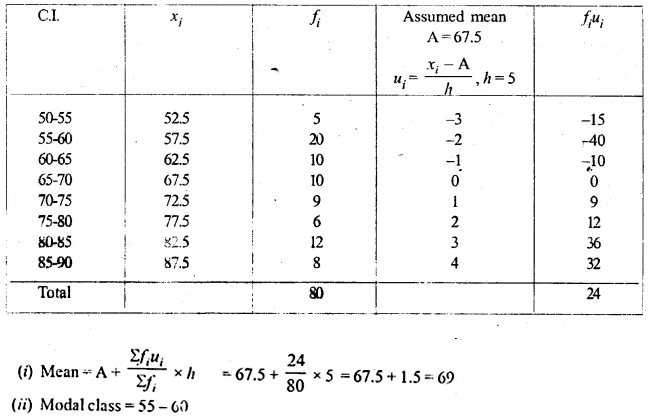
(i) Using step-deviation method, calculate the mean marks of the following distribution.
(ii) State the modal class.

Solution:

Question 13.
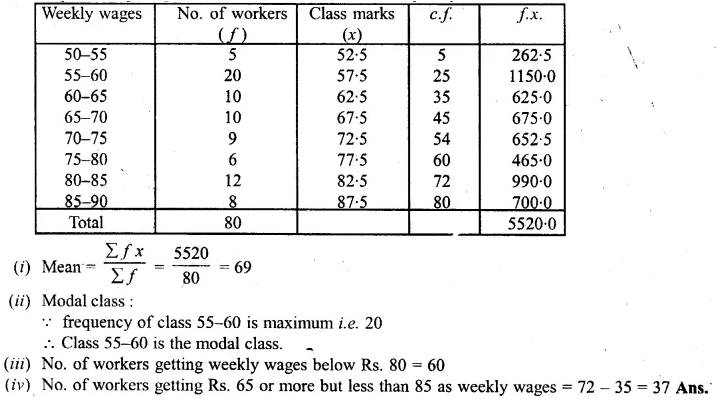
The following table gives the weekly wages (in Rs.) of workers in a factory :

Calculate:
(i) The mean.
(ii) the modal class
(iii) the number of workers getting weekly wages below Rs. 80.
(iv) the number of workers getting Rs. 65 or more but less than Rs. 85 as weekly wages.
Solution:
Representing the given distribution in cumulative frequency distribution

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3, drop a comment below and we will get back to you at the earliest.