ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Given that M = \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix} \) and N = \(\begin{bmatrix} 2 & 0 \\ -1 & 2 \end{bmatrix}\),find M + 2N
Solution:
M = \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix} \)
N = \(\begin{bmatrix} 2 & 0 \\ -1 & 2 \end{bmatrix}\)

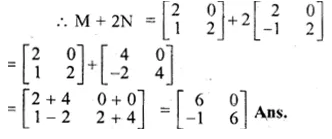
Question 2.
If A = \(\begin{bmatrix} 2 & 0 \\ -3 & 1 \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & 1 \\ -2 & 3 \end{bmatrix} \)
find 2A – 3B
Solution:
A = \(\begin{bmatrix} 2 & 0 \\ -3 & 1 \end{bmatrix} \)
B = \(\begin{bmatrix} 0 & 1 \\ -2 & 3 \end{bmatrix} \)

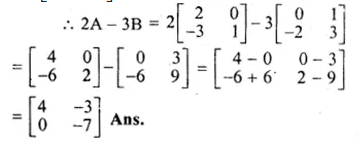
Question 3.
If A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \)
Compute 3A + 4B
Solution:
A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)
B = \(\begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \)

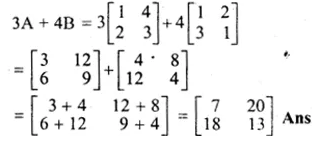
Question 4.
Given A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix} \)
(i) find the matrix 2A + B
(ii) find a matrix C such that C + B = \(\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)
B = \(\begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix} \)

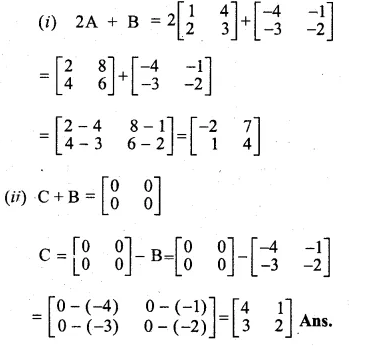
Question 5.
A = \(\begin{bmatrix} 1 & 2 \\ -2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & -1 \\ 1 & 2 \end{bmatrix} \) , C = \(\begin{bmatrix} 0 & 3 \\ 2 & -1 \end{bmatrix} \)
Find A + 2B – 3C
Solution:
A = \(\begin{bmatrix} 1 & 2 \\ -2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & -1 \\ 1 & 2 \end{bmatrix} \) , C = \(\begin{bmatrix} 0 & 3 \\ 2 & -1 \end{bmatrix} \)
∴ A + 2B – 3C

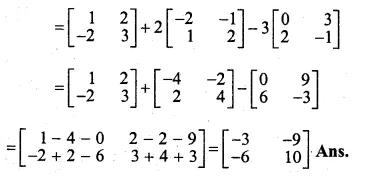
Question 6.
If A = \(\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix} \)
Find the matrix X if :
(i) 3A + X = B
(ii) X – 3B = 2A
Solution:
A = \(\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix} \)
B = \(\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix} \)
(i) 3A + X = B
⇒ X = B – 3A

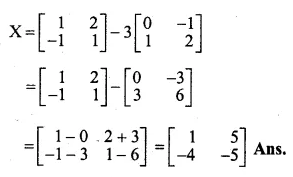
Question 7.
Solve the matrix equation
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-3X=\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}\)
Solution:
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-3X=\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}\)
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}=3X\)

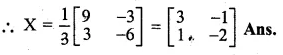
Question 8.
If \(\begin{bmatrix} 1 & \quad 4 \\ -2 & \quad 3 \end{bmatrix}+2M=3\begin{bmatrix} 3 & \quad 2 \\ 0 & -3 \end{bmatrix}\), find the matrix M
Solution:
\(\begin{bmatrix} 1 & \quad 4 \\ -2 & \quad 3 \end{bmatrix}+2M=3\begin{bmatrix} 3 & \quad 2 \\ 0 & -3 \end{bmatrix}\)
2M =

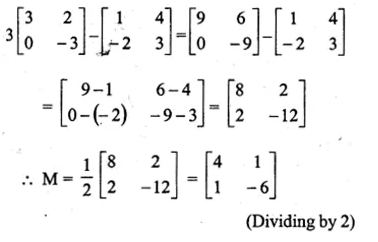
Question 9.
A = \(\begin{bmatrix} 2 & -6 \\ 2 & 0 \end{bmatrix} \) and B = \(\begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \) , C = \(\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
Find the matrix X such that A + 2X = 2B + C
Solution:
A = \(\begin{bmatrix} 2 & -6 \\ 2 & 0 \end{bmatrix} \) and B = \(\begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \) , C = \(\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
let X = \(\begin{bmatrix} x & y \\ z & t \end{bmatrix}\)

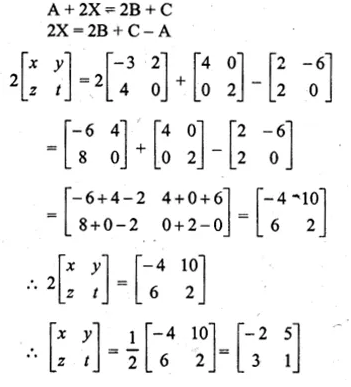
Question 10.
Find X and Y if X + Y = \(\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}\) and X – Y = \(\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\)
Solution:
X + Y = \(\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}\)…..(i)
X – Y = \(\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\)…….(ii)

Question 11.
If \(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\) Find the values of x and y
Solution:
\(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\)
\(\begin{bmatrix} 6 & 8 \\ 10 & 2x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\)

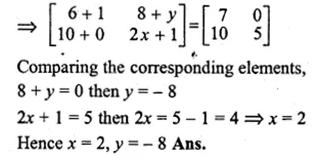
Question 12.
If \(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\) Find the values of x and y
Solution:
\(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\)
\(\begin{bmatrix} 6 & 8 \\ 10 & 2x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\)

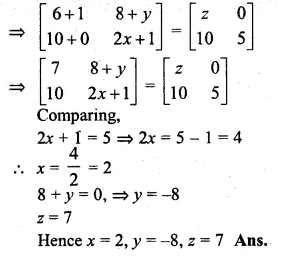
Question 13.
If \(\begin{bmatrix} 5 & 2 \\ -1 & \quad y+1 \end{bmatrix}-2\begin{bmatrix} 1 & 2x-1 \\ 3 & -2 \end{bmatrix}=\begin{bmatrix} 3 & -8 \\ -7 & 2 \end{bmatrix}\) Find the values of x and y
Solution:
\(\begin{bmatrix} 5 & 2 \\ -1 & \quad y+1 \end{bmatrix}-2\begin{bmatrix} 1 & 2x-1 \\ 3 & -2 \end{bmatrix}=\begin{bmatrix} 3 & -8 \\ -7 & 2 \end{bmatrix}\)

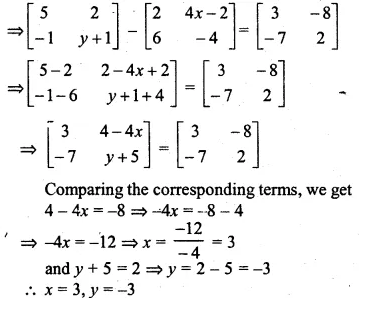
Question 14.
If \(\begin{bmatrix} a & \quad 3 \\ 4 & \quad 2 \end{bmatrix}+\begin{bmatrix} 2 & \quad b \\ 1 & -2 \end{bmatrix}-\begin{bmatrix} 1\quad & 1 \\ -2\quad & c \end{bmatrix}=\begin{bmatrix} 5 & 0 \\ 7 & 3 \end{bmatrix}\)
Find the value of a,b and c
Solution:
\(\begin{bmatrix} a & \quad 3 \\ 4 & \quad 2 \end{bmatrix}+\begin{bmatrix} 2 & \quad b \\ 1 & -2 \end{bmatrix}-\begin{bmatrix} 1\quad & 1 \\ -2\quad & c \end{bmatrix}=\begin{bmatrix} 5 & 0 \\ 7 & 3 \end{bmatrix}\)

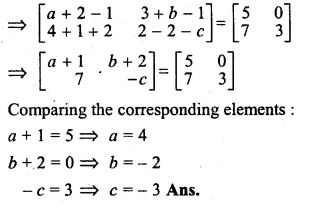
Question 15.
If A = \(\begin{bmatrix} 2 & a \\ -3 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & 3 \\ 7 & b \end{bmatrix} \) , C = \(\begin{bmatrix} c & 9 \\ -1 & -11 \end{bmatrix} \) and 5A + 2B = C, find the values of a,b,c
Solution:
A = \(\begin{bmatrix} 2 & a \\ -3 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & 3 \\ 7 & b \end{bmatrix} \) , C = \(\begin{bmatrix} c & 9 \\ -1 & -11 \end{bmatrix} \)
and 5A + 2B = C

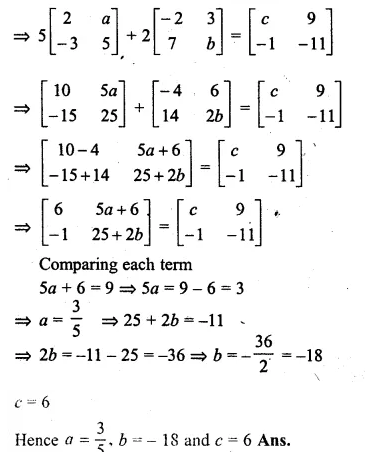
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.