RS Aggarwal Class 9 Solutions Chapter 3 Introduction to Euclid’s Geometry Ex 3A
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 3 Introduction to Euclid’s Geometry Ex 3A.
Question 1.
Solution:
A theorem is a statement that requires a proof while an axiom is the basic fact which is taken for granted without proof.
Question 2.
Solution:
(i) Line segment: The straight line between two points A and B is a called a line segment \(\overline { AB } \)
![]()
(ii) Ray : A line segment \(\overline { AB } \) when extended indefinitely is one direction is called a ray \(\overrightarrow { AB } \) It has no definitely length.
![]()
(iii) Intersecting lines : Two lines having one common point are called intersecting lines and the common point is called the point of intersection.
(iv) Parallel Lines : If two lines lying in the same plane do not intersect each other when produced on either side, then these two lines are called parallel lines. The distance between two parallel hues always remains the same.

(v) Half line : If we take a point P on a line \(\overleftrightarrow { AB } \), its divides the line into two parts. Each part is called half line or two ray i.e. \(\overrightarrow { PA } \) and \(\overrightarrow { PB } \) .
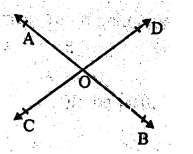
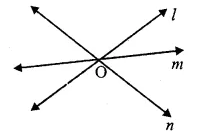
(vi) Concurrent lines : Three or more lines intersecting at the same point are called concurrent lines.
(vii) Collinear points : Three or more points lying on the same line are called collinear points.
(viii) Plane : A plane is a surface such that every point of the line joining any two points on it, lies on it.
Question 3.
Solution:
(i) Six points are : A, B, C, D, E and F
(ii) Five line segments are : \(\overline { EG }\), \(\overline { FH }\), \(\overline { EF }\), \(\overline { GH }\) and \(\overline { MN }\)
(iii) Four rays are : \(\overrightarrow { EP } \) , \(\overrightarrow { GR } \),\(\overrightarrow { GB } \) and \(\overrightarrow { HD } \)
(iv) Four lines are : \(\overrightarrow { AB } \),\(\overrightarrow { CD } \),\(\overrightarrow { PQ } \) and \(\overrightarrow { RS } \)
(v) Four collinear points are M, E, G, B. Ans
Question 4.
Solution:
(i) \(\overleftrightarrow { EF } \) and \(\overleftrightarrow { GH } \) is a pair of intersecting line whose point of intersection is R
and second pair of intersecting lines is \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { CD } \) and point of intersection is P.
(ii) Three concurrent lines are \(\overleftrightarrow { AB } \), \(\overleftrightarrow { EF } \) and \(\overleftrightarrow { GH } \) and the point of intersection is R.
(iii) Three rays are \(\overleftrightarrow { RB } \),\(\overleftrightarrow { RH } \) and \(\overleftrightarrow { RG } \)
(iv) Two line segments are \(\overleftrightarrow { RQ } \) and \(\overleftrightarrow { RP } \)
Question 5.
Solution:
(i) Through a given point, infinitely many lines can be drawn.
(ii) Only one line can be drawn to pass through two given points.
(iii) Two lines can intersect each other at the most one point
(iv) A, B and C are three collinear points. Then the line segments will be \(\overline { AB } \), \(\overline { BC } \) and \(\overline { AC } \).
Question 6.
Solution:
(iv), (vi), (vii), (viii) and (ix) are true and others are not true.
Hope given RS Aggarwal Class 9 Solutions Chapter 3 Introduction to Euclid’s Geometry Ex 3A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.