NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3.

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 13
Chapter Name	Surface Areas and Volumes
Exercise	Ex 13.3
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3

Question 1.
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Solution:
We have, diameter = 10.5 cm
Radius (r) = \(\frac { 10.5 }{ 2 }\) = 5.25 cm
and slant height l= 10 cm
Curved surface area = πrl= \(\frac { 22 }{ 7 }\) x 5.25 x 10 = 165 cm²

Question 2.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution:
We have, slant height l = 21 m
and diameter = 24 cm

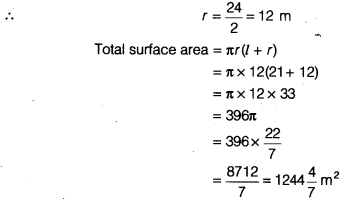
Question 3.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find
(i) radius of the base and
(ii) total surface area of the cone.
Solution:
We have, slant height, l= 14cm
Curved surface area of a cone = 308 cm²

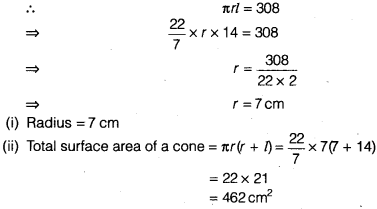
Question 4.
A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹70.
Solution:
We have, h = 10 m

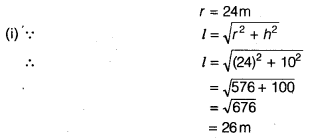
Hence, the slant height of the canvas tent is 26 m.
(ii) Canvas required to make the tent = Curved surface area of tent
= πrl
= π x 24 x 26 = 624π m²
∵ Cost of 1 m2 canvas = ₹ 70
Cost of 624n m2 canvas = ₹ 70 x 624π
= ₹ 70x 624 x \(\frac { 22 }{ 7 }\)
= ₹ 10 x 624 x 22
= ₹ 137280
Hence, the cost of the canvas is ₹ 137280.

Question 5.
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use π = 3.14)
Solution:
Let r, h and l be the radius, height and slant height of the tent, respectively.

The extra material required for stitching margins and cutting = 20 cm = Q² m Hence, the total length of tarpaulin required = 62.8 + Q² = 63 m

Question 6.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m².
Solution:
We have, slant height, l = 25m
and diameter = 14m
∴ Radius, r= 7m

Question 7.
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Solution:

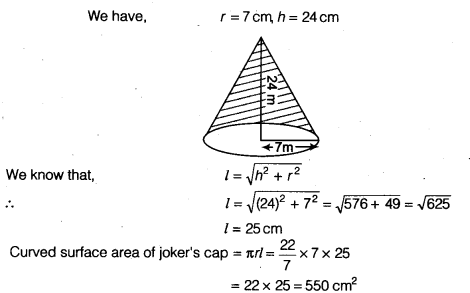
∵ The sheet required to make 1 cap = 550 cm²
∴ The sheet required to make 10 caps = 550 x 10= 5500 cm²

Question 8.
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹12 per m², what will be the cost of painting all these cones? (Use π = 3.14 and take \( \sqrt{104} \) = 102)
Solution:

Curved surface area of a cone = πrl = 3.14 x 0.2 x 1.02 = 0.64056 m²
Cost of painting per m2 = ₹12
Cost of painting 0.64056 m2 = ₹12 x 0.64056= ₹ 7.68672
Cost of painting for 1 cone = ₹ 7.68672
Cost of painting 50 cones = ₹ 7.68672x 50= ₹ 384.336= ₹ 384.34

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3, drop a comment below and we will get back to you at the earliest.