Selina Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 15 Triangles

Triangles Exercise 15A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Stale, if the triangles are possible with the following angles :
(i) 20°, 70° and 90°
(ii) 40°, 130° and 20°
(iii) 60°, 60° and 50°
(iv) 125°, 40° and 15°
Solution:

Question 2.
If the angles of a triangle are equal, find its angles.
Solution:

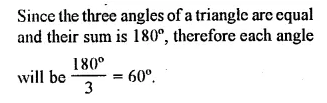
Question 3.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
Solution:

Question 4.
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Solution:

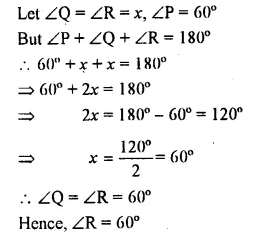
Question 5.
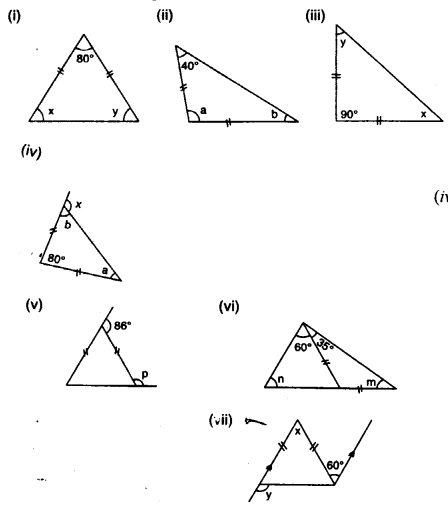
Calculate the unknown marked angles in each figure :

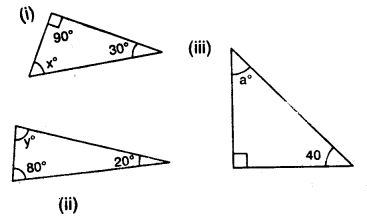
Solution:

Question 6.
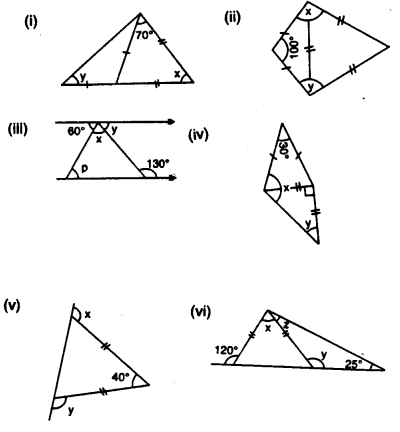
Find the value of each angle in the given figures:

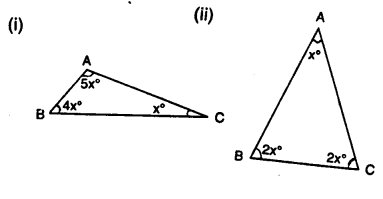
Solution:

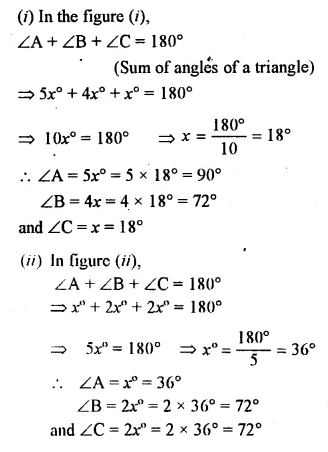
Question 7.
Find the unknown marked angles in the given figure:

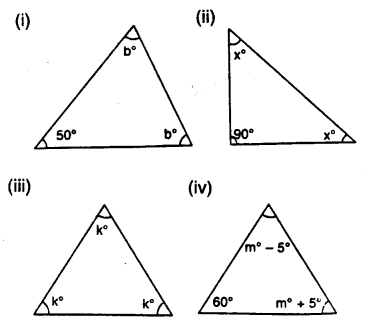
Solution:

Question 8.
In the given figure, show that: ∠a = ∠b + ∠c

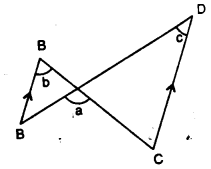
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
Solution:

Question 9.
Calculate the angles of a triangle if they are in the ratio 4 : 5 : 6.
Solution:

Question 10.
One angle of a triangle is 60°. The, other two angles are in the ratio of 5 : 7. Find the two angles.
Solution:

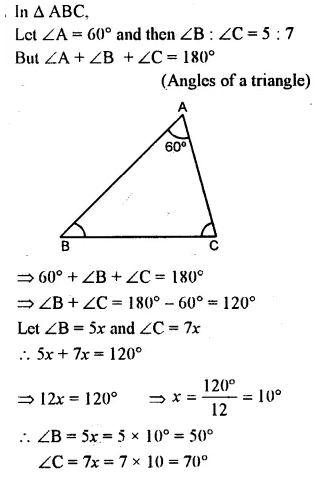
Question 11.
One angle of a triangle is 61° and the other two angles are in the ratio 1\(\frac { 1 }{ 2 }\) : 1 \(\frac { 1 }{ 3 }\). Find these angles.
Solution:

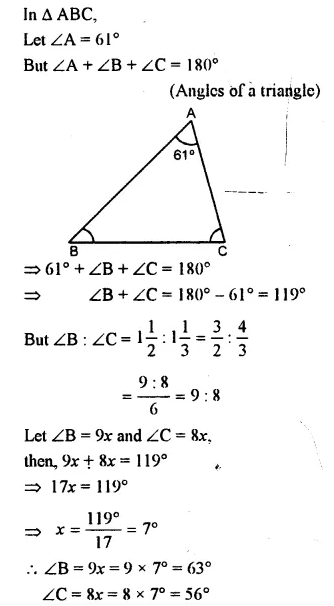
Question 12.
Find the unknown marked angles in the given figures :

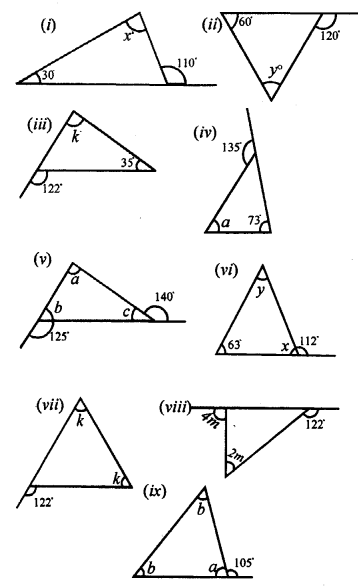
Solution:

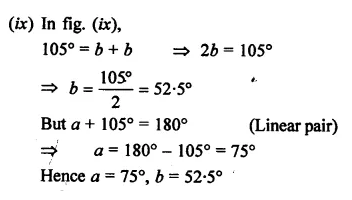
Triangles Exercise 15B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Find the unknown angles in the given figures:

Solution:

Question 2.
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figures :

Solution:

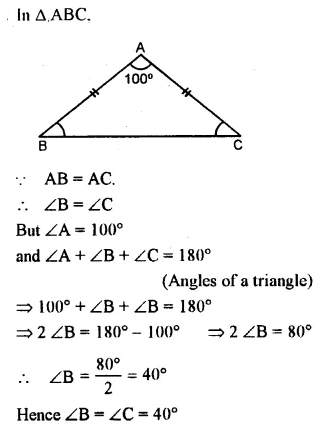
Question 3.
The angle of vertex of an isosceles triangle is 100°. Find its base angles.
Solution:

Question 4.
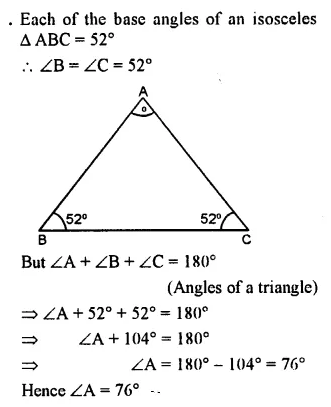
One of the base angles of an isosceles triangle is 52°. Find its angle of vertex.
Solution:

Question 5.
In an isosceles triangle, each base angle is four times of its vertical angle. Find all the angles of the triangle.
Solution:

Question 6.
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
Solution:

Question 7.
The base angle of an isosceles triangle is 15° more than its vertical angle. Find its each angle.
Solution:

Question 8.
The vertical angle of an isosceles triangle is three times the sum of its base angles. Find each angle.
Solution:

Question 9.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1 : 4. Find each angle of the triangle.
Solution:

Question 10.
In the given figure, BI is the bisector of∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.

Solution:

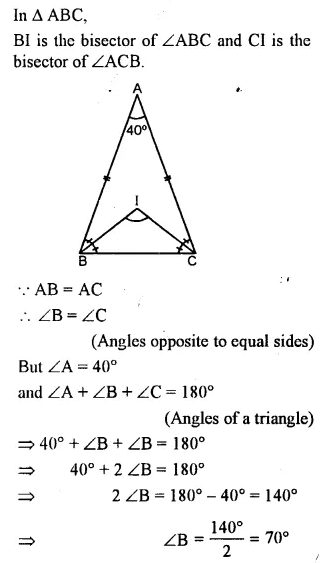
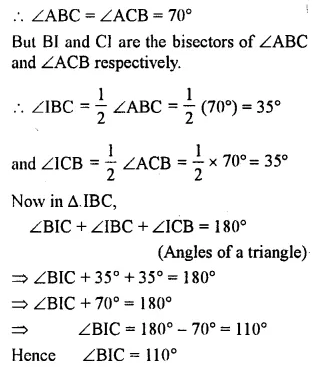
Question 11.
In the given figure, express a in terms of b.

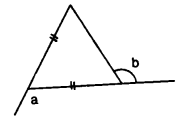
Solution:

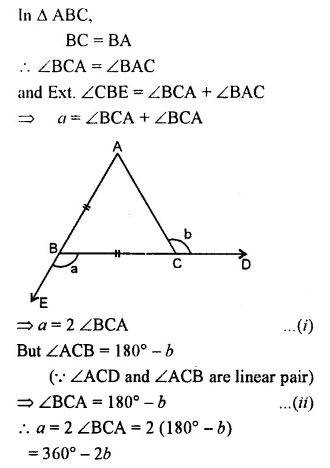
Question 12.
(a) In Figure (i) BP bisects ∠ABC and AB = AC. Find x.
(b) Find x in Figure (ii) Given: DA = DB = DC, BD bisects ∠ABC and∠ADB = 70°.

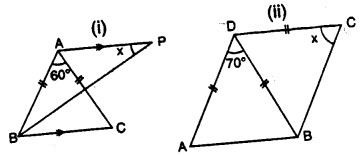
Solution:

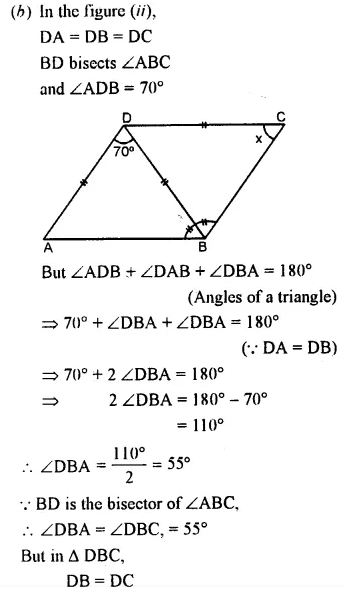
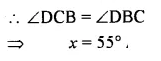
Question 13.
In each figure, given below, ABCD is a square and ∆ BEC is an equilateral triangle.
Find, in each case : (i) ∠ABE(ii) ∠BAE

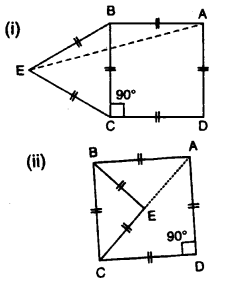
Solution:

Question 14.
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.

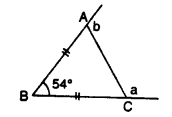
Solution:

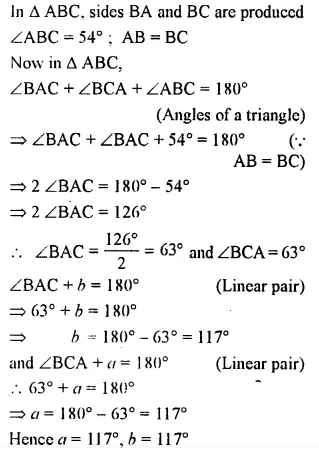
Triangles Exercise 15C – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Construct a ∆ABC such that:
(i) AB = 6 cm, BC = 4 cm and CA = 5.5 cm
(ii) CB = 6.5 cm, CA = 4.2 cm and BA = 51 cm
(iii) BC = 4 cm, AC = 5 cm and AB = 3.5 cm
Solution:

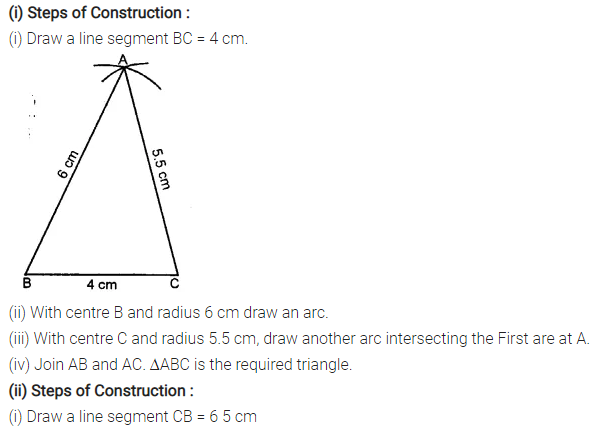
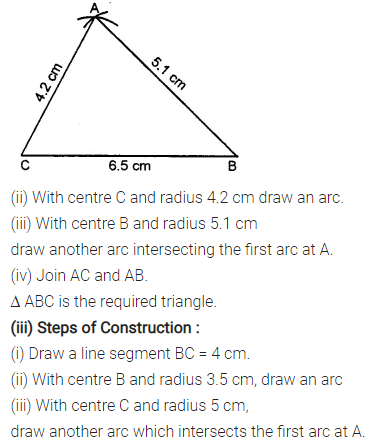
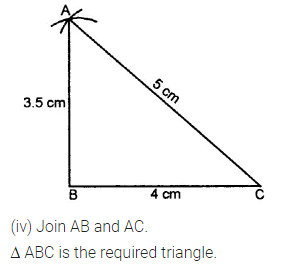
Question 2.
Construct a A ABC such that:
(i) AB = 7 cm, BC = 5 cm and ∠ABC = 60°
(ii) BC = 6 cm, AC = 5.7 cm and ∠ACB = 75°
(iii) AB = 6.5 cm, AC = 5.8 cm and ∠A = 45°
Solution:

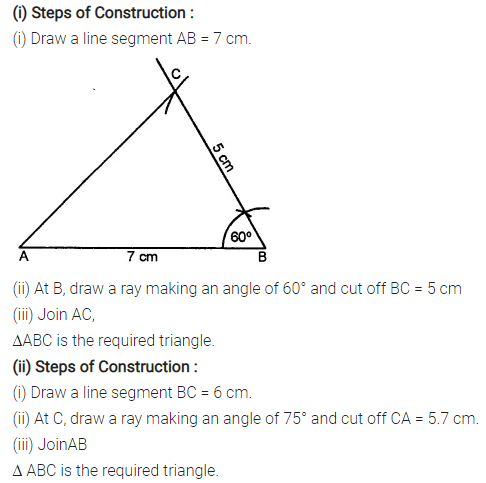
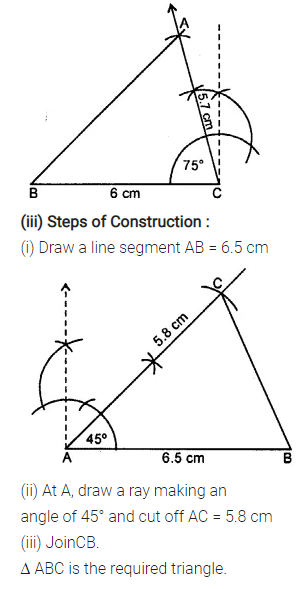
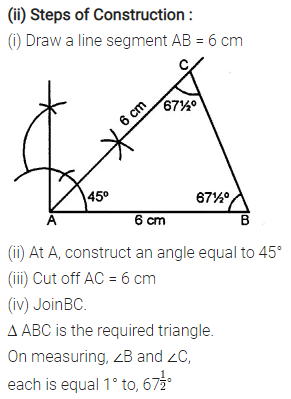
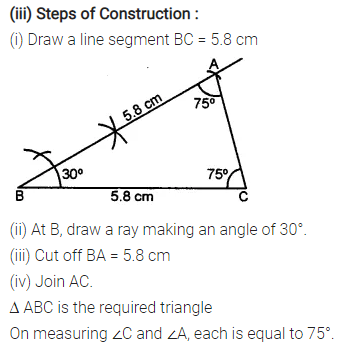
Question 3.
Construct a ∆ PQR such that :
(i) PQ = 6 cm, ∠Q = 60° and ∠P = 45°. Measure ∠R.
(ii) QR = 4.4 cm, ∠R = 30° and ∠Q = 75°. Measure PQ and PR.
(iii) PR = 5.8 cm, ∠P = 60° and ∠R = 45°.
Measure ∠Q and verify it by calculations
Solution:

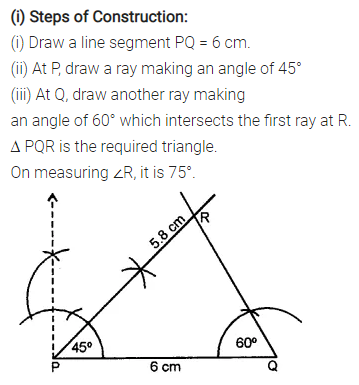
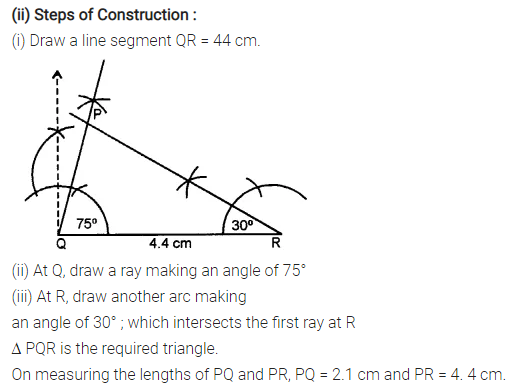
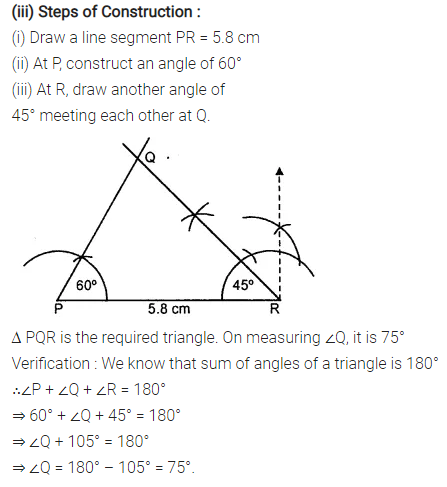
Question 4.
Construct an isosceles A ABC such that:
(i) base BC = 4 cm and base angle = 30°
(ii) base AB = 6-2 cm and base angle = 45°
(iii) base AC = 5 cm and base angle = 75°.
Measure the other two sides of the triangle.
Solution:

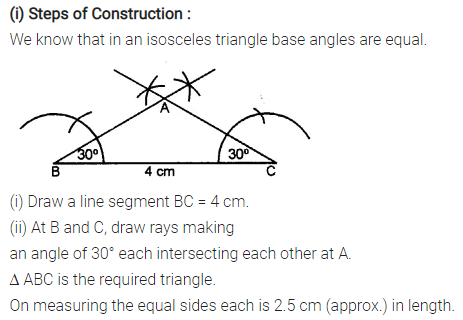
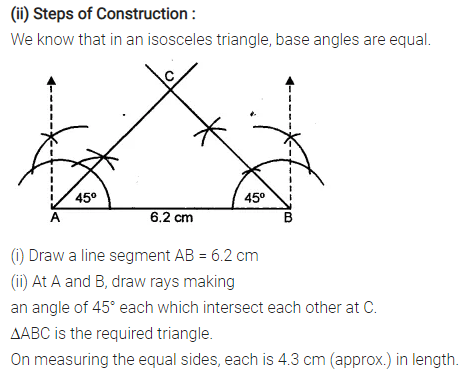
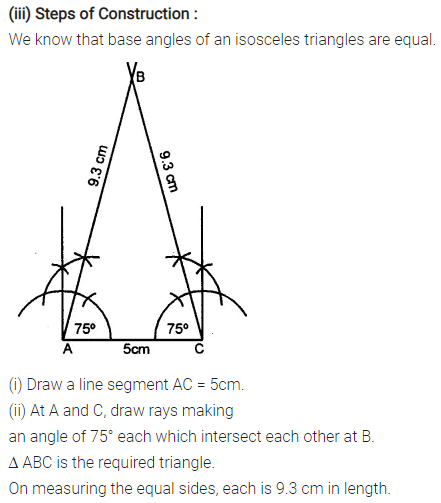
Question 5.
Construct an isosceles ∆ABC such that:
(i) AB = AC = 6.5 cm and ∠A = 60°
(ii) One of the equal sides = 6 cm and vertex angle = 45°. Measure the base angles.
(iii) BC = AB = 5-8 cm and ZB = 30°. Measure ∠A and ∠C.
Solution:

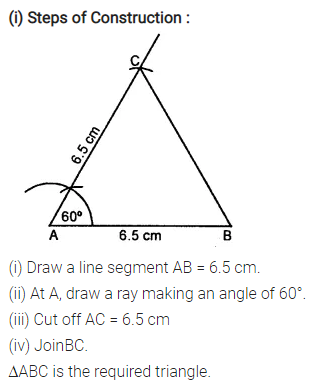
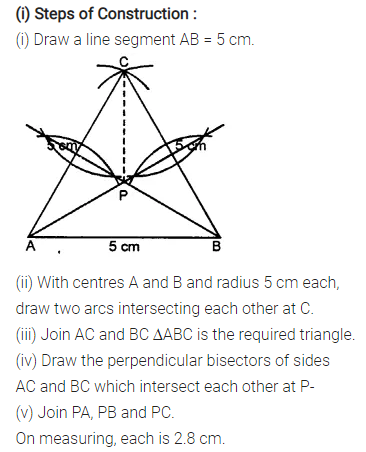
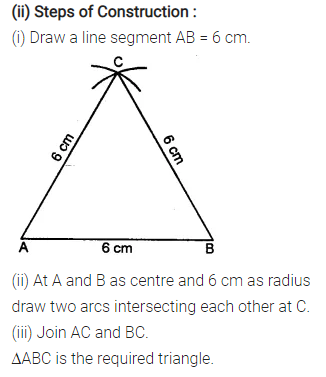
Question 6.
Construct an equilateral A ABC such that:
(i) AB = 5 cm. Draw the perpendicular bisectors of BC and AC. Let P be the point of intersection of these two bisectors. Measure PA, PB and PC.
(ii) Each side is 6 cm.
Solution:

Question 7.
(i) Construct a ∆ ABC such that AB = 6 cm, BC = 4.5 cm and AC = 5.5 cm. Construct a circumcircle of this triangle.
(ii) Construct an isosceles ∆PQR such that PQ = PR = 6.5 cm and ∠PQR = 75°. Using ruler and compasses only construct a circumcircle to this triangle.
(iii) Construct an equilateral triangle ABC such that its one side = 5.5 cm.
Construct a circumcircle to this triangle.
Solution:

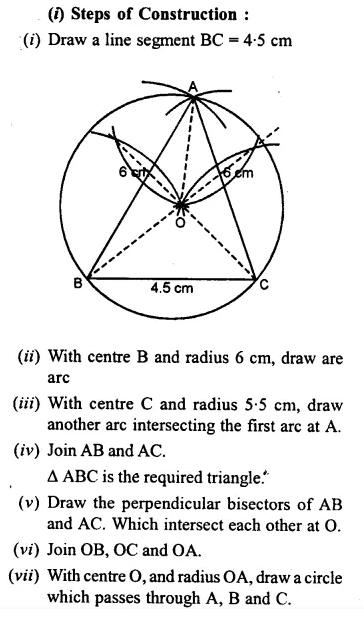
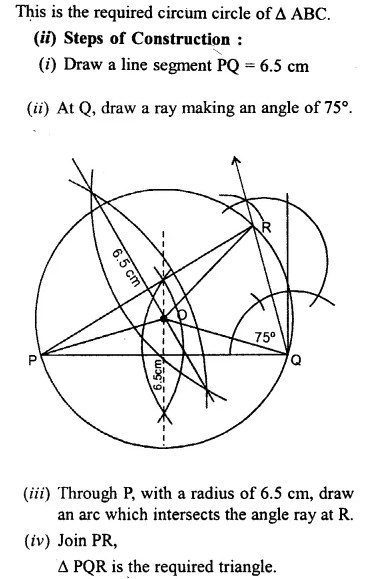
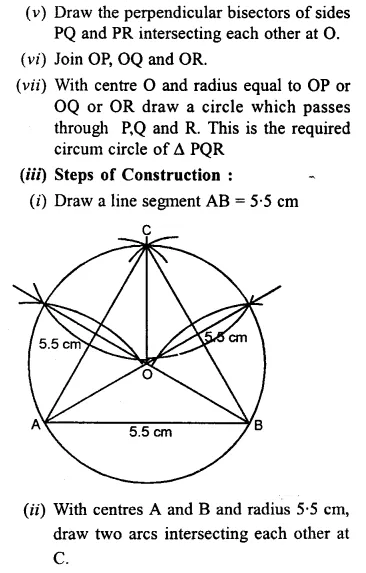
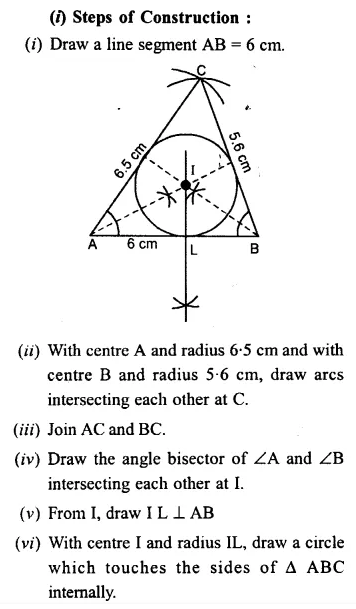
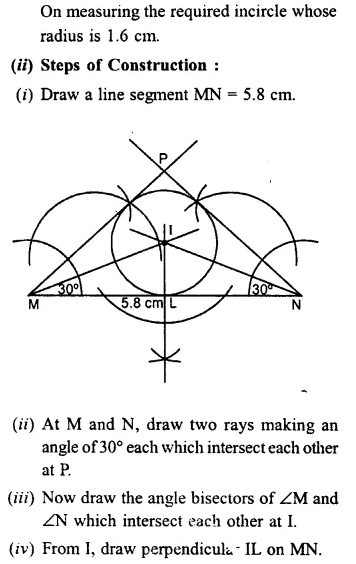
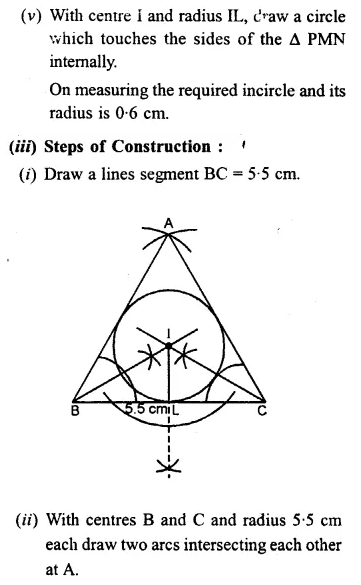
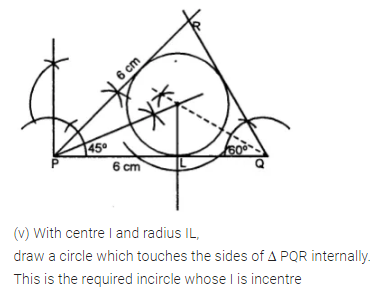
Question 8.
(i) Construct a ∆ABC such that AB = 6 cm, BC = 5.6 cm and CA = 6.5 cm. Inscribe a circle to this triangle and measure its radius.
(ii) Construct an isosceles ∆ MNP such that base MN = 5.8 cm, base angle MNP = 30°. Construct an incircle to this triangle and measure its radius.
(iii) Construct an equilateral ∆DEF whose one side is 5.5 cm. Construct an incircle to this triangle.
(iv) Construct a ∆ PQR such that PQ = 6 cm, ∠QPR = 45° and angle PQR = 60°. Locate its incentre and then draw its incircle.
Solution:

Selina Concise Mathematics Class 7 ICSE Solutions