Category: ICSE

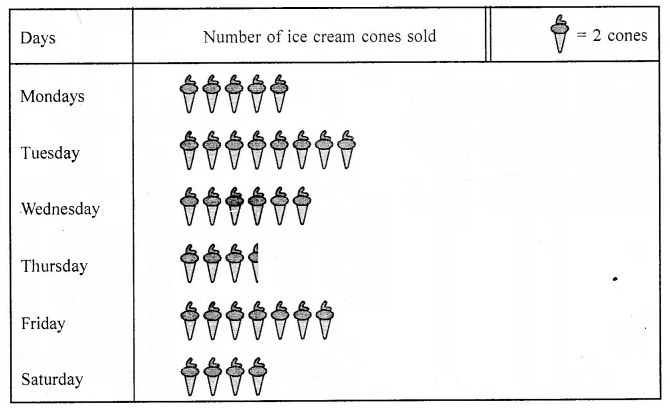
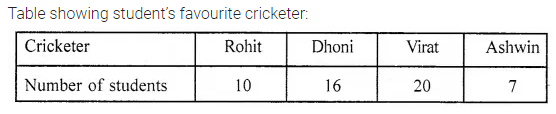
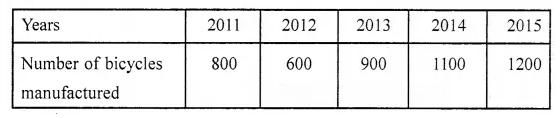
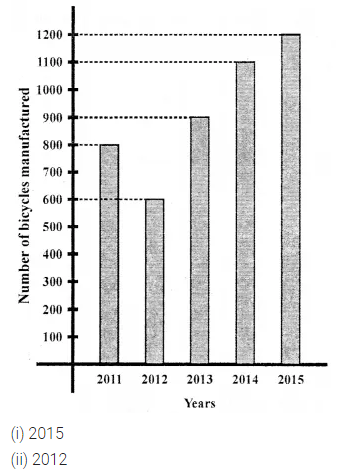
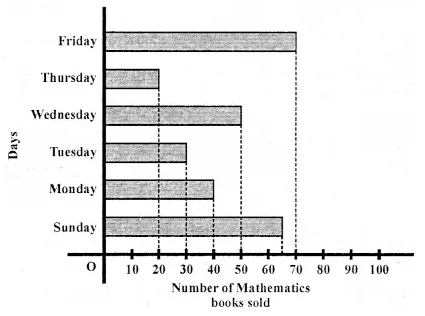
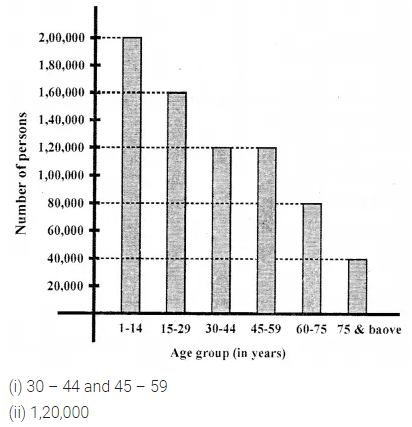
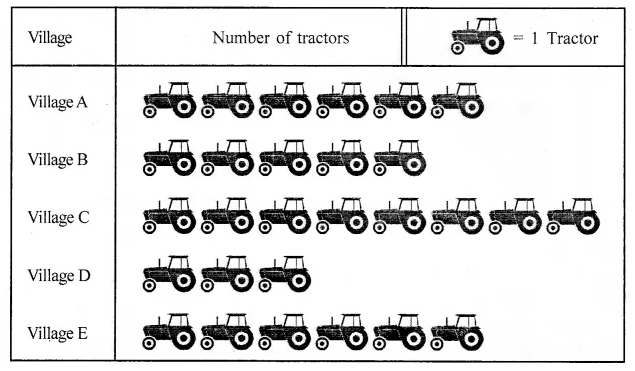
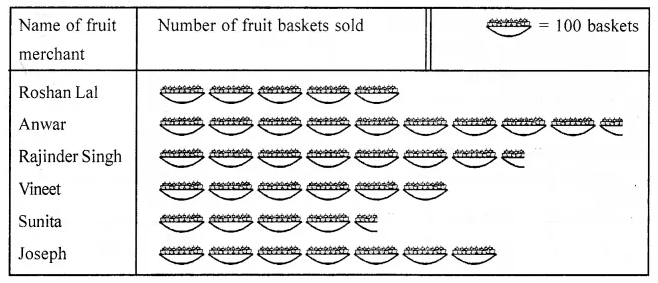
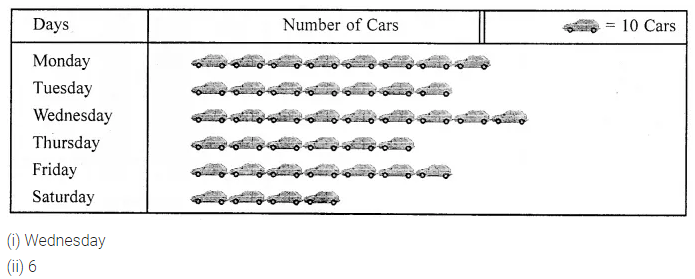
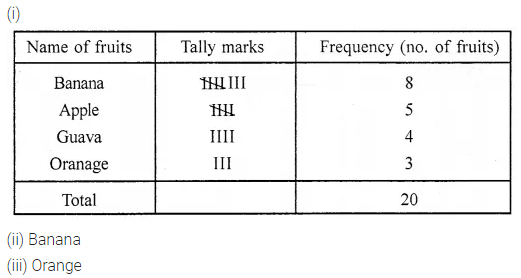
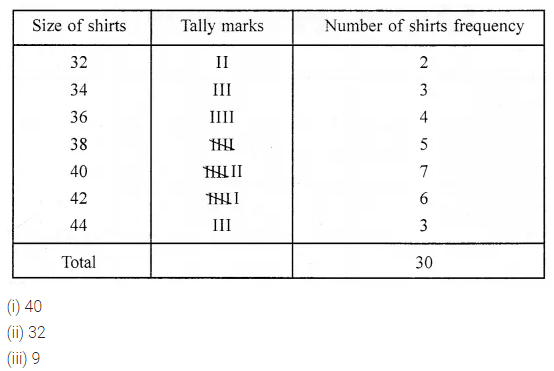
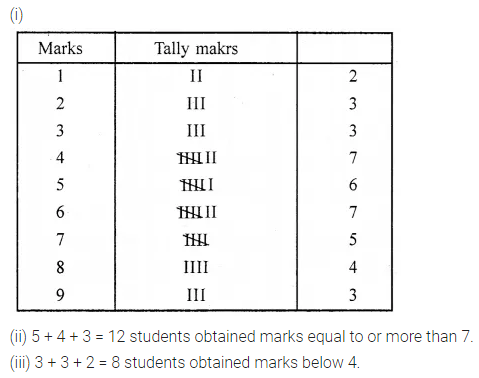
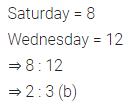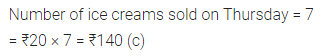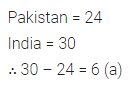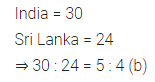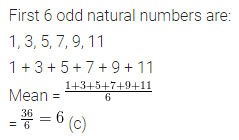ML Aggarwal Class 7 Solutions Chapter 7 Percentage and Its Applications Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 7 Percentage and Its applications Check Your Progress

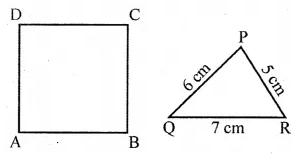
Question 1.
Convert the following percentages into fractions in the simplest form:
(i) 12\(\frac { 1 }{ 2 }\) %
(ii) 66\(\frac { 2 }{ 3 }\) %
(iii) 8\(\frac { 1 }{ 3 }\) %
Solution:

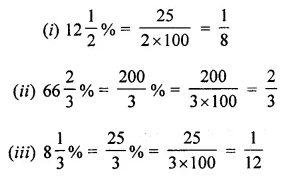
Question 2.
Express each of the following fractions as a percentage:
(i) \(\frac { 5 }{ 8 }\)
(ii) \(\frac { 13 }{ 40 }\)
(iii) \(\frac { 7 }{ 6 }\)
Solution:

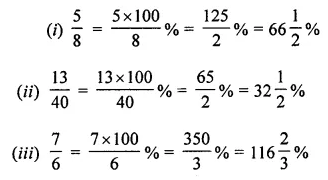
Question 3.
Express each of the following percentages as a decimal:
(i) 122%
(ii) 2.2%
(iii) 3\(\frac { 1 }{ 8 }\) %
Solution:

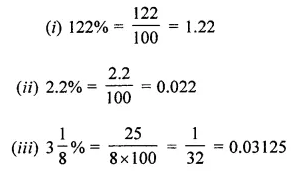
Question 4.
Express 0.0345 as a percentage.
Solution:

Question 5.
Convert each part of the ratio 5 : 6 : 9 to a percentage.
Solution:

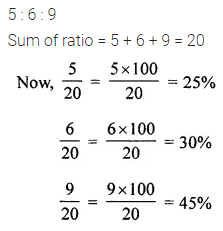
Question 6.
(i) What percent of a day is half an hour?
(ii) What percent is \(\frac { 3 }{ 4 }\) metres of 4\(\frac { 1 }{ 2 }\) metres?
Solution:

Question 7.
The population of a town decreased from 25000 to 24500. Find the percentage decrease.
Solution:

Question 8.
Arun bought a car for ₹ 350000. The next year, the price went upto ₹ 370000. What was the precentage increase in the price?
Solution

Question 9.
The population of a village has decreased by 6%. If the original population was 3650, find the population after decrease.
Solution:

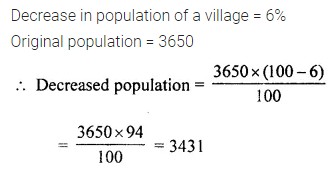
Question 10.
43% of the students in a school are girls. If the number of boys is 1482, find:
(i) the total strength of the school
(ii) number of girls in the school.
Solution:

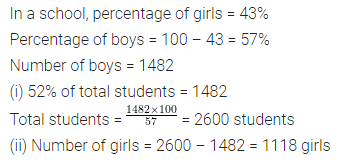
Question 11.
Rohan bought a calculator for ₹ 760 and sold it for ₹ 874. Find his profit and profit percentage.
Solution:

Question 12.
On selling an article for ₹ 1027, Meena suffered a loss of ₹ 273. Find her loss percentage.
Solution:

Question 13.
By selling a fan for ₹ 710, a trader suffers a loss of ₹ 40. Find the cost price of the fan. At what price this fan should be sold in order to gain 10%?
Solution:

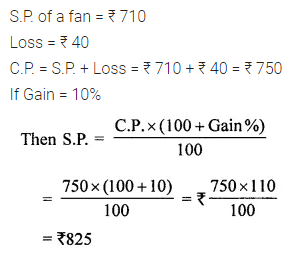
Question 14.
A shopkeeper sells an article at ₹ 300, thus earning a profit of 20%. Find the cost price of the article.
Solution:

Question 15.
A shopkeeper sells an article at ₹ 320, thus suffering a loss of 20%. Find the cost price of the article.
Solution:

Question 16.
If ₹ 6000 is borrowed at 6.5% per annum simple interest, find the interest and the amount to be paid at the end of 3 years.
Solution:

Question 17.
How long will it take for ₹ 1860 invested at the rate of 9.5% per annum simple interest to amount to ₹ 2449?
Solution:

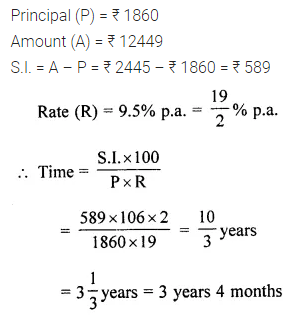
Question 18.
At what rate will ₹ 7200 fetch a simple interest of ₹ 3024 in 4 years?
Solution:

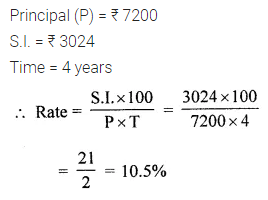
Question 19.
What sum of money will yield a simple interest of ₹ 1155in 3 years 6 months at 11% p.a.?
Solution:

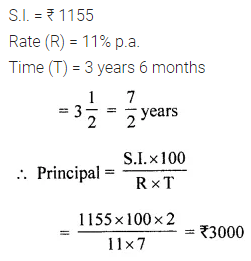
Must Refer:

BSOFT Pivot Calculator

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Check Your Progress

Question 1.
A die is thrown 25 times and the scores were as given below :
2, 1, 4, 6, 2, 3, 1, 5, 6, 3, 4, 5, 2, 1, 6, 6, 6, 3, 2, 2, 2, 4, 3, 2, 2
(i) Construct a data array.
(ii) Construct a tally chart and frequency distribution table.
Solution:

Question 2.
In primary school, the number of students in different classes is as follows:

Represent this data by a pictograph, using  ≃ 20 students.
Solution:

Question 3.
Observe the following bar graph, showing the marks scored by Gurmeet in the annual examination in different subjects: Answer the following questions:

(i) What is the scale of this bar graph?
(ii) In which subject Gurmeet obtained maximum marks?
(iii) In which subject she obtained minimum marks?
(iv) Name the subject(s) in which she got 80 or more marks.
Solution:

Question 4.
The following table shows the monthly expenditure of a family on various items:

Represent the data by a bar graph.
Solution:

Question 5.
Find the mean and the median of the following data:
5, 3, 12, 0, 7, 11, 4, 3, 9
Solution:

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) A ……. is a collection of numerical figures to give some information.
(ii) Each numerical figure in data is called an ………..
(iii) The number of times a particular observation occurs in a data is called … of the observation.
(iv) A data arranged in ascending or descending order is called an ………… data.
(v) A pictorial representation of a data is called a …………
(vi) If represent 5 students then  represent ………… students.
(vii) In a pictograph, if one bicycle represents 20 bicycles then 140 bicycles can be represented by ………… bicycles.
(viii)In a pictograph, if one electric bulb represents 10 bulbs then the picture of half a bulb will represent ………… bulbs.
(ix) In a pictograph, if the symbol represents 50 fruits baskets, then  represent ………… fruit baskets.
(x) The frequency of 8 is written symbolically as ………… using tally marks.
(xi) In a bar graph, the bars are of uniform …………
(xii) The mean of the first 8 natural numbers is …………
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) If the data is large, it is difficult to get information from raw data.
(ii) Pictographs and bar graphs help us in understanding and analyzing a data.
(iii) In a bar graph, bars can be drawn either vertically or horizontally.
(iv) In a bar graph, width of a bar has no significance. It is only for eye attraction.
(v) Usually, the tally marks are recorded in bunches of 5.
(vi) The frequency 9 is represented as filtlll using tally marks.
(vii) Mentioning of scale is necessary in pictographs.
(viii) Mean is always one of the number in a given data.
(ix) Median is always one of the numbers in a given data.
Solution:

Multiple Choice Questions
Observe the following pictograph which shows the number of ice cream cones sold by school canteen during a week. Chose the correct answer from the given options for questions 3 to 7:

Question 3.
The minimum number of ice cream cones were sold on:
(a) Monday
(b) Saturday
(c) Tuesday
(d) Thursday
Solution:
Thursday (d)

Question 4.
The maximum number of ice cream cones were sold on:
(a) Tuesday
(b) Friday
(c) Wednesday
(d) Thursday
Solution:
Tuesday (a)

Question 5.
Ratio of the number of ice cream cones sold on Saturday to the number of ice cream cones sold on Wednesday is.
(a) 3 : 2
(b) 2 : 3
(c) 4 : 5
(d) 4 : 7
Solution:

Question 6.
Total number of ice cream cones sold during the whole week was:
(a) 33
(b) 67
(c) 65
(d) 57
Solution:

Question 7.
If the cost of one ice cream cone is ₹20, then the sale value on Thursday was:
(a) ₹70
(b) ₹100
(c) ₹140
(d) ₹1340
Solution:

Observe the adjoining bar graph, showing the number of one-day international matches played by cricket teams of different countries. Choose the correct answer from the given four options for questions 8 to 11:

Question 8.
Which country played a maximum number of matches?
(a) India
(b) England
(c) Pakistan
(d) Australia
Solution:
Australia (d)

Question 9.
How many matches did South Africa play?
(a) 16
(b) 18
(c) 20
(d) 24
Solution:
18 (b)

Question 10.
How many more matches were played by India than Pakistan?
(a) 6
(b) 12
(c) 24
(d) 30
Solution:

Question 11.
Ratio of the number of matches played by India to the number of matches played by Sri Lanka is
(a) 4 : 5
(b) 5 : 4
(c) 4 : 3
(d) 7 : 6
Solution:

Choose the correct answer from the given four options for questions 12 and 13:
Question 12.
The mean of the first 6 odd natural numbers is
(a) 5
(b) 5.5
(c) 6
(d) 6.5
Solution:

Question 13.
The median of the numbers 4, 4, 7, 5, 7, 6, 1, 3, 11 is
(a) 7
(b) 6
(c) 5
(d) 4
Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) A ……. is a collection of numerical figures to give some information.
(ii) Each numerical figure in data is called an ………..
(iii) The number of times a particular observation occurs in a data is called … of the observation.
(iv) A data arranged in ascending or descending order is called an ………… data.
(v) A pictorial representation of a data is called a …………
(vi) If represent 5 students then represent ………… students.
(vii) In a pictograph, if one bicycle represents 20 bicycles then 140 bicycles can be represented by ………… bicycles.
(viii)In a pictograph, if one electric bulb represents 10 bulbs then the picture of half a bulb will represent ………… bulbs.
(ix) In a pictograph, if the symbol represents 50 fruits baskets, then represent ………… fruit baskets.
(x) The frequency of 8 is written symbolically as ………… using tally marks.
(xi) In a bar graph, the bars are of uniform …………
(xii) The mean of the first 8 natural numbers is …………
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) If the data is large, it is difficult to get information from raw data.
(ii) Pictographs and bar graphs help us in understanding and analyzing a data.
(iii) In a bar graph, bars can be drawn either vertically or horizontally.
(iv) In a bar graph, width of a bar has no significance. It is only for eye attraction.
(v) Usually, the tally marks are recorded in bunches of 5.
(vi) The frequency 9 is represented as filtlll using tally marks.
(vii) Mentioning of scale is necessary in pictographs.
(viii) Mean is always one of the number in a given data.
(ix) Median is always one of the numbers in a given data.
Solution:

Multiple Choice Questions
Observe the following pictograph which shows the number of ice cream cones sold by school canteen during a week. Chose the correct answer from the given options for questions 3 to 7:

Question 3.
The minimum number of ice cream cones were sold on:
(a) Monday
(b) Saturday
(c) Tuesday
(d) Thursday
Solution:
Thursday (d)

Question 4.
The maximum number of ice cream cones were sold on:
(a) Tuesday
(b) Friday
(c) Wednesday
(d) Thursday
Solution:
Tuesday (a)

Question 5.
Ratio of the number of ice cream cones sold on Saturday to the number of ice cream cones sold on Wednesday is.
(a) 3 : 2
(b) 2 : 3
(c) 4 : 5
(d) 4 : 7
Solution:

Question 6.
Total number of ice cream cones sold during the whole week was:
(a) 33
(b) 67
(c) 65
(d) 57
Solution:

Question 7.
If the cost of one ice cream cone is ₹20, then the sale value on Thursday was:
(a) ₹70
(b) ₹100
(c) ₹140
(d) ₹1340
Solution:

Observe the adjoining bar graph, showing the number of one-day international matches played by cricket teams of different countries. Choose the correct answer from the given four options for questions 8 to 11:

Question 8.
Which country played a maximum number of matches?
(a) India
(b) England
(c) Pakistan
(d) Australia
Solution:
Australia (d)

Question 9.
How many matches did South Africa play?
(a) 16
(b) 18
(c) 20
(d) 24
Solution:
18 (b)

Question 10.
How many more matches were played by India than Pakistan?
(a) 6
(b) 12
(c) 24
(d) 30
Solution:

Question 11.
Ratio of the number of matches played by India to the number of matches played by Sri Lanka is
(a) 4 : 5
(b) 5 : 4
(c) 4 : 3
(d) 7 : 6
Solution:

Choose the correct answer from the given four options for questions 12 and 13:
Question 12.
The mean of the first 6 odd natural numbers is
(a) 5
(b) 5.5
(c) 6
(d) 6.5
Solution:

Question 13.
The median of the numbers 4, 4, 7, 5, 7, 6, 1, 3, 11 is
(a) 7
(b) 6
(c) 5
(d) 4
Solution:

ML Aggarwal Class 6 Solutions Chapter 11 Understanding Symmetrical Shapes Ex 11.6 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 11 Understanding Symmetrical Shapes Ex 11.6

Question 1.
What is the shape of
(i) your geometry box?
(ii) a brick?
(iii) a matchbox?
(iv) a dum?
(v) a playing die?
(vi) a sweet laddu?
Solution:

Question 2.
Match the following:

Solution:

Question 3.
Fill in the blanks:
(i) A cube has ……… square faces, ……… edges and ……… vertices.
(ii) A triangular prism has ……… triangular faces, ……… rectangular faces, ……… edges and ……… vertices.
(iii) A triangular pyramid has ……… faces, ……… edges and vertices.
Solution:

ML Aggarwal Class 6 Solutions Chapter 11 Understanding Symmetrical Shapes Ex 11.5 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 11 Understanding Symmetrical Shapes Ex 11.5

Question 1.
State whether the following statements are true (T) or false (F):
(i) Each angle of a rectangle is a right angle.
(ii) The opposite sides of a rectangle are equal in length.
(iii) The diagonals of a square are perpendicular to one another.
(iv) All sides of a rhombus are equal in length.
(v) All sides of a parallelogram are equal in length.
(vi) The opposite sides of a trapezium are parallel.
(vii) The diagonal of a parallelogram are equal.
Solution:

Question 2.
Examine whether the following figures are polygons. Give reasons.

Solution:

Question 3.
Name each of the following polygons:

Solution:

Question 4.
Draw a rough sketch of a pentagon and draw its diagonals.
Solution:

Question 5.
Draw a rough sketch of a regular hexagon. Connecting three of its vertices draw:
(i) an isosceles triangle
(ii) a light angled triangle.
Solution:

Question 6.
Can you identify the regular quadrilateral?
Solution:

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Ex 15.5 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Ex 15.5

Question 1.
Find the median of the following data:
(i) 3, 1, 5, 6, 3, 4, 5
(ii) 3, 1, 5, 6, 3, 4, 5, 6
Solution:

Question 2.
Calculate the mean, the median and the mode of the numbers :
1, 3, 2, 6, 2, 3, 1, 3
Solution:

Question 3.
Calculate the mean, the median and the mode of the following numbers :
3, 7, 2, 5, 3, 4, 1, 5, 3, 6
Solution:

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Ex 15.4 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Ex 15.4

Question 1.
Find the mean of the following data:
(i) 40, 30, 30, 0, 26, 60
(ii) 3, 5, 7, 9, 11, 13, 15
Solution:

Question 2.
Find the mean of the first five even whole numbers.
Solution:

Question 3.
A batsman scored the following number of runs in six innings:
36, 35, 50, 46, 60, 55
Calculate the mean runs scored by him in an inning.
Solution:

Question 4.
The enrolment in a school for six consecutive years was as follows :
1555, 1670, 1750, 2013, 2540, 2825
Find the mean enrolment of the school for this period.
Solution:

Question 5.
The marks (out of 100) obtained by a group of students in a science test are :
85, 76, 90, 85, 39, 48, 56, 95, 81, 75
Find the:
(i) highest and lowest marks obtained by the students.
(ii) mean marks obtained by the students.
Solution:

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Ex 15.3 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Ex 15.3

Question 1.
Observe the adjoining bar graph showing the number of students in a particular class of a school.

Answer the following questions:
(i) What is the scale of this graph?
(ii) How many new students are added every year?
(iii) Is the number of students in the year 2015 is twice than that of in the year 2012?
Solution:

Question 2.
Observe the bar graph given below which is showing the sale of shirts in a readymade garment shop from Monday to Saturday.

Answer the following questions:
(i) What information does the above bar graph give?
(ii) What is the scale chosen on the horizontal line representing a number of shirts?
(iii) On which day were the maximum number of shirts sold? How many shirts were sold on that day?
(iv) n which day was the minimum number of shirts sold?
(v) How many shirts were sold on Thursday?
Solution:

Question 3.
Make a table corresponding to the following graph:

Solution:

Question 4.
The following table shows the number of bicycles manufactured in a factory during the years 2011 to 2015. Illustrate this data by using a bar graph. Choose a scale of your choice.

(i) In which year was the maximum number of bicycles manufactured?
(iii) In which year was the minimum number of bicycles manufactured?
Solution:

Question 5.
The number of Mathematics books sold by a shopkeeper on six consecutive days is given below:

Draw a horizontal bar graph to represent the above information choosing the scale of your choice.
Solution:

Question 6.
The number of persons in various age (in years) groups in a town is given in the following table:

Draw a bar graph to represent the above information and answer the following questions (take 1 unit height = 20,000 people):
(i) Which age groups have the same population?
(ii) All persons in the age group of 60 and above are called senior citizens. How many senior citizens are there in the town?
Solution:

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Ex 15.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Ex 15.2

Question 1.
Following pictograph shows the number of tractors in five villages.

Observe the pictograph and answer the following questions.
(i) Which village has the minimum number of tractors?
(ii) Which village has the maximum number of tractors?
(iii) How many more tractors village C has as compared to village B.
(iv) What is the total number of the tractor in all the five villages?
Solution:

Question 2.
The number of girl students in each class of a co-educational middle school is depicted by the pictograph.

Observe this pictograph and answer the following questions :
(a) Which class has the minimum number of girl students?
(b) Is the number of girls in Class VI less than the number of girls in Class V?
(c) How many girls are there in Class VII?
Solution:

Question 3.
In a village, the following pictograph shows the number of fruit baskets sold by six merchants in a particular season:

Observe the above pictograph and answer the following questions:
(i) Which merchant sold the maximum number of baskets?
(ii) How many baskets were sold by Rajinder Singh?
(iii) The merchants who have sold 700 or the number of baskets are planning to buy a cold store for the next season. Can you name them?
Solution:

Question 4.
In Gurgaon, the number of cars sold during a particular week was as follows:

Prepare a pictograph of the cars sold using a symbol of car representing 10 cars and answer the following questions:
(i) On which day the maximum number of cars were sold?
(ii) How many pictures of cars will represent the number of cars sold on Thursday?
Solution:

Question 5.
Total number of animals in five villages are as follows:

Prepare a pictograph of these animals using one symbol ® to represent 10 animals and answer the following questions:
(i) How many symbols represent animals of village E?
(ii) Which village has the maximum number of animals?
(iii) Which village has more animals: village A or village C?
Solution:

ML Aggarwal Class 6 Solutions Chapter 15 Data Handling Ex 15.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 15 Data Handling Ex 15.1

Question 1.
Following is the choice of 20 students of class VI of a school:
Banana, Apple, Guava, Orange, Apple, Banana, Orange, Guava, Banana, Banana, Apple, Banana, Apple, Banana, Orange, Guava, Apple, Banana, Guava, Banana.
(i) Arrange the name of fruits in a table using tally marks.
(ii) Which fruit is liked by the maximum number of students?
(iii) Which fruit is liked by the minimum number of students?
Solution:

Question 2.
In a ready-made garment shop, on a particular day the following sizes of shirts were sold:
34, 38, 42, 40, 44, 32, 34, 36, 42, 40, 44, 36, 38, 42, 44, 40, 38, 40, 42, 32, 34, 38, 42, 40, 36, 42, 40, 38, 36, 40.
Arrange the above data in ascending order and construct a frequency distribution table. Also, answer the following questions:
(i) Which shirt size had the maximum sale?
(ii) Which shirt size had the minimum sale?
(iii) The number of shirts sold of size 42 or greater than size 42.
Solution:

Question 3.
In a Mathematics test, the following marks were obtained by 40 students. Arrange these marks in a table using tally marks.

(i) Construct a frequency distribution table for the above data.
(ii) Find how many students obtained 7 marks or more than 7 marks.
(iii) How many students obtained marks below 4?
Solution:

ML Aggarwal Class 6 Solutions Chapter 14 Mensuration Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 14 Mensuration Check Your Progress

Question 1.
Look at the given figure and fill in the following blanks:

(i) The contribution in the estimation of the given area due to completely covered squares is
(ii) The contribution in the estimation of the given area due to more than half covered squares is
(iii) The contribution in the estimation of the given area due to the exactly half-covered square is
(iv) The contribution in the estimation of the given area due to less than half covered squares is
(v) The total estimated area is
Solution:

Question 2.
The perimeter of a square ABCD is twice the perimeter of ∆PQR. Find the area of the square ABCD.

Solution:

Question 3.
A wire is in the shape of a square of side 10 cm. If the wire is rebent into a rectangle of length 12 cm, find its breadth. Which encloses more area, the square or the rectangle and by how much?
Solution:

Question 4.
A rectangular room is 9 m long and 6 m wide. Find the cost of covering the floor with carpet 2 m wide at ₹35 per metre.
Solution:

Question 5.
If the cost of fencing a square plot at the rate of ₹ 2.50 per metre is ₹ 200, then find the length of each side of the field.
Solution:

Question 6.
If the cost of fencing a rectangular park at the rate of ₹7.50 per metre is ₹600 and the length of the park is 24 m, find the breadth of the park.
Solution:

Question 7.
By splitting the following figures into a rectangle, find their areas (The measures are given in centimetres).

Solution: