Category: ICSE

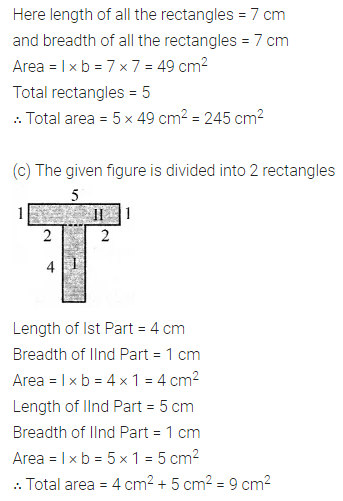
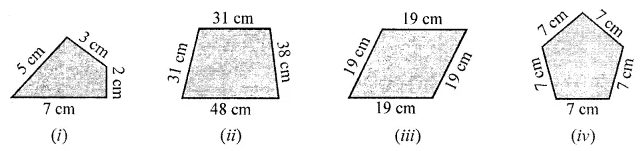
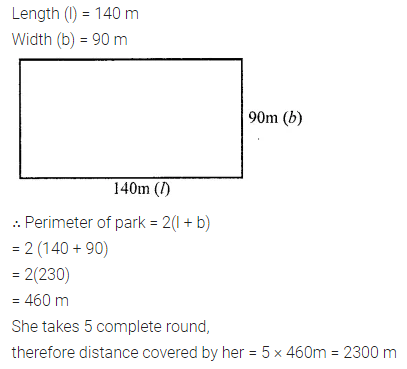
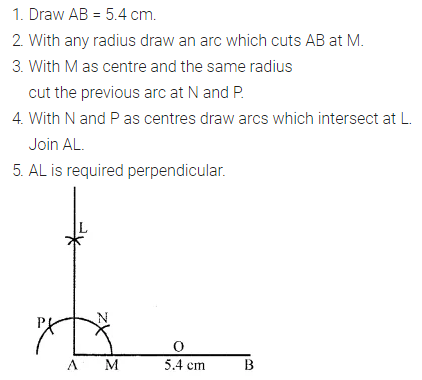
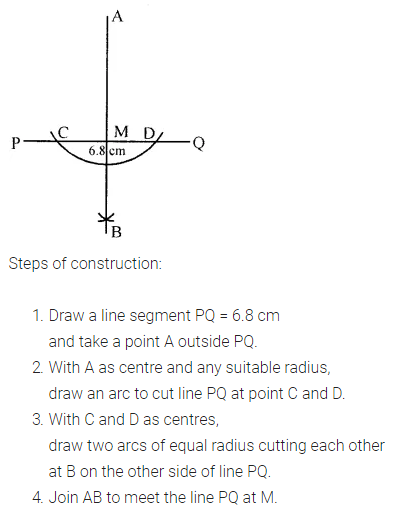
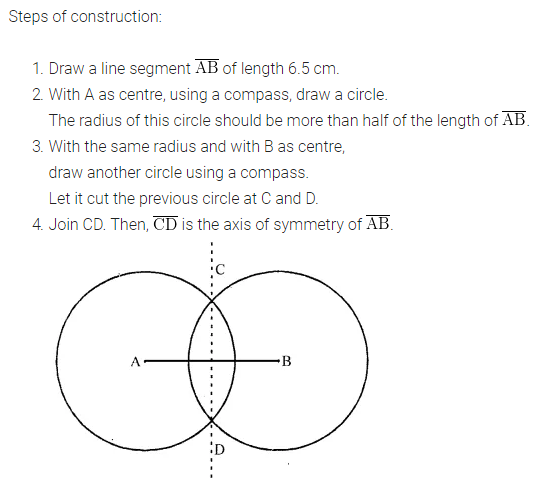
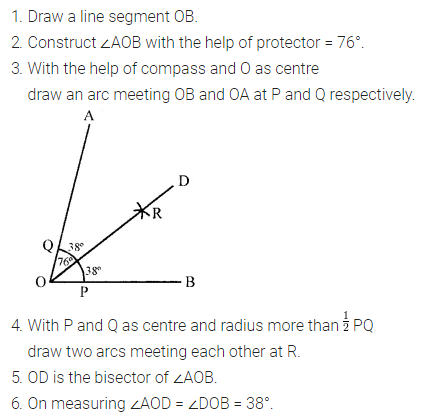
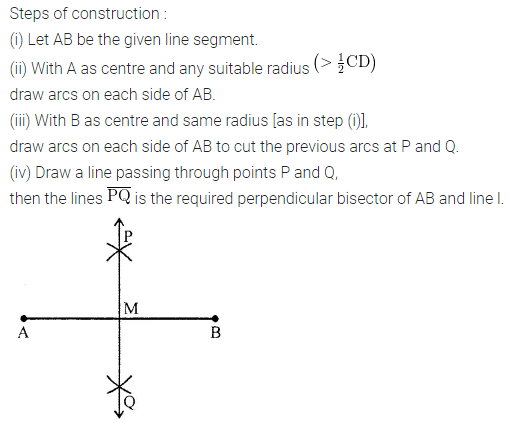
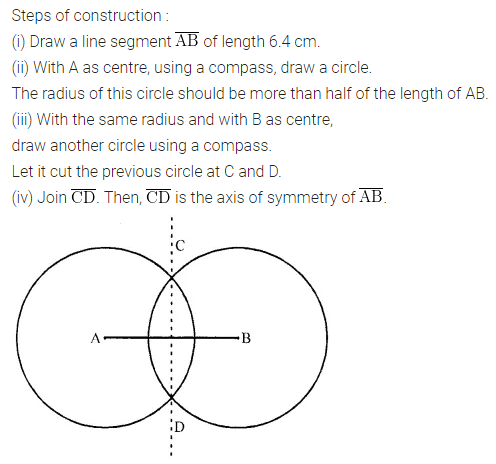
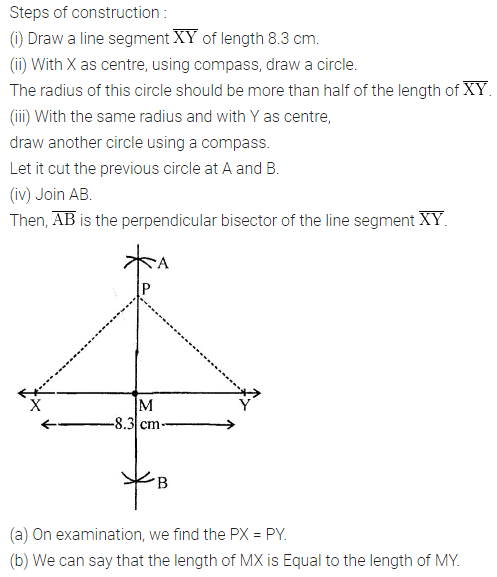
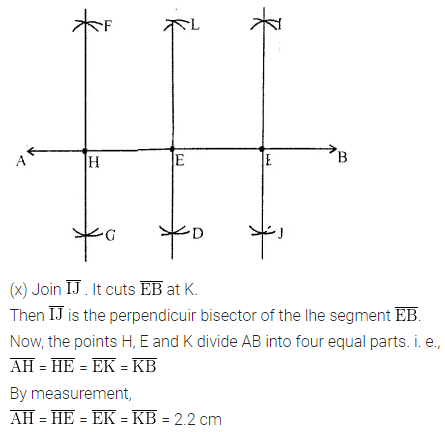
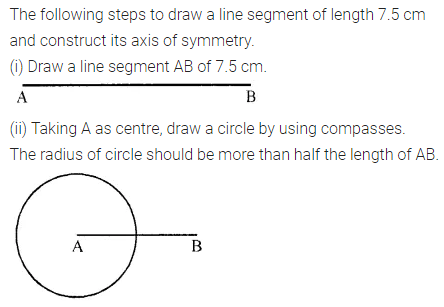
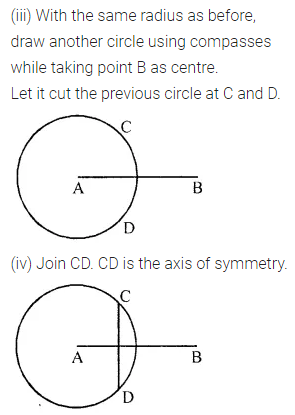
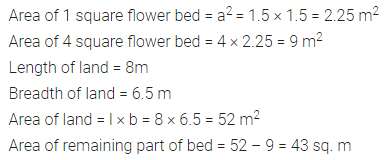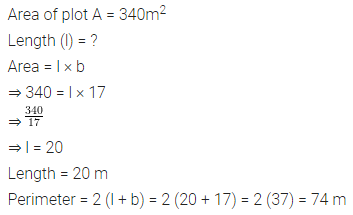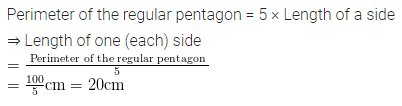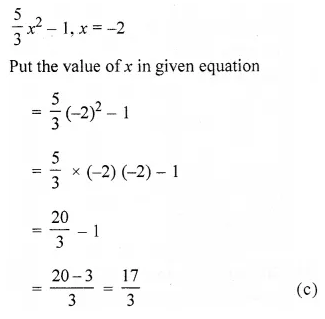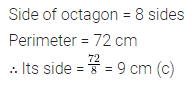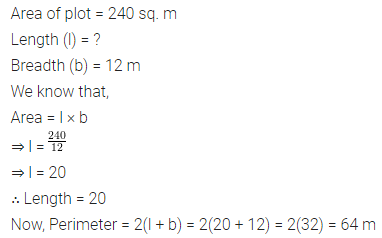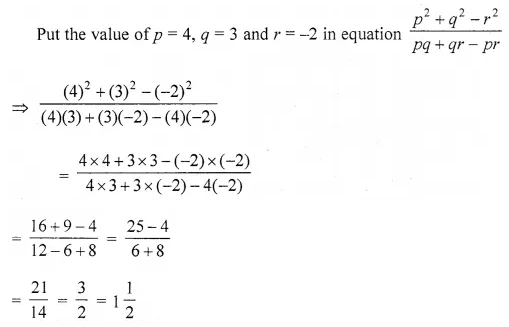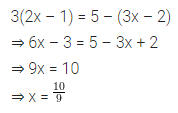ML Aggarwal Class 6 Solutions Chapter 14 Mensuration Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 14 Mensuration Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) The perimeter of a closed plane figure is the length of its ……….
(ii) The unit of measurement of the perimeter is the same as that of ……….
(iii) If the side of a rhombus is 7 cm then its perimeter is ……….
(iv) The area of a closed plane figure is measured in ……….
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) A centimetre is the unit of area.
(ii) The sum of lengths of a polygon is called its area.
(iii) If the sides of a rectangle are given in centimetres, then its perimeter is measured in square centimetres.
(iv) If the side of a square is doubled, then its perimeter is also doubled.
(v) If the side of a square is doubled, then its area is also doubled.
(vi) To find the cost of constructing a road, we find its area.
(vii) To find the cost of fencing a field, we find its perimeter.
Solution:

Multiple Choice Questions
Choose the correct answer from, the given four options (3 to 15):
Question 3.
If the perimeter of a square is 50 cm, then its side is
(a) 200 cm
(b) 150 cm
(c) 25 cm
(d) 12.5 cm
Solution:

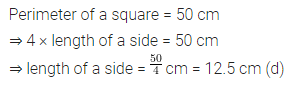
Question 4.
The area of the rectangle with length 25 cm and breadth 12 cm is
(a) 300 sq. m
(b) 74 cm
(c) 300 sq. cm
(d) 74 sq. cm
Solution:

Question 5.
If the perimeter of a square is 36 cm, then its area is
(a) 6 sq. cm
(b) 9 sq. cm
(c) 18 sq. cm
(d) 81 sq. cm
Solution:

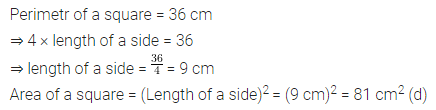
Question 6.
If the area of a rectangular plot is 180 sq. m and its length is 15 m, then its breadth is
(a) 12 m
(b) 12 cm
(c) 60 m
(d) 9 m
Solution:

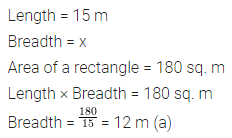
Question 7.
If the length and the breadth of a rectangle are doubled, then its perimeter
(a) remains the same
(b) doubles
(c) becomes four times
(d) becomes half
Solution:

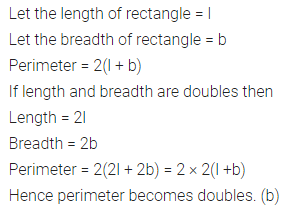
Question 8.
If the length and the breadth of a rectangular are doubled then its area
(a) remains the same
(b) becomes half
(c) doubles
(d) becomes four times.
Solution:

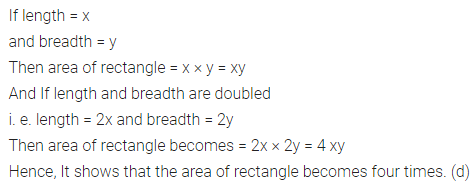
Question 9.
If the sides of a square are halved, then its area
(a) remains the same
(b) becomes half
(c) becomes one-fourth
(d) doubles
Solution:

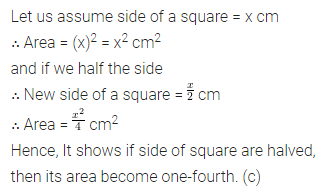
Question 10.
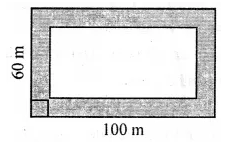
A square-shaped park ABCD of side 100 m has two equal flower beds of size 10 m x 5 m as shown in the given figure. The perimeter of the remaining park is

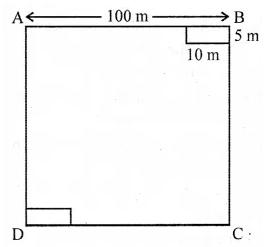
(a) 340 m
(b) 370 m
(c) 400 m
(d) 430 m
Solution:

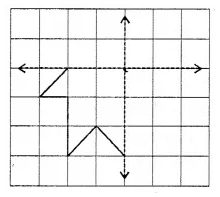
Question 11.
In the given figure, a square of side 1 cm is joined to a square of side 3 cm. The perimeter of the new figure is

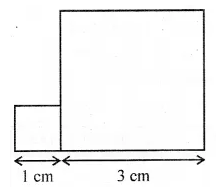
(a) 13 cm
(b) 14 cm
(c) 15 cm
(d) 16 cm
Solution:

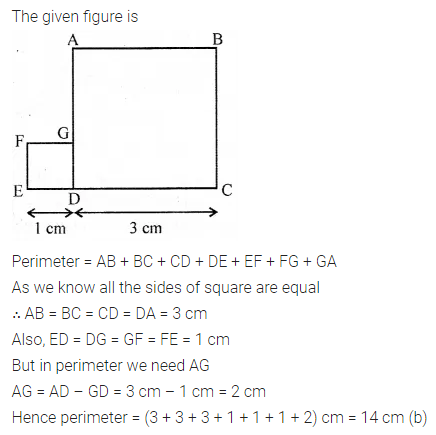
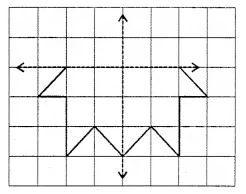
Question 12.
Two regular hexagons of perimeter 30 cm each are joined as shown in the given figure. The perimeter of the new figure is

(a) 65 cm
(b) 60 cm
(c) 55 cm
(d) 50 cm
Solution:

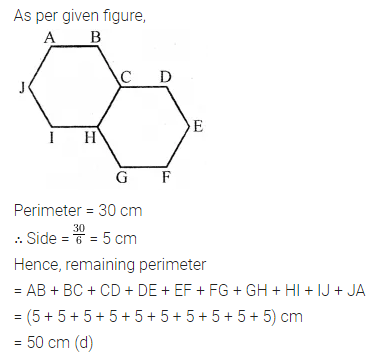
Question 13.
If the area of a square is numerically equal to its perimeter, then the length of each side is
(a) 1 unit
(b) 2 units
(c) 3 units
(d) 4 units
Solution:

Question 14.
If a ribbon of length 10 m is stitched around a rectangular table cloth making 2 rounds along its boundary, then the perimeter of the table cloth is
(a) 20 m
(b) 10 m
(c) 5 m
(d) 2.5 m
Solution:

Question 15.
A picture is 60 cm wide and 1.8 m long. The ratio of its width to its perimeter in lowest form is
(a) 1 : 2
(b) 1 : 3
(c) 1:6
(d) 1 : 8
Solution:

Higher Order Thinking Skills (Hots)
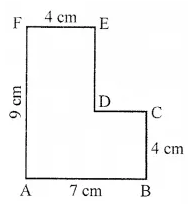
Question 1.
How many envelopes of size 25 cm x 15 cm can be made from a rectangular sheet of size 4 m x 1.2 m?
Solution:

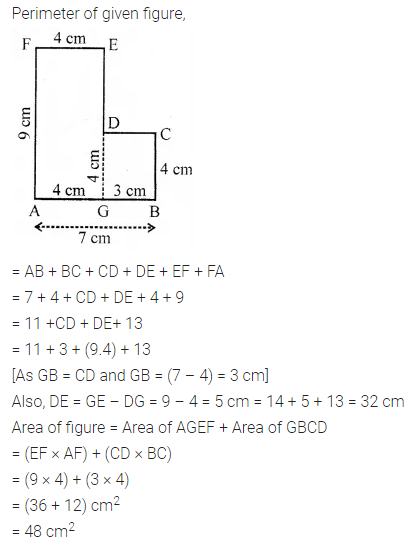
Question 2.
The perimeter of a rectangle is 36 cm. What will be length and breadth (in natural number) of that rectangle whose area is
(i) maximum?
(ii) minimum?
Solution:

ML Aggarwal Class 6 Solutions Chapter 14 Mensuration Ex 14.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 14 Mensuration Ex 14.2

Question 1.
Find the area of the region enclosed by the following figures by counting squares:

Solution:

Question 2.
Find the area of the following closed figures by counting squares:

Solution:

Question 3.
Find the areas of the rectangles whose lengths and breadths are:
(i) 9 m and 6 m
(ii) 17 m and 3 m
(iii) 14 m and 4 m
Which one has the largest area and which one has the smallest area?
Solution:

Question 4.
Find the areas of the rectangles whose two adjacent sides are:
(i) 14 cm and 23 cm
(ii) 3 km and 4 km
(iii) 2 m and 90 cm
Solution:

Question 5.
Find the areas of the squares whose sides are:
(i) 8 cm
(ii) 14 m
(iii) 2 m 50 cm
Solution:

Question 6.
A room is 4 m long and 3 m 25 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Solution:

Question 7.
What is the cost of tiling a rectangular field 500 m long and 200 m wide at the rate of ₹7.5 per hundred square metres?
Solution:

Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:

Question 9.
In the given figure, find the area of the path (shown shaded) which is 2 m wide all around.

Solution:

Question 10.
Four square flower beds of side 1 m 50 cm are dug on a rectangular piece of land 8 m long and 6 m 50 cm wide. What is the area of the remaining part of the land?
Solution:

Question 11.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to cover a rectangular region whose length and breadth are respectively :
(i) 70 cm and 36 cm
(ii) 144 cm and 1 m.
Solution:

Question 12.
The area of a rectangular plot is 340 sq. m. If its breadth is 17 m, find its length and the perimeter.
Solution:

Question 13.
If the area of a rectangular plot is 144 sq. m and its length is 16 m. Find the breadth of the plot and the cost of fencing it at the rate of ₹ 6 per metre.
Solution:

Question 14.
Split the following shapes into rectangles and find their areas. (The measures are given in centimetres).

Solution:

ML Aggarwal Class 6 Solutions Chapter 14 Mensuration Ex 14.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 14 Mensuration Ex 14.1

Question 1.
Find the perimeter of each of the following figures:

Solution:

Question 2.
Find the perimeter of each of the following shapes:
(i) A triangle of sides 3 cm, 4 cm and 6 cm.
(ii) A triangle of sides 7 cm, 5.4 cm and 10.2 cm.
(iii) An equilateral triangle of side 11 cm.
(iv) An isosceles triangle with equal sides 10 cm each and third side 7 cm.
Solution:

Question 3.
The lid of a rectangular box of sides 40 cm by 10 cm is sealed all round with tape. What is the length of the tape required?
Solution:

Question 4.
Table-Top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?
Solution:

Question 5.
A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
Solution:

Question 6.
Find the perimeter of a regular hexagon with each side measuring 7.5 m.
Solution:

Question 7.
The lengths of two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is the length of its third side?
Solution:

Question 8.
The perimeter of a regular pentagon is 100 cm. How long is its every side?
Solution:

Question 9.
A piece of string is 30 cm long. What will be the length of each side if the string is used to form:
(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?
Solution:

Question 10.
Find the cost of fencing a rectangular park of length 225 m and breadth 115 m at the rate of ₹13 per metre.
Solution:

Question 11.
Meera went to a rectangular park 140 m long and 90 m wide. She took 5 complete rounds on its boundary. What is the distance covered by her?
Solution:

Question 12.
Pinky runs 8 times around a rectangular park with length 80 m and breadth 55 m while Pankaj runs 7 times around a square park of side 75 cm. Who covers more distance and by how much?
Solution:

ML Aggarwal Class 6 Solutions Chapter 13 Practical Geometry Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress

Question 1.
Draw a line segment AB = 5.4 cm. Construct a perpendicular at A by using ruler and compass.
Solution:
Steps of Construction:

Question 2.
Draw a line segment PQ = 6.8 cm. Draw a perpendicular to it from a point A outside PQ by using ruler and compass.
Solution:

Question 3.
Draw a line segment of length 6.5 cm and construct its axis of symmetry.
Solution:

Question 4.
Draw ∠AOB = 76° with the help of a protractor. Bisect this angle by using a ruler and compass. Measure the two parts by your protractor and see how accurate you are.
Solution:
Steps of Construction:

Question 5.
By using and compass, construct an angle of 135° and bisect it. Measure any one part by protractor and see how accurate you are.
Solution:

ML Aggarwal Class 6 Solutions Chapter 13 Practical Geometry Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) A ruler is used to draw a line and to measure their …………
(ii) A divider is used to compare …………
(iii) A compass is used to draw circles or arcs of …………
(iv) A protractor is used to draw and measure …………
(v) The set squares are two triangular pieces having angles of ………… and …………
(vi) To bisect a line segment of length 7 cm, the opening of the’ compass should be more than …………
(vii) The perpendicular bisector of a line segment is also its line of …………
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) There is only one set square in a geometry box.
(ii) An angle can be copied with the help of a ruler and compass.
(iii) The perpendicular bisector of a line segment can be drawn by paper folding.
(iv) Perpendicular to a line from a given point not on it can be drawn by paper folding.
(v) A 45° – 45° – 90° set square and a protractor have the same number of line(s) of symmetry.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 13):
Question 3.
A circle of any radius can be constructed with the help of a:
(a) ruler
(b) divider
(c) compass
(d) protractor
Solution:
compass (c)

Question 4.
The instrument in a geometry box having the shape of a semicircle is :
(a) ruler
(b) divider
(c) compass
(d) protractor
Solution:

Question 5.
The instrument to measure an angle is
(a) ruler
(b) protractor.
(c) divider
(d) compass
Solution:
protractor (b)

Question 6.
Which of the following angles cannot be constructed using a ruler and compass?
(a) 15°
(b) 45°
(c) 75°
(d) 85°
Solution:
85° (d)

Question 7.
The number of perpendiculars that can be drawn to a line from a point not on it is
(a) 1
(b) 2
(c) 4
(d) infinitely many
Solution:
1 (a)

Question 8.
The number of perpendicular bisectors that can be drawn of a given line segment is :
(a) 0
(b) 1
(c) 2
(d) infinitely many
Solution:
1 (b)

Question 9.
The number of lines of symmetry in a picture of a divider is The number of lines of symmetry in a picture of a compass is
(a) 0
(b) 1
(c) 2
(d) 4
Solution:
1 (b)

Question 10.
The number of lines of symmetry in a picture of a compass is
(a) 0
(b) 1
(c) 2
(d) none of these
Solution:
0 (a)

Question 11.
The number of lines of symmetry in a ruler is
(a) 0
(b) 1
(c) 2
(d) 4
Solution:
2 (c)

Question 12.
The number of lines of symmetry in a 30° – 60° – 90° set square is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
0 (a)

Question 13.
The number of lines of symmetry in a protractor is
(a) 0
(b) 1
(c) 2
(d) more than 2
Solution:
1 (b)

ML Aggarwal Class 6 Solutions Chapter 13 Practical Geometry Ex 13.3 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Ex 13.3

Question 1.
Draw an angle of 80° and make a copy of it using ruler and compass.
Solution:

Question 2.
Draw an angle of measure 127° and construct its bisector.
Solution:

Question 3.
Draw ∠POQ = 64°. Also, draw its line of symmetry.
Solution:

Question 4.
Draw a right angle and construct its bisector.
Solution:

Question 5.
Draw an angle of 152° and divide it into four equal parts.
Solution:

Question 6.
Draw an angle of measure 45° and bisect it.
Solution:

ML Aggarwal Class 6 Solutions Chapter 13 Practical Geometry Ex 13.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Ex 13.2

Question 1.
Draw a line segment \(\overline{\mathrm{PQ}}\) =5.6 cm. Draw a perpendicular to it from a point A outside \(\overline{\mathrm{PQ}}\) by using ruler and compass.
Solution:

Question 2.
Draw a line segment \(\overline{\mathrm{AB}}\) = 6.2 cm. Draw a perpendicular to it at a point M on \(\overline{\mathrm{AB}}\) by using ruler and compass.
Solution:

Question 3.
Draw a line l and take a point P on it. Through P, draw a line segment \(\overline{\mathrm{PQ}}\) perpendicular to l. Now draw a perpendicular to \(\overline{\mathrm{PQ}}\) at Q (use ruler and compass).
Solution:

Question 4.
Draw a line segment \(\overline{\mathrm{AB}}\) of length 6.4 cm and construct its axis of symmetry (use ruler and compass).
Solution:

Question 5.
Draw the perpendicular bisector of \(\overline{\mathrm{XY}}\) whose length is 8.3 cm.
(i) Take any point P on the bisector drawn. Examine whether PX = PY.
(ii) If M is the mid-point of \(\overline{\mathrm{XY}}\), what can you say about the lengths MX and MY?
Solution:

Question 6.
Draw a line segment of length 8.8 cm. Using ruler and compass, divide it into four equal parts. Verify by actual measurement.
Solution:

Question 7.
With \(\overline{\mathrm{PQ}}\) of length 5.6 cm as diameter, draw a circle.
Solution:

Question 8.
Draw a circle with centre C and radius 4.2 cm. Draw any chord AB. Construct the perpendicular bisector of AB and examine if it passes through C.
Solution:

Question 9.
Draw a circle of radius 3.5 cm. Draw any two of its (non-parallel) chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution:

ML Aggarwal Class 6 Solutions Chapter 13 Practical Geometry Ex 13.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Ex 13.1

Question 1.
Construct a circle of radius:
(i) 2 cm
(ii) 3.5 cm
Solution:

Question 2.
With the same centre O, draw two circles of radii 2.6 cm and 4.1 cm.
Solution:

Question 3.
Draw any circle and mark points A, B and C such that
(i) A is on the circle.
(ii) B is in the interior of the circle.
(iii) C is in the exterior of the circle.
Solution:

Question 4.
Draw a circle and any two of its (non-perpendicular) diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
Solution:

Question 5.
Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D.
Examine whether \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are at right angles.
Solution:

Question 6.
Construct a line segment of the length of 6.3 cm using ruler and compass.
Solution:

Question 7.
Construct \(\overline{\mathrm{AB}}\) of length 8.3 cm. From this cut off \(\overline{\mathrm{AC}}\) of length 5.6 cm. Measure the length of BC . .
Solution:

Question 8.
Draw any line segment \(\overline{\mathrm{PQ}}\). Without measure \(\overline{\mathrm{PQ}}\), construct a copy of \(\overline{\mathrm{PQ}}\).
Solution:

Question 9.
Given some line segment \(\overline{\mathrm{AB}}\), whose length you do not know, construct \(\overline{\mathrm{PQ}}\) such that the length of \(\overline{\mathrm{PQ}}\) is twice that of \(\overline{\mathrm{AB}}\).
Solution:

Question 10.
Take a line segment \(\overline{\mathrm{PQ}}\) of length 10 cm. From \(\overline{\mathrm{PQ}}\), cut of \(\overline{\mathrm{PA}}\) of length 4.3 cm and \(\overline{\mathrm{BQ}}\) of length 2.5 cm. Measure the length of segment \(\overline{\mathrm{AB}}\).
Solution:

Question 11.
Given two line segments \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) of length 7.5 cm and 4.6 respectively. Construct line segments.
(i) \(\overrightarrow { PQ } \) of length equal to the sum of the lengths of \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\).
(ii) \(\overline{\mathrm{XY}}\) of length equal to the difference of the lengths of \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\). Verify these lengths by measurements.
Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 6 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 6

Questions 1 to 8 are of 1 mark each.
Choose the correct answer from the given four options (1 to 8):
Question 1.
The value of the expression \(\frac{5}{3}\)x² – 1 when x = -2 is

Solution.

Question 2.
By joining any two points of a circle, we obtain its
(a) radius
(b) circumference
(c) diameter
(d) chord
Solution:
chord (d)

Question 3.
Which of the following statement is true?
(a) Every closed curve is a polygon
(b) Every closed simple curve is a polygon
(c) Every simple curve made up entirely of line segment is a polygon
(d) Every simple closed curve made up entirely of line segments is a polygon.
Solution:

Question 4.
The median of the numbers 3, 1,0, 6, 5, 3, 4, 1, 2, 2 is
(a) 2
(b) 2.5
(c) 3
(d) none of these
Solution:

Question 5.
If the perimeter of a regular octagon is 72 cm, then its side is
(a) 6 cm
(b) 8 cm
(c) 9 cm
(d) 12 cm
Solution:

Question 6.
If Anandi’s present age is x years and her father’s age is 3 years less than 4 times her age, then her father’s present age is
(a) (4x – 3) years
(b) (3x – 4) years
(c) 4(x – 3) years
(d) (4x + 3) years
Solution:

Question 7.
The number of lines of symmetry which a quadrilateral cannot have is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 8.
The number of bisectors that can be drawn of a given angle is
(a) 1
(b) 2
(c) 4
(d) infinitely many
Solution:
1 (a)

Section-B
Questions 9 to 14 are of 2 marks each.
Question 9.
A cuboidal box has height h cm. Its length is 4 times the height and the breadth is 7 cm less than the length. Express the length and the breadth of the box in terms of its height.
Solution:

Question 10.
In the given figure, name the point(s)
(i) in the interior of ∠EOD.
(ii) in the exterior of ∠FOE.

Solution:

Question 11.
Write the following statement in mathematical form using literals, numbers and the signs of basic operations:
“Three times a number x is equal to 12 less than twice the number y.”
Solution:

Question 12.
If the area of a rectangular plot is 240 sq. m and its breadth is 12 m, then find the perimeter of the plot.
Solution:

Question 13.
On a squared paper, sketch a hexagon with exactly one line of symmetry.
Solution:

Question 14.
Find the area of the region enclosed by the given polygon.

Solution:

Section-C
Questions 15 to 24 are of 4 marks each.
Question 15.
In the given figure, count the number of segments and name them.

Solution:

Question 16.
In the given figure, state which of the angles marked with small letters are acute, obtuse, reflex or right angle (you may judge the nature of angle by observation).

Solution:

Question 17.
There are 40 employees in a Government Office. They were asked how many children they have. The result was:
1, 2, 3, 1, 0, 2, 0, 1, 2, 2, 1, 3, 5, 2, 0, 0, 2. 4, 1, 1
2, 2, 0, 3, 0, 0, 2, 1, 3, 6, 0, 2, 1, 0, 3, 2, 2, 2, 1, 4
(i) Arrange the above data in ascending order.
(ii) Construct frequency distribution table for the given data.
Solution:

Question 18.
A survey was carried out on 32 students of class VI in a school. Data about different modes of transport used by them to travel to school was displayed in a pictograph as under:

Observe the pictograph and answer the following questions:
Observe the pictograph and answer the following questions:
(i) Which is the most popular mode of transport?
(ii) What is the number of students who travel either by cycle or walking?
(iii) What are the advantages of using a school bus as a mode of transport?
(iv) What mode of transport would you suggest and why?
Solution:

Question 19.
If p = 4, q = 3 and r = -2, then find the value of the algebraic expression \(\frac{p^{2}+q^{2}-r^{2}}{p q+q r-p r}\).
Solution:

Question 20.
A room is 5 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room completely?
Solution:

Question 21.
Solve the linear equation
3(2x – 1) = 5 – (3x – 2).
Solution:

Question 22.
Copy the given figure on a squared paper and complete the figure such that the resultant figure is symmetrical about the dotted line.

Solution:

Question 23.
Draw a net of a square pyramid.
Solution:

Question 24.
Draw a line segment of length 7.5 cm and construct its axis of symmetry.
Solution:

Section-D
Questions 25 to 29 are of 6 marks each.
Question 25.
A survey was carried out on 150 families of a colony about the consumption of milk per day. The result was recorded as:

Represent the above data by a vertical bar graph, choosing scale: 1 unit height = 6 families. What are the advantages of taking milk every day?
Solution:

Question 26.
Draw a rough sketch of a regular hexagon. Connecting three of its vertices, draw
(i) an isosceles triangle
(ii) an equilateral triangle
(iii) a right-angled triangle.
Solution:

Question 27.
The cost of cultivating a rectangular field at the rate of ₹5 per square metre is ₹2880. If the length of the field is 32 m, find the cost of fencing the field at the rate of ₹11.25 per metre.
Solution:

Question 28.
By using a ruler and compass, construct an angle of 45° and bisect it. Measure any one part.
Solution:

Question 29.
Look at the following matchstick pattern of polygons. Complete the table. Also, write the general rule that gives the number of matchsticks.

Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 5 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 5

Choose the correct answer from the given four options (1-2):
Question 1.
The number of lines of symmetry of a protractor is
(a) 0
(b) 1
(c) 2
(d) unlimited
Solution:
1 (b)

Question 2.
If the perimeter of a regular pentagon is 60 cm, then its every side is
(a) 10 cm
(b) 12 cm
(c) 15 cm
(d) 20 cm
Solution:

Question 3.
If the perimeter of a square is 42 cm, then find its area.
Solution:

Question 4.
Using a ruler and compass, construct an angle of 90°.
Solution:
Steps of Construction:

Question 5.
On a squared paper, sketch a quadrilateral with exactly two lines of symmetry. Also, sketch the lines of symmetry.
Solution:

Question 6.
If the area of a rectangular plot is 396 sq. m and its breadth is 18 m. Find the length of the plot and the cost of fencing it at the rate of ₹7.50 per metre.
Solution:

Question 7.
Draw a line segment AB of length 6.4 cm. Take a point P on AB such that AP = 4.5 cm. Draw a perpendicular to AB at P. (use ruler and compass).
Solution:

Question 8.
Copy the given figure. How many lines of symmetry it has? Draw its all lines of symmetry.

Solution:

Question 9.
In the given figure, all adjacent sides are at right angles. Find:
(i) the perimeter of the figure.
(ii) the area enclosed by the figure.

Solution:

Question 10.
Copy the given figure on a squared paper and complete the figure such that the resultant figure is symmetrical about both the dotted lines.

Solution:

https://ncertsolutionsguru.dreamwidth.org/
https://www.racked.com/users/NCERTSolutionsGuru
https://github.com/NCERTSolutionsGuru

ML Aggarwal Class 9 Solutions Chapter 1 Rational Numbers Ex 1.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 1 Rational Numbers Ex 1.2

Question 1.
Prove that \(\sqrt{5}\) is an irrational number. Hence show that \(\frac {2}{3}\)\(\sqrt{5}\) is an irrational number.
Solution:
Let \(\sqrt{5}\) is a rational number
Let \(\sqrt{5}\) = \(\frac {p}{q}\) where p and q are integer and q > 0, p and q have no common factor except 1
Squaring both sides

⇒ p² = 5q²
∴ 5q² is divisible by 5
∴ p² is also divisible by 5
⇒ p is divisible by 5
Let p = 5k where k is an integer
squaring both sides
p² = 25 k²
⇒ 5q² = 25k²
⇒ q² = 5k²
∴ 5k² is divisible by 5
∴ q² is also divisible by 5
⇒ q is divisible by 5
∴ p and q are both divisible by 5
our supposition is wrong as p and q have no common factor
∴ \(\sqrt{5}\) is an irrational number
Now in \(\frac {2}{3}\)\(\sqrt{5}\) , \(\frac {2}{3}\) is a rational number and \(\sqrt{5}\) is an irrational number.

But product of a rational number and an irrational number is also an irrational number
∴ \(\frac {2}{3}\)\(\sqrt{5}\) is an irrational number.
Hence proved.

Question 2.
Prove that \(\sqrt{7}\) is an irrational number.
Solution:
Let \(\sqrt{7}\) is a rational number
Let \(\sqrt{7}\) = \(\frac {p}{q}\)
Where p and q are integers, q ≠ 0 and p and q have no common factor
Squaring both sides,

⇒ p² = 7q²
∴ p² is a multiple of 7
⇒ p is multiple of 7
Let p = 7 m
Where m is an integer
∴ Then (7 m)² = 7q² ⇒ 49 m² = 7q²
⇒ q² = 7 m²
∴ q² is multiple of 7
⇒ q is multiple of 7
p and q both are multiple of 7
Which is not possible
Hence \(\sqrt{7}\) is not a reational number
∴ \(\sqrt{7}\) is an irrational number

Question 3.
Prove that \(\sqrt{6}\) is an irrational number.
Solution:
Let \(\sqrt{6}\) is a rational number
and \(\sqrt{6}\) = \(\frac {p}{q}\) where p and q are integers and q ≠ 0 and have no common factor

= p² = 6q² ………(i)
∴ p² is divisible by 2 which is a prime
p is also divisible by 2
Let p = 2k where k is an integer
∴ Substituting the value of p in (i)
(2k)² = 6q² ⇒ 4k² = 6q²
⇒ 2k² = 3q²
∴ q² is divisible by 2
⇒ q is divisible
p and q both are divisible by 2
Which is not possible as p and q both have
no common factor
Hence \(\sqrt{6}\) is an irrational number

Question 4.
Prove that \(\frac{1}{\sqrt{11}}\) is an irrational number.
Solution:
Let \(\frac{1}{\sqrt{11}}\) is a rational number
Let \(\frac{1}{\sqrt{11}}\) = \(\frac {p}{q}\) where p and q are integers
and q ≠ 0 and have no common factor Squaring both sides

∴ q² is divisible by 11
⇒ q is divisible by 11
Let q = 11k where k is an integer squaring
q² = 121k²
Substituting the value of q in (i)
∴ 121k² = 11p²
⇒ 11k² = p²
∴ p² is divisible by 11
⇒ p is divisible by 11
∴ p and q both are divisible by 11
But it is not possible
∴ \(\frac{1}{\sqrt{11}}\) is an irrational number

Question 5.
Prove that \(\sqrt{2}\) is an irrational number. Hence show that 3 – \(\sqrt{2}\) is an irrational number.
Answer:
(i) Let \(\sqrt{2}\) be a rational number, then by definition
\(\sqrt{2}\) = \(\frac {p}{ q}\) where p, q are integers ,q>0, p and q have no common factor.
Since, 1² – 1, 2² = 4 and 1 < 0 < 4, It follows that

In particular, if q = 1, then we get 1 < p < 2 But, there is no integer between 1 and 2. ∴ q ≠ 1 so q > 1

As 2 and q are both integers, 2q is an integer. On the other hand, q > 1 and p,q have no common factor. So p² and q have no common factor. It follows that \(\frac {p}{q}\) is not an integer. Thus, we arrive at a contradiction. Hence \(\sqrt{2}\) is not a rational number.

If possible, let 3 – \(\sqrt{2}\) is an rational number say r (r ≠ 0), then
3 – \(\sqrt{2}\) = r ⇒ – \(\sqrt{2}\) = r – 3 ⇒ \(\sqrt{2}\) = 3 – r
As r is a rational number and r ≠ 0, Then 3 – r is rational
⇒ \(\sqrt{2}\) is rational, which is wrong, Hence 3 – \(\sqrt{2}\) is irrational number.

Question 6.
Prove that \(\sqrt{3}\) is an irrational number. Hence, show that \(\frac{2}{5}\)\(\sqrt{3}\) is an irrational number.
Solution:
Let \(\sqrt{3}\) is a rational number
and let \(\sqrt{3}\) = \(\frac{p}{q}\) where p and q are integers,
q ≠ 0 and have no common factors both sides
Squaring both sides

p² is divisible by 3
⇒ p is divisible by 3
Let p = 3k where k is an integer
Squaring both sides
p² = 9k²
Substituting the value of p² in (i)
9k² = 3q² ⇒ q² = 3k²
∴ q² is divisible by 3
⇒ q is divisible by 3
∴ p and q both are divisible by 3
But it is not pissible
∴ \(\sqrt{3}\) is an irrational number
Now in \(\frac{2}{5}\)\(\sqrt{3}\)
2 and 5 both are rational numbers.
∴ \(\frac{2}{5}\)\(\sqrt{3}\) is irrational number as product of rational and irrational is irrational
Hence \(\frac{2 \sqrt{3}}{5}\) is an irrational number.

Question 7.
Prove that √5 is an irrational number.
Hence, show that -3 + 2√5 is an irrational number.
Answer:
Let \(\sqrt{5}\) is a rational number
and let \(\sqrt{5}\) = \(\frac {p}{q}\) where p and q are integers,
q ≠ 0 and have no common factors both sides
Squaring both sides

p² is divisible by 5
⇒ p is divisible by 5
Let p = 5k where k is an integer
Squaring both sides
p² = 25k²
Substituting the value of p² in (i)
25k² = 5q² => q² = 5k²
q² is divisible by 5
⇒ is divisible by 5
∴ p and q both are divisible by 5
But it is not possible
\(\sqrt{5}\) is an irrational number
Now in – 3 + 2\(\sqrt{5}\)
– 3 and 2 both are rational numbers
∴ 2\(\sqrt{5}\) is irrational number as product of a rational and irrational is irrational
Hence – 3 + 2\(\sqrt{5}\) is an irrational number

Question 8.
Prove that the following numbers are irrational:

Answer:
(i) Suppose that 5 + \(\sqrt{2}\) is rational number Say r (r ≠ 0) then
5 + \(\sqrt{2}\) = r \(\sqrt{2}\) = r – 5
As r is rational number, then r – 5 is also rational number.
⇒ \(\sqrt{2}\) is rational number, which is wrong,
∴ our supposition is wrong.
Hence, 5 + \(\sqrt{2}\) is irrational number.

(ii) 3 – 5\(\sqrt{3}\)
Suppose 3 – 5\(\sqrt{3}\) is a rational
and let 3 – 5\(\sqrt{3}\) = r
⇒ 5\(\sqrt{3}\) = 3 – r = > 73 = \(\sqrt{3}=\frac{3-r}{5}\)
∵ r is a rational number 3-r
∴ \(\frac{3-r}{5}\) is also a rational number
But \(\sqrt{3}\) is an irrational number
∴It is not possible
∴ 3 – 5\(\sqrt{3}\) is an irrational number

(iii) 2\(\sqrt{3}\) – 7
Let 2\(\sqrt{3}\) – 7 is a rational number
and let 2\(\sqrt{3}\) – 7 = r
= > 2\(\sqrt{3}\) = r + 7 ⇒ \(\sqrt{3}=\frac{r+7}{2}\)
∴ r is a rational number
∴ \(\frac{r+7}{2}\) is also a rational number
But \(\sqrt{3}\) is an irrational number
∴ It is not possible
2\(\sqrt{3}\) – 7 is an irrational number

(iv) \(\sqrt{2}\) + \(\sqrt{5}\)
Suppose \(\sqrt{2}\) + \(\sqrt{5}\) isa rational number and
let x = \(\sqrt{2}\) + \(\sqrt{5}\)
Squaring both sides,

\(\sqrt{10}\) is a rational number
But it is not true as \(\sqrt{10}\) is an irrational number
∴ Our supposition is wrong
∴ \(\sqrt{2}\) + \(\sqrt{5}\) is an irrational number.