Category: ICSE

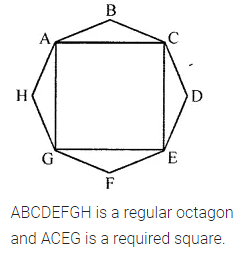
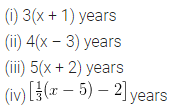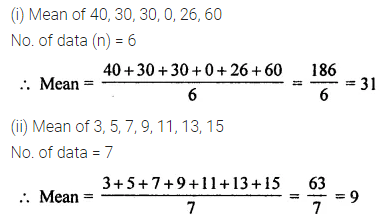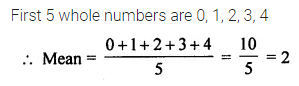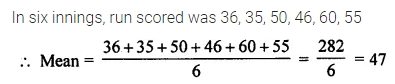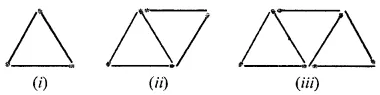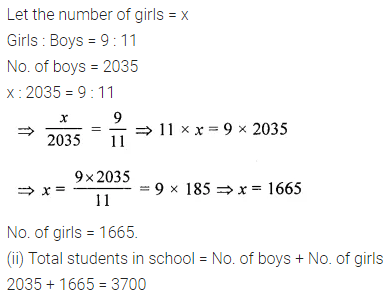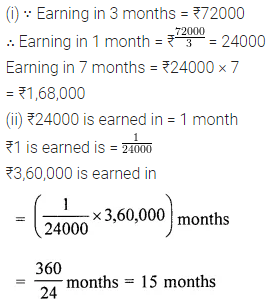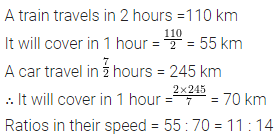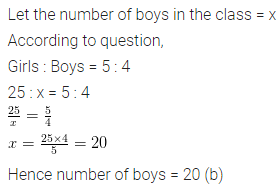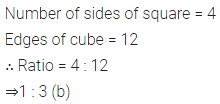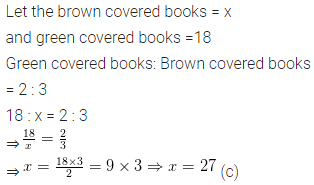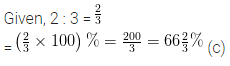ML Aggarwal Class 6 Solutions Chapter 12 Symmetry Ex 12.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 12 Symmetry Ex 12.1

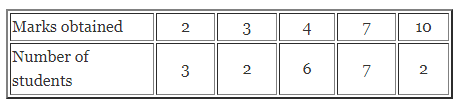
Question 1.
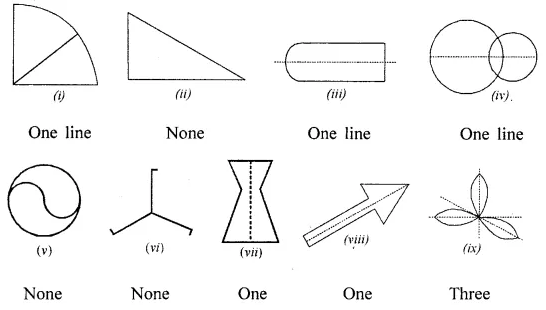
Draw the line (or lines) of symmetry, if any, of the following shapes and count their number.

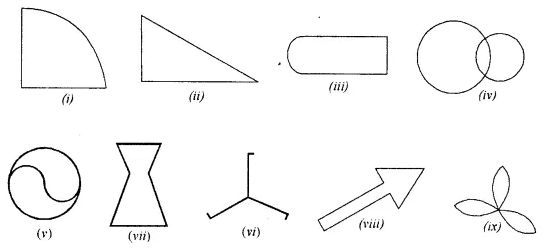
Solution:

Question 2.
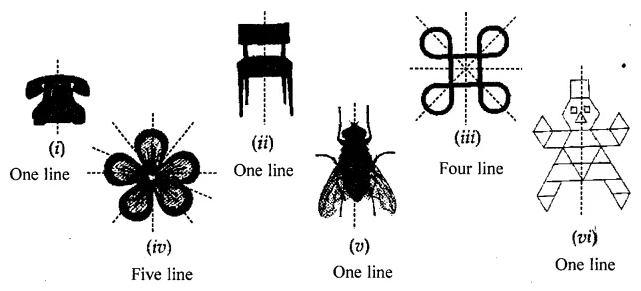
Draw the line (or lines) of symmetry, if any, of the following pictures (of objects) and count their number:

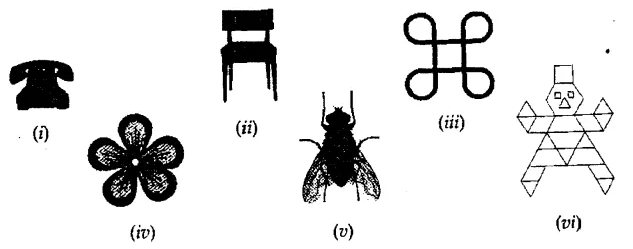
Solution:

Question 3.
Draw the line (or lines) of symmetry, if any, of the following road signs and count their number:

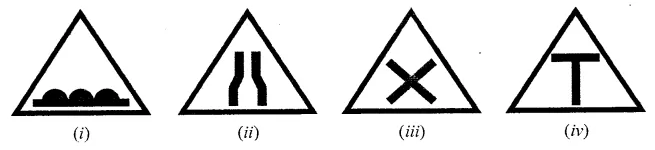
Solution:

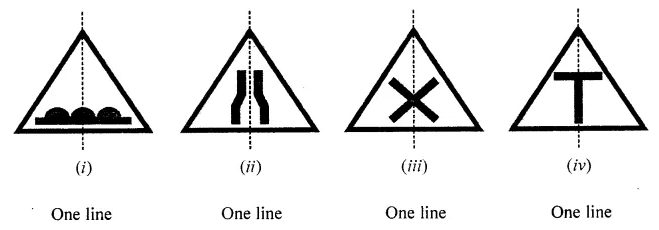
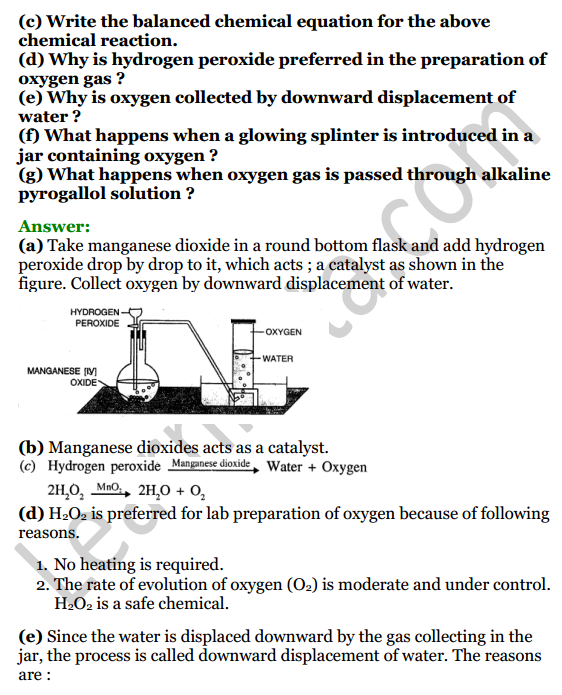
Question 4.
Draw the line (or lines) of symmetry, if any, of the following numerals and count their number:

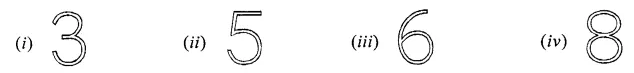
Solution:

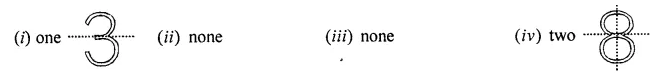
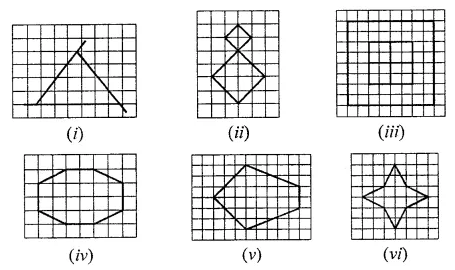
Question 5.
Copy the following figures on a squared paper and draw the lines of symmetry (if any) and count their number:

Solution:

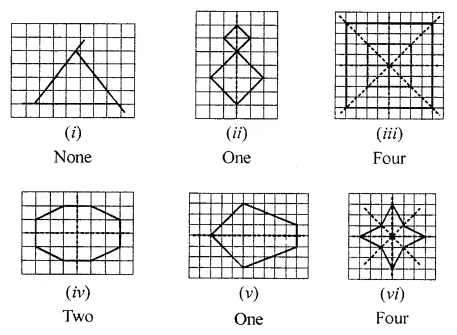
Question 6.
Write the letters of words ‘JUST LOOK’ which have no line of symmetry.
Solution:

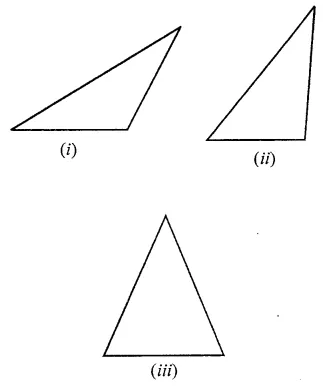
Question 7.
Can you draw a triangle which has
(i) exactly one line of symmetry?
(ii) exactly two lines of symmetry?
(iii) exactly three lines of symmetry?
(iv) no lines of symmetry?
Sketch a rough figure in each case and name the triangle.
Solution:

ML Aggarwal Class 6 Solutions Chapter 9 Algebra Ex 9.3 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 9 Algebra Ex 9.3

Question 1.
Form four expressions with numbers 7, 5 and 8 (no variables) using operations of addition, subtraction or multiplication with the condition that every number should be used but not more than once.
Solution:

Question 2.
Which out of following are expressions with numbers only?
(i) 2y + 3
(ii) (7 × 20) – 82
(iii) 5 × (21 – 7) + 9 x 2
(iv) 5 -11 n
(v) (5 × 4) – 45 + p
(vi) 3 × (11 + 7) – 24 + 3
Solution:

Question 3.
Identify the operations (addition, subtraction, multiplication, division) in forming the following expressions and tell how the expressions have been formed:
(i) x + 5
(ii) y – 7
(iii) 3z
(iv) \(\frac{p}{5}\)
(v) 2x + 17
(vi) 3y – 5
(vii) \(-7 m+\frac{2}{3}\)
(viii) \(\frac{x}{3}-15\)
Solution:

Question 4.
Write expression for the following:
(i) 7 added to p
(ii) p subtracted from 7
(iii) p multiplied by 7
(iv) p divided by 7
(v) 7 divided by p
(vi) 7 subtracted from -m
(vii) p multiplied by -5
(viii) -p divided by 5
Solution:

Question 5.
Write expression for the following:
(i) 11 added to 2 m
(ii) 11 subtracted from 2 m
(iii) 3 added to 5 times y
(iv) 3 subtracted from 5 times y
(v) y is multiplied by -8 and then 5 is added to the result
(vi) y is multiplied by 5 and then the result is subtracted from 16.
Solution:

Question 6.
Write the following in mathematical form using signs and symbols:
(i) 6 more than thrice a number x.
(ii) 7 taken away from y.
(iii) 3 less than quotient of x by y.
Solution:

Question 7.
Form six expressions using t and 4. Use not more than one number operation and every expression must have t in it.
Solution:

Question 8.
Form expressions using y, 2 and 7. Use only two different number operations and every expression must have y in it.
Solution:

Question 9.
A student scored x marks in English but the teacher deducted 5 marks for bad handwriting. What was the student’s final score in English?
Solution:

Question 10.
Raju’s father’s age is 2 years more than 3 times Raju’s age. If Raju’s present age is y years, then what is his father’s age?
Solution:

Question 11.
Mohini is x years old. Express the following in algebraic form:
(i) three times Mohini’s age next year.
(ii) four times Mohini’s age 3 years ago.
(iii) the present age of Mohini’s uncle, if his uncle is 5 times as old as Mohini will be two years from now.
(iv) the present age of Mohini’s cousin, if her cousin is two years less than one-third of Mohini’s age five years ago.
Solution:

Question 12.
A cuboidal box has height h cm. Its length is 5 times the height and breadth is 10 cm less than the length. Express the length and the breadth of the box in terms of the height.
Solution:

Question 13.
A bus travels at v km per hour. It is going from Delhi to Jaipur. After the bus has travelled 5 hours, Jaipur is still 20 km away. What is the distance from Delhi to Jaipur?
Solution:

Question 14.
Change the following statements using expressions into statements in ordinary language:
(i) A notebook cost ₹ p. A book costs ₹ 3p.
(ii) The cost of rice per kg is ₹ p. The cost of oil per litre is ₹5p.
(iii) The speed of a truck is v km per hour. The speed of a bus is (v + 10) km per hour.
(iv) Tony’s box contains 8 times the marbles he puts on the table.
(v) The total number of students in the school is 20 times that of our class.
(vi) Raju is x years old. His uncle is 4x years old and his aunt is (4x – 3) years old.
(vii) In arrangement of dots there are r rows. Each row contains 5 dots.
Solution:

ML Aggarwal Class 6 Solutions Chapter 11 Understanding Symmetrical Shapes Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 11 Understanding Symmetrical Shapes Check Your Progress

Question 1.
In the given figure, identify the longest and shortest line segments by measuring their lengths.

Solution:

Question 2.
Where will the hour hand of a clock stop if it starts from 10 and turns through 3 right angles?
Solution:
7

Question 3.
Classify the angles whose measures are given below:
(i) 56°
(ii) 125°
(iii) 90°
(iv) 180°
(v) 215°
(vi) 328°
Solution:

Question 4.
Name the types of the following triangles:
(i) ∆ABC with AB = 8 cm, AC = 7 cm and BC = 5.5 cm.
(ii) ∆PQR with PQ = PR = 5 cm and QR = 7.3 cm.
(iii) ∆DEF with D = ∠90°.
(iv) ∆XYZ with ∠Y = 90° and XY = YZ.
(v) ∆LMN with ∠L = 30°, ∠M = 70° and ∠N = 80°.
Solution:

Question 5.
Name each of the following triangles in two different ways (you may use ruler and protractor):

Solution:

Question 6.
State whether the following statements are true or false:
(i) A rectangle is a regular quadrilateral.
(ii) A rhombus is a regular quadrilateral.
(iii) Every parallelogram is a rhombus.
(iv) The diagonals of a rhombus intersect at right angles.
(v) A polygon having 6 sides is called an octagon.
(vi) A road roller has two plane circular faces and one curved face.
(vii) A rectangular pyramid has 5 rectangular faces.
Solution:

Question 7.
Draw a rough sketch of a regular octagon and draw a square by joining exactly four of its vertices.
Solution:

ML Aggarwal Class 7 Solutions Chapter 17 Data Handling Ex 17.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 17 Data Handling Ex 17.2

Question 1.
Find the mean of the following data:
(i) 40, 30, 30, 0, 26, 60
(ii) 3, 5, 7, 9, 11, 13, 15
Solution:

Question 2.
Find the mean of the first five whole numbers.
Solution:

Question 3.
A batsman scored the following number of runs in six innings:
36, 35, 50, 46, 60, 55
Calculate the mean runs scored by him in an inning.
Solution:

Question 4.
The enrolment in a school for six consecutive years was as follows:
1555, 1670, 1750, 2013, 2540, 2825
Find the mean enrolment of the school for this period.
Solution:

Question 5.
The marks (out of 100) obtained by a group of students in a science test are:
85, 76, 90, 85, 39, 48, 56, 95, 81, 75
Find the:
(i) highest and lowest marks obtained by the students.
(ii) range of the marks obtained.
(iii) mean marks obtained by the students.
Solution:

Question 6.
The heights of 10 girls were measured in cm and the results are as follows:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141
(i) What is the height of the tallest girl?
(ii) What is the height of the shortest girl?
(iii) What is the mean height of the girls?
(iv) How many girls have heights more than the mean height?
Solution:

Question 7.
If the arithmetic mean of 8, 4, 6, x, 2, 7 is 5, then find the value of x.
Solution:

Question 8.
Find the mean of the following data:

Solution:

ML Aggarwal Class 6 Solutions Chapter 9 Algebra Ex 9.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 9 Algebra Ex 9.2

Question 1.
If the side of an equilateral triangle is l, then express the perimeter of the triangle in terms of l.
Solution:

Question 2.
The side of a regular hexagon is l. Express its perimeter in terms of l.
Solution:

Question 3.
The length of an edge of a cube is l. Find the formula for the sum of lengths of all the edges of the cube.

Solution:

Question 4.
If the radius of a circle is r units, then express the length of a diameter of the circle in terms of r.
Solution:

ML Aggarwal Class 6 Solutions Chapter 11 Understanding Symmetrical Shapes Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 11 Understanding Symmetrical Shapes Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) An angle whose measure is less than that of a right angle is …………
(ii) An angle whose measure is the sum of the measures of two right angles is …………
(iii) When the sum of measures of two angles is that of a right angle, then each on of them is …………
(iv) When the sum of measures of two angles is that of a straight angle and if one of them is acute then the other is …………
(v) A triangle having one of its angles as right angle and with lengths of two sides equal is called ………… triangle.
(vi) A cuboid has ………… faces, ………… edges and ………… vertices.
(vii) A rectangular pyramid has ………… faces, ………… edges and ………… vertices.
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) Each angle of an equilateral triangle is a right angle.
(ii) The adjacent sides of a rectangle are equal in length.
(iii) The diagonals of a rectangle are equal in length.
(iv) The diagonals of a rectangle are perpendicular to one another.
(v) The diagonals of a rhombus are equal in length.
(vi) Any three line segments make up a triangle.
(vii) All the faces of a triangular prism are triangles.
(viii)All the faces of a triangular pyramid are triangles.
Solution:

Question 3.
State whether the following statement is true or false. Justify your answer.
‘An angle whose measure is greater than that of a right angle is obtuse’.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (4 to 15):
Question 4.
Comparison of lengths is possible in case of
(a) two lines
(b) two line segments
(c) two rays
(d) a ray and a line segment
Solution:

Question 5.
A reflex angle measures
(a) more than 90° but less than 180°
(b) more than 180° but less than 270°
(c) more than 180° but less than 360°
(d) none of these
Solution:

Question 6.
A scalene triangle cannot be
(a) an acute angled triangle
(b) an obtuse angled triangle
(c) a right angled triangle
(d) an equilateral triangle
Solution:

Question 7.
An obtuse angled triangle can be
(a) right angled
(b) isosceles
(c) equilateral
(d) none of these
Solution:

Question 8.
If you are facing north and turn through \(\frac{3}{4}\) of a turn in anti-clockwise direction, which direction will you face?
(a) east
(b) south
(c) west
(d) north
Solution:

Question 9.
Open any two adjacent fingers of your hand. What kind of angle you get?
(a) acute
(b) right
(c) obtuse
(d) straight
Solution:

Question 10.
In the given figure, the number of obtuse angles is

(a) 2
(b) 3
(c) 4
(d) 5
Solution:

Question 11.
If the sum of two angles is an obtuse angle, then which of the following is not possible? one right angle and one acute angle one obtuse angle and one acute angle two acute angles two right angles
(a) two right angles
(b) one obtuse angle and one acute angle
(c) two acute angles
(d) two right angles
Solution:

Question 12.
If the sum of two angles is greater than 180°, then which of the following is not possible?
(a) two obtuse angles
(b) two right angles
(c) one obtuse and one acute angle
(d) one reflex and one acute angle
Solution:

Question 13.
Which of the following statements is false?
(a) Every quadrilateral triangle is an isosceles triangle.
(b) Every isosceles triangle is an equilateral triangle.
(c) Every parallelogram is a trapezium.
(d) Every trapezium is a quadrilateral.
Solution:

Question 14.
Which of the following statement is correct?
(a) Every rhombus is a square
(b) Every parallelogram is a rectangle
(c) Every square is a rhombus
(d) Every rectangle is a square
Solution:

Question 15
A quadrilateral whose each angle is a right angle is a
(a) trapezium
(b) parallelogram
(c) rhombus
(d) rectangle
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
If the lengths of two sides of an isosceles triangle are 3 cm and 7 cm, then what is the lengths of the third side?
Solution:

Question 2.
If the lengths of three consecutive sides of an isosceles trapezium are 5 cm, 6 cm and 8 cm, then what is the length of the fourth side?
Solution:

ML Aggarwal Class 6 Solutions Chapter 9 Algebra Ex 9.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 9 Algebra Ex 9.1

Question 1.
Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.

Solution:

Question 2.
If there are 24 mangoes in a box, how will you write the number of mangoes in terms of the number of boxes? (use b for the number of boxes.)
Solution:

Question 3.
Anuradha is drawing a dot Rangoli (a beautiful pattern of lines joining dots). She has 8 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 12 rows?
Solution:

Question 4.
Anu and Meenu are sisters. Anu is 5 years younger than Meenu. Can you write Anu’s age in terms of Meenu’s age? Take Meenu’s age as x years.
Solution:

Question 5.
Oranges are to be transferred from larger boxes to smaller boxes. When a larger box is empited, the oranges from it fill 3 samller boxes and still 7 oranges are left. If the number of oranges in a small box are taken to be x, then what is the number of oranges in the larger box?
Solution:

Question 6.
Harsha’s score in Mathematics is 15 more than three-fourth of her score in Science. If she scores x marks in Science, find her score in Mathemstics?
Solution:

Question 7.
Look at the following matchstick pattern of equilateral triangles. The triangles are not separate. Two neighbouring triangles have a common matchstick. Observe the pattern and find the rule that gives the number of matchsticks.

Solution:

Question 8.
Look at the following matchstick pattern of letter A. The A’s are not separate. Two neighbouring A’s have two common matchsticks. Observe the pattern and find the rule that gives the number of matchsticks.

Solution:

ML Aggarwal Class 6 Solutions Chapter 8 Ratio and Proportion Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 8 Ratio and Proportion Check Your Progress

Question 1.
From the given figure, find the ratio of

(i) Number of triangles to the number of circles inside the rectangle.
(ii) Number of squares to the number of all the figures inside the rectangle.
(iii) Number of circles to the number of remaining figures inside the rectangle.
Solution:

Question 2.
The length of a pencil is 16 cm and its diameter is 6 mm. What is the ratio of the diameter of the pencil to that of its length?
Solution:

Question 3.
A certain club has 100 members, out of which 25 play tennis, 28 play badminton, 12 play chess and the rest do not play any game. Find the ratio of number of members who play
(i) badminton to the number of those who play chess.
(ii) badminton to the number of those who do not play any game.
(iii) tennis to the number of those who do not play any game.
(iv) tennis to the number of those who play either badminton or chess.
Solution:

Question 4.
Do the ratios 15 cm to 3 m and 25 seconds to 3 minutes from a proportion?
Solution:

Question 5.
Divide ₹500 among Suresh and Awanti in the ratio 3 : 7.
Solution:

Question 6.
The ratio of the number of girls to that of boys in a school is 9 : 11. If the number of boys in the school is 2035, find:
(i) the number of girls in the school,
(ii) the number of students in the school.
Solution:

Question 7.
The ratio of income to expenditure of a family is 7 : 6. Find the savings if the income of family is ₹42000.
Solution:

Question 8.
An employee earns ₹72,000 in 3 months.
(i) How much does he earn in 7 months?
(ii) In how many months will he earn ₹3,60,000?
Solution:

Question 9.
A train travels 110 km in 2 hours and a car travels 245 km in \(3 \frac{1}{2}\) hours. What is the ratio of the speed of the train to that of the car?
Solution:

Selina Publishers Concise Chemistry Class 7 ICSE Solutions Chapter 7 Air and Atmosphere

Selina Concise Chemistry Class 7 ICSE Solutions

ML Aggarwal Class 6 Solutions Chapter 11 Understanding Symmetrical Shapes Ex 11.4 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 11 Understanding Symmetrical Shapes Ex 11.4

Question 1.
Name the following triangles with regards to sides :

Solution:

Question 2.
Name the following triangles with regards to angles :

Solution:

Question 3.
Name each of the following triangles in two different ways (you may judge the nature of the angle by observation):

Solution:

Question 4.
Match the following:

Solution:

Question 5.
State which of the following statement are true and which are false :
(i) A triangle can have two right angles.
(ii) A triangle cannot have more than one obtuse angle.
(iii) A triangle has atleast two actue angles.
(iv) If all the three sides of a triangle are equal, it is called a scalene triangle.
(v) A triangle has four sides.
(vi) An isosceles triangle is an equilateral triangle also.
(vii) An equilateral triangle is an isosceles triangle also.
(viii)An scalene triangle has all its angles equal.
Solution:

ML Aggarwal Class 6 Solutions Chapter 8 Ratio and Proportion Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 8 Ratio and Proportion Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) In the ratio 3 : 5, the first term is …………. and second term is ………..
(ii) In a ratio, the first term is also called ……….. and second term is also called …….
(iii) If two terms of a ratio have no common factor (except 1), then the ratio is said to be in …….
(iv) To simplify a ratio, we divide the two terms by their …….
(v) The simplest form of the ratio 8 : 12 is ……
(vi) 90 cm : 1.5 m = ……….
(vii) Method of comparison of two quantities of the same kind (in same units) by division is known as …………
(viii) When two ratios are equal, they are said to be in ………
(ix) When four quantities are in proportion, then the product of ………… is equal to product of middle terms.
(x) 4.5 omo is equal to ………
Solution:

Question 2.
State whether the following statemtns are true (T) or false (F):
(i) Ratio exists only between two quantities of the same kind.
(ii) Ratio has no units.
(iii) If a ≠ b, then the ratio a: bis different from the ratio b : a.
(iv) If we multiply or divide both terms of a ratio by the same non-zero number, then the ratio remains the same.
(v) The ratio a: b is said to be in simplest form if HCF of a and b is 1.
(vi) In some situations, comparison of two quantities (of same kind) by difference does not make much sense.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 18):
Question 3.
A ratio equivalent to 5 : 7 is
(a) 10:21
(b) 15 : 14
(c) 20 : 28
(d) 25 : 49
Solution:

Question 4.
The ratio 384 : 480 in the simplest form is
(a) 2 : 5
(b) 3 : 5
(c) 5 : 4
(d) 4 : 5
Solution:

Question 5.
The ratio of 20 minutes to 1 hour is
(a) 20 : 1
(b) 1 : 3
(c) 1 : 4
(d) 2 : 5
Solution:

Question 6.
The ratio of 150 g to 2 kg is
(a) 75 : 1
(b) 40 : 3
(c) 3 : 40
(d) 3 : 200
Solution:

Question 7.
In a class of 40 students, 25 students play cricket and the remaining play tennis. The ratio of number of students playing crickets to the number of students playing tennis is
(a) 5 : 8
(b) 5 : 3
(c) 3 : 5
(d) 8 : 5
Solution:

Question 8.
Two numbers are in the ratio 3 : 5. If the sum of numbers is 144, then the smaller number is
(a) 54
(b) 72
(c) 90
(d) 48
Solution:

Question 9.
The ratio of number of girls to the number of boys in a class is 5 : 4. If there are 25 girls in the class, then the number of boys in the class is
(a) 15
(b) 20
(c) 30
(d) 40
Solution:

Question 10.
The ratio of the number of sides of a square and the number of edges of a cube is
(a) 1 : 2
(b) 1 : 3
(c) 1 : 4
(d) 2 : 3
Solution:

Question 11.
In shelf, the books with green cover and that with brown cover are in the ratio 2:3. If there are 18 books with green cover, then the number of books with brown cover is
(a) 12
(b) 24
(c) 27
(d) 36
Solution:

Question 12.
In a box, the ratio of the number of red marbles to that of blue marbles is 4 :7. Which of the following could be the total number of marbles in the box?
(a) 14
(b) 21
(c) 22
(d) 28
Solution:

Question 13.
If a, b, c and d are in proportion, then
(a) ab = cd
(b) ad = be
(c) ac = bd
(d) none of these
Solution:

Question 14.
If the weight of 5 bags of rice is 272 kg, then the weight of 1 bag of rice is
(a) 50.4 kg
(b) 54.4 kg
(c) 54.004 kg
(d) 54.04 kg
Solution:

Question 15.
If 7 pencils cost ₹35, then the cost of one dozen pencils is
(a) ₹60
(b) ₹70
(c) ₹30
(d) ₹5
Solution:

Question 16.
The ratio 2 : 3 expressed as percentage is
(a) 40%
(b) 60%
(c) \(66 \frac{2}{3} \%\)
(d) \(33 \frac{1}{3} \%\)
Solution:

Question 17.
0.025 when expressed as percentage is
(a) 250%
(b) 25%
(c) 4%
(d) 2.5%
Solution:

Question 18.
In a class, 45% of the students are girls. If there are 18 girls in the class, then the total number of students in the class is
(a) 44
(b) 40
(c) 36
(d) 30
Solution:

Value Based Questions
Question 1.
Students of a colony decided to go to an old age home in their vicinity to wish Happy New year and get blessings from old people.
They carried the following items with them:
Bouquets 63, New Year Cards 70 and chocolates bars 140. Answer the following questions:
(i) What is the ratio of number of bouquets to the number of chocolate bars?
(ii) What is the ratio of number of cards to the number of sum of all items?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
Divide ₹6000 among Irfan, Nagma and Ishan in the raito 3 : 5 : 7.
Solution:

Question 2.
Sapna weighs 54 kg on earth and 9 kg on moon. If a monkey weighs 3.5 kg on moon, then how much will it weigh on the earth?
Solution:

Question 3.
If 5 men can do a certain construction work in 14 days, then how long will 7 men take to complete the same construction work?
Solution: