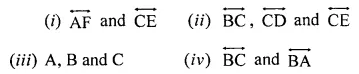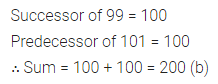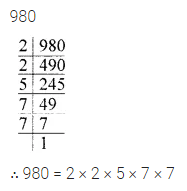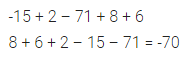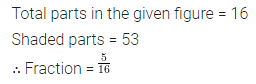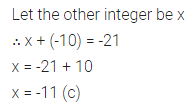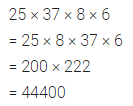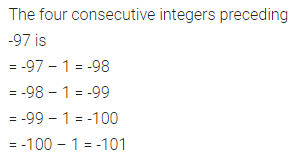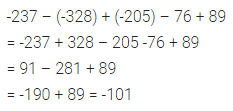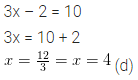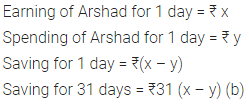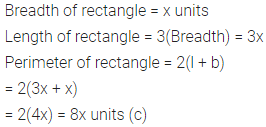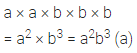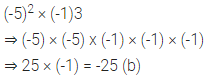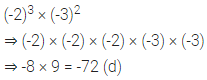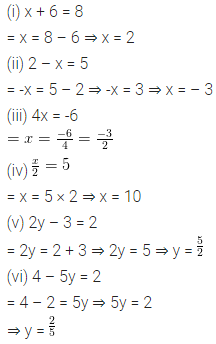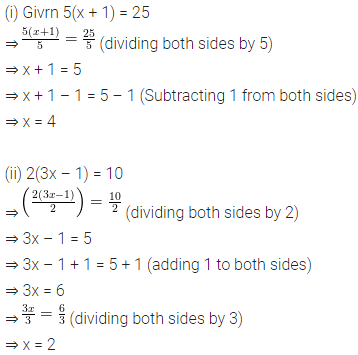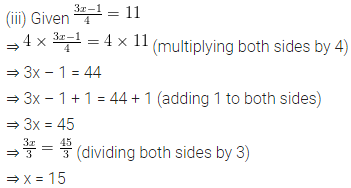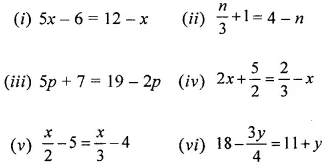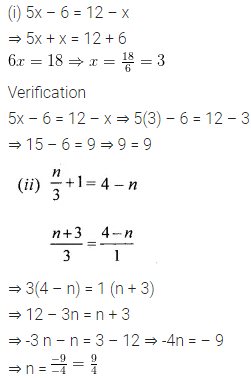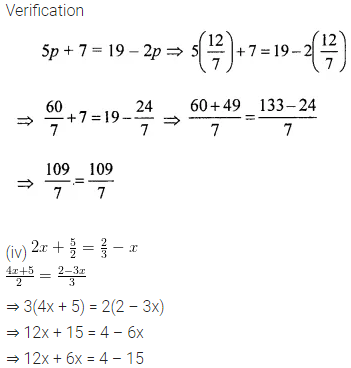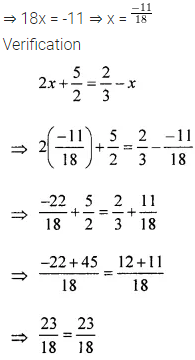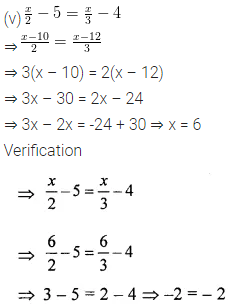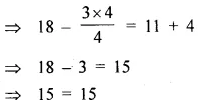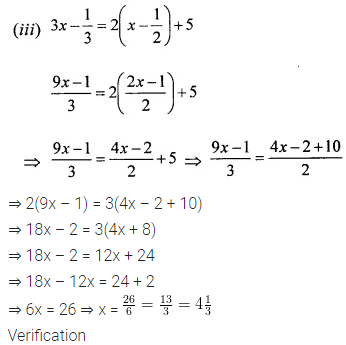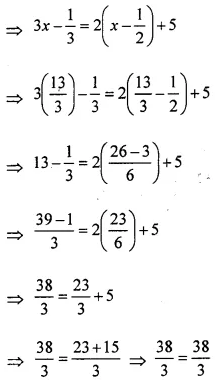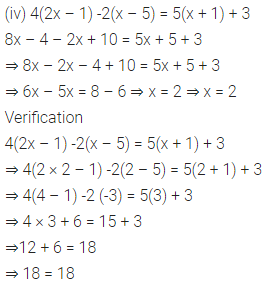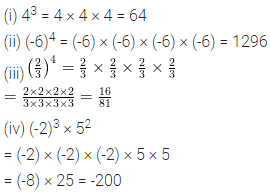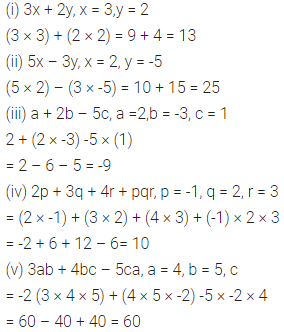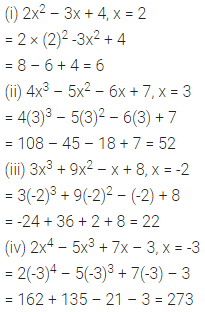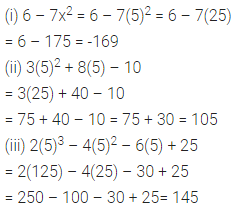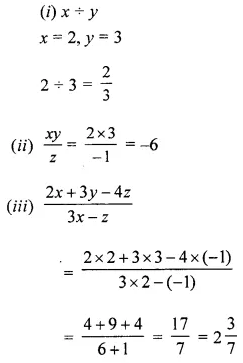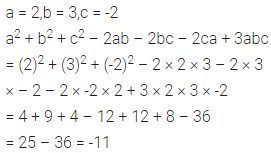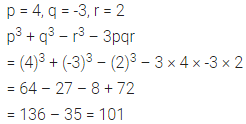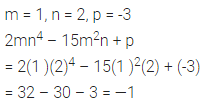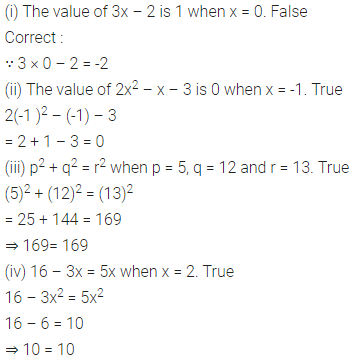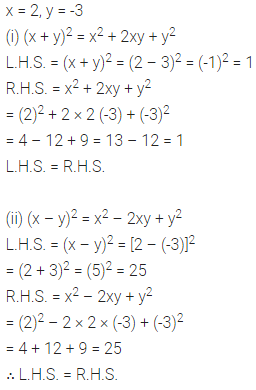Category: ICSE

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 4 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 4

Choose the correct answer from the given four options (1-2):
Question 1.
Avanti’s present age is y years and her mother’s age is 4 years less than 3 times her age, then her mother’s present age is
(a) (3y + 4) years
(b) (4y – 3) years
(c) (3y – 4) years
(d) 3(y – 4) years
Solution:

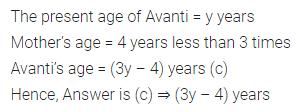
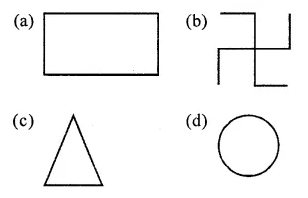
Question 2.
Which of the following statements is false?
(a) Every square is a rhombus.
(b) An equilateral triangle is a regular polygon.
(c) A triangle having all acute angles is scalene.
(d) Every square is a regular polygon.
Solution:

Question 3.
If = 3, q = -2 and r = -1, find the value of: 2p² + 3q – r² + 2pr – 5pqr.
Solution:

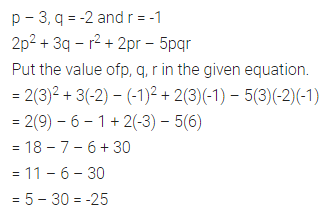
Question 4.
Fill in the following blanks:
(i) A polygon is a closed simple curve made up of entirely ………….
(ii) A cuboid has 6 rectangular faces, edges and ………. vertices.
Solution:

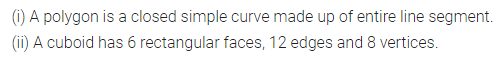
Question 5.
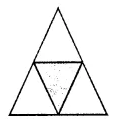
Give reason(s) of using triangular shapes and not polygonal shapes consisting of four or more sides in constructing structures like electric towers and bridges. What value is added in using triangular shapes?
Solution:

Question 6.
Look at the following pattern of squares fonned by matchsticks:

Find the rule that gives the number of matchsticks required in terms of the number of squares formed.
Solution:

Question 7.
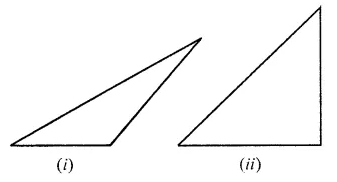
Name each of the following triangles in two ways (you may judge by observation or use ruler and protractor):

Solution:

Question 8.
Draw a net of a regular tetrahedron.
Solution:

Question 9.
Solve the linear equation:
4 – 3(5x + 2) = 4(7 – 3x).
Also, verify the solution.
Solution:

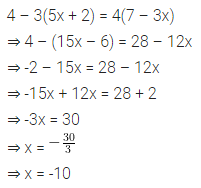
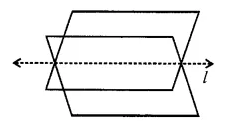
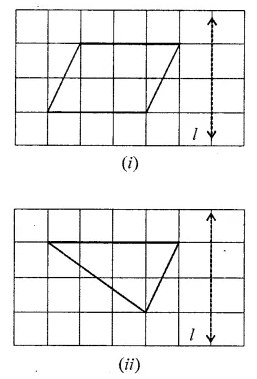
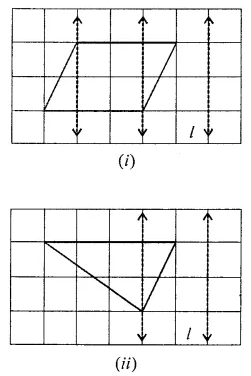
Question 10.
Use the given figure to name:
(i) parallel lines
(ii) concurrent lines
(ii) collinear points
(iv) two opposite rays.

Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 3 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 3

Section-A
Questions 1 to 8 is of 1 mark each.
Choose the correct answer from the given four options (1 to 8):
Question 1.
The difference between the place value and face value of 5 in the numeral 70542 is:
(a) 0
(b) 42
(c) 495
(d) 537
Solution:

Question 2.
he sum of the successor of 99 and the predecessor of 101 is
(a) 198
(b) 200
(c) 201
(d) 199
Solution:

Question 3.
If x and y are two co-prime numbers, then their LCM is

Solution:

Question 4.
Which of the following statement is true?
(a) |15 – 6| = |15| + |-6|
(b) Additive inverse of-3 is 3
(c) -1 lies on the right of 0 on the number line
(d) -4 is greater than -3
Solution:

Question 5.
The fraction equivalent to \(\frac{360}{540}\) is

Solution:

Question 6.
Which of the following numbers is divisible by 6?
(a) 5372
(b) 6495
(c) 7632
(d) 7568
Solution:

Question 7.
5 kg 5g is equal to
(a) 5.5 kg
(b) 5.05 kg
(c) 5.005 kg
(d) 5.0005 kg
Solution:

Question 8.
The ratio of a number of girls to the number of boys in a class is 7 : 5. If there are 15 boys in the class, then the number of girls in the class is
(a) 14
(b) 21
(c) 28
(d) 36
Solution:

Section-B
Questions 9 to 14 are of 2 marks each.
Question 9.
Write the greatest and the smallest 4-digit numbers using four different digits with the condition that the digit 4 occurs at tens place.
Solution:

Question 10.
Find the prime factorisation of 980.
Solution:

Question 11.
Find the value of-15 – (-2) – 71 – (-8) + 6.
Solution:

Question 12.
What fraction of the given figure is the shaded part?

Solution:

Question 13.
Write the mixed fraction \(7 \frac{3}{40}\) as a decimal number.
Solution:

Question 14.
The length of a pencil is 14 cm and its diameter is 7 mm. What is the ratio of the diameter of the pencil to that of its length?
Solution:

Section-C
Questions 15 to 24 are of 4 marks each.
Question 15.
Estimate the product 2459 x 653 by rounding off each factor to its
(i) greatest place
(ii) nearest hundreds.
Solution:

Question 16.
By using distributive laws, find 257 × 1007.
Solution:

Question 17.
Using number line, subtract (-3) from (-8).
Solution:

Question 18.
Find the greatest number that will divide 76, 113 and 186 leaving remainders 4, 5 and 6 respectively.
Solution:

Question 19.
Arrange the following integers in descending order:
-506, 2376, 2367, -311, -509, 245.
Solution:

Question 20.
Arrange the following fractions in ascending order \(\frac{5}{12}, \frac{1}{4}, \frac{7}{8}, \frac{5}{6}\).
Solution:

Question 21.
Simplify: \(3 \frac{5}{6}+4 \frac{3}{4}-5-1 \frac{3}{8}\).
Solution:

Question 22.
Write all possible natural numbers using the digits 3, 0, 8. Repetition of digits is not allowed. Also, find their sum.
Solution:

Question 23.
Munna and Munni are aged 14 years and 10 years. Their mother wants to divide ?180 between them in the ratio of their ages. How much does each get?
Solution:

Question 24.
Do the ratios 15 cm to 3 m and 15 seconds to 3 minutes form a proportion? Justify your answer.
Solution:

Section-D
Questions 25 to 29 are of 6 marks each.
Question 25.
To stitch a shirt, 2 m 25 cm cloth is needed. Out of 30 m cloth, how many shirts can be stitched and how much cloth will remain?
Solution:

Question 26.
Four bells are ringing at intervals of 40, 30, 36 and 45 minutes respectively. At what time will they ring together again if they start ringing simultaneously at 9 A.M.?
Solution:

Question 27.
I bought fruits worth ₹\(27 \frac{3}{4}\) and vegetables worth ₹\(10 \frac{1}{2}\). If I gave a fifty-rupee note to the shopkeeper, how much will I get back?
Solution:

Question 28.
Javed purchased vegetables weighing 10 kg. Out of this, 3 kg 450 g was potatoes, 2 kg 10 g was onions, 1 kg 750 g was tomatoes and the rest were green vegetables. What was the weight of green vegetables?
Solution:

Question 29.
To get a closer finish in a 100 m race, the runners are given different starting positions, depending upon how fast they can run. A starting position of +10 means that the runner starts 10 m in front of the starting line and -5 means that the runner starts 5 m behind the start line. The competitors starting positions are :
Abbas 0 Mohan -3 Rishi -20
Pete  + 10 Tarush + 15 Sahel + 5
(i) Who starts farthest from the finish line?
(ii) How far does Tarush have to run to reach the finish line?
(iii) How far Mohan has to run to reach the finish line?
(iv) How many metres are there between the starting positions of Rishi and Peter?
(v) What value is added if the students are asked to run 1 km daily?
Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 2 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 2

Choose the correct answer from the given four options (1-2):
Question 1.
Every composite number has at least
(a) 1 factor
(b) 2 factors
(c) 3 factors
(d) 4 factors
Solution:

Question 2.
Which of the following collections form a set?
(a) Collection of 5 odd prime numbers
(b) Collection of 3 most intelligent students of your class
(c) Collection of 4 vowels in the English alphabet
(d) Collection of months of a year having less than 31 days.
Solution:

Question 3.
Find the prime factorisation of 1320.
Solution:

Question 4.
If A = {x : x is a positive multiple of 3 less than 20} and B = {x : x is an odd prime number less than 20}, then find n(A) + n(B).
Solution:

Question 5.
Reduce the fraction \(\frac{714}{1386}\) in its simplest form.
Solution:

Question 6.
Simplify the following:
\(2 \frac{3}{14}-3 \frac{5}{6}-\frac{2}{5}+2 \frac{1}{2}\)
Solution:

Question 7.
A number is divisible by 5 and 8 both. By what other numbers with that number be always divisible?
Solution:

Question 8.
Arrange the fractions \(\frac{2}{3}, \frac{7}{9}, \frac{5}{8}, \frac{3}{5}\) in ascending order.
Solution:

Question 9.
Find the smallest number of 5-digits which is divisible by 12, 15 and 18.
Solution:

Question 10.
Three bells are ringing continuously at intervals of 30, 40 and 45 minutes respectively. At what time will they ring together if they ring simultaneously at 5 A.M.?
Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 1 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Model Question Paper 1

Choose the correct answer from the given four options (1-2):
Question 1.
If the sum of two integers is -21 and one of them is -10 then the other is
(a) -32
(b) 32
(c) -11
(d) 11
Solution:

Question 2.
The number of natural numbers between the smallest natural number and the greatest 2-digit number is
(a) 90
(b) 97
(c) 98
(d) 99
Solution:

Question 3.
Find the value of 25 × 37 × 8 × 6 by suitable arrangement.
Solution:

Question 4.
Write four consecutive integers preceding -97.
Solution:

Question 5.
Write the greatest and the smallest 4-digit numbers using four different digits with the condition that 5 occurs at ten’s place.
Solution:

Question 6.
Write all possible natural numbers formed by the digits 7, 0 and 3. Repetition of digits is not allowed.
Solution:

Question 7.
Find the value of: -237 – (-328) + (-205) – 76 + 89.
Solution:

Question 8.
Abhijeet’s school is 3 km 520 m away from his home. One day while returning from his school, just after covering 1 km 370 m distance, he saw a woman who was bleeding, he took her to the nearest hospital which was 2 km 775 m away from that place and got her admitted. He came back to his home which was 4 km 565 m from the hospital.
(i) Find the distance covered by Abhijeet on that day.
(ii) What value of life is depicted by Abhijeet?
Solution:

Question 9.
Arrange the following integers in descending order:
-353, 207, -289, 702, -335, 0, -77.
Solution:

Question 10.
Find the smallest five-digit number which is exactly divisible by 254.
Solution:

ML Aggarwal Class 9 Solutions Chapter 1 Rational Numbers Ex 1.1 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 1 Rational Numbers Ex 1.1

Question 1.
Insert a rational number between \(\frac {2}{9}\) and \(\frac {3}{8}\), and arrange in descending order.
Solution:
A rational number between \(\frac {2}{9}\) and \(\frac {3}{8}\)

Question 2.
Insert two rational numbers between, \(\frac {1}{3}\) and \(\frac {1}{4}\), and arrange in ascending order.
Solution:
A rational number between and \(\frac {1}{3}\) and \(\frac {1}{4}\)

A rational number between and \(\frac {1}{4}\) and \(\frac {7}{24}\)

Question 3.
Insert two rational numbers between – \(\frac {1}{3}\) and – \(\frac {1}{2}\) and arrange in ascending order.
Solution:
L.C.M. of 3 and 2 is 6

∴ Two rational numbers between \(\frac {- 2}{6}\) and \(\frac {- 3}{6}\)

Question 4.
Insert 3 rational numbers between \(\frac {1}{3}\) and \(\frac {4}{5}\) and arrange in descending order.
Solution:
A rational number between \(\frac {1}{3}\) and \(\frac {4}{5}\)

Question 5.
Insert three rational numbers between 4 and 4.5.
Solution:

∵ 4 < 4.0625 < 4.125 < 4.25 < 4.5
∴ Three rational numbers between 4 and 4.5 are 4.0625, 4.125, 4.25

Question 6.
Find six rational numbers between 3 and 4.
Solution:
Six rational numbers between 3 and 4
First rational number between 3 and 4

Question 7.
Find five rational numbers between \(\frac {3}{5}\) and \(\frac {4}{5}\).
Solution:
Five rational numbers between \(\frac {3}{5}\) and \(\frac {4}{5}\)
Multiplying and dividing by 5 + 1 = 6

Question 8.
Find ten rational numbers between \(\frac {- 2}{5}\) and \(\frac {1}{7}\)
Solution:
Ten rational numbers between \(\frac {- 2}{5}\) and \(\frac {1}{7}\)
LCM of 5 and 7 = 35

Question 9.
Find six rational numbers between \(\frac {1}{2}\) and \(\frac {2}{3}\).
Solution:
Six rational number between \(\frac {1}{2}\) and \(\frac {2}{3}\)
LCM of 2, 3 = 6

ML Aggarwal Class 7 Solutions Chapter 17 Data Handling Check Your Progress for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 17 Data Handling Check Your Progress

Question 1.
State whether the following statement is true or false. Justify your answer:
“The median is always one of the numbers in data.”
Solution:

Question 2.
Marks obtained by five students of class VII in quarterly and half-yearly examination in Mathematics (out of 25) are given below:

Represent the above data by a bar graph and answer the following questions:
(i) Do you see any improvement? Justify your answer.
(ii) Who has not done better?
Solution:

Question 3.
Find the mean of the factors of 12.
Solution:

Question 4.
Find the median and the mode of the following data:
2, 14, 16, 12, 13, 14, 16, 13, 10, 14, 18, 9
Solution:

Question 5.
Heights (in cm) of 25 students are given below:
168, 165, 163, 160, 163, 161, 162, 164, 163, 162, 164, 163, 160, 163, 157, 165, 148, 163, 164, 160, 165, 163, 152, 155, 163.
What is the mode of their heights?
Solution:

Question 6.
A die is thrown, what is the probability of getting an odd prime number?
Solution:

Question 7.
A letter is chosen at random from the letters of the word MATHEMATICS, what is the probability of getting
(i) letter M
(ii) a vowel
(iii) a consonant?
Solution:

ML Aggarwal Class 6 Solutions Chapter 9 Algebra Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 9 Algebra Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) In algebra, we use …………… to represent variables (generalized numbers).
(ii) A symbol or letter which can be given various numerical values is called a ……………
(iii) If Jaggu’s present age is x years, then his age 7 years from now is ……………
(iv) If one pen costs ₹X x, then the cost of 9 pens is ……………
(v) An equation is a statement that the two expressions are ……………
(vi) Trial an error is one of methods to obtain …………… of an equation.
(vii) 7 less than thrice a number y is ……………
(viii) If 3x + 4 = 19, then the value of x is ……………
(ix) The number of pencils bought for ₹ x at the rate of ₹2 per pencil is ……………
(x) In the expression (-7)⁵, base = …………… and exponent = ……………
(xi) If base = 6 and exponent = 5, then the exponential form = …………… .
Solution:

Question 2.
State whether the following statements are ture (T) or false (F):
(i) If x is variable then 5x is also variable.
(ii) If y is variable then y – 5 is also variable.
(iii) The number of angles in a triangle is a variable.
(iv) The value of an algebraic expression changes with the change in the value of the variable.
(v) If the length of a rectangle is twice its breadth, then its area is a constant.
(vi) An equation is satisfied only for a definite value of the variable.
(vii) If x toffees are distributed equally among 5 children, then each child gets 5x toffees.
(viii) t minutes are equal to 60 t seconds.
(ix) If x is a negative integer, then -x is a positive integer.
(x) x = 5 is a solution of the equation 3x + 2 = 13.
(xi) 2y- 7 > 13 is an equation.
(xii) ‘One third of a number x added to itself gives 8’ can be expressed as \(\frac{x}{3}\) + 8 = x.
(xiii)The difference between the ages of two sisters Lata and Asha is a variable.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 19):
Question 3.
I think of a number x, add 5 to it. The result is then multiplied by 2 and the final result is 24. The correct algebraic statement is
(a) x + 5 × 2 = 24
(b) (x + 5) × 2 = 24
(c) 2 × x + 5 = 24
(d) x + 5 = 2 × 24
Solution:

Question 4.
Which of the following is an equation?
(a) x + 5
(b) 7x
(c) 2y + 3 = 11
(d) 2p < 1
Solution:

Question 5.
If each matchbox contains 48 matchsticks, then the number of matchsticks required to fill n such boxes is
(i) 48 + n
(b) 48 – n
(c) 48 ÷ n
(d) 48n
Solution:

Question 6.
If the perimeter of a regular hexagon is x metres, then the length of each of its sides is
(a) (x + 6) metres
(b) (x – 6) metres
(c) (x ÷ 6) metres
(d) (6 ÷ x) metres
Solution:

Question 7.
x = 3 is the solution of the equation
(a) x + 7 = 4
(b) x + 10 = 7
(c) x + 7 = 10
(d) x + 3 = 7
Solution:

Question 8.
The solution of the equation 3x – 2 = 10 is
(a) x = 1
(b) x = 2
(c) x = 3
(d) x = 4
Solution:

Question 9.
The operation not involved in forming the expression 5x + \(\frac{5}{x}\) from the variable x and number 5 is
(a) addition
(b) subtraction
(c) multiplication
(d) division
Solution:

Question 10.
The quotient of x by 3 added to 7 is written as

Solution:

Question 11.
If there are x chairs in a row, then the number of persons that can be seated in 8 rows are
(a) 64
(b) x + 8
(c) 8x
(d) none of these
Solution:

Question 12.
If Arshad earns ₹ x per day and spends ₹ y per day, then his saving for the month of March is
(a) ₹(31x – y)
(b) ₹31(x – y)
(c) ₹31 (x + y)
(d) ₹31 (y – x)
Solution:

Question 13.
If the length of a rectangle is 3 times its breadth and the breadth is x units, then its perimeter is
(a) 4x units
(b) 6x units
(c) 8x units
(d) 10x units
Solution:

Question 14.
Rashmi has a sum of ₹ x. She spend ₹800 on grocery, ₹600 on cloths and ₹500 on education and received as ₹200 as a gift. How much money (in ₹) is left with her?
(a) x – 1700
(b) x – 1900
(c) x + 200
(d) x – 2100
Solution:

Question 15.
For any two integers a and b, which of the following suggests that the operation of addition is commutative?
(a) a × b = b × a
(b) a + b = b + a
(c) a – b = b – a
(d) a + b > a
Solution:

Question 16.
In \(\left(\frac{3}{4}\right)^{5}\), the base is
(a) 3
(b) 4
(c) 5
(d) \(\frac{3}{4}\)
Solution:

Question 17.
a × a × b × b × b can be written as
(a) a²b³
(b) a³b²
(c) a³b³
(d) a⁵b⁵
Solution:

Question 18.
(-5)² × (-1)³ is equal to
(a) 25
(b) -25
(c) 10
(d) -10
Solution:

Question 19.
(-2)³ × (-3)² is equal to
(a) 6⁵
(b) (-6)⁵
(c) 72
(d) -72
Solution:

ML Aggarwal Class 6 Solutions Chapter 9 Algebra Ex 9.5 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 9 Algebra Ex 9.5

Question 1.
State which of the following are equations with a variable. In case of an equation with a variable, identify the variable.
(i) 17 + x = 5
(ii) 2b – 3 = 7
(iii) (y – 7) > 5
(iv) \(\frac{9}{3}=3\)
(v) 7 × 3 – 19 = 2
(vi) 5 × 4 – 8 = 31
(vii) 2p < 15
(viii) 7 = 11 × 5 – 12 × 4
(ix) \(\frac{3}{2} q=5\)
Solution:

Question 2.
Solve each of the following equations :
(i) x + 6 = 8
(ii) 2 – x = 5
(iii) 4x = -6
(iv) \(\frac{x}{2}=5\)
(v) 2y – 3 = 2
(vi) 4 – 5y = 2
Solution:

Question 3.
Solve the following linear equations:
(i) 5(x + 1) = 25
(ii)2(3x – 1) = 10
(iii) \(\frac{3 x-1}{4}=11\)
Solution:

Question 4.
Solve the following linear equations:

Solution:

Question 5.
Solve the following equations and verify your answers:
(i) 3(x + 7) = 18
(ii) 2(x- 1) = x + 2
(iii) \(3 x-\frac{1}{3}=2\left(x-\frac{1}{2}\right)+5\)
(iv) 4(2x – 1) -2(x – 5) = 5(x + 1) + 3
Solution:

ML Aggarwal Class 6 Solutions Chapter 12 Symmetry Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 12 Symmetry Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) The subtraction symbol – has …….. lines of symmetry.
(ii) The addition symbol + has …….. lines of …….. symmetry.
(iii) Line of symmetry is also known …….. line or …….. of symmetry.
(iv) A kite has …….. line(s) of symmetry:
(v) A parallelogram has …….. line(s) of symmetry.
(vii) A rectangle is symmetrical about the lines joining the …….. of the opposite sides.
(viii)The number of capital letters of the English alphabet having only vertical line of symmetry is ……..
(ix) The number of capital letters of the English alphabet having only horizontal line of symmetry is ……..
(x) The number of capital letters of the English alphabet having both horizontal and vertical lines of symmetry is ……..
(xi) The digits having two lines of symmetry are …….. and ……..
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) The letter N has one line of symmetry.
(ii) Every hexagon has six lines of symmetry.
(iii) All right-angled triangles have one line of symmetry.
(iv) A triangle with more than one line of symmetry must be an equilateral triangle.
(v) A line of symmetry divides a figure into two identical parts.
(vi) A circle has only 8 lines of symmetry.
(vii) A regular octagon has 10 lines of symmetry.
(viii) A square and a rectangle have the same number of lines of symmetry.
(ix) A right-angled triangle can have at most one line of symmetry.
(x) If an isosceles triangle has more than one line of symmetry, then it must be rn equilateral triangle.
(xi) If a rectangle has more than two lines of symmetry, then it must be a square.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 15):
Question 3.
The number of lines of symmetry of a scalene triangle is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:

Question 4.
The letter F has
(a) one horizon line of symmetry
(b) one vertical line of symmetry
(c) two lines of symmetry
(d) no line of symmetry
Solution:
no line of symmetry (d)

Question 5.
The number of lines of symmetry of a rectangle is
(a) 0
(b) 1
(c) 2
(d) 4
Solution:

Question 6.
A rhombus is symmetrical about
(a) each of its two diagonals
(b) each of its two lines joining the mid-points of opposite sides
(c) each of the perpendicular bisector of its sides
(d) none of these.
Solution:

Question 7.
The number of lines of symmetry of a circle is
(a) 4
(b) 8
(c) 16
(d) unlimited
Solution:

Question 8.
Which of the following letters does not have any line of symmetry?
(a) B
(b) T
(c) Z
(d) Y
Solution:
Z (c)

Question 9.
Which of the following letters does not have the vertical line of symmetry?
(a) A
(b) H
(c) M
(d) E
Solution:

Question 10.
Which figure from the following figures is not symmetrical with respect to any line?

Solution:

Question 11.
In which of the given figures is the dotted line of symmetry?

Solution:

Question 12.
Amongst the given figures, the one having a maximum number of lines of symmetry is:

Solution:

Question 13.
The angle between the mirror line l and the line segment joining a point and its reflection (image) is:
(a) 0°
(b) 45°
(c) 60°
(d) 90°
Solution:
90° (d)

Question 14.
Which of two figures are image of each other (mirror line shown dotted)?

Solution:

Question 15.
Which of the two figures are mirror images of each other (mirror line showed dotted)?

Solution:

ML Aggarwal Class 6 Solutions Chapter 12 Symmetry Ex 12.2 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 12 Symmetry Ex 12.2

Question 1.
Copy the following figures on a squared paper. Complete each of them such that the dotted line is the line of symmetry:

Solution:

Question 2.
Copy the following figures on a squared paper. Complete each of them such that the resultant figure has two dotted lines as the lines of symmetry:

Solution:

Question 3.
In the given figure, l is the line of symmetry. Complete the diagram to make it symmetrical.

Solution:

Question 4.
In the given figure, l is the line of symmetry. Draw the image of the parallelogram and complete the diagram so that it becomes symmetrical.

Solution:

Question 5.
Copy the following figures on a squared paper and find their reflections in the mirror line l.

Solution:

ML Aggarwal Class 6 Solutions Chapter 9 Algebra Ex 9.4 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 9 Algebra Ex 9.4

Question 1.
Find the value of the following:
(i) 4³
(ii) (-6)⁴
(iii) \(\left(\frac{2}{3}\right)^{4}\)
(iv) (-2)³ × 5²
Solution:

Question 2.
Find the value of:
(i) 3x + 2y when x = 3 and y – 2
(ii) 5x – 3y when x = 2 and y = -5
(iii) a + 2b – 5c when a = 2, b = -3 and c = 1
(iv) 2p + 3q + 4r + pqr when p = -1, q = 2 and r = 3
(v) 3ab + 4bc – 5ca when a = 4, 6 = 5 and c = -2.
Solution:

Question 3.
Find the value of:
(i) 2x² – 3x + 4 when × = 2
(ii) 4x³ – 5x² – 6x + 7 when x = 3
(iii) 3x³ + 9x² – x + 8 when x = -2
(iv) 2x⁴ – 5x³ + 7x – 3 when x = -3
Solution:

Question 4.
If x = 5, find the value of:
(i) 6 – 7x²
(ii) 3x² + 8x – 10
(iii) 2x³ – 4x² – 6x + 25
Solution:

Question 5.
If x = 2, y = 3 and z = -1, find the values of:
(i) x + y
(ii) \(\frac{x y}{z}\)
(iii) \(\frac{2 x+3 y-4 z}{3 x-z}\)
Solution:

Question 6.
If a = 2, b = 3 and c = -2, find the value of a² + b² + c² – 2ab – 2bc – 2ca + 3abc.
Solution:

Question 7.
If p = 4, q = -3 and r = 2, find the value of: p³ + q³ – r³ – 3pqr.
Solution:

Question 8.
If m = 1, n = 2 and p = -3, find the value of 2mn⁴ – 15m²n + p.
Solution:

Question 9.
State true or false:
(i) The value of 3x – 2 is 1 when x = 0.
(ii) The value of 2x² – x – 3 is 0 when x = -1.
(iii) p² + q² – r² when p = 5, q = 12 and r = 13.
(iv) 16 – 3x = 5x when x = 2.
Solution:

Question 10.
For x = 2 and y = -3, verify the following:
(i) (x + y)² = x² + 2xy + y²
(ii) (x – y)² = x² – 2xy + y²
(iii) x² – y² = (x + y) (x – y)
(iv) (x + y)² = (x – y)² + 4xy
(v) (x + y)³ = x³ + y³ + 3x²y + 3xy²
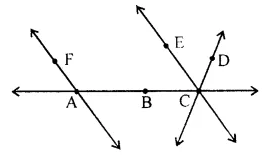
Solution: