RS Aggarwal Class 9 Solutions Chapter 12 Geometrical Constructions Ex 12A
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 12 Geometrical Constructions Ex 12A.
Question 1.
Solution:
Steps of Constructions :
(i) Draw a line segment AB = 5cm.
(ii) With A as centre and a radius equal to more than half of AB, drawn two arcs one above and other below of AB.
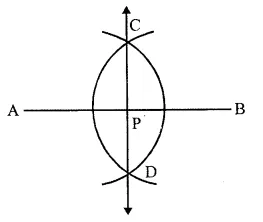
(iii) With centre B, and with same radius, draw two arcs intersecting the previously arcs at C and D respectively.
(iv) Join CD, intersecting AB at P.
Then CD is the perpendicular bisector of AB at the point P.
Question 2.
Solution:
Steps of constructions.
(i) Draw a line segment AB.
(ii) With A as centre and with small radius drawn arc cutting AB at P.
(iii) With P as centre and same radius draw another arc cutting the previous arc at Q and then R.
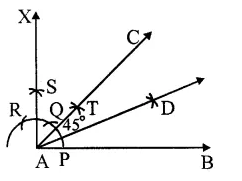
(iv) Bisect arc QR at S.
(v) Join AS and produce it to X such that ∠ BAX = 90°.
(vi) Now with centres P and S and with a suitable radius, draw two arcs intersecting each other at T.
(vii) Join AT and produced it to C Then ∠BAC = 45°.
(viii) Again with centres P and T and suitable radius draw two arcs intersecting each at D.
(ix) Join AD.
AD is the bisector of ∠ BAC
Question 3.
Solution:
Steps of construction.
(i) Draw a line segment AB.
(ii) With centre A and same radius draw an arc which meets AB at P.
(iii) With centre P and same radius, draw arcs first at Q and then at R.
(iv) With centres Q and R, draw arcs intersecting each other at C intersecting the first arc at T.
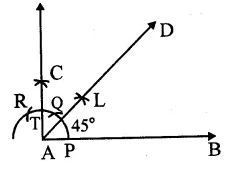
(v) Join AC
Then ∠BAC = 90°
(vi) Now with centres P and T and with some suitable radius, draw two arcs intersecting each other at L.
(vii) Join AL and produce it to D.
Then AD is the bisector of ∠ BAC.
Question 4.
Solution:
Steps of construction.
(i) Draw a line segment BC = 5cm.
(ii) With centres B and C and radius
5cm, draw two arcs intersecting each other at A.
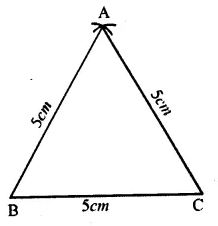
(iii) Join AB and AC.
Then ∆ ABC is the required equilateral triangle.
Question 5.
Solution:
We know that altitudes of equilateral triangle are equal and each angle is 60°.
Steps of construction.
(i) Draw a line XY and take a point D on it.
(ii) At D, draw a perpendicular and cut off DA = 5.4cm.
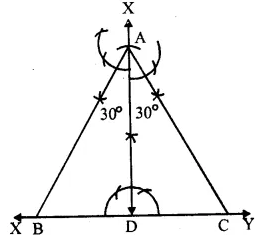
(iii) At A draw angles of 30° on each side of AD which meet XY at B and C respectively.
Then ∆ ABC is the required triangle.
Question 6.
Solution:
Steps of construction :
(i) Draw a line segment BC = 5cm
(ii) With centre B and radius 3.8 cm draw an arc.
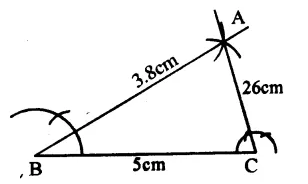
(iii) With centre C and radius 2.6 cm draw another arc intersecting the first arc at A.
(iv) Join AB and AC.
Then ∆ ABC is the required triangle.
Question 7.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.7cm.
(ii) At B, draw a ray BX making an angle of 60° with BC.
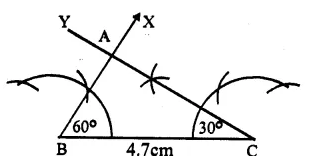
(iii) At C, draw another ray, CY making an angle of 30° which intersects the ray BX at A ,
Then ∆ ABC is the required triangle On measuring ∠ A, it is 90°.
Question 8.
Solution:
Steps of Construction :
(i) Draw a line segment QR * 5cm.
(ii) With centres Q and R and radius equal to 4.5cm, draw arcs intersecting eachother at P.
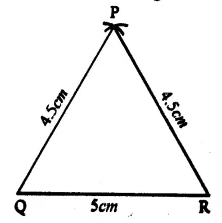
(iii) Join PQ and PR.
Then ∆ PQR is the required triangle.
Question 9.
Solution:
We know that in an isosceles triangle, two sides are equal and so their opposite angles are also equal.
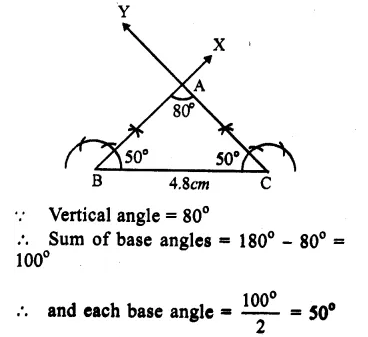
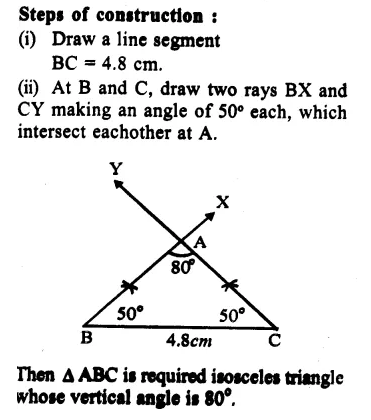
Question 10.
Solution:
Steps of constructions :
(i) Draw a line segment BC = 4.5cm.
(ii) At B, draw a ray BX making an angle of 90° with BC.
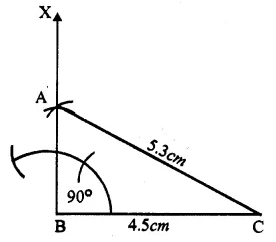
(iii) With centre C and radius 5.3 cm, draw an arc intersecting BX at A.
(iv) Join AC.
Then ∆ ABC is the required right angled triangle.
Question 11.
Solution:
Steps of constructions :
(i) Draw a line XY.
(ii) Take a point D on XY.
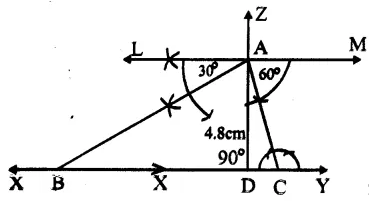
(iii) Draw a perpendicular at D and cut off DA = 4.8 cm
(iv) At A, draw a line LM parallel to XY.
(v) At A, draw an angle of 30° with LM on one side and an angle of 60° with LM on other side meeting XY at B and C respectively
Then ∆ ABC is the required triangle.
Question 12.
Solution:
Steps of constructions :
(i) Draw a line segment EF = 12cm.
(ii) At E, draw a ray EX making an acute angle with EF.
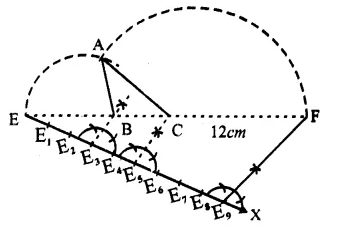
(iii)From EX,cut off 3+2+4=9 equal parts.
(iv) Join E9 F.
(v) From E5 and E3, draw lines parallel to E9 F meeting EF at C and B respectively.
(vi) With centre B and radius EB and with centre C and radius CF, draw arcs intersecting eachother at A.
(vii) Join AB and AC.
Then ∆ ABC is the required triangle.
Question 13.
Solution:
Steps of constructions :
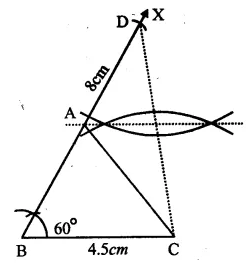
(i) Draw a line segment BC = 4.5cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BD = 8cm.
(iii) Join DC.
(iv) Draw the perpendicular bisector of BD which intersects BX at A.
(v) Join AC.
Then ∆ ABC is the required triangle.
Question 14.
Solution:
Steps of Constructions :
(i) Draw a line segment BC = 5.2 cm.
(ii) At B draw a ray BX making an angle of 30°.
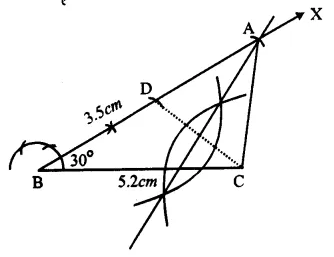
(iii) From BX, cut off BD = 3.5cm.
(iv) Join DC.
(v) Draw perpendicular bisector of DC which intersects BX at A.
(vi) Join AC.
Then ∆ ABC is the required triangle.
Hope given RS Aggarwal Class 9 Solutions Chapter 12 Geometrical Constructions Ex 12A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.