RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
Other Exercises
- RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.1
- RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2
- RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.3
- RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.4
- RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.5
Question 1.
Compute the amount and the compound interest in each of the following by using the formula when :
(i) Principal = Rs 3,000, Rate = 5%, Time = 2 years
(ii) Principal = Rs 3,000 Rate = 18%, Time = 2 years
(iii) Principal = Rs 5,000 Rate = 10 paise per rupee per annum, Time = 2 years
(iv) Principal = Rs 2,000, Rate = 4 paise per rupee per annum, Time = 3 years.
(v) Principal = Rs 12,800, Rate = 7\(\frac { 1 }{ 2 }\) %, Time = 3 years
(vi) Principal = Rs 10,000, Rate = 20% per annum compounded half-yearly, time = 2 years
(vii) Principal = Rs 1,60,000, Rate = 10 paise per rupee per annum compounded half- yearly, Time = 2 years.
Solution:
(i) Principal (P) = Rs 3,000
Rate (R) = 5% p.a.
Time (n) = 2 years
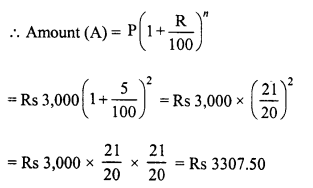
and compound interest (C.I) = A – P = Rs 3307.50 – Rs 3,000 = Rs 307.50
(ii) Principal (P) = Rs 3,000
Rate (R) = 18% p.a.
Time (n) = 2 years
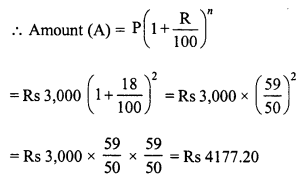
and compound interest (C.I.) = A – P = Rs 4177.20 – Rs 3,000 = Rs 1177.20
(iii) Principal (P) = Rs 5,000
Rate (R) =10 paise per rupee or 10% p.a.
Time (n) = 2 years.
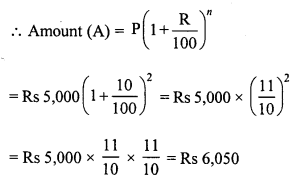
C.I. = A – P = Rs 6,050 – Rs 5,000 = Rs 1,050
(iv) Principal (P) = Rs 2,000
Rate (R) = 4 paise per rupee or 4% p.a.
Time (n) = 3 years
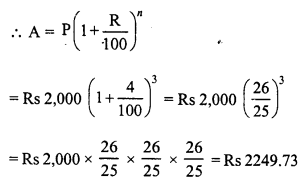
C.I. = A – P = Rs 2249.73 – Rs 2,000 = Rs 249.73
(v) Principal (P) = Rs 12,800
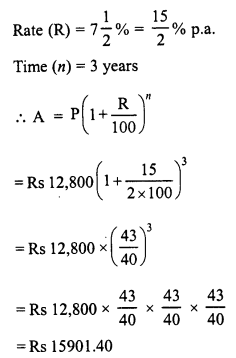
C.I. = A – P = Rs 15901.40 – Rs 12,800 = Rs 3101.40
(vi) Principal (P) = Rs 10,000
Rate (R) = 20% p.a. or 10% half-yearly
Time = 2 years or 4 half-years

C.I. = A – P = Rs 14,641 – Rs 10,000 = Rs 4,641
(vii) Principal (P) = Rs 1,60,000
Rate (R) = 10 paise per rupee or 10% p.a. or 5% half-yearly
Time (n) = 2 years or 4 half-years.

C.I. = A – P = Rs 1,94,481 – Rs 1,60,000 = Rs 34,481
Question 2.
Find the amount of Rs 2,400 after 3 years, when the interest is compounded annually at the rate of 20% per annum.
Solution:
Principal (P) = Rs 2,400
Rate (R) = 20%
Time (n) = 3 years
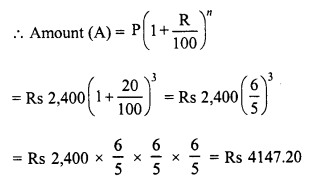
Question 3.
Rahman lent Rs 16,000 to Rasheed at the rate of 12\(\frac { 1 }{ 2 }\) % per annum compound interest. Find the amount payable by Rasheed to Rahman after 3 years.
Solution:
Principal (P) = Rs 16,000
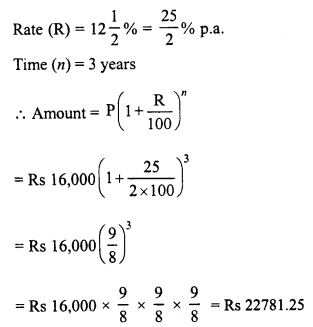
Question 4.
Meera borrowed a sum of Rs 1,000 from Sita for two years. If the rate of interest is 10% compounded annually find the amount that Meera has to pay back.
Solution:
Amount of loan (P) = Rs 1,000
Rate (R) = 10% p.a.
Period (n) = 2 years
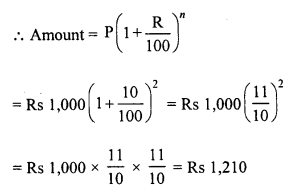
Question 5.
Find the difference between the compound interest and simple interest. On a sum of Rs 50,000 at 10% per annum for 2 years.
Solution:
Principal (P) = Rs 50,000
Rate (R) = 10% p.a.
Period (n) = 2 years.

Difference between C.I. and S.I. = Rs 10,500 – Rs 10,000 = Rs 500
Question 6.
Amit borrowed Rs 16,000 at 17\(\frac { 1 }{ 2 }\) % per annum simple interest on the same day, he lent it to Ashu at the same rate but compounded annually. What does he gain at the end of 2 years ?
Solution:
Amount of loan (P) = Rs 16,000

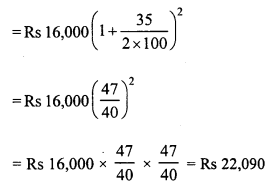
C.I. = A – P = Rs 22,090 – Rs 16,000 = Rs 6,090
Now gain = C.I. – S.I = Rs 6,090 – 5,600 = Rs 490
Question 7.
Find the amount of Rs 4,096 for 18 months at 12\(\frac { 1 }{ 2 }\) % per annum, interest being compounded semi-annually ?
Solution:
Principal (P) = Rs 4,096
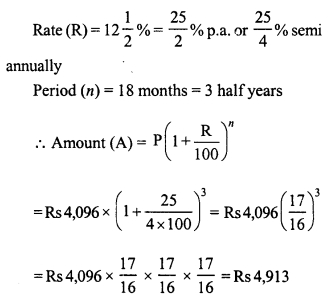
Question 8.
Find the amount and the compound interest on Rs 8,000 for 1\(\frac { 1 }{ 2 }\) years at 10% per annum, compounded half-yearly.
Solution:
Principal (P) = Rs 8,000
Rate (R) = 10% p.a. or 5% half yearly
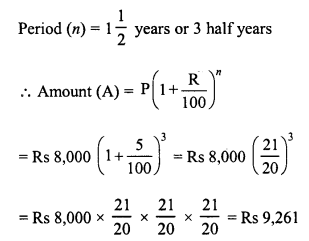
and C.I. = A – P = Rs 9,261 – Rs 8,000 = Rs 1,261
Question 9.
Kamal borrowed Rs 57,600 from LIC against her policy at 12\(\frac { 1 }{ 2 }\) % per annum to build a house. Find the amount that she pays LIC after 1\(\frac { 1 }{ 2 }\) years if the interest is calculated half-yearly.
Solution:
Amount of loan (P) = Rs 57,600
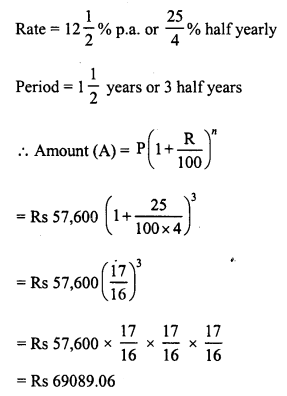
Question 10.
Abha purchased a house from Avas Parishad on credit. If the cost of the house is Rs 64,000 and the rate of interest is 5% per annum compounded half-yearly, find the interest paid by Abha after one year and a half.
Solution:
Price of house (P) = Rs 64,000
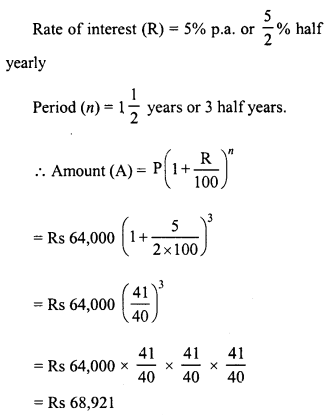
Compound interest (C.I.) = A – P = Rs 68,921 – Rs 64,000 = Rs 4,921
Question 11.
Rakesh lent out Rs 10,000 for 2 years at 20% per annum compounded annually. How much more he could earn if the interest be compounded half-yearly ?
Solution:
Principal (P) = Rs 10,000
Rate (R) = 20% p.a. or 10% half-yearly
Period (n) = 2 years or 4 half-years
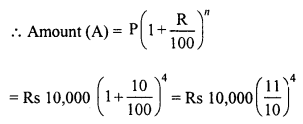

C.I. = Rs 14,400 – Rs 10,000 = Rs 4,400
Now difference in C.I. = Rs 4,641 – Rs 4,400 = Rs 241
Question 12.
Romesh borrowed a sum of Rs 2,45,760 at 12.5% per annum compounded annually. On the same day, he lent out his money to Ramu at the same rate of interest but compounded semi-annually. Find his gain after 2 years.
Solution:
In first case,
Principal (P) = Rs 2,45,760
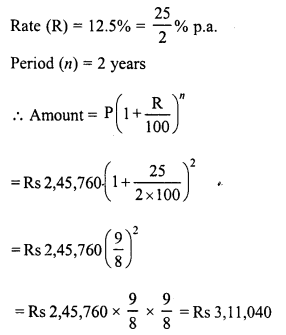
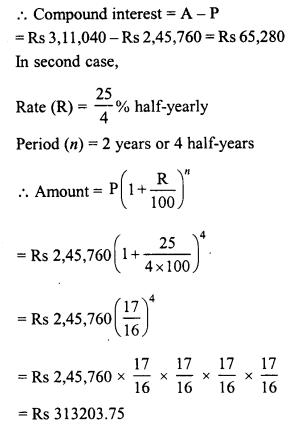
C.I. = A – P = Rs 313203.75 – Rs 2,45,760 = Rs 67443.75
Gain = 67443.75 – Rs 65,280 = Rs2163.75
Question 13.
Find the amount that David would receive if he invests Rs 8,192 for 18 months at 12\(\frac { 1 }{ 2 }\) % per annum, the interest being compounded half-yearly.
Solution:
Principal (P) = Rs 8,192
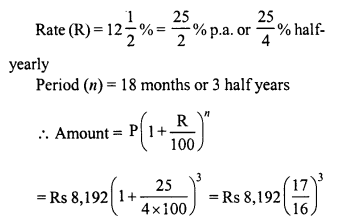
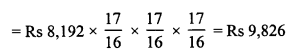
Question 14.
Find the compound interest on Rs 15,625 for 9 months at 16% per annum, compounded quarterly.
Solution:
Principal (P) = Rs 15,625
Rate (R) = 16% p.a. or 4% quarterly
Period (n) = 9 months or 3 quarters
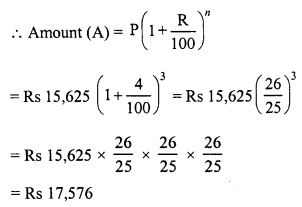
Compound interest = A – P = Rs 17,576 – Rs 15,625 = Rs 1,951
Question 15.
Rekha deposited Rs 16,000 in a foreign bank which pays interest at the rate of 20% per annum compounded quarterly, find the interest received by Rekha after one year.
Solution:
Principal (P) = Rs 16,000
Rate (R) = 20% p.a. or 5% quarterly
Period (n) = one year or 4 quarters
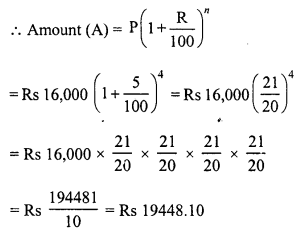
C.I. = A – P = Rs 19448.10 – Rs 16,000 = Rs 3448.10
Question 16.
Find the amount of Rs 12,500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
Solution:
Principal (P) = Rs 12,500
Rate (R1) = 15% p.a. for first year
R2 = 16% p.a. for second year
Period = 2 years
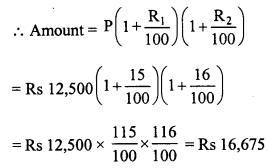
Question 17.
Ramu borrowed Rs 15,625 from a finance company to buy a scooter. If the rate of interest be 16% per annum compounded annually, what payment he will have to make after 2\(\frac { 1 }{ 4 }\) years ?
Solution:
Principal (P) = Rs 15,625
Rate (R) = 16%
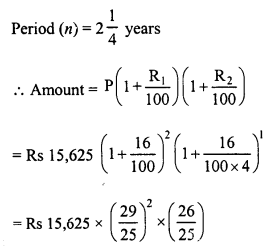
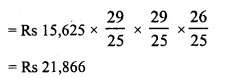
Question 18.
What will Rs 1,25,000 amount to at the rate of 6% if interest is calculated after every 4 months for one year ?
Solution:
Principal (P) = Rs 1,25,000

Question 19.
Find the compound interest at the rate of 5% for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 12,000 as simple interest.
Solution:
In first case,
S.I. = Rs 12,000
Rate (R) = 5% p.a.
Period (T) = 3 years
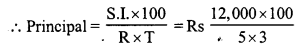
= Rs 80,000
In second case,
Principal (P) = Rs 80,000
Rate (R) = 5% p.a.
Period (n) = 3 years
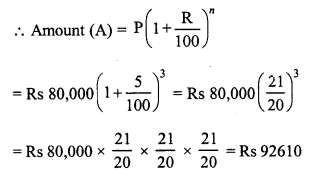
C.I. = A – P = Rs 92,610 – 80,000 = Rs 12,610
Question 20.
A sum of money was lent for 2 years at 20% compounded annually. If the interest is payable half-yearly instead of yearly, then the interest is Rs 482 more. Find the sum.
Solution:
Let Sum (P) = Rs x
Rate (R) = 20% p.a. or 10% half-yearly
Period (n) = 2 years or 4 half years
In first case,

Interests = A – P = Rs 146.41 – Rs 100 = Rs 46.41
Now difference in interests = Rs 46.41 – Rs 44.00 = Rs 2.41
If difference is 2.41 then sum is 100 If difference is Rs 482, then sum
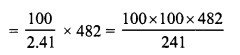
Question 21.
Simple interest on a sum of money for 2 years at 6\(\frac { 1 }{ 2 }\) % per annum is Rs 5,200. What will be the compound interest on the sum at the same rate for the same period ?
Solution:
In first case,
S.I. = Rs 5,200

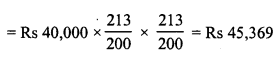
Compound interest = A – P = Rs 45,369 – Rs 40,000 = Rs 5,369
Question 22.
Find the compound interest at the rate of 5% per annum for 3 years on that principal which in 3 years at the rate of 5% per annum gives Rs 1,200 as simple interest.
Solution:
In first case,
S.I. = Rs 1,200
Rate (R) = 5% p.a.
Period (T) = 3 years
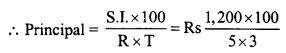
In second case,
Principal (P) = Rs 8,000
Rate (R) = 5% p.a.
Period (n) = 3 years
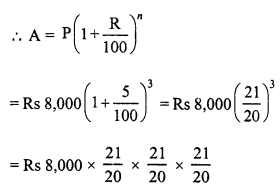
= Rs 9,261
C.I. = A – P = Rs 9,261 – Rs 8000 = Rs 1,261
Hope given RD Sharma Class 8 Solutions Chapter 14 Compound Interest Ex 14.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.