NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 13 |
| Chapter Name | Surface Areas and Volumes |
| Exercise | Ex 13.4 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4
Unless stated otherwise, take π = \(\frac { 22 }{ 7 }\)
Question 1.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular .ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Given: upper diameter = 4 cm ⇒ upper radius = \(\frac { 1 }{ 2 }\) = 2 cm = R
lower diameter = 2 cm ⇒ lower radius = \(\frac { 2 }{ 2 }\) = 1 cm = r
height of glass = 14 cm
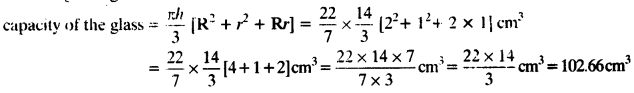
Question 2.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:
Given: upper circumference of the frustum = 18 cm

Slant height (l) = 4 cm
We have C.S.A of the frustum = π (r1 + r2)l
Putting values from equation (i) and (ii), we get
Curved surface area = (πr1 + πr2)l = (9 + 3) x 4 = 12 x 4 = 48 cm²
Question 3.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see figure). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
Solution:
Radius of open side (r1) = 10 cm
Radius of upper base (r2) = 4 cm
Slant height (l) = 15 cm
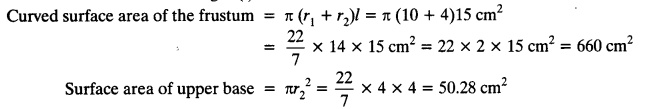
Total surface area of the cap = C.S.A. of the frustum + Area of upper base
= 660 cm² + 50.28 cm² = 710.28 cm²
Question 4.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm2. (Take π = 3.14)
Solution:
Radius of the lower end (r1) = 8 cm
Radius of the upper end (r2) = 20 cm
Height of the frustum (h) = 16 cm
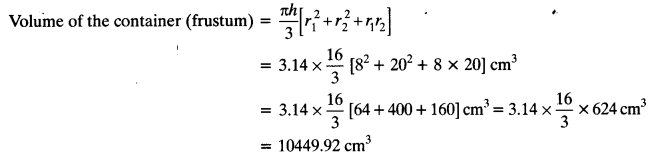

Question 5.
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \(\frac { 1 }{ 16 }\) cm, find the length of the wire.
Solution:
Let ADC is a cone with vertical angle 600.
Now, cone is cut into two parts, parallel to its base at height 10 cm.
Radius of larger end of the frustum = R1
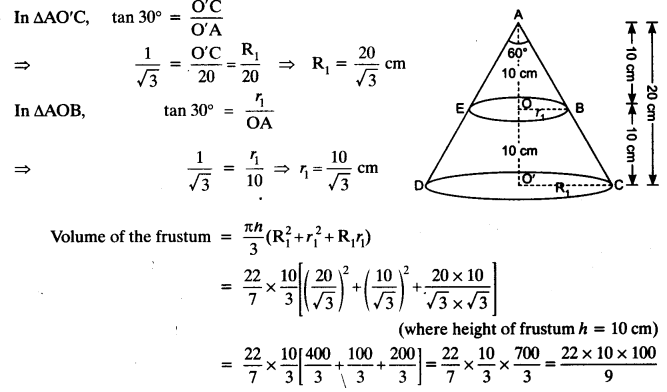
A wire be formed having diameter \(\frac { 1 }{ 16 }\) cm and length be H cm
Volume of wire so obtained = πr²H
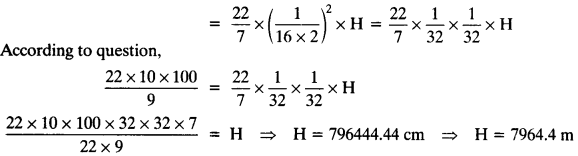
We hope the NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4, drop a comment below and we will get back to you at the earliest.