RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1

Other Exercises

Solve each of the following equations and also verify your solution :
Question 1.
9\(\frac { 1 }{ 4 }\) = y – 1\(\frac { 1 }{ 3 }\)
Solution:
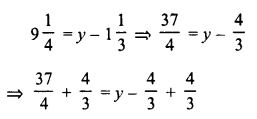
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 1

Question 2.
\(\frac { 5x }{ 3 }\) + \(\frac { 2 }{ 5 }\) = 1
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 4

Question 3.
\(\frac { x }{ 2 }\) + \(\frac { x }{ 3 }\) + \(\frac { x }{ 4 }\) = 13
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 5

Question 4.
\(\frac { x }{ 2 }\) + \(\frac { x }{ 8 }\) = \(\frac { 1 }{ 8 }\)
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 6

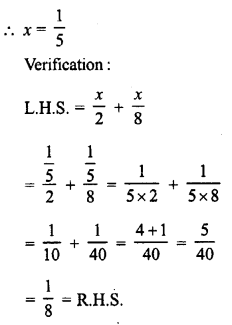
Question 5.
\(\frac { 2x }{ 3 }\) – \(\frac { 3x }{ 8 }\) = \(\frac { 7 }{ 12 }\)
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 8

Question 6.
(x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1) = 0
Solution:
(x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1) = 0
⇒ [x² + (2 + 3) x + 2 x 3] + [x² + (-3 – 2) x + (-3) (-2)] – 2x² – 2x = 0
⇒ x² + 5x + 6 + x² – 5x + 6 – 2x² – 2x = 0
⇒ x² + x² – 2x² + 5x – 5x – 2x + 6 + 6 = 0
⇒ -2x + 12 = 0
Subtracting 12 from both sides,
-2x + 12 – 12 = 0 – 12
⇒ -2x = -12
Dividing by -2,
x = 6
Verification:
L.H.S. = (x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1)
= (6 + 2) (6 + 3) + (6 – 3) (6 – 2) – 2 x 6 (6 + 1)
= 8 x 9 + 3 x 4 – 12 x 7
= 72 + 12 – 84
= 84 – 84
= 0
= R.H.S.

Question 7.
\(\frac { x }{ 2 }\) – \(\frac { 4 }{ 5 }\) + \(\frac { x }{ 5 }\) +\(\frac { 3x }{ 10 }\) = \(\frac { 1 }{ 5 }\)
Solution:
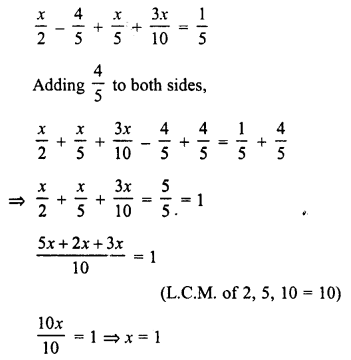
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 9

Question 8.
\(\frac { 7 }{ x }\) + 35 = \(\frac { 1 }{ 10 }\)
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 11

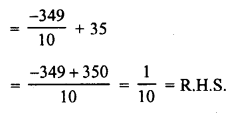
Question 9.
\(\frac { 2x – 1 }{ 3 }\) – \(\frac { 6x – 2 }{ 5 }\) = \(\frac { 1 }{ 3 }\)
Solution:
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 13

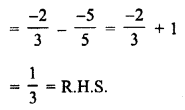
Question 10.
13 (y – 4) – 3 (y – 9) – 5 (y + 4) = 0
Solution:
13 (y – 4) – 3 (y – 9) – 5 (y + 4) = 0
⇒ 13y – 52 – 3y + 27 – 5y – 20 = 0
⇒ 13y – 3y – 5y – 52 + 27 – 20 = 0
⇒ 13y – 8y – 72 + 27 = 0
⇒ 5y – 45 = 0
Dividing by 5,
y = 9
Verification:
L.H.S. = 13 (y – 4) – 3 (y – 9) – 5 (y + 4)
= 13 (9 – 4) – 3 (9 – 9) – 5 (9 + 4)
= 13 x 5 – 3 x 0 – 5 x 13
= 65 – 0 – 65
= 0
= R.H.S.

Question 11.
\(\frac { 2 }{ 3 }\) (x – 5) – \(\frac { 1 }{ 4 }\) (x – 2) = \(\frac { 9 }{ 2 }\)
Solution:
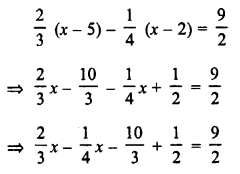
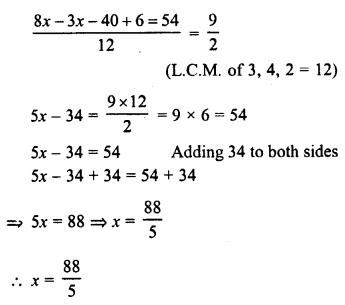
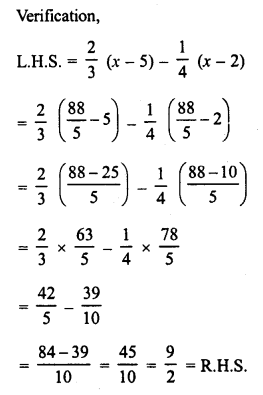
RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1 16