Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations (In one variable) Ex 4A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B

Question 1.
State, true or false :

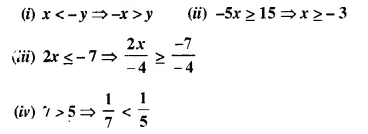
Solution:

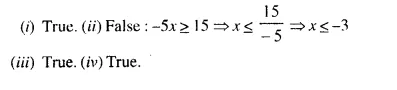
Question 2.
State whether the following statements are true or false:
(i) If a < b, then a – c < b – c (ii) If a > b, then a + c > b + c
(iii) If a < b, then ac > bc
(iv) If a > b, then \(\frac { a }{ b }\) < \(\frac { b }{ c }\) (v) If a – c > b – d; then a + d > b + c
(vi) If a < b, and c > 0, then a – c > b – c where a, b, c and d are real numbers and c ≠ 0.
Solution:
(i) True
(ii) True
(iii) False
(iv) False
(v) True
(vi) False

Question 3.
If x ∈ N, find the solution set of inequations,
(i) 5x + 3 ≤ 2x + 18
(ii) 3x – 2 < 19 – 4x
Solution:

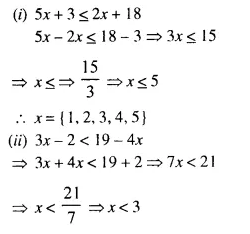
x = {1, 2}

Question 4.
If the replacement set is the set of whole numbers, Solve:
(i) x + 7 ≤ 11
(ii) 3x – 1 > 8
(iii) 8 – x > 5
(iv) 7 – 3x ≥ – \(\frac { 1 }{ 2 }\)
(v) x – \(\frac { 3 }{ 2 }\) < \(\frac { 3 }{ 2 }\) – x
(vi) 18 ≤ 3x – 2
Solution:

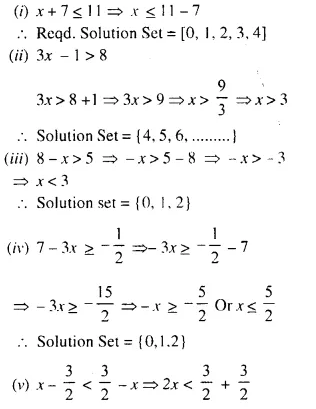
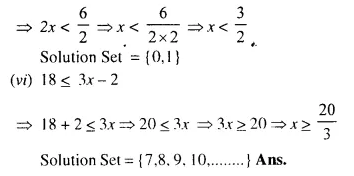
Question 5.
Solve the inequation :
3 – 2x ≥ x – 12 given that x ∈ N. [1987]
Solution:
3 – 2x ≥ x – 12
⇒ – 2x – x ≥ – 12 – 3
⇒ – 3x ≥ -15
⇒ – x ≥ – 5
⇒ x ≤ 5
Solution Set= {1, 2, 3, 4, 5} or {x ∈ N : x ≤ 5}

Question 6.
If 25 – 4x ≤ 16, find:
(i) the smallest value of x, when x is a real number
(ii) the smallest value of x, when x is an integer.
Solution:
25 – 4x ≤ 16
⇒ – 4x ≤ 16 – 25
⇒ – 4x ≤ – 9
⇒ 4x ≥ 9
x ≥ \(\frac { 9 }{ 4 }\)
(i) The smallest value of x, when x is a real number \(\frac { 9 }{ 4 }\) or 2.25
(ii) The smallest value of x, when x is an integer 3.

Question 7.
If the replacement set is the set of real numbers, solve:

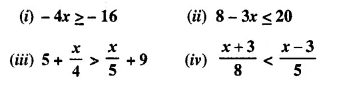
Solution:

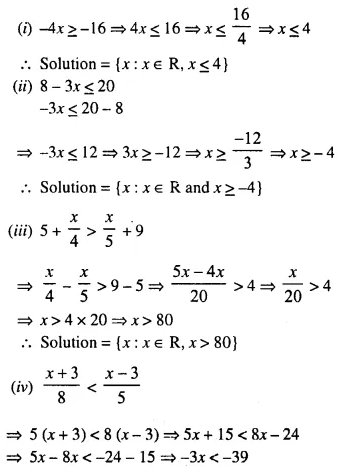
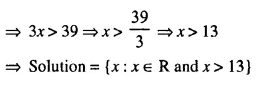
Question 8.
Find the smallest value of x for which 5 – 2x < 5\(\frac { 1 }{ 2 }\) – \(\frac { 5 }{ 3 }\) x, where x is an integer.
Solution:

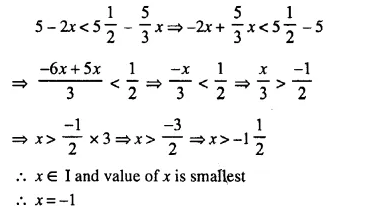
Question 9.
Find the largest value of x for which 2 (x – 1) ≤ 9 – x and x ∈ W.
Solution:
2 (x – 1) ≤ 9 – x
⇒ 2x – 2 ≤ 9 – x
⇒ 2x + x ≤ 9 + 2
⇒ 3x ≤ 11
⇒ x ≤ \(\frac { 11 }{ 3 }\)
⇒ x ≤ 3\(\frac { 2 }{ 3 }\)
x ∈ W and value of x is largest x = 3

Question 10.
Solve the inequation:
12 + 1\(\frac { 5 }{ 6 }\) x ≤ 5 + 3x and x ∈ R. (1999)
Solution:

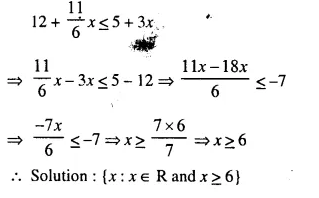
Question 11.
Given x ∈ (integers), find the solution set of: -5 ≤ 2x – 3 < x + 2.
Solution:
-5 ≤ 2x – 3 < x + 2
(i) -5 ≤ 2x – 3
⇒ -2x ≤ -3 + 5
⇒ -2x ≤ 2
⇒ x ≤ -1
⇒ -1 ≤ x
(ii) 2x – 3 < x + 2
⇒ 2x – x < 2 + 3
⇒ x < 5
From (i) and (ii),
-1 ≤ x < 5
x = {-1, 0, 1, 2, 3, 4}

Question 12.
Given x ∈ (whole numbers), find the solution set of: -1 ≤ 3 + 4x < 23.
Solution:
-1 ≤ 3 + 4x < 23
(i) -1 ≤ 3 + 4x
⇒ -1 – 3 ≤ 4x
⇒ -4 < 4x
⇒ -1 ≤ x
(ii) 3 + 4x < 23
⇒ 4x < 23 – 3
⇒ 4x < 20
⇒ x < 5
From (i) and (ii)
-1 ≤ x < 5 and x ∈ W
Solution set = {0, 1, 2, 3, 4}

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.