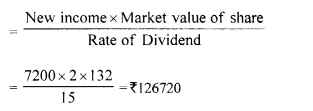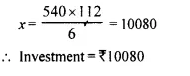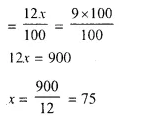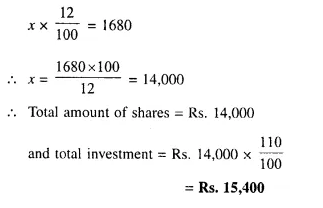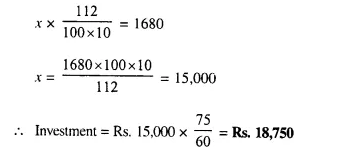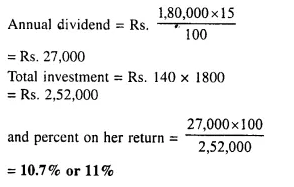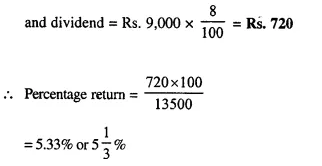Tag: Selina Concise ICSE Class 10 Maths Solutions

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C

Question 1.
How much money will be required to buy 400, ₹ 12.50 shares at a premium of ₹ 1?
Solution:
Number of shares purchased = 400
Rate of each share = ₹ 12.50
M.V. = ₹ 1 premium = ₹ 12.50 + ₹ 1 = ₹ 13.50
Amount of in vestment = ₹ 400 x ₹ 13.50 = ₹ 5400

Question 2.
How much money will be required to buy 250, ₹ 15 shares at a discount of ₹ 1.50?
Solution:
Number of shares = 250
M.V. = at ₹ 15 at a discount of ₹ 1.50 = ₹ 15 – ₹ 1.50 = ₹ 13.50
Amount of investment = ₹ 13.50 x 250 = ₹ 3375

Question 3.
A person buys 120 shares at a nominal value of ₹ 40 each, which he sells at ₹ 42.50 each. Find his profit and profit percent.
Solution:
No. of shares = 120
Nominal value of each share = ₹ 40.00
Profit at each share = ₹ 42.50 – ₹ 40.00 = ₹ 2.50
Total profit = 2.50 x 120 = ₹ 300
Cost price of 120 shares = ₹ 40 x 120 = ₹ 4,800

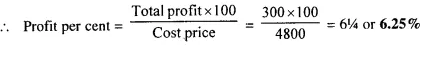
Question 4.
Find the cost of 85 shares of Rs. 60 each when quoted at ₹ 63.25
Solution:
No. of shares = 85
Market value of cach share = ₹ 63.25
Total cost = ₹ 63.25 x 85 = ₹ 5,376.25

Question 5.
A man invests ₹ 800 in buying 75 shares and when they are selling at a premium of ₹ 1.15, he sells all the shares. Find his profit and profit percent.
Solution:
Investment = ₹ 800
In first case face value of each share = ₹ 5
and market value of each share = ₹ 5.00 + ₹ 1.15 = ₹ 6.15
Gain on each share of ₹ 5 = ₹ 1.15

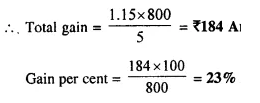
Question 6.
Find the annual income derived from 125, ₹ 120 shares paying 5% dividend.
Solution:
Amount of investment = ?
Number of shares purchased = 125 at ₹ 120, 5% dividend
Amount of investment = ₹ 125 x 120 = ₹ 15000
His annual income = 15000 x \(\frac { 5 }{ 100 }\) = ₹ 750

Question 7.
A man invests ₹ 3,072 in a company paying 5% per annum when its ₹ 10 share can be bought for ₹ 16 each. Find:
(i) his annual income;
(ii) his percentage income on his investment.
Solution:
Total investment = ₹ 3,072
Market value of each shares = ₹ 16

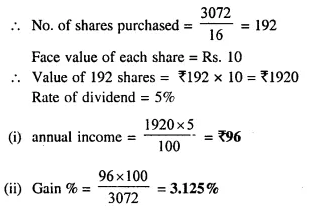
Question 8.
A man invests ₹ 7,770 in a company paying 5 percent dividend when a share of nominal value of ₹ 100 sells at a premium of ₹ 5. Find :
(i) the number of shares bought;
(ii) annual income ;
(iii) percentage income ;
Solution:
Investment = ₹ 7770
Nominal value of each share = 100
Market value = 100 + 5 = 105

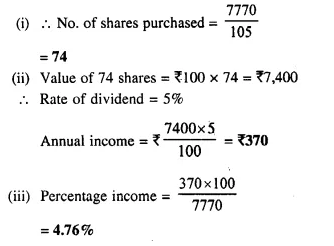
Question 9.
A man buys ₹ 50 shares of a company paying 12 percent dividend, at a premium of ₹ 10. Find :
(i) the market value of 320 shares ;
(ii) his annual income ;
(iii) his profit percent.
Solution:
(i) Market value of each share = ₹ 50 + ₹ 10 = ₹ 60
Market value of 320 shares = ₹ 60 x 320 = ₹ 19,200
(ii) Rate of dividend = 12%
Face value of 320 shares = Rs. 50 x 320 = Rs. 16,000

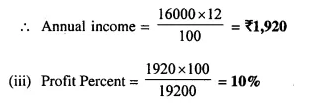
Question 10.
A man buys of Rs. 75 shares at a discount of Rs. 15 of a company paying 20% dividend. Find :
(i) the market value of 120 shares ;
(ii) his annual income ;
(iii) his profit percent.
Solution:
(i) Market value of one share = Rs. 75 – 15 = Rs. 60
Market value of 120 shares = Rs. 60 x 120 = Rs. 7,200
(ii) Rate of dividend = 20%
Face value of 120 shares = Rs. 75 x 120 = Rs. 9,000

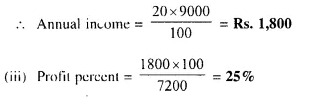
Question 11.
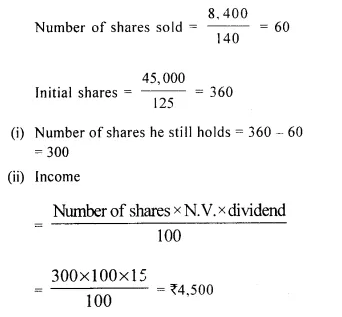
A man has 300, ₹ 50 shares of a company paying 20% dividend. Find his net income after paying 3% income tax.
Solution:
No. of shares = 300
Face value of 50 shares = Rs. 50 x 300 = Rs. 15,000
Rate of dividend = 20%

Question 12.
A company pays dividend of 15 % on its ten-rupee shares from which it deducts income tax at the rate of 22%. Find the annual income of a man who owns one thousand shares of this company.
Solution:
No. of shares = 1,000
Face Value of each share = Rs. 10
Rate of dividend = 15%
Rate of income tax = 22%
Face value of 1,000 shares = 1,000 x 10 = Rs. 10,000
Total dividend = Rs. 10,000 x \(\frac { 15 }{ 100 }\) = Rs. 1,500
Income tax deducted = Rs. 1500 x \(\frac { 22 }{ 100 }\) = Rs. 330
Net income = Rs.1500 – Rs. 330 = Rs. 1170

Question 13.
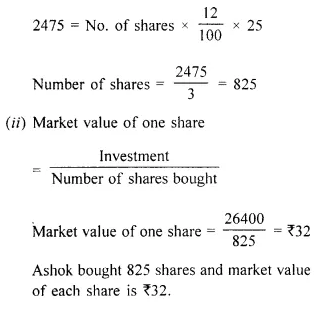
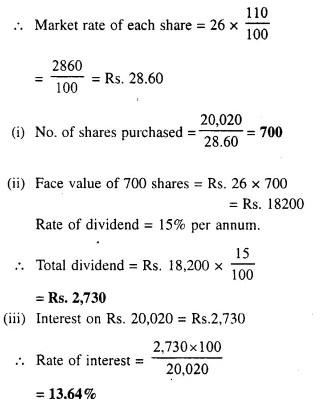
A man invests Rs. 8,800 in buying shares of a company of face value of rupees hundred each at a premium of 10%. If he earns Rs. 1,200 at the end of the year as dividend find:
(i) the number of shares he has in the company;
(ii) the dividend percent per share. [2001]
Solution:
Investment = Rs. 8,800
Face value of each share = Rs. 100
Market value of each share = Rs. 100 + 10 = Rs. 110

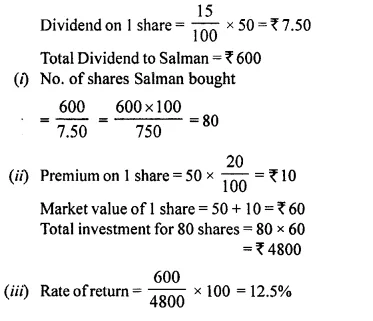
Question 14.
A man invests Rs. 1,680 in buying shares of nominal value Rs. 24 and selling at 12% premium. The dividend on the shares is 15% per annum. Calculate :
(i) The number of shares he buys ;
(ii) The dividend he receives annually. [1999]
Solution:
Investment = Rs. 1680
Nominal value of each share = Rs. 24
Market value of each share = Rs. 24 + 12% of 24
= Rs. 24 + 2.88 = Rs. 26.88
Rate of dividend = 15%
(i) No. of shares = \(\frac { 1680 }{ 26.88 }\) = 62.5
(ii) Face value of 62.5 shares = 62.5 x 24 = Rs. 1500
Amount of dividend = 1500 x \(\frac { 15 }{ 100 }\) = Rs. 225

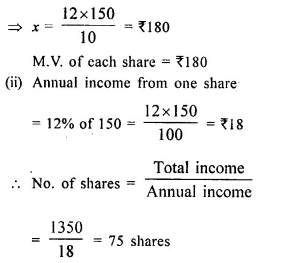
Question 15.
By investing Rs. 7,500 in a company paying 10 percent dividend, an annual income of Rs. 500 is received. What price is paid for each of Rs. 100 share? [1990]
Solution:
Investment = Rs. 7,500
Rate of dividend = 10%
Total income = Rs. 500

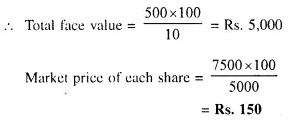
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking (Recurring Deposit Accounts) Ex 2B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2B

Question 1.
Pramod deposits ₹ 600 per month in a Recurring Deposit Account for 4 years. If the rate of interest is 8% per year; calculate the maturity value of his account.
Solution:
Deposit per month (P) = ₹ 600
Rate of interest (r) = 8%
Period (n) = 4 years = 48 months.
According to formula,

Maturity value = ₹ 600 x 48 + ₹ 4,704 = ₹ 28,800 + ₹ 4,704 = ₹ 33504

Question 2.
Ritu has a Recurring Deposit Account in a bank and deposits ₹ 80 per month for 18 months. Find the rate of interest paid by the bank if the maturity value of this account is ₹ 1,554.
Solution:
Let rate of interest = r%,
n = 18,
P = ₹ 80
and A is maturity value.
Using formula

Question 3.
The maturity value of a R.D. Account is ₹ 16,176. If the monthly installment is ₹ 400 and the rate of interest is 8%; find the time (period) of this R.D. Account.
Solution:
Here maturity value (A) = ₹ 16,176
Rate = 8%,
P = ₹ 400
Let period = n (No. of months)
Using formula :
I = A – P x n = 16,176 – 400 x n = 16,716 – 400n.

⇒ 48,528 – 1,200n = 4n² + 4n
⇒ 4n² + 4n + 1200n – 48,528 = 0
⇒ 4n² + 1,204n – 48,528 = 0
⇒ n² + 301n — 12,132 = 0 (dividing by 4)
⇒ n² – 36n + 337n – 12,132 = 0
⇒ n (n – 36) + 337 (n – 36) = 0
⇒ (n – 36) (n + 337) = 0
Either n = 36 months or n = -337, which is not possible.
Time = 36 months = 3 years

Question 4.
Mr. Bajaj needs ₹ 30,000 after 2 years. What least money (in multiple of ₹ 5) must he deposit every month in a recurring deposit account to get required money at the end of 2 years, the rate of interest being 8% p.a. ?
Solution:
Amount of maturity = ₹ 30000
Period (n) = 2 years = 24 months
Rate = 8% p.a.
Let x be the monthly deposit

Amount of monthly deposit in the multiple of ₹ 5 = ₹ 1155

Question 5.
Rishabh has a recurring deposit account in a post office for 3 years at 8% p.a. simple interest. If he gets ₹ 9,990 as interest at the time of maturity, find :
(i) the monthly installment.
(ii) the amount of maturity.
Solution:
Total interest = ₹ 9990
Period (n) = 3 years = 36 months
Rate of interest (r) = 8%
(i) Let monthly installment = x

Monthly installment = ₹ 2250
(ii) Amount of maturity = Principal + Interest
= 36 x 2250 + 9990
= ₹ 81000 + 9990 = ₹ 90990

Question 6.
Gopal has a cumulative deposit account and deposits ₹ 900 per month for a period of 4 years. If he gets ₹ 52,020 at the time of maturity, find the rate of interest.
Solution:
Maturity value = ₹ 52,020
Monthly installment (P) = ₹ 900
Total principal = ₹ 900 x 48 = ₹ 43200
Amount of interest = ₹ 52020 – ₹ 43200 = ₹ 8820
Let rate of interest = r%

Question 7.
Deepa has a 4 year recurring deposit account in a bank and deposits ₹ 1,800 per month. If she gets ₹ 1,800 per month. If she gets ₹ 1,08,450 at the time of maturity, find the rate of interest.
Solution:
Deposit per month = ₹ 1800
Period = 4 years = 48 months
Maturity value = ₹ 108450
Total principal = ₹ 1800 x 48 = ₹ 86400
Amount of interest = ₹ 108450 – 86400 = ₹ 22050
Let r be the rate of interest

Question 8.
Mr. Britto deposits a certain sum of money each month in a Recurring Deposit Account of a bank. If the rate of interest is of 8% per annum and Mr. Britto gets ₹ 8,088 from the bank after 3 years, find the value of his monthly installment. (2013)
Solution:
Let monthly installment = ₹ x
Period (n) = 3 x 12 months = 36 months

Question 9.
Sharukh opened a Recurring Deposit Account in a bank and deposited ₹ 800 per month for 1\(\frac { 1 }{ 2 }\) years. If he received ₹ 15,084 at the time of maturity, find the rate of interest per annum. (2014)
Solution:
Money deposited per month (P) = ₹ 800
r = ?

Question 10.
Katrina opened a recurring deposit account with a Nationalised Bank for a period of 2 years. If the bank pays interest at the rate of 6% per annum and the monthly installment is ₹ 1,000, find the :
(i) interest earned in 2 years
(ii) maturity value. (2015)
Solution:
Period (n) = 2 years = 2 x 12 = 24 months
Rate of interest (r) = 6%
Monthly installment (P) = ₹ 1000

Question 11.
Mohan has a recurring deposit account in a bank for 2 years at 6% p.a. simple interest. If he gets ₹ 1200 as interest at the time of maturity, find :
(i) the monthly installment
(ii) the amount of maturity
Solution:
(i) Interest = ₹ 1200,
n = 2 x 12 = 24 months,
r = 6%

⇒ P = ₹ 800
So the monthly installment is ₹ 800
(ii) Total sum deposited = P x n = ₹ 800 x 24 = ₹ 19200
The amount that Mohan will get at the time of maturity = Total sum deposited + Interest Received
= ₹ 19200 + ₹ 1200 = ₹ 20400
Hence, the amount of maturity is ₹ 20400

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking (Recurring Deposit Accounts) Ex 2A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2B

Question 1.
Manish opens a Recurring Deposit Account with the Bank of Rajasthan and deposits ₹ 600 per month for 20 months. Calculate the maturity value of this account, if the bank pays interest at the rate of 10% per annum.
Solution:
Recurring Deposit per month = ₹ 600
Period (n) = 20 months
Rate of interest (r) = 10% p.a.
Total principal for 1 month

Maturity value = ₹ 600 x 20 + ₹ 1,050 = ₹ 12,000 + ₹ 1,050 = ₹ 13,050

Question 2.
Mrs. Mathew opened a Recurring Deposit Account in a certain bank and deposited ₹ 640 per month for 4\(\frac { 1 }{ 2 }\) years. Find the maturity value of this account, if the bank pays interest at the rate of 12% per year.
Solution:
Recurring deposit per month = ₹ 640
Period (n) = 4\(\frac { 1 }{ 2 }\) years = 54 months
Rate of interest (r) = 12%
Total principal for 1 month

Maturity value = ₹ 640 x 54 + ₹ 9,504 = ₹ 34,560 + ₹ 9,504 = ₹ 44,064

Question 3.
Each of A and B opened a recurring deposit accounts in a bank. If A deposited ₹ 1,200 per month for 3 years and B deposited ₹ 1,500 per month for 2\(\frac { 1 }{ 2 }\) years; find, on maturity, who will it get more amount and by how much ? The rate of interest paid by the bank is 10% per annum.
Solution:
A’s deposit per month (P) = ₹ 1200
Period = 3 years = 36 months
Total principal for one month


and maturity value = ₹ 1500 x 30 + Interest
= ₹ 45000 + 5812.50
= ₹ 50812.50
It is clear that B’s maturity value is greater Difference = ₹ 50812.50 – ₹ 49860 = ₹ 952.50

Question 4.
Ashish deposits a certain sum of money every month in a Recurring Deposit Account for a period of 12 months. If the bank pays interest at the rate of 11% p.a. and Ashish gets ₹ 12,715 as the maturity value of this account, what sum of money did he pay every month ?
Solution:
Let Recurring deposit per month = ₹ x
Period (n) = 12 months
Rate of interest (r) = 11%
Maturity value = ₹ 12,715 ………. (i)
Total principal for one month

Recurring deposit per month ₹ 1000 p.m.

Question 5.
A man has a Recurring Deposit Account in a bank for 3\(\frac { 1 }{ 2 }\) years. If the rate of interest is 12% per annum and the man gets ₹ 10206 on maturity, find the value of monthly installments.
Solution:
Let Recurring deposit per month = ₹ x
Period (n) = 3\(\frac { 1 }{ 2 }\) years = 42 months
Rate of interest (r) = 12% p.a.
Amount of maturity = ₹ 10206 ……… (i)

Amount of each installment = ₹ 200

Question 6.
(i) Puneet has a Recurring Deposit Account in the Bank of Baroda and deposits ₹ 140 per month for 4 years If he gets ₹ 8,092 on maturity, find the rate of interest given by the bank.
(ii) David opened a Recurring Deposit Account in a bank and deposited ₹ 300 per month for two years. If he received ₹ 7725 at the time of maturity, find the rate of interest per annum. (2008)
Solution:
(i) Recurring deposit per month = ₹ 140
Period (n) = 4 years = 48 months
Let Rate of interest (r) = r % p.a.
Amount of maturity = ₹ 8,092
Total principal for one month

Question 7.
Amit deposited ₹ 150 per month in a bank for 8 months under the Recurring Deposits Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% per annum and interest is calculated at the end of every month ? [I.C.S.E. 2001]
Solution:
Amount of Recurring deposit = ₹ 150
Period (n) = 8 months
Rate of interest (r) = 8% p.a.
Total principal for one month

Amount of maturity value = ₹ 150 x 8 + ₹ 36 = ₹ 1,200 + ₹ 36 = ₹ 1,236

Question 8.
Mrs. Geeta deposited ₹ 350 per month in a bank for 1 year and 3 months under the Recurring Deposit Scheme. If the maturity value of her deposits is ₹ 5,565; find the rate of interest per annum.
Solution:
Amount of recurring deposit per month = ₹ 350
Period (n) = 1 year 3 months = 15 months
Let rate of interest = r % p.a.
Amount of maturity = ₹ 5565
Amount of interest = ₹ 5,565 – ₹ 350 x 15 = ₹ 5,565 – 5,250 = ₹ 315 ….(i)
Now, total principal for one month

Question 9.
A recurring deposit account of ₹ 1,200 per month has a maturity value of ₹ 12,440. If the rate of interest is 8% and the interest is calculated at the end of every month; find the time (in months) of this Recurring Deposit Account.
Solution:
Amount of recurring deposit per month = ₹ 1,200
Rate of interest (r) = 8% p.a.
Let period = n months
Amount of maturity = ₹ 12,440
Amount of interest = ₹ 12440 – ₹ 1200 x n ….(i)
Total principal for one month

from (i) and (ii), we get,
4n (n + 1) = 12440 – 1200n
⇒ 4n² + 4n = 12440 – 1200n
⇒ 4n² + 1204n – 12440 = 0
Dividing by 4,
⇒ n² + 301n – 3110 = 0
⇒ n² + 311n – 10n – 3110 = 0
⇒ n (n + 311) – 10 (n + 311) = 0
⇒ (n + 311) (n – 10) = 0
Given n + 311 = 0, then n = – 311 Which is not possible,
or n – 10 = 0, then n = 10
Period = 10 months.

Question 10.
Mr. Gulati has a Recurring Deposit Account of ₹ 300 per month. If the rate of interest is 12% and the maturity value of this account is ₹ 8,100; find the time (in years) of this Recurring Deposit Account.
Solution:
Amount of recurring deposit per month = ₹ 300
Let Period = n months
Rate of interest (r) = 12% p.a.
Amount of maturity = ₹ 8,100
Interest = 8,100 – 300 x n ……. (i)
Total principal for 1 month

⇒ 3n (n + 1) = 16,200 – 600 n
⇒ 3n² + 3n = 16,200 – 600 n
⇒ 3n² + 603n – 16,200 = 0
Dividing by 3, we get,
⇒ n² + 201n – 5,400 = 0
⇒ n² + 225n – 24n – 5,400 = 0
⇒ n(n + 225) – 24 (n + 225) = 0
⇒ (n + 225) (n – 24) = 0
Either n + 225 = 0, then n = – 225 Which is not possible
or n – 24 = 0, then n = 24
Period = 24 months or 2 years.

Question 11.
Mr. Gupta opened a recurring deposit account in a bank. He deposited ₹ 2,500 per month for two years. At the time of maturity he got ₹ 67,500. Find :
(i) the total interest earned by Mr. Gupta.
(ii) the rate of interest per annum. (2010)
Solution:
(i) Total amount deposited by Mr. Gupta in 24 months = ₹ 2500 x 24 = ₹ 60,000
Maturity amount = ₹ 67,500
Total interest earned by Mr. Gupta = ₹ 67,500 – ₹ 60,000 = ₹ 7,500
(ii) Total principal for 1 month

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1C

[In this exercise, all the prices are excluding tax/VAT unless specified].
Question 1.
Madan purchases a compact computer system for ₹ 47,700 which includes 10% rebate on the marked price and then 6% Sales Tax on the remaining price. Find the marked price of the computer.
Solution:
Sales price of the computer = ₹ 47700
Rate of Sales Tax = 6%

Hence marked price = ₹ 50,000

Question 2.
An article is marked at ₹ 500. The wholesaler sells it to a retailer at 20% discount and charges sales-tax on the remaining price at 12.5%. The retailer, in turn, sells the article to a customer at its marked price and charges sales-tax at the same rate. Calculate :
(i) the price paid by the customer.
(ii) the amount of VAT paid by the retailer.
Solution:
Marked price of an article = ₹ 500
Rate of discount = 20%

(i) Price paid by-the customer = ₹ 500 + ₹ 62.50 = ₹ 562.50
(ii) VAt paid by the retailer = ₹ 62.50 – ₹ 50.00 = ₹ 12.50

Question 3.
An article is marked at ₹ 4,500 and the rate of sales-tax on it is 6%. A trader buys this article at some discount and sells it to a customer at the marked price. If the trader pays ₹ 81 as VAT; find :
(i) how much per cent discount does the trader get ?
(ii) the total money paid by the trader, including tax, to buy the article.
Solution:
Marked price = ₹ 4500
Rate of S.T. = 6%
VAT paid by the trader = ₹ 81
C.P. for the customer = ₹ 4500

Question 4.
A retailer sells an article for ₹ 5,350 including 7% Sales Tax on the listed price. If he had bought it at a discount and has made a profit of 25% on the whole, And the rate of discount he gets.
Solution:
S.P. of an article of the retailer (including S.T.) = ₹ 5350
Rate of S.T. = 7%

Question 5.
A shopkeeper buys a camera at a discount of 20% from the wholesaler, the printed price of the camera being ₹ 1600 and the rate of sales tax is 6%. The shopkeeper sells it to the buyer at the printed price and charges tax at the same rate. Find :
(i) The price at which the camera can be bought from the shopkeeper.
(ii) The VAT (Value Added Tax) paid by the shopkeeper. (2008)
Solution:
Printed price (M.P) = ₹ 1600
Rate of discount = 20%

(i) The buyers bought the camera = ₹ 1600 + ₹ 96 = ₹ 1696
(ii) VAT paid by the shopkeeper = ₹ 96 – ₹ 76.80 = ₹ 19.20

Question 6.
Tarun bought an article for ₹ 8000 and spent ₹ 1000 for transportation. He marked the article at ₹ 11,700 and sold it to a customer. If the customer had to pay 10% sales tax, find:
(i) The customer’s price
(ii) Tarun’s profit percent.
Solution:
Tarun’s cost price = ? 8000
Transportation charges = ₹ 1000
Tarun’s total cost = (₹ 8000 + ₹ 1000) = ₹ 9000
Tarun’s selling price = ₹ 11,700
Rate of sales tax = 10%

Question 7.
A shopkeeper sells an article at the listed price of ₹ 1,500 and the rate of VAT is 12% at each stage of sale. If the shopkeeper pays a VAT of ₹ 36 to the Government, what was the price, inclusive of Tax, at which the shopkeeper purchased the articles from the wholesaler?
Solution:
Tax charged by shopkeeper

Question 8.
A shopkeeper bought a washing machine at a discount of 20% from a wholesaler, the printed price of the washing machine being ₹ 18,000. The shopkeeper sells it to a consumer at a discount of 10% on the printed price. If the rate of sales tax under is 8%, find:
(i) the VAT paid by the shopkeeper.
(ii) the total amount that the consumer pays for the washing machine. (2014)
Solution:
(i) S.P. of washing machine

VAT paid by shopkeeper = Tax charged – Tax paid = ₹ 1296 – ₹ 1152 = ₹144
(ii) Price paid by customer = ₹ 16200 + ₹ 1296 = ₹ 17496

Question 9.
Mohit, a dealer in electronic goods, buys a high class TV set for ₹ 61,200. He sells this TV set to Geeta, Geeta to Rohan and Rohan sells it to Manoj. If the profit at each stage is ₹ 2,000 and the rate of VAT at each stage is 12.5%, find :
(i) total amount of tax (under VAT) paid to the Government.
(ii) Money paid by Manoj to buy the TV set.
Solution:
For Mohit,
C.P. of electronic goods = ₹ 61200
Amount of profit in each case = ₹ 2000

Net VAT = ₹ 8400 – ₹ 8150 = ₹ 250
(i) Total amount of VAT paid to govt. = ₹ 7650 + ₹ 250 + ₹ 250 + ₹ 250 = ₹ 8400
(ii) Money paid by Manoj to buy the T.V. set = ₹ 67200 + ₹ 8400 = ₹ 75600

Question 10.
A shopkeeper buys an article at a discount of 30% of the list price which is ₹ 48,000. In turn, the shopkeeper sells the article at 10% discount. If the rate of VAT is 10%, find the VAT to be paid by the shopkeeper.
Solution:
Market value (M.P.) of an article = ₹ 48000
Rate of discount = 30%
Amount of discount = ₹ 48000 x \(\frac { 30 }{ 100 }\) = ₹ 14400
(i) Cost price of shopkeeper = ₹ 48000 – ₹ 14400 = ₹ 33600
(ii) C.P. for shopkeeper = ₹ 33600
Rate of VAT = 10%
Amount of VAT paid by shopkeeper

Net VAT paid by the shopkeeper = VAT recovered from customer – VAT paid to dealer
= ₹ 4320 – ₹ 3360 = ₹ 960

Question 11.
A company sells an article to a dealer for ₹ 40,500 including VAT (sales-tax). The dealer sells it to some other dealer for ₹ 42,500 plus tax. The second dealer sells it to a customer at a profit of ₹ 3,000. If the rate of sales-tax under VAT is 8%, find :
(i) the cost of the article (excluding tax) to the first dealer.
(ii) the total tax (under VAT) received by the Government.
(iii) the amount that a customer pays for the article.
Solution:
For a company,
S.P. of an article including VAT = ₹ 40500
Rate of VAT = 8%
(i) Amount of article excluding VAT

= ₹ 425 x 108 = ₹ 45900
Total tax (VAT) = ₹ 45900 – ₹ 42500 = ₹ 3000
S.P. for the second dealer = ₹ 42500 + ₹ 3000 = ₹ 45500
(ii) VAT = ₹ \(\frac { 45500 x 8 }{ 100 }\) = ₹ 3640
(iii) Total amount paid by customer = ₹ 45500 + ₹ 3640 = ₹ 49140

Question 12.
A wholesaler buys a TV from the manufacturer for ₹ 25,000. He marks the price of the TV 20% above his cost price and sells it to a retailer at 10% discount on the marked price. If the rate of VAT is 8%, find the :
(i) marked price.
(ii) retailer’s cost price inclusive of tax.
(iii) VAT paid by the wholesaler. (2015)
Solution:
S.P. for the manufactures = ₹ 25000
or C.P. for a whole seller a T.V. = ₹ 25000

C.P. for the retailer = ₹ 27000 + ₹ 2160 = ₹ 29160
(iii) VAT paid by the whole seller = ₹ 2160 – ₹ 2000 = ₹ 160

Question 13.
A dealer buys an article at a discount of 30 % from the wholesaler, the marked price being ₹ 6,000. The dealer sells it to a shopkeeper at a discount of 10% on the marked price. If the rate of VAT is 6%, find :
(i) the price paid by the shopkeeper including the tax.
(ii) the VAT paid by the dealer. (2016)
Solution:
Market price of the article = ₹ 6000
A dealer buys an article at a discount of 30% from the wholesaler.
Price of the article which the dealer paid to the wholesaler = 6000 – 30% of 6000

Amount of the article inclusive of sales tax at which the dealer bought it
= ₹ 4200 + ₹ 252 = ₹ 4452
Dealer sells the article at a discount of 10% to the shopkeeper.
Price of the article which the shopkeeper paid to the dealer = ₹ 6000 – 10% of 6000

Amount of the article inclusive of sales tax at which the shopkeeper bought it
= ₹ 5400 + ₹ 324 = ₹ 5724
The value added by dealer = ₹ 5400 – ₹ 4200 = ₹ 1200
Amount of VAT paid by dealer = 6% of 1200
= \(\frac { 6 }{ 100 }\) x 1200 = ₹ 72
Price paid by shopkeeper including tax is ₹ 5724
VAT paid by dealer is ₹ 72

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1B

 

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1C

[In this exercise, all the prices are excluding tax/VAT unless specified].
Question 1.
A shopkeeper purchases an article for ₹ 6,200 and sells it to a customer for ₹ 8,500. If the sale tax (under VAT) is 8%; find the VAT paid by the shopkeeper.
Solution:
C.P. of article = ₹ 6200
Rate of VAT = 8%

Amount of VAT paid by the shopkeeper = ₹ 680 – ₹ 496 = ₹ 184

Question 2.
A purchases an article for ₹ 3,600 and sells it to B for ₹ 4,800. B, in turn, sells the article to C for ₹ 5,500. If the sale tax (under VAT) is 10%, find the VAT levied on A and B.
Solution:
C.P. of an article for A = ₹ 3600
C.P. of the article for B = ₹ 4800
and C.P. for C = ₹ 5500
Rate of VAT in each case = 10%

Now VAT levied on A = ₹ 480 – ₹ 360 = ₹ 120
and VAT levied on B = ₹ 550 – ₹ 480 = ₹ 70

Question 3.
A manufacturer buys raw material for ₹ 60,000 and pays 4% tax. He sells the ready stock for ₹ 92,000 and charges 12.5% tax. Find the VAT paid by the manufacturer.
Solution:
C.P. of raw material = ₹ 60000
Rate of tax = 4%

VAT paid by the manufacturer = ₹ 11500 – ₹ 2400 = ₹ 9100

Question 4.
The cost of an article is ₹ 6,000 to a distributor. He sells it to a trader for ₹ 7,500 and the trader sells it to a customer for ₹ 8,000. If the VAT rate is 12.5% ; find the VAT paid by the :
(i) distributor
(ii) trader.
Solution:
Cost price of an article to a distributor = ₹ 6000
and selling price of distributor = ₹ 7500
and selling price of trader = ₹ 8000
Rate of VAT = 12.5% = \(\frac { 25 }{ 2 }\) %
Now, VAT for two distributor

(i) Now VAT paid by distributor = ₹ 937.50 – ₹ 750 = ₹ 187.50
(ii) and VAT paid by trader = ₹ 1000 – ₹ 937.50 = ₹ 62.50

Question 5.
The printed price of an article is ₹ 2,500. A wholesaler sells it to a retailer at 20% discount and charges sales-tax at the rate of 10%. Now the retailer, in turn, sells the article to a customer at its list price and charges the sales-tax at the same rate. Find :
(i) the amount that retailer pays to the wholesaler.
(ii) the VAT paid by the retailer.
Solution:
M.P. of an article = ₹ 2500
Rebate = 20%

Question 6.
A retailer buys an article for ₹ 800 and pays the sales-tax at the rate of 8%. The retailer sells the same article to a customer for ₹ 1,000 and charges sales- tax at the same rate. Find :
(i) the price paid by a customer to buy this article.
(ii) the amount of VAT paid by the retailer.
Solution:
C.P. of an article for retailer = ₹ 800
Rate of S.T. = 8%

(i) Cost price of the customer = ₹ 1000 + ₹ 80 = ₹ 1080
(ii) VAT paid by the retailer = ₹ 80 – ₹ 64 = ₹ 16

Question 7.
A shopkeeper buys 15 identical articles for ₹ 840 and pays sales-tax at the rate of 8%. He sells 6 of these articles at ₹ 65 each and charges sales-tax at the same rate. Calculate the VAT paid by the shopkeeper against the sale of these six articles.
Solution:
C.P. of 15 articles = ₹ 840

VAT paid by the retailer = ₹ 31.20 – ₹ 26.88 = ₹ 4.32

Question 8.
The marked price of an article is ₹ 900 and the rate of sales-tax on it is 6%. If on selling the article at its marked price, a retailer has to pay VAT = ₹ 4.80; find the money paid by him (including sales-tax) for purchasing this article.
Solution:
M.P. an article = ₹ 900
Rate of S.T. = 6%

Amount paid including S.T. = ₹ 820 + ₹ 49.20 = ₹ 869.20

Question 9.
A manufacturer marks an article at ₹ 5,000. He sells this article to a wholesaler at a discount of 25% on the marked price and the wholesaler sells it to a retailer at a discount of 15% on its marked price. If the retailer sells the article without any discount and at each stage the sales-tax is 8%, calculate the amount of VAT paid by :
(i) the wholesaler.
(ii) the retailer.
Solution:
M.P. of an article = ₹ 5000
Rate of discount = 25%
S.R of the manufacturer or C.P of


Now VAT paid by
(i) The wholesaler = ₹ 340 – ₹ 300 = ₹ 40
(ii) Retailer = ₹ 400 – ₹ 340 = ₹ 60

Question 10.
A shopkeeper buys an article at a discount of 30% and pays sales-tax at the rate of 8%. The shopkeeper, in turn, sells the article to a customer at the printed price and charges sales tax at the same rate. If the printed price of the article is ₹ 2,500; find :
(i) the price paid by the shopkeeper.
(ii) the price paid by the customer.
(iii) The VAT (Value Added Tax) paid by the shopkeeper.
Solution:
Printed price of an article = ₹ 2500
Discount = 30%
C.P of the article for shopkeeper

(i) Price paid by the shopkeeper = ₹ 1750 + ₹ 140 = ₹ 1890
(ii) Price paid by the customer = ₹ 2500 + ₹ 200 = ₹ 2700
(iii) VAT paid by the shopkeeper = ₹ 200 – ₹ 140 = ₹ 60

Question 11.
A shopkeeper sells an article at its list price (₹ 3,000) and charges sales-tax at the rate of 12%. If the VAT paid by the shopkeeper is ₹ 72, at what price did the shopkeeper buy the article inclusive of sales-tax ?
Solution:
S.P. or list price of an article = ₹ 3000
Rate of sales tax = 12%

C.P paid by the shopkeeper including S.T. = ₹ 2400 + ₹ 288 = ₹ 2688

Question 12.
A manufacturer marks an article for ₹ 10,000. He sells it to a wholesaler at 40% discount. The wholesaler sells this article to a retailer at 20% discount on the marked price of the article. If retailer sells the article to a customer at 10% discount and the rate of sales-tax is 12% at each stage; find the amount of VAT paid by the :
(i) wholesaler
(ii) retailer
Solution:
Marked price of an article = ₹ 10000
Rate of discount = 40%
C.P of the wholesaler


Now
(i) Vat paid by wholesaler = ₹ 960 – ₹ 720 = ₹ 240
(ii) Vat paid by retailer = ₹ 1080 – ₹ 960 = ₹ 120

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1C

Question 1.
Rajat purchases a wrist-watch costing ₹ 540. The rate of Sales Tax is 8%. Find the total amount paid by Rajat for the watch.
Solution:
Cost of watch = ₹ 540
Rate of Sales Tax = 8%

Total Amount of Watch = ₹ 540 + ₹ 43.20 = ₹ 583.20

Question 2.
Ramesh paid ₹ 345.60 as Sales Tax on a purchase of ₹ 3,840. Find the rate of Sales Tax.
Solution:
On ₹ 3840, sales-tax is = ₹ 345.60

Question 3.
The price of a washing machine, inclusive of sales tax is ₹ 13,530/-. If the Sales Tax is 10%, find its basic (cost) price. [2003]
Solution:
Selling price of washing machine = ₹ 13,530.
Rate of Sales Tax = 10%

Question 4.
Sarita purchases biscuits costing ₹ 158 on which the rate of Sales Tax is 6%. She also purchases some cosmetic goods costing ₹ 354 on which the rate of Sales Tax is 9%. Find the total amount to be paid by Sarita.
Solution:
Cost of biscuits = ₹ 158.

Total cost of cosmetic goods = ₹ 354 + ₹ 31.86 = ₹ 385.86
Total amount paid by Sarita = ₹ 167. 48 + ₹ 385.86 = ₹ 553. 34

Question 5.
The marked price of two articles A and B together is ₹ 6,000. The sales tax on article A is 8% and that on article B is 10%. If on selling both the articles, the total sales tax collected is ₹ 552, find the marked price of each of the articles A and B.
Solution:
M.P of two articles A and B = ₹ 6000
Rate of S.T. on A = 8%
and rate of S.I. on B = 10%
Total sales tax on A and B = ₹ 552
Let MP of A be = ₹ x
and then of MP of B = ₹ (6000 – x)
according to the condition,

M.P. of article A = ₹ 2400
and MP of article B = ₹ 6000 – ₹ 2400 = ₹ 3600

Question 6.
The price of a T.V. set inclusive of sales tax of 9% is ₹ 13,407. Find its marked price. If Sales Tax is increased to 13%, how much more does the customer has to pay for the T.V. ? [2002]
Solution:
Sale price of T.V. set = ₹ 13,407
Rate of sales tax = 9%
Let marked price of T.V. = x
Then sale price

Sale price = ₹ 12,300 + ₹ 1,599 = ₹ 13,899
Difference between the two sales price = ₹ 13,899 – ₹ 13,407 = ₹ 492

Question 7.
The price of an article is ₹ 8,250 which includes Sales Tax at 10%. Find how much more or less does a customer pay for the article, if the Sales Tax on the article:
(i) increases to 15%
(ii) decreases to 6%
(iii) increases by 2%
(iv) decreases by 3%
Solution:
Price of an article = ₹ 8,250
Rate of Sales Tax = 10%
Let the list price = x


The customer will have to pay less = ₹ 8,250 – ₹ 8,025 = ₹ 225

Question 8.
A bicycle is available for ₹ 1,664 including Sales Tax. If the list price of the bicycle is ₹ 1,600, find :
(i) the rate of Sales Tax
(ii) the price a customer will pay for the bicycle if the Sales Tax is increased by 6%.
Solution:
Sale price of bicycle = ₹ 1,664.
List price = ₹ 1,600
Amount of Sales Tax = ₹ 1,664 – ₹ 1,600 = ₹ 64.

Sales price = ₹ 1,600 + ₹ 160 = ₹ 1,760

Question 9.
When the rate of sale-tax is decreased from 9% to 6% for a coloured T.V.; Mrs Geeta will save ₹ 780 in buying this T.V. Find the list price of the T.V.
Solution:
Rate of sales tax in the beginning = 9%
and Reduced rate = 6%
Diff. = 9 – 6 = 3%
Total saving = ₹ 780
List, price of TV = Total saving x \(\frac { 100 }{ 3 }\)
= \(\frac { 780 x 100 }{ 3 }\) = ₹ 26000

Question 10.
A trader buys an unfinished article for ₹ 1,800 and spends ₹ 600 on its finishing, packing, transportation, etc. He marks the article at such a price that will give him 20% profit. How much will a customer pay for the article including 12% sales tax.
Solution:
Cost price of an unfinished article = ₹ 1800
Cost on finishing, packing etc or over head charges = ₹ 600
Total C.P. = ₹ 1800 + ₹ 600 = ₹ 2400
Gain = 20%

Total sale price = ₹ 2880 + ₹ 345.60 = ₹ 3225.60

Question 11.
A shopkeeper buys an article for ₹ 800 and spends ₹ 100 on its transportation, etc. He marks the article at a certain price and then sells it Tor ₹ 1,287 including 10% sales tax. Find this profit as per cent.
Solution:
C.P. of an article = ₹ 800
Over head charges = ₹ 100
Total C.P. = ₹ 800 + ₹ 100 = ₹ 900
Sale price = ₹ 1287 including S.T.
Rate of S.T. = 10%

Question 12.
A shopkeeper announces a discount of 15% on his goods. If the marked price of an article, in his shop, is ₹ 6000 ; how much a customer has to pay for it, if the rate of Sales Tax is 10% ?
Solution:
Marked price of an article = ₹ 6000
Rate of discount = 15%

Question 13.
The catalogue price of a music system is ₹ 24,000. The shopkeeper gives a discount of 8% on the list price. He gives a further off-season discount of 5% on the balance. But Sales Tax at 10% is charged on the remaining amount. Find:
(a) the Sales Tax a customer has to pay.
(b) the final price he has to pay for the music system. (2001)
Solution:
List price of colour music system = ₹ 24,000
First rate of discount = 8%

(b) Final price of music system = ₹ 20,976 + ₹ 2,097.60 = ₹ 23,073.60

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 1 Value Added Tax Ex 1A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C

Question 1.
By investing 745,000 in 10% 7100 shares, Sharad gets 73,000 as divided. Find the market value of each share.
Solution:
Total investment = ₹ 45000 at 10% of ₹ 100 shares
and amount of dividend = ₹ 3000

Question 2.
Mrs. Kulkarni invests ₹ 1,31,040 in buying ₹ 100 shares at a discount of 9%. She sells shares worth ₹ 72,000 at a premium of 10% and the rest at a discount of 5%. Find her total gain or loss on the whole.
Solution:
Total investment = ₹ 1,31,040 in ₹ 100 share at discount of 9%
Market value of each share = ₹ 100 – ₹ 9 = ₹ 91

Question 3.
A man invests a certain sum in buying 15% ₹ 100 shares at 20% premium. Find:
(i) his income from one share.
(ii) the number of shares bought to have an income, from the dividend, ₹ 6,480.
(iii) sum invested.
Solution:
Face value of each share = ₹ 100
Market value of each share = ₹ 100 + ₹ 20 = ₹ 120
Rate of dividend = 15%
(i) Income from one share = ₹ 15
(ii) and number of shares when amount of dividend
= \(\frac { 6480 }{ 15 }\) = 432
(iii) and sum invested = ₹ 432 x 120 = ₹ 51,840

Question 4.
Gagan invested 80% of his savings in 10% ₹ 100 shares at 20% premium and the rest of his savings in 20% ₹ 50 shares at 20% discount. If his incomes from these shares is ₹ 5,600, calculate:
(i) his investment in shares on the whole.
(ii) the number of shares of first kind that he bought
(iii) percentage return, on the shares bought, on the whole.
Solution:
(i) Total income = ₹ 5600
Let total investment = ₹ x

Question 5.
Aishwarya bought 496, ₹ 100 shares at ₹ 132 each. Find:
(i) investment made by her.
(ii) income of Aishwarya from these shares, if the rate of dividend is 7.5%.
(iii) how much extra must Aishwarya invest in order to increase her income by ₹ 7,200?
Solution:
Number of shares = 496
Market value of each share = ₹ 132
(i) Total investment = 496 x 132 = ₹ 65472
(ii) Rate of dividend = 7.5%
Income = 496 x 7.5 = ₹ 3720
(iii) New income (increase in income) = ₹ 7200
Market value of share = ₹ 132
Rate of income = 7.5%
Exit investment

Question 6.
Gopal has some ₹ 100 shares of company A, paying 10% dividend. He sells a certain number of these shares at a discount of 20% and invests the proceeds in ₹ 100 shares at ₹ 60 of company B paying 20% dividend. If his income, from the shares sold, increases by ₹ 18,000, find the number of shares sold by Gopal.
Solution:
Let number of share purchased = x
Face value of these shares = ₹ 100 x x = 100x
dividend = 10%

Question 7.
A man invests a certain sum of money in 6% hundred rupee shares at ₹ 12 premium. When the shares fell to ₹ 96, he sold out all the shares bought and invested the proceed in 10%, ten rupee shares at ₹ 8. If the change in his income is ₹ 540, find the sum invested originally.
Solution:
Let investment = ₹ x
Dividend at the rate of 6% at 12% premium

Question 8.
Mr. Gupta has a choice to invest in ten rupee shares of two firms at ₹ 13 or at 716. If the first firm pays 5% dividend and the second firm pays 6% dividend per annum, find:
(i) which firm is paying better ?
(ii) If Mr. Gupta invests equally in both the firms and the difference between the returns from them is ₹ 30, Find how much in all does he invest ?
Solution:
Face value of each share = ₹ 10
Market value of first firm’s share = ₹ 13
and market value of second firm’s share = ₹ 16
Dividend from first firm = 5%
and dividend from second firm = 6%
(i) Let investment in each firm = ₹ 13 x 16
Income from first firm’s shares

It is clear from the above that first firm’s shares are better.
(ii) Difference in income = ₹ 8.00 – ₹ 7.80 = ₹ 0.20
If difference is ₹ 0.20 then investment in each firm = ₹ 13 x 16
and if difference is ₹ 30, then investment

Total investment in both firms = ₹ 31200 x 2 = ₹ 62,400

Question 9.
Ashok invested ₹ 26,400 in 12%, ₹ 25 shares of a company. If he receives a dividend of ₹ 2,475, find the :
(i) number of shares he bought.
(ii) market value of each share.
Solution:
(i) Given,
Investment = ₹ 26400
Rate of dividend = 12%
Dividend earned = ₹ 2475
Face value of one share = ₹ 25
Total dividend earned = No. of shares x Rate of dividend x Face value of one share

Question 10.
A man invested ₹ 45,000 in 15% ₹ 100 shares quoted at ₹ 125. When the market value of these shares rose to Rs. 140, he sold some shares, just enough to raise ₹ 8,400. calculate :
(i) the number of shares he still holds;
(ii) the dividend due to him on these remaining shares. [2004]
Solution:

Question 11.
Mr. Tiwari invested ₹ 29,040 in 15% ₹100 shares quoted at a premium of 20%. Calculate :
(i) the number of shares bought by Mr. Tiwari.
(ii) Mr. Tiwari’s income from the investment.
(iii) the percentage return on his investment.
Solution:
Mr. Tiwari’s investment = ₹ 29040
Face value of each share = ₹ 100
Market value of each share = ₹ 100 + ₹ 20 = ₹ 120
Rate of income = 15%
(i) Number of shares purchased

Question 12.
A dividend of 12% was declared on ₹ 150 shares selling at a certain price. If the rate of return is 10%, calculate :
(i) the market value of the shares.
(ii) the amount to be invested to obtain an annual dividend of ₹ 1,350.
Solution:
Let market value of each share = x
Rate of return on investment = 10%
Face value of each share = ₹ 150
Dividend rate = 12%
(i) Now, rate of return x market value = Rate of dividend x Face value
⇒ 10 x x = 12 x 150

Amount of investment in ₹ 5 shares = ₹ 5 x ₹ 180 = ₹ 13500

Question 13.
Divide ₹ 50,760 into two parts such that if one part is invested in 8% ₹ 100 shares at 8% discount and the other in 9% ₹ 100 shares at 8% premium, the annual incomes from both the investments are equal.
Solution:
Total investment = ₹ 50,760
Let first part of investment = x
Then second part = ₹ 50,760 – x
Rate of dividend in first part = 8% ₹100 at discount = 8%
M.V. of each share = ₹ 100 – 8 = ₹ 92
Rate of dividend second part = 9% ₹ 100 at premium = 8%
M.V. of each share = 100 + 8 = ₹ 108
But annual income from both part is same

Question 14.
Mr. Shameem invested 33\(\frac { 1 }{ 3 }\) % of his savings in 20% ₹ 50 shares quoted at ₹ 60 and the remainder of the savings in 10% ₹ 100 shares quoted at ₹ 110. If his total income from these investments is ₹ 9,200 ; find :
(i) his total savings
(ii) the number of ₹ 50 shares.
(iii) the number of ₹ 100 shares.
Solution:
Let total investment = x

Question 15.
Vivek invests ₹ 4500 in 8% ₹ 10 shares at ₹ 15. He sells the shares when the price rises to ₹ 30, and invests the proceeds in 12% ₹ 100 shares at ₹ 125. Calculate,
(i) the sale proceeds
(ii) the number of ₹ 125 shares he buys.
(iii) the change in his annual income from dividend.
Solution:
(i) By investing ₹ 15, share bought = ₹ 10
By investing ₹ 4500, share bought = \(\frac { 10 }{ 15 }\) x 4500 = ₹ 3000
Total face value of ₹ 10 shares = ₹ 3000, Income = 8%
= \(\frac { 8 }{ 100 }\) x 3000 = ₹ 240
By selling Rs. 10 share money received = ₹ 30
By selling Rs. 3000 shares money = \(\frac { 30 }{ 10 }\) x 3000 = ₹ 9000
(ii) By investing ₹ 125, no. of share of ₹ 100 bought = 1
By investing ₹ 9000, no. of share of ₹ 100 bought = \(\frac { 1 }{ 125 }\) x 9000 = 72
No. of ₹ 125 shares bought = 72
(iii) By investing ₹ 125 in Rs. 100 share, income = ₹ 12
By investing ₹ 9000 in ₹ 100 share, income = \(\frac { 12 }{ 125 }\) x 9000 = ₹ 864
Increase in income = ₹ 864 – ₹ 240 = ₹ 624

Question 16.
Mr. Parekh invested ₹ 52,000 on ₹ 100 shares at a discount of ₹ 20 paying 8% dividend. At the end of one year he sells the shares at a premium of ₹ 20. Find
(i) The annual dividend.
(ii) The profit earned including his dividend.
Solution:
Investment = ₹ 52000,
N.V. of 1 share = ₹ 100
M.V. of 1 share for 1 st year = ₹ 100 – 20 = ₹ 80
No. of shares = \(\frac { 52000 }{ 80 }\) = 650
(i) Annual dividend = \(\frac { 8 }{ 100 }\) x 650 x 100 = ₹ 5200
(ii) S.P of 1 share = ₹ 100 + 20 = ₹ 120
S.P. of 650 shares = ₹ 120 x 650 = ₹ 78000
C.P. of 650 shares = ₹ 100 x 650 = ₹ 65000
Profit = S.P. – C.P. = ₹ 78000 – ₹ 65000 = ₹ 13000
Profit including dividend = ₹ 13000 + ₹ 5200 = ₹ 18200

Question 17.
Salman buys 50 shares of face value ₹ 100 available at ₹ 132.
(i) What is his investment ?
(ii) If the dividend is 7.5%, what will be his annual income ?
(iii) If he wants to increase his annual income by ₹ 150, how many extra shares should he buy?
Solution:
F.V. = ₹ 100
(i) M. V. = ₹ 132,
no. of shares = 50
Investment = no. of shares x M.V. = 50 x 132 = ₹ 6600
(ii) Income per share = 7.5% of N.V.
= \(\frac { 75 }{ 10 x 100 }\) x 100 = ₹ 7.5
Annual incomes = 7.5 x 50 = ₹ 375
(iii) New annual income = 375 + 150 = ₹ 525
No. of shares = \(\frac { 525 }{ 7.5 }\) = 70
No. of extra share = 70 – 50 = 20

Question 18.
Salman invests a sum of money in ₹ 50 shares, paying 15% dividend quoted at 20% premium. If his annual dividend is ₹ 600, calculate:
(i) the number of shares he bought
(ii) his total investment
(iii) the rate of return on his investment. (2014)
Solution:
Nominal value = ₹ 50

Question 19.
Rohit invested ₹ 9,600 on ₹ 100 shares at ₹ 20 premium paying 8% dividend. Rohit sold the shares when the price rose to ₹ 160. He invested the proceeds (excluding dividend) in 10% ₹ 50 shares at ₹ 40. Find the :
(i) original number of shares.
(ii) sale proceeds.
(iii) new number of shares.
(iv) change in the two dividends. (2015)
Solution:
Investment by Rohit = ₹ 9600
Rate of dividend = 8% on 100 shares at ₹ 20 premium
Market value = ₹ 100 + ₹ 20 = ₹ 120

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B

 

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C

Question 1.
A man buys 75, Rs. 100 shares paying 9 per cent dividend. He buys shares at such a price that he gets 12 per cent of his money. At what price did he buy the shares?
Solution:
No. of shares = 75
Value of each share = Rs. 100
Rate of dividend = 9%
Let the market value of each share = x
Thus. 12% of x = 9% of 100

Market value of each share = Rs. 75

Question 2.
By purchasing Rs. 25 gas shares for Rs. 40 each, a man gets 4 per cent profit on his investment. What rate per cent is the company paying ? What is his dividend if he buys 60 shares?
Solution:
Face value of each share = Rs. 25
Market value of each share = Rs. 40
Profit = 4% of his investment
Let the rate of dividend = x %

Question 3.
Hundred rupee shares of a company are available in the market at a premium of Rs. 20. Find the rate of dividend given by the company, when a man’s return on his investment is 15 percent.
Solution:
Face value of each share = Rs. 100
Market value of each share = Rs. 120
Total dividend = 15% on his investment
Let the rate of dividend = x %
Then x % of 100 = 15 % of 120

x = 18%
Rate of dividend = 18%

Question 4.
Rs. 50 shares of a company are quoted at a discount of 10%. Find the rate of dividend given by the company, the return on the investment on these shares being 20 percent.
Solution:
Face value of each share = Rs. 50

Rate of dividend = 18%

Question 5.
A company declares 8 per cent dividend to the share holders. If a man receives Rs. 2,840 as his dividend, find the nominal value of his shares.
Solution:
Rate of dividend = 8%
Total dividend = Rs. 2.840
Let Nominal value of shares = x
Then 8% of x = Rs. 2840

Nominal value of his shares = Rs. 35,500

Question 6.
How much should a man invest in Rs. 100 shares selling at Rs. 110 to obtain an annual income of Rs. 1,680, if the dividend declared is 12% ?
Solution:
Face value of each share = Rs. 100
Market value of each share = Rs. 110
Total annual income = Rs. 1,680.
Rate of dividend = 12%
Let total amount of shares = x
Then x x 12% = 1,680

Question 7.
A company declares a dividend of 11.2% to all its share-holders. If its Rs. 60 share is available in the market at a premium of 25%, how much should Rakesh invest in buying the shares of this company in order to have an annual income of Rs. 1,680 ?
Solution:
Face value of each share = Rs. 60
Market value = Rs. 60 x \(\frac { 125 }{ 100 }\) = Rs. 75
Rate of dividend = 11.2%
Annual income = Rs. 1,680
Let the face value of shares = x
Dividend = x x 11.2%
x x 11.2% = 1680

Question 8.
A man buys 400, twenty rupee shares at a premium of Rs. 4 each and receives a dividend of 12%. Find :
(i) the amount invested by him.
(ii) his total income from the shares.
(iii) percentage return on his money.
Solution:
No. of shares = 400
Face value of one share = Rs. 20
Market value of one share = Rs. 20 + 4 = Rs. 24
Rate of dividend = 12%
(i) Amount invested by the man = Rs. 24 x 400 = Rs. 9600

Question 9.
A man buys 400, twenty-rupee shares at a discount of 20% and receives a return of 12% on his money. Calculate
(i) the amount invested by him.
(ii) the rate of dividend paid by the company.
Solution:
No. of shares = 400
Face value of one share = Rs. 20
Market value of one share = Rs. 20 x \(\frac { 80 }{ 100 }\) = Rs. 16
Amount of shares = Rs. 20 x 400 = Rs. 8,000
(i) Amount invested = Rs. 16 x 400 = Rs. 6,400
(ii) Total dividend = Rs. 6,400 x \(\frac { 12 }{ 100 }\) = Rs. 768
Rate of dividend = \(\frac { 768 x 100 }{ 8000 }\)= 9.6 %

Question 10.
A company with 10,000 shares of Rs. 100 each, declares an annual dividend of 5%.
(i) What is the total amount of dividend paid by the company ?
(ii) What should be the annual income of a man who has 72 shares, in the company ?
(iii) If he received only 4% of his investment, find the price he paid for each share.
Solution:
No. of shares = 10000
Face value of each share = 100
Rate of dividend = 5%
Amount of shares = Rs. 100 x 10,000 = Rs. 10,00,000

Question 11.
A lady holds 1800, Rs. 100 shares of a company that pays 15 % dividend annually. Calculate her annual dividend. If she had bought these shares at 40% premium, what is the return she gets as percent on her investment. Give your answer to the nearest integer.
Solution:
No. of shares = 1800
Face value of each share = Rs. 100
Rate of dividend = 15 %
Market value of each share Rs. 140
Total value of shares = Rs. 1800 x 100 = Rs. 1,80,000

Question 12.
A man invests Rs. 11,200 in a company paying 6 percent per annum when its Rs. 100 shares can be bought for Rs. 140 find:
(i) his annual dividend.
(ii) his percentage return on his investment.
Solution:
Investment = Rs. 11,200
Rate of dividend = 6%
Market value of a share = Rs. 140
No. of shares = Rs. 11,200 ÷ Rs. 140 = 80
Face value of 80 shares = 80 x Rs. 100 = Rs. 8,000

Question 13.
Mr. Sharma has 60 shares of N.V. ₹ 100 and sells them when they are at a premium of 60%. He invests the proceeds in shares of nominal value ₹ 50, quoted at 4% discount, and paying 18% dividend annually. Calculate:
(i) the sale proceeds ;
(ii) the number of shares he buys and
(iii) his annual dividend from the shares.
Solution:
(i) No. of shares = 60
Face value of each share = Rs. 100
Total amount = Rs. 100 x 60 = Rs. 6,000
Market value = Rs. 160
His sale proceed = Rs. 160 x 60 = Rs. 9,600
(ii) In second case :
Nominal value of each share = Rs.50
and Market value = Rs. 50 x \(\frac { 96 }{ 100 }\) = Rs. 48
Rate of dividend = 18%
No. of shares he purchased = \(\frac { 9600 }{ 48 }\) = 200
(iii) Face value of 200 shares = 200 x Rs. 50 = Rs. 10,000
Dividend = Rs. 10000 x \(\frac { 18 }{ 100 }\) = Rs. 1,800

Question 14.
A company with 10,000 shares of nominal value ₹ 100 declares an annual dividend of 8% to shareholders.
(i) Calculate the total amount of dividend paid by the company.
(ii) Ramesh had bought 90 shares of the company at ₹ 150 per share. Calculate the dividend he receives and the percentage of return on his investment.
Solution:
(i) No. of shares = 10,000
Nominal value of each share = Rs. 100
Dividend = 8%
Total face value of 10,000 shares = Rs. 100 x 10,000 = Rs. 10,00,000
and amount of dividend = Rs. \(\frac { 1000000 x 8 }{ 100 }\) = Rs. 8000
(ii) In second case :
Ramesh bought = 90 shares
Market value of each share = Rs. 150
His investment = Rs. 150 x 90 = Rs. 13,500
Face value of 90 shares = Rs. 100 x 90 = Rs. 9,000

Question 15.
Which is the better investment:
16% Rs. 100 shares at 80 or 20% Rs. 100 shares at 120 ?
Solution:
In first case :
Income on Rs. 80 = Rs. 16

From above, it is clear that first investment is better.

Question 16.
A man has a choice to invest in hundred rupee shares of two firms at Rs. 120 or at Rs. 132. The first firm pays r. dividend of 5% per annum and the second firm pays a dividend of 6% per annum. Find :
(i) Which company is giving a better return.
(ii) If a man invests Rs. 26,400 with each firm, how much will be the difference between the annual returns from the two firms.
Solution:
In first case :
Market value of share = Rs. 120
and dividend = 5%
Income on Rs. 120 = Rs. 5

= Rs. 1,200
Difference = Rs. 1,200 – Rs. 1,100 = Rs. 100

Question 17.
A man bought 360, ten rupee shares of a company paying 12 percent per annum. He sold the shares when their price rose to Rs. 21 per share and invested the proceeds in five rupee shares paying 4.5 per cent per annum at Rs 3.50 per share. Find the annual change in his income.
Solution:
No. of shares bought = 360
Face value of each share = Rs. 10
Dividend = 12%
Cost price of 360 shares = Rs. 360 x 10 = Rs. 3,600
Market value = Rs. 21
Selling price = Rs. 21 x 360 = Rs. 7,560
In second case :
Face value of each share = Rs. 5
Market value of each share = Rs. 3.5

Difference in his income = Rs. 486 Rs. 432 = Rs. 54

Question 18.
A man sold 400 (Rs. 20) shares of a company paying 5% at Rs. 18 and invested the proceeds in (Rs. 10) shares of another company paying 7% at Rs. 12. How many (Rs. 10) shares did he buy and what was the change in his income?
Solution:
In first case :
No. of shares sold = 400
Face value of each share = Rs. 20
Market value = Rs. 18
Income = 5%
Amount of his investment = Rs. 18 x 400 = Rs. 7,200
and amount of shares = Rs. 20 x 400 = Rs. 8000
In second case :
Market value of each share = Rs. 12
Face value of each share = Rs. 10
Rate of dividend = 7%
No. of shares purchased = \(\frac { 7200 }{ 12 }\) = 600
Face value of 600 shares = Rs. 10 x 600 = Rs. 6,000
Now, income in first case = Rs. 8000 x \(\frac { 5 }{ 100 }\) = Rs. 400
and income in second case = Rs. 6000 x \(\frac { 7 }{ 100 }\) = Rs. 420
Increase in income = Rs. 420 – 400 = Rs. 20

Question 19.
Two brothers A and B invest Rs. 16,000 each in buying shares of two companies. A buys 3% hundred-rupee shares at 80 and B buys ten rupee shares at par. If they both receive equal dividend at the end of the year, find the rate percent of the dividend received by B.
Solution:
A’s investment = Rs. 16,000
Face value of each share = Rs. 100
Market value of each share = Rs. 80
and rate of dividend = 3%
No. of shares purchased = \(\frac { 16000 }{ 80 }\) = 200
Amount of shares = 200 x Rs. 100 = Rs. 20,000
and amount of dividend = 20,000 x \(\frac { 3 }{ 100 }\) = Rs. 600
B’s investment = Rs. 16,000
Face value of each share = Rs. 10
and amount of dividend = Rs. 600
Rate of dividend = \(\frac { 600 }{ 16000 }\) x 100 = 3.75 %

Question 20.
A man invests Rs. 20,020 in buying shares of nominal value Rs. 26 at 10% premium. The dividend on the shares is 15% per annum Calculate :
(i) The number of shares he buys.
(ii) The dividend he receives annually.
(iii) The rate of interest he gets on his money [2003]
Solution:
Total investment = Rs. 20,020
Nominal value of each share = Rs. 26.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 25 Probability Ex 25C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C

Question 1.
A bag contains 3 red balls, 4 blue balls and one yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it : find the probability that die ball is :
(i) yellow
(ii) red
(iii) not yellow
(iv) neither,yellow nor red
Solution:
In a bag. there are 8 balls in which there are Red balls = 3
blue balls = 4
and yellow ball = 1
Total possible out come = 8
(i) Yellow balls = 1
∴ Number of favourable outcome = 1

(ii) Red balls = 3

(iii) Not yellow balls = 3+4 = 7
∴ Number of favourable outcome = 8

(iv) Neither yellow nor red can be blue ball.
∴ Number of favourable outcome = 4

Question 2.
A dice is thrown once. What is the probability of getting a number :
(i) greater than 2 ?
(iii) less than or equal to 2 ?
Solution:
A die is thrown once
Numbers marked on the faces of a die are 1, 2,3,4, 5, 6
∴ Number of possible outcome = 6
(i) Greater than 2 number = 3, 4, 5, 6 = 4 numbers

(ii) Less than or equal to 2 are 2, 1 which are 2 in numbers.

Question 3.
From a well-shuffled deck of 52 cards* one card is drawn. Find the probability that the card drawn is :
(i) a face card.
(ii) not a face card. ,
(iii) a queen of black colour.
(iv) a card with number 5 or 6.
(v) a card with number less than 8.
(vi) a card with number between 2 and 9.
Solution:
A deck of playing cards has 52 cards
∴ Number of possible outcome = 52
(i) A face card ; face cards in the deck are = 3 x 4 = 12
∴ Number of favourable outcome = 12

(ii) Not a face card which are 52 – 12 = 40
∴ Number of favourable outcome = 40

(iii) A queen of black color which are 2 in numbers in the deck
∴ Number of favourable outcome = 2

(iv) A card with number 5 or 6 are 2 x 4 numbers
∴ Number of favourable outcome = 8

(v) A card with number less than 8 which can be 2, 3, 4, 5, 6, 7 = 6

(vi) A card with number between 2 and 9 can be 3, 4, 5, 6, 7, 8 = 6
∴ Number of favourable outcome = 6

Question 4.
In a match between A and B.
(i) the probability of winning of A is 0.83. What is the probability of winning of B ?
(ii) the probability of losing the match is 0.49 for
B. What is the probability of winning of A?
Solution:
A match is played between two persons A and B
∴ Number of possible outcome = 1
(i) The probability of winning of A is 0.83
∴ Probability of winning of B = 1 – 0.83 = 0.17 [∵ P(E) + P(\(\bar { E }\) )=1]
(ii) The probability of losing the match is 0.49 by B.
∴ Probability of losing of B or winning of A = 0.49

Question 5.
A and B are friends. Ignoring the leap year, find the probability that both friends will have :
(i) different birthdays ?
(ii) the same birthdays ? (Ignore a leap year)
Solution:
Number of days in a year = 365
and birthday of a person can be on one day only.
(i) Different birthdays can be 365 – 1 = 364

Question 6.
A man tosses two different coins (one of Rs. 2 and another of Rs. 5) simultaneously. What is the probability that he gets :
(i) at least one head ?
(ii) at most one head?
Solution:
There are two coins : one of two rupees and
other is of 5-rupees
∴ Number of Heads =1 + 1=2
and number of tails are 2 i.e., 2 and 5
∴ Number of possible outcome = 2 x 2 = 4
(i) Atleast one head.
Number of favourable outcome = 3

(ii) At the most one head = 3

Question 7.
A box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is :
(i) white
(ii) neither red nor white
Solution:
Number of balls in a box are 20 in which 7 are red, 8 are green and 5 are white
∴ Number of possible outcome = 20
(i) White = 5
∴ Number of favourable outcome = 5

(ii) Neither red not white
i.e., all the green which are 8

Question 8.
All the three face cards of spades are removed from a well-shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting :
(i) a black face card
(ii) a queen
(iii) a black card.
Solution:
A deck of playing cards = 52
Cards which are removed = 3 (3 face cards of spades)
Balance cards in the deck = 52 – 3 = 49
(i) A black face card which are 6 – 3 = 3 in number
∴ Number of favourable outcome = 3

(ii) A queen : In the deck there are 4 – 1 = 3 queen

(iii) A black cards : which are 26 – 3 = 23 cards in number

Question 9.
In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start.
What is the probability that the music will stop within the first 15 seconds ?
Solution:
Total time for the musical race = 0 to 40 seconds = 40 seconds.
Time taken by a player =15 seconds. (0 to 15 seconds)

Question 10.
In a bundle of 50 shirts, 44 are good, 4 have minor defects and 2 have major defects. What is the probability that :
(i) it is acceptable to a trader who accepts only a good shirt ?
(ii) it is acceptable to a trader who rejects only a shirt with major defects ?
Solution:
Total number of shirts in a bundle = 50
No. of good shirts = 44
Minor defected = 4
Major defected = 2
∴ Number of possible outcome = 50
(i) Acceptance of only for a good shirt = 44

(ii) Rejecting of totally defected shirts, number of remaining shirts = 44 + 4 = 48

Question 11.
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is :
(i) 8
(ii) 13
(iii) less than or equal to 12
Solution:
Two dice are thrown at the same time and each dice has 6 numbers 1, 2, 3, 4, 5, 6 on its faces
∴Number of possible outcome = 6 x 6 = 36
(i) Sum of two numbers on the top is 8 i.e..(2, 6), (3, 5), (4,4), (5, 3), (6, 2)
∴ Number of favourable outcome = 5

(ii) Sum of two number on the top is 13.
At the most, then sum can be (6, 6) = 12
∴ number of favourable outcome = 0
∴ P(E) = 0
(iii) Sum is less than or equal to 12 i.e.(1, 1), (1,2), (1,3), (1,4), (1,5), (1,6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3). (3, 4), (3. 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5,
6) , (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) = 36
∴ Number of favourable outcome = 36

Question 12.
Which of the following cannot be the probability of an event ?
(i) \(\frac { 3 }{ 7 }\)
(ii) 0.82
(iii) 37%
(iv) -2.4
Solution:
(i) ∵ \(\frac { 3 }{ 7 }\) is between 0 and 1
∴ It is a probability event
(ii) ∵ 0.82 is between 0 and 1
∴ It is a probability event.
(iii) 37% = \(\frac { 37 }{ 100 }\)
∵It is between 0 and 1
∴ It is a probability event.
(iv) -2.4
∵It is less than 0.
∴ It is not a probability event.

Question 13.
If P(E) = 0.59; find P(not E).
Solution:
P(E) = 0.59
But P(E) + P(\(\bar { E }\) )= 1
or P(E) + P(not E) = 1
⇒ 0.59 + P(not E) = 1
⇒ ∴ P(not E) = 1 – 0.59 = 0.41

Question 14.
A bag contains a certain number of red balls. A ball is drawn. Find the probability that the ball drawn is :
(i) black
(ii) red.
Solution:
In a bag, there are certain number red balls. Let it be x balls.
One ball is drawn out
(i) A black
∵ There is no black ball in the bag
∴ Probability of black ball = 0
(ii) A red ball

Question 15.
The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday ?
Solution:
Probability of two boys do not have the same birthday [P (E)] = 0.897
Let Probability of those boys having the same birthday = P(not E)
= P(\(\bar { E }\) )
But P(E) + P(\(\bar { E }\) )= 1
⇒ 0.897 +P(\(\bar { E }\) ) = 1
⇒P(\(\bar { E }\) )= 1 -0.897 = 0.103
Hence probability having the same birthday = 0.103

Question 16.
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability tharthe ball drawn will be :
(i) not red ?
(ii) neither red nor green ?
(iii) white or green ?
Solution:
In a bag, there are 10 red balls, 16 white and 8 green balls
∴ Total balls =10 + 16 + 8= 34 ball
∴ Number of possible outcome = 34
(i) Not red ball
Number of favourable outcome = 16 + 8 = 24

(ii) Neither red nor green
∴ Number of outcome = 34 – (10 + 8)
= 34-18=16

(iii) White or green
∴ Number of outcome = 16 + 8 = 24

Question 17.
A bag contains twenty Rs. 5 coins, fifty Rs. 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin :
(i) will be a Re 1 coin ?
(ii) will not be a Rs. 2 coin ?
(iii) will neither be a Rs. 5 coin nor be a Re 1 coin ?
Solution:
In a bag, there are
5-rupee coins = 20
2-rupee coins = 50
1-rupee coin =30
Total number of coins in the bag = 20 + 50 + 30 = 100
∴ Number of possible outcome =100
(i) one-rupee coin = 30

(ii) When there is no 2-rupee coins
∴ Number of coins = 20 + 30 = 50

(iii) Neither be Rs. 5 coins nor be Re-one coin = 100 – (20 + 30) = 100 – 50 = 50

Question 18.
A game consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.

If the outcomes are equally likely, find the probability that the pointer will point at :
(i) 6
(ii) an eve., number.
(iii) a prime number.
(iv) a number greater than 8.
(v) a number less than or equal to 9.
(vi) a number between 3 and 11.
Solution:
There are 12 numbers on the spinning game.
∴ Number of possible outcome = 12
(i) 6 which is one

(ii) an even number which are 6 i.e. 2, 4, 6, 8, 10, 12

(iii) A prime number which are 2, 3, 5, 7, 11 and 5 in number

(iv) A number greater than 8 are 9, 10, 11, 12
which are 4 in number.

(v) A number less than or equal to 9 are
1, 2, 3, 4, 5, 6, 7, 8, 9 which are 9 in number

(vi) A number between 3 and 11 are 4, 5, 6, 7, 8, 9, 10 which are 7 in number

Question 19.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting :
(i) a queen of red colour.
(ii) a black face card.
(iii) the jack or the queen of hearts.
(iv) a diamond.
(v) a diamond or a spade.
Solution:
Number of cards in a deck of playing card = 52
∴ Number of possible outcome = 52
(i) A queen of red colour
Number of favourable outcome = 2
(As there are 2 red queens in the deck)

(ii) A black face card.
There are 3 + 3 = 6 black face cards in the deck.

(iii) The jack or the queen of hearts which are two in numbers

(iv) A diamond.
There are 13 cards of diamond in the deck.

(v) A diamond or a spade.
There are 13 cards of diamond and 13 cards of spade in the deck
∴ Number of favourable outcome = 13 + 13 = 26

Question 20.
From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is :
(i) a black card.
(ii) 8 of red color.
(iii) a king of black color.
Solution:
Number of cards is a deck of playing card = 52
All face cards are removed. Which are 3 x 4 = 12
(i) A black card which are 10 in numbers

(ii) 8 of red colors

(iii) A king of black color.
∵ In the deck of playing cards, face cards are removed
∴ There is no face cards.
∴ P(E) = 0.

Question 21.
Seven cards : – the eight, the nine, the ten, jack, queen, king and ace of diamonds are well shuffled. One card is then picked up at random.
(i) What is the probability that the card drawn is the eight or the king ?
(ii) If the king is drawn and put aside, what is the probability that the second card picked up is
(a) an ace ?
(b) a king ?
Solution:
There are 7 cards which are the eight, the nine, the ten, the jack, the’ queen, the king and the ace of diamond.
∴ Number of possible outcome = 7
(i) card having the eight or a king which are 2.

(ii) If king is drawn, then number of remaining playing cards = 7-1=6
(a) An ace.

(b) A king
There is no card of king
∴ P(E) = 0

Question 22.
A box contains 150 bulbs out of which 15 are defective. It is not possible to just look at a bulb and tell whether or not it is defective. One bulb is taken out at random from this box. Calculate the probability that the bulb taken out is :
(i) a good one
(ii) a defective one.
Solution:
Number of bulbs in a box = 150
No. of defective bulbs = 15
∴ No of good bulbs = 150 – 15 = 135
∴ Number of possible outcome = 150
(i) A good bulb and number of good bulbs =135

(ii) A defective bulb. Number of defective bulb = 15

Question 23.
(i) 4 defective pens are accidentally mixed with 16 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is drawn at random from the lot. What is the probability that the pen is defective ? (ii) Suppose the pen drawn in (i) is defective and is not replaced. Now one more pen is drawn at random from the rest. What is the probability that this pen is :
(a) defective
(b) not defective ?
Solution:
Number of defective pens = 4
(i) and number of good pens = 16
∴ Total pens = 4 + 16 = 20
∴ Number of possible outcome = 20
One defective pen, no. of defective pens = 4

(ii) One defective pen is drawn
∴ Remaining pens = 20 – 1 = 19
(a) Defective one
Number of remaining defective pens =4-1=3

(b) Not defective, number of good pens =16

Question 24.
A bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears :
(i) a perfect square number.
(ii) a number divisible by 4.
(iii) a number divisible by 5.
(iv) a number divisible by 4 or 5.
(v) a number divisible by 4 and 5.
Solution:
Total number of stones = 100
On which numbers 1 to 100 are marked
∴ Number of possible outcome = 100
(i) A perfect square = which are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 which are 10 inmumbers

(ii) A number divisible by 4 are 4, 8, 12, 16, …, 96, 100 which one 25 in numbers

(iii) A number divisible by 5, are 5, 10, 15, 20, ….., 95, 100 which are 20 in numbers,

(iv) A number divisible by 4 or 5 are 4, 5, 8, 10,12, 15, 16, 20, 24, 25, 28, 30, 32, 35, 36, 40, 96,95, 100 which are 40 in numbers

(v) A number divisible by 4 and 5 are 20, 40, 60, 80 and 100 which are 5 in numbers

Question 25.
A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on table top and a die, very small in size, is dropped on the rectangular paper without seeing towards it. If the die falls and lands on the paper only, find the probability that it will fall and land :
(i) inside the circle.
(ii) outside the circle.
Solution:
Diameter of the circle = 20 cm
Length of rectangular paper = 40 cm
and width = 30 cm
Area of rectangle = 40 x 30 = 1200 cm2
∴ Number of possible out come = 1200

Question 26.
Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the upper-most faces of two dice is :
(i) 4 or 5
(ii) 7, 8 or 9.
(iii) between 5 and 8
(iv) more than 10
(v) less than 6
Solution:
Two dice having numbers 1 to 6 are rolled together.
∴ Number of possible outcome = 6 x 6 = 36
(i) If sum is 4 or 5 of numbers on the upper most face,
Their number of favourable outcome = (1,3), (2, 2), (3, 1), (1, 4), (2, 3), (3, 2), (4, 1) which are 7 in numbers

(ii) If sum of number on the upper faces by 7, 8 or 9, then these can be (1, 6), (2, 6), (3, 6), (4, 3), (5. 2). (6, 1). (4, 3), (2, 5), (3, 4), (4, 4), (5, 3), (5, 4), (6, 2), (6, 3), (4, 5) which are total 15 in numbers.

(iii) Sum is between 5 and 8.
i.e. sum is 6 or 7.
These can be.
(1, 5), (2, 5), (1, 6), (5, 1), (5, 2), (6, 1), (3, 3), (3, 4), (4, 3), (2, 4), (4, 2) which are 11 in number.
∴ Number of favourable outcome = 11

(iv) If sum is more than 10, then these can be (5. 6), (6, 5), (6, 6) which are 3 in number

(v) If sum is less than 6, then there can be (1, 2), (2, 1), (1, 3), (3, 1), (4, 1), (1, 4), (2, 3), (3, 2), (2, 4), (4, 2)

Question 27.
Three coins are tossed together. Write all the possible outcomes. Now, find the probability of getting :
(i) exactly two heads.
(ii) at least two heads.
(iii) atmost two heads.
(iv) all tails.
(v) at least one tail.
Solution:
3 coins one tossed together.
∴ Number of possible outcome = 23 = 2 x 2 x 2 = 8
i.e. HHH, HHT, HTH, HTT, TTT, THH, THT, TTH
(i) exactly two heads these can be HHT, THH, HTH = 3 in numbers

(ii) At least two heads : These can be HHH,HHT, HTH, THH = 4 in numbers

(iii) Atmost two heads : These can be THH, HHT, HTH, HTT, THT, TTH, TTT which is 7 in numbers.

(iv) All tails : There can be TTT i. e., only one

(v) At least one tail : There can be HHT, HTH, HTT, TTT, THH, THT, TTH = 7 in number

Question 28.
Two dice are thrown simultaneously. What is the probability that :
(i) 4 will not come up either time ?
(ii) 4 will come up at least once ?
Solution:
Two dice are thrown simultaneous,
and each dice has 1-6 numbers on its faces
∴ Number of possible outcome = 6 x 6 = 36
(i) 4 will not come up either time
∴ Number of favourable outcomes = (6 – 1)² = (5)² = 25

(ii) 4 will come up at least once
∴ These can be (1, 4), (2, 4), (3, 4), (4, 4), (4, 5),(4, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6)
∴ Number of favourable outcome =11

Question 29.
Cards marked with numbers 1, 2, 3, 4, …,20 are well shuffled and a card is drawn at random. What is the probability that the number on the card is
(i) a prime number
(ii) divisible by 3
(iii) a perfect square ?
Solution:

Question 30.
Offices in Delhi are open for five days in a week (Monday to Friday). Two employees of an office remain absent for one day in the same particular week. Find the probability that they remain absent on :
(i) the same day
(ii) consecutive day
(iii) different days.
Solution:
∵ Office are open for 5 days a week
∴ Number of possible outcomes for 2 employees = 5 x 5 = 25
Let the five days of working be denoted by M, T, W, Th, F for Mondays, Tuesday, Wednesday Thursday and Friday respectively
(i) On Same day.
Favourable outcome will be M;T;T;M;T;W;W;T;W;H; TH.W ; TH ; F and F, TH which are 8 in all

(iii) Absent on different days : Then = 1- P(absent on the same day)
= 1 – \(\frac { 1 }{ 5 }\)= \(\frac { 4 }{ 5 }\) [from (i)]
∵ P(E) + P(not E) = 1

Question 31.
A box contains some black balls and 30 white balls. If the probability of drawing a black ball is two-fifths of white ball; find the number of black balls in the box.
Solution:
In a box, some balls are black while 30 balls are white
Let number of black balls = x
Then number of possible outcome = x + 30
Probability of drawing a black ball = \(\frac { 2 }{ 5 }\) of a white balls.
Now, In case of black ball,


Either x + 30 = 0, then x = -30 which is not possible
or x – 12 = 0, then x = 12
Hence number of black balls = 12

Question 32.
From a pack of 52 playing cards all cards whose numbers are multiples of 3 are removed. A card is now drawn at random.
What is the probability that the card drawn is
(i) a face card (King, Jack or Queen)
(ii) an even numbered red card ? (2011)
Solution:
No. of total cards = 52 cards removed of 4 colors = 3, 6, 9, 12 = 4 x 4 = 16
Remain using cards = 52 – 16 = 36
(i) No. of faces cards = 2 x 4 = 8 cards (excluding queen)
∴ Probebility P(E) = \(\frac { 8 }{ 36 }\) = \(\frac { 2 }{ 9 }\)
(ii) An even number red cards = 2, 4, 8, 10 = 4×2 = 8 cards
∴ Probebility P(E) = \(\frac { 8 }{ 36 }\) = \(\frac { 2 }{ 9 }\)

Question 33.
A die has 6 faces marked by the given numbers as shown below:

The die is thrown once. What is the probability of getting
(i) a positive integer.
(ii) an integer greater than -3.
(iii) the smallest integer.
Solution:
Total outcomes n(S)= 6
(i) a positive integer = (1, 2, 3)
No. of favourables n(E) = 3

Question 34.
A bag contains 5 white balls, 6 red balls and 9 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is :
(i) a green ball.
(ii) a white or a red ball.
(iii) neither a green ball nor a white ball. (2015)
Solution:
A bag contains 5 white balls, 6 red balls and 9 green balls.
∴ Total number of balls = 5 + 6 + 9 = 20 balls
One ball is drawn at random.
(i) Probability of a green ball = \(\frac { 9 }{ 20 }\)
(ii) Probability of a white or a red ball = \(\frac { 5 + 6 }{ 20 }\) = \(\frac { 11 }{ 20 }\)
(iii) Probability of neither a green ball nor a white ball = \(\frac { 6 }{ 20 }\) = \(\frac { 3 }{ 10 }\) (Only red balls )

Question 35.
A game of numbers has cards marked with 11, 12, 13, , 40. A card is drawn at random. Find the probability that the number on the card drawn is :
(i) A perfect square
(ii) Divisible by 7
Solution:
(i) The perfect squares lying between 11 and 40 and 16, 25 and 36.
So the number of possible outcomes is 3.
Total number of cards from 11 to 40 is 40 – 11 + 1 = 30
Probability that the number on the card drawn is a perfect square

So, the probability that the number on the
card drawn is a perfect square is \(\frac { 1 }{ 10 }\) .
(ii) The numbers lfom 11 to 40 that are divisible by 7 are 14, 21, 28 and 35.
So the number of possible outcomes is 4. Total number of cards from 11 to 40 is 30.
Probability that the number on the card drawn is divisible by 7

So, the probability that the number on the card drawn is divisible by 7 is \(\frac { 2 }{ 15 }\).

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

 

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Question 1.
Solve each of the following equations, using the formula:
Solution:

Question 2.
Solve each of the following equations for x and give, in each case, your answer correct to one decimal place :
(i) x² – 8x + 5 = 0
(ii) 5x² + 10x – 3 = 0
Solution:

Question 3.
Solve each of the following equations for x and give, in each case, your answer correct to 2 decimal places :
(i) 2x² – 10x + 5 = 0
(ii) 4x² + \(\frac { 6 }{ x }\) + 13 = 0
(iii) x² – 3x – 9 = 0 [2007]
(iv) x² – 5x – 10 = 0 [2013]
Solution:

Question 4.
Solve each of the following equations for x, giving your answer correct to 3 decimal places:
(i) 3x² – 12x – 1 = 0
(ii) x² – 16x + 6 = 0
(iii) 2x² + 11x + 4 = 0
Solution:

Question 5.
Solve:
(i) x⁴ – 2x² – 3 = 0
(ii) x⁴ – 10x² + 9 = 0
Solution:

Question 6.
Solve:
(i) (x² – x)² + 5 (x² – x) + 4 = 0
(ii) (x² – 3x)² – 16 (x² – 3x) – 36 = 0
Solution:

Question 7.
Solve :

Solution:

Question 8.
Solve the equation : 2x – \(\frac { 1 }{ x }\) = 7. Write your answer correct to two decimal places.
Solution:

Question 9.
Solve the following equation and give your answer correct to 3 significant figures : 5x² – 3x – 4 = 0
Solution:

Question 10.
Solve for x using the quadratic formula. Write your answer correct to two significant figures, (x – 1)² – 3x + 4 = 0
Solution:

Question 11.
Solve the quadratic equation x² – 3 (x + 3) = 0; Give your answer correct to two significant figures.
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

Question 1.
Describe the locus for questions 1 to 13 given below: 1. The locus of a point at a distance 3 cm from a fixed point.

Solution:
The locus of a point which is 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is called the centre of the circle.

Question 2.
The locus of points at a distance 2 cm from a fixed line.
Solution:
A pair of straight lines 1 and m which are parallel to the given line at a distance of 2 cm, from it is the locus.

Question 3.
The locus of the centre of a wheel of a bicycle going straight along a level road.
Solution:

The locus of the centre of a wheel which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.

Question 4.
The locus of the moving end of the minute hand of a clock.
Solution:

The locus of the moving end of the minute hand of the clock will be a circle where radius will be of the length of the minute hand.

Question 5.
The locus of a stone dropped from the top of a tower.
Solution:

The locus of stone which is dropped from the top of the tower will be a vertical line through the point from which the stone is dropped.

Question 6.
The locus of a runner running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Solution:

The locus of the runner running round a circular track at a distance of 1.5 m from the inner edge will be the circum¬ference of a circle whose radius is equal to the radius of the inner circular track plus 1.5 m

Question 7.
The locus of the door-handle as the door opens.
Solution:

The locus of the door handle will be the circumfer-ence of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.

Question 8.
The locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution:

The locus of the points inside the circle which are equidistant from the fixed points on the circumference of the circle will be the diameter which is perpendicular bisector of the line joining the two fixed points on the circle.

Question 9.
The locus of the centres of all circles passing through two fixed points.
Solution:

The locus of the centre of all the circles which pass through two fixed points will be the perpendicular bisector of the line segment joining the two fixed points which are given.

Question 10.
The locus of vertices of all isosceles triangles having a common base.
Solution:

The locus of vertices of all isosceles triangles have a common base will be the perpendicular bisector of the common base of the triangles.

Question 11.
The locus of a point in space, which is always at a distance of 4 cm from a fixed point.
Solution:
The locus of a point in space is the surface of the sphere whose centre is the fixed point and radius equal to 4 cm.

Question 12.
The locus of a point P, so that:
AB² = AP²+ BP², where A and B are two fixed points.
Solution:


The locus of the point P is the circumference of a circle with AB as diameter and satisfies the condition AB² = AP²+ BP².

Question 13.
The locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC ; (ii) B and D.
Solution:
Locus of the point in a rhombus ABCD which is equidistant from.

Question 14.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly after one second.
Solution:
The locus of all the people on earth’s surface is the circumference of a circle whose radius is 332 m and centre is the point where the gun is fired.

Question 15.
Describe:
(i) The locus of points at distances less than 3 cm from a given point.
(ii) The locus of points at distances greater than 4 cm from a given point.
(iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
(iv) The locus of points at distances greater than or equal to 35 mm from a given point.
(v) The locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
(vi) The locus of the centres of all circles that are tangent to both the arms of a given angle.
(vii) The locus of the mid-points of all chords par-allel to a given chord of a circle.
(viii) The locus of points within a circle that are equidistant from the end points of a given chord.
Solution:
(i) The space inside of the circle whose radius is 3 cm and centre is the fixed point which is given.
(ii) The space outside of the circle whose radius is 4 cm and centre is the fixed point which is given.
(iii) The space inside and circumference of the circle with a raduis of 2.5 cm and centre is the given fixed point.
(iv) The space outside and the circumference of a circle with a radius of 35 mm and centre is the given fixed point.
(v) Circumference of the circle concentric with

the second circle whose radius is equal to the sum of the radii of the two given circles.
(vi) The locus of the centre of all circle whose tan-gents are the arms of a given angle is the bisector of that angle.

(vii) The locus of the mid-points of the chords which are parallel to a given chords is the diameter perpendicular to the given circle.


The locus of points within a circle that are equidistant from the end points of a given chord is a diameter which is perpendicular bisector of the given chord.

Question 16.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
Solution:
Steps of Construction:

Draw a line XY parallel to the base BC from the vertex A.
This line is the locus of vertex A. All the tri-angles which have the base BC and altitude (length) equal to AD.

Question 17.
In the given figure, obtain all the points equidistant from lines m and n ; and 2.5 cm from O.

Solution:

Draw angle bisector PQ and XY of angles formed by the lines m and n. From O, draw arcs with radius 2.5 cm, which intersects the angle bisectors at A, B, C and D respectively.
Hence A, B, C and D are the required points.
P.Q.
By actual drawing obtain the points equidistant from lines m and n ; and 6 cm from a point P, where P is 2 cm above m, m is parallel to – n and m is 6cm above n
Solution:
Steps of construction:

(i) Draw a line n.
(ii) Take a point P on n and draw a perpendicular to n. ,
(iii) Cut off LM = 6 cm and draw a line q, the per pendicu lar bisector of LM
(iv) At M, draw a line n making an angle of 900 at.
(v) Produce LM and take a point P such that PM =2 cm.
(vi) From P, draw are an with 6 cm radius which intersects the line q, (he perpendicular bisector cf LM, atA and B.
A and B are the required points which are equidisant from rn and n and is at a distance of 6 cm from P

Question 18.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is :
(i) always 4 cm from the line AB.
(ii) equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Solution:
Steps of Construction:

(i) Draw a line segment AB equal to 8 cm.
(ii) Draw two parallel lines  ℓ and m to AB at a distance of 4cm

(iii) Draw the perpendicular bisector of AB which intersects the parallel lines  ℓ and m at X and Y respectively then X and Y are the required points.
(iv) Join AX.AY, BX and BY.
The figure so formed is a square as its diago¬nals are equal and intersect at 90°.

Question 19.
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respec¬tively. Draw and describe the locus of a point which is :
(i) equidistant from BA and BC.
(ii) 4 cm from M.
(iii) 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
Solution:
(i) Draw an angle of 60° with AB = BC = 8 cm.
(ii) Draw the angle bisector BX of ∠ABC.

(iii) With centre M and N, draw circles of radius equal to 4 cm, which intersect each other at P. P is the required point.
(iv) Join MP, NP.
BMPN is a rhombus.
∵ MP = PM = BN = PN = 4 cm.

Question 20.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label :
(i) the locus of the centres of all circles which touch AB and AC ;
(ii) the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC.
Solution:

(i) Draw a line segment BC = 4.5 cm
(ii) With centre B and radius 6 cm and with centre C and radius 5 cm, draw arcs which intersects each other at point A
(iii) Join AB and AC.
ABC is a required triangle.
(iv) Draw the angle bisector of ∠BAC.
(v) Draw a lines parallel to AC and AB at a distance of 2 cm. which intersects each other AD at O.
(vi) With centre O and radius 2 cm, draw a circle which touches AB and AC.

Question 21.
Construct a triangle ABC, having given AB = 4.8 cm. AC = 4 cm and ∠A = 75°. Find a point P.
(i) inside the triangle ABC.
(ii) outside the triangle ABC.
equidistant from B and C; and at a distance of 1.2 cm from BC.
Solution:

(i) Draw a line segment AB = 4.8 cm.
(ii) At, A draw a ray AX making an angle of 75°.
(iii) Cut off AC = 4 cm from AX.
(iv) Join BC.
(v) Draw two lines  ℓ and m parallel to BC at a distance of 1.2 cm.
(vi) Draw the perpendicular bisector of BC which intersect  ℓ and m at P and P .
P and P1 are the required points which are in¬side and outside the given triangle ABC.

P.Q.
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Solution:
O is fixed point. P moves along AB; a fixed line. OP is joined and produced it to Q such that OP = PQ, Now we have to prove that locus of P is a line parallel to AB.

Proof:
∵ P moves along AB, and Q moves in such a way that PQ is always equal to OP.
P is the mid-point of OQ.
Now is A OQQ’
P and P’ are the mid-point of OQ and OQ’
AB || OQ’
Locus of Q is a line CD, which is parallel to AB.

Question 22.
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Solution:

Steps of Construction:
(i) Draw a ray BC.
(ii) At B, draw a ray BA making an angle of 75° with BC.
(iii) Draw a line  ℓ parallel to AB at a distance of 2 cm.
(iv) Draw another line m parallel to BC at a distance of 1.5 cm. which intersects m at P.
∴ P is the required point.

Question 23.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Solution:

(i) Draw a line segment AB = 5.6 cm.
(ii) From A and B, as centres and radius 9.2 cm, draw the arcs which intersect each other at C.
(iii) Join CA and CB.
(iv) Draw two lines m and n parallel to BC at a distance of 2 cm each.
(v) Draw the angle bisector of ∠CAB which inter-sects the parallel lines m and n at P and Q respectively.
P and Q are the required points which are equi-distant from AB and AC.
On measuring the distance between P and Q is 4.3 cm.

Question 24.
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
Solution:

(iii) Join CA and CB.
(iv) Draw the perpendicular bisector of BC.
(v) A as centre and radius 4 cm, draw an arc which intersect the perpendicular bisector of BC, at P.
P is the required point which is equidistant from B and C and at a distance of 4 cm from A.

Question 25.
thythtyhRuler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
(ii) Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
(iv) Mark the point Q, in your construction, which would make A QBC equal in area to A ABC, and isosceles.
(v) Measure and record the length of CQ. [1998]
Solution:
(i) Draw a line segument BC = 6 cm.
(ii) At B, draw a ray BX making an angle of 60H and cut off BA = 9 cm.
(iii) Join AC, then A ABC is the given triangle. ..(i)
(iv) Draw perpendicular bisector of BC which
intersects BA in M, then any point on LM, is the equidistant from B and C. ….(ii)

(v) Though A, draw a line m II BC.
(vi) The perpendicular bisector of BC and the par-allel line intersect each other at Q.
(vii) Join QB and QC.
Then A QBC is equal in the area of A ABC and through any point on line m, and bace BC, every triangle is equal in area to the given triangle ABC. Length of CQ, on measuring.

Question 26.
State the locus of a point in a rhombus ABCD, wi.r’ch is equidistant
(i) from AB and AD; (ii) from the vertices A and C.
[1998]
Solution:
In rhombus ABCD, draw the angle bisector of ∠A which meets in C
∴ Join BD, which intersects AC at O.
O is the required locus.
From O, draw OL ⊥ AB and OM ⊥ AD.
In Δ AOL and Δ AOM

∴ O is equidistant from AB and AD.
∵ Diagonal AC and BD bisect each other at O at right angles.
∴ AO = OC
O is equidistant from A and C.

Question 27.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
(i) Plot the points A (1,1), B (5,3) and C (2.7).
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from ABandAC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
[1999]
Solution:

Plot the points A (1, 1), B (5, 3) and C (2, 7) on the graph and join AB, BC and CA.
Draw the perpendicular bisector of AB and angle bisector of ∠A which intersect each other at P. P is the required point,
∵ P lies on the perpendicular bisector of AB.
∴P is equidistant from A and B.
Again,
∵ P lies on the angle bisector of ∠A
∴ P is equidistant’from AB and AC
Now, on measuring the length of PA, it is 5.2 cm
(Approx.)

Question 28.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Biscet ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB. [2001]
Solution:
(i) Draw a line segment AB = 6 cm.
(ii) With centres A and B and radius 4 cm, draw two arcs which intersect each other at C.

(iii) Join CA and CB.
(iv) Draw the angle bisector of ∠C and cut off CP – 5 cm.
(v) A line m is drawn parallel to AB at a distance of 5 cm.
(vi) P as centre and radius 5 cm, draw arcs which
intersect the line m at Q and R.
(vii) Join PQ, PR and AQ.
Q and R are the required points.
P.Q
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC. [1995]
Solution:

(i) Draw a circle with radius = 4 cm and O is the centre.
(ii) Take a point A on it.
(iii) A as centre and radius 6 cm draw an arc which intersects the circle at B.
(iv) Again A as centre and radius 5 cm, draw another arc which intersects the circle at C.
(v) Join AB and AC.
(vi) Draw the perpendicular bisector of AC, which intersects AC at M and meets the circle at E and F. EF is the locus of the points inside the circle which are equidistant from A and C.
(vii) Join AE, AF, CE and CF.
Proof:

Similarly, we can prove that CF = AF Hence EF is the locus of points which are equidistant from A and C.
(ii) Again draw the bisector of ∠A which meets the circle at N.
∴ Locus of points inside the circle which are equidistant from AB and AC is the perpendicular bisector of ∠A.

Question 29.
Plot the points A (2,9), B (-1,3) and C (6,3) on a graph paper. On the same graph paper, draw the locus of point A so that the area of ΔABC remains the same as A moves.
Solution:

Draw axis XOX’ and YOY’ on the graph paper. Plot the points A (2, 9), B (-1,3) and C (6, 3) Join AB, BC and CA which form a ΔABC. From A, draw a line l parallel to BC on x-axis The locus of point A is the line l.
∵ l || BC and triangles on the same base BC and between the same parallel are equal in area.
∴ l is the required locus of point A.

Question 30.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
(i) Complete the rectangle ABCD such that:
(a) P is equidistant from A B and BC.
(b) P is equidistant from C and D.
(ii) Measure and record the length of AB.
(2007)
Solution:
(i) Draw a line segment BC = 5 cm.
(ii) At B, draw a ray making an angle of 45° and cut off BP = 4 cm.
(iii) Join PC.
(iv) v P is equidistant from AB and BC.
∴ P lies on the bisector of ∠ABC.
Now draw a ray BY making an angle of 90°.
P is equidistant from C and D P lies on the perpendicular bisector of CD.

(v) From C, draw CZ ⊥ BC which intersect the perpendicular bisector at Q.
(vi) Cut off QD = CQ and from BP, cut off BA = CD.
(vii) Join AD.
Then ABCD is the required rectangle. Measuring the length of AB, it is 5.7 cm approximately.

Question 31.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown.
(i) Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
(ii) Construct the locus of points at a distance of 3.5 cm from A.
(iii) Construct the locus of points equidistant from AC and BC.
(iv) Mark 2 points X and Y which are at
distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY. (2016)
Solution:
(i) Steps of construction :
(1) Draw BC = 6.5 cm using a ruler.
(2) At B, draw ∠CBP = 60°
From BP, cut off BA = 5 cm.
(3) Join AC to get the required triangle.
(4) With A as a centre and radius equal to 3.5 cm, draw a circle. This circle is the required
locus of points at a distance of 3.5 cm from A.
(5) Draw the bisector of ∠ACB. This bisector is the locus of points equidistant from AC and BC.
(6) The angle bisector drawn above cuts the circle at X and Y. These are the points which are at a distance of 3.5 cm from A and also equidistant from AC and BC. On measuring, the length of XY comes out to be 5.2 cm.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B Heights and Distances Ex 22C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.