Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C
Question 1.
By investing 745,000 in 10% 7100 shares, Sharad gets 73,000 as divided. Find the market value of each share.
Solution:
Total investment = ₹ 45000 at 10% of ₹ 100 shares
and amount of dividend = ₹ 3000
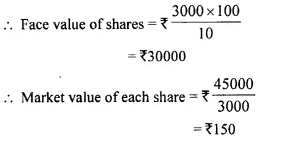
Question 2.
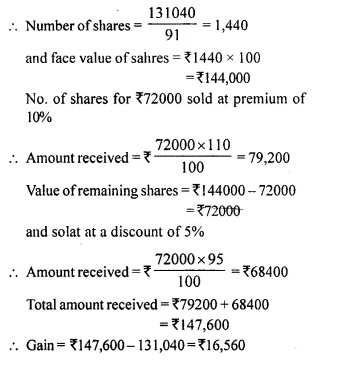
Mrs. Kulkarni invests ₹ 1,31,040 in buying ₹ 100 shares at a discount of 9%. She sells shares worth ₹ 72,000 at a premium of 10% and the rest at a discount of 5%. Find her total gain or loss on the whole.
Solution:
Total investment = ₹ 1,31,040 in ₹ 100 share at discount of 9%
Market value of each share = ₹ 100 – ₹ 9 = ₹ 91
Question 3.
A man invests a certain sum in buying 15% ₹ 100 shares at 20% premium. Find:
(i) his income from one share.
(ii) the number of shares bought to have an income, from the dividend, ₹ 6,480.
(iii) sum invested.
Solution:
Face value of each share = ₹ 100
Market value of each share = ₹ 100 + ₹ 20 = ₹ 120
Rate of dividend = 15%
(i) Income from one share = ₹ 15
(ii) and number of shares when amount of dividend
= \(\frac { 6480 }{ 15 }\) = 432
(iii) and sum invested = ₹ 432 x 120 = ₹ 51,840
Question 4.
Gagan invested 80% of his savings in 10% ₹ 100 shares at 20% premium and the rest of his savings in 20% ₹ 50 shares at 20% discount. If his incomes from these shares is ₹ 5,600, calculate:
(i) his investment in shares on the whole.
(ii) the number of shares of first kind that he bought
(iii) percentage return, on the shares bought, on the whole.
Solution:
(i) Total income = ₹ 5600
Let total investment = ₹ x

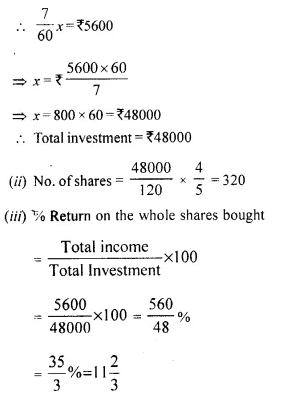
Question 5.
Aishwarya bought 496, ₹ 100 shares at ₹ 132 each. Find:
(i) investment made by her.
(ii) income of Aishwarya from these shares, if the rate of dividend is 7.5%.
(iii) how much extra must Aishwarya invest in order to increase her income by ₹ 7,200?
Solution:
Number of shares = 496
Market value of each share = ₹ 132
(i) Total investment = 496 x 132 = ₹ 65472
(ii) Rate of dividend = 7.5%
Income = 496 x 7.5 = ₹ 3720
(iii) New income (increase in income) = ₹ 7200
Market value of share = ₹ 132
Rate of income = 7.5%
Exit investment
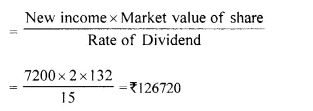
Question 6.
Gopal has some ₹ 100 shares of company A, paying 10% dividend. He sells a certain number of these shares at a discount of 20% and invests the proceeds in ₹ 100 shares at ₹ 60 of company B paying 20% dividend. If his income, from the shares sold, increases by ₹ 18,000, find the number of shares sold by Gopal.
Solution:
Let number of share purchased = x
Face value of these shares = ₹ 100 x x = 100x
dividend = 10%

Question 7.
A man invests a certain sum of money in 6% hundred rupee shares at ₹ 12 premium. When the shares fell to ₹ 96, he sold out all the shares bought and invested the proceed in 10%, ten rupee shares at ₹ 8. If the change in his income is ₹ 540, find the sum invested originally.
Solution:
Let investment = ₹ x
Dividend at the rate of 6% at 12% premium

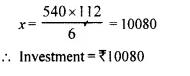
Question 8.
Mr. Gupta has a choice to invest in ten rupee shares of two firms at ₹ 13 or at 716. If the first firm pays 5% dividend and the second firm pays 6% dividend per annum, find:
(i) which firm is paying better ?
(ii) If Mr. Gupta invests equally in both the firms and the difference between the returns from them is ₹ 30, Find how much in all does he invest ?
Solution:
Face value of each share = ₹ 10
Market value of first firm’s share = ₹ 13
and market value of second firm’s share = ₹ 16
Dividend from first firm = 5%
and dividend from second firm = 6%
(i) Let investment in each firm = ₹ 13 x 16
Income from first firm’s shares
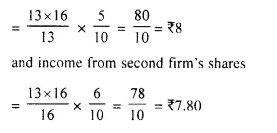
It is clear from the above that first firm’s shares are better.
(ii) Difference in income = ₹ 8.00 – ₹ 7.80 = ₹ 0.20
If difference is ₹ 0.20 then investment in each firm = ₹ 13 x 16
and if difference is ₹ 30, then investment
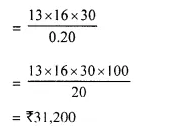
Total investment in both firms = ₹ 31200 x 2 = ₹ 62,400
Question 9.
Ashok invested ₹ 26,400 in 12%, ₹ 25 shares of a company. If he receives a dividend of ₹ 2,475, find the :
(i) number of shares he bought.
(ii) market value of each share.
Solution:
(i) Given,
Investment = ₹ 26400
Rate of dividend = 12%
Dividend earned = ₹ 2475
Face value of one share = ₹ 25
Total dividend earned = No. of shares x Rate of dividend x Face value of one share
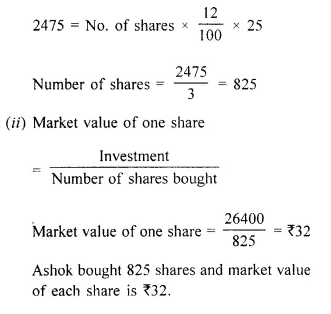
Question 10.
A man invested ₹ 45,000 in 15% ₹ 100 shares quoted at ₹ 125. When the market value of these shares rose to Rs. 140, he sold some shares, just enough to raise ₹ 8,400. calculate :
(i) the number of shares he still holds;
(ii) the dividend due to him on these remaining shares. [2004]
Solution:
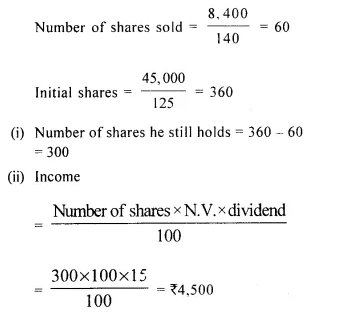
Question 11.
Mr. Tiwari invested ₹ 29,040 in 15% ₹100 shares quoted at a premium of 20%. Calculate :
(i) the number of shares bought by Mr. Tiwari.
(ii) Mr. Tiwari’s income from the investment.
(iii) the percentage return on his investment.
Solution:
Mr. Tiwari’s investment = ₹ 29040
Face value of each share = ₹ 100
Market value of each share = ₹ 100 + ₹ 20 = ₹ 120
Rate of income = 15%
(i) Number of shares purchased

Question 12.
A dividend of 12% was declared on ₹ 150 shares selling at a certain price. If the rate of return is 10%, calculate :
(i) the market value of the shares.
(ii) the amount to be invested to obtain an annual dividend of ₹ 1,350.
Solution:
Let market value of each share = x
Rate of return on investment = 10%
Face value of each share = ₹ 150
Dividend rate = 12%
(i) Now, rate of return x market value = Rate of dividend x Face value
⇒ 10 x x = 12 x 150
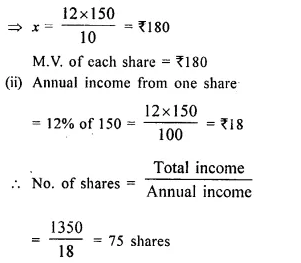
Amount of investment in ₹ 5 shares = ₹ 5 x ₹ 180 = ₹ 13500
Question 13.
Divide ₹ 50,760 into two parts such that if one part is invested in 8% ₹ 100 shares at 8% discount and the other in 9% ₹ 100 shares at 8% premium, the annual incomes from both the investments are equal.
Solution:
Total investment = ₹ 50,760
Let first part of investment = x
Then second part = ₹ 50,760 – x
Rate of dividend in first part = 8% ₹100 at discount = 8%
M.V. of each share = ₹ 100 – 8 = ₹ 92
Rate of dividend second part = 9% ₹ 100 at premium = 8%
M.V. of each share = 100 + 8 = ₹ 108
But annual income from both part is same

Question 14.
Mr. Shameem invested 33\(\frac { 1 }{ 3 }\) % of his savings in 20% ₹ 50 shares quoted at ₹ 60 and the remainder of the savings in 10% ₹ 100 shares quoted at ₹ 110. If his total income from these investments is ₹ 9,200 ; find :
(i) his total savings
(ii) the number of ₹ 50 shares.
(iii) the number of ₹ 100 shares.
Solution:
Let total investment = x


Question 15.
Vivek invests ₹ 4500 in 8% ₹ 10 shares at ₹ 15. He sells the shares when the price rises to ₹ 30, and invests the proceeds in 12% ₹ 100 shares at ₹ 125. Calculate,
(i) the sale proceeds
(ii) the number of ₹ 125 shares he buys.
(iii) the change in his annual income from dividend.
Solution:
(i) By investing ₹ 15, share bought = ₹ 10
By investing ₹ 4500, share bought = \(\frac { 10 }{ 15 }\) x 4500 = ₹ 3000
Total face value of ₹ 10 shares = ₹ 3000, Income = 8%
= \(\frac { 8 }{ 100 }\) x 3000 = ₹ 240
By selling Rs. 10 share money received = ₹ 30
By selling Rs. 3000 shares money = \(\frac { 30 }{ 10 }\) x 3000 = ₹ 9000
(ii) By investing ₹ 125, no. of share of ₹ 100 bought = 1
By investing ₹ 9000, no. of share of ₹ 100 bought = \(\frac { 1 }{ 125 }\) x 9000 = 72
No. of ₹ 125 shares bought = 72
(iii) By investing ₹ 125 in Rs. 100 share, income = ₹ 12
By investing ₹ 9000 in ₹ 100 share, income = \(\frac { 12 }{ 125 }\) x 9000 = ₹ 864
Increase in income = ₹ 864 – ₹ 240 = ₹ 624
Question 16.
Mr. Parekh invested ₹ 52,000 on ₹ 100 shares at a discount of ₹ 20 paying 8% dividend. At the end of one year he sells the shares at a premium of ₹ 20. Find
(i) The annual dividend.
(ii) The profit earned including his dividend.
Solution:
Investment = ₹ 52000,
N.V. of 1 share = ₹ 100
M.V. of 1 share for 1 st year = ₹ 100 – 20 = ₹ 80
No. of shares = \(\frac { 52000 }{ 80 }\) = 650
(i) Annual dividend = \(\frac { 8 }{ 100 }\) x 650 x 100 = ₹ 5200
(ii) S.P of 1 share = ₹ 100 + 20 = ₹ 120
S.P. of 650 shares = ₹ 120 x 650 = ₹ 78000
C.P. of 650 shares = ₹ 100 x 650 = ₹ 65000
Profit = S.P. – C.P. = ₹ 78000 – ₹ 65000 = ₹ 13000
Profit including dividend = ₹ 13000 + ₹ 5200 = ₹ 18200
Question 17.
Salman buys 50 shares of face value ₹ 100 available at ₹ 132.
(i) What is his investment ?
(ii) If the dividend is 7.5%, what will be his annual income ?
(iii) If he wants to increase his annual income by ₹ 150, how many extra shares should he buy?
Solution:
F.V. = ₹ 100
(i) M. V. = ₹ 132,
no. of shares = 50
Investment = no. of shares x M.V. = 50 x 132 = ₹ 6600
(ii) Income per share = 7.5% of N.V.
= \(\frac { 75 }{ 10 x 100 }\) x 100 = ₹ 7.5
Annual incomes = 7.5 x 50 = ₹ 375
(iii) New annual income = 375 + 150 = ₹ 525
No. of shares = \(\frac { 525 }{ 7.5 }\) = 70
No. of extra share = 70 – 50 = 20
Question 18.
Salman invests a sum of money in ₹ 50 shares, paying 15% dividend quoted at 20% premium. If his annual dividend is ₹ 600, calculate:
(i) the number of shares he bought
(ii) his total investment
(iii) the rate of return on his investment. (2014)
Solution:
Nominal value = ₹ 50
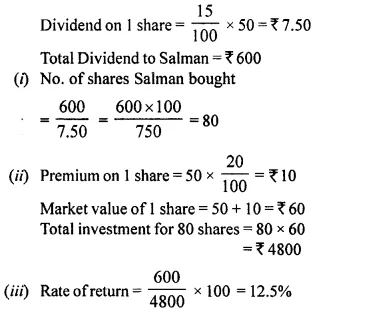
Question 19.
Rohit invested ₹ 9,600 on ₹ 100 shares at ₹ 20 premium paying 8% dividend. Rohit sold the shares when the price rose to ₹ 160. He invested the proceeds (excluding dividend) in 10% ₹ 50 shares at ₹ 40. Find the :
(i) original number of shares.
(ii) sale proceeds.
(iii) new number of shares.
(iv) change in the two dividends. (2015)
Solution:
Investment by Rohit = ₹ 9600
Rate of dividend = 8% on 100 shares at ₹ 20 premium
Market value = ₹ 100 + ₹ 20 = ₹ 120
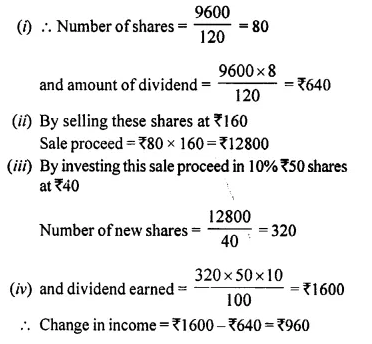
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.