Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 25 Probability Ex 25A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C
Question 1.
A coin is tossed once. Find the probability of:
(i) getting a tail
(ii) not getting a tail
Solution:
On tossing a coin once,
number of possible outcome = 2
(i) Favourable outome getting a tail = 1
⇒ number of favourable outcome = 2
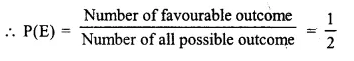
(ii) Similarly favourable outcome not getting a tail = 1
But no. of possible out come = 2
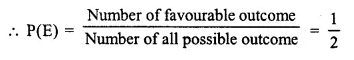
Question 2.
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is :
(i) a black ball.
(ii) a red ball.
(iii) a white ball.
(iv) not a red ball.
(v) not a black ball.
Solution:
In a bag, 3 balls are white
2 balls are red
5 balls are black
Total number of balls = 3 + 2 + 5 = 10
(i) Number of possible outcome of one black ball = 10
and number of favouable outcome of one black ball = 5
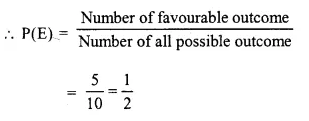
(ii) Number of possible outcome of one red ball = 10
and number of favourable outcome = 2
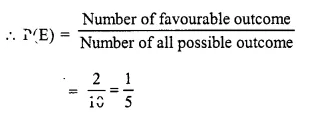
(iii) Number of possible outcome of white ball = 10
and number of favourable outcome = 3

(iv) Number of possible outcome = 10
Number of favourable outcome = 3+5 = 8
not a red ball
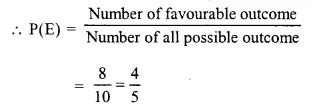
(v) Number of possible outcomes =10 Number of favourable outcome
not a black ball = 3 + 2 = 5
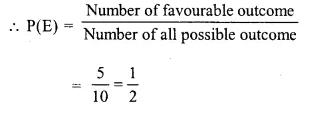
Question 3.
In a single throw of a die, find the probability of getting a number :
(i) greater than 4.
(ii) less than or equal to 4.
(iii) not greater than 4.
Solution:
A die has numbers 1, 2, 3, 4, 5, 6 on its sides
∴ Number of possible outcome = 6
(i) Number of favourable outcome = greater than four i.e. two number 5 and 6
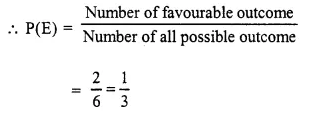
(ii) Number of favourable outcome = less than or equal to 4 i.e. 1, 2, 3, 4 which are 4 in number
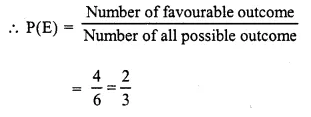
(iii) Number of favourable outcome = not greater than 4 or numbers will be 1, 2, 3, 4 which are 4 in numbers
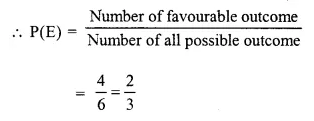
Question 4.
In a single throw of a die, find the probability that the number :
(i) will be an even number.
(ii) will not be an even number.
(iii) will be an odd number.
Solution:
A die has six numbers : 1, 2, 3, 4, 5, 6
∴ Number of possible outcome = 6
(i) Number of favourable outcome = an even number i.e. 2, 4, 6 which are 3 in numbers
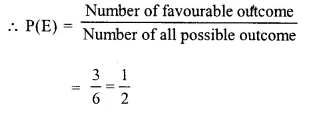
(ii) & (iii) Number of favourable outcome = not an even number i.e. odd numbers : 1, 3, 5 which are 3 in numbers
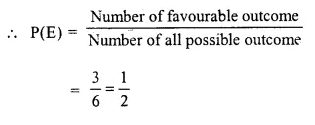
Question 5.
From a well-shuffled deck of 52 playing-cards, one card is drawn. Find the probability that the card drawn will :
(i) be a black card.
(ii) not be a red card.
(iii) be a red card.
(iv) be a face card.
(v) be a face card of red color.
Solution:
Number of cards in a playing card deck =52
number of possible outcomes = 52
(i) Number of favourable outcomes = black cards = 26 cards
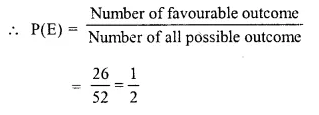
(ii) Number of favourable outcomes = Not be a red card = black cards = 26
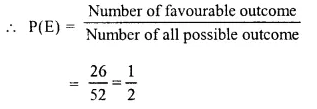
(iii) Number of favourable outcome = Number of red cards = 26
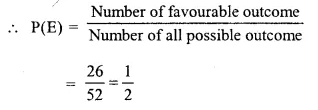
(iv) Number of favourable outcome = face cards = 3×4=12
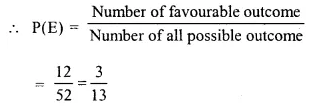
(v) Number of favourable outcome = face cards of red colour = 3 x2 = 6
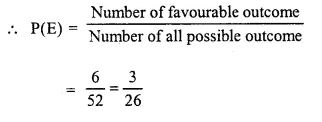
Question 6.
(i) If A and B are two complementary events then what is the relation between P(A) and P(B)?
(ii) If the probability of happening of an event A is 0.46. What will be the probability of not happening of the event A ?
Solution:
(i) A and B are two complementary events
Then A = P(E) and B = P(\(\bar { E }\) )
ButP(E) + P(\(\bar { E }\)) = 1
or P(A) + P(B) = 1
(ii) ∵ P(A) + P(B) = 1 (Complementary events)
But P(A) = 0.46
∴ P(B) = 1 – P (A)
= 1 – 0.46 = 0.54
Question 7.
In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of :
(i) winning of Geeta.
(ii) not winning of Ritu.
Solution:
∵ Match of T.T. is played between Geeta and Ritu
∴ Probability of winning of Geeta + Probability of winning of Ritu = 1
Probability of winning of Ritu = 0.73
(i) Probability of winning of Geeta
= 1 – probability of winning of Ritu
= 1 – 0.73 = 0.27
(ii) Probability of not winning of Ritu
= Probability of winning of Geeta = 0.27
Question 8.
In a race between Mahesh and John ; the probability that John will lose the race is 0.54.
Find the probability of :
(i) winning of Mahesh.
(ii) winning of John.
Solution:
∵ A Race is run between Mahesli and John
∴ P(E) + P(\(\bar { E }\) )=1
Where P(E) is the probability of lose the race by John
and P(\(\bar { E }\) ) is the probability of not losing or winning the race by Mahesh
But P( \(\bar { E }\) ) = 0.54
then 0.54 + P(E) = 1
⇒ P(E) = 1 – 0.54 = 0.46
∴ Probability of winning the race by John = 0.46 .
Question 9.
(i) Write the probability of a sure event.
(ii) Write the probability of an event which is impossible.
(iii) For an event E. write a relation representing the range of values of P(E).
Solution:
(i) We know that if the probability of an event is 1 then the probability is called a certain event or a sure event
Hence probability of a sure event = 1
(ii) The probability of an event which is impossible = 0
(iii) Probability of no event can be less than 0 and more than 1 and E be any event then
0 ≤ P(E) ≤ 1
Question 10.
In a single throw of a die, find the probability of getting :
(i) 5 (ii) 8
(in) a number less than 8.
(iv) a prime number.
Solution:
On a die the numbers are 1, 2, 3, 4, 5, 6 i.e. six.
∴ Number of possible outcome = 6
(i) Number of favourable outcome = 1 i.e. 5
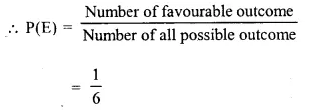
(ii) Number of favourable outcome = 0 (∵ 8 is not possible)
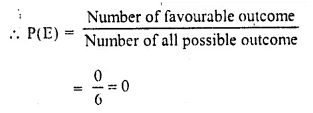
(iii) Number less than 8 will be 1,2, 3, 4, 5, 6
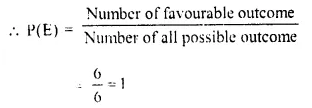
(iv) A prime number will be = 2. 3, 5
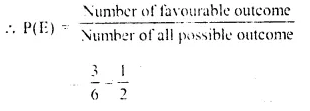
Question 11.
A die is thrown once. Find the probability of getting :
(i) an even number.
(ii) a number between 3 and 8.
(iii) an even number or a multiple of 3.
Solution:
The number on die are 1. 2. 3. 4. 5. 6
(i) Number of even numbers on the die = 2, 4, 6 = 3
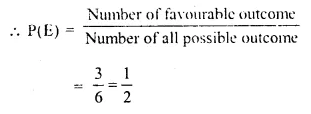
(ii) A number between 3 and 8 on the die = 3, 4, 5, 6 = 4
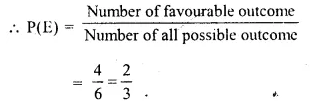
(iii) An even number or a multiple of 3 = 2, 3, 4, 6 = 4
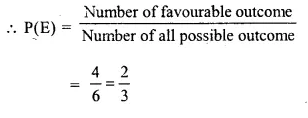
Question 12.
Which of the following cannot be the probability of an event ?
(i) \(\frac { 3 }{ 5 }\)
(ii) 2.7
(iii) 43%
(iv) -0.6
(v) -3.2
(vi) 0.35
Solution:
We know that probability of no event can be less than 0 and more than 1
∴ If probability of any event can be less than 0 or more than 1 now
(i) \(\frac { 3 }{ 5 }\) which is between 0 and 1
∴ It is the probability of an event
(ii) 2.7 which is greater than 1
∴ It is not the probability of an event.
(iii) 43% = \(\frac { 43 }{ 100 }\) which is between 0 and 1
∴ It is the probability of an event.
(iv) -0.6 which is less than 0
∴ It is not the probability of an event
(v) -3.2 which is less than 0.
∴ It is not the probability of an event
(vi) 0.35 = \(\frac { 35 }{ 100 }\) which is between 0 and 1
∴ It is the probability of an event
Hence (ii), (iv) and (v) are not probability of an event Ans.
Question 13.
A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:
(i) a white ball
(ii) a black ball
Solution:
∵ There are 6 black balls in a bag
∴ number of possible outcome = 6
(i) A white ball
As there is no white ball in the bag
∴ Its probability is zero (0) = or P(E) = 0
(ii) a black ball
∴ Number of favourable outcome = 1

Question 14.
A single letter is selected at random from the word ‘Probability’. Find the probability that it is a vowel.
Solution:
In the word, Probability, number of letters are
i.e. P, R, O, B, A, I, L, T, Y
and number of favourable outcome = o.a.i = 3
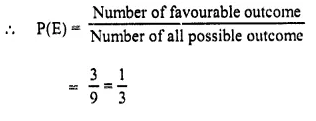
Question 15.
Ramesh chooses a date at random in January for a party (see the following figure).

Find the probability that he chooses :
(i) A Wednesday (ii) A Friday (iii) A Tuesday or a Saturday
Solution:
We are given the days of the month of January which has 31 days.
∴ Number of possible outcome = 31
(i) Number of Wednesday in the month = 5
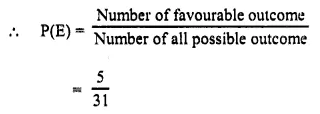
(ii) Number of Friday in the month = 5

(iii) Number of Tuesday = 4
and number of Saturday = 4
Total number of Tuesday and Saturday = 4 + 4 = 8
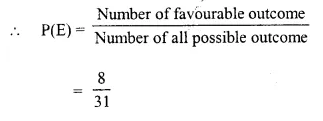
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.