Here we are providing Areas of Parallelograms and Triangles Class 9 Extra Questions Maths Chapter 9 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-9-maths/
Extra Questions for Class 9 Maths Areas of Parallelograms and Triangles with Answers Solutions
Extra Questions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles with Solutions Answers
Areas of Parallelograms and Triangles Class 9 Extra Questions Very Short Answer Type
Areas Of Parallelograms And Triangles Class 9 Extra Questions With Answers Question 1.
Two parallelograms are on equal bases and between the same parallels. Find the ratio of their areas.
Solution:
1:1 [∵ Two parallelograms on the equal bases and between the same parallels are equal in
area.]
Class 9 Maths Chapter 9 Extra Questions Question 2.
In ∆XYZ, XA is a median on side YZ. Find ratio of ar(∆XYA) : ar(∆XZA).
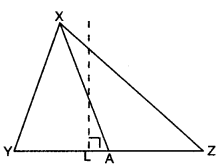
Solution:
Here, XA is the median on side YZ.
∴ YA = AZ
Draw XL ⊥ YZ
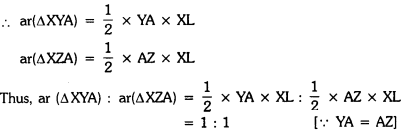
Parallelogram Questions For Class 9 Question 3.
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (fig.). E and F are the mid-points of the non parallel sides. Find the ratio of ar(ABFE) and ar(EFCD).
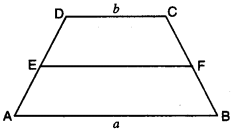
Solution:
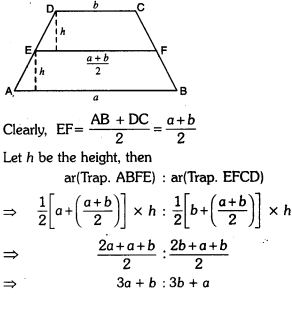
Area Of Parallelograms And Triangles Class 9 Extra Questions Question 4.
ABCD is a parallelogram and Q is any point on side AD. If ar(∆QBC) = 10 cm2, find ar(∆QAB) + ar(∆QDC).
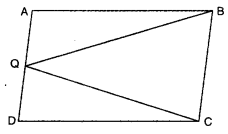
Solution:
Here, ∆QBC and parallelogram ABCD are on the same base BC and lie between the same parallels BC || AD.
∴ ar(||gm ABCD) = 2 ar(∆QBC) ar(∆QAB) + ar(∆QDC) + ar(∆QBC) = 2 ar(∆QBC)
ar(∆QAB) + ar(∆QDC) = ar(∆QBC)
Hence, ar(∆QAB) + ar(∆QDC) = 10 cm2 [∵ ar(∆QBC) = 10 cm2 (given)]
Areas Of Parallelograms And Triangles Class 9 Questions With Answers Question 5.
WXYZ is a parallelogram with XP ⊥ WZ and ZQ ⊥ WX. If WX = 8 cm, XP = 8 cm and ZQ = 2 cm, find YX.
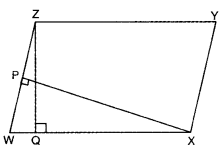
Solution:
ar(||gm WXYZ) = ar(||gm WXYZ)
WX × ZQ = WZ × XP
8 × 2 = WZ × 8
⇒ WZ = 2 cm
Now, YX = WZ = 2 cm [∵ opposite sides of parallelogram are equal]
Questions On Areas Of Parallelograms And Triangles Class 9 Question 6.
In figure, TR ⊥ PS, PQ || TR and PS || QR. If QR = 8 cm, PQ = 3 cm and SP = 12 cm, find ar(quad. PQRS).
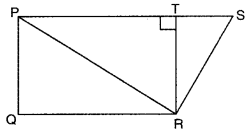
Solution:
Here,
PS || QR [given]
∴ PQRS is a trapezium
Now, TR ⊥ PS and PQ || TR [given]
⇒ PQ ⊥ PS
∴ PQ = TR = 3 cm [given]
Now, ar(quad. PQRS) = \(\frac{1}{2}\) (PS + QR) × PQ = \(\frac{1}{2}\)(12 + 8) × 3 = 30 cm2
Area Of Parallelogram Class 9 Extra Questions Question 7.
In the given figure, ABCD is a parallelogram and L is the mid-point of DC. If ar(quad. ABCL) is 72 cm, then find ar(∆ADC).
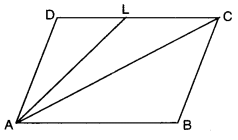
Solution:
In ||gm ABCD, AC is the diagonal

Areas Of Parallelograms And Triangles Questions With Answers Question 8.
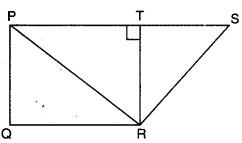
In figure, TR ⊥ PS, PQ || TR and PS || QR. If QR = 8 cm, PQ = 3 cm and SP = 12 cm, find ar (PQRS).
Solution:
Here, PS || QR
∴ PQRS is a trapezium in which PQ = 3 cm, QR = 8 cm and SP = 12 cm
Now, TR I PS and PQ || TR
∴ PQRT is a rectangle [∵ PQ || TR, PT || QR and ∠PTR = 90°]
⇒ PQ = TR = 3 cm
Now, ar(PQRS) = \(\frac{1}{2}\)(PS + QR) × TR = \(\frac{1}{2}\)(12 + 8) × 3 = 30 cm2.
Areas of Parallelograms and Triangles Class 9 Extra Questions Short Answer Type 1
Area Of Parallelogram Class 9 Questions Question 1.
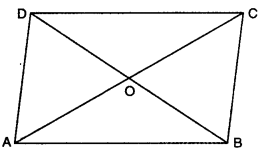
ABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(A AOD) = 4 cm\(2\) find area of parallelogram ABCD.
Solution:
Here, ABCD is a parallelogram in which its diagonals AC and BD intersect each other in O.
∴ O is the mid-point of AC as well as BD.
Now, in ∆ADB, AO is its median
∴ ar(∆ADB) = 2 ar(∆AOD)
[∵ median divides a triangle into two triangles of equal areas]
So, ar(∆ADB) = 2 × 4 = 8 cm2
Now, ∆ADB and ||gm ABCD lie on the same base AB and lie between same parallels AB and CD
∴ ar(ABCD) = 2 ar(∆ADB).
= 2 × 8
= 16cm2
Areas Of Parallelograms And Triangles Question 2.
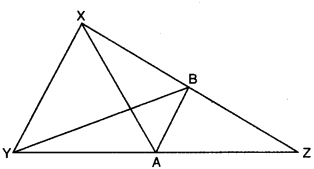
In the given figure of ∆XYZ, XA is a median and AB || YX. Show that YB is also a median.
Solution:
Here, in ∆XYZ, AB || YX and XA is a median.
∴ A is the mid-point of YZ. Now, AB is a line segment from mid-point of one side (YZ) and parallel to another side (AB || YX), therefore, it bisects the third side XZ.
⇒ B is the mid-point of XZ.
Hence, YB is also a median of ∆XYZ.
Question 3.
ABCD is a trapezium. Diagonals AC and BD intersect each other at O. Find the ratio ar (∆AOD) : ar (∆BOC).
Solution:
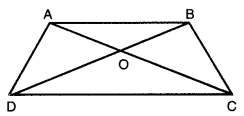
Here, ABCD is a trapezium in which diagonals AC and BD intersect each other at O. ∆ADC and ABCD are on the same base DC and between the same ‘parallels i.e., AB || DC.
∴ ar(∆ADC) = ar(∆BCD)
⇒ ar(∆AOD) + ar(∆ODC)
= ar(ABOC) + ar(AODC)
⇒ ar(∆AOD) = ar(∆BOC)
⇒ \(\frac { ar(∆AOD) }{ ar(∆BOC) } \) = 1
Question 4.
ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ (fig.). If AQ intersects DC at P, show that ar(∆BPC) = ar(∆DPQ).
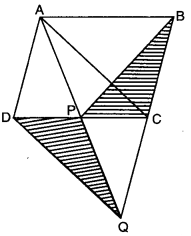
Solution:
In ||gm ABCD,
ar(∆APC) = ar(∆BCP) …(i)
[∵ triangles on the same base and between the same parallels have equal area]
Similarly, ar(∆ADQ) = ar(∆ADC) i …(ii)
Now, ar(∆ADQ) – ar(∆ADP) = ar(∆ADC) – ar(∆ADP)
ar(∆DPQ) = ar(∆ACP) … (iii)
From (i) and (iii), we have
ar(∆BCP) = ar(∆DPQ)
or ar(∆BPC) = ar(∆DPQ)
Question 5.
In the figure, PQRS is a parallelogram with PQ = 8 cm and ar(∆PXQ) = 32 cm2. Find the altitude of gm PQRS and hence its area.
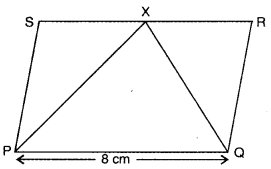
Solution:
Since parallelogram PQRS and APXQ are on the same base PQ and lie between the same
parallels PQ || SR
∴ Altitude of the ∆PXQ and ||gm PQRS is same.
Now, \(\frac{1}{2}\)PQ × altitude = ar(∆PXQ)
⇒ \(\frac{1}{2}\) × 8 × altitude = 32
altitude = 8 cm
ar(||gm PQRS) = 2 ar(∆PXQ)
= 2 × 32 = 64 cm2
Hence, the altitude of parallelogram PQRS is 8 cm and its area is 64 cm2.
Question 6.
In ∆ABC. D and E are points on side BC such that CD = DE = EB. If ar(∆ABC) = 27 cm, find ar(∆ADE)
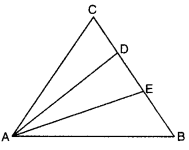
Solution:
Since in ∆AEC, CD = DE, AD is a median.
∴ ar(∆ACD) = ar(∆ADE)
[∵ median divides a triangle into two triangles of equal areas]
Now, in ∆ABD, DE = EB, AE is a median
ar(∆ADE) = ar(∆AEB)… (ii)
From (i), (ii), we obtain
ar(∆ACD) = ar(∆ADE) = ar(∆AEB)\(\frac{1}{3}\)ar(∆ABC)
∴ ar(∆ADE) = \(\frac{1}{3}\) × 27 = 9 cm2
Areas of Parallelograms and Triangles Class 9 Extra Questions Short Answer Type 2
Question 1.
For the given figure, check whether the following statement is true or false. Also justify your answer. PQRS is a trapezium with PQ || SR, PS || RU and ST || RQ, then ar(PURS) = ar(TQRS)
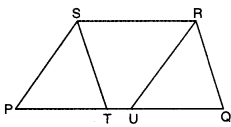
Solution:
Since ST || RQ and SR || TQ [given]
⇒ STQR is a ||gm
Similarly, PS || UR and SR || PU [given]
⇒ PSRU is a ||gm
Also, similarly, ||gm STQR and ||gm PSRU lie on same base SR and between same parallels PQ and SR.
∴ ar(||gm STQR) = ar(||gm PSRU)
Hence, the given statement is true.
Question 2.
In the given figure, WXYZ is a quadrilateral with a point P on side WX. If ZY || WX, show that :
(i) ar(∆ZPY) = ar(∆ZXY)
(ii) ar(∆WZY) = ar(∆ZPY)
(iii) ar(∆ZWX) = ar(∆XWY)
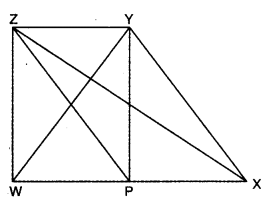
Solution:
∆ZPY and ∆ZXY lie on same base ZY and between same parallels ZY and WX
∴ ar(∆ZPY) = ar(∆ZXY)
Again, (∆WZY) and (∆ZPY) lie on same base ZY and between same parallels ZY and WX
∴ ar(∆WZY) = ar(∆ZPY)
Also, ∆zwX and ∆XWY lie on same base XW and between same parallels ZY and WX
∴ ar(∆ZWX) = ar(∆XWY)
Question 3.
In ∆ABC ; D, E and F are mid-points of sides BC, AC and AB respectively. A line through C drawn parallel to DE meets FE produced to G. Show that ar(∆FDE) = ar(∆EGC).
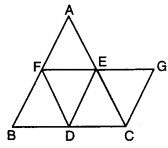
Solution:
Here, in ∆ABC; D, E and F are the mid-points of sides BC, AC and AB respectively. A line through C is drawn parallel to DE meets FE produced at G.
Since a line segment drawn through the mid-points of two sides, is parallel to third side and is half of it.
∴ DE || AB, EF || BC and FD || AC
⇒ AEDF, EFDC and EFDB are parallelograms
Also, a diagonal of a parallelogram divides it into two congruent triangles
∴ ∆AFE ≅ ∆DEF
∆DEF ≅ ∆FDB and
∆DEF ≅ ∆EDC
∴ ar(∆FDE) ≅ ar(∆EDC) …(i)
Again, in quad. EGCD, we have
CG || DE and DC || EG [given]
∴ EGCD is a parallelogram .
∴ ∆EDC = ∆CGE
⇒ ar(AEDC) = ar(ACGE) … (ii)
From (i) and (ii), we obtain
ar(∆FDE) = ar(∆EGC)
Question 4.
In ∆PQR, A and B are points on side QR such that they trisect QR. Prove that ar(∆PQB) = 2ar(∆PBR).
Solution:
Here, in ∆PQR, A and B are points on side QR
such that QA = AB = BR.
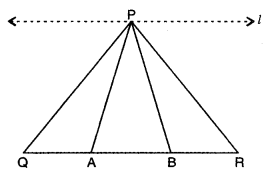
Through P, draw a line / parallel to QR
Now, APQA, APAB and APBR on the equal bases
and between the same parallels l || QR
⇒ ar(∆PQA) = ar(∆PAB) = ar(∆PBR) …. (i)
Now, ar(∆PQB) = ar(∆PQA) + ar(∆PAB)
= 2ar(∆PQA)[using (i)]
= 2ar(∆PBR) [using (i)]
Question 5.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q, then parallelogram PBQR is completed (see figure). Show that ar(||gm ABCD) = ar(||gm PBQR).
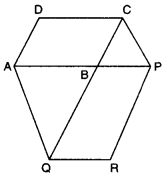
Solution:
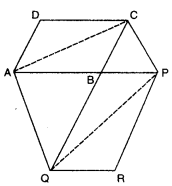
Join AC and QP, also it is given that ∆Q || CP
∴ ∆ACQ and ∆APQ are on the same base ∆Q and lie between the same parallels ∆Q || CP.
∴ ar(∆ACQ) = ar(∆APQ)
or ar(∆ABC) + ar(∆ABQ) = ar(ABPQ) + ar(∆ABQ)
ar(∆ABC) = ar(ABPQ)
or \(\frac{1}{2}\)ar(||gm ABCD) = \(\frac{1}{2}\)ar (||gm PBQR)
or ar(||gm ABCD) = ar(||gm PBQR)
Areas of Parallelograms and Triangles Class 9 Extra Questions Long Answer Type
Question 1.
EFGH is a parallelogram and U and T are points on sides EH and GF respectively. If ar(∆EHT) = 16 cm, find ar(∆GUF).
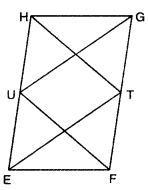
Solution:
∴ ar(∆EHT) = \(\frac{1}{2}\) ar(||gm EFGH) …..(i)
Similarly, ∆GUF and parallelogram EFGH are on the same base GF and lie between the same parallels GF and HE
∴ ar(∆GUF) = \(\frac{1}{2}\) ar(||gm EFGH) …..(ii)
From (i) and (ii), we have
ar(∆GUF) = ar(∆EHT)
= 16 cm2 [∵ ar(∆EHT) = 16 cmcm2] [given]
Question 2.
ABCD is a parallelogram and P is any point in its interior. Show that :
ar(∆APB) + ar(∆CPD) = ar(∆BPC) + ar(∆APD)
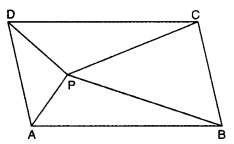
Solution:
Through P, draw a line LM || DA and EF || AB
Since ∆APB and ||gm ABFE are on the same base AB and lie between the same parallels AB and EF.
∴ ar(∆APB) = \(\frac{1}{2}\) ar(||gm ABFE) … (i)
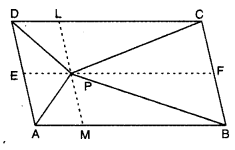
Similarly, ACPD and parallelogram DCFE are on the same base DC and between the same parallels DC and EF.
∴ ar(∆CPD) = \(\frac{1}{2}\) ar(||gm DCFE) … (ii)
Adding (i) and (ii), we have
ar(∆APB) + ar(∆CPD) = \(\frac{1}{2}\) ar (||gm ABFE) + ar(||gm DCFE)
= \(\frac{1}{2}\) ar(|lgm ABCD) … (iii)
Since ∆APD and parallelogram ADLM are on the same base AB and between the same parallels AD and ML
∴ ar(∆APD) = \(\frac{1}{2}\) ar(||gm ADLM) …..(iv)
Similarly, ar(∆BPC) = \(\frac{1}{2}\) = arc||gm BCLM) ….(v)
Adding (iv) and (u), we have
ar(∆APD) + ar (∆BPC) = \(\frac{1}{2}\) ar(||gm ABCD) ….(vi)
From (iii) and (vi), we obtain
ar(∆APB) + ar(∆CPD) = ar(∆APD) + ar(ABPC)
Question 3.
In the given figure, ABCD is a square. Side AB is produced to points P and Q in such a way that PA = AB = BQ. Prove that DQ = CP.
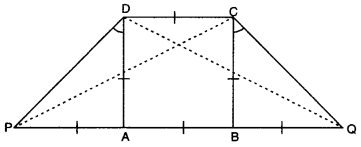
Solution:
In ∆PAD, ∠A = 90° and DA = PA = AB
⇒ ∠ADP = ∠APD = \(\frac{90^{\circ}}{2}\) = 45°
Similarly, in ∆QBC, ∠B = 90° and BQ = BC = AB
⇒ ∠BCQ = ∠BQC = \(\frac{90^{\circ}}{2}\) = 45°
In ∆PAD and ∆QBC, we have
PA = BQ [given]
∠A = ∠B [each = 90°]
AD = BC [sides of a square]
⇒ ∠PAD ≅ ∆QBC [by SAS congruence rule]
⇒ PD = QC [c.p.c.t.]
Now, in APDC and ∆QCD
DC = DC [common]
PD = QC [prove above]
∠PDC = ∠QCD [each = 90° + 45° = 135°]
⇒ ∆PDC = ∆QCD [by SAS congruence rule]
⇒ PC = QD or DQ = CP
Areas of Parallelograms and Triangles Class 9 Extra Questions HOTS
Question 1.
In the given figure, PQRS, SRNM and PQNM are parallelograms, Show that :
ar(∆PSM) = ar(∆QRN).
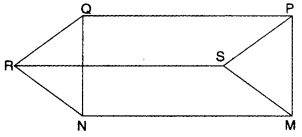
Solution:
Since PQRS is a parallelogram.
∴ PS = QR and PS || QR
Since SRNM is also a parallelogram.
∴ SM = RN and SM || RN
Also, PQNM is a parallelogram
∴ PM || QM and PM = QM
Now, in APSM and ∆QRN
PS = QR
SM = RN
PM = QN
∆PSM ≅ ∆QRN [by SSS congruence axiom]
∴ ar (∆PSM) = ar (∆QRN) [congruent triangles have same areas)
Areas of Parallelograms and Triangles Class 9 Extra Questions Value Based (VBQs)
Question 1.
Naveen was having a plot in the shape of a quadrilateral. He decided to donate some portion of it to construct a home for orphan girls. Further he decided to buy a land in lieu of his donated portion of his plot so as to form a triangle.
(i) Explain how this proposal will be implemented?
(ii) Which mathematical concept is used in it?
(iii) What values are depicted by Naveen?
Solution:
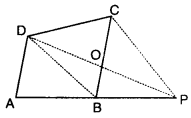
(i) Let ABCD be the plot and Naveen decided to donate some portion to construct a home for orphan girls from one corner say C of plot ABCD. Now, Naveen also purchases equal amount of land in lieu of land CDO, so that he may have triangular form of plot. BD is joined. Draw a line through C parallel to DB to meet AB produced in P.
Join DP to intersect BC at 0.
Now, ABCD and ABPD are on the same base and between same parallels CP || DB.
ar(∆BCD) = ar(∆BPD) ar(∆COD) + ar(∆DBO) = ar(∆BOP) + ar(∆DBO)
ar(ACOD) = ar(ABOP) ar(quad. ABCD)
= ar(quad. ABOD) + ar(∆COD)
= ar(quad. ABOD) + ar(∆BOP)
[∵ ar(ACOD) = ar(ABOP)] (proved above]
= ar(∆APD)
Hence, Naveen purchased the portion ABOP to meet his requirement.
(ii) Two triangles on the same base and between same parallels are equal in area.
(iii) We should help the orphan children.
Question 2.
A flood relief camp was organized by state government for the people affected by the natural calamity near a city. Many school students volunteered to participate in the relief work. In the camp, the food items and first aid centre kits were arranged for the flood victims. The piece of land used for this purpose is shown in the figure.
(a) If EFGH is a parallelogram with P and Q as mid-points of sides GH and EF respectively, then show that area used for first aid is half of the total area.
(b) What can you say about the student volunteers working for the relief work?
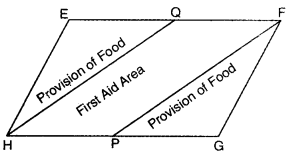
Solution:
(a) Here, EFGH is a ||gm
∴ EF = GH and EF || GH
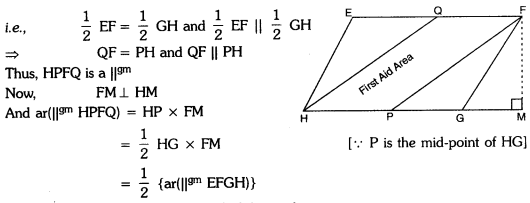
Hence, area used for first aid is half of the total area.
(b) Students working for the noble cause show compassion towards the affected people. They also realize their social responsibility to work for helping the ones in need.
