On this page, you will find Areas of Parallelograms and Triangles Class 9 Notes Maths Chapter 10 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 10 Areas of Parallelograms and Triangles will seemingly help them to revise the important concepts in less time.
CBSE Class 9 Maths Chapter 9 Notes Areas of Parallelograms and Triangles
Areas of Parallelograms and Triangles Class 9 Notes Understanding the Lesson
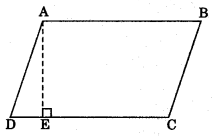
1. Area of a parallelogram = base x height
= DC x AE
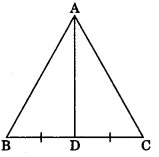
2. Area of a triangle = \(\frac{1}{2}\)base x height
\(\frac{1}{2}\) BC x AD
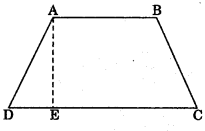
3. Area of a trapezium = x (Sum of parallel sides) x Distance between them
\(\frac{1}{2}\) (AB + DC) x AE
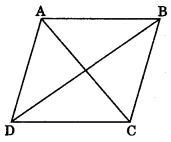
4. Area of a rhombus =\(\frac{1}{2}\) \(\frac{1}{2}\) x product of diagonals A B
\(\frac{1}{2}\) x AC x BD
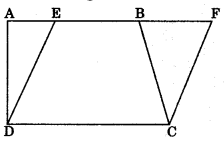
5. Two figures are said to be on the same base and between the same parallels, if they have a common side (base) and the vertices (or the vertex) opposite to the common base of each figure He on a line parallel to the base.
Theorem 9.1: Parallelograms on the same base and between the same parallels are equal in area.
ar(ABCD) = ar(EFCD)
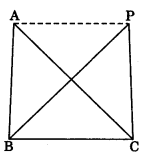
Theorem 9.2: Triangles on the same base and between the same parallels are equal in area.
ar(ΔABC) = ar(ΔPBC)
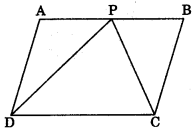
Theorem 9.3: Two triangles having the same base and equal areas lie between the same parallels.
If a triangle and a parallelogram are on the same base and between the same parallels, then
(i) Area of triangle = \(\frac{1}{2}\) x area of the parallelogram
ar(ΔPDC) = \(\frac{1}{2}\) ar(||gmABCD)
(ii) A diagonal of parallelogram divides it into two triangles of equal areas.
ar(ΔABD) = ar(ΔBCD)

(iii) If each diagonal of a quadrilateral separates it into two triangles of equal area, then the quadrilateral is a parallelogram.
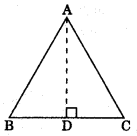
(iv) A median AD of a ΔABC divides it into two triangles of equal areas.
ar(ΔABD) = ar(ΔACD)