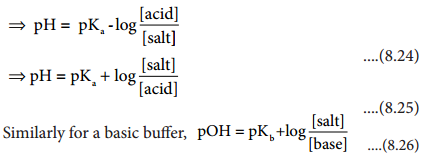Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.
Buffer Solution
Do you know that our blood maintains a constant pH, irrespective of a number of cellular acid – base reactions. Is it possible to maintain a constant hydronium ion concentration in such reactions? Yes, it is possible due to buffer action.
Buffer is a solution which consists of a mixture of a weak acid and its conjugate base (or) a weak base and its conjugate acid. This buffer solution resists drastic changes in its pH upon addition of a small quantities of acids (or) bases, and this ability is called buffer action. The buffer containing carbonic acid (H2CO3) and its conjugate base HCO–3 is present in our blood. There are two types of buffer solutions.
1. Acidic Buffer Solution:
A solution containing a weak acid and its salt.
Example: Solution containing acetic acid and sodium acetate
2. Basic Buffer Solution:
A solution containing a weak base and its salt.
Example: Solution containing NH4OH and NH4Cl
Buffer Action
To resist changes in its pH on the addition of an acid (or) a base, the buffer solution should contain both acidic as well as basic components so as to neutralize the effect of added acid (or) base and at the same time, these components should not consume each other. Let us explain the buffer action in a solution containing CH3COOH and CH3COONa. The dissociation of the buffer components occurs as below.
If an acid is added to this mixture, it will be consumed by the conjugate base CH3COO– to form the undissociated weak acid i.e, the increase in the concentration of H+ does not reduce the pH significantly.
CH3COO–(aq) + H+(aq) → CH3COOH(aq)
If a base is added, it will be neutralized by H3O+, and the acetic acid is dissociated to maintain the equlibrium. Hence the pH is not significantly altered.
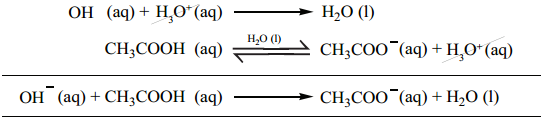
These neutralization reactions are identical to those reactions that we have already discussed in common ion effect.
Les us analyse the effect of the addition of 0.01 mol of solid sodium hydroxide to one litre of a buffer solution containing 0.8 M CH3COOH and 0.8 M CH3COONa. Assume that the volume change due to the addition of NaOH is negligible. (Given: K4 for CH3COOH is 1.8 × 10-5).
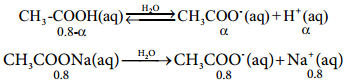
The dissociation constant for CH3COOH is given by
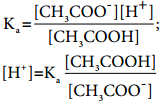
The above expression shows that the concentration of H+ is directly proportional to
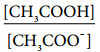
Let the degree of dissociation of CH3COOH be α then,
[CH3OOH] = 0.8 – α and [CH3COO–]
= α + 0.8
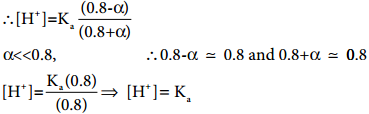
Given that
Kafor CH3COOH is 1.8 × 10-5
∴ [H+] = 1.8 × 10-5; pH = – log (1.8 × 10-5)
= 5 – log 1.8
= 5 – 0.26
pH = 4.74
Calculation of pH after adding 0.01 mol NaOH to 1 litre of buffer.
Given that the volume change due to the addition of NaOH is negligible
∴[OH–] = 1.8 × 10-5; pH = – log (1.8 × 10-5)
= 5 – log 1.8
= 5 – 0.26
pH = 4.74
Caluculation of pH after adding 0.01 mol NaOH to 1 litre of buffer.
Given that the volume change due to the addition of NaOH is negligible
∴ [OH–] = 0.01 M.
The consumption of OH– are expressed by the following equations.
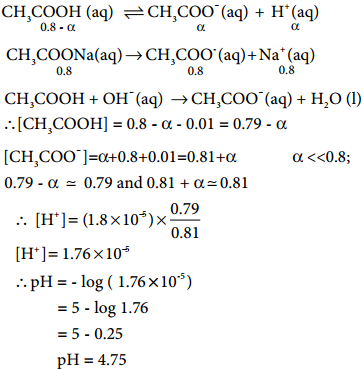
The addition of a strong base (0.01 M NaOH) increased the pH only slightly ie., from 4.74 to 4.75 . So, the buffer action is verified.
Buffer Capacity and Buffer Index
The buffering ability of a solution can be measured in terms of buffer capacity. Vanslyke introduced a quantity called buffer index, β , as a quantitative measure of the buffer capacity. It is defined as the number of gram equivalents of acid or base added to 1 litre of the buffer solution to change its pH by unity.
Here, β = \(\frac{dB}{d(pH)}\) …………. (8.19)
dB = number of gram equivalents of acid / base added to one litre of buffer solution.
d(pH) = The change in the pH after the addition of acid / base.
Henderson – Hassel Balch Equation
We have already learnt that the concentration of hydronium ion in an acidic buffer solution depends on the ratio of the concentration of the weak acid to the concentration of its conjugate base present in the solution i.e.,
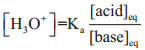………….. (8.20)
The weak acid is dissociated only to a small extent. Moreover, due to common ion effect, the dissociation is further suppressed and hence the equilibrium concentration of the acid is nearly equal to the initial concentration of the unionised acid. Similarly, the concentration of the conjugate base is nearly equal to the initial concentration of the added salt.
…………… (8.21)
Here [acid] and [salt] represent the initial concentration of the acid and salt, respectively used to prepare the buffer solution. Taking logarithm on both sides of the equation
……………. (8.22)
Reverse the sign on both sides
…………….. (8.23)
We know that
pH = – log [H3O+] and pKa = – logKa
