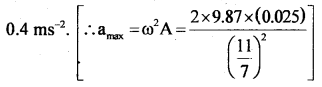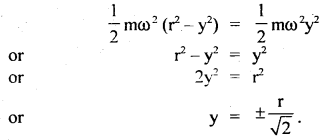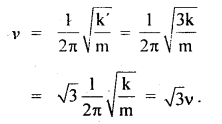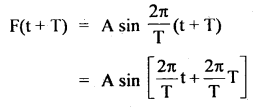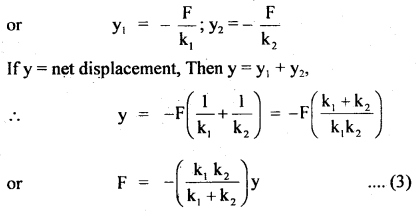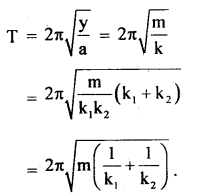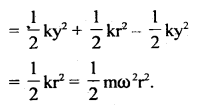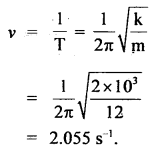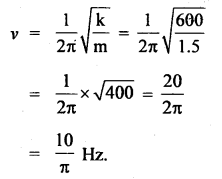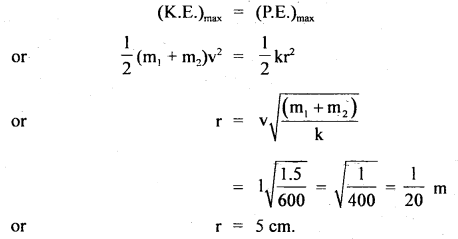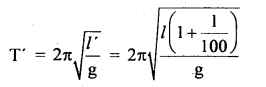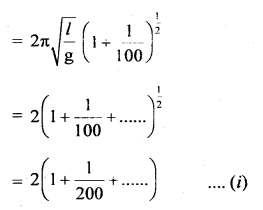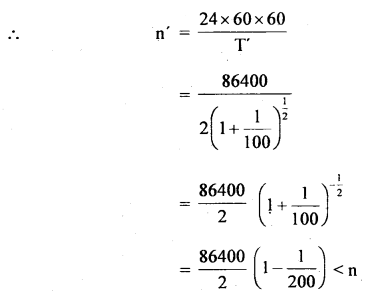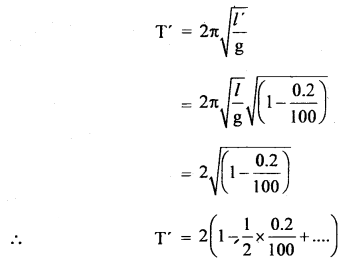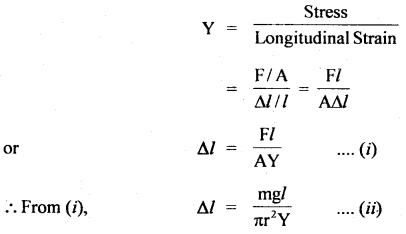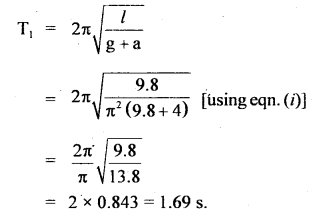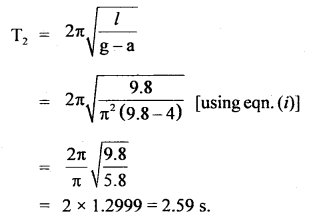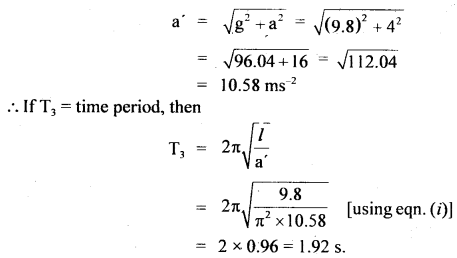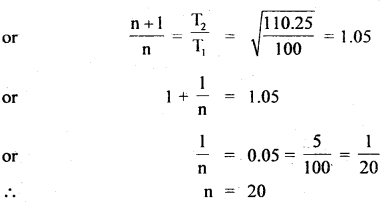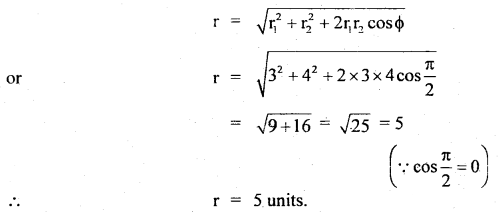Category: CBSE Class 11

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 10 Mechanical Properties of Fluids. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 10 Important Extra Questions Mechanical Properties of Fluids

Mechanical Properties of Fluids Important Extra Questions Very Short Answer Type

Question 1.
(a) Why density increases with the fall of temperature?
Answer:
Because the volume of the given mass decreases.

(b) Can you estimate the exact fractional volume of an ice cube in water when the system is falling freely? Why?
Answer:
No. The effective value of g in the given case is zero.

Question 2.
Why two holes are made to empty an oil tin?
Answer:
If only one hole is made, then the pressure inside the tin would be less than the atmospheric pressure. So oil would not come out. If two holes are made, then the pressure inside the tin is equal to atmospheric pressure.

Question 3.
(a) What is one torr of pressure?
Answer:
It is the pressure exerted by 1 mm of mercury column.

(b) Suppose a few’ drops of water are introduced in the barometer tube, what would be the effect on the barometric height?
Answer:
The barometric height would decrease due to the pressure of water vapors.

Question 4.
(a) What are the values of systolic and diastolic blood pressure of a healthy human being?
Answer:
Nearly 120 mm of Hg and 80 mm of Hg respectively.

(b) At what temperature is the density of water maximum and what is its value?
Answer:
At 4°C and the maximum value is 10³ kg m^-3.

Question 5.
What is indicated by:
(a) Gradual increase of atmospheric pressure?
Answer:
It indicates dry weather.

(b) Gradual fall of atmospheric pressure?
Answer:
This indicates the possibility of rain as the atmospheric pressure falls when the water vapors increase in air.

(c) Sudden fall of atmospheric pressure?
Answer:
It indicates the possibility of a storm.

Question 6.
Why water does not come out of a dropper unless its rubber head is pressed hard?
Answer:
Water would come out only if the pressure exerted on the rubber head is greater than the atmospheric pressure.

Question 7.
What is 105 Nm^-2 pressure called? What is the value of 1 torr?
Answer:
It is called 1 bar. Torr is the unit of atmospheric pressure.
1 torr = 1 mm of Hg column
= 1.33 × 10^-4 Nm^-2
= 1.33 × 10^-3dyne cm^-2.

Question 8.
(a) Why Hg is used in the barometer?
Answer:
Due to the large density of mercury, the barometer is of convenient size.

(b) A steel ball is floating in a trough of mercury. If we fill the empty part of the trough with water, what will happen to the steel ball?
Answer:
It will move up.

Question 9.
The two thigh bones (femurs) each of cross-section area 10cm² support the upper part of a human body of mass 40 Kg. Estimate the pressure sustained by the femurs.
Answer:

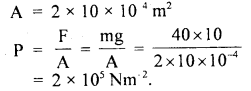
Question 10.
How can you check whether the barometer tube contains air or not?
Answer:
The barometer tube is raised or lowered in a trough of mercury. If the height of the mercury column changes, then the barometric tube contains air.

Question 11.
When air is blown in between the two balls suspended from a string such that they don’t touch each other, the balls come nearer to each other. Why?
Answer:
Pressure decreases with an increase in velocity between the balls.

Question 12.
What is the effect of temperature on the viscosity of liquid?
Answer:
The viscosity of liquid decreases with the increase in temperature and vice-versa.

Question 13.
Why you can’t remove the filter paper from the funnel shown here by blowing from the narrow end?
Answer:
When the air enters the wider and velocity is reduced and pressure is increased.

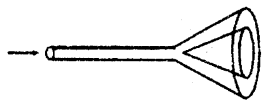
Question 14.
Why a raindrop falling freely does not acquire a high velocity?
Answer:
This is because the raindrop acquires terminal velocity after having fallen through a certain height.

Question 15.
(a) Why do the clouds float in the sky?
Answer:
They have zero terminal velocity.

(b) Why machines are sometimes jammed in winter?
Answer:
Due to change in viscosity with temperature.

(c) Why a hot liquid moves faster than a cold liquid?
Answer:
Due to a decrease in viscosity with an increase in temperature.

Question 16.
(a) A flask contains glycerine and the other one contains water. Both are stirred rapidly and kept on the table. In which flask will the liquid come to rest earlier than the other one and why?
Answer:
Glycerine due to greater viscosity.

(b) What is the effect on the viscosity of a gas of the temperature?
Answer:
There is a decrease in the viscosity of gas with the decrease in temperature and increases with an increase in temperature.

Question 17.
How does the viscous force between two layers of a liquid depend upon the relative velocity between two layers?
Answer:
The viscous force between two layers increases with the ¡ñcreasc in relative velocity.

Question 18.
(a) Why firefighters have a jet attached to the head of their water pipes?
Answer:
This is done to increase the velocity of water flowing out of the pipe.

(b) Why the airplanes and cars are given a streamlined shape?
Answer:
This is done to reduce the backward drag of the atmosphere.

Question 19.
People living in houses far removed from a municipal water tank often find it difficult to get water on the top floor even if it is situated lower than the level of water tank. Why?
Answer:
This is because there is a loss of pressure when water is flowing.

Question 20.
(a) Why a small air bubble rises slowly through a liquid whereas the bigger one rises rapidly?
Answer:
Terminal velocity is proportional to the square of radius i.e. v_T ∝ R².

(b) Why flags flutter on a windy day?
Answer:
Velocity increases and pressure decreases on a windy day.

Question 21.
(a) Why more viscous mobile oil is used in summer than in winter in scooters?
Answer:
Due to high temperature, viscosity is less, so more viscous oil is used in summer than in winter.

(b) Why air bubble in a liquid rises up?
Answer:
Because the terminal velocity of the air bubble is negative.

Question 22.
What are the values of Reynolds number (N_g) for different types of flows?
Answer:
For streamline or laminar flow 0 < N_R < 2000, for turbulent flow, N_R > 3000

If NR lies between 2000 to 3000, the flow is unstable i.e. change from streamline flow to turbulent flow.

Question 23.
Explain why:
(a) Is sand drier than clay?
Answer:
Due to capillary action.

(b) Is it that a needle may float on clear water but will sink when some detergent is added to water?
Answer:
The detergents reduce surface tension.

(c) Mercury (Hg) does not wet glass?
Answer:
For cohesion is greater than the force of adhesion.

(d) Two mercury drops coalesce when brought together?
Answer:
Due to the strong force of cohesion.

(e) The end of a glass rod becomes round on heating?
Answer:
Due to surface tension.

(f) Antiseptics have low surface tension.
Answer:
As they have to spread over a large area.

(g) Oil is poured to calm sea waves?
Answer:
When oil is poured on water, the surface tension of water is reduced, thus water tends to spread over a larger area.

(h) Is it possible to produce a fairly vertical film of soap solution but not of water?
Answer:
It is due to the reason that the surface tension of soap solution is lesser as compared to the surface tension of water and thus it spreads over a larger area.

(i) Is it easier to spray water when soap is added to it?
Answer:
Due to less surface tension.

Question 24.
(a) Why the liquid in the surface film has special importance?
Answer:
The phenomenon of surface tension is due to the given portion i.e. surface film of the liquid.

(b) Why cotton dresses should be preferred in summer?
Answer:
Due to the reason that they have fine pores which act as capillaries for the sweat.

Question 25.
(a) What shape does a liquid take when it weighs nothing?
Answer:
Spherical shape.

(b) Why the nib of a pen is split?
Answer:
For capillary action.

Question 26.
What is the effect:
(a) of highly soluble impurities on the surface tension of a liquid?
Answer:
The surface tension is increased.

(b) of less soluble impurities on the surface tension of a liquid?
Answer:
The surface tension decreases.

(c) on the angle of contact when the temperature of a liquid is increased?
Answer:
The angle of contact decreases.

Question 27.
Is the pressure:
(a) of air inside a soap bubble greater than the atmospheric pressure?
Answer:
Yes.

(b) inside a mercury drop greater than the atmospheric pressure?
Answer:
Yes.

(c) A cylinder is filled with non-viscous liquid of density p, height h, and a hole is made at a height h2 from the bottom of the cylinder? What is the velocity of the liquid coming out of the hole?
Answer:
\(\sqrt{2 \mathrm{~g}\left(\mathrm{~h}_{1}-\mathrm{h}_{2}\right)}\)

Question 28.
(a) What happens to the work done to increase the surface area?
Answer:
It is stored as potential energy.

(b) What is the work done in blowing a soap bubble of radius. r and surface tension T?
Answer:
8πr²T.

Question 29.
(a) How trees draw water from the ground?
Answer:
Trees draw water from the ground by capillary action.

(b) The radius of a capillary tube is doubled. What change will take place in the height of the capillary rise?
Answer:
Capillary rise will be halved as h ∝ \(\frac{1}{r}\)

(c) In the capillary tube water descends and not rises. Guess the material of the capillary tube.
Answer:
Paraffin wax.

Question 30.
(a) Smaller the angle of contact better is the detergent. Is it correct?
Answer:
Yes, because the smaller the angle of contact, the more is the area over which it can spread.

(b) When a glass window is smeared with glycerine, the raindrops don’t stick to the glass. Why?
Answer:
The smearing of glycerine increases the angle of contact from acute to obtuse.

Question 31.
(a) Why is it difficult to fill mercury in the glass tube of a mercury thermometer?
Answer:
This is because mercury descends and not ascends in the glass tube.

(b) Can you decide whether a liquid will rise or get depressed in a capillary tube by observing the shape of the liquid meniscus?
Answer:
If the liquid meniscus is concave then the liquid will rise and if it is convex, then the liquid will be depressed.

Question 32.
(a) Why water rises to different heights in capillaries of different bores?
Answer:
This is because the capillary rise is inversely proportional to the radius of the capillary tube.

(b) Why clothes become waterproof when the wax is rubbed on them?
Answer:
When the wax is rubbed on clothes, the capillaries formed in the threads disappear.

Question 33.
Why Teflon is coated on the surface of a non-stick pan?
Answer:
The Teflon coating increases the angle of contact from acute to obtuse as the adhesive force between Teflon and most of the dishes is very small as compared to uncoated pan and dishes.

Question 34.
‘How a damp proof layer increases the life of the plaster of the wall?
Answer:
Bricks have fine capillaries through which water rises. The damp-proof layer breaks these capillaries.

Question 35.
Why wet ink is absorbed by blotting paper?
Answer:
Blotting paper has fine pores which act as capillaries. The ink rises in these capillaries and hence is absorbed by the blotting paper.

Question 36.
Why greased cotton soaks less than ordinary cotton?
Answer:
This because the presence of grease reduces the effect of surface tension.

Question 37.
A capillary tube is dipped vertically in water in a state of weightlessness. To what height shall the water rise?
Answer:
The water shall rise to the full available length of the capillary tube.

Question 38.
Why the addition of flux makes soldering easy?
Answer:
The addition of flux reduces the surface tension of the molten tin. So the molten tin can spread easily. This makes soldering easy.

Question 39.
A tiny liquid drop is spherical but a larger drop has an oval shape. Why?
Answer:
In the case of a tiny drop, the force of surface tension dominates the force of gravity. But in the case of a large drop, the force of gravity dominates the force of surface tension.

Question 40.
If instead of freshwater, seawater is filled in the tank, will the velocity of efflux change?
Answer:
No, because the velocity of efflux is independent of the density of the liquid.

Question 41.
What is coming out of a hole made in the wall of a freshwater tank? If the size of the hole is increased,
(a) will the velocity of efflux of water change?
Answer:
The velocity of efflux will remain the same as it only depends upon the depth of orifice below the free surface of the water.

(b) will the volume of the water come out per second change?
Answer:
The volume will change since the volume of the liquid flowing out per second is equal to the product of the area of the hole and the velocity of the liquid flowing out.

Question 42.
(a) What is the effect on the equilibrium of a physical balance when air is blown below one pan?
Answer:
Velocity increases and thus pressure will decrease below that pan, hence it will go down.

(b) At what temperature, the surface tension of a liquid is zero?
Answer:
At the critical temperature, the surface tension of a liquid is zero.

Question 43.
What is the effect of solute on the surface tension of liquid?
Answer:
In case, the solute is very easily soluble, then the surface tension of liquid increases e.g. when salt is dissolved in water. If the solute is less soluble, then the surface tension of liquid decreases e.g. by adding soap or phenol in water.

Question 44.
What is the effect of pressure on the coefficient of viscosity of fluids?
Answer:
With the increase in pressure, the viscosity of liquids increases but the viscosity of water decreases, whereas the viscosity of gases remains unchanged.

Question 45.
Why the force required by a man to move his limbs immersed in water is smaller than the force required for the same movement in air?
Answer:
The upthrust of water apparently reduces the weight of a man in the water. So it is easier for him to move his limbs in water than in air.

Question 46.
What is:
(a) velocity head,
Answer:
\(\frac{\mathrm{v}^{2}}{2 \mathrm{~g}}\)

(b) pressure head,
Answer:
\(\frac{P}{\rho g}\)

(c) gravitational head?
Answer:
h

(d) Write down the following liquids in the order of increasing surface tension at a given temperature: w^ter, mercury, soap solution?
Answer:
soap solution, water, mercury.

(e) Is Bernoulli’s Theorem valid for viscous liquids?
Answer:
No.

Question 47.
What are the characteristics of a non-viscous fluid?
Answer:

1. It must be incompressible i.e. density should be constant.
2. It should have no viscosity.

Question 48.
Why hot soup tastes better than cold soup?
Answer:
Hot soup has comparatively less surface tension than cold soap. So hot soap spreads over a larger area than cold soap.

Question 49.
(a) Define critical velocity.
Answer:
It is defined as the velocity of flow of a liquid up to which its flow is streamlined and above which its flow becomes turbulent.
i.e. V_c = \(\frac{N_{R} \eta}{\rho D}\)

(b) What is Reynolds number?
Answer:
It is a pure number that determines the nature of the flow of the liquid through a pipe.
N_R = \(\frac{\mathrm{V}_{\mathrm{c}} \rho \mathrm{D}}{\eta}\)

Question 50.
The accumulation of snow on the wings of an airplane reduces the lift. Why?
Answer:
When snow accumulates on the wings of an airplane, the structure of the wings no longer remains as that of an aerofoil. Hence, the lift is reduced.

Mechanical Properties of Fluids Important Extra Questions Short Answer Type

Question 1.
A glass bulb is balanced by an iron weight in an extremely sensitive beam balance covered by a bell jar. What shall happen when the bell jar is evacuated?
Answer:
The upthrust on the bulb is larger than the upthrust on the iron weight. When the bell jar has evacuated the upthrust on both the bulb and the iron weight become zero. Clearly, the bulb is affected more than the iron weight. Thus the pan containing the bulb shall go down.

Question 2.
It is easier to swim in seawater than in river water. Why?
Answer:
Due to the presence of salt, the density of seawater is more than that of river water. Hence seawater offers more upthrust as compared to river water. Therefore a lesser portion of our body is submerged in, seawater as compared to river water. Hence it is easier to swim in sea-water than in river water.

Question 3.
Does Archimedes’ Principle hold in a vessel in free fall or in a satellite moving in a circular orbit?
Answer:
A vessel in free fall or in a satellite moving in a circular orbit is in the state of weightlessness. It means the value of ‘g’ is zero. Thus the weight of the vessel and upthrust will be zero. Hence Archimedes’ Principle does not hold good.

Question 4.
A block of wood floats in a pan of water in an elevator. When the elevator starts from rest and accelerates downward, does the 1 block floats higher above the water surface? What happens when the elevator accelerates upward? *
Answer:
When the elevator accelerates downward, the weight of the block of wood decreases. Hence it will float higher above the water’s surface.

When the elevator accelerates upward, the weight of the block increases, and hence it will float lower the water surface.

Question 5.
The thrust on a human being due to atmospheric pressure is about 15 tons. How human being can withstand such an enormous thrust while it is impossible for him to carry a load of even one ton?
Answer:
There is a large number of pores and openings on the skin of a body. Through these openings, air goes within the system and there is free communication between the inside and the outside. The presence of; the air inside the body counterbalances the pressure outside.

Question 6.
Why are sleepers used below the rails? Explain.
Answer:
When sleepers are placed below the rails, the area of the cross- p section is increased. We know that P = F/A, so when the train runs on the rails, the pressure exerted on the ground due to the weight of the train is small because of a large area of cross-section of the sleeper. Hence the ground will not yield under the weight of the train.

Question 7.
The passengers are advised to remove the ink from their f pens while going up in an airplane. Explain why?
Answer:
With the increase in height, the atmospheric pressure decreases. The ink in the pen is filled at the atmospheric pressure on the surface of the earth. So as the plane rises up, the pressure decreases \ and the ink will flow out of the pen from higher pressure to the low ‘pressure region. This will spoil the clothes of passengers.

Question 8.
Why a sinking ship often turns over as it becomes immersed in water?
Answer:
When the ship is floating, the metacenter of the ship is above the center of gravity. While sinking the ship takes in water and as a result, the center of gravity is raised above the metacenter. The ship turns over due to the couple formed by the weight and the buoyant force.

Question 9.
Explain why a balloon filled with helium does not rise in the air indefinitely but halts after a certain height?
Answer:
The balloon initially rises in the air because the weight of the displaced air i.e> upthrust is greater than the weight of the helium and the balloon. Since the density of air decreases with height, therefore, the balloon halts at a particular height where the density of air is such that the weight of air displaced is just equal to the weight of helium gas and the balloon. Hence the net force acting on the balloon is zero and the balloon stops rising.

Question 10.
A light ball can remain suspended in a vertical jet of water flow?
Answer:
The region where the ball and the vertical jet of water are in contact is a region of low pressure because of higher velocity. The pressure on the other side of the ball is larger. Due, to the pressure difference, the ball remains suspended.

Question 11.
In the case of an emergency, a vacuum brake is used to stop the train. How does this brake work?
Answer:
Steam at high pressure is made to enter the cylinder of the vacuum brake. Due to high velocity, pressure decreases in accordance with Bernoulli’s principle. Due to this decrease in pressure, the piston gets lifted. Hence the brake gets lifted.

Question 12.
Why dust generally settles down in a closed room?
Answer:
Dust particles may be regarded as tiny spheres. They acquire terminal velocity after having fallen through some distance in the air. Since the terminal velocity varies directly as the square of the radius therefore the terminal velocity of dust particles is very small. So they settle down gradually.

Question 13.
How will the rise of a liquid be affected if the top of the capillary tube is closed?
Answer:
The air trapped between the meniscus of the liquid and the closed end of the tube will be compressed. The compressed air shall oppose the rise of liquid in the tube.

Question 14.
What are buoyancy and the center of buoyancy?
Answer:

1. The upward thrust acting on the body immersed in a liquid is called buoyancy or buoyant force.
2. The center of buoyancy is the center of gravity of the displaced liquid by the body when immersed in a liquid.

Question 15.
Under what conditions:
(a) Centre of buoyancy coincides with the center of gravity?
Answer:
For a solid body of uniform density, the center of gravity coincides with the center of buoyancy.

(b) The center of buoyancy does not coincide with the center of gravity?
Answer:
For a solid body having different densities over different parts, its center of gravity does not coincide with the
center of buoyancy.

Question 16.
Why small pieces of camphor dance about on the surface of the water?
Answer:
When the camphor is dissolved in water, the surface tension of water is reduced. Since camphor has an irregular shape therefore it may dissolve more at one end than at the other end. This produces an unbalanced force due to which it moves. When it reaches a different region, the same process is repeated.

Question 17.
On what factors does the critical velocity of the liquid depend?
Answer:
Critical velocity (v_c) of a liquid is:

1. Directly proportional to the coefficient of viscosity of the liquid.
2. Inversely proportional to the density of the liquid i.e. v_c ∝ \(\frac{1}{ρ}\)
3. Inversely proportional to the diameter of the tube through which it flows
   i. e. vc ∝ \(\frac{1}{D}\)

Question 18.
What are the two forces which determine the shape of a liquid drop?
Answer:
The shape of a liquid drop is determined by the interplay of two forces – gravitational force and the force of surface tension. The gravitational force tries to flatten the drop so that the center of gravity comes at the lowest point.

On the other hand, the force of surface tension tends to give the drop a spherical shape.

Question 19.
A drop of oil placed on the surface of water spreads out. But a drop of water placed on oil contracts to a spherical shape. Explain both the phenomenon
Answer:
A drop of oil placed on the surface of water spreads because the force of adhesion between water molecules and oil molecules dominates the cohesive force-of oil molecules. So oil drop on water spreads.

On the other hand, the cohesive force of water molecules dominates the adhesive force between water and oil molecules. So drop of water c on oil contracts to a spherical shape.

Question 20.
Why are the droplets of mercury when brought in contact pulled together to form a bigger drop? Also, a state with reasons whether the temperature of this bigger drop will be the same or more or less than the temperature of the smaller drop.
Answer:
It is due to large cohesive forces acting between the molecules of mercury that the droplets of mercury when brought in contact pulled together to form a bigger drop.

Question 21.
Oil spreads over the surface of the water. Why?
Answer:
The surface tension of oil is smaller than that of water. When oil is dropped on the surface of the water, the force stretches the oil drops on all sides. Hence the oil spreads over the surface of the water.

Question 22.
Why is it easier to skate on ice than on a smooth aluminum sheet?
Answer:
The ice below the feet of the person smelts on account of increased pressure. Tiny drops of water are formed. These behave like ‘rollers’ and thus it is easier to skate on ice. No such thing is possible in the case of aluminum sheets.

Question 23.
What are the factors on which angle of contact depends?
Answer:
It depends upon the following factors:

1. The nature of the solid and the liquid in contact.
2. The cleanliness of the surfaces in contact.
3. The medium above the free surface of the liquid.

Question 24.
Prove Archimedes’ Principle mathematically.
Answer:
Let W₁ and W₂ be the weights of the body in the air and when completely immersed in a liquid respectively.

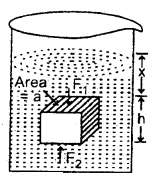
∴ Loss in weight of body inside the liquid = W₁ – W₂.

Proof: Let h = height of a body lying at a depth X below the free surface of a liquid of density p.
Let a = area of the face of the body parallel to the horizontal.

If P₁ and P₂ be the pressures at the upper and lower face of the
P₁ = x ρg ….(i)
P₂ = (x + h) ρg …(ii)

If F₁ and F₂ be the thrust on the upper and lower face of the body, then
F₁ = P₁a = xρag …(iii)
and acts vertically downward.

and F₂ = P₂a = (x + h) ρag …. (iv)
and acts vertically upward.

As F₂ > F₁, so net thrust acts on the body in the upward direction and is called upthrust (U)

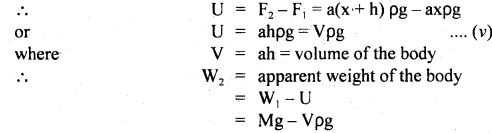
As V = volume of the body = volume of liquid displaced by the body, so Vρ is the mass of the liquid displaced
∴ Vρg = weight of the displaced liquid

Thus loss in weight of the body when sunk in the liquid = weight of the liquid displaced.

Question 25.
Derive the condition of floatation of the body.
Answer:
When a body floats in a liquid with a part submerged in the liquid, the weight of the liquid displaced by the submerged part is always equal to the weight of the body.

Let V = volume of the body
σ = density of its material
ρ = density of the liquid in which the body floats such that its volume V ‘ is outside the liquid

Then the volume of the body inside the liquid = V – V’
Weight of the displaced liquid = (V – V’) ρg
Also weight of the body = Vσg

For the body to float,
weight of the liquid displaced by the submerged part = weight of the body.

Question 26.
(a) Why the wings of an airplane are rounded outwards (i.e. more curved) while flattened inwards? What is this shape called?
Answer:
The special design of the wings which is slightly convex upward and concave downward increases velocity at the upper surface and decreases it at the lower surface. So according to Bernoulli’s Theorem, the pressure on the upper side is less than the pressure on the lower side.

This difference of pressure provides the additional thrust on the foil called lift. This is called airfoil or aerofoil. It is a solid piece that is so shaped that it an upward vertical. force is produced on it when it moves horizontally through the air.

(b) What is an ideal liquid?
Answer:
A liquid is said to be ideal if:

1. It is incompressible.
2. It is non-viscous.
3. Its flow is steady i.e. stream-line.

Question 27.
What is a hydrostatic paradox? Explain. Is it really a paradox?
Answer:
It is defined as the inability of a liquid to flow from a vessel having more liquid to a vessel having lesser liquid when the liquid level is the same. Consider three vessels of different shapes but the same base area as shown., The level of water is kept the same in A, B, and C. So the quantity of water is different in the vessels. However, the thrust on the bottom is the same in all of them. It may appear paradoxical

We know that

1. the pressure at a point depends on the height of the liquid column.
2. It does not depend on the quantity of the liquid and
3. thrust is the product of pressure and area of the surface. ,

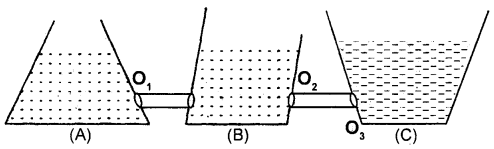
In the given three cases the pressure at the base is hρg and since the area of the base is the same in all the three cases hence the thrust = hρg a where a = area of the base

So, we see that the thrust is the same in A, B, and C even though the quantity of liquid is different in them.

No. In fact, there is no paradox as such because the pressure depends on the depth of point and not on the quantity of liquid. Here O₁, O₂, and O₃ lie in the same horizontal plane, so the pressure is the same.

Question 28.
State Pascal’s law. How does it get changed in the presence of gravity?
Answer:
Pascal’s law states that for a liquid in equilibrium, the pressure is the same everywhere (provided the effect of gravity can be neglected), It may also be stated as “the pressure applied anywhere on an enclosed fluid is transmitted equally in all directions throughout the fluid”.

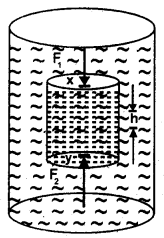
Effect of gravity: Consider a liquid of density p contained in a vessel. Let us find the pressure difference between the points x and y. Let us imagine a cylinder of liquid whose faces 1 and 2 are at height h. The cylinder is in equilibrium.

Let P₁ = Pressure at face 1, pressure P₂ at face 2 and the weight of the liquid in cylinder mg. Here m is the mass of the imaginary fluid cylinder. If F, and F, be the forces on the upper and lower faces of the cylinder, then F₁ = P₁ A₁, F₂ = P₂A₂. As the cylinder of liquid is in equilibrium, so the net force on it is zero.
i.e. (F₁ + mg) – F₂ = 0
or P₁A + mg – P₂A = 0
or (P₂ – P₁)A = mg

where A is the base area of the imaginary cylinder. Since mass of the liquid cylinder
m = Vρ = Ahρ (∵ V = Ah)
∴ (P₂ – P₁)A = Ahρg
or (P₂ – P₁) = hρg

If the point x lies on the surface, then P₁ = 0 and Let P₂ = P
∴ P = hρg
Equation (1) gives the expression for the pressure applied by a liquid column of height h.

Question 29.
Draw a diagram showing the construction of a hydraulic brake.$Iow does it work?
Answer:
The diagram showing various parts of a hydraulic brake is given here.

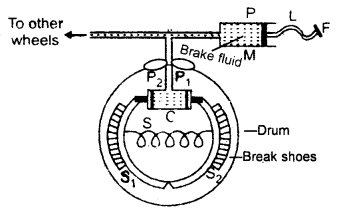
On applying foot pressure on the pedal, the brake fluid flows*from the master cylinder transmitting the pressure from P₁ to P₂ equally.

This expands the brake shoe and stops the wheel. When pressure is released at the foot pedals, the spring brings the brake shoe to its original position and brake fluid is forced back to the master cylinder.

Question 30.
Stake’s law deals with spherical bodies moving through a viscous fluid. Give its statement and derive it dimensionally.
Answer:
Stake’s law may be stated as “the viscous drag experienced by a spherical body of radius r moving in a fluid of viscosity η with a terminal velocity v is given by
F = 6πηrv

Derivation: Let F depends on η, r, and v, we can write
F = kη_ar_bv_c ….(1)
where k = Proportionality constant.
On writing dimensional formula on both sides, we have

∴ a = 1, b = 1, c = 1

∴ Putting values of a, b, c in equation (1), we get
F = kη₁r₁V₁
= kηrv.

For spherical bodies Stoke found k to be 6π
∴ F = 6ηπrv
Hence, derived.

Mechanical Properties of Fluids Important Extra Questions Long Answer Type

Question 1.
(a) Derive the expression for excess pressure inside:
(i) a liquid drop.
Answer:
Let r = radius of a spherical liquid drop of center O.
T – surface tension of the liquid. Let p_i and p₀ be the values of pressure inside and outside the drop.

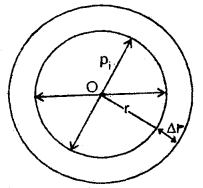
∴ Excess of pressure inside the liquid drop = p_i – p₀

Let Δr be the increase in its radius due to excess pressure. It has one free surface outside it.
∴ increase in surface area of the liquid drop.
= 4π (r + Δr)² – 4πr²
= 4π [r² +(Δr)² + 2r Δr – r²]
= 8πr Δr ….(i)
(∵ Δr is small Δr² is neglected.)

∴ increase in surface energy of the drop is
W = surface tension × increase in area
= T × 8πr Δr ….(ii)

Also W = Force due to excess of pressure × displacement
= Excess of pressure × area of drop × increase in radius

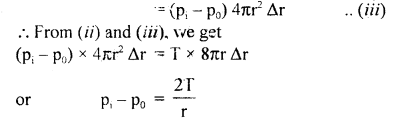
(ii) a liquid bubble.
Answer:
In a liquid bubble: A liquid bubble has air both inside and outside it and therefore it has two free surfaces.
r, Δr, T = ? as above
Thus increase in its surface area

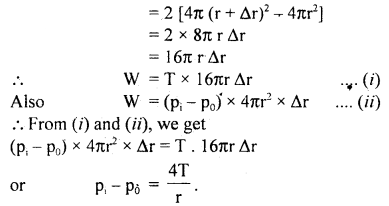
(iii) an air bubble.
Answer:
Inside an air bubble: Air bubble is formed inside the liquid, thus an air bubble has one free surface inside it and a liquid is outside.
If r = radius of the air bubble.
Δr = increase in its radius due to excess pressure (p_i – p₀) inside it.
T = surface tension of the liquid in which bubble is formed.

∴ increase in surface area

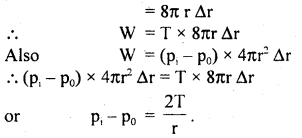
(b) Derive the relation between the surface tension and the surface energy.
Answer:
Let ABCD be a rectangular frame of wire. Let LM be a slidable cross-piece. Now dip the wireframe in the soap solution so that a film is formed over the frame. Due to surface tension, -the film has a tendency to shrink, and thereby, the cross-piece LM will be pulled in an inward direction which can be kept in its position by applying an equal and opposite force F on it.
F = T × 2l
where T = surface tension and l = length of LM.

It has been taken 2l as the film has two free surfaces.
Let x = small distance by which LM moves to L’M’.

∴ 21 × x = increase in the area of the film if W – work done in increasing the area by 2l × x, then
W = F × x = (T × 2l) × x

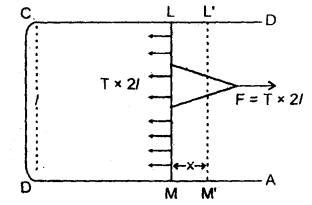
If U be the surface energy, then by definition
U = \(\frac{\text { Work done in increasing the surface area }}{\text { increase in surface area }}\)
= \(\frac{\mathrm{T} \times 2 l \times \mathrm{x}}{2 l \times \mathrm{x}}\)
U = T
Thus U is numerically equal to the surface energy.

Question 2.
(a) Derive the expression for terminal velocity.
Answer:
When a spherical body is dropped in a viscous fluid, it is first accelerated and then the acceleration becomes zero and it attains a constant velocity VT called terminal velocity.

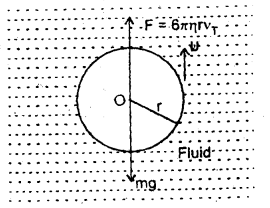
Let r = radius of the spherical body falling through a viscous medium having a coefficient of viscosity η and density σ.
Let ρ = density of the material of the body.

The various forces acting on it are:
(i) its weight (W) acting in a vertically downward direction and

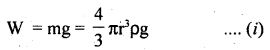
(ii) Upthrust (U) equal to the weight of the fluid displaced and is given by
U = \(\frac{4π}{3}\)r3 σg …..(ii)
and its acts vertically upward.

(iii) Viscous force (F) acting upward and according to Stoke’s Law,
F = 6πηrv₁ …. (iii)

where v_T = terminal velocity
when the body attains v_T, the net force on it is zero.
i.e. upward force = downward force

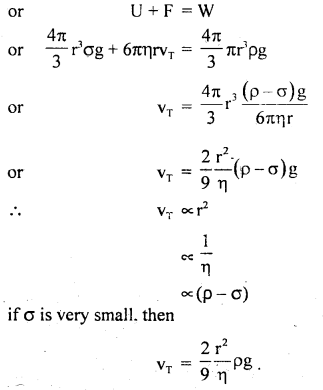
(b) Derive the equation of continuity.
Answer:
Consider a liquid flowing through a pipe AB of the varying area of cross-section.

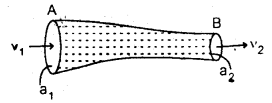
Let a₁ and a₂ be its area of the cross-section at points A and B respectively.

Let v₁ and v₂ be the velocities of the liquid at A and B respectively whereas ρ₁ and ρ₂ are the densities of the liquid at A and B respectively.

∴ The volume of liquid entering per second at point A = a₁v₁
and Volume of liquid leaving per second at point B = a₂V₂

∴ masses of the liquid per second entering at A and leaving at B are given by
m₁ = a₁v₁ρ₁
and m₂ = a₂v₂ρ₂

If there is no source or sink of the liquid along the length of the pipe, then

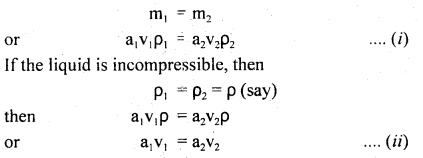
Equation (ii) is the required expression for the equation of continuity for the steady flow of an incompressible and non-viscous liquid.

(c) Describe the principle and action of a hydraulic lift giving a simple diagram.
Answer:
Principle: This device uses Pascal’s law. It is an arrangement used to multiply force. It consists of two cylinders C and C’ of different areas of cross-section fitted with frictionless pistons connected to each other with a pipe.

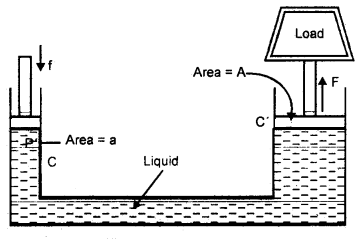
Action: In hydraulic lift greater force is generated using a smaller force.

Let a, A = area of cross-section of smaller and bigger cylinders respectively,
f = force applied on the smaller piston.
P = pressure applied on the liquid f
∴ P = \(\frac{f}{a}\)

According to Pascal’s law, the same pressure is transmitted to the larger piston.
If F be the force transmitted to the larger piston, then

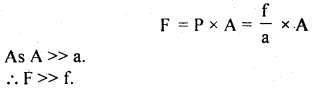
Thus a heavy load placed on the larger piston is lifted easily.

Question 3.
(a) Prove mathematically Bernoulli’s Theorem.
Answer:
It states that

Proof: Imagine an incompressible and non-viscous liquid flowing through a pipe AB of varying cross¬sectional area as shown in Fig. It enters from A and leaves

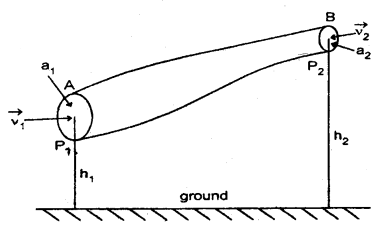
Let a₁ and a₂ be its area of the cross-section at A and B respectively such that a₁ > a₂.

P₁ and P₂ be the pressures due to liquid at ends A and B respectively such that P₁ > P₂ as the liquid flows from high to low pressure.

Also, let v₁ and v₂ be the velocities of the liquid at A and B respectively.
ρ = density of the liquid,
m = mass of liquid flowing per second from A to B.

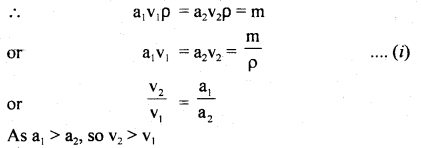
Work done per second on the liquid at end A
= pressure × area × velocity
= P₁a₁v₁ …. (ii)
and work done per second by the liquid at end B
= P₂a₂v₂ …. (iii)

∴ Net work done per second on the liquid by the pressure energy in moving the liquid from A to B

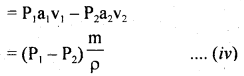
When m flows in one second from end A to B, its height increases from h₁ to h₂, and velocity increases from v₁ to
v₂.

∴ increase in potential energy / second from end A to B
= mgh₂ – mgh₁ …. (v)

∴ increase in K.L. second from end A to B

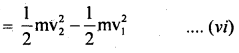
∴ According to the work-energy theorem, work done by pressure energy/second = increase in (K.E. + P.E.) per second

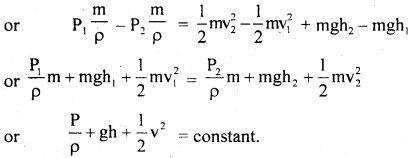
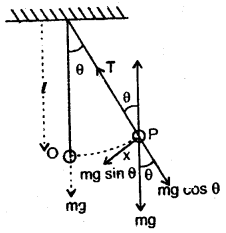
(b) Derive the Ascent formula.
Answer:
Let r = radius of a capillary tube immersed in a liquid
like water having surface tension T.
θ = angle of contact
ρ = density of liquid
R = radius of the meniscus
P = atmospheric pressure
Let h = height up to which the liquid rises in the capillary tube.

Let A and B be two points in the capillary tube where A is just above the meniscus and B is just below it. Now the pressure on the convex side is less than that on the concave side.
Pressure at A = P
Pressure at B = P – \(\frac{2T}{R}\)

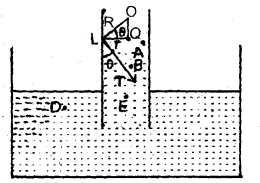
The liquid rises in the capillary tube so that pressure at points D and E which lie at the same horizontal level in the liquid become equal.

i.e. Pressure at E = Pressure at D = P
∴ Pressure at E = Pressure at B + Pressure due to liquid column of height h

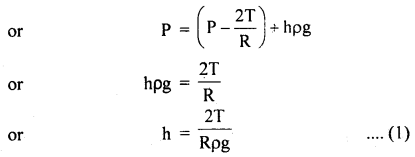
To calculate R: Let O be the center of curvature of the liquid meniscus.
∴ θ = angle of contact

Now in rt. angled ΔOQL

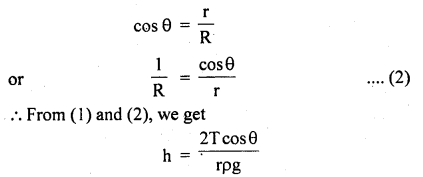
which is the required formula.

Numerical Problems:

Question 1.
Express standard atmospheric pressure in
(a) Nm^-2
(b) bars
(c) millibars
(d) Torr
Answer:
We know that standard atmospheric pressure is
P = 76 cm of Hg
h = 760 cm = 0.76 m
p = 13.6 × 10³ kg m^-3
g = 9.8 ms^-2

Question 2.
A piece of alloy haš a mass of 250 g in air. When immersed in water, it has an apparent weight of 1.96 N and when immersed in oil, it has an apparent weight of 2.16 N. Calculate the density of
(a) metal
Answer:
Weight of metal in the air.

weight of metal in water,
W_w = 1.96N
weight of metal in oil, W_oil = 2.16N

(a) weight of water displaced = W_a – W_w
= 2.45 – 1.96 = 0.49 N

∴ mass of water displaced,

= 5000 kg m³
= 5 gm cm³

(b) oil.
Answer:

Question 3.
A copper cube of mass 0.50 kg is weighed in water (ρ = 10³ kg m^-3). The mass comes out to be 0.40 kg. Is the cube hollow or solid? Given density of copper = 8.96 × 10³ kg m^-3.
Answer:
Let V be the volume of the cube, then according to Archimedes’ principle,
Loss of weight in water = weight of water displaced …. (i)

Here, mass in air, m_a = 0.5 kg
mass in water, m_w = 0.4 kg …. (ii)
ρ of water = 10³ kg m³.
∴ From (i) and (ii), we get

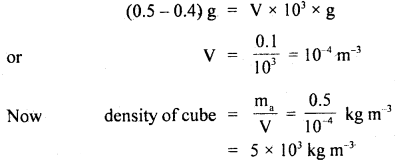
which is less than the density of copper (8.96 × 10³ kg m^-3). So the cube must be hollow.

Question 4.
A piece of pure gold (ρ = 9.3 g cm^-3) is suspected to be hollow. It weighs 38.250 g in air and 33.865 in water. Calculate the volume of the hollow portion in gold, if any.
Answer:
Density of pure gold, ρ = 9.3 g cm³ ,
mass of gold piece, M = 3 8.250 g

∴ volume of the gold piece, V = \(\frac{\mathrm{M}}{\mathrm{p}}=\frac{38.250}{9.3}\)
= 4.113 cm³

Also mass of gold piece in water
m’ = 33.865 g
∴ apparent loss in mass of the gold piece in water = (M – m’)
= (38.250 – 33.865)g
= 4.3.85 g

ρ_water = 1 g Cm^-3

∴ volume of displaced water = \(\frac{\mathrm{m}}{\rho}=\frac{4.385}{1}\)cm^-3
= 4.385 cm^-3

∴ volume of the hollow portion in the gold piece
= 4.385 – 4.113
= 0.272 cm^-3.

Question 5.
A glass plate of length 20 cm, breadth 4 cm, and thickness 0.4 cm weights 40 g in air. If it is held vertically with the long side horizontal and the plate half breadth immersed in water, what will be its apparent weight, the surface tension of water = 70 dyne cm^-1.
Answer:
Here, l = 20 m, b = 4 cm , t = 0.4 cm, T = 70 dyne cm^-1

Following three forces are acting on the plate:

1. Weight of the plate, W = 40 grand actings vertically downward.
2. Force due to surface tension acting vertically downward.

If F be the force due to surface tension, then

(iii) Upthrust, U = Vρg


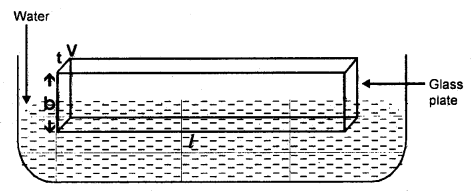
∴ Net weight = W + F – U
= 40 + 2.9143 – 16
= 26.9143 gf

Question 6.
(a) What is the work done in blowing a soap bubble of diameter 0.07 m?

Answer:
(a) Here, initial radius of soap bubble, r₁ = 0
Final radius of soap bubble, r₂ = 0.035 m (∵ D₂ = 0.07m)
Increase in surface area of soap bubble

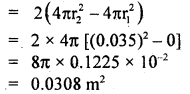
surface tension of soap solution = T = 0.04 Nm^-1
∴ work done to blow soap bubble = increase in area × T
= 0.0308 × 0.04
= 1.232 × 10^-3

(b) If 3.6960 × 10³ J of work is done to blow it further, find the new radius. Surface tension of soap solution is 0.04 Nm1.
Answer:
Let r be the new radius =?

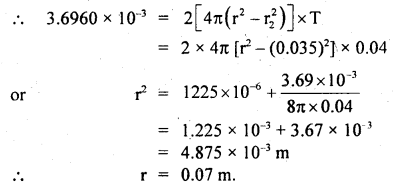
Question 7.
Aspherical mercury drop of 10^-3 m radius is sprayed into million drops of the same size. Find the energy used in doing so. Surface tension of Hg = 0.55 Nm^-1.
Answer:
Here, R = 10^-3 m
Number of small drops, n = 106
T = 0.55 Nm^-1

Let r = radius of small drop
Since volume before spraying = volume after spraying

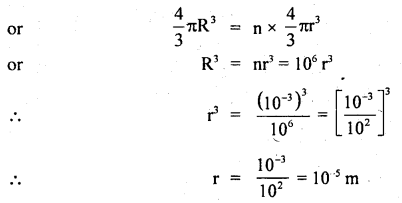
Also the surface area of bigger drop = 4πR²
The surface area of 106 smaller drops = 106 × πr²

∴ increase in surface area,

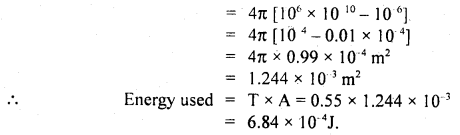
Question 8.
A liquid drop of diameter D breaks up into 27 tiny drops. Find the resulting change in energy.
Answer:
Let R be the radius of a bigger drop.
and r be the radius of smaller drop.


∴ Increase in area = 3πD² – πD² = 2πD²
T = surface tension of the liquid

∴ increase in energy = increase in area × T
= 2πD² × T.

Question 9.
Find the height to which water at 4°C will rise in a capillary tube of 10^-3 m diameter. Take g = 9.8 ms^-1. Angle of contact, θ = 0° and T = 0.072 Nm^-1.
Answer:
Here,

Question 10.
If a 5 cm long capillary tube with 0.1 mm internal diameter and open at both ends is slightly dipped in water having surface tension = 75 dynes cm^-1, explain whether water will flow out of the upper end of the capillary or not.
Answer:
Here,

Let h = height up to which water rises =?

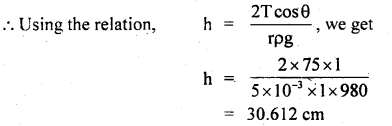
Let h’ be the height of the capillary tube
∴ h’ = 5 cm
‘ Now water will rise to ..the upper end but will not overflow. It will adjust its radius of curvature (R) such that

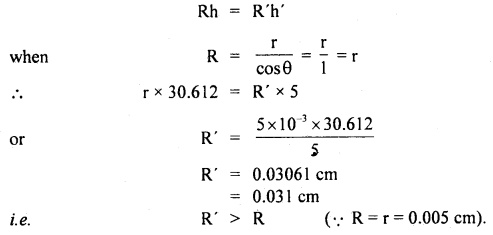
Question 11.
Water is escaping from a vessel through a horizontal capillary tube 20 cm long and 0.2 mm radius at a point 100 cm below the free surface of the water in the vessel. Calculate the rate of flow if the coefficient of viscosity of water is 1 × 10^-3 PaS.
Answer:
Here, l = 20 cm = 0.20 m
r = 0.2mm = 2 × 10⁴ m
h = 100 cm = 1 m
p = 10³ kg m³
η = 1 × 10³ PaS
∴ P = hpg= 1 × 10³ × 9.8 Nm^-2

Let V = rate of flow = volume of water flowing per second =?

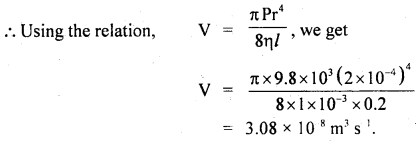
Question 12.
8 spherical raindrops of equal size are falling vertically through the air with a terminal velocity of 6.1 ms^-1. What should be the velocity if these 8 drops were to combine to form a bigger spherical drop.
Answer:
Here, v_T = 0.1 ms^-1
= terminal vol. of small drop

Let v ‘T be the terminal velocity of bigger drop Let r and R be the radius of smaller and bigger drop respectively.
Using the relation,

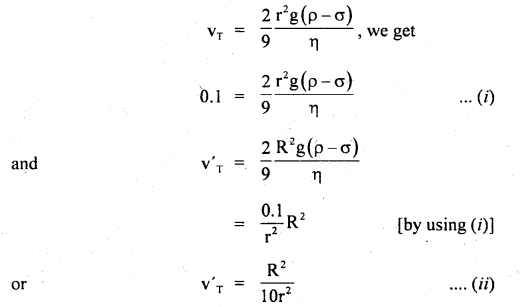
Also volume of bigger drop = Volume of 8 small drops

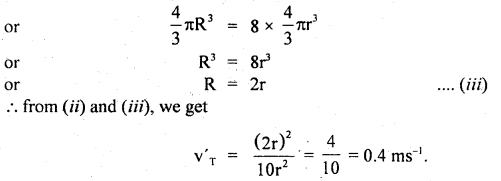
Question 13.
A pitot tube is mounted on an airplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm as shown here. What is the speed of the plane relative to air? Given relative density of alcohol = 0.8 and density of air = 1 kg m^-3.

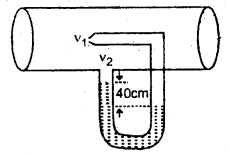
Answer:
Here, the density of air, ρ = 1 kg m^-3
relative density of alcohol = 0.8

∴ density of alcohol = 0.8 × 10³ kg m^-3
Let P₁ = pressure of air at the nozzle.
P₂ = pressure of air at the other end.

P₁ – P₂ = 40 cm of alcohol
= 0.4 m of alcohol
= 0.4 × density of alcohol × g
= 0.4 × 800 × 9.8 Nm^-2.

Let v1 and v2 be the velocity of air at the nozzle and another end respectively. Then using Bernoulli’s theorem,

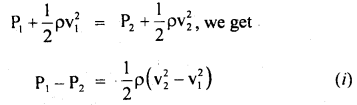
Now as the nozzle of the tube is parallel to the direction of motion of air,

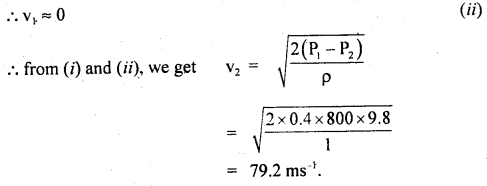
Question 14.
A piece of metal 102 m2 ¡n area rests on a layer of Castrol oil 2 × 10 m thick whose η = 1.55 PaS. Calculate the horizontal force required to move the plate with a speed of 3 × 10² ms^-1.
Answer:

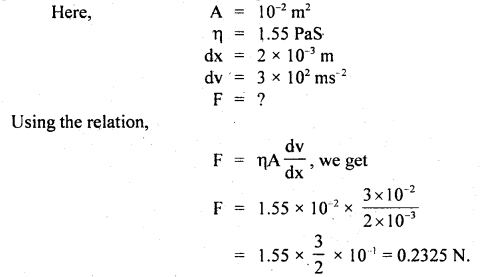
Question 15.
What should be the maximum average velocity of water in a tube of diameter 2 cm so that flow is laminar? The viscosity of water is 0.001 Nm^-2s.
Answer:
Here, D = 2 cm = 0.02 m
ρ = 10³ kg m³
η = 0.001 Nm^-2 s
= 10^-3 Nm^-2 s

Flow of water will be laminar if
N_R = 1000
where N_R is Reynold number

Let v = maximum average velocity.
∴ Using the relation

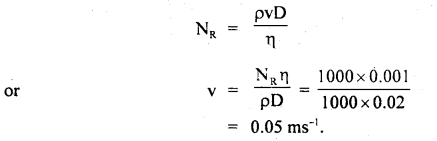
Question 16.
A non-viscous liquid flows through a horizontal pipe of varying cross-section at the rate of 22 m^-3 s^-1. Calculate the velocity at the cross-section where the radius is 5 cm.
Answer:
Here, the volume of liquid flowing per second,

Question 17.
(a) A fish weighs 348 g in air and 23 g in pure water. Calculate the relative density of fish.
Answer:
Here, the weight of fish in air = 348 g
weight of fish in water = 23 g

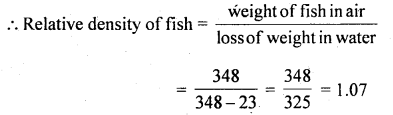
(b) A piece of solid weighs 120 g in air, 80 g in water, and 60 g in a liquid. Calculate the relative density of the solid and that of liquid.
Answer:
Here, the weight of solid in air = 120 g
weight of solid in water = 80 g
weight of liquid = 60 g

∴ (i) Relative density of solid

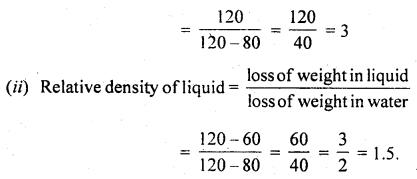
Question 18.
(a) A cubical block of wood of specific gravity 0.5 and a chunk of concrete of specific gravity 2.5 are fastened together. Calculate the ratio of the mass of wood to the mass of concrete which makes the combination float with its entire volume Submerged underwater.
Answer:
(a) Let m_w and m_c be the masses of wood and concrete respectively. Then according to law of floatation, Weight of the water displaced = weight of the body immersed.

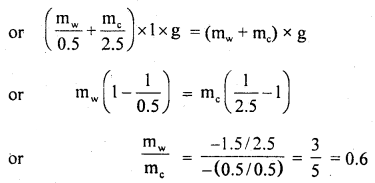
(b) A spring balance reads 10 kg when a bucket of water is suspended from it. What is the reading on the spring? balance when:
(i) an ice cube of mass 1.5 kg is put into the bucket.
Answer:
When the ice cube is put in the bucket, then the total mass of the system suspended from the spring balance will be
10 kg + 1.5 kg = 11.5 kg
so the balance will read 11.5 kg.

(ii) an iron piece of mass 7.8 kg suspended by another string is immersed with half its volume inside the water in the bucket. (Relative density of iron = 7.8)?
Answer:
Relative density of iron = 7.8
so the density of iron = 7.8 × 10³ kg m^-1

This is the buoyant force experienced by iron pieces due to water. The iron piece will exert an equal force on the water in the downward direction. So the reading of the balance will increase by 0.5 kg. Thus the spring will read 10 kg +0.5 kg= 10.5 kg.

Question 19.
The flow rate from the tap of diameter 1.25 cm ¡s 3l/mm. The coefficient of viscosity of water is 10 PaS. Characterize the flow.
Answer:
The volume of liquid flowing per unit time = area × velocity



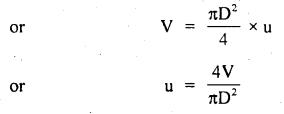
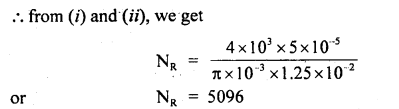
As N_R > 3000, so clearly, the flow will be turbulent.

Question 20.
The flow of blood in a large artery of an anesthetized dog is diverted through a Venturimeter. The wider part of the meter has a cross-sectional area equal to that of the artery, A = 8 mm². The narrow part has an area, a = 4 mm². The pressure drop in the artery is 24 Pa. What is the speed of the blood in the artery? (Given: density of blood = 1.06 × 10³ kg m^-3).
Answer:
Here, a₂= a = 4 mm²
a₁ = A =8 mm²
r = 1.06 × 10³ kg m^-3
P₁ – P₂ = 24 Pa
v₁ = ?

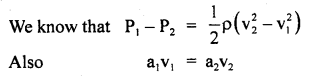
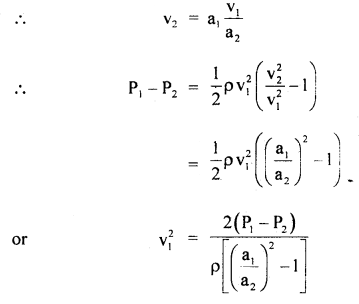
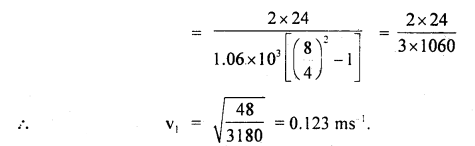
Question 21.
Calculate the minimum pressure required to force the blood from the heart to the top of the head (vertical distance 0.5 m). Assume the density of blood to be 1040 kg m^-3. Friction is neglected, g = 9.8 ms^-2.
Answer:
Here,

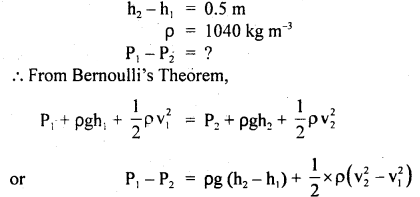
let v₁ = v₂ for minimum pressure difference

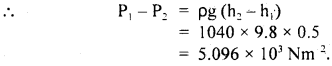
Question 22.
The density of air in the atmosphere decreases with height and can be expressed by the relation p = ρ₀e^-αh where ρ₀ is the density at sea level, a is the constant and h is the height. Calculate the atmospheric pressure at sea level. Assume g to be constant. The numerical values of constants are g = 9.8 ms^-2, ρ₀ = 1.3 kg m^-3 α = 1.2 × 10^-4 m^-1.
Answer:
Here, g = 9.8 ms^-2
ρ₀ = 1.3 kg m^-3
α = 1.2 × 10-4 m^-1
ρ = ρ₀e^-αh

Let dp = pressure due to small air column of length dh at a height h, then
dP = ρ dh g = (ρ₀e^-αh) g dh

∴ Total atmospheric pressure is given by

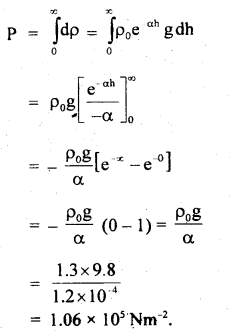
Question 23.
A ring is cut from a platinum tube having 8.5 cm internal and 8.7 cm external diameter. It is supported horizontally from a pan of balance so that it comes in contact with water in a glass vessel. What is the surface tension of water if an extra 3.97 g weight is required to pull it away from water (g = 980 ms^-2)?
Answer:
Here, m = 3.97 gm
r₁ = 8.5 cm
r₂ = 8.7 cm
T = ?
The water is in contact with the inner and outer circumference of the ring. To pull it out, work has to be done against forces due to surface tension.

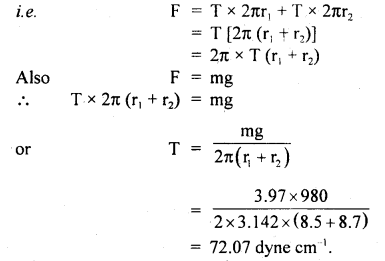
Question 24.
Consider the horizontal acceleration of a mass of liquid in an open tank. Acceleration of this kind causes the liquid surface to drop at the front of the tank and to rise at the rear. Show that the liquid surface slopes at an angle θ with the horizontal where tan θ = \(\frac{a}{g}\), where ‘a’ is the horizontal acceleration, g
Answer:
This situation is shown in the figure here.

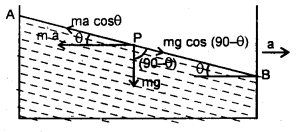
Let a liquid molecule of mass m lies at point P on the sloped surface AB of the liquid.
The different forces acting on this molecule are shown in the figure.
The force ma is due to the reaction and mg is the weight of the molecule.

For equilibrium of the molecule along the sloped surface AB,
ma cos θ = mg cos(90 – θ)
= mg sin θ

As the surface AB is in equilibrium, sp every liquid molecule on it is at rest.
The surface AB becomes inclined to the horizontal at angle 0 s.t.
tan θ = \(\frac{a}{g}\)

Question 25.
A stone of density 2.5 g cm^-3 completely immersed in seawater is allowed to sink from rest. Calculate the depth to which the stone would sink in 2s. The specific gravity of seawater is 1.025 and acceleration due to gravity is 980 cm s^-2. Neglect the effect of friction.
Answer:
Here, g = 980 cm s^-2 .
ρ₁ = density of stone = 2.5 g cm^-3.
Specific gravity of sea water = 1.025
∴ ρ₂ = density of sea water = 1.025 g cm^-3.

Now let m = mass of stone.
∴ V = volume of stone = \(\frac{\mathrm{m}}{\rho}=\frac{\mathrm{m}}{2.5}\) cm .
and this is equal to the volume of the displaced seawater.

∴ M = mass of seawater displaced.
= ρ₂ × V
= 1.025 × \(\frac{m}{2.5}\) gram

∴ Weight of sea water displaced = \(\frac{1.025 \times \mathrm{m}}{2.5}\) × g
If W₁ be the weight of the stone in seawater, then
W₁ = weight of stone – the weight of seawater displaced.

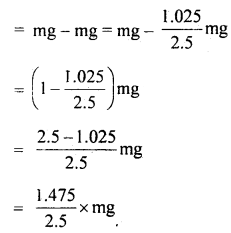
∴ Downward acceleration ‘a’ of stone in seawater is given by

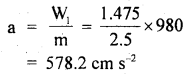
Now let S = depth to which stone sinks. t = 2s, u = 0

∴ Using the relation,

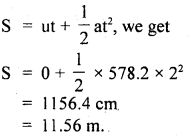
Value-Based Type:

Question 1.
Krishna went sightseeing to a nearby river along with his physics teacher. He noticed that the wind was blowing from the side and the sailboat still continue to move forward. He was surprised. He asked his physics teacher an explanation of this situation. The teacher has noticed his “interest explained the concept through a small example.

The physics of sailing is very interesting in that sailboats do not need the wind to push from behind in order to move. The wind can blow from the side and the sailboat can still move forward.

The answer lies in the well-known principle of aerodynamic
lift Imagine you are a passenger in a car as it’s moving along, and you place your right hand out the window, ff you tilt your hand in the clockwise sense your hand will be pushed backward and up. This is due to the force of the air which has a sideways component and upwards component (therefore your hand is pushed backward and up).
(a) What values could you find- in Krishna?
Answer:
Krishna is very interested in learning the subject; also he is interested in knowing how science helps in understanding the day-to-day experiences, observant, has the courage to ask questions.

(b) Also explain what the Magnus effect is.
Answer:
The difference in velocities of air above the ball is relatively larger than below. Hence, there is a pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called the Magnus effect.

Question 2.
Seema’s mother was suffering from blood pressure but she did not consult any doctor. Prabha was a student of class XI who came to Visit Seema’s mother. Seema was upset as her mother did not want to go to hospital. Prabha convinced her mother by telling the effects of blood pressure on the heart. Finally, both of them able to brought Seema’s mother to a hospital and consulted a doctor.
(i) What values were displayed by Seema?
Answer:
Seema’s values are:
Caring, Sensible, love, and affection to her mother.

(ii) What values were exhibited by Prabha?
Answer:
Prabha’s values are Good knowledge of diseases and their ef- feet, a Helping attitude, willingness to convince and serve someone who needs, Friendly behavior, etc.

(iii) State Bernoulli’s theorem.
Answer:
It states that the total energy (sum of pressure energy, K.E, and P.E) per unit mass is always constant for an ideal fluid.
i.e. \(\frac{\mathrm{P}}{\mathrm{\rho}}\) + gh + \(\frac{1}{2}\)v² = constant

Question 3.
Salma’s little sister was crying. Then she took a piece of camphor and put it in water. By seeing the camphor piece dancing on surface on the surface of the water, the little one stopped crying.
(a) What can you say about the qualities of Salma?
Answer:
Salma is responsible, helps her mother in looking after her younger sister.

(b) Why do small pieces of camphor dance on the surface of the water?
Answer:
When camphor is dissolved in water, the surface tension of water is reduced, Since camphor has an irregular shape, therefore, it may dissolve more at one end than at the other end. This produces an unbalanced force due to which it moves. When it reaches a different region, the same process is repeated.

(c) Define surface tension.
Answer:
It is the property of the liquid by virtue of which the free surface of the liquid at rest tends to have minimum area and as such it behaves like a stretched elastic membrane.

Question 4.
(a)Savitawas surprised to see oil spreading onto the surface of the water and asked her mother to explain why oil spreads onto the surface of the water. Her mother explained to her daughter the reason behind it. By going through the explanation she thought of learning more about the other scientific phenomenon also. What qualities do you can find in Savita?
Answer:
She has inquisitiveness; she wants to know the scientific reason behind the phenomena.

(b) Oil spreads over the surface of water whereas water does not spread over the surface of the oil. Why?
Answer:
The surface tension of the water is more than that of oil, therefore when oil is poured over water the greater value of surface tension of water, pulls the oil in all directions. On the other hand, when water is poured over oil, it does not spread over it because the surface tension of oil is less than that of water.

Question 5.
Vineet saw his uncle planting seeds in the land. His uncle does not know the methods of growing plants. Then he decided to make his uncle aware of this. He explained the importance of plowing the land before planting the seeds. Uncle is convinced with his ideas. He planted accordingly. The plants are grown successfully.
(a) What can you say about Vineet?
Answer:
Vineet has good knowledge of agriculture. He is very much interested in putting his ideas into practice, uses his knowledge to convince his uncle.

(b) What is the utility of plowing a field? Does it help the soil to retain moisture?
Answer:
When the field is plowed, the capillaries are broken. So water cannot rise to the surface and the soil is able to retain its moisture.

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 14 Oscillations. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 14 Important Extra Questions Oscillations

Oscillations Important Extra Questions Very Short Answer Type

Question 1.
(a) A particle has maximum velocity in the mean position and zero velocity at the extreme position. Is it a sure test for S.H.M.?
Answer:
No.

(b) Is restoring force necessary in S.H.M.?
Answer:
Yes.

Question 2.
Imagine a situation where the motion is not simple harmonic but the particle has maximum velocity in the mean position and zero velocity at the extreme position.
Answer:
Projection of a particle in non-uniform circular motion satisfies all the given conditions.

Question 3.
We know that in S.H.M., the time period is given by
T = 2π\(\sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\)
Does T depend upon displacement?
Answer:
No. T is independent of displacement as the displacement term is also contained in acceleration.

Question 4.
(a) Two simple pendulums of equal lengths cross each other at the mean position. What is their phase difference?
Answer:
180° i.e. it radians.

(b) Can a simple pendulum vibrate at the center of Earth? Why?
Answer:
No. This is because the value of g at the center of Earth is zero.

Question 5.
(a) A particle is in S.H.M. of amplitude 2 cm. At the extreme position, the force is 4N. What is the force at a mid-point i.e. midway between mean and extreme position?
Answer:
2N.

(b) What happens to the time period of a simple pendulum if its length is doubled?
Answer:
The time period is increased by a factor of 4l.

Question 6.
Can & simple pendulum be used in an artificial satellite? Why?
Answer:
No. This is because there exists a state of weightlessness in the artificial satellite.

Question 7.
What fraction of the total energy is potential energy when the displacement is one-half of the amplitude?
Answer:
\(\frac{1}{4}\left[\because \frac{P . E}{\text { Total energy }}=\frac{\frac{1}{2} \operatorname{m\omega}^{2}\left(\frac{a}{2}\right)^{2}}{\frac{1}{2} m \omega^{2} a^{2}}\right]\)

Question 8.
What fraction of the total energy is kinetic energy, when the displacement is one-half of the amplitude?
Answer:
\(\frac{3}{4}\left[\because \frac{\text { K.E. }}{\text { Total energy }}=\frac{\frac{1}{2} m \omega^{2}\left(a^{2}-\left(\frac{a}{2}\right)^{2}\right)}{\frac{1}{2} m \omega^{2} a^{2}}=\frac{3}{4}\right]\)

Question 9.
(a) When a particle oscillates simply harmonically, its potential energy varies periodically. If v be the frequency of oscillation of the particle, then what is the frequency of vibration of P.E.?
Answer:
2v

(b) A body executes S.H.M. with a period of \(\frac{11}{7}\) seconds and an amplitude of 0.025 m. What is the maximum value of acceleration?
Answer:

Question 10.
A body of mass m when hung on a spiral spring stretches it by 20 cm. What is its period of oscillation when pulled down, and released?
Answer:
T = 2π\(\sqrt{\frac{20}{980}}=\frac{2 \pi}{7} \mathrm{~s}=\frac{44}{49} \mathrm{~s}\)

Question 11.
A spring-mass system oscillating vertically has a time period T. What shall be the time period if oscillating horizontally?
Answer:
T i.e. it remains the same.

Question 12.
The time period of a body executing S.H.M. is 0.05 s and the amplitude of vibration is 4 cm. What is the maximum velocity of the body?
Answer:
1.6 π ms^-1

Question 13.
A spring-controlled wristwatch is taken from Earth to Moon. What shall be the effect on the watch?
Answer:
There will be no effect on g as the time period of spring is independent of g.

Question 14.
(a) At what displacement, the P.E. of a simple harmonic oscillator is maximum?
Answer:
At the extreme position.

(b) At what displacement, the K.E. of a simple harmonic oscillator is maximum? ‘
Answer:
At the mean position.

Question 15.
What is the total energy of a simple harmonic oscillator?
Answer:
\(\frac{1}{2}\)m ω² r², where r = amplitude, ω = angular frequency, m = mass of the oscillator.

Question 16.
Name the trigonometric functions which are suitable for the analytical treatment of periodic motions. ,
Answer:
Sine and Cosine functions or their linear combination.

Question 17.
How is acceleration (a) related to the displacement (y) in S.H.M.?
Answer:
aα – y.

Question 18.
At what position, the velocity of a particle executing S.H.M. is maximum?
Answer:
At mean position.

Question 19.
What is Force constant (k)? What are its units in the S.I. system?
Answer:
k = Force per unit displacement.
S.I unit of k is Nm^-1

Question 20.
(a) What ¡s the phase difference between displacement and velocity of a particle executing S.H.M.?
Answer:
90° or \(\frac{π}{2}\) radian.

(b) What is the phase difference between displacement and acceleration of a particle executing S.H.M.?
Answer:
180° or π radian.

Question 21.
(a) What will be the change in the time period of a loaded spring when taken to Moon?
Answer:
No change because T = 2π\(\sqrt{\frac{m}{k}}\) i.e. T ¡s independent of g.

(b) Why does the time period (T) of the swing not change when two boys sit on it instead of one?
Answer:
T is independent of the mass of the swing as T = 2π\(\sqrt{\frac{l}{g}}\).

Question 22.
Why are the vibrations of a simple pendulum damped?
Answer:
Because the energy of the pendulum is used to overcome air resistance.

Question 23.
A pendulum clock is taken on a lift moving down with a uniform Velocity. Will it gain dr lose time?
Answer:
It neither gains nor loses time.

Question 24.
What role do shock absorbers play in oscillations of vehicles on a bumpy road?
Answer:
They act as damping devices and save vehicles from resonant oscillations.

Question 25.
When do you apply force as the spring descends while swinging on a swing?
Answer:
To counter the effect of the damping force on the amplitude of oscillations of the swing at an appropriate point.

Question 26.
The time period of oscillation of a sphere hung from a wire attached to a rigid support and given slight rotation about the wire is given by T = 2π\(\sqrt{\frac{I}{C}}\). Which factor out of these is equivalent to the mass factor of an oscillator in S.H.M.?
Answer:
I (moment of inertia) of the sphere is equivalent to m, the mass of an ordinary oscillator in S.H.M.

Question 27.
At what points is the energy entirely K.E. and entirely P.E. in S.H.M.?
Answer:
At mean position and extreme position respectively.

Question 28.
What provides the restoring force for simple harmonic motion in the following cases?
(i) Simple pendulum.
(ii) Spring.
(iii) Column of mercury in a U-tube.
Answer:
The restoring force is provided by:
(a) gravity in simple pendulum i.e. weight of the pendulum.
(b) elasticity in spring.
(c) weight in the column of Hg in a U-tube.

Question 29.
Which single characteristics of a periodic motion distinguishes it as S.H.M?
Answer:
If acceleration is directly proportional to the negative- displacement, then the motion is said to be S.H.M.

Question 30.
(a) Does the bursting of air bubbles at the surface of boiling water show a periodic motion of the surface molecules?
Answer:
No.

(b) Do all periodic motions are S.H.M.?
Answer:
No.

Question 31.
At what point the velocity and acceleration are zero in S.H.M.?
Answer:
The velocity is zero at the extreme points of motion and acceleration is zero at the mean position of motion.

Question 32.
On what factors does the force constant of a spring depend?
Answer:
It Depends Upon the following factors:

1. Nature of the material of the spring.
2. Elasticity (i.e. coefficient of elasticity) of the material of spring.

Question 33.
Which factors determine the natural frequency of an oscillator?
Answer:
The dimensions and the elastic properties of the oscillator.

Question 34.
When a high-speed plane passes by, the windows of the plane start producing sound due to
(i) S.H.M.,
(ii) damped oscillations,
(iii) maintained oscillations. Why?
Answer:
(ii) Damped oscillations are caused due to air pressure on the glass window panes.

Question 35.
A motorcyclist while trying to loop a loop of maximum radius in a death trap goes round in the globe. Is it his projection on diameter in S.H.M.?
Answer:
Yes.

Question 36.
Sometimes on the screen of a cathode-ray oscilloscope, we see rectangular or triangular waves. Are these formed due to S.H.M. of the oscillator connected to it?
Answer:
No, these are not S.H.M. but are periodic waves.

Question 37.
Is oscillation of a mass suspended by a spring simple harmonic?
Answer:
Yes, only if the spring is perfectly elastic.

Question 38.
A diver wearing an electronic digital watch goes down into seawater with terminal velocity v. How will the time in the waterproof watch be affected?
Answer:
It will not be affected as its action is independent of gravity and buoyant force.

Question 39.
When is the tension maximum in the string of a simple pendulum?
Answer:
The tension in the string is maximum at the mean position because the tension in the string = mg cos θ = mg. (∵ θ = 0 at mean position).

Question 40.
Is the damping force constant on a system executing S.H.M.?
Answer:
No, because damping force depends upon velocity and it is more when the system moves fast and is less when the system moves slow.

Question 41.
What is the (a) distance covered by (b) displacement of, a body executing S.H.M. in a time equal to its period if its
amplitude is r?
Answer:
A body executing S.H.M. completes one vibration in a time equal to its period, so the body reaches its initial position after a time equal to its period.
Thus the
(a) total distance traveled is 4r and
(b) displacement is zero.

Question 42.
Can a motion be oscillatory but not simple harmonic? If yes give an example and if no explain, why?
Answer:
Yes. Uniform circular motion is an example of it.

Question 43.
How will the period of a pendulum change when its length is doubled?
Answer:
The time period becomes \(\sqrt{2}\) times the original value as T ∝ \(\sqrt{l}\).

Question 44.
Determine whether or not the following quantities can be in the same direction for a simple harmonic motion;
(a) displacement and velocity,
Answer:
Yes, when the particle in S.H.M. is moving from equilibrium position to extreme position.

(b) velocity and acceleration,
Answer:
Yes, when the particle executing S.H.M. is moving from an extreme position to a mean position.

(c) acceleration and displacement?
Answer:
No, because acceleration is always directed opposite to the displacement.,

Question 45.
Can a body have zero velocity and maximum acceleration in S.H.M.?
Answer:
Yes. In S.H.M., at the extreme position, the velocity of the body is zero and acceleration is maximum.

Question 46.
A passing airplane sometimes causes the rattling of windows of a house. Explain why?
Answer:
When the frequency of the sound waves produced by the engine of the airplane strikes the windows panes, they start vibrating due to forced oscillations. This causes rattling of windows.

Question 47.
Identify periodic, non-periodic, and S.H.M. out of the following:
(a) fluttering tree leaves due to wind.
Answer:
Non-periodic

(b) fluttering of honeybee’s wings for a microsecond.
Answer:
S.H.M.

(c) rising and falling of water drops at the bottom of a waterfall.
Answer:
Non-periodic

(d) the sound produced by a motorcycle in a small interval of time.
Answer:
Periodic

(e) the motion of the wheels of a canon during rapid fire.
Answer:
Periodic

(f) jerks in a machine gun during rapid fire.
Answer:
periodic

(g) vibrations of a drum membrane in a music band.
Answer:
Non-periodic.

Question 48.
Why pendulum clocks are not suitable for spaceships?
Answer:
The time period of a pendulum clock is given by
T = 2π\(\sqrt{\frac{l}{g}}\)

In a spaceship g = 0, so T = ∞,
It means the pendulum clock will not oscillate and hence are not suitable for spaceships.

Question 49.
A glass window may be broken by a distant explosion. Is it correct?
Answer:
Yes. The sound waves can cause forced vibrations in glass due to the difference between the frequency of sound waves and the natural frequency of the glass. This can break the glass window.

Question 50.
The bob of a simple pendulum is positively charged. The pendulum is made to oscillate over a negatively charged plate. How shall the time period change as compared to the natural time period of the simple pendulum?
Answer:
Due to the electric force of attraction between the bob and the plate, the effective value of acceleration due to gravity will increase T = 2π\(\sqrt{\frac{l}{g}}\) therefore T will decrease.

Oscillations Important Extra Questions Short Answer Type

Question 1.
Why does the body of a bus begin to rattle sometimes when the bus is accelerated?
Answer:
At some speed of the bus, the frequency of vibrations produced by the bus-engine is equal to the natural frequency of the bus. This produces resonant vibrations which have quite a large amplitude and\ence the bus begins to rattle.

Question 2.
The displacement of a particle in S.H.M. may be given by x = A sin (ωt + Φ) Show that if the time t is increased by \(\frac{2π}{ω}\), the value of x remains the same.
Answer:
The displacement of a particle in S.H.M. at a time t is given
x = A sin (ωt + Φ) …. (i)

Let x be the displacement of the-particle at time t’ = ( t + \(\frac{2π}{ω}\)),
To prove x₁ = x

From equation (i), we get
x₁ = A sin [ω( t + \(\frac{2π}{ω}\)) + Φ)]
= A sin [ωt + 2π + Φ]
= A sin [2π + (ωt + Φ)]
= A sin (ωt + Φ)
[ ∵ sin (2π + θ) = sin θ]

i.e. the displacement of the particle in S.H.M. is same for times t and t + \(\frac{2π}{ω}\) .
Hence proved.

Question 3.
A hollow sphere is filled with water through a small hole in it. It is hung by a long thread and as water slowly flows out of the hole at the bottom, one finds that the period of oscillations first increases and then decreases. Explain why?
Answer:
When the sphere is filled with water, its C.G. is at the center of the sphere. We know that the time period (T) of oscillation is directly proportional to the square root of the effective length of the pendulum
i.e. T ∝ \(\sqrt{l}\).

Due to the flow out of the water through the hole at the bottom of the sphere, the first effective length l increases, and then it decreases because of the lowering of the center of gravity in the first case and rising up in the second case. The first case corresponds to the lowering of the water level up to the center of the sphere. The second case corresponds to the lowering of the water level from the center of the sphere to its bottom.

Question 4.
A girl is swinging in the sitting position. How will the period ^ of the swing be changed if she stands up?
Answer:
This can be explained using the concept of a simple pendulum.
We know that the time period of a simple pendulum is given by
T = 2π \(\sqrt{\frac{l}{g}}\) i.e. T ∝ \(\sqrt{l}\)

When the girl stands up, the distance between the point of suspension arid the center of mass of the swinging body decreases i. e. l decreases, so l will also decrease.

Question 5.
At what displacement, a particle in S.H.M. possesses half K.E. and half P.E.?
Answer:
We know that in any position for a displacement of y from the mean position, the K.E. and P.E. are given by the expressions:
E_k = \(\frac{1}{2}\) mω² (r² – y²) ….(1)
E_p = \(\frac{1}{2}\)mω²y² …..(2)
Where m = mass of the particle
y = displacement from the mean position
ω = its angular frequency
r = amplitude of oscillation of the particle

Now for E_k = E_p, we get

Question 6.
Explain why marching troops are asked to break their steps while crossing a bridge?
Answer:
This is done so as to avoid setting the bridge into resonant oscillations of large amplitude. If troops march in step, then the frequency of the steps of the marching troops may become equal to the natural frequency of vibration of the bridge. Hence it may oscillate with high amplitude due to the phenomenon of resonance, resulting in damage to the bridge.

Question 7.
What is the direction of acceleration at the mean and extreme positions of an oscillating simple pendulum?
Answer:
When the simple pendulum oscillates, its bob moves along a circular path with the point of suspension at its center. At the mean position, bob possesses centripetal acceleration which acts along the thread towards the point of suspension. At an extreme position, the bob is at rest for a moment. The acceleration on the bob acts along the tangent to the circular path and is directed towards its mean position. This acceleration results due to the restoring force arising due to the weight of the bob.

Question 8.
You are provided with a light spring, a meter scale, and a known mass. How will you find the time period of oscillation of mass attached to the spring without the use of a clock?
Answer:
With the help of metre scale, we can note the length and extension produced. Since
F = – kl
and F = mg
or
∴ mg = – k l
or
\(\frac{\mathrm{m}}{\mathrm{k}}=\frac{l}{\mathrm{~g}}\) (numerically)
∴ T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{l}{g}}\) …(1)

∴ By knowing the extension l, T can be calculated from equation (1) w ithout the use of clock.

Question 9.
Why does the time period of a pendulum change when taken to the top of a mountain or deep in a mine? Will clocks keep the correct time?
Answer:
Time period of a pendulum is given by
T = 2π\(\sqrt{\frac{l}{g}}\)
As the value of ‘g’ on the top of a mountain or deep in a mine decreases, so the time period of the pendulum increases on the top of a mountain or deep in a mine and hence the pendulum clocks will run slow,

Question 10.
What is the source of potential energy in a loaded elastic spring?
Answer:
As the load is put at the end of the spring, it gets extended. To increase the length, the load does work against the elastic restoring force. This work done is stored in the spring in the form of its potential energy,

Question 11.
Why cannot we construct an ideal simple pendulum?
Answer:
An ideal simple pendulum is made up of a heavy point mass suspended to a weightless, inextensible string fastened to a rigid support. In actual practice geometrical point mass is not realized so is a weightless and inextensible string. Hence ideal simple pendulum cannot be constructed in actual practice.

Question 12.
When a fast railway train passes over a river bridge, we hear a loud sound, why?
Answer:
Fast railway train vibrations are passed to the air column between the bridge and the river water through railway lines and slippers. The vertical air column starts resonating with train vibrations, so a loud sound is heard. ‘

Question 13.
If the amplitude of vibration of an oscillator is made half, how will its time period and energy be affected?
Answer:
Since the time period of an oscillator is independent of its amplitude, so it remains unaffected. However, the total energy is directly proportional to the square of the amplitude, so the energy of the oscillator will become a quarter of its original value on making amplitude half.

Question 14.
A bead is mounted on a vertical stand placed attached to the rim of a record player and its shadow is cast on the wall with the help of light from a lamp. The record player is set in motion. Describe the motion of the shadow of the bead.
Answer:
As the bead executes circular motion with the record player, its shadow on the wall will execute whose period depends on the speed of rotation of the record player.

Question 15.
In Boyle’s law apparatus, if the open end tube is quickly moved up and down what will happen to the mercury column in the closed tube?
Answer:
Due to quick compression and expansion of air column above mercury column in the closed tube, the mercury column is set into damped harmonic motion. Damping is caused due to friction in the air layer and mercury with the glass wall.

Question 16.
Alcohol in a U-tube is executing S.H.M. of time period T. Now alcohol is replaced by water up to the same height in U-tube. What will be the effect on the time period?
Answer:
As the time period (T) of oscillation of a liquid column in a U-tube does not depend upon the density of the liquid, so T is independent of the nature of liquid in a U-tube, hence there will be no effect on the time-period of replacing alcohol by water.

Question 17.
A spring having a force constant k and a mass m is suspended. The spring is cut into three halves and the $ame mass is suspended from one of the halves. Is the frequency of vibration the same before and after the spring is cut? Give reason.
Answer:
No. This can be explained as follows:
The spring constant k = \(\frac{F}{x}\), when the spring is cut inito three parts, the hew force constant will be k’ = \(\frac{\mathrm{F}}{\frac{\mathrm{x}}{3}}=\frac{3 \mathrm{~F}}{\mathrm{x}}\) = 3k.

If v = frequency of oscillation when the spring was not divided,
Then

i.e. frequency of oscillation after cutting the spring into 3 parts is \(\sqrt{3}\) times the frequency of oscillation before cutting. It is now clear to us that this is due to the reason that v ∝ \(\sqrt{k}\) and k increases on cutting the spring, so frequency increases.

Question 18.
Oscillatory motion is periodic but the reverse is not always true. Justify.
Answer:
The motion of planets and comets like Hailey’s comet, satellites, merry-go-round, etc. all are periodic but not oscillatory as these are not to and fro motions about a mean position. But the motion of the simple pendulum is not only oscillatory but periodic too as it is also to and fro and repeats itself at regular intervals of time.

Question 19.
Why a restoring force is a must for S.H.M.?
Answer:
A restoring force is a force that restores or tends to restore or bring back a body or particle to its equilibrium position. When a body executing S.H.M. crosses its mean position due to its kinetic energy, the restoring force starts acting towards the equilibrium position and brings the oscillator towards the mean position from the extreme position of motion. The same thing happens when the body goes to the other side of the equilibrium position. So, a restoring force is a must for any oscillatory motion including S.H.M.

Question 20.
What is a periodic function, explain?
Answer:
A mathematical function that repeats itself after a definite period is called a periodic function, e.g. f (t) = f (t + T), here T = period of the function.

Let F(t) fie a periodic function such that F(t) = A sin \(\frac{2π}{T}\) t or F(t) = A cos \(\frac{2π}{T}\) t which are periodic functions. If t is replaced by t + T, we get once again the same value of the function. Thus


Hence f(t) is a periodic function having a time period T.

Question 21.
Distinguish between forced vibrations and maintained vibrations.
Answer:
A body vibrating under the effect of an external applied periodic force and oscillating with a frequency other than its natural frequency is said to be performing forced vibrations.

If energy is supplied to the oscillator at the same rate at which it is dissipated, the amplitude of the oscillator remains unchanged. Such oscillations are called maintained oscillations e.g. The oscillations of the pendulum clock of a watch or the balance wheel of a watch are examples of maintained oscillations.

Question 22.
Will a pendulum go slower or faster at
(a) Moon,
(b) planet Jupiter?
The time period of oscillation of a pendulum on Earth is given by
T_e = 2π\(\sqrt{\frac{1}{g_{e}}}\)
Answer:
(a) On moon gm = \(\frac{1}{6}\) of the Earth = \(\frac{\mathrm{g}_{\mathrm{c}}}{6}\).Since g_m < g_e, so T_m > T_e. Thus due to increase in time period of oscillation of pendulum, it will go slower on the moon.

(b) The value of acceleration due to gravity g_j on Jupiter is more than g_e, so the time period T_J of oscillation of the pendulum will be less than what it is on the earth. Thus due to a decrease in the time period of oscillation of a pendulum, it will go faster on Jupiter.

Question 23.
The mass M attached to a spring oscillates with a period of 2s. If the mass is increased by 2 kg, the period increases by 1 s. Find the initial mass m assuming that Hooke’s law is obeyed.
Answer:
Let the initial mass and time period be M and T respectively. If the Hook’s law is obeyed, then the oscillations of the spring will be simple harmonic having time period T given by
T = 2π\(\sqrt{\frac{M}{k}}\)

Given T = 2s
∴ 2 = 2π\(\sqrt{\frac{M}{k}}\); k = spring constant ….(1)

On increasing the mass by 2 kg, T’ = 2 + 1 = 3s.
∴ 3 = 2π\(\sqrt{\frac{M+2}{k}}\)

Squaring and dividing equation (2) by (1), we have

Question 24.
The displacement of a particle having periodic motion is given by
y = r sin ωt
Show that the motion of the particle is simple harmonic for small values of v.
Answer:
Since y = r sin(ωt – Φ) ….(1)
∴ \(\frac{dy}{dt}\) = rω cos(ωt – Φ) …(2)
and \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}\) = – rω² sin(ωt – Φ)
= – ω² y …(3) [by (i)]

where,a = \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}\) is called acceleration.
ω = angular frequency
∴ a = – ω²y

Now as a ∝ y and acts towards mean position. This is the characteristic of S.H.M. Hence the given equation y = r sin (ωt – Φ) represents an S.H.M. of the oscillator.

Question 25.
We have a very strong string and of sufficient length making a pendulum with a metal ball (e.g. a shot put). What will be the effect on the time period if
(a) the length of the pendulum is doubled and
Answer:
If the length of the pendulum is doubled, then
T = 2π\(\sqrt{\frac{2l}{g}}\)
= 2π\(\sqrt{\frac{l}{g}}\) \(\sqrt{2}\) = \(\sqrt{2}\)T.
The period of oscillation will increase.

(b) the ball is replaced by an elephant?
Answer:
Since mass does not come in relation to the time period of oscillation of a pendulum therefore instead of shot put if we make a pendulum of some length with an elephant there will be no effect on the time period of its oscillation.

Question 26.
The angular frequency of damped harmonic motion is given by ω = \(\sqrt{\frac{k}{m}-\left(\frac{b}{2 m}\right)^{2}}\) where b is know as damping constant. The displacement in such a motion is given by x = A e^-bt/2m cos (ωt + Φ) and the retarding force is F = – b v, where v is the speed of the particle. Could you guess from the given equations?
(a) How the amplitude of vibration change?
Answer:
The amplitude of vibration decreases continuously due to damping force. The amplitude decreases exponentially as is evident from the displacement equation the damping force is velocity-dependent.

(b) Does the time period of vibration change with displacement?
Answer:
The time period of oscillation does not change in damped oscillations.

Question 27.
Apart from the danger of being burnt which other factors make the re-entry of a space vehicle difficult in Earth’s atmosphere?
Answer:
The Earth’s thick atmospheric layer offers buoyant force and space vehicles suffer from damped harmonic oscillations, making the re-entry difficult.

Question 28.
If the amplitude of vibration is not small in the simple pendulum experiment will it not be executing periodic harmonic oscillations? How will the time period be affected?
Answer:
The simple pendulum will still be executing periodic harmonic oscillation even if the amplitude is large. However, the time period of oscillation will be slightly greater than what it is for small amplitudes
i.e. T > 2π\(\sqrt{\frac{l}{g}}\) ,

(The derivation of formulae is beyond the scope of this course),

Question 29.
Can you give some examples where an anharmonic oscillator does not possess potential energy?
Answer:
The thermal radiation enclosed in a black body of fixed dimensions and photons in solids behave like harmonic oscillators where they don’t have potential energy.

Question 30.
A man is standing on a platform executing S.H.M. in the vertical direction and attached to a weighing machine. Will there be any change in his weight?
Answer:
Depending on the motion of the platform from its mean position, the weight of the man will change when the platform moves down from the mean position to the lowermost point and return back to the mean position, ‘ the acceleration acts vertically upwards and hence the weight of the man j will increase. But when the platform moves up from its mean position to [ the uppermost point and returns back to the mean position, the acceleration in S.H.M. acts downwards, so the weight of the man is decreased.

Oscillations Important Extra Questions Long Answer Type

Question 1.
(a) What is the effect on the time period of a simple pendulum when:
(i) it is immersed in a liquid of density σ.
Answer:
Let p = density of the material of the pendulum bob.
σ = density of the liquid in which the pendulum bob is immersed such that p > σ. Let it is made oscillate with a time period T’. The effective value of ‘g’ in the liquid is given by

where T = time period of the simple pendulum when it oscillates in air.
or
\(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}=\sqrt{\frac{\rho}{\rho-\sigma}}\)
∴ ρ > σ
or
ρ – σ > 0

∴ \(\frac{\rho}{\rho-\sigma}\) > 1
or
\(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}\) > 1
or
T’ > T
i.e. its time period increases.

(ii) the temperature of wire through which the bob is suspended increased?
Answer:
When the temperature of the wire with which the bob of the pendulum is suspended increases, the length of the wire increases due to its thermal expansion. As
T ∝ \(\sqrt{l}\), so T will also increase as shown below:
Let l = original length of the wire
dθ = rise in its temperature
α = coefficient of linear expansion of the material of the wire
If l’ = new length
and dl = increase in its length = l’ – l, then

(Using Binomial expansion)
or increase in Time period = T’ – T = \(\frac{\mathrm{T} \alpha \mathrm{d} \theta}{2}\)

(b) Derive the differential equation of Simple Harmonic Oscillation.
Answer:
When an oscillator is displaced, say in the x-direction, the restoring force tends to bring it in its equilibrium position. It is well known that restoring force is directly proportional to the displacement, thus
Fα – x or F = – k x(t) .
where, the negative sign indicates! that the force always acts towards equilibrium position and opposes displacement, k is known as the force constant.

According to Newton’s law of motion if x (t) is the displacement then \(\frac{\mathrm{dx}(\mathrm{t})}{\mathrm{dt}}\) is the velocity and \(\frac{\mathrm{d}^{2} \mathrm{x}(\mathrm{t})}{\mathrm{dt}^{2}}\) is the acceleration of the oscillating particle.

Now Force = mass × acceleration

Equations (A) and (B) are known as the differential equations of simple harmonic oscillator, GO is the angular velocity given by
ω = \(\frac{2π}{T}\)
Also
ω = \(\sqrt{\frac{k}{m}}\)

So, the time period of oscillation of the oscillator is given by
\(\frac{2π}{T}\) = \(\sqrt{\frac{k}{m}}\)
or
T = 2π\(\sqrt{\frac{m}{k}}\)

(c) Distinguish briefly between natural, forced and , resonant vibrations. What are damped and undamped / vibrations?
Answer:
Natural vibrations: The vibrations of a body in the absence of any resistive, damping, or external) forces are said to be its natural vibrations. The body once vibrated continues to vibrate with its natùral frequency and undiminished amplitude.

Forced vibrations: A body at rest or vibrating with some frequency changes its frequency of vibration and amplitude when an external force is impressed on it. If the applied force is periodic the body oscillates with a period which is the period of the impressed force.

The vibrations of the body are not natural or free vibrations but are forced vibrations. If the external periodic force is removed, the body executes its natural oscillations after a while.

Resonant vibrations: If a body is set in vibrations such that a periodic force creates vibrations in it and the frequency of such vibrations becomes equal to the natural frequency of vibration of the body (i.e. the frequency of its free vibrations in the absence of the applied periodic force), its amplitude of vibration increases vigorously. The body is said to be in resonance with the second oscillating body or the applied periodic force.

The frequencies of the two oscillators become equal. Resonant oscillations are not only set up in mechanical oscillators but in electrical circuits and atomic oscillators too.

Damped vibrations: If a body vibrates in the presence of a resistive force such as fluid friction or electromagnetic damping force, its amplitude of oscillation decreases, and ultimately the oscillations die out i.e. the body stops oscillating. Such an oscillation is called damped oscillation as shown in the figure. The amplitude of vibration decreases with time.

Undamped Oscillations: The free oscillations of an oscillator in the absence of any resistive or damping force have constant amplitude over time. Such oscillations are called undamped oscillations. Most vibrations in ‘ daily life are damped vibrations because the oscillator experiences one or the other type of force acting on it. So, its vibrations become damped.

Question 2.
(a) Discuss the effect of driving force frequency on the driven frequency. How does friction affect the oscillation of an oscillator?
Answer:
Driving force is a time-dependent force represented by
F(t) = f_o cos 2πvt …..(1)
where v = frequency of driving force. This frequency is different from the natural frequency of the oscillation v_n of the oscillator. v_n is also called driven frequency. Thus motion depends on driving force.

Thus the motion of the particle is now under the action of: (a) linear restoring force, (b) time dependent (or periodic) force given in equation (1) so that using Newton’s law, we have for the oscillator:
ma(t) = – k x(t) + f_o cos2πvt …. (2)
and v_n² = \(\frac{1}{\mathrm{~T}^{2}}=\frac{\mathrm{k}}{4 \pi^{2} \mathrm{~m}}\) ….(3)

where m = mass of oscillator,
k = force constant,
v = frequency of the driving force,
ω = 2πvt,
vn = natural frequency of the oscillator,

Let the displacement be given by, x = C cos ωt,
where C = constant, .

This shows that the mass m will execute S.H.M. whose frequency is equal to the frequency of the driving force. The amplitude of oscillation too depends on the frequency of the driving force and is independent of time.

If there is a large difference between v and v_n, then the amplitude of oscillation will be too small. But if v_n ~ v, the amplitude of oscillation will become infinite, which does not actually happen as some sort of unaccounted force breaks the oscillations down. But if v – v_n, the amplitude becomes very large. This phenomenon is called resonance. There are several examples of resonance in daily life such as playing musical instruments, marching of troops in steps, etc.

Effect of the force of friction on S.H.M.: The real oscillations of almost all oscillators are known as damped oscillations. The energy of the system is continuously dissipated but nevertheless, oscillations remain periodic. This dampens oscillations. It is an additional restoring force that is proportional to the velocity of the particle rather than its displacement i.e. F = – bv(t), where b is a positive constant called damping constant. The oscillator is now under the combined action of F(t) and f(t) so that
ma(t) = – k x(t) – bv(t) …. (5)

The solution of this equation gives

(b) Derive an expression for
(1) angular velocity
(2) time period,
(3) frequency of a particle executing S.H.M. in terms of spring factor and inertia factor.
Answer:
Let m = mass of a particle executing S.H.M. The restoring force F is directly proportional to the displacement and acts opposite to it so that
F ∝ – x
or
F = – k x
where k is called the force constant. If the mass m is attached to an elastic spring, then k is called the spring constant for a given spring. From Newton’s second law of motion,
F = ma
Therefore F = ma = – kx
or
a = – \(\frac{k}{m}\)x
⇒ a ∝ – x

Hence the motion is S.H.M., we can write
a = – ω² x
where ω² = \(\frac{k}{m}\)
or
ω = \(\left(\frac{k}{m}\right)^{\frac{1}{2}}\)

This gives ω in terms of spring and constant mass factor.
we know that ω = \(\frac{2π}{T}\)

⇒ T = \(\frac{2π}{ω}\)

Substituting the value of ω from above we have
T = 2π\(\sqrt{\frac{m}{k}}\)

This is the expression for time period.
The frequency v = \(\frac{1}{T}\) = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\)

If the body executing S.H.M. has angular motion, then mass is replaced by the moment of inertia L and the force constant k is replaced by C, the restoring couple per unit twist, hence ω, T and v become
ω = \(\sqrt{\frac{C}{I}}\)

T = 2π\(\sqrt{\frac{C}{I}}\)
and v = \(\frac{1}{2 \pi} \sqrt{\frac{C}{I}}\)

Thus ω, T and v are found in terms of the spring factor and moment of inertia factor.

Question 3.
Calculate the effective spring constant and time period of a parallel and series combination of two different types of springs that are loaded.
Answer:
(a) When springs are connected in parallel with weight mg, hanging at the lower end.

Both the springs are pulled down through the same displacement say y.

Let F₁ and F₂ be the restoring forces acting on the spring.
Then F₁ = – k₁y
and F₂ = – k₂y

If F = total restoring force, then
F = F₁ + F₂
= – (k₁ + k₂)y ….(1)

Let k = spring constant of the combination, then
F = – ky ….(2)

∴ From (1) and (2), we get
k = k₁ + k₂

The motion of the weight will be simple harmonic in nature. Its time period is given by
T = 2π\(\sqrt{\frac{m}{k}}\)
= 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{1}+\mathrm{k}_{2}}}\)

(b) When the springs are connected in series, the springs suffer different displacement y₁ and y₂ when the weight mg is pulled down. But the restoring force is the same in each spring.
∴ F = – k₁y₁
and F = -k₂y₂

If k be the spring constant of the combination, then
F = -ky …..(4)
∴ From (3) and (4), we get
k = \(\frac{\mathbf{k}_{1} \mathbf{k}_{2}}{\mathbf{k}_{1}+\mathbf{k}_{2}}\) …(5)

If ‘a’ be the acceleration produced in the body of mass m, then
a = \(\frac{\mathrm{F}}{\mathrm{m}}=\frac{-\mathrm{k}}{\mathrm{m}}\)y ⇒ motion of S.H.M. having time period T given by

(c) The weight ‘mg’ is connected in between the two springs which themselves are connected in series.

When the weight is pulled to one side, one spring gets compressed and the other is extended by the same amount. The restoring force acts in the same direction due to both the springs.

Let y = extension or compression produced in the springs,
F₁, F₂ = restoring forces produced in the springs, then
F₁ = – k₁y
F₂ = – k₂y
If F = F₁ + F₂ = – (k₁ + k₂)y

If k = spring constant of the combination, then
F = – ky;
∴ k = k₁ + k₂
a = \(\frac{F}{m}\) = – \(\frac{\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right)}{\mathrm{m}}\)y
and T = 2π\(\sqrt{\frac{M}{k}}\) = 2π\(\sqrt{\frac{M}{k_{1}+k_{2}}}\)

Question 4.
(a) Obtain the expression for a time period of a simple pendulum.
(b) Calculate the total energy of a particle executing S.H.M.
Answer:
(a) Let l = length of the string of the pendulum.
mg = weight of the bob acting vertically downward.
θ = angle by which the bob be displaced from the vertical position.
O = equilibrium position of the bob.

At any position P, the various forces acting on the bobs are:

1. mg, the weight of the bob acting in a vertically downward direction.
2. Tension (T) in the string acting along the string towards the support from which the pendulum is suspended.

mg is resolved into two rectangular components.

1. mg cos θ opposite to T.
2. mg sin θ perpendicular to T and directed towards the mean position O.

T – mg cos θ provides the centripetal force = \(\frac{\mathrm{mv}^{2}}{l}\) to the bob to move it in the circular path of radius l.

∴ T – mg cos θ = \(\frac{\mathrm{mv}^{2}}{l}\)
At extreme position P, bob is momentarily at rest i.e. v = 0

∴ T – mg cos θ = 0
or
T = mg cos θ ….(1)
mg sin θ provides restoring force (F), i.e.
F = – mg sin θ …. (2)

It acts towards the mean position. Here -ve sign shows that F tends to decrease θ. If θ is small, then
sin θ ~ θ
∴ F = – mg θ
Or
\(\frac{F}{m}\) = – gθ
or
a = – gθ = – g. \(\frac{x}{l}\) (∵ x = lθ)

where a = acceleration produced in the bob.
Now as a ∝ x and acts towards mean position, so its motion is S.H.M. having timC period (T) given by

T = 2π\(\sqrt{\frac{x}{a}}\) = 2π\(\sqrt{\frac{l}{g}}\)

(b) A particle executing S.H.M. has two types of energy

1. P.E. due to its displacement from mean position.
2. K.E. due to its velocity.

Let M = mass of the particle executing S.H.M.
r = amplitude of S.H.M.
ω = angular frequency of S.H.M.
y = displacement after a time t. k = force constant of S.H.M.
F = ky, restoring force acting at any position A.

Let the body is displaced from A to B s.t. AB = dy
If dW = work is done on the body when displaced by dy, then
dW = F dy = ky dy

If W = work done when the body is displaced through y, then

This work is stored in the particle in the form of P.E.
i.e. E₁ = P.E. = \(\frac{1}{2}\)ky²

KE. Let y = velocity of the particle executing S.H.M. at a displacement y from the mean position. Then
v = ω\(\sqrt{r^{2}-y^{2}}\)


Thus the total energy in S.H.M. remains constant.

Numerical Problems:

Question 1.
A particle executing S.H.M. along a straight line has a velocity of 4 ms^-1 at a distance of 3 m from its mean position and 3 ms^-1 at a distance of 4 m from it. Determine its angular speed and time period of oscillation.
Answer:
Here, y₁ = 3 m
v₁ = 4 ms^-1
y₂ = 4 m
v₂ = 3 ms^-1
ω =?

We know that the velocity of a particle executing S.H.M. is given by

∴ From (ii),
4 = ω \(\sqrt{25-9}\) = 4ω
∴ ω = 1 rad s^-1
∴ T = \(\frac{2π}{ω}\) = 2π second.

Question 2.
A harmonic oscillation is represented by y = 0.34 cos (3000 t + 0.74) where y and t are in cm and s respectively. Deduce
(i) amplitude,
(ii) frequency and angular frequency,
(iii) time period,
(iv) initial phase.
Answer:
The given equation is y 0.34 cos (3000 t + 0.74) …. (1)
Comparing eqn. (i) with the standard equation of displacement of harmonic oscillation,
y = r cos (ωt + Φ_o), we get
r = amplitude = 0.34 cm

Question 3.
A particle vibrates simply harmonically with an amplitude of 4 cm.
(a) Locate the position of the point where its speed is half its maximum speed.
(b) At what displacement ¡s P.E. = K.E.?
Answer:
Here, r = 4 cm
v_max = maximum speed of the particle
m = mass of the particle
(a) let v = speed of the particle when its displacement is y and
v = \(\frac{1}{2}\)v_max …(i)
Let y = required position w.r.t. mean pcsition =?

∴ maximum P.E = \(\frac{1}{2}\)kr²
Also maximum K.E = \(\frac{1}{2}\)mv²_max

According to the law of conservation of energy,

(b) Let y₁ be the displacement from the mean position at which
P.E.=KE.

Question 4.
A body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant 2.0 × 10³ Nm^-1. What is the stretched length of the spring? 1f the body is pulled down further stretching the spring to a length of 59 cm and then released, what is the frequency of oscillation of the suspended mass? (Neglect the mass of the spring) .
Answer:
Here, k = 2 × 10³ Nm^-1
m = 12 kg
L = original length of the spring
= 50 cm = 0.50 m

Let l = elongation produced in the spring when 12 kg mass is suspended.
∴ F = kl = mg
or
l = \(\frac{\mathrm{mg}}{\mathrm{k}}=\frac{12 \times 9.8}{2 \times 10^{3}}\)
= 0.0588 m = 5.88 cm

∴ stretched length of the spring = L + l = 50.00 + 5.88 = 55.88 cm

The time period of a loaded spring does not change even if the spring is further stretched. So when it is stretched to 59 cm, its time period will be given by
T= 2π\(\sqrt{\frac{m}{k}}\)

∴ Frequency of oscillation is given by

Question 5.
A body of mass of 1.0 kg is suspended from a weightless spring having a force constant of 600 Nm^-1. Another body of mass 0.5 kg moving vertically upward hits the suspended body with a velocity of 3.0 ms^-1 and gets embedded in it. Find the frequency of oscillations and amplitude of motion.
Answer:
Here, m₁ = 1 kg
m₂ = 0.5 kg
k = force constant = 600 Nm^-1
v₁ = 0
v₂ = 3 ms^-1

As the mass m2 gets embedded after collision; so
m = total mass = inertia factor = m₁ + m₂ = 1 + 0.5 = 1.5 kg
If v = frequency of oscillation, then

According to the law of conservation of linear momentum, pf = pi.
(m₁ + m₂)V = m₁v₁ + m₂v₂ = m₂v₂ (∵ v₁ = 0)
∴ V = \(\frac{\mathrm{m}_{2} \mathrm{v}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}=\frac{0.5 \times 3}{1.5}\) = 1 ms^-1

Let r = amplitude of motion
Also according to the law of conservation of mechanical energy

Question 6.
(a) If the length of a second’s pendulum is increased by 1%, how many beats will it lose in one day?
(b) A pendulum clock normally shows the correct time. On an extremely cold day, its length decreases by 0.2%. Compute the error in time per day.
Answer:
(a) Time period of a pendulum is
T = 2π\(\sqrt{\frac{l}{g}}\)

For second’s pendulum, T = 2s
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\) …(i)

Let l’ = new length of the second’s pendulum. When l is increased by 1%, then
l’ = l + l% of l = l +\(\frac{1}{100}\)l

If T’ = new time period, then


(Using Binomial Expansion Theorem)
= 2 + \(\frac{1}{100}\)

No. of oscillations initially produced by the pendulum is
n = no. of seconds in one day/time
= \(\frac{24 \times 60 \times 60}{2}=\frac{86400}{2}\) …(ii)

No. of oscillations produced by the pendulum after increasing its length.

Number of oscillations lost per day = no. of seconds lose per day
= 216 × 2 = 432 s.

(b) The correct time period of the pendulum clock 2s.
Let l be its correct length
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\) ….(iii)

Decrease in length = 0.2% of l = \(\frac{2}{100}\)l
If l’ be the new length than
l’ = l – \(\frac{0.2}{100}\)l = l(1 – \(\frac{0.2}{100}\))

If T’ be the new time period, then

= (2 – \(\frac{0.2}{100}\)) < 2
∴ Clock gains time,
Time gained in 2 seconds = \(\frac{0.2}{100}\)s

∴ Time gained per day = \(\frac{0.2}{100}\) × \(\frac{1}{2}\) × 24 × 60 × 60 = 86.4 s.

Question 7.
A simple pendulum is made by attaching a 1 kg bob to a 5 cm copper wire of diameter 0.08 cm and it has a certain period of oscillation. Next, a 10 kg bob is substituted for a 1 kg bob. Calculate the change in period if any. Young’s modulus of Copper is 12.4 × 1010 Nm^-2.
Answer:
Here, F = mg
A = πr²
The original length of the pendulum, l = 5 m

Case I: m = 1 kg, l = 5 m, r = \(\frac{0.08}{2}\) cm = 0.04 cm = 4 × 10^-4 m, Y = 12.4 × 10¹⁰ Nm^-2
∴ Δl1 = \(\frac{1 \times 9.8 \times 5}{3.14 \times(0.04)^{2} \times 12.4 \times 10^{10}}\)
= 0.0787 × 10^-2 m
= 0.00079 m.

∴ Total length of the pendulum,
l₁ = l + Δl₁ = 5 m + 0.00079 m
= 5.00079 m.

If T1 be the initial time period of the pendulum, then
T₁ = 2π\(\sqrt{\frac{l_{1}}{g}}\)
= 2 × \(\frac{22}{7} \sqrt{\frac{5.00079}{9.8}}\)
= 6.28 × 0.714 = 4.486 s

CaseII: M = 10kg, l = 5 m, r = 0.04 × 10^-4m, Y = 12.4 × 1010 Nm^-2
∴ Δl₂ = \(\frac{10 \times 5 \times 9.8}{3.14 \times 16 \times 10^{-8} \times 12.4 \times 10^{10}}\)
= 0.0079 m
∴ l₂ = l + Δl₂ = 5 + 0.0079 = 5.0079 m

If T2 be the new time period of the pendulum, then
T₂ = 2π\(\sqrt{\frac{l_{2}}{g}}\)
= 2 × 3.14\(\sqrt{\frac{5.00079}{9.8}}\)
= 4.489 s.

∴ Increase in time = T₂ – T₁ = 4.489 – 4.486 = 0.003s.

Question 8.
A second’s pendulum is taken in a carriage. Find the period of oscillation when the carriage moves with an acceleration of 4 ms^-2.
(i) Vertically upwards,
(ii) Vertically downwards,
(iii) in a horizontal direction.
Answer:
Here, T = 2s
using T = 2π\(\sqrt{\frac{l}{g}}\), we get
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\)
or
1 = 2π\(\frac{l}{g}\)
or
l = \(\frac{\mathrm{g}}{\pi^{2}}=\frac{9.8}{\pi^{2}}\) …(i)

(i) When carriage moves up, a = 4 ms^-2
∴ If T₁ be the time period, then

(ii) When the carriage moves down with a = 4 ms^-2
If T₂ be the time period, then

(iii) When the carriage moves horizontally, then g and a are at right angles to each other and hence the net acceleration is

Question 9.
A block is kept on a horizontal table. The table is undergoing S.H.M. of frequency 3 Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. Find the maximum amplitude of the table at which the block does not slip on the surface (g = 10 ms^-2).
Answer:
Here, v = 3 Hz.
μ = 0.72
g = 10 ms^-2

Maximum acceleration of the block is
amax = rω²
where r = amplitude of the table
ω = its angular frequency = 2πv
= 2π × 3

∴ Maximum force on the block is given by
F = mamax = mrω²

Frictional force on the block,
f_s = μmg

The block will not slip on the surface of the table if
F = f_s
or
mrω² = μmg
or
r = \(\frac{\mu g}{\omega^{2}}\)
or
r = \(\frac{0.72 \times 10.0}{(6 \pi)^{2}}\) = 0.02 m

Question 10.
The pendulum bob has a speed of 3 ms^-1 at its lowest position. The pendulum is 0.5 m long. What will be the speed of the bob when the length makes an angle of 60° with the vertical?
Answer:
Let m = mass of the bob
y = speed of the bob at the lowest position = 3ms^-1.

l = length of the pendulum
= 0.5 m = \(\frac{1}{2}\)m

∴ K.E at the lowest position O = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)m × 3² = \(\frac{9}{2}\)m …(i)

When the length (i) makes an angle O ( 60°) to the vertical, the bob of the pendulum will have both K.E. and P.E.

If v₁ be the velocity of the bob in this position and h= height of the bob with respect to O, then
SC = l cos θ
∴ h = OS – SC = l – l cos θ
= l(l – cos θ)
= l(1 – \(\frac{1}{2}\))
= \(\frac{l}{2}=\frac{1}{2} \times \frac{1}{2}\)m
= \(\frac{1}{4}\)m.

Total energy of the bob = K.E. + P.E.
= \(\frac{1}{2}\)mv₁² + mgh
= \(\frac{1}{2}\)mv₁² + m × 9.8 × \(\frac{1}{4}\) …(iii)

∴ According to the law of conservation of energy,
K.E. at O = Total energy at A
\(\frac{9}{2}\) m = \(\frac{1}{2}\)mv12 + \(\frac{\mathrm{m} \times 9.8}{4}\)
or
v₁² = 9 – \(\frac{9.8}{2}\) = 9 – 4.9 = 4.1
∴ v₁ = 2.025 = 2.03 ms-1.

Question 11.
A person stands on a weighing machine placed on a horizontal platform. The machine reads 60 kg. When the platform executes S.H.M. at a frequency of 2.0 s^-1 and amplitude 5.0 cm, what will be the effect on the reading of the weighing machine? Take g = 10 ms^-2.
Answer:
Here, m = 60 kg
v = 2 s^-1
r = 5 cm = 0.05 m
ω = 2πv = 2π × 2 = 4π rad^-1 s

Here A and B are the extreme positions between which the platform vibrates and O = mean position.
∴ acceleration is maximum at A or B and is given by
a_max = rω² = 0.05 × (4π)²
= 0.05 × 16 × 9.87
= 7.9 ms^-2

∴ restoring force, F = ma_max
= m × 7.9 N
= 7.9 m N

At point A, both weight and restoring force are directed towards the mean position, so the effective weight is maximum at A i.e. reading will be maximum and is given by
W₁ = mg + ma_max = m(g + a_max)
= 60 (10 + 7.9)
= 60 × 17.9 N
= 1074.0 N
= 107.4 kgf

At point B, the weight and the restoring force are opposite to each other, so the effective weight i.e. reading of the weighing machine is minimum at B and is given by

Question 12.
If earth were a homogeneous sphere and a square hole was bored in it through its center, show that a body dropped in the hole will execute S.H.M. and calculate its period if the radius of earth = 6400 km.
Answer:
Let R = radius of earth 6400 × 10³ m
O = center of the earth

Let AB be a tunnel bored along the diameter of the earth and a body be dropped from point A.

Let it reaches point C at a depth d from the surface of the earth.
∴ OC = R — d = distance of the object from the center of earth displacement of the body.

If gd be the acceleration due to gravity at a depth ‘d’ then we know, that
g_d = g(1 – \(\frac{d}{R}\)) = g\frac{(R-d)}{R}\(\)

If R – d = y = displacement from O, then
g_d = \(\frac{g}{R}\)y

Now as the acceleration of the body is proportional to its displacement from the center of earth i.e. O. Hence the motion of the body is S.H.M. and its time period is given by

Question 13.
A horizontal spring block system of mass M executes S.H.M. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration.
Answer:
The frequency of oscillation of spring block system of mass M is given by
v = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{M}}}\) …..(i)
where k = force constant of the spring.

Let r = initial amplitude of oscillation.
V_o = velocity of the system in equilibrium position,
according to the law of conservation of energy,
∴ \(\frac{1}{2}\)MV₀² = \(\frac{1}{2}\)kr²
or
V_o = \(\sqrt{\frac{k}{M}}\)r ….(ii)

When mass m is put on the system, then total mass = M + m.

If V = velocity of the combination in equilibrium, then according to the law of conservation of linear momentum,
MV_o = (M + m)V
or
V = \(\frac{\mathrm{MV}_{0}}{\mathrm{M}+\mathrm{m}}\) ….(iii)

Let r₁ be the new amplitude, then


If v’ be the new frequency of oscillation, then
v’ = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{M}+\mathrm{m}}}\)

Question 14.
A tray of mass 12 kg is supported by two parallel vertical identical springs. When the tray is pressed down slightly and released, it executes S.H.M. with a time period of 1.5 s. What is the force constant of each spring? When a block of mass m is placed in the tray, the period of S.H.M. changes to 3 s. What is the mass of the block?
Answer:
Let k be the spring constant of each of the identical springs connected in parallel.
M = mass of tray = 12 kg
T₁ = time period of oscillation of the tray = 1.5 s

Let T₂ = time period of oscillation of the tray + block of mass ‘m’
∴ T₂ = 3 s
m = ?
k =?

If k’ = spring constant of the combination, then
k’ = k + k = 2k (a)

Dividing (ii) and (i), we get

Question 15.
Two pendulums of lengths 100 cm and 110.25 cm start oscillating in phase simultaneously. After how many oscillations will they again be in phase together?
Answer:
Here, l₁ = 100 cm
l₂ = 110.25 cm
using T = 2π\(\sqrt{\frac{l}{g}}\)

For smaller pendulum, T₁ = 2π\(\sqrt{\frac{100}{g}}\) …(i)

For larger pendulum, T₂ = 2π\(\sqrt{\frac{110.25}{g}}\) …(ii)
where T₁ and T₂ are the time periods of the two pendulums.

Let these pendulums oscillate in phase again if the larger pendulum completes n oscilLations, It means the smaller pendulum must complete (n + 1) oscillations.
nT₂ = (n + 1)T₁

Hence both pendulums will again oscillate in phase after 20 oscillations of the larger or 21 oscillations of the smaller pendulum.

Question 16.
Springs of spring constants k, 2k, 4k., 8k, are connected in series. A mass m kg ¡s attached to the lowér end to the last spring and the system is allowed to vibrate. Calculate the approximate time period of vibration.
Answer:
The time period of vibration of series loaded spring is given by
T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{\mathrm{s}}}}\) …(1)
Where k is the force constant of the series combination of springs.

In a series combination of springs, the combined spring constant k is given by

or
ks = \(\frac{k}{2}\)

m mass attached to the lower end of the spring.
∴ From (1) and (2), we get
T = 2π\(\sqrt{\frac{2 m}{k}}\)

Question 17.
A point particle of mass 0.1 kg is executing S.H.M. of amplitude 0.1 m. When the particle passes through the mean position, its kinetic energy is 8 × 10^-2 J. Obtain the equation of motion of this article if the initial phase of oscillation is 45°
Answer:
Since the kinetic energy is maximum at the mean position and is equal to

The standard equation of motion of a particle executing S.H.M. is
y = A sin(ωt + Φ₂)
or
x = A cos(ωt + Φ₂)
Given r = 0.1 m, ω = 4 rad s-1 and Φ₂ = 45° = \(\frac{π}{4}\)

∴ The required cquation of motion is
y = 0.1 sin (4t + \(\frac{π}{4}\))
or
x = 0.1 cos (4t + \(\frac{π}{4}\)).

Question 18.
A cubical body (side 0.1 m and mass 0.002 kg) floats in water. It is pressed and then released so that it oscillates vertically. Show that the motion of the body is simple harmonic and And the time period.
Answer:
Here, m = mass of body = 0.002 kg
L = side of body = 0.1 m
In the absence of any given indication it is assumed that the body floats (just sunk), so

The mass of water displaced = volume × density of water
= V ρ = (0.1 )3 ρ.

The upward thrust exerted by water displaced
i.e. buoyant force = Vρg=(0.1 )3 × 10³ × 9.8 (∴ ρ ofwater = 10³ kg m³)
W₁ = Downward weight = mg
Net downward force, F = (0.002 g -Vρg)
or
F = [0.002g – (1)³ × 10³g
= (0.002 – 1)g
= – 0.998 × 9.8 N …. (1)

Suppose the block is depressed by y,
hence restoring force F₁ = – (0.1 + y)k

When the body floats on the water the force acting is F = 0.1 k, where k is the force constant
The net downward force
F – F’ = 0.1 k – (0.1 + y)k
= – yk ….(2)

Thus force ∝ (- y)
Force = ma, where a = acceleration of the body.
∴ ma = – y k
or a = – \(\frac{k}{m}\) y
m
or a ∝ -y …. (3)

Hence the motion-ofthe block is S.H.M.
The time period of oscillation is given by
T = 2π\(\frac{m}{k}\) …(4)

From eqn. (1), k = \(\frac{\mathrm{F}}{\mathrm{L}}=\frac{0.998 \times 9.8}{0.1}\)Nm^-1 …(5)
m = 0.002 kg

∴ T = 2π\(\sqrt{\frac{0.002 \mathrm{~kg} \times 0.1}{0.998 \times 9.8 \mathrm{Nm}_{1}}}\)
= 0.0284 s.

Question 19.
Two simple harmonic motions are represented by the following equations:
y₁ = 10 sin \(\frac{π}{4}\) (12t + 1); y² = 5 (sin 3πt + \(\sqrt{3}\) cos 3πt).
(a) Find out the ratio of their amplitudes.
(b) What are the time periods of two motions?
(c) Also find the phase difference between two motions.
Answer:
The two given displacements may be written as

(a) The amplitudes of the two S.H.M. are A₁ = 10 units. and A₂ = 10 units
Hence \(\frac{\mathrm{A}_{1}}{\mathrm{~A}_{2}}=\frac{10}{10}\) = 1

(b) Comparing the given equation with the normal sine function of S.H.M.
i.e. y = A sin(\(\frac{2πt}{T}\) + Φ) …(3)

Here we get \(\frac{2πt}{T}\) = 3πt
or
T = \(\frac{2}{3}\) s

i.e. Time period for two motions is same i.e. T = 0.67 s.

(c) Phase difference between two motions:
Phase (Φ₁) of motion represented by y₁ is
Φ₁ = 3πt + \(\frac{π}{4}\) …(4)

Phase (Φ₂) of motion represented by y₂ is
Φ₂ = 3πt + \(\frac{π}{3}\) …(5)

∴ Phase difference is given by
dΦ = Φ₂ – Φ₁ = (3πt + \(\frac{π}{3}\)) – (3πt + \(\frac{π}{4}\))
= (4 – 3)\(\frac{π}{12}\)
= \(\frac{π}{12}\) = 15°

Question 20.
Two particles execute- S.H.M. of the same amplitude at time period along the same straight line. They cross each other in opposite directions at half the amplitude. What is the phase difference between them?
Answer:
Let the displacement of one particle executing S.H.M. be
y₁ = A sin ωt …. (1)

when y₁ = \(\frac{A}{2}\)
From equation (1), we get.
\(\frac{A}{2}\) = A sin ωt
or
sin ωt = \(\frac{1}{2}\) = sin 30°
∴ ωt = 30° = \(\frac{π}{6}\) radian.

If Φ₁ be the phase of first particle then Φ = \(\frac{π}{6}\) radian. Also let the displacement of second particle executing S.H.M. be
y₁ = r sin (π – ωt) = r sin Φ₂ ….(2)
where Φ₂ = π – ωt = π – \(\frac{π}{6}\) = \(\frac{5}{6}\)π radian

If dΦ be the phase difference between the two particle when they cross each other, then
dΦ = Φ₂ – Φ₁
= \(\frac{5}{6}\)π – \(\frac{π}{6}\) = \(\frac{4π}{6}\) = \(\frac{2}{3}\)π radian
= 120°.

Question 21.
A spring compressed by 10 cm develops a restoring force of 5N. A body of mass of 2 kg is placed on it. Find
(i) Force constant,
(ii) depression of a spring,
(iii) time period and
(iv) the frequency of oscillations, if the body is disturbed.
Answer:
Here, F = 5N
x = 10 cm = 0.1 m
m = 2 kg
(i) k = force constant = \(\frac{F}{x}=\frac{5 N}{0.1}\) = 50 Nm^-1.

(ii) depression, l = \(\frac{\mathrm{mg}}{\mathrm{k}}=\frac{2 \times 9.8}{50}\) = 0.392 m

(iii) T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{2}{50}}\) = \(\sqrt{\frac{2π}{5}}\)s

(iv) v = \(\frac{1}{\mathrm{~T}}=\frac{5}{2 \pi}\) Hz

Question 22.
The S.H.M. of a particle is given by the equation y = 3 sin cot + 4 cos cot. Find its amplitude.
Answer:
The equation y = 3 sin ωt + 4 cos ωt is due to the superposition of two waves,
y₁ = 3 sin ωt
and
y₂ = 4 cos ωt = 4 sin(ωt + \(\frac{π}{2}\))

If r₁ and r₂ be the amplitudes of the two w’aves respectively, then r₁= 3 units and r₂ = 4 units.
Φ = phase difference between them = \(\frac{π}{2}\)

If r be the amplitude of the resultant wave, then

Question 23.
Two masses m₁ = 1.0 kg and m₂ = 0.5 kg arc suspended together by a massless spring of spring constant k as shown in the figure. When masses are in equilibrium, m, is removed without disturbing the system. Calculate the amplitude of oscillation and angular frequency of m2. (g = 10 ms^-2 and k = 12.5 Nm^-1).
Answer:
Let y = extension in length of the spring when both m1 and m2 are suspended with it, then
(m₁ + m₂)g = ky
or
y = \(\frac{\left(m_{1}+m_{2}\right) g}{k}\) …(1)

Let y’ extension in the length of the spring when only m is suspended.
∴ m₂g = ky’
or
y’ = \(\frac{\mathrm{m}_{2} \mathrm{~g}}{\mathrm{k}}\) …(2)

(1) – (2) gives y – y’ = \(\frac{\left(m_{1}+m_{2}\right) g}{k}-\frac{m_{2} g}{k}=\frac{m_{1} g}{k}\)

This represents the amplitude of oscillation (r)
i.e. r = y – y’ = \(\frac{\mathrm{m}_{1} \mathrm{~g}}{\mathrm{k}}\) …(3)
Here, m₁ = 1.0 kg
k = 12.5 Nm^-1
g = 10 ms^-2

Putting these values in equation (3), we get
r = \(\frac{1 \times 10}{12.5}\) = 0.8 m

If ω be the angular frequency of m₂, then
ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}_{2}}}=\sqrt{\frac{12.5}{0.5}}\) (∵ m₂ = 0.5 kg)
ω = 5 s^-1.

Question 24.
Prove that T = 84.6 minutes for a simple pendulum of infinite length.
Answer:
T = 2π\(\sqrt{\frac{l}{g}}\) …(1)
eqn. (1) hold good till l << R (radius of the earth).

When l is large, the curvature of the earth had also to be taken into account. In that case,

Question 25.
For damped oscillator, m = 200 gm, k = 90 Nm b = 40 gs^-1.
Calculate (a) time period of oscillation,
(b) time is taken for its amplitude of vibration to become \(\frac{l}{2}\) of its initial value.
(c) time is taken for its mechanical energy to drop to half of its initial value.
Answer:
Here, m = 200 g = 0.200 kg
k = 90 Nm^-1
b = 40gs^-1.
(a) \(\sqrt{km}\) = \(\sqrt{90 \times 0.2}=\sqrt{18}\) = 4.243 kg s^-1
b = 0.04 kg s^-1
∴ b << \(\sqrt{km}\)

(b) Let T_1/2 = time taken for the amplitude to drop to half of its initial value.

(c) Let T’_1/2 be the time for its mechanical energy to drop to half of its initial value,
∴ Using equation,

which is just half of T_1/2. (i.e. decay period for amplitude).

Value-Based Type:

Question 1.
A sports teacher was training the children to march- past On their way they come across a bridge. Then the physical education teacher stopped the children from marching on the bridge.
(a) Comment upon the values of sports teachers.
Answer:
The sports teacher is responsible, cares not only for public property but also for children.

(b) Also explain what is meant by Resonance.
Answer:
When the frequency of marching coincides with the natural frequency of oscillation of the bridge then the bridge oscillates with maximum amplitude to such an extent that the bridge may even collapse. The condition is called “Resonance”.

Question 2.
The Physics teacher of class XI has assigned the work finding the resultant spring constant when two springs of spring constants K₁, K₂ are joined in series. Two students Sabita and Shirin. Sabita made a theoretical study as well as verified it experimentally. Whereas Shirin could not complete the work. When th~ teacher enquired the next day Sabita could give the answer. Whereas Shirin could not.
(a) Comment upon the qualities of Sabita.
Answer:
Sabita is Sincere and hardworking and has a scientific temper.

(b) Two springs are joined in series and connected to a mass m. If spring constants are Kj and K2, Calculate the period of oscillation of mass m.
Answer:
Since K₁ and K₂ are joined in series.

Question 3.
Adarsh a student of class XI has found the factors on which the time period of oscillation of a pendulum depends and arrived at the expression T – (constant) × (l/g)^1/2. He wants to know how the length of the pendulum gets affected on the surface of the moon for the same pendulum and arrived at the conclusion that it is 1/6.
(a) What values does Adarsh possesses?
Answer:
Adarsh is hardworking, thinks logically, having a scientific temper, able to find solutions with patience.

(b) The length of a second pendulum on the surface of the moon?
Answer:
Since l is proportional to ‘g’ the pendulum on the surface of the moon will be 1/6m.

Question 4.
In a physics class, the teacher told that everyone has to finish the homework and assignment within a weak. But only five students including Dinesh did their homework on time. A few questions from the assignment are as under:
(i) Derive the expression for velocity in S.H.M.
Answer:
Let the displacement in S.H.M is given by

(ii) On what factors time period of a simple pendulum depends.
Answer:
The time period of a simple pendulum depends on
(a) Length of the pendulum.
(b) The acceleration due to gravity.

(iii) What values are shown by Dinesh?
Answer:
Values shown by Dinesh are Punctuality and Sincerity.

Studying from CBSE Class 11 English Hornbill Snapshots Notes Summary of All Chapters in Hindi Pdf Download helps students to prepare for the exam in a well-structured and organised way. Making Hornbill Snapshots Class 11 Chapters Summary saves students time during revision as they don’t have to go through the entire textbook. In CBSE Notes, students find the summary of the complete chapters in a short and concise way. Students can refer to the NCERT Solutions for Class 11 English, to get the answers to the exercise questions.

English Class 11 Notes Summary | Summary of Class 11 English Hornbill Snapshots

Hornbill Class 11 Chapters Summary | Class 11 English Hornbill Summary

• The Portrait of A Lady Summary
• We Are Not Afraid To Die If We Can All Be Together Summary
• Discovering Tut: The Saga Continues Summary
• Landscape of The Soul Summary
• The Ailing Planet: The Green Movements Role Summary
• The Browning Version Summary
• The Adventure Summary
• Silk Road Summary
• A Photograph Poem Summary
• The Laburnum Top Poem Summary
• The Voice of The Rain Poem Summary
• Childhood Poem Summary
• Father To Son Poem Summary

Snapshots Class 11 Chapters Summary | Class 11 English Snapshots Summary

• The Summer of The Beautiful White Horse Summary
• The Address Summary
• Ranga’s Marriage Summary
• Albert Einstein At School Summary
• Mother’s Day Summary
• The Ghat of The Only World Summary
• Birth Summary
• The Tale of Melon City Summary

We hope students have found this Summary of Class 11 English Hornbill Snapshots useful for their studies. If you have any queries related to English Class 11th Notes Summary, drop your questions below in the comment box.

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 8 Structural Organisation in Animals. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 8 Important Extra Questions Structural Organisation in Animals

Structural Organisation in Animals Important Extra Questions Very Short Answer Type

Question 1.
What is a ligament?
Answer:
It is a connective tissue that joins one bone to another bone.

Question 2.
Name the tissue which forms the inner lining of blood vessels
Answer:
Squamous epithelium

Question 3.
Name the functional unit of a muscle.
Answer:
Sarcomere.

Question 4.
Name any two granulocytes
Answer:
Eosinophils and basophils.

Question 5.
What are cell junctions?
Answer:
Cell junctions are the structures that hold the adjacent cells of tissue together when they are not separated widely by extracellular material.

Question 6.
Name the tissue that lines the intestinal wall.
Answer:
Columnar epithelium.

Question 7.
State the function of neuroglial cells.
Answer:
Serves as packing and supporting material between the nerve cells.

Question 8.
Name few epidermal structures.
Answer:
Hair, nails, claws and scales.

Question 9.
Define organ.
Answer:
Organ: A number of tissues together form an organ that works as a unit for the benefit of an organism.

Question 10.
What is the function of the ligament?
Answer:
The ligament is a dense fibrous connective tissue that connects bones at the joints.

Question 11.
Give an example of a heterochrony gland.
Answer:
Pancreas.

Question 12.
Name the cells from which thrombocytes are produced.
Answer:
Megakaryocytic cells.

Question 13.
Where are W.B.C. formed?
Answer:
In the bone marrow, lymph nodes and spleen.

Question 14.
What are the endocrine glands?
Answer:
They are ductless glands that secrete hormones directly into the bloodstream.

Question 15.
What is the function of antithrombin in our blood?
Answer:
It acts as an anticoagulant that prevents the clotting of blood in our blood vessels.

Question 16.
In which type of nerve fibre, the nerve impulse will move faster?
Answer:
Myelinated nerve fibre.

Question 17.
State the role of ligaments in the human body.
Answer:
It joins bones at the joints

Question 18.
Name the protein found in the white fibres,
Answer:
Collagen.

Question 19.
What do ESR and EDTA stand for?
Answer:
Erythrocytes Sedimentation Rate, Ethylene Diamine Tetra Acetic Acid.

Question 20.
What are myoepithelial cells?
Answer:
Cells showing the peculiar characteristics of both muscles and epithelial tissues.

Question 21.
What do fibroblasts synthesise? j
Answer:
The fibroblast in areolar tissue synthesizes collagen and elastin proteins.

Question 22.
How is coagulation prevented in an uninjured blood vessel?
Answer:
It is due to the secretion of heparin by most cells.

Question 23.
Name the two fundamental types of smooth muscles.
Answer:

1. Single unit smooth muscle.
2. Multi-unit smooth muscle.

Question 24.
What is double circulation?
Answer:
The blood passes twice through the heart to move through the body.

Question 25.
What is the trachea?
Answer:
It is a tube that is a part of the breathing apparatus of air-breathing animals.

Question 26.
What is clitellum?
Answer:
It is a prominent circular band of glandular tissue which surrounds the 14th to 16th segments in the earthworm body.

Question 27.
What is worm casting?
Answer:
It is the insoluble and undigested food that is given out along with soil through the anus.

Question 28.
What is the scientific name of an earthworm?
Answer:
Pheretima Posthuma.

Question 29.
Why is cockroach called Urecotelic?
Answer:
It is called Urecotelic because it excretes in the form of uric acid.

Question 30.
What is the function of Malpighian tubules?
Answer:
It helps in excretion.

Question 31.
What is the trachea?
Answer:
It is a tube that is a part of the breathing apparatus of air-breathing animals.

Question 32.
What are nephridia?
Answer:
Excretory organs of earthworm.

Question 33.
Define the term—hermaphrodite.
Answer:
It is the condition in which both testes and ovaries are produced by the same individual

Question 34.
Name the mouthparts of earthworm.
Answer:
Mandibles, maxillae, labium, labrum and hypopharynx.

Question 35.
Does the rat possess tonsils?
Answer:
No, the rat does not possess tonsils.

Question 36.
What is the functional unit of the cockroach eye?
Answer:
Ommatidium.

Question 37.
What is coelom?
Answer:
It is the true body cavity, space between the body wall and the alimentary canal.

Question 38.
State the difference between male and female frog.
Answer:
The male frog bears copulatory pads and well developed local sacs whereas they are absent in the female.

Question 39.
What are Pilitactiles?
Answer:
They are bristles found on both the sides of nostrils in the rat.

Question 40.
Name the larval stage in the life history of the frog.
Answer:
Tadpole.

Structural Organisation in Animals Important Extra Questions Short Answer Type

Question 1.
What is the utility of transitional epithelium in constituting the surface layer of the urinary bladder?
Answer:
Transitional epithelium is. highly stretchable and it does not allow the urinary bladder to get torn off when it is completely filled with urine. It undergoes considerable expansion to accommodate the maximum quantity of urine.

Question 2.
Classify the muscular tissue into different types.
Answer:
The muscular tissues can be divided into two broad categories depending upon their cytologic characteristic.
These are

1. Striated muscles and
2. Non-striated.

Striated muscle cells, in turn, may be subdivided into two additional categories-skeletal and cardiac.

So these are summarised into three different types:

1. Striated or striped-skeletal and voluntary muscle fibres.
2. Non-striated or unstriped plain or smooth and involuntary muscle fibres.
3. Cardiac – striated and involuntary muscle fibres.

Question 3.
What is the major function of haemoglobin?
Answer:
Functions of haemoglobin:

1. It is essential for oxygen carrier from the lungs to the tissue in the form of oxyhaemoglobin, Each molecule of haemoglobin carries about 1.33 ml of oxygen.
2. It plays an important part in the transport of CO₂ as Carbomino haemoglobin from tissue to the lungs. About 23 per. cent of CO₂ is transported back to the lungs through the haemoglobin.
3. It acts as a buffer arid regulates’•the blood reactions by maintaining a constant pH.

Question 4.
What are the general characteristics of epithelial tissue?
Answer:

1. It consists of closely packed cells of various types and shapes which forms the lining membrane of several organs.
2. The cells of the epithelial membrane are arranged in one or more layers resting upon the thin non-cellular basement membrane and these cells are supported by intercellular cementing substance and close vascular connective tissues.
3. The basement membrane is formed of protein fibres interspersed in the matrix of polysaccharide. The matrix is secreted by underlying connective tissue.
4. The cementing substance between the cells is formed of mucoprotein containing hyaluronic and calcium salts.

Question 5.
What are oligodendrocytes? What their functions?
Answer:
Oligodendrocytes are a type of neuroglia cells that hold the neurons in position in the central nervous system. Their process spirally wraps around the nerve fibres to form a myelin sheath in the absence of Schwann cells in the central nervous system.

Question 6.
Why does oedema occur in persons suffering from a dietary deficiency of proteins?
Answer:
Albumin and globulin proteins are necessary for retaining water in the blood plasma by their, osmotic effects. In the dietary deficiency of proteins, enough water is not retained in the blood plasma and it gets filtered out from the blood into the tissue and leads to the swelling of hands and feet.

Question 7.
Name the specific tissue that forms the outermost exposed surface of the human skin. State any two advantages of this tissue being there.
Answer:
Keratinised squamous epithelium. It contains insoluble protein-keratin which is impervious to water and so prevents the loss of water. It also provides protection to the skin against mechanical pressure, friction, injury and water loss.

Question 8.
Write a short note on erythropoiesis.
Answer:
The formation of new erythrocytes is called erythropoiesis and if takes place from the haemopoietic tissue. The haemopoietic tissue in the young foetus is the liver and spleen whereas in the adults it is the bone marrow, of long bones.

The haemopoietic tissue synthesises millions of RBCs every minute to replace the worn-out erythrocytes promoted by erythropoietin, a glycoprotein produced by renal tissue in response to the liberation of ACTH. The deficiency of iron, folic add and vitamin B leads to anaemia, megaloblastic anaemia and pernicious anaemia etc. 12

Question 9.
How is blood prevented from clotting in the blood banks?
Answer:
In the blood banks, the various anticoagulants like.

1. Sodium oxalate, sodium citrate and EDTA (Ethylene diamine tetraacetic acid) are used which prevent coagulation by removal of calcium ions.
2. Clotting can also be prevented by removing free calcium ions from the whole blood as this metallic ion is a critical requirement in several stages of the coagulation mechanism.

Question 10.
How does saltatory conduction take place along a nerve fibre?
Answer:
Along with a myelinated nerve fibre, the conduction of impulse is called saltatory conduction. This is so because the ionic changes and consequent depolarisation taking place only at the nodes of Ranvier free from myelin sheath leading to the jumping of action potential from one node to the next.

Question 11.
State the important function of platelets.
Answer:

1. During injury to any tissue, the platelets disintegrate and liberate a thromboplastin which is concerned with the activation of prothrombin to thrombin.
2. The platelets are quite sticky and they get adhered to the roughened surfaces of foreign bodies as bacteria. This response tends to increase the bodily defence as leukocytes can phagocytize these microorganisms more easily.

Question 12.
Write a note on the body wall of the earthworm.
Answer:
The body wall of the earthworm: The body wall of the earthworm is covered by a thin non-cellular cuticle. The cuticle is followed by an epidermis, two muscle layers and innermost coelomic epithelium. The epidermis consists of a single layer of columnar epithelial cells. It contains many other types of cells, including the secretory gland cells. Muscle layers are made of circular and longitudinal muscle fibres.

Question 13.
How does the earthworm move?
Answer:
Earthworm moves with the help of an S-shaped stopped setae, embedded in the epidermal pit at the middle of each segment. These are made up of chitin and help in locomotion by gripping the earth. Locomotion is thus, performed by contraction and relaxation of the muscles and used of setae for gripping on-die soil.

Question 14.
What is the main difference between the blood of earth¬worm and man?
Answer:
The blood of the earthworm is red due to haemoglobin that is dissolved in plasma. Corpuscles are colourless and nucleated. Man blood is also red but haemoglobin is dissolved in RBGs. The corpuscles are denucleated and biconcave disc-like.

Question 15.
Name the main excretory organ in the cockroach. How does it help in excretion?
Answer:
The main excretory organ in the cockroach is the malpighian tubules. Each malpighian tubule is lined by glandular, ciliated cells with a brush border. They absorb the nitrogenous waste product and convert them into uric acid through various biochemical processes. The uric acid is excreted through the hindgut. The fat bodies, nephrocytes, cuticle and Urecose glands also help in the excretion

Question 16.
What is the mosaic vision?
Answer:
Each ommatidium produces a separate image or a small part of the object present just in front of it. Thus, the image of the object formed in a compound eye is actually made of several small pieces. Such a picture or image is called a mosaic image and the vision is called mosaic vision. The nature of the image depends upon the intensity of light. In bright light, an apposition image is formed and in dim light, it is superposition.

Question 17.
Write briefly about the female reproductive system in the cockroach.
Answer:
It consists of two large ovaries lying laterally in the 4th, 5th and 6th segment. Each ovary is made up of a group of 8 ovarian tubules containing a chain of developing ova. Oviducts of each ovary unite into a single median oviduct that is also called the vagina that opens into the genital chamber. The female accessory glands are a pair of branched, collateral glands, that open into the dorsal side of the genital chamber:

Question 18.
What is a portal system?
Answer:
It consists of a vein and its capillaries that collect deoxygenated blood from some organ and pour it into some other organ instead of supplying it directly to the heart. Such a vein is called a portal vein and these veins along with their capillaries constitute the portal system.

Question 19.
Write briefly about the brain of the frog.
Answer:
The frog’s brain consists, of the fore-brain, mid-brain and hind-brain. It is enclosed in a bony structure, which has two occipital condyles for attachment with the first vertebra. Fore-brain is made up of olfactory lobes, paired cerebral hemispheres and unpaired diencephalon.

The mid-brain has characteristic paired ‘optic lobes. The hind-brain consists of the cerebellum and medulla oblongata. The medulla oblongata passes out through the foramen magnum and continues into the spinal cord that is contained in the vertebral column.

Question 20.
What is the interaction of frog with mankind?
Answer:

1. Frogs eat up insects and thus, protect the crop.
2. Frogs are largely used as experimental material for teaching and research.
3. The muscular legs of the frog are largely used as food by man in some parts of India and many other countries.

Question 21.
What are nephridia? In which animal they are present? Name a different kind of nephridia by indicating their location.
Answer:
Nephridia are the excretory organs and they are found in earth-worm.

There are three types of nephridia:

1. Septal nephridia: These are present on both sides of the intersegmental septa and open into the intestine.
2. Integumentary nephridia: These are found attached to the lining of the body wall and open on the body surface.
3. Pharyngeal nephridia: These are found in the 4th, 5th and 6th segments in the form of paired tufts.

Question 22.
What are the ear ossicles in the rat?
Answer:
Ear ossicles in the rat:
The ear of a rat is divided into three parts:

1. external ear,
2. the middle ear, and
3. internal ear.

The outermost is the external ear or pinna has the middle ear three small bones called ear ossicles. The third internal ear is related to hearing and equilibrium. The semicircular canals are lined with sensory epithelial cell in the internal ear of the rat.

Question 23.
How is earthworm known as the “friend of farmers”?
Answer:

1. Earthworm makes small burrows in the soil and so the soil becomes porous facilitating respiration and penetration of developing plant roots.
2. They chum up the soil on swallowing at their mouth end and pass the soil out at their anal end. Thus, the soil becomes finer and capable of holding more soil water.
3. They cultivate the soil by bringing its deeper layer of the surface.
4. Earthworms are also used as food in some countries. Many tribal communities in India use earthworms in the form of medicine to cure bladder stones, jaundice, piles, diarrhoea etc.

Question 24.
Name the main excretory organ in the cockroach. How does it help in excretion?
Answer:
The main excretory organ in the cockroach is the malpighian tubules.

Each malpighian tubule is lined by glandular, ciliated cells with a brush border. They absorb the nitrogenous waste product and convert them into uric acid through various biochemical processes. The uric acid is excreted through the hindgut. The fat bodies, nephrocytes, cuticle and Urecose glands also help in excretion.

Question 25.
Describe briefly the male reproductive organs in the cockroach.
Answer:
The male reproductive organs consist of a pair of testes lying one on each lateral side in the 4th-5th abdominal segments, A vas deferens, a thin tube arises from each testis and opens into the male gonophore situated ventral to the anus. A mushroom-shaped gland is present at the 6th-7th abdominal segments that function as an accessory reproductive gland.

The external genitalia is represented by chitinous asymmetrical structures, surrounding the male gonopore, at the end of the abdomen, called male gonapophysis or phylloxera. The sperms are stored in seminal vesicles and are glued together in the form of bundles called spermatophores.

Question 26.
Give the possible reason for the following statements.
(i) A transparent nictitating membrane is present in the eyes of a frog.
Answer:
Nictitating membrane protects the eyes of the frog when it undergoes mud during hibernation, aestivation and swimming.

(ii) The first finger of the male frog is swollen.
Answer:
The first finger in the male frog is swollen in the form of a copulatory pad to hold up the female frog firmly during copulation.

(iii) The skin of the frog is moist and slippery
Answer:
The skin of the frog is moist and slippery to perform the cutaneous respiration as well as to slip away from the grip of predators.

(iv) Webs are present between the toes of frog,
Answer:
The webs are present between the toes because these act as paddles when the frog is swimming.

Question 27.
Name the three types of respiration in the frog. How does frog respire during hibernation?
Answer:
The three types of respiration in a frog are:

1. Cutaneous respiration
2. Buccal respiration
3. Pulmonary respiration

The frog’s skin is moist, slimy and highly vascularized which is especially useful for respiration in hibernation and aestivation. The oxygen of the atmosphere enters the thin film of skin moisture where it goes to the blood capillaries of the skin. The oxygen mixes with the blood and passes to the different organs of the body. The carbon dioxide formed in the body organs is taken up by the blood capillaries to the skin from where it diffuses out into the air.

Structural Organisation in Animals Important Extra Questions Long Answer Type

Question 1.
Enumerate the various functions of epithelial tissue.
Answer:
Function:

1. Protection: It protects the underlying or overlying soft tissues against heat, injury, chemicals, virus and bacteria etc.
2. Absorption: It absorbs the digestive food especially with columnar cells of the intestine.
3. Secretion: The glandular epithelial cells lining the inner cavities secrete various substances like mucous, enzymes and hormones which are necessary for various metabolic activities.
4. Excretion: The epithelial cells of kidney tubules and sweat glands help in the excretion of wastes from the body.
5. Sensation: The nerve ending in the epithelial cells of the retina, olfactory organs and nasal chamber etc. receive the stimuli from the external atmosphere and transfer them to the brain for interpretation.
6. Other functions: The trachea contains the ciliated epithelium to facilitate the transport of mucous and other substances from one part of the body to another. The lungs’ epithelium helps in the exchange of gases during respiration and the germinal epithelium of testes and ovaries form the sperms and ova respectively. The epithelium also forms the exoskeleton structure as scales, feathers, hairs, nails, claws, horns etc.

Question 2.
What is a gland? Differentiate between simple and compound exocrine gland.
Answer:
Any organ or structure that secretes specific useful substances is known as a gland.

A gland develops from the epithelium tissues and is generally cubical, short columnar or polyhedral in shape.
1. Simple exocrine gland: Simple exocrine gland has no branch but consists of a single unbranched duct lined by epithelial cells. The secretory part of the gland also consists of epithelial cells arranged in a simple tube, coiled tube in a flask which send their secretion into a single duct.

So these are simple tubular glands, simple coiled tubular glands and simple alveolar glands respectively.

2. Compound exocrine gland: Compound exocrine gland has a branched system of ducts. The secretory part consists of tubules-Com-pound tables, many acini or alveoli-compound alveolar glands or a combination of both tubules and acini-compound tubuloalveolar gland.

Question 3.
What is connective tissue? Give its important functions.
Answer:
Connective tissue is mesodermal in origin and form of matrix, fibres and cells. It constitutes the extracellular ground substance and fills up the intercellular spaces between the cells.

Functions of connective tissue: The connective tissue perform various functions and these are:

1. It serves the function of packing material nearly for all organs.
2. It binds one tissue or organ to another and serves the purpose of a strong elastic rope.
3. It provides skeletal support and shape to the body.
4. It protects the vital organs of the cranial and thoracic cavities, deep blood vessels and nerves from mechanical injuries.
5. The adipose connective tissue stores fat and represent stored energy.
6. It provides defence against foreign particles like bacteria. The phagocytes of leucocytes ingest the bacteria and germs and protect the body against infection.
7. The lymphocytes from the antibodies against the action of antigens and provide immunity to the body.

Question 4.
What is adipose tissue? Where does it lie in the human body? Give its important functions.
Answer:
Adipose tissue: It is the specialized form of areolar tissue where it contains fat cells or adipocytes in the matrix. Each fat cell is large, rounded occupied by big fat droplets and its nucleus and cytoplasm are pushed towards the periphery of the cell. This imparts a ‘signet’ ring-like look to the fat cell.

These fat cells can easily be stained by Sudan III or osmic acid. The matrix is supported by a loose framework of areolar tissue containing fibroblasts, macrophage, white collagen fibres of small size, elastic fibres; lymphatics and blood vessels.

The lactating tissue lies in the subcutaneous tissue of the skin, in the mesentery and in the perinephric and sub periodical tissue of the body. The lactating mammary gland of human also contain abundant amounts of adipose tissue but these are quite lacking in penis, scrotum, eyelids and in the cranial cavity.

Adipose tissue

Functions: It synthesises, stores and metabolises the fat and forms the insulating layer beneath the skin. It collects around the viscera especially kidneys and prevents them from shock and injury.

Question 5.
Plasma contains three classes of proteins. What are these? Give their functions.
Answer:
The major classes of plasma proteins are

1. Albumin,
2. Globulins and
3. Fibrinogen

Functions of Plasma Proteins:

1. The immune bodies are mainly an important constituent of the globulin fraction which provide defence against infection.,
2. Fibrinogen and prothrombin are necessary for the coagulation of blood.
3. The plasma proteins normally have an osmotic effect of 25 mm Hg and thus influence the exchange of fluid between blood and tissue spaces.
4. Plasma proteins mainly globulins are responsible for the viscosity of blood and this help in maintaining peripheral resistance and arterial blood pressure for efficient heart functioning.
5. Plasma, proteins act as buffers in maintaining acid-base balance.
6. Albumin and globulin proteins retain water in the blood plasma by their osmotic effects and their deficiency lead to oedema.
7. Plasma proteins especially the fibrinogen are concerned with erythrocyte sedimentation rate.
8. Plasma proteins help in the transport of certain substances like hormones, enzymes, iron and copper etc. in the blood.
9. Plasma proteins distribute heat uniformly all over the body.

Question 6.
Describe briefly the external features of cockroach.
Answer:
The cockroach is a nocturnal cursorial and omnivorous insect. It is generally reddish-brown in colour and its entire body is covered by tough chitin. Its body is divided into head, thorax and abdomen.

Head: It is somewhat pear-shaped and is six segmented. It lies at a right angle to the body with the broad side upwards. It articulates with the thorax by the flexible neck. On each side of the head is a large compound eye. A pair of antennae articulate Inspite close to the notches of the compound eyes.

The top of the head is termed a vertex. Mouthparts are chewing and surrounded by five kinds of appendages. These include, the labrum, mandibles, first maxillae, second maxillae and hypopharynx. The neck is slender, flexible and supported by chitinous cervical plates.

Thorax: The thorax consists of three segments – Prothorax, mesothorax and metathorax. Each segment of the thorax is covered by four sclerites. There is a tergum on the dorsal side, a sternum on the ventral side and a pleuron on either lateral side.

The thorax bears three pairs of jointed walking legs, a pair per segment and two pairs of wings in meso and metathorax. Each leg is made of a number of parts-coxa; the trochanter, femur, tibia and tarsus. Their leg is made of a number of parts coxa, trochanter, femur, tibia and tarsus: They are formed as lateral expansions of the

(a) External features of cockroach

integument between the tergum and the pleuron. Each wing is supported by a network of hollow veins. The mesothorax wings are narrow, thick, opaque and leathery and not used in flight.
Head

(b) External features of cockroach

Abdomen: The abdomen is ten segmented and covered by four sclerites. There are is all ten-terga, but 9th terga of the male and 8th and 9th terga of the female are covered by 7th tergum. In the female-only the first seven sterna are visible, the seventh, eighth and ninth sterna together form a brood pouch.

The 10th tergum bears a pair of a long tapering structure called anal cerci. In male 9th sternum bears a pair of short unjointed anal styles. They are absent in females. The gonapophyses are very small, irregular arising from the 9th sternum in the male and from the eighth and ninth sterna in the female.

At the posterior end of the abdomen, below the tenth terga, is situated the anus. There, are ten pairs of spiracles on the lateral sides of the body, two on the thorax, eight on the abdomen.

Question 7.
Describe briefly the alimentary canal and digestive glands of the frog.
Answer:
The alimentary canal of the frog is short. It starts with a mouth that is terminal in position. It opens into the buccopharyngeal cavity which contains the maxillary and vomerine teeth and carries the openings of the eustachian tube, vocal sac, gullet and glottis. The gullet opens in a narrow and short tubed Oesophagus which continues In the large stomach. Stomach walls arc highly muscular that help In converting the food into chyme.

The stomach is followed by a coiled small intestine. The small intestine bears a number of finger-like folds called villi and microvilli which increase the surface area for absorption of digested food. Intestine continues into a wider section, opening into the cloaca. The urinary bladder opens into the cloaca. The urinary opens into the cloacal chamber through the ureter.

Alimentary canal and digestive glands of the frog

The gastric glands of the stomach bring about the digestion of protein. The liver secretes bile that is temporarily stored in the gall bladder. Bile helps in the digestion of food by changing its pH from acidic to alkaline and by emulsifying the fat. The liver does not secrete any enzyme. The pancreas is situated in a thin mesentery and lies parallel to the stomach.

It secretes pancreatic juice that causes the digestion of protein starch and fats with the help of trypsin, amylase and lipase. Similarly, intestinal juices with their peptidases, lipase and sugar enzymes bring about the digestion of peptides, fats and sugars.

Question 8.
Describe briefly the blood vascular system of the cockroach.
Answer:
The cockroach has an open circulatory system. Blood is colourless and contains plasma with colourless cells, the leucocytes. It does not contain haemoglobin and thus, plays no role in respiration.

The heart is thirteen chambered which is long, narrow, muscular and tube-like structure. The three chambers of the heart lie in the thorax and ten in the abdomen. The posterior end is closed and the anterior end is continued forwards as the anterior aorta. It opens into a haemocoel in the head.

There is a small hole, the Ostia at the posterior side of each chamber. Ostia is guided by valves to allow blood flow only in one direction i.e., from the haemocoel to the inner chamber of the heart.

All the visceral organs are bathed in blood. It consists of a colourless liquid part, plasma containing many corpuscles called haemocytes.

Question 9.
Describe the male reproductive organs in the frog.
Answer:
It consists of a pair of the yellowish testis that is attached to the upper part of the kidneys by a double fold of peritoneum called mesorchium.

Reproductive organs of the male frog

Each testis contains about 10 to 12 vasa efferentia that run through the mesorchium and enter the kidneys of their side. In kidneys, these open into the bidder’s canal that finally joins with the urinogenital ducts. This cones of the kidneys and finally opens into the cloaca. The cloaca is a small, medium chamber that is used to pass faecal matter, urine and sperms to the exterior.

Question 10.
Draw a labelled diagram of the reproductive organs of an earthworm.
Answer:
Reproduction in Earthworm: The earthworm is hermaphrodite (bisexual). The testes and ovaries are present in the same individual. There are two testes present in the 10th and 11th segments. Ducts that arise from them are called vasa deferentia. The run-up to the 18th segment where they join the ventral side of the 17th and 19th segments.

The prostate and spermatic duct open to the exterior by a pair of male genital pores on the ventrolateral side of the 18th segment. The spermathecae are found one in each of the 6th to 9th segments. They are 4 pairs, they receive and store spermatozoa during copulation.

Two ovaries are attached at the intersegmental septum of the 12th and 13th segments. Ovarian funnels are found beneath the ovaries. They continue into oviducts, join together and open on the ventral side as a single female genital pore on the 14th segment. The development is direct. There are no larval forms in earthworm.

The reproductive system of earthworm

Question 11.
Describe the alimentary canal of an earthworm and interactions with mankind.
Answer:
Alimentary canal of earthworm: Alimentary canal is a straight tube starting from 1st segment to the last segment of the body. It consists of the mouth, buccal cavity, pharynx, oesophagus, gizzard, stomach, intestine and anus. The mouth lies in the first segment.

The mouth opens into the buccal cavity (1 – 3 segment). The buccal cavity leads into the pharynx. The pharynx leads into the oesophagus which is continued into the gizzard. The stomach extends from the 9th 14th segment. The intestine starts from the 15th segment and continues up to the last segment. The alimentary canal opens to the outside by an aperture called the anus.

Interaction of earthworm with mankind:

1. Earthworms are the friends of farmers. They make burrows in the soil and make it porous to facilitate respiration and penetration of plant root. Earthworm increases the fertility of the soil by vermicomposting.
2. In China, Japan, Burma, Australia, earthworms are used for food.
3. Earthworms are used as bait for game fishing.
4. In India, earthworms are used for the treatment of stones, jaundice, piles, diarrhoea.
5. Earthworms also cause harm by making burrows in the land (damage tender plant).

Alimentary canal of the earthworm

By going through these CBSE Class 11 Maths Notes Chapter 7 Permutations and Combinations Class 11 Notes, students can recall all the concepts quickly.

Permutations and Combinations Notes Class 11 Maths Chapter 7

Fundamental Principle of Counting (F.P.C.): If an event can occur in m different ways, following which another event can occur in n different ways, following which another event can occur in r different ways and so forth, then the total number of different ways of occurrence of the events in the given order is m x n x r x …

Note : The principle is also known as multiplication principle.

Factorial Notation:
Important Definition : Factorial is a convenient notation for representing the product of first natural numbers. The notation for the product uses a mark of exclamation (!) suffixed to the highest natural number in the product. Thus

4! = 4 × 3 × 2 × 1.
6! = 6 × 5 × 4 × 3 × 2 × 1.
In general, n! = n(n – l)(ra – 2)… (3)(2)(1).
It is read as ‘factorial n

Important formula:
(i) 6(5!) = 6(5 × 4 × 3 × 2 × 1)
= 6!
n[(n-l)!] = n!
(it) 0! = 1. [By definition]

Permutations:
Important Definition : A permutation is an arrangement in definite order of a number of objects taken when some or all at a time.

Important Formulae : (i) The number of permutations of n different objects taken all at a time, denoted by nPn is given by ⁿP_n = n(n – l)(n – 2)… 3.2.1
= n!

(ii) The number of permutations of n different objects taken r at a time denoted by ⁿP_r (n > r) is given by
ⁿP_r or P(n, r) = n(n – 1)(n – 2)… (n + 1 – r).
or ⁿP_r = \(\frac{n !}{(n-r) !}\) (when all objects are different)

(iii) Value of 0!
Putting r = n in \(\frac{n !}{(n-r) !}\), we have :
ⁿP_n= \(\frac{n !}{(n-n) !}\) or n! = \(\frac{n !}{0 !}\)
or 0! = \(\frac{n !}{n !}\) = 1
∴ 0! = 1.

(iv) Permutations of n objects all at a time, when n1 are alike, n2 are alike, and so on but different from n1 and n2 are given by
P = \(\frac{n !}{n_{1} ! n_{2} ! n_{3} !}\)

(v) Circular permutations : If we consider arrangements of objects in a circle, instead of a line, then we speak of circular permutations.

If n distinct objects are arranged in a circle, each object can shift position n times and returns to its original without disturbing the arrangement. Thus, each circular permutation gives n linear permutations and the number of distinguishable circular permutations, p is given by p = \(\frac{n !}{n}\) = (n – 1)!.

Combinations :
Important Definition: (i) A combination is a selection of some or all of a number of different objects. In a combination, the order of selection of the objects is immaterial.

(ii) The difference between a permutation and a combination of the objects is the “Order” does matter in a permutation, while it does not matter in case of a combination.

(iii) Relation between permutations and combinations is
C(n, r) = \(\frac{\mathrm{P}(n, r)}{r !}\), where C(n,r)
is the number of combinations of n objects taken r at a time.

or P(n,r) = (r!)C(n, r)
Note : ⁿP_r and ⁿC_r may also be denoted as P(n, r) and C(n, r) respectively.

Important Formulae:
(i) C(n, r) = \(\)
Note : (a) C(n, n)= 1 (b) C(n, 0) = \(\frac{n !}{0 !(n-0) !}\) = 1.
(ii) Complementary combinations
C (n, r) = C(n, n-r)
(;iii) Pascal’s rule
C(n, r) + C(n, r – 1) = C(n + 1, r).

By going through these CBSE Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations Class 11 Notes, students can recall all the concepts quickly.

Complex Numbers and Quadratic Equations Notes Class 11 Maths Chapter 5

Imaginary Numbers: A number whose square is negative, is known as an imaginary number, e.g. : \(\sqrt{-1}, \sqrt{-2}\), etc.
\(\sqrt{-1}\) is denoted by the Greek letter i (iota).

Powers of i : i¹ = – 1; i²= – 1; i³ = — i, i⁴ = 1, etc.

An Important Result : For any two real numbers a and b,
\(\sqrt{a} \times \sqrt{b}=\sqrt{a b}\) is true only when at least one of a and b is either 0 or positive.
In fact, \(\sqrt{-a} \times \sqrt{-b}=(i \sqrt{a})(i \sqrt{b})=i^{2} \sqrt{a b}=-\sqrt{a b}\), where a and b are positive real numbers.

Complex Number : Any number of the form x + iy, where x, y are real numbers and i \(\sqrt{-1}\) is called a complex number.

It is denoted by z, i.e., z = x + iy. The real and imaginary parts of a complex number z are denoted by Re(z) and Im(z) respectively. Thus, if z = x + iy, then Re(z) = x and Im(z) = y.

Note : Every real number is a complex number, for if a e R, it can be written as a – a + i0.

Purely Real and Purely Imaginary Numbers : A complex number z is said to be
(i) purely real, if Im(z) = 0.
(ii) purely imaginary, if Re(z) = 0.

Conjugate of a Complex Number : The conjugate of a complex number z, denoted by \(\bar{z}\) is the complex number obtained by changing the sign of imaginary part of z i.e., if z = a + ib, then \(\bar{z}\) = a-ib.

Modulus of a Complex Number: The modulus of a complex number, z- a + ib, denoted by |z |, is defined as |z | = \(\sqrt{x^{2}+y^{2}}\)

Sum, Difference and Product of Complex Numbers : For any complex numbers z₁ = a + ib and z₂ = c + id, it is defined as
(i) Z₁ + z₂ = (a + ib) + (c + id) = (a + c) + i(b + d).
(ii) z₁ – z₂ = (a + ib) – (c + id) = (a -c) + i(b – d).
(iii) z₁z₂ = (a + ib)(c + id) = (ac -bd) + i(ad – bc).

Properties of Complex Numbers:

1. A real number can never be equal to an imaginary number.
2. (a + ib) = 0 ⇔ a = 0 and 6 = 0.
3. Two complex numbers are equal only when their real and imaginary parts are separately equal.
i.e., if a + ib = c + id, then a = c and b = d.

4. If z is a complex number, then :
(i) (\(\bar{z}\)) = z
(ii) (z + \(\bar{z}\)) is real.
(iii) (z – \(\bar{z}\)) is zero or an imaginary number.
(iv) z + \(\bar{z}\) = 2Re(z) and (z – \(\bar{z}\)) = 2iIm(z).
(v) z\(\bar{z}\) – |z |² and, therefore, z\(\bar{z}\) is real.

5. If z₁ and z₂ are complex numbers, then :
(i) \(\left(\overline{z_{1}+z_{2}}\right)=\overline{z_{1}}+\overline{z_{2}}\)
(ii) \(\left(\overline{z_{1}-z_{2}}\right)=\overline{z_{1}}-\overline{z_{2}}\)
(iii) \(\left(\overline{z_{1} z_{2}}\right)=\overline{z_{1}} \cdot \overline{z_{2}}\)
(iv) \(\left|z_{1} z_{2}\right|=\left|z_{1}\right|\left|z_{2}\right|\)

6. For any complex number z, |z | = 0 ⇔ z = 0.
7. The sum and product of two complex numbers are real if and only if they are conjugate of each other.
8. The conjugate and the reciprocal of a non-zero complex number z are equal if and only if | z | = 1.
9. Reciprocal or multiplicative inverse of a + ib
= \(\frac{1}{a+i b}=\frac{1}{a+i b} \times \frac{a-i b}{a-i b}=\frac{a}{a^{2}+b^{2}}-i\left(\frac{b}{a^{2}+b^{2}}\right)\)

10. For any integer k,
(i) i^2k = (-1)^k , i^{2k+ 1} = (- 1)^ki
(ii) i^4k = (i⁴)^k = 1, i^{4k+ 1} = i^4k+2 = i² = -1,
i^4k+3 = i³ = i² x i = -i

Geometrical Representation of a Complex Number : To every complex number z = x + iy, there is one and only one point P(x, y) in the plane, and conversely to every point (x,y) in the plane, there is one and only one complex number z = x + iy.

The plane, representing the complex numbers, as an ordered pair of real numbers is called the Complex plane or Gaussian plane or Argand plane.

Modulus and Amplitude of a Complex Number : Let a poin^ P represents a complex number z = x + iy in the complex plane. Then, the length OP is called the modulus of the complex number z and is denoted by |z|.

∴ |z| = OP = |x + iy|
= \(\sqrt{x^{2}+y^{2}}\) .

The angle XOP = θ is called the amplitude or argument of 2 and is written as amp. z or arg. z. The value of θ satisfying – π < θ < π is called the principal value of amp z.

Polar Form of a Complex Number : Let z – a + ib be represented by P(a, b).
Let OP = r, ∠XOP = θ.
Then, a – rcos θ,
b = rsinθ
= r² = a² + b²
⇒ r = |2|
and tanθ = \(\frac{b}{a}\)
⇒ cosθ = \(\frac{a}{r}\) ,sinθ = \(\frac{b}{r}\).
The form 2 = r(cos θ + isin θ) is called the Polar Form.

Polynomial Equation : A polynomial equation of a degree x has n roots.

Solutions of Quadratic Equation: The solutions of quadratic equation
ax² + bx + c = 0,
where a, b, c ∈ R, a ≠ 0, b2² – 4ac < 0 are given by
x = \(\frac{-b \pm\left(\sqrt{4 a c-b^{2}}\right) i}{2 i}\)

D = b² – 4ac is called the discriminant of the quadratic equation.

By going through these CBSE Class 11 Maths Notes Chapter 4 Principle of Mathematical Induction Class 11 Notes, students can recall all the concepts quickly.

Principle of Mathematical Induction Notes Class 11 Maths Chapter 4

Mathematical induction is a technique for proving general results or theorem involving positive integers.

The word induction means the method of inferring a general statement from the validity of particular cases.

Statement : A sentence which can be judged to be true or false is called a statement.
A statement holding for n ∈ N is generally denoted by P(n).

Principle of mathematical induction : Let P(n) be a statement involving the natural number n. Then,
(i) P( 1) is true and
(ii) P(k + 1) is true whenever P(k) is true, then P(n) is true for all natural numbers n.

For proving that statement P(n) holds for all n ∈ N :
Following steps are applied :

Step 1 : Verification that P(n.) holds for n = 1, i.e., P( 1) is true.
Step 2 : Suppose that P(re) holds for every k ∈ N.
Step 3 : Prove that P(n) holds for n = k + 1 also.

By going through these CBSE Class 11 Maths Notes Chapter 3 Trigonometric Functions Class 11 Notes, students can recall all the concepts quickly.

Trigonometric Functions Notes Class 11 Maths Chapter 3

Important Definitions:

Angle: An angle is considered as a figure obtained by rotating a given ray about its initial point. The original position of the ray is called the initial side and the final position is called the terminal side of the angle. The point of rotation is called the vertex.

Positive Angle : If the direction of the rotation is anticlockwise, the angle is said to be positive.

Negative Angle : If the direction of the rotation is clockwise, the angle is said to be negative.

Degree measure of an angle: If a rotation from initial side of the terminal side is (\(\frac{1}{360}\))th of a revolution, the angle is said to have a measure of one degree, written as 1°.

1° = 60′ [One degree = 60 minutes]
1′ = 60″ [One minute = 60 seconds]

Radian Measure : An angle with its vertex at the centre of a circle which intercepts an arc equal in length to the radius of the circle is said to have a measure of 1 radian.

Important Formulae:

1. θ = \(\frac{l}{r}\)
   where θ = angle subtended by arc of length l at the centre of the circle and
   r = radius of the circle.
2. π radians = 180°.
3. 1 radian = \(\left(\frac{180}{\pi}\right)^{\circ}\)
4. 1° = radian = 0.01746 (app.)

Circular Functions: Let a circle of unit radius be drawn with centre O. A line segment OP = 1 is rotated from the initial position OX, in the anticlockwise direction.

Let OP makes an angle θ with OX. The x-coordinate of P gives the value of cos θ and y – coordinate will give the value of sin θ. P may be any where on the circle and hence θ may acquire any value from 0 to 2π radians. Thus, we get the value of cos θ and sin θ for any value of θ.
These trigonometric functions are known as circular functions.

Important Formulae :

1. sin² θ – co² θ = 1
2. 1 + tan² θ = sec² θ
3. 1 + cot² θ = cosec² θ

Periodic Functions : A function f is said to be periodic, if there exists a real number T > 0 such that f(x + T) = f(x) for all values of x. Then, T is called the period of the function.
Trigonometric actions are also periodic.
Here, cos (2nπ + x) = cos x
sin (2 nn + x) = sin x

Trigonometric Ratios (T-Ratios) Of Angle (-x)

1. sin(-x) = -sin x,
2. cos (- x) = cos x,
3. tan (-x) = -tan x,
4. cosec (- x) = – cosec x,
5. sec(-x) = sec x,
6. cot (- x) = – cot x.

T-Ratios of (\(\frac{\pi}{2}\) – x)

1. sin (\(\frac{\pi}{2}\)-x) = cos x
2. cosec (\(\frac{\pi}{2}\)-x) = sec x
3. cos (\(\frac{\pi}{2}\)-x) = sin x
4. tan (\(\frac{\pi}{2}\)-x) = cot x
5. sec (\(\frac{\pi}{2}\)-x) = cosec x
6. cot (\(\frac{\pi}{2}\)-x) = tan x

T-Ratios of (\(\frac{\pi}{2}\) + x)

1. sin (\(\frac{\pi}{2}\)-x) = cos x
2. cos (\(\frac{\pi}{2}\)-x) = -sin x
3. tan (\(\frac{\pi}{2}\)-x) = -cot x
4. cosec (\(\frac{\pi}{2}\)-x) = sec x
5. sec (\(\frac{\pi}{2}\)-x) = -cosec x
6. cot (\(\frac{\pi}{2}\)-x) = -tan x

T-Ratios of (π -x)

1. sin (π – x) = sin x,
2. cos (π – x) = – cos x,
3. tan (π – x) = – tan x,
4. cosec (π – x) = cosec x,
5. sec (π – x) = – sec x,
6. cot (π – x) = – cot x.

T-Ratios of (π+ x)

1. sin (π + x) = – sin x,
2. cos (π + x) = – cos x,
3. tan (π + x) = tan x,
4. cosec (π + x) = – cosec x,
5. sec (π + x) = – sec x,
6. cot (π + x) = cot x.

T-Ratios of (2π – x)

1. sin (2π – x) = – sin x,
2. cos (2n – x) = cos x,
3. tan (2π – x) = – tan x,
4. cosec (2π – x) = – cosec x,
5. sec (2π – x) = sec x,
6. cot (2π -x) = – cot x.

T-Ratios of (2π + x)

1. sin (2π + x) = sin x,
2. cos (2π + x) = cos x,
3. tan (2π + x) = tan x,
4. cosec (2π + x) = cosec x,
5. sec (2π + x) = sec x,
6. cot (2π+x)=cotx.

Note : To learn these formulae by heart, we adopt the following method :

I. First of all, we determine the sign of t-ratio under consideration.
The phrase Add Sugar To Coffee is quite helpful. We write Add, Sugar, To,
Coffee in I, II, III, IV quadrants respectively.

1. The letter A of word ‘add’ indicates all the f-ratios of angles lying in the first quadrant are positive.
2. The letter S of word ‘sugar’ indicates sin and cosec of the angle lying in II quadrant are positive and rest of t-ratios are negative.
3. T of word ‘to’ indicates tan and cot of the angle lying in the third quadrant are positive and rest of the t-ratios of such angles are negative.
4. C of the word coffee shows that cos and sec of the angles lying in IV quadrant are positive and rest of t-ratios are negative of such angles.

II. (i) For -angle – x, π – x, π + x, 2π – x, 2π + x, the t-ratios remains to be the same.
sin (- x) = – sin x, tan (π + x) = tan x, cos (2π -x) = cos x.

(ii) For angles \(\frac{\pi}{2}\) – x, \(\frac{\pi}{2}\) + x, \(\frac{3\pi}{2}\) – x, \(\frac{3\pi}{2}\)+ x the t-ratio changes from cos to sin , tan to cot and sec to cosec and vice versa.
e.g., sin(\(\frac{\pi}{2}\) + x) = cosx, tan(\(\frac{\pi}{2}\) – x) = cot x,
sec(\(\frac{\pi}{2}\) + x) = -cosec x etc.

T-Ratios of (x + y)

1. sin (x + y) = sin x cos y + cos x sin y
2. cos (x + y) = cos x cos y – sin x sin y
3. tan (x + y) = \(\frac{\tan x+\tan y}{1-\tan x \tan y}\)
4. cot(x + y) = \(\frac{\cot x \cot y-1}{\cot x+\cot y}\)

T-Ratios of (x – y)

1. sin Or – y) = sin x cos y – cos x- sin y
2. cos (x -y) = cos x cos y + sin x sin y
3. tan(x – y) = \(\frac{\tan x-\tan y}{1+\tan x \tan y}\)
4. cot(x – y) = \(\frac{\cot x \cot y+1}{\cot y-\cot x}\)

T-Ratios of (2x)

1. sin 2x = 2sin x cos x = \(\frac{2 \tan x}{1+\tan ^{2} x}\)
2. cos 2x = cos² x – sin² x = 2cos² x – 1 = 1 – 2sin² x
   = \(\frac{1-\tan ^{2} x}{1+\tan ^{2} x}\)
3. tan 2x = \(\frac{2 \tan x}{1-\tan ^{2} x}\)

T-Ratios of (3x)

1. sin 3x = 3sin x – 4sin³ x.
2. cos 3x = 4cos³ x – 3 cos x.
3. tan3 x = \(\frac{3 \tan x-\tan ^{3} x}{1-3 \tan ^{2} x}\)

Sum and Difference of two like ratios :

1. sm x + sin y = 2sin\(\frac{x+y}{2}\) cos \(\frac{x-y}{2}\)
2. sin x – sin y = 2cos \(\frac{x+y}{2}\) sin \(\frac{x-y}{2}\)
3. cos x + cos y = 2cos \(\frac{x+y}{2}\) cos\(\frac{x-y}{2}\)
4. cos x – cos y = – 2sin\(\frac{x+y}{2}\) sin\(\frac{x-y}{2}\)

Product of T-Ratios:

1. 2 sin x cos y = sin (x + y) + sin (x – y).
2. 2 cos x sin y = sin (x + y) – sin (x – y).
3. 2 cos x cos y = cos (x + y) + cos (x – y).
4. 2 sin x sin y = cos (x – y) – cos (x + y).

General solution of an equation :

1. If sin x = 0, then x = nπ, n ∈ Z.
2. If cos x = 0, then x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
3. If tan x = 0, then x = nπ, n ∈ Z.
4. sin x = sin y ⇒ x = nπ + (- 1 )ⁿy, n ∈ Z.
5. cos x = cos y ⇒ x = 2nπ ±y, n ∈ Z.
6. tan x = tan y ⇒ x = nπ+y, n ∈ Z,
   where y is the principal value of x.

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 13 Photosynthesis in Higher Plants. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 13 Important Extra Questions Photosynthesis in Higher Plants

Photosynthesis in Higher Plants Important Extra Questions Very Short Answer Type

Question 1.
What is the full form of NADP?
Answer:
Nicotinamide Adenine Dinucleotide phosphate.

Question 2.
What are the complete photosynthetic units of plants?
Answer:
Chloroplasts.

Question 3.
Give one difference between chlorophyll ‘a’ and chlorophyll ‘b’.
Answer:
Chlorophyll (a) has a methyl group (CH₃) whereas chlorophyll (b) has an aldehyde group (CHO).

Question 4.
How many ATP molecules are required for the synthesis of one molecule of glucose in the C₃ pathway?
Answer:
18 ATP molecules are required for the synthesis of one molecule of glucose.

Question 5.
In which part of the leaves chlorophyll is found?
Answer:
In the thylakoid membrane of the chloroplast.

Question 6.
What is the primary acceptor of C02 in the C₃ plant? ,
Answer:
RiBulose 1.5 biphosphate (RuBP).

Question 7.
In which part of chloroplast light reaction takes place?
Answer:
Grana.

Question 8.
What is the relation between photosynthetic units and reaction centers?
Answer:
A photosynthetic unit consists of P6g0 and P700 reaction centers of photosystems.

Question 9.
What is the compensation point?
Answer:
The point at which the rate of photosynthesis is equal to the rate of respiration.

Question 10.
What is Kranz’s anatomy?
Answer:
It is a type of leaf structure in which the vascular bundle is surrounded by bundle sheath and mesophyll cells.

Question 11.
Which kinds of reactions of photosynthesis occur in the grana and stroma of chloroplasts?
Answer:

• Grana light reaction
• Stroma dark reaction

Question 12.
Give the overall general chemical equation of photosynthesis?
Answer:

Question 13.
Expand the abbreviation RuBP, NADP
Answer:
RuBP: Ribulose biphosphate
NADP: Nicotinamide Adenine Dinucleotide Phosphate

Question 14.
Give two points of difference between sun plants and shade plants.
Answer:
Sun plants need relatively high light intensity to saturate their photosynthetic rates while shade plants reach saturation at low intensities.

Question 15.
Name the process which is responsible for converting solar energy into chemical energy.
Answer:
Photosynthesis

Question 16.
Wherefrom does oxygen come out during photosynthesis?
Answer:
From water

Photosynthesis in Higher Plants Important Extra Questions Short Answer Type

Question 1.
Expand the abbreviation RuBP. What is its role in photosynthesis?
Answer:
The full form of RuBP is ribulose 1,5 biphosphate; RuBP is the first acceptor of atmospheric CO₂ during the dark reaction of photosynthesis. The reaction is called carboxylation.

RuBP is regenerated during the final formation of sugar molecules.

Question 2.
What is the porphyrin system?
Answer:
The porphyrin system consists of

1. A complex ring structure of alternating single and double bonds called a porphyrin ring having four pyrrole rings containing a magnesium atom in the center.
2. A lengthy hydrocarbon tail attached to the porphyrin group called phytol.

Question 3.
What are the two main functions of pigments other than chlorophyll in green leaves?
Answer:
The functions of pigments other than chlorophyll are:

1. to absorb light energy and transfer it to chlorophyll for photosynthesis.
2. to protect the chlorophyll molecule from photooxidation.

Question 4.
What is the significance of chlorophyll-a in photosynthesis carried out by higher plants?
Answer:
In higher plants, all the pigments carotenes, xanthophylls, and chlorophyll-b transfer the absorbed solar energy to chlorophyll-a. It is the chlorophyll-a molecule, which initiates the process of photosynthesis.

Question 5.
Write two differences between cyclic and non-cyclic photophosphorylation?
Answer:
Differences between cyclic and non-cyclic photophosphorylation:

Cycle-photophosphorylation	Non-cyclic-photophosphorylation
(i) Reaction center P700 is the electron emitter and also electron acceptor	(i) Reaction center P680 is the electron emitter and P700 is the electron acceptor.
(ii) It synthesizes only ATP.	(ii) It forms both ATP and NADPH,

Question 6.
What are the steps that are common to C₃ and C₄ photosynthesis?
Answer:
The following steps are common in both C₃ and C₄ photosynthesis.

1. Photolysis of H₂O and photophosphorylation in the light reaction.
2. The dark reaction occurs in the stroma in both cases.
3. Carboxylation-but in C₃ plants CO₂ acceptor is RuBP whereas in C₄ it is phosphoenolpyruvic acid.
4. The Calvin cycle resulting in the formation of starch occurs in both C₃ and C₄ photosynthesis.

Question 7.
What is the coupling factor in photosynthesis?
Answer:
These are similar to the F₀– F₁ complex of mitochondria present in appressed and non-appressed regions, granular and stromal thylakoids. These participate in the photophosphorylation process.

Question 8.
What is 3 – PGA?
Answer:
It is a protein molecule located on the outer surface of the thylakoid membrane. It is the first stable intermediate product of photosynthesis. It comprises 16% of the chloroplast protein, which is the most abundant protein of the biological world on earth.

Question 9.
What is the Emerson effect or photosynthetic enhancement?
Answer:
Emerson in 1957 showed that the rate of photosynthesis can be increased if monochromatic beams of two different wavelengths i.e. long and short are used simultaneously around a trap center in a photosynthetic unit. This phenomenon is known as the Emerson effect or photosynthetic enhancement.

Question 10.
What is translocation in plants?
Answer:
The process of long-distance movement of organic substances synthesized during photosynthesis from chlorophyll-containing cells or leaf which serve as regions of supply or source to different plant organs as regions of their utilization of sink is known as translocation. The term translocation is generally restricted to movements of solutes in the tissues of the phloem and xylem of plants.

Question 11.
Describe the process of photorespiration.
Answer:
It is a process of loss of photosynthetically fixed carbons, occurring in some plants during intense heat and low carbon dioxide concentrations. Under these conditions the enzyme RuBP oxygenase and converts Ribulose Bisphosphate (5 carbon), into phospho-glyceric acid (3 carbon) and phosphoglycolate (2 carbon). Soon glycolate is formed of phosphoglycolate. In peroxisomes, glycolate soon changes into glycine and glycine into serine and CO₂ without the production of assimilatory powers (ADT and NADPH₂). All the changes taking place as follows.

Photorespiration is also called the C₂ cycle because 2 carbon compounds are formed during the process. This process does not field any unstable or free energy in the form of ATP.

Question 12.
Explain the following:
(i) There will be no life without photosynthesis.
Answer:
For the existence of life, food and O₂ are very essential. Photosynthesis is the only process that can trap solar energy and can synthesis food for own and all other organisms. During photosynthesis, O₂ is given out and CO₂ is taken. So, it keeps the balance of O₂ and CO₂ in nature. Thus, photosynthesis is essential for the existence of life.

(ii) There is no oxygen evolution in bacterial photosynthesis.
Answer:
In bacterial photosynthesis, the raw material for the supply of proton (H⁺) is H₂S than H₂O. Thus, there are productions of S than O₃ during splitting in light reaction.
2 H₃S → 2 HS + 2H+
HS + HS → H₂S + S

(iii) Chlorophyll is an essential photosynthetic pigment.
Answer:
Chlorophyll-b and other pigments of a reaction center of photosystem absorb solar energy and transfer it to chlorophyll-a. Ultimately it is the chlorophyll-a that initiates the photosynthesis process. Solar energy enters into the ecosystem only through photosynthesis.

Question 13.
What is the role of NADP in photosynthesis?
Answer:
NADP is a co-enzyme useful in photosynthesis when non-cyclic photophosphorylation occurs, water is split. [n such a situation NADP acts as an acceptor of electrons and protons to form NADPH. This NADPH is used as reducing power for the fixation of CO₂ in the dark reaction. If the dark reaction is slow, then oxidized NADP will not be available and the non-cyclic cycle will then cease to operate.

Question 14.
Give four important differences between photosynthesis and respiration.
Answer:

Photosynthesis	Respiration
1. Occurs only in green cells.	1. Occurs in all Living cells.
2. Occurs in chloroplasts in the cell.	2. Occurs in mitochondria.
3. Needs light to occur.	3. Does not need light.
4. Uses CO2 and water.	4. Uses glucose and oxygen releases CO2 and water.
5. It ïs a constructive process.	5. It is a destructive process.

Question 15.
Explain the principle of limiting factor with a suitable graph.
Answer:
Law of limiting factor: When a chemical reaction is conditioned as to its rapidity by a number of separate factors then the rate of reaction is as rapid as the slowest factor permits.

As is clear that as the light intensity is increased the rate of photosynthesis increases proportionately until some other factor like CO, becomes limiting. Ultimately the plant becomes light-saturated indicating that light is no more the limiting factor. If now the cone, of CO, is increased the rate of photosynthesis increases until the light becomes a limiting factor.

Question 16.
(i) List the three categories of photosynthetic pigments.
Answers:
Chlorophylls, Carotenoids, Phycobilins.

(ii) Which pigments are known as accessory pigments and why?
Answer:
Carotenoids and phycobilins.
They absorb light in the wavelength range not absorbed by chlorophyll and transfer it to chlorophyll.

Question 17.
(i) What does chlorophyll do to the light falling on it?
Answer:
Chlorophyll molecule becomes excited as soon as light falls on it. It was given out an electron acceptor which returns to release gradually energy in the form of ATP.

(ii) Which pigment system absorbs the red wavelength of light?
Answer:
Photosystem I.

Question 18.
Name the two main sets of reactions in photosynthesis in which light energy is required write down the reaction.
Answer:
(i) Photolysis for breaking down of water molecule.
energy

(ii) Photophosphorylation for the conversion of light energy into chemical energy.
ADP + iP → ATP

Photosynthesis in Higher Plants Important Extra Questions Long Answer Type

Question 1.
What is photorespiration? Describe the process in detail and link it with the Calvin cycle.
Answer:
Enzyme Rubisco catalyzes the carboxylation reaction where CO₂ combines with RuBP. This enzyme catalyzes the combination of O₂ with RuBP called oxygenation. Respiration that is initiated in chloroplasts and occurs in light only is called photorespiration.

The oxygenation of RuBP in presence of O₂ is the first of photorespiration, which leads to the formation of one molecule of phosphoglycolate, a two-carbon compound, and one molecule of PGA. While PGA is used up in the Calvin cycle, the phosphoglycolate is dephosphorylated to form glycolate in the chloroplast and in turn diffused to peroxide, where it is oxidized to glyoxylate.

In the peroxide, the glyoxylate is used to form amino acid and glycine-calycine enters mitochondria where two glycine molecules (4 carbon) give rise to one molecule of serine (3 carbon) and one CO₂ (one carbon). The serine is taken up by peroxisome and converted into glycerate. The glycerate enters the chloroplast where it is phosphorylated to form PGA. PGA molecules enter the Calvin cycle to make carbohydrates releasing one molecule of CO₂ In mitochondria photorespiration is also called the photosynthetic carbon oxidation cycle.

Increased O₂ level increases photorespiration whereas increased CO₂ level increases photorespiration ( and increases C₂ photosynthesis).

In C₃ plants photosynthesis occurs only in one cell type i.e. mesophyll cells. Both light reactions and carbon reactions occur in mesophyll cells in C₃ plants. In C₄ plant photosynthesis requires the presence of two types of photosynthesis cells that is mesophyll cells and bundle sheath cells. The C₄ plants contain dimorphic chloroplasts, which means chloroplasts in mesophyll cells are granular. Therefore C₂ pathway does not operate in the C₄ pathway.

All the important changes can be summarised as

Question 2.
Describe carbon reactions of the C₃ pathway. Does this pathway operate also in C₄ plants?
Answer:
The reactions catalyzing the assimilation of CO₂ to carbohydrates take place in the stroma where all the necessary enzymes are localized. These reactions are referred to as ‘carbon reactions’ (also called dark reactions) leading to the photosynthetic reduction of carbon to carbohydrates.

In the first phase of carbon reaction, C02 enters the leaf through the stroma. This CO₂ is accepted by a 5-carbon molecule, ribulose-1-5 bisphosphate (RuBP) already present in the leaf. It forms two molecules of 3-carbon, compound, 3- phosphoglycerate (PGA). This 3-carbon molecule is the first stable product of this pathway and hence it is called C, PATHWAY.

The formation of (PGA) with CO₂ combining with RuBP is called carboxylation. This reaction is catalyzed by an enzyme called ribulose bisphosphate carboxylase (Rubisco). This enzyme also possesses oxygenase activity and hence abbreviated as Rubisco. This activity allows O, to compete with C02 for combining with RuBP.

After the carboxylation reduction of PGA occurs and ATP and NADPH, formed during photochemical reactions with the reduction of PGA, glyceraldehyde-3 phosphate-a carbohydrate is formed. These 3-carbon molecules, also called triose phosphates act as precursors for the synthesis of sucrose and starch. To complete the cycle, and to continue it, regeneration of the 5-carbon acceptor molecule, that is RuBP takes place.

The C₃ type of carbon reaction occurs in the stroma of the chloroplast. This pathway is called the Calvin cycle.

The CO₂concentrating mechanism is called the C₄  pathway. Operation of the C₄ pathway requires the cooperation of both cell-type mesophyll and bundle sheath cells. The objective of the C. pathway is to build up a high concentration of CO₂ which suppresses photorespiration. This C. pathway is more efficient than the C₃ pathway. Hence C? pathway does not operate C₄ plants. (See the table)

Schematic representation of C₃ pathway Calvin cycle.

Question 3.
Describe briefly the experiment conducted by the scientist, T.W. Englemann.
Answer:
T.W. Englemann plotted the action spectrum of photosynthesis.

Photosynthesis can occur in visible light of wavelength varying between 390 to 763 nm. The rate of photosynthesis is not uniform in light of all wavelengths.

It varies depending upon their relative absorption by chlorophyll pigments. The graph showing the relative yield or rate of photosynthesis in plants exposed to monochromic light of different wavelengths is termed as ACTION SPECTRUM. The rate of photosynthesis, as shown in the action spectrum is maximum in the blue region of light.

Curves showing a comparison of absorption and action spectra of chlorophyll pigments during photosynthesis

Question 4.
What is a photosystem? Which is the pigment that acts as a reaction center? Describe the interaction of photosystem 1 and photosystem II.
Answer:
The light is entrapped by a group of chlorophyll molecules which together constitute a photosystem. Each pigment system has a trap or reaction center, which is either P₇₀₀ or P₆₈₀ ao. In this ‘P’ stands for pigment and figures 680 and 700 for the wavelength of light. Chlorophyll molecule acts as a trap center with the transfer of high energy electron to electron transport system (ETS).

The high-energy electrons return rapidly to their normal low energy orbitals in the absence of light and the excited chlorophyll molecule reverts to its original stable condition. These two photosystems: photosystem-I and photosystem-11 exist with different forms of chlorophyll ‘a’ as the reaction center. The PS-II is located in the appressed regions of grana thylakoids and the PS-I in the stroma thylakoids and non-appressed regions of grana.

The function of two photosystems that interact with each other is to trap light energy and convert it to chemical energy (ATP). This chemical energy stored in the form of ATP is used by living cells.

Distribution of pigment in photosystem I and Photosystem II.

Question 5.
What led to the evolution of the C₄ pathway of photosynthesis? Describe in detail.
Answer:
Kortschak (1965) observed that in sugarcane, the compound in which CO, got incorporated was oxaloacetic acid or oxaloacetate (OAA), a 4-carbon compound instead of phosphoglyceric acid, a 3-carbon com¬pound.

Hatch and Slack (1965-1967) found it a regular mode of CO₂ fIxation in a number of monocots such as sugar cane, maize, sorghum, and Pennisetum. They found that the initial acceptor of CO₂ in such plants is Phosphoenalpymvic acid instead of RuBP and the first stable compound is oxaloacetate acid, a 4-carbon compound. These plants are termed C₄ plants as the first stable compound is a 4-carbon compound and other plants are termed C₃ plants.

Hatch and Slack observed that these plants have another pathway of CO₂ a fixation that precedes the Calvin cycle occurring in C₃ plants. This cycle is known as the C₄ pathway.

Question 6.
Describe in detail how ATP and NADPH2 are formed during photochemical reactions?
Answer:
Photosynthesis at present is thus considered basically an oxidation-reduction process during which water is oxidized to release oxygen and CO₂ is reduced to carbohydrates. Photosynthesis involves two steps- the first step is light-dependent called Light reaction or Hill reaction or photochemical phase. The second step is the Dark reaction or Blankman’s reaction or the Biosynthetic phase, which does require light.

Light Reaction or Hill Reaction: During this process, solar energy is converted into chemical energy, light is trapped by chlorophyll and carotenoid pigments and is converted into chemical energy which is stored in the form of ATP energy-rich molecule.

Photolysis of water occurs that leads to the evolution of oxygen and formation of H⁺ ions, the latter combining with NADP to form NADPH₂ often termed as reducing power. ATP and NADPH together termed assimilatory power as CO₂ fixation during the dark reaction.

Photolysis of water takes place in presence of light and water oxidizing enzyme as follow:

The unstable OH” combines to form water and molecular oxygen after losing the electrons which are accepted by oxidized chlorophyll molecule. (P₆₈₀ of PS₁₁) through an unknown electron acceptor compound “Z”. This step requires the presence of Mn⁺⁺ and Cl’ ions.

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 20 Locomotion and Movement. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 20 Important Extra Questions Locomotion and Movement

Locomotion and Movement Important Extra Questions Very Short Answer Type

Question 1.
What is a tendon?
Answer:
The dense connective tissue joins bone and skeletal muscle.

Question 2.
What are antagonistic muscles?
Answer:
The. pair of muscles which at a joint produce opposite movements.

Question 3.
What is tetanus?
Answer:
The continued state of muscular contraction is called tetanus.

Question 4.
What is threshold stimulus?
Answer:
The stimulus of minimum strength which is required to bring about muscular contraction is called the threshold stimulus.

Question 5.
What is a muscle twitch?
Answer:
The single contraction of muscle upon receiving the stimulus is called muscle twitch. (Contraction is followed by relaxation).

Question 6.
What is sarcomere?
Answer:
The functional unit of myofibril contracts and causes the shortening of muscle fibre.

Question 7.
How many bones are present in the human skeleton?
Answer:
The human skeleton contains 206 bones.

Question 8.
What are synovial joints?
Answer:
These are freely movable joints due to the presence of synovial fluid in the synovial cavity.

Question 9.
What is locomotion?
Answer:
The bodily movement in animals from one place to the other is called locomotion.

Question 10.
What is rigour mortis?
Answer:
Stiffening of muscle after death.

Question 11.
Name the proteins which help in muscle contraction.
Answer:
Myosin and actin.

Question 12.
What is the function of synovial fluid?
Answer:
Synovial fluid acts as a lubricant.

Question 13.
What is a pivot joint?
Answer:
The joint allows the turning or rotational movements, e.g., between atlas and axis vertebra.

Question 14.
Which of the movable joint makes the hip joint?
Answer:
Ball and socket joint.

Question 15.
Which muscle contracts to make your palm face upwards?
Answer:
Supinator.

Question 16.
How many bones are there in the human skull?
Answer:
29

Question 17.
Which type of movable joint is the knee joint?
Answer:
Hinge joint.

Question 18.
Name the band of the skeletal joint which permits movements in a single plane only.
Answer:
Hinge joint.

Question 19.
Differentiate between A-band and I-band.
Answer:

• A-band is a dark band having myosin filaments.
• I-band is a light band having thin filaments.

Question 20.
What is the total number of bones in our body?
Answer:
206.

Question 21.
Name the five different categories of vertebrae in your backbone.
Answer:

1. Cervical,
2. thoracic,
3. lumber,
4. sacral and
5. coccygeal.

Question 20.
Where inside the bones are blood cells produced?
Answer:
The bone marrow of long bones.

Question 23.
Give one example of a ball and socket joint.
Answer:
Shoulder joint.

Locomotion and Movement Important Extra Questions Short Answer Type

Question 1.
List the mechanical function of the skeleton.
Answer:

1. It provides a rigid framework of the body and definite shape to organs.
2. It supports the weight of the body.
3. It protects the internal organs.
4. Its long bones function as a lever.
5. Skeletal muscles with flexible connective tissue bands called tendons in association with endoskeleton and joints give locomotion and movements to different body parts.

Question 2.
List some biological function of the skeleton.
Answer:

1. Provides attachment surface to muscles.
2. Serves as storage depot of calcium and phosphate minerals.
3. Act in erythropoiesis.
4. Ear ossicles help in sound wave propagation.
5. Redbone marrow present inside the marrow cavity of long bones such as femur, humerus and in interstices of spongy bones of vertebrae, sternum, scapula etc. help in the formation of RBCs, WBCs and platelets of the blood. This process is known as Haemopoiesis.

Question 3.
List different modes of locomotion and movement in hydra.
Answer:

1. Contraction and expansion
2. Bending and swaying
3. Looping
4. Somersaulting.
5. Floating
6. Gliding
7. Swimming
8. Walking.

Question 4.
What are the different molecules present in muscles?
Answer:

1. Contractile proteins viz. actin, myosin and tropomyosin.
2. Enzymes and other proteins like troponin.
3. Carbohydrate as a substrate for energy.
4. Energy carries viz. ATP, ADP, AMP and CP.
5. Ions viz. Na⁺, K⁺, Mg⁺⁺, Ca⁺, CI⁺.

Question 5.
Differentiate between isotonic and isometric contraction
Answer:

Isotonic contraction	Isometric contraction
1. There is a change in the shape of muscles.	1. There is no change in the shape of muscles
2. Muscles maintains tension.	2. Muscles maintains length.
3. Muscles contracts and the load is lifted	3. Muscles contracts against a load that can’t be lifted.

Question 6.
A red muscles fibre works for a prolonged period, whereas a white muscle fibre gets fatigued, why?
Answer:
Red muscle fibres contain oxygen storing pigment myoglobin and a large number of mitochondria, so they can have O₂ supply for aerobic respiration and release of energy for a longer period.

White muscles fibres do not have myoglobin pigment. They face a short supply of O₂ and much depends on anaerobic respiration, so they get fatigued soon.

Question 7.
What are the main types of joints present in the human body?
Answer:
The types of joints present in the body of man are:
1. Fixed or fibrous joints: There is no movement at all in articulating joints, because of the presence of tough, inextensible, white fibrous tissue, e.g., skull bones.

2. Slightly movable or cartilaginous joints: A limited movement is possible in articulating bones. A dense disc of white cartilage joins the articulating surfaces, e.g., vertebrae and public symphysis.


Different types of joints

3. Freely movable or synovial joints: Free movement is possible due to the presence of synovial fluid in the synovial cavity, between the articulating bones, e.g., hinge joint, ball and socket joint.

Question 8.
What are the advantages of the movement of body parts?
Answer:
The movement has the following advantages:

1. With change in body posture and limb movement, equilibrium of the body is maintained.
2. Limb movement causes locomotion.
3. Food is captured by movement of tentacles, limbs, jaw, tongue etc. in different animals.
4. Changes in environment surrounding can be sensed by the movement of the eyeball, pinna etc.
5. Blood circulation is possible by heart movement.
6. Movement of the diaphragm causes inhales and exhale (breathing).

Question 9.
What are the advantages of locomotion?
Answer:
The bodily movements or locomotion has the following advantages:

1. It enables the body to shift it entirely from one place to the other.
2. It protects the organism from predation.
3. It helps the animals to make the search for their food and other nutritional requirements.
4. It helps the animal to seek a mate for reproduction.

Question 10.
Draw a labelled diagram of the joint found between the pelvic girdle and femur. Also, write the type of this joint.
Answer:
Type of the joint: The joint between pelvic and femur bones is a ball and socket synovial joint.

Synovial ball and socket joint between pelvic and femur

Question 11.
Why movement and locomotion are necessary among animals?
Answer:
Movement and locomotion are necessary among animals for the survival of them. It enables, them to procure food, search for shelter, find mates, protect themselves from predatory and perform many other life activities.

Question 12.
Elucidate the types of movements found among the animals.
Answer:
Movements among animals vary greatly. Movement involves three basic mechanisms.
These are:

1. amoeboid,
2. ciliary and
3. muscular.

Amoeboid movement is typical of Amoeba. Amoeba moves with the help of pseudopodia. Amoeboid movement helps in the food capture and change of place as well.

The same method of movement is also employed by the leucocytes, like phagocytes and macrophages of the human lymphatic system for engulfment of antigen and migration of circulatory fluid. In protozoan ciliary movement is seen. Muscular movement is the basic mechanism used in the majority of vertebrates including humans. Most multicellular animals possess muscle fibres for the movement of different organs and at¬taining locomotion.

Question 13.
What is muscle? Write the names of different types of muscles?
Answer:
Locomotion in humans depends on the movements of muscle fibres (muscle cells). Muscles are made up of contractile fibres which in turn formed of myofibrils. In humans, muscles constitute nearly 40 – 50 per cent of the total body weight.

Muscles are broadly classified into three categories.

1. Skeletal muscles: These are attached to the bones by tendons and help in the movement of the part of the skeleton. These muscles are under the control of the conscious mind and can be moved to the wall.
   Skeletal muscles are termed voluntary muscles.
2. Cardiac muscles: These are also striated and occur exclusively on the heart.
3. Smooth muscles: These are involuntary and non-striated muscles and are innervated by the autonomic nervous system.

Question 14.
How the skeletal muscle contracts?
Answer:
During contraction, the actin and myosin filaments slide past each other to reduce the length of the sarcomeres. The actin filaments move inwards towards the centre of the sarcomere. The heads of the myosin filaments operate as ‘hooks’, attaching to the F-actin they form cross-bridges, then change their relative configuration and pull the actin filaments.

As 3 result, the Z-lines limiting the sarcomeres are drawn closer together, but the length of A-bands remain unchanged. The I-bands reduce in length.

However, the net result is the shortening of the sarcomere. The actin filament slides out from the A-band resulting in the lengthening of the sarcomere.

Question 15.
What is arthritis? How is it caused?
Answer:
It is a disorder of bones in which fibrous tissues are attached with bones- and become ossified, making the joints immovable.

It is caused by the inflammation of the joints. It is of several types, e.g., rheumatoid arthritis, osteoarthritis ‘and gouty arthritis.

Question 16.
Write the names of the factors which are responsible for osteoporosis.
Answer:
Imbalances of hormones like thyrocalcitonin, parathyroid and sex hormones, deficiencies of calcium and vitamin D are the major Causativetors.

Question 17.
How do the joints help in the movement? Explain.
Answer:
A synovial or movable joint is a joint which allows the movement of collating bones such that they can move extensively upon each other. In joints, there is a space called a synovial cavity. This cavity remains filled in a fluid called synovial fluid.

The movement of an organ occurs due to the pulling of bones. Movement takes place along the joints which act as the fulcrum of the liver. In fact, the joints function as a lever. Due to the presence of a number of joints movement of the different body parts and the whole body is possible.

Question 18.
How calcium affects the process of muscle contraction?
Answer:
Muscle fibres are excitable. Normally, a nerve impulse arriving at the neuromuscular junction initiates a contractile response. A neurotransmitter released at the neuromuscular junction enters into the sarcomere through its membrane channel. The opening of the channel also results in the inflow of Na⁺ inside the sarcomere and generates an action potential in the muscle fibre.

The sarcoplasmic reticulum releases the stored Ca⁺⁺, which binds with the specific sites present on the troponin component of the thin filament. As a result, the active sites present on the F-actin molecules are exposed. These sites are specific to the myosin head, which exhibits Mg⁺⁺ dependent ATP as activity.

During relaxation of the muscle, the Ca⁺⁺ is pumped back into the sarcoplasmic reticulum. As a result, the troponin component becomes free. The cross-bridge breaks and the thin filament occupies its normal position. The muscle relaxes.

Question 19.
Write the difference between movable and immovable joints.
Answer:

Movable joints	Immovable joints
1. The articulating surfaces are kept in close contact by a fibrous capsule and a slippery synovial fluid occurs in the space between the articulating surfaces of the bone.	1. The articulating bones at this joint are firmly held together by dense bands of tough inextensible white fibrous tissue.
2. It permits considerable movement of the articulating bones.	2. It does not permit any movement of the articulating bones.

Question 20.
Fill in the blanks:
Answer:

1. Troponin is a part of Myosin filament.
2. The Head of the myosin has AT passive activity.
3. Humerus Radius and Ulna bones are found in the forearm.
4. The acetabulum is present in the Pelvic girdle.
5. The ball and socket joint is a Movable girdle.

Question 21.
Match column I with column II

Column I	Column- II
(a) Smooth muscle	(i) Myoglobin
(b) Tropomyosin	(ii) Third class lever
(c) Red muscle	(iii) Thin filament
(d) Skull	(iv) Sutures
(e) Forearm	(v) Involuntary

Answer:

Column I	Column- II
(a) Smooth muscle	(v) Involuntary
(b) Tropomyosin	(iii) Thin filament
(c) Red muscle	(i) Myoglobin
(d) Skull	(iv) Sutures
(e) Forearm	(ii) Third class lever

Question 22.
What is a joint? Write its type with an example.
Answer:
Joints are the place of articulation between two or more bones or between a bone and cartilage. Due to the presence of a number of joints, the movement of the different body parts and the whole body is possible.

There are three types of joints:

1. Fixed or immovable joints: There is no space between the bones. They are attached very tightly with the help of white fibrous connective tissue.
2. Slightly movable or cartilaginous: It is an articulation between the bones that allow a very little movement.
3. Movable joints or synovial: It is a joint which allows the movement of articulating bones such that they can move extensively upon each other. In such joints a synovial vanity is present.

Question 23.
What is the role of the girdle in the skeleton?
Answer:
Girdle bones provide a connection between the axial skeleton and limbs. The two girdles are named pectoral and pelvic girdles. Each girdle is formed of two halves.

Locomotion and Movement Important Extra Questions Long Answer Type

Question 1.
(a) During muscular contraction what are the chemical changes that take place. Describe in a listed form.
Answer:
The main chemical events that happen during muscular contraction described by Albert Szent Gyorgi are
1. Acetylcholine is released from vesicles at the neuromuscular junction. It stimulates the muscle.

2. Hydrolysis of ATP in the presence of Ca⁺⁺ and Mg⁺⁺ Energy used up in muscle contraction.

3. ADP is charged again by taking phosphate from creatine phosphate (CP).

4. During relaxation, creatine is phosphorylated, energy being provided by anaerobic conversion of muscle glycogen into lactic acid.
Creatine + ATP— Creating-phosphate + ADP

5. Energy released by hydrolysis of ATP causes rotation of myosin heads and bring near the actin filaments, actomyosin complex is formed, eventually, sarcomere shortens.

6. Ca⁺⁺ are actively transported to the sarcoplasmic reticulum, no more Ca⁺⁺ available for ATP breakdown, no further energy available for further contraction of the sarcomere.

7. Part of the energy is utilized by breaking of cross-bridges and the muscle relaxes.

(b) What are the main groups of vertebrae in the vertebral column of man?
Answer:
There are 5 groups of vertebrae namely cervical, thoracic, lumbar, sacral and coccygeal vertebral.
(The vertebral formula is C₇, T₁₂, L₅, C_3-5 = 32 – 34).

Question 2.
(a) What purposes does movement of external body parts in relation to body axis serve in animals?
Answer:

1. The movement of limbs, appendages, head and trunk serves to change the body posture to maintain equilibrium against gravity.
2. Limb movements are prerequisites for carrying out locomotion.
3. Prehension of food involves movement of tongue, jaws, snout, tentacles, limbs and appendages in different animals.
4. Movement of eyeballs and pinna of ear help to collect information from the external environment.

(b) What are fibrous joint and cartilaginous joints and their biological function?
Answer:

1. Fibrous joint: The articulating bones are firmly held together by the dense bands of tough, inextensible white fibrous tissues. They provide strength and support for the body or protection of delicate structures which cannot withstand any kind of deformation.
2. Cartilaginous joints: In cartilaginous joints, a dense disc of white fibrocartilage joins the opposing surfaces of the articulating bones to each other. This allows a limited movement at the joints.

(c) Explain Antagonistic muscles.
Answer:
Antagonistic muscles: Antagonistic muscles are those which contract to produce opposite movements at the same joint. When a muscle contract to produce a movement, its antagonistic must relax to allow that movement to take place, e.g., the bicep is a FLEXER for the elbow joint and the tricep is it’s antagonistic and an EXTENSOR for that joint.

During flexion at the elbow, the biceps contract and the tricep relax, during extension at the same joint the tricep contracts and the biceps relaxes.

(d) Distinguish between muscles twitch and tetanus or explain muscle twitch and tetanus.
Answer:
A single isolated contraction caused by a single nerve impulse or electric shock is called a muscle twitch. Immediately after the brief twitch, the muscle fibres relax.

Tetanus is a continued state of concentration caused by many repeated stimuli. Much higher tension is developed in tetanus than in an isolated twitch. Almost all our daily activities are carried out by tetanic contractions of muscles.

Question 3.
How thick and thin filaments are arranged in a muscle fibre?

relationship between actin and myosin filaments in stretched and contracted states
Answer:
Each striated muscle contains thin actin and thick myosin filaments. These filaments are longitudinally arranged inside light I bands and dark A bands respectively. The actin and myosin filaments remain cross-linked with each other in the myofibril. Sarcomeres are the rows of functional unit in each myofibril, each extending from the dark Z- line of the next I band. Each sarcomere thus comprises of A band in the middle with 2 half I band on its two sides.

From each Z line, the actin filaments through half of the I band intermingles with the ends of myosin filaments in the A band. The myofibril is surrounded at each I band by the tubules and cisternae of sarcoplasmic reticulum and at each junction of A and I bands by a TI tubule communicating with the cell exterior, which is shown in the figure. The relationship between actin (thin filament) and myosin (thick filament).

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 19 Excretory Products and their Elimination. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 19 Important Extra Questions Excretory Products and their Elimination

Excretory Products and their Elimination Important Extra Questions Very Short Answer Type

Question 1.
What is a nephron?
Answer:
The functional unit of the kidney.

Question 2.
What is a flame cell?
Answer:
The excretory unit in planaria, tapeworm, and liver fluke.

Question 3.
What is micturition?
Answer:
It is the act of void of the urinary bladder, the activity under nervous and voluntary control.

Question 4.
What are ammonotelic animals?
Answer:
The animals which excrete nitrogenous wastes as ammonia are ed ammonotelic animals, e.g., certain fishes.

Question 5.
What is a green gland and in which animal it is found?
Answer:
It is an excretory structure found in prawns.

Question 6.
What is an antidiuretic hormone?
Answer:
It is the hormone that helps in the reabsorption of water in the nephron, also called vasopressin (Secreted by post pituitary gland).

Question 7.
Define excretion.
Answer:
Excretion is the process of elimination of metabolic wastes from the body.

Question 8.
What is the color rendering substance found in urine?
Answer:
Urochrome.

Question 9.
What are diuretics?
Answer:
The substances which increase the volume of water, to be excreted as urine, are called diuretics, e.g., tea, coffee, alcoholic beverages.

Question 10.
What is osmoregulation?
Answer:
It is the maintenance of water and osmotic concentration of blood.

Question 11.
Name the organ of the excretory system, which stores urine before its removal from the body.
Answer:
Urinary bladder.

Question 12.
In which part of the nephron does filtration occur?
Answer:
Glomerulus.

Question 13.
What happens to the useful substances that get filtered into the renal tubule?
Answer:
They are reabsorbed into the blood.

Question 14.
Point out the main excretory organ?
Answer:
Kidney.

Question 15.
Write down the products excreted by the following organs.
(a) Lung
Answer:
Lung: Carbon dioxide and water vapor

(b) Skin,
Answer:
Skin: Urea, water, and some salts

(c) Intestine.
Answer:
Intestine: Some salts like calcium and iron.

Question 16.
What is excreted by the kidney in urine?
Answer:
Urea.

Question 17.
In which part of the nephron does filtration occur?
Answer:
Glomemle.

Question 18.
Who filters the blood?
Answer:
The kidney filters the blood, which takes place between the glomerulus and Bowman’s capsule.

Question 19.
Why it is necessary to remove waste products by excretion?
Answer:
It is essential and necessary because all waste products are toxic and harmful.

Excretory Products and their Elimination Important Extra Questions Short Answer Type

Question 1.
Differentiate between sweat and sebum.
Answer:

Sweat	Sebum
1. It is a liquid state excretion of tin.	1. It is semisolid excretion
2. NaCl. urea, amino-acids are excreted.	2. Waxes, fatty acids, and sterol are excreted.
3. Excreted in large amounts	3. Excreted in small amounts
4. Also thermoregulatory role.	4. No thermoregulatory role.

Question 2.
What consequences will follow with the failure of tubular reab¬sorption in nephrons?
Answer:
Nephrons are the structural and functional units of each kidney. With the failure of reabsorption in nephrons, much-needed substances like glucose, amino acids, water, salts, etc. will be excreted along with urine.

The biological functioning of organs and body will be impaired, ultimately death will occur.

Question 3.
How the net filtration pressure is obtained?
Answer:
The pressure of blood in afferent arterioles is (+ mm Hg 75). This is opposed by the osmotic pressure of plasma proteins by (-) 30 mm Hg and intertubular pressure of (-) 20 mm Hg. The net filtration pressure is (+) 25 mm Hg that acts in glomerular filtration as a driving force. About 172 liters of glomerular filtrate are produced in 24 hrs. which is nearly 4-1/ 2 times the total fluid in the human body.

Question 4.
List some important functions of kidneys?
Answer:
Kidneys play a vital role as follows:
(a) It removes nitrogenous wastes from the blood.
(b) It regulates fluid balance, between intake and fluid loss.
(c) It removes drugs, penicillin, poisons, etc. from blood.
(d) It maintains acid-base (pH) balance
(e) It regulates electrolyte balance.

Question 5.
Differentiate between ureter and urethra?
Answer:

Ureter	Urethra
1. It is a muscular tube.	1. It is a membranous tube.
2. It is long.	2. It is short.
3. It arises from the renal pelvis of the kidney.	3. It arises from the urinary bladder.
4. It carries urine to the urinary bladder.	4. It eliminates stored urine of the exterior.
5. No muscular splincter.	5. Muscular splinter keeps urethra-closed except for micturition.

Question 6.
How does the excretion of uric acid take place in birds and reptiles?
Answer:
In birds and reptiles, uric acid is formed mostly in the liver, transported to the kidney through blood. It is separated by renal tubules and temporarily stored in cloacae. Water is absorbed by cloacal walls, needing only a minimum amount of water for excretion. In birds, urine is eliminated in a paste-like form along with feces.

Question 7.
Name and state in brief the processes involved in the formation of urine.
Answer:
The urine is formed by the combined processes as follows:
(a) Glomerular filtration: Metabolism wastes and other substances are filtered out by glomerulus due to the generation of net filtration pressure.
(b) Re-absorption: Water and other required substances are selectively reabsorbed from the filtrate, so that urine becomes concentrated.
(c) Tubular secretion: Tubules secrete certain ions (like K⁺ in exchange for Na⁺), urea, creatinine, uric acid, ammonia, etc. This process is of more significance in marine fishes and desert amphibians than mammals.

Question 8.
Differentiate between ureotelism and Uricotelism.
Answer:

Ureotelism	Uricotelism
1. The process of elimination of main urea.	1. The process of elimination of mainly uric acid.
2. Water moderately required for excretion.	2. Much less water required for excretion.
3. Synthesis of urea requires less energy expenditure.	3. Synthesis of uric acid needs more energy expenditure.

Question 9.
What is Polynephritis? What is uremia?
Answer:
It is a bacterial infection that causes inflammation of the renal pelvis, nephrons, and medullary tissues of the kidney. It affects the counter-current mechanism. Its main symptoms are frequent and painful urination, fever, and pain in the lumbar region.

A high concentration of urea, uric acid, creatinine, etc. in the blood due to some bacteria infection or some obstruction in the passage of the urinary system is called uremia.

Question 10.
Indicate whether the following statements are True or False
(a) Micturition is carried out by a reflex.
Answer:
True

(b) ADH helps in water elimination, making the urine hypotonic.
Answer:
False

(c) Protein-free fluid is filtered from blood plasma into the Bowman’s capsule
Answer:
True

(d) Henle’s loop plays an important role in concentrating the urine.
Answer:
True
(e) Glucose is actively reabsorbed in the proximal convoluted tubule.
Answer:
True

Question 11.
Match the items of Column I with these of Column II.

Column I	Column-II
(a) Ammonotelism	(i) Birds
(b) Bowman’s Capsule	(ii) Hypertonic   urine
(c) Micturition	(iii) Counter-current system
(d) Uricotelism	(iv) Bony fish
(e) Vasa recta	(v) Urinary bladder
(f) Sebum	(vi) Glucose
(g) ADH	(vii) Glomerular Alteration
(h) Tubular reabsorption	(viii) Skin

Answer:

Column I	Column-II
(a) Ammonotelism	(iv) Bony fish
(b) Bowman’s Capsule	(vii) Glomerular Alteration
(c) Micturition	(v) Urinary bladder
(d) Uricotelism	(i) Birds
(e) Vasa recta	(iii) Counter-current system
(f) Sebum	(viii) Skin
(g) ADH	(ii) Hypertonic   urine
(h) Tubular reabsorption	(vi) Glucose

Question 12
Fill in the blanks with appropriate words:
(a) During micturition, the urinary bladder, and the urethral sphincters contract, and relax
(b) Flame cells and malpighian tubules are found in and Bowman’s capsule and glomerulus respectively.
(c) Blood enters the glomerulus through the renal arteriole and leaves via the afferent arteriole.
(d) Two counter-current systems formed in the kidney are the Renal medulla and the renal cortex
(e) Sweat serves to eliminate mainly water and salt

Question 13.
Compare and contrast the osmoregulatory problems and adaptations of a marine bony fish with a freshwater bony fish.
Answer:
Osmoregulation in freshwater Marine bony fish, do not drink water to reduce the need to expel excess water. In this case, water uptake and salt loss are minimized by a specialized body covering. Freshwater animals have the ability to take up salts from the environment. The active transport of ions takes place against the concentration gradient, specialized cells called monocytes or chloride cells in the gill membrane of freshwater fish. These can import Na⁺ and CI^– from the surrounding water containing less than 1 mm NaCl when their plasma concentration of NaCl exceeds 100 mm.

Osmoregulation in marine environment Seawater has an osmolarity of about 1000m Osm L The osmoregulatory problems in marine water are opposite to those in a freshwater environment. Marine bony fish have the body fluids hypotonic to seawater and thereby, they tend to lose water from the body through permeable surfaces.

To compensate for the water loss, marine bony fish drink seawater, which results in a gain of excess salts. The monocytes or chloride cells of the gill membrane of marine bony fish help to eliminate excess monovalent ions from the body fluid to the seawater. Divalent cations are generally eliminated with feces.

Question 14.
State the importance of counter-current systems in renal functioning.
Answer:
Vasa rectal is responsible for the concentration of urine. The vase rectal is in the form of loops. Therefore, the blood flows in the opposite directions in two limbs of each vasa Fecta; the blood entering its descending limb comes into close contact with the outgoing blood in the ascending limb. This is called a Counter-Current System. The two limbs of the loops of Henle form another Counter-Current System.

Importance: The counter-current system significantly contributes to concentrating urine in mammals.

Question 15.
State the position and function of the juxtaglomerular apparatus?
Answer:
This is a specialized cellular apparatus located where the distal convoluted tubule passes close to the Bowman’s capsule between the afferent and efferent arterioles. JGA cells secrete substance like renin that modulates blood pressure and renal blood flow and thus, GFR is regulated.

Question 16.
Describe the hormonal feedback circuits in controlling renal functions.
Answer:
Two important hormonal control of the kidney function by negative feedback circuits can be identified:
1. Control by Antidiuretic Hormone ADH: ADH produced in the hypothalamus of the brain and released into the blood from the pituitary gland, enhances fluid retention by making the kidneys reabsorb more water. The release of ADH is triggered when osmoreceptors in the hypothalamus detect an increase in the osmolarity of the blood.

The osmoreceptors cells also promote thirst. Drinking reduces the osmolarity of the blood which inhibits the secretion of ADB, thereby completing the feedback circuit.

2. Control by Juxtaglomerular Apparatus (JGH): It operates a multihormonal Renin-Angiotensin-Aldosterone System (RAAS). JGA responds to decrease the blood pressure and release enzyme renin into the blood. In the blood, the enzyme initiates chemical reactions that convert a plasma protein called angiotensinogen to a peptide called angiotensin II which works as a hormone.

Angiotensin II increases blood pressure and stimulates the adrenal gland to release aldosterone, a hormone. This leads to an increase in blood volume and pressure completing the feed¬back circuit by supporting the release of renin.

Still another hormone, a peptide called Atrial Natriuretic Factor ANF), opposes the regulation by RAAS.

Thus, ADH, the RAAS, and ANF provide an elaborate system of checks and balance that regulate the kidney functioning to control body fluid, osmolarity, salt concentration, blood pressure, and blood volume.

Question 17.
State the normal and abnormal constituents of human urine.
Answer:
Urine is a pale yellow colored slightly acidic watery fluid.

• Abnormal Urine: Various metabolic errors of kidney malfunctioning changes the composition of urine.
• Proteinuria: Excess of protein level.
• Albuminuria: The presence of albumin, usually occurs in nephritis.
• Glycosuria: Presence of glucose in urea as in case of diabetes mellitus.
• Ketonuria: Presence of abnormally high ketone bodies.
• Hematuria: Presence of blood or blood cells in urine.
• hemoglobinuria: Presence of hemoglobin in urine.
• Uremia: Presence of excess urea.
• Normal Urine: Normal urine is slightly heavier than water. It gives an aromatic odor due to the presence of volatile, bad-smelling organic substances, the ruined water, organic and inorganic materials are the main constituents of normal urine.

The other nitrogenous constituents of normal urine are ammonia, uric acid, hippuric acid, and creatinine.

Non-nitrogenous substances are vitamin C, oxalic acid, phenolic substances. In inorganic substances, sodium chloride is the principal mineral salt in the urine.

Question 18.
State the role of skin and lungs in excretion.
Answer:
Role of Skin: Human skin possesses glands for secreting sweat and sebum (from the sebaceous gland). Sweat contains NaCl, lactic acid, urea, amino acids, and glucose. The volume of sweat various negligible to 14 L a day. The principal function of sweat is the evaporative cooling of the body surface.

Sebum is a waxy protective secretion to keep the skin oily and this secretion eliminates some lipids, such as waxes, sterols, other hydrocarbons, and fatty acids. Integument in many animals is excreting ammonia into the surrounding by diffusion.

Role of lungs in excretion: Human lungs eliminate around 18L of CO₂ per day and about 400 ml of water in normal resting conditions. Water loss via lungs is small in hot humid climates and large in cold dry climates. The rate of ventilation and ventilation pattern also affects the water loss through the lungs. Different volatile materials are also readily eliminated through the lungs.

Excretory Products and their Elimination Important Extra Questions Long Answer Type

Question 1.
Briefly state the mechanism of urine formation in the human kidney.
Answer:
Three main processes are involved in urine formation
1. Glomerular filtration: Kidneys filter the equivalent of blood volume every 4 – 5 minutes. Filtration slits are formed by the assemblages of fine cellular processes of podocytes (foot cells). The process of ultra-filtration depends upon two main factors, first the net hydrostatic pressure difference between the lumen of the capillary and the lumen of the Bowman’s capsule favor filtration.

The glomerular ultrafiltrate contains essentially all the constituents of the blood except for blood corpuscles and plasma proteins. Nearly 15% – 25% of the water and salutes are removed from the plasma that flows through the glomerulus. The glomerular filtration rate is about 125 ml min1 or about 180 L day^-1 in human kidneys.

2. Two important intrinsic mechanisms provide autoregulation of glomerular filtration rate.
(a) Myogenic mechanism: Increase in blood pressure will tend to stretch the efferent arteriole, which would increase the blood flow to the glomerulus. The diameter of the arteriole is reduced, increasing the resistance to flow. This myogenic mechanism thus reduced variations inflow to the glomerulus in case of fluctuations in blood pressure.

(b) Juxtaglomerular apparatus (JGA): This specialized cellular apparatus is located where the distal convoluted tubule passes close to the Bowman’s capsule between the afferent and efferent arterioles. JGA cells secrete substances like renin that modulate blood pressure and renal blood flow and GFR are regulated.

Myogenic and juxtaglomerular mechanisms work together to autoregulate the GFR over a wide range of blood pressure. In addition to these extrinsic neural control also regulates the filtration rate.

3. Tubular re-absorption: The selective transport of substances across the epithelium of the excretory tubule from the ultrafiltrate to the interstitial fluid is called re-absorption. Nearly all the sugar, vitamins, organic substances (nutrients), and most of the water are reabsorbed.

4. Tubular secretion: It is a very selective process involving both passive and active transport. The filtrate travel through the nephron, substances that are transported across the epithelium from the surrounding interstitial fluid and join it. The net effect of renal secretion is the addition of plasma solutes to the filtrate within the tubule.

Question 2.
Explain the following:
(a) Skin functions as an accessory excretory organ.
Answer:
The skin retains some excretory role in many animals. Human skin possesses two glands for secreting fluid on its surface. These are; sweat from sweat glands and sebum from sebaceous glands.

(b) Mammals can eliminate hypotonic and hypertonic urine according to body needs.
Answer:
When the animal takes a large quantity of water the kidneys excrete a very high amount of hypotonic urine. At the same time when the animal takes a small number of water kidneys to excrete a very high amount of hypertonic urine.

At the same time when the animal takes a small number of water kidneys to excrete a small amount of hypertonic urine, as kidneys need to conserve water. In this way, the osmotic concentration of blood is maintained by the kidneys. This flexibility of kidney nephrons is highly observed in mammals.

Hypotonic urine removes excess water from the body in order to raise the osmotic concentration of the blood to normal. Excess of water in body fluids generally lowers the osmotic pressure of blood and increases the volume of blood. This increase in the volume of blood raises the blood pressure and hydrostatic pressure which increases the rate of ultrafiltration. In this way, a large amount of hypotonic urine is produced in order to bring the volume of fluids to normal.

(c) Micturition is a reflex process but is under some voluntary control.
Answer:
It is the process of passing out urine. Nephrons produce urine and drain. When enough urine collects in the bladder the distension of its walls raises enough pressure which generates a spontaneous nervous activity under the stimulation of the sympathetic and parasympathetic nervous system. This nervous stimulation causes the smooth muscles on the urinary bladder to rise too high to control.

Similarly, micturition can voluntarily be initiated even before enough urine has accumulated in the bladder. Backflow of the urine into the ureters from the urinary bladder is prevented because the terminal part of each ureter passes through the bladder and gets closed as soon as the contraction of the bladder occurs.

(d) Mammals are ureotelic, but birds are uricotelic.
Answer:
Mammals are ureotelic animals as they eliminate nitrogen mainly urea. It is very soluble in water and needs a considerable amount of water for its elimination. Mammals can thus form hypertonic urine which they excrete. While the birds cannot excrete urine as hypertonic since nitrogen occurs mainly in the form of uric acid. The uric acid is insoluble in water and does not require much water for its elimination.

Question 3.
Describe the functional anatomy of a human nephron.
Answer:
Nephrons are structural and functional units of each kidney to form the urine. Each nephron is fine; microscopic highly coiled tubular structure differentiated into malpighian body and the renal tubule. The malpighian body comprises a large double-walled cup-shaped structure the Bowman’s capsule present in the renal cortex. It is lined by thin, semipermeable epithelial cells, the podocytes. Bowman’s capsule receives the blood supply through a branch of the renal artery.

The afferent arteriole forms a fine capillary network in the form of glomerules with high hydrostatic pressure. The lumen between two layers of Bowman’s capsule is continuous with the lumen of the tubule. The Bowman’s capsule and the glomerulus together form a globular body, the Malpighian body or the renal capsules.

The capillaries forming the glomerulus at the exit of Bowman’s capsule unite to form a narrow efferent arteriole which breaks up into a peritubular network of capillaries with low hydrostatic pressure.

The renal tubule is a long highly coiled tubular structure differentiated into proximal convoluted tubule (PCT) Henle’s loop, distal convoluted tubule (DCT). The U-shaped loop-like structure, descending and ascending from the renal tubule is called Henle’s loop.

Collecting tubules of several nephrons open into a wider duct called the collecting duct. A number of collecting ducts unite with each other in the medulla to form the ducts of Bellini, which drains down the urine into the ureter from each kidney to be stored in the urinary bladder.

The efferent arteriole emerges out from the glomerules breaks up into a peritubular capillary network around the renal tubule in the cortex. These capillaries also form a thin-walled, straight capillary the vasa recta. The vasa recta help in retaining the reabsorbed ions and urea in medullary interstitial fluid to maintain high osmotic pressure in kidneys.

Glomerular filtrate undergoes tubular reabsorption and tubular secretion for the formation of urine. (See diagram opposite page)

Uriniferous tubules Or nephron of the kidney

Question 4.
Describe the gross anatomical features of the human kidney with a suitable diagram.
Answer:
Kidney: Kidney is chocolate brown, bean-shaped, large-sized about 10 cm long and 5 – 7 cm broad, 3 – 4cm thick flattened, metamorphic. The weight of each kidney is 150 to 170 gm. They are situated against the back wall of the abdominal cavity, just below the diaphragm, between the 12th thoracic and 3rd lumbar vertebrae.

The outer margin is convex. The inner concave presents a longitudinal opening called the hilum. The renal artery and renal vein respectively enter and leave the kidney through its hilum.

The two kidneys are slightly asymmetrical in position because the right kidney is slightly at a lower level than the left. Kidneys are held in position by a mass of adipose tissue called Renal fat. These rest against the abdominal muscles. Each kidney is covered on the ventral side by the peritoneum and is thus retroperitoneal in nature.

Surrounding the kidneys and the renal fat is a sheath of fibro elastic tissue known as renal fascia or capsule. They protect the kidney. The renal fat forms a shock-absorbing cushion. The renal fascia fixes the kidney to the abdominal wall.

Longitudinal section (Diagrammatic of Kidney)

Question 5.
(a)What is the role of the liver in excretion in mammals?
Answer:
Role of liver in excretion: The liver changes ammonia into urea which is less toxic than ammonia. Urea is eliminated from the body by the kidneys through urine.

The liver is the principal organ of excretion of cholesterol, bile pigments (bilirubin and biliverdin) some vitamins, drugs, and inactivated products of steroid hormones. The liver excretes these substances in the bile which carries them to the small intestine. Ultimately, these substances get eliminated along with feces.

(b) What are the diseases associated with the urinary system?
Answer:
Diseases associated with the urinary system:
1. Polynephritis: It is a bacterial infection, which causes inflammation of renal pelvic nephrons and medullary tissues of the kidney. It affects the counter-current mechanism. Its main symptoms are frequent and painful urination, fever, and pain in the lumbar region.

2. Uremia: It causes the presence of a high concentration of urea, uric acid, creatinine, etc, in the blood due to some bacterial infection or some obstruction in the passage of the urinary system. Urea poisons the cells. It is not passed in the urine and accumulates in the blood.

3. Renal stones: When uric acid precipitates and accumulates in the nephrons of kidneys in the form of renal stones or when calcium phosphates and oxalates accumulate in the nephrons of the kidneys in the form of renal stones. It causes blockage or frequent painful urination along with blood in the urine. Renal stone causes severe colic pain starting in the back and radiating down to the front of the thigh or vulva or testicle on that side.

4. Glomerulonephritis: It is characterized by the inflammation of Glomeruliduct, some injury to the kidney, abnormal allergic reaction, or by some streptococci bacteria infection. Proteins and red blood corpuscles become filtered into the glomerular filtrate. It may lead to kidney failure in severe infection.

5. Oedema: It is characterized by the increased volume of interstitial fluid mainly caused by retention of excess Na+ ions which in turn causes water retention. Blood pressure increases dining edema.

Question 6.
Write a short account on hemodialysis.
Answer:
In case of renal failure, an artificial kidney is used for removing excess urea from the blood of the patient by a process called hemodialysis. Blood is taken out from the artery of the patient, cooled to 0°C, mixed with an anticoagulant such as heparin, and then pumped into the apparatus called artificial kidney. In this apparatus, blood flows through channels

Working of artificial kidneys for hemodialysis

bounded by cellophane membrane. The membrane is impermeable to macromolecules but permeable to small solutes. The membrane separates the blood flowing inside the channels from a dialyzing fluid flowing outside the membrane. The wastes like urea, uric acid, and creatinine diffuse from the blood to the dialyzing fluid across the cellophane membrane.

Thus the blood is considerably cleared of nitrogenous waste products without losing plasma proteins. Such a processor separation of macromolecules from small solute particles with the help of a permeable membrane is called dialysis. The blood coming out of the artificial kidney is warmed to body temperature, mixed with an Antiheparin to restore its normal coagulability, and returned to a vein of the patient.

Haemodialysis saves and prolongs the life of many uremic patients.