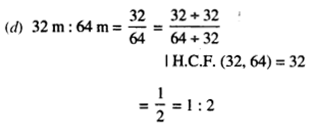Category: CBSE Class 6

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3.

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 13
Chapter Name	Symmetry
Exercise	Ex 13.3
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3

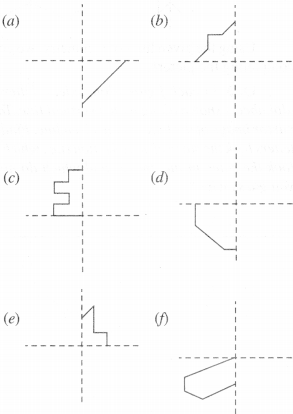
Question 1.
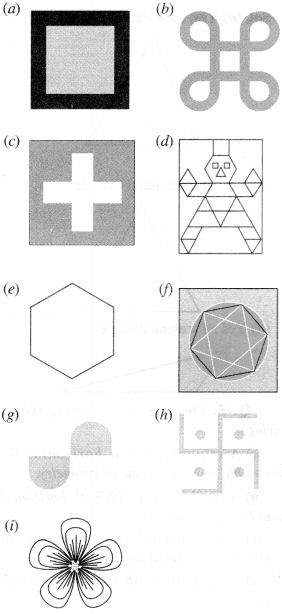
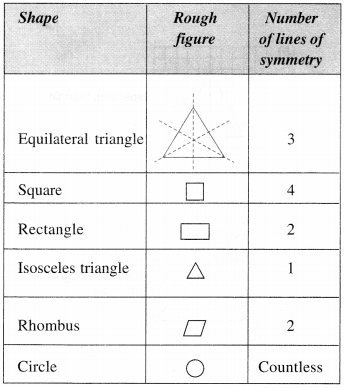
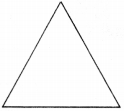
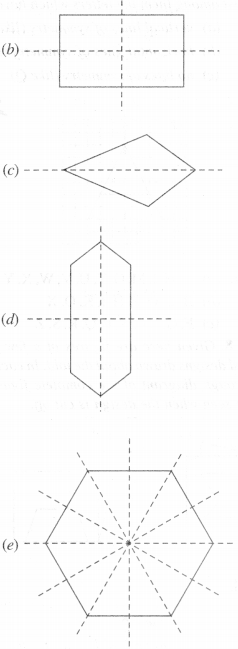
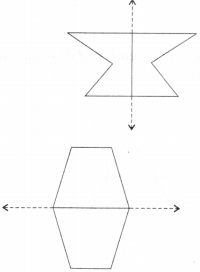
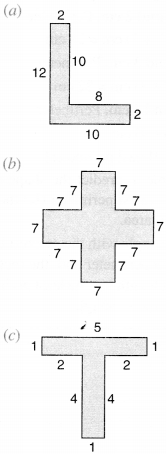
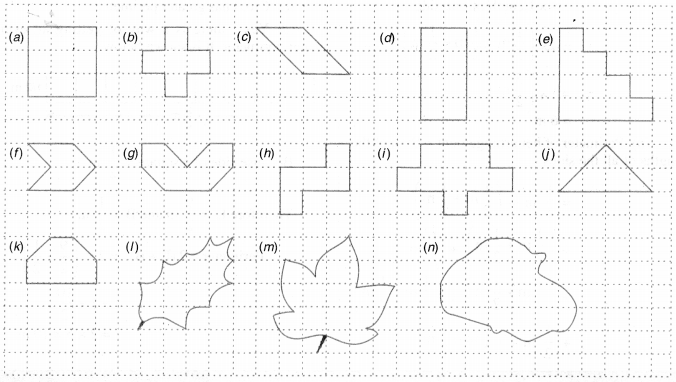
Find the number of lines of symmetry in each of the following shapes. How will you check your answers?


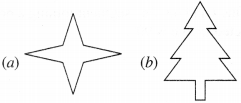
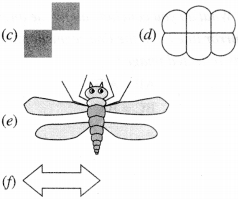
Solution :
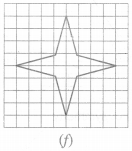
(a)

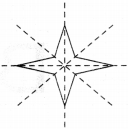
Number of lines of symmetry = 4
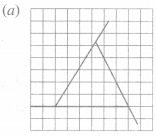
(b)

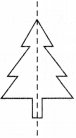
Number of lines of symmetry = 1
(c)

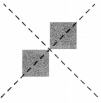
Number of lines of symmetry = 2
(d)

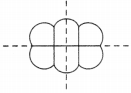
Number of lines of symmetry = 2
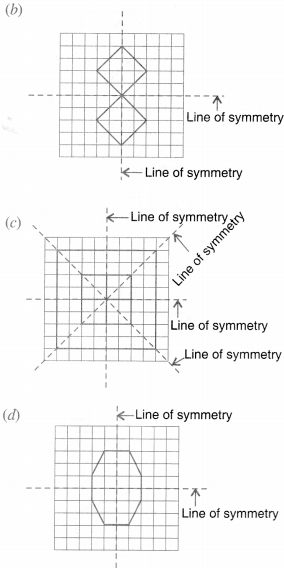
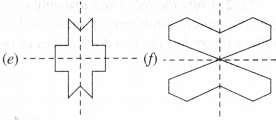
(e)

Number of lines of symmetry = 1
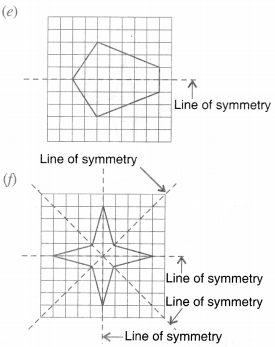
(f)

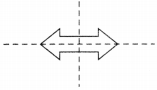
Number of lines of symmetry = 2

Question 2.
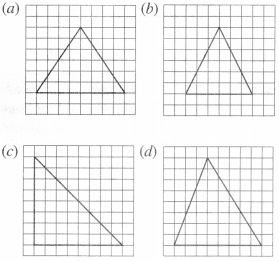
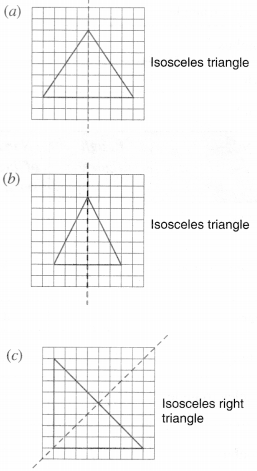
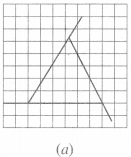
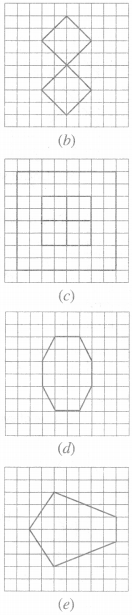
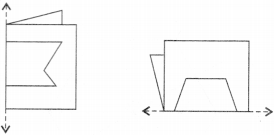
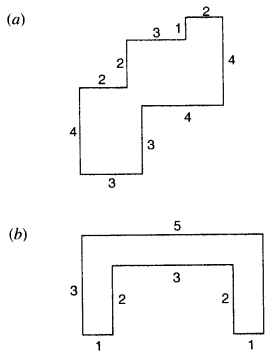
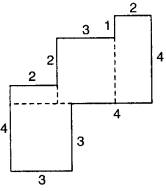
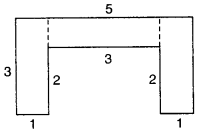
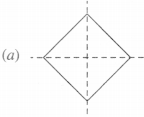
Copy the following drawing on squared paper. Complete each one of them such that the resulting figure has the two dotted lines as two lines of symmetry :

How did you go about completing the picture?
Solution :




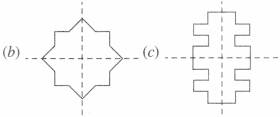
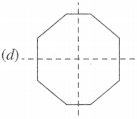
Using the given lines of symmetry, we go about completing the picture.

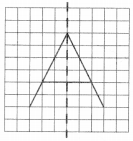
Question 3.
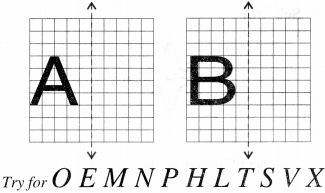
In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e., which letters look the same in the image) and which do not. Can you guess why?

Solution :
The letter A looks the same after reflection but not the letter B. The reason is that in reflection, the sense of direction changes. In the given letters, the letters O, M, N, H, T, V, and X look the same after reflections because these letters have a vertical line of symmetry.

We hope the NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2.

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 13
Chapter Name	Symmetry
Exercise	Ex 13.2
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2

Question 1.
Find the number of lines of symmetry for each of the following shapes :

Solution :

Question 2.
Copy the triangle in each of the following figures, on squared paper. In each case, draw the line(s) of symmetry if any and identify the type of triangle. (Some of you may like to trace the figures and try paper-folding first!)

Solution :

Question 3.
Complete the following table :

Solution :

Question 4.
Can you draw a triangle which has
(a) exactly one line of symmetry?
(b) exactly two lines of symmetry?
(c) exactly three lines of symmetry?
(d) no lines of symmetry?
Sketch a rough figure in each case.
Solution :
(a) Yes; an isosceles triangle

(b) No
(c) Yes; an equilateral triangle

(d) Yes, an equilateral triangle

Question 5.
On a squared paper, sketch the following:
(a) A triangle with a horizontal line of symmetry’ but no vertical line of symmetry.
(b) A quadrilateral with both horizontal and vertical lines of symmetry.
(c) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(d) A hexagon with exactly two lines of symmetry.
(e) A hexagon with six lines of symmetry.
(Hint: It will be helpful if you first draw the lines of symmetry and then complete the figures.)
Solution :


Question 6.
Trace each figure and draw the lines of symmetry, if any :



Solution :

no line symmetry


Question 7.
Consider the letters of English alphabets A to Z. List among them the letters which have
(a) vertical lines of symmetry (like A)
(b) horizontal lines of symmetry (like B)
(c) no lines of symmetry (like Q)

Solution :
(a) A, H, I, M, O, T, U, V, W, X, Y
(b) B, C, D, E, H, I, K, O, X
(c) F, G, J, L, N, P, Q, R, S, Z

Question 8.
Given here are figures of a few folded sheets and designs drawn about the fold. In each case, draw a rough diagram of the complete figure that would be seen when the design is cut off.

Solution :

 

We hope the NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 13 Symmetry Ex 13.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2.

• Ratio and Proportion Class 6 Ex 12.1
• Ratio and Proportion Class 6 Ex 12.3

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 12
Chapter Name	Ratio and Proportion
Exercise	Ex 12.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2

Question 1.
Determine if the following are in proportion:
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
Solution :





Question 2.
Write True (T) or False (F) against each of the following statements :
(a) 16: 24: : 20: 30
(b) 21: 6: 35: 10
(c) 12: 18: 28: 12
(d) 8: 9: : 24: 27
(e) 5.2: 3.9: : 3: 4
(f) 0.9: 0.36: : 10: 4
Solution :




Question 3.
Are the following statements true₹ I
(a) 40 Persons : 200 Persons =₹ 15: ₹75 ;
(b) 7.5 litre : 15 litre = 5 kg : 10 kg 1
(c) 99 kg : 45 kg = f 44 : ₹20
(d) 32 m : 64 m = 6 sec: 12 sec
(e) 45 km: 60 km = 12 hours : 15 hours.
Solution :


Since the two ratios are equal, therefore, the given statement is true.

Since the two ratios are equal, therefore, the given statement is true.

Since, the two ratios are equal, therefore, the given statement is true.


Since the two ratios are equal, therefore the given statement is true.

Since the two ratios are not equal, therefore the given statement is false.

Question 4.
Determine if the following ratios form a proportion. Also, write the middle terms and extreme terms where the ratios form a proportion.
(a) 25 cm: 1 m and 7 40 : 7160
(b) 39 litre : 65 litre and 6 bottle : 10 bottle
(c) 2 kg : 80 kg and 25 g : 625 g
(d) 200 ml: 2.5 litre and ₹4 ; ₹ 50.
Solution :
(a)
∴ 1 m= 100 cm

Since the two ratios are equal, therefore, the given ratios are in proportion. Middle terms are 1 m and ₹ 40. Extreme terms are 25 cm and ₹ 160.

Since the two ratios are equal, therefore, the given ratios are in proportion. Middle terms are 65 liters and 6 bottles. Extreme terms are 39 liters and 10 bottles.


Since the two ratios are not equal, therefore, the given ratios are not in proportion.

Since the two ratios are equal, therefore, the given ratios are in proportion. Middle terms are 2.5 litres and ₹ 4. Extreme terms are 200 ml and ₹ 50.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 12 Ratio and Proportion Ex 12.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5.

• Algebra Class 6 Ex 11.1
• Algebra Class 6 Ex 11.2
• Algebra Class 6 Ex 11.3
• Algebra Class 6 Ex 11.4

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 11
Chapter Name	Algebra
Exercise	Ex 11.5
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5

Question 1.
State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t-7)> 5
(c) \(\frac { 4 }{ 2 } \) =2
(d) (7 x 3)-19 = 8
(e) 5 x 4 – 8 =2x
(f) x – 2 =0
(g) 2m<30
(h) 2n+1=11
(i) 7=(11 x 5) -(12x 4)
(j) 7=(11×2)+p
(k) 20=5y
(l) latex]\frac { 3q }{ 2 } [/latex]<5
(m) z+12>24
(n) 20-(10-5)=3×5
(o) 7-x =5
Solution.

Question 2.
Complete the entries in the third column of the table.


Solution.
(a) Yes
(b) Yes
(c) No
(d) No
(e) No
(f) Yes
(g) No
(h) No
(i)  Yes
(j) Yes
(k) No
(l) No
(m) No
(n) No
(o) No
(p) No
(q) Yes

Question 3.
Pick out the solution from the values given bracket next to each equation. Show that the values do not satisfy the equation.
(a) 5m – 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p-5 = 5 (0, 10, 5,-5)
(d) \(\frac { q }{ 2 } \) = 7 (7, 2, 10, 14)
(e) r-4- 0 (4, – 4. 8, 0)
(f) x + 4 – . y (-2, 0, 2. 4)
Solution.
(a) Solution is 12
For m = 10
L.H.S. = 5 x 10 = 50 which is not equal to R.H.S.
For m = 5
L.H.S. = 5 x 5 = 25 which is not equal to R.H.S.
For m = 15
L.H.S. = 5 x 15 = 75 which is not equal to R.H.S.

(b) Solution is 8
For n = 12
L.H.S. = 12+12
= 24 which is not equal to R.H.S.
For n = 20
L.H.S. = 20+12
= 32 which is not equal to R.H.S.
For n =0
L.H.S. = 0+12
= 12 which is not equal to R.H.S.

(c) Solution is 10
For p = 0
L.H.S. = 0 – 5 = – 5 which is not equal to R.H.S.
For p = 5
L.H.S. = 5-5 = 0 which is not equal to R.H.S.
For p = – 5
L.H.S. = – 5 – 5 = – 10 which is not equal to R.H.S.

(d) Solution is 14
For g = 7
L.H.S. = \(\frac { q }{ 2 } \) which is not equal to R.H.S.
For q = 2
L.H.S. = \(\frac { 2 }{ 2 } \) = 1 which is not equal to R.H.S.
For q = 10
L.H.S. = \(\frac { 10 }{ 2 } \) = 5 which is not equal to R.H.S.

(e) Solution is 4
For r = – 4
L.H.S. = -4-4
= – 8 which is not equal to R.H.S.
For r = 8
L.H.S. = 8-4 = 4 which is not equal to R.H.S.
For r = 0
L.H.S. = 0 – 4 = – 4 which is not equal to R.H.S.

(f) Solution is – 2
For x = 0
L.H.S. = 0 + 4 = 4 which is not equal to R.H.S. For x = 2
L.H.S. = 2 + 4 = 6 which is not equal to R.H.S.
For x : = 4
L.H.S. = 4 + 4 = 8 which is not equal to R.H.S.

Question 4.
(a) Complete the table and by inspection of the table find the solution to the equation m + 10 = 16

(b) Complete the table and by inspection of the table find the solution to the equation 5t = 35

(c) Complete the table and find using the table the solution of the equation z/3 = 4

(d) Complete the table and find the solution to the equation m-7=3

Solution.

Question 5.
Solve the following riddles, you may yourself construct such riddles.
Who am I?
(i) Go round a square
Counting every corner
Thrice and no more!
Add the count to me
To get exactly thirty four!

(ii) For each day of the week
Make an account from me
If you make no mistake
You will get twenty three!

(iii) I am a special number
Take away from me a six!
A whole cricket team
You will still be able to fix!

(iv) Tell me who I am
I shall give a pretty clue!
You will get me back
If you take me out of twenty-two!
Solution.
(i) Let the required number be x.
Number of corners of the square = 4
Number obtained on counting every comer thrice = 4 x 3=12
According to the question, x + 12 = 34 ⇒ x = 34 -12 = 22
Hence, I am 22.

(ii) Let the required number be x.
Number of players in a cricket team = 11
According to the question.
x – 6 = 11  ⇒ x =11+6=17
Hence, lam 17.

(iii) Let the required number be v.
Number of days of a week = 7
According to the question.
x + 7 = 23    ⇒ x = 23-7 =16
Hence, lam 16.

(iv) Let the required number be x.
According to the question.
22 – x = x ⇒ x + x = 22
2x = 22    ⇒ x = \(\frac { 10 }{ 2 } \) = 11
Hence, lam 11.

We hope the NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4.

• Algebra Class 6 Ex 11.1
• Algebra Class 6 Ex 11.2
• Algebra Class 6 Ex 11.3
• Algebra Class 6 Ex 11.5

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 11
Chapter Name	Algebra
Exercise	Ex 11.4
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4

Question 1.
Answer the following :
(a) Take Sarita’s present age to he y years
(i) What will be her age 5 years from now?
(ii) What was her age 3 years back?
(iii) Sarita ‘s grandfather is 6 times her age. What is the age of her grandfather?
(iv) Grandmother is 2 years younger than grandfather. What is grandmother’s age?
(v) Sarita’sfather’s age is 5years more than 3 times Sarita’s age. What is her father’s age?
(b) The length of a rectangular hall is 4 meters less than 3 times the breadth of the hall. What is the length, if the breadth is b meters?
(c) A rectangular box has height h cm. Its length is 5 times the height and breadth is 10 cm less than the length. Express the length and the breadth of the box in terms of the height.
(d) Meena, Beena, and Leena are climbing the steps to the hilltop. Meena is at step s, Beena is 8 steps ahead and Leena7 steps behind. Where are Beena and Leena? The total number of steps to the hilltop is 10 less than 4 times what Meena has reached. Express the total number of steps using.
(e) A bus travels at v km per hour. It is going from Daspur to Beespur. After the bus has traveled 5 hours,
Beespur is still 20 km away. What is the distance from Daspur to Beespur? Express it using.

Solution.
(a) (y + 5) years
(ii) (y – 3) years
(iii) 6y years
(iv) (6y – 2) years
(v) (3y + 5) years
(b) Length (l) = (3b – 4) meters
(c) Length of the box = 5h cm
Breadth of the box = (5h – 10) cm
(d) Beena is at step (s + 8)
Leena is at step (s – 7)
Total number of steps = 4s – 10.
(e) Speed of the bus = v km/hr
Distance travelled in 5 hours = 5v km.
∴Total distance = (5v + 20) km

Question 2.
Change the following statements using expressions into statements in the ordinary language.
(For example, Given Salim scores r runs in a cricket match, Nalin scores (r+ 15) runs. In ordinary language—Nalin scores 15 runs more than Salim.)
(a) A notebook costs Rs p. A book costs Rs 3 p.
(b) Tony puts q marbles on the table. He has 8 q marbles in his box.
(c) Our class has n students. The school has 20n students.
(d) Jaggu is z years old. His uncle is 4z years old and his aunt is (4z- 3) years old.
(e) In an arrangement of dots, there are r rows. Each row contains 5 dots.
Solution.
(a) A book costs three times the cost of a notebook.
(b) Tony’s box contains 8 times the marbles on the table.
(c) The total number of students in the school in 20 times that of our class.
(d) Jaggu’s uncle is 4 times older than Jaggu and Jaggu’s aunt is 3 years younger than his uncle.
(e) The total number of dots in an arrangement is 5 times the number of rows.

Question 3.
(a) Given Munnu ’s age to be x years, can you guess what (x – 2) may show?
(Hint: Think of Munnu’s younger brother.) Can you guess what (x + 4) may show? What (3x + 7) may show?
(b) Given Sara’s age today to be y years. Think of her age in the future or in the past. What will the
following expression indicate? y + 7, y-3, y + 4\(\frac { 1 }{ 2 } \) ,y-2\(\frac { 1 }{ 2 } \).
(c) Given n students in the class like football, what may 2n show? What may — show?(Hint: Think of games other than football).
Solution.
(a) (x – 2) may show the age is Munnu’s younger brother. (a + 4) may show the age of Munnu’s elder brother. (3a+ 7) may show the age of Munnu’s grand mother.
(b) y + l indicates her age 7 years from now.
y – 3 indicates her age 3 years back.
y+ 4\(\frac { 1 }{ 2 } \) indicates her age 4\(\frac { 1 }{ 2 } \) years from now
y-2\(\frac { 1 }{ 2 } \) indicates her age 2\(\frac { 1 }{ 2 } \) years back.
(c) 2n may show the number of students who like cricket.
\(\frac { n }{ 2 } \)may show the number of students who like hockey.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.3 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.3.

• Algebra Class 6 Ex 11.1
• Algebra Class 6 Ex 11.2
• Algebra Class 6 Ex 11.4
• Algebra Class 6 Ex 11.5

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 11
Chapter Name	Algebra
Exercise	Ex 11.3
Number of Questions Solved	6
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.3

Question 1.
Make up as many expressions with numbers (no variables) as you conform with three numbers 5, 7 and 8. Every number should be used not more than once. Use only addition, subtraction and multiplication.(Hint: Three possible expressions are 5 + (8­7), 5 – (8-7), 5 x 8 + 7; make the other expressions.)
Solution.
The possible expressions are 5 + (8 – 7), 5 – (8 – 7), (5 + 8) + 7, 5 + (8 + 7),
5 x 8 + 7, 5 x 7 + 8, 5 x 8-7, 5 x 7-8,
5 x (8 – 7), 5 x (8 + 7), 8 x (7 – 5), 8 x (7 + 5) etc.

Question 2.
Which out of the following are expressions with numbers only ?
(a) y + 3
(b) 7 x 20- 8z
(c) 5(21 -7)+ 7 x 2
(d) 5
(e) 3x
(f) 5 – 5n
(g) 7 x 20 – 5 x 10 – 45 + p.
Solution.
(c), (d).

Question 3.
Identify the operations (addition, subtraction, division, multiplication) in forming the following expressions and tell how the expressions have been formed:
(a) z + 1, z-1, y + 17, y-17
(b) 17y, \(\frac { y }{ 17 } \), 5z
(c) 2y + 17, 2y – 17
(d) 7m, -7m + 3, -7m- 3.
Solution.
(a) Addition, subtraction, addition, subtraction
(b) Multiplication, division, multiplication.
(c) Multiplication and addition, multiplication and subtraction.
(d) Multiplication, multiplication and addition,multiplication and subtraction.

Question 4.
Give expressions for the following cases :
(a) 7 added to p
(b) 7 subtracted from p
(c) p multiplied by 7
(d) p divided by 7
(e) 7 subtracted from – m
(f) -p multiplied by 5
(g) -p divided by 5.
(h) p multiplied by – 5.
Solution.
(a) p + 7
(b) p-1
(c) 7p
(d) \(\frac { p }{ 7 } \)
(e) -m-1
(f) -5p
(g) – \(\frac { p }{ 5 } \)
(h) – 5p.

Question 5.
Give expressions in the following cases :
(a) 11 added to 2m
(b) 11 subtracted from 2m
(c) 5 times y to which 3 is added
(d) 5 times v from which 3 is subtracted
(e) y is multiplied by – 8
(f) y is multiplied by – 8 and then 5 is added to the result
(i) y is multiplied by 5 and the result is subtracted from 16
(j) y is multiplied by-5 and the result is added to 16.
Solution.
(a) 2m +11
(b) 2m – 11
(c) 5y + 3
(d) 5v – 3
(e) -8v
(f) -8y + 5
(g) 16 – 5y
(h) -5y + 16.

Question 6.
(a) Form expressions using t and 4. Use not more than one number operation. Every expression must have t in it.
(b) Form expressions using y, 2 and 7. Every expression must have y in it. Use only two number operations. These should be different.
Solution.
(a) t + 4, t – 4,4t, \(\frac { t }{ 4 } \) , \(\frac { 4 }{ t } \)  , 4 -1,4 +1 4 t
(b) 2y + 7, 2y – 7, 7y + 2

 

We hope the NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.3 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.2.

• Algebra Class 6 Ex 11.1
• Algebra Class 6 Ex 11.3
• Algebra Class 6 Ex 11.4
• Algebra Class 6 Ex 11.5

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 11
Chapter Name	Algebra
Exercise	Ex 11.2
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.2

Question 1.
The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.
Solution.
Perimeter (p) of the equilateral triangle with side l = Sum of the lengths of sides of the equilateral triangle = 1 + 1 + 1 = 31.

Question 2.
The side of a regular hexagon (Fig.) is denoted by l. Express the perimeter of the hexagon using l. (Hint: A regular hexagon has all its six sides equal in length.)

Solution.
Perimeter (p) of the regular hexagon with side
= Sum of the lengths of all sides of the regular hexagon
=l+l+l+l+l+l
= 6 l.

Question 3.
A cube is a three-dimensional figure as shown in Fig. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the
edges of a cube.

Solution.
Total length (L) of the edges of a cube
= Sum of the lengths of all (12) edges of the cube
= l+l+l+l+l+l+l+l+l+l+l+l
=12 l

Question 4.
The diameter of a circle is a line which joins two points on the circle and also passes through the center of the circle. (In the adjoining figure (Fig.) AB is a diameter of the circle; C is its center.) Express the diameter of the circle (d) in terms of its radius (r).

Solution.
AB = AC + CB
⇒ d=r+r ⇒ d=2r

Question 5.
To find the sum of three numbers 14, 27 and 13, we can have two ways.
(a) We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or
(b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus,
(14 + 27) + 13 = 14 + (27 + 13)
This can be done for any three numbers. This property is known as the associativity of the addition of
numbers. Express this property which we have already studied in the chapter on Whole Numbers, in a general way, by using variables a, b and c.
Solution.
Let a, b and c be three variables, each of which can take any numerical value. Then.
(a + b) + c = a + (b + c)
This property is known as the associativity of the addition of numbers.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.2 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 11 Algebra Ex 11.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3.

• Mensuration Class 6 Ex 10.1
• Mensuration Class 6 Ex 10.2

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 10
Chapter Name	Mensuration
Exercise	Ex 10.3
Number of Questions Solved	12
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3

Question 1.
Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21m
(c) 2 km and 3 km
(d) 2 m and 70 cm.
Solution :
(a) Area of the rectangle
= Length × Breadth = 3 × 4 sq cm = 12 sq cm
(b) Area of the rectangle = Length × Breadth
= 12 m × 21 m = 252 sq m
(c) Area of the rectangle = Length × Breadth
= 2 km × 3 km = 6 sq km
(d) 2 m = 2 × 100 cm = 200 cm
Area of the rectangle = Length × Breadth
= 200 × 70 sq cm
14000 sq cm.

Question 2.
Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m.
Solution :
(a) Area of the square = Side × Side
= 10 cm × 10 cm – 100 sq cm
(b) Area of the square = Side × Side
= 14 cm × 14 cm = 196 sq cm
(c) Area of the square = Side × Side
= 5 m × 5 m = 25 sq m.

Question 3.
The length and breadth of three rectangles are as given below:
(a) 9 m and 6 m
(b) 3 m and 17 m
(c) 4 m and 14 m.
Which one has the largest area and which one has the smallest?
Solution :
(a) Area of the rectangle = Length × Breadth = 9 m × 6 m = 54 sq m
(b) Length of the rectangle = Length × Breadth = 3 m × 17 m = 51 sq m
(c) Length of the rectangle = Length × Breadth = 4m × 14m = 56 sq m
The rectangle (c) has the largest area and the rectangle (b) has the smallest area.

Question 4.
The area of a rectangular garden 50 m long is 300 sq. m. Find the width of the garden.
Solution :
Area of the rectangular garden = 300 sq m Length of the rectangular garden = 50 m
∴ Width of the rectangular garden

Question 5.
What is the cost of tiling a rectangular piece of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.
Solution :
Length of the rectangular piece of land
500 m
Breadth of the rectangular piece of land
200 m
∴ Area of the rectangular piece of land
= Length × Breadth
= 500 m × 200 m
= 100000 sq m
Cost of tiling 100 sq m = ₹ \(\frac{ 8 }{ 100 }\)
Cost of tiling 100000 sq m
= ₹ \(\frac{ 8 }{ 100 }\) × 100000
= ₹ 8000.

Question 6.
A table-top measures 2 m by 1 m 50 cm. What is its area in square meters?
Solution :
Length of the table-top = 2 m Breadth of the table-top = 1 m 50 cm = 1.50 m
∴ Area of the table-top
= Length × Breadth = 2 m × 1.50 m
= 3.0 sq m.

Question 7.
A room is 4 m long and 3 m 50 cm wide. How many square meters of carpet is needed to cover the floor of the room?
Solution :
Length of the room = 4 m Breadth of the room = 3 m 50 cm = 3.50 m
∴ Area of the room = Length × Breadth
= 4 × 3.5 sq. m
= 14.0 sq m
Hence, 14.0 square meters of carpet is needed to cover the floor of the room.

Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution :
Length of the floor = 5 m Breadth of the floor = 4 m
∴ Area of the floor = Length × Breadth
= 5m × 4m = 20sqm Area of the square carpet = Side × Side
= 3m × 3m = 9sqm
∴ Area of the floor that is not carpeted = 20 sq m – 9 sq m = 11sq m.

Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of land?
Solution :
Area of square flower bed
= Side × Side = 1 m × 1 m
= 1 sq m
∴ Area of 5 square flower beds
= 5 × 1 sq m = 5 sq m
Length of the piece of land = 5 m
Breadth of the piece of land = 4 m
∴ Area of the piece of land
= Length × Breadth = 5 m × 4 m
= 20 sq m
∴ Area of the remaining part of the land
= 20 sq m – 5 sq m
= 15 sqm.

Question 10.
By splitting the following figures into rectangles, find their areas (The measures are given in centimeters).

Solution :
(a) Area of the figure
= (3 × 3 + 1 × 2 + 3 × 3 + 4 × 2) sqcm
= (9 + 2 + 9 + 8) sq cm = 28 sq cm

(b) Area of the figure
= (3 × 1 + 3 × 1 + 3 × 1) sqm
= (3 + 3 + 3) sq m
= 9 sqm

Question 11.
Split the following shapes into rectangles and find the area of each (The measures are given in centimeters).

Solution :
(a) Area of the shape
= (8 × 2 + 12 × 2) sq cm = (16 + 24) sq cm = 40 sq cm
(b) Area of the shape
= (17 × 7 + 7 × 7 + 7 × 7 + 7 × 7 + 7 × 7) sq cm
= (49 + 49 + 49 + 49 + 49) sq cm
= 245 sq cm
(c) Area of the shape = ( 5 × 1 + 4 × 1) sq cm
= (5 + 4) sq cm
= 9 sq cm.

Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively :
(a) 100 cm and 144 cm?
(b) 70 cm and 36 cm?
Solution :
(a) Length of the region = 100 cm Breadth of the region = 144 cm
∴ Area of the region = Length × Breadth
= 100 cm × 144 cm
= 14400 sq cm
Length of a tile = 12 cm Breadth of a tile = 5 cm
∴ Area of a tile = Length × Breadth = 12 × 5 sq cm
= 60 sq cm
∴ Number of tiles needed to fit the region

(a) Length of the region = 70 cm Breadth of the region = 36 cm
∴ Area of the rectangular region = 70 × 36 sq cm
= 2520 sq cm Area of a tile = 60 sq cm
∴ Number of tiles needed to fit the region

A challenge!
On a centimeter squared paper, make as many rectangles as you can such that the area of the rectangle is 16 sq cm (consider only whole number lengths).
(a) Which rectangle has the greatest perimeter?
(b) Which rectangle has the least perimeter? If you take a rectangle of area 24 sq. cm., what
will be your answers?
Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter? With the least perimeter? Give example and reason.
Solution :
Three rectangles can be made as follows:
(i) Sides 16 cm and 1 cm. Perimeter
= 2 × (Length + Breadth)
= 2 × (16 + 1) cm = 34 cm
(ii) Sides 8 cm and 2 cm. Perimeter
= 2 × (Length + Breadth)
= 2 × (8 + 2) cm = 20 cm
(iii) Sides 4 cm and 4 cm. Perimeter
= 2 × (Length + Breadth)
= 2 (4 + 4) cm = 16 cm

(a) The rectangle (i) has the greatest perimeter.
(b) The rectangle (iii) has the least perimeter.
For Area 24 sq. cm, four rectangles can be made as follows :
(i) Sides 24 cm and 1 cm. Perimeter
= 2 × (24 + 1)cm = 50 cm [Greatest perimeter]
(ii) Sides 12 cm and 2 cm. Perimeter
= 2 × (12 + 2) cm = 28 cm
(iii) Sides 8 cm and 3 cm. Perimeter
= 2 × (8 + 3) cm = 22 cm
(iv) Sides 6 cm and 4 cm. Perimeter
= 2 × (6 + 4) cm = 20 cm [Least perimeter]
Yes ! it is possible to predict the shape of the rectangle with (i) the greatest perimeter (iv) the least perimeter for any given area.
Reason: The rectangle with the greatest length has the maximum perimeter and the rectangle with the smallest length has the least perimeter, for a given area of the rectangle.

We hope the NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.2.

• Mensuration Class 6 Ex 10.1
• Mensuration Class 6 Ex 10.3

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 10
Chapter Name	Mensuration
Exercise	Ex 10.2
Number of Questions Solved	1
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.2

Question 1.
Find the areas of the following figures:

Solution :
(a)

	Cover	Number estimate	Area
(i)	Full-filled squares	9	9 squares
(ii)	Half-filed squares	–	–
(iii)	More than half-filed squares	–	–
(iv)	Less than half-filed squares	–	–

∴ Total area of the figure = 9 sq units

(b)

	Cover	Number estimate	Area
(i)	Full-filled squares	5	5 squares
(ii)	Half-filed squares	–	–
(iii)	More than half-filed squares	–	–
(iv)	Less than half-filed squares	–	–

∴ Total area of the figure = 9 sq units

(c) Full-filled squares = 2
Half-filled squares = 4
Area covered by full squares
= 2 × 1 sq unit = 2 sq units
Area covered by half squares = 4 × \(\frac{ 1 }{ 2 }\) sq unit = 2 sq units
∴ Total area = 2 sq units + 2 sq units = 4 sq units.

(d) Full-filled squares = 8
Total area = Area covered by full squares = 8 × 1 sq unit = 8 sq units.

(e) Full-filled squares =10
∴ Total area = Area covered by full squares = 10 × 1 sq unit = 10 sq units.

(f) Full-filled squares = 2 Half-filled squares = 4 Area covered by full squares
= 2 × 1 sq unit = 2 sq units Area covered by half squares
= 4 × \(\frac{ 1 }{ 2 }\) sq unit = 2 sq units
Total area = 2 sq units + 2 sq units = 4 sq units.

(g) Full-filled squares = 4 Half-filled squares = 4 Area covered by full squares
= 4 × 1 sq unit = 4 sq units Area covered by half squares
= 4 × \(\frac{ 1 }{ 2 }\) sq unit = 2 sq units
∴ Total area = 4 sq units + 2 sq units.
= 6 sq units

(h) Full-filled squares = 5
∴ Total area = Area covered by full squares = 5 × 1 sq unit = 5 sq units.

(i) Full-filled squares = 9
∴ Total area = Area covered by full squares = 9 × 1 sq unit = 9 sq units.

(j) Full-filled squares = 2 Half-filled squares = 4 Area covered by full squares
= 2 × 1 sq unit = 2 sq units Area covered by half squares
= 4 × \(\frac{ 1 }{ 2 }\) sq unit = 2 sq units
∴ Total area = 2 sq units + 2 sq units = 4 sq units.

(k) Full-filled squares = 4 Half-filled squares = 2 Area covered by full squares
= 4 × 1 sq unit = 4 sq units Area covered by half squares
= 2 × \(\frac{ 1 }{ 2 }\) sq unit = 1 sq unit
∴ Total area = 4 sq units + 1 sq unit = 5 sq units.
(l)

	Cover	Number estimate	Area
(i)	Full-filled squares	4	4 × 1 sq unit = 4 sq units
(ii)	Half-filed squares	2	2 × \(\frac{ 1 }{ 2 }\) sq unit = 1 sq unit
(iii)	More than half-filed squares	3	3 × 1 sq unit = 3 sq units
(iv)	Less than half-filed squares	4	–

(m)

	Cover	Number estimate	Area
(i)	Full-filled squares	9	9 × 1 sq unit = 9 sq units
(ii)	Half-filed squares	2	2 × \(\frac{ 1 }{ 2 }\) = 1 sq unit
(iii)	More than half-filed squares	6	6 × 1 sq unit = 6 sq units
(iv)	Less than half-filed squares	4	–

∴ Total Area = 9 sq units + 1 sq. unit + 6 sq units = 16 sq units
(n)

	Cover	Number estimate	Area
(i)	Full-filled squares	11	11 × 1 sq unit = 11 sq units
(ii)	Half-filed squares	6	6 × \(\frac{ 1 }{ 2 }\) = 3 sq unit
(iii)	More than half-filed squares	9	9 × 1 sq unit = 9 sq units
(iv)	Less than half-filed squares	–	–

∴ Total area = 11 sq units + 3 sq units + 9 sq units = 23 sq units.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 9 Data Handling Ex 9.4 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 9 Data Handling Ex 9.4.

• Data Handling Class 6 Ex 9.1
• Data Handling Class 6 Ex 9.2
• Data Handling Class 6 Ex 9.3

Board	CBSE
Textbook	NCERT
Class	Class 6
Subject	Maths
Chapter	Chapter 9
Chapter Name	Data Handling
Exercise	Ex 9.4
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 9 Data Handling Ex 9.4

Question 1.
A survey of 120 school students was done to find which activity they prefer to do in their free time:

Preferred activity	Number of students
Playing	45
Reading story books	30
Watching T.V.	20
Listening to music	10
Painting	15

Draw a bar graph to illustrate the above data taking the scale of 1 unit length = 5 students.
Which activity is preferred by most of the students other than playing?
Solution.
(i) Draw two perpendicular lines—one vertical and one horizontal.
(ii) Along horizontal line mark the “Preferred activity” and along vertical line mark the “No. of students”
(iii) Take bars of same width keeping the uniform gap between them.
(iv) Take scale of 1 unit length = 5 students along the vertical line and then mark the corresponding values.
(v) Calculate the heights of the bars for various activities preferred as shown below :
Playing                      :  45÷5= 9 units
Reading story books :  30÷5= 6 units
Watching T.V.           :   20÷4 =4 units
Listening to Music    :   10÷5= 2 units
Painting                    :   15÷5=3 units
(vi) Now draw various bars.

The activity “Reading story books” is preferred by most of the students other than playing.

Question 2.
The number of Mathematics books sold by a shopkeeper on six consecutive days is shown below:

Days	Sun­day	Mon­day	Tues­day	Wednes­day	Thurs­day	Fri­day
Number of books sold	65	40	30	50	20	70

Draw a bar graph to represent the above information choosing the scale of your choice.
Solution.
(i) Draw two perpendicular lines—one vertical and one horizontal.
(ii) Along horizontal line mark the “days” and along vertical line mark the “number of books sold.”
(iii) Take bars of same width keeping the uniform gap between them.
(iv) Take scale of 1 unit length = 5 books along the vertical line and mark the corresponding values.
(v) Calculate the heights of the bars for various days as shown below:
Sunday   : 65÷5=13 units
Monday  : 40÷5=8 units
Tuesday  : 30÷5=6 units
Wednesday : 50÷5=10 units
Thursday : 20÷5=4 units
Friday : 70÷5=14 units
(vi) Now draw various bars.

Question 3.
Following table shows the number of bicycles manufactured in a factory during the years 1998 to 2002. Illustrate this data using a bar graph. Choose a scale of your choice.

Year	Number of bicycles manufactured
1998	800
1999	600
2000	900
2001	1100
2002	1200

(i) In which year was the maximum number of bicycles manufactured?
(ii) In which year was the minimum number of bicycles manufactured?
Solution.
Steps for drawing a bar graph
(i) Draw two perpendicular lines — one vertical and one horizontal.
(ii) Along horizontal line marks the Year and along vertical line mark the “No. of bicycles manufactured”.
(iii) Take bars of same width keeping uniform gaps between them.
(iv) Take scale of 1 unit length = 100 bicycles along the vertical line and then mark the corresponding values.
(v) Calculate the heights of the bars for various years as shown below:
1998: 800÷100=8 units
1999: 600÷100=6 units
2000: 900÷100=9 units
2001: 1100÷100=11 units
2002: 1200÷100=12 units
(vi) Now draw various bars.

(i) The maximum number of bicycles were manufactured in the year 2002.
(ii) The minimum number of bicycles were manufactured in the year 1999.

Question 4.
A number of persons in various age groups in a town is given in the following table:

Age group	Number of persons
1-14	2 lakhs
15-29	1 lakh 60 thousand
30-44	1 lakh 20 thousand
45-59	1 lakh 20 thousand
60-74	80 thousand
75 and above	40 thousand

Draw a bar graph to represent the above information and answer the following questions. (take 1 unit length = 20 thousands):
(i) Which two age groups have the same population?
(ii) All persons in the age group of 60 and above are called senior citizens. How many senior citizens are there in the town?
Solution.
(i) Draw two perpendicular lines — one vertical and one horizontal.
(ii) Along horizontal line mark the “Age group” and along vertical line mark the “Number of persons”.
(iii) Take bars of same width keeping uniform gap between them.
(iv) Take scale of 1 unit length = 20 thousand along the vertical line and then mark the corresponding values.
(v) Calculate the heights of the bars for various of groups as shown below:
1- 14 : \(\frac { 200000 }{ 20000 } \) =10 units
15- 29 : \(\frac { 160000 }{ 20000 } \) = 8 units
30- 44 : \(\frac {120000 }{ 20000 } \) = 6 units
45- 59 : \(\frac {120000}{ 20000 } \) = 6 units
60- 74 : \(\frac { 80000 }{ 20000 } \) = 4 units
75 and above : \(\frac { 40000 }{ 20000 } \) = 2 units
(vi) Now draw various bars.

(i) The two age-groups 30-44 and 45-59 have the same population.
(ii) Number of senior citizens in the town
= 80000 + 40000
= 120000

We hope the NCERT Solutions for Class 6 Maths Chapter 9 Data Handling Ex 9.4 help you. If you have any query regarding. NCERT Solutions for Class 6 Maths Chapter 9 Data Handling Ex 9.4, drop a comment below and we will get back to you at the earliest.